Mechanical Analysis of Rock Tunnels Reinforced by Grouted Rockbolts Considering the Blasting Damage Effect

Abstract

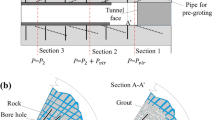
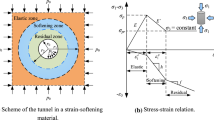
Tunnelling using drilling and blasting method inevitably disturbs the surrounding rock and induces a blasting damaged zone around the tunnel. Conventional mechanical analyses assume that the entire ground is damaged, leading to an underestimation of the surrounding rock stability and a conservative support design of the tunnel. This study developed a new analytical model to analyze the displacement, stress, and plastic radius of tunnels reinforced by grouted rockbolts considering the blasting damage effect. The blasting damaged zone was assumed to take a cylindrical shape with a finite radius. First, four different states of an unsupported tunnel based on the plastic zone distribution within the damaged and undamaged zones were distinguished and solved. Subsequently, ten different forms of a bolt-supported tunnel considering the ground state at bolt installation and the relative ranges of the bolt length and plastic zone were established. A method for determining the evolution paths of these possible forms for a specific tunnel project was developed using the critical displacements and longitudinal positions that define the transition between the different states and forms. Finally, an analytical algorithm for the rockbolt–surrounding rock interaction was established by introducing the concept of a fictitious pressure to simulate tunnel advancement. The proposed analytical model was verified by 3D numerical simulation and field monitoring results. Illustrative examples were presented to investigate the effect of the bolt length on tunnel displacement in both hard and soft rocks. Finally, the performance and advantages of the proposed model were investigated by comparing with the conventional analytical model. The proposed method can be used in the rockbolt design of tunnels constructed using the drilling and blasting method.

Highlights

• Interaction between rock and grouted rockbolts considering blasting damage zone is analyzed.

• Ground reaction curves for four different ground states and ten forms are derived.

• Analytical algorithm for possible evolution paths and critical transitions is presented.

• Effects of blasting damage zone and bolt length on tunnel displacement is illustrated.

• Proposed model validated by numerical and field test results excels existing models in rockbolts design.

Appendices

Appendix 1: GRC Solutions for Different Ground States

1.1 State A

The boundary conditions for State A are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(44)

The radial displacement at the tunnel boundary can be written as

$$u_{r_0 } = \frac{{\left( {1 + \nu^{\prime}} \right)r_0 }}{{E^{\prime}(r_1^2 - r_0^2 )}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {p_{r_1 } r_1^2 - p_i r_0^2 } \right) - \left( {p_i - p_{r_1 } } \right)r_1^2 } \right] - u_0$$

(45)

with

$$p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_0^2 p_i + E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_0^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_0^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_0^2 } \right]}}$$

(46)

where $p_{r_1 }$ is the radial stress at r = r₁.

1.2 State B

The boundary conditions for State B are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \left( {\sigma_r + \sigma_\theta } \right)\left| {_{r = r_p - {\text{d}}r} } \right. = \left( {\sigma_r + \sigma_\theta } \right)\left| {_{r = r_p + {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_p + {\text{d}}r} } \right. = u_r \left| {_{r = r_p - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(47)

The radial displacement at the tunnel boundary can be written as

$$u_{r_0 } = \frac{{m^{\prime}\sigma^{\prime}_c r_0 }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_p }{{r_0 }}} \right)\left( {\frac{r_p }{{r_0 }}} \right)^{K^{\prime}_\psi + 1} + \frac{{\sigma^{\prime}_c r_0 }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_0^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_0 } \right] - u_0$$

(48)

where $K^{\prime}_\psi = \frac{{1 + \sin \psi^{\prime}}}{{1 - \sin \psi^{\prime}}}$, $A_i = 2\sqrt {{\frac{p_i }{{m^{\prime}\sigma^{\prime}_c }} + \frac{{s^{\prime}}}{{m^{\prime2} }}}} - \frac{1}{{K^{\prime}_\psi + 1}} + \nu^{\prime}$, $D_0 = \sqrt {{p_i \frac{{m^{\prime}}}{{\sigma^{\prime}_c }} + s^{\prime}}}$.

The plastic radius $r_p$ is given by

$$\left\{ \begin{array}{l} r_p = r_1 \left[ {\frac{{2\sigma^{\prime}_c \left( {D_p^2 - s^{\prime}} \right) + \sigma^{\prime}_c D_p m^{\prime} - 2m^{\prime}p_{r_1 } }}{{2\sigma^{\prime}_c \left( {D_p^2 - s^{\prime}} \right) + \sigma^{\prime}_c D_p m^{\prime} - 2m^{\prime}p_{r_p } }}} \right]^{0.5} \hfill \\ p_{r_p } = \frac{{\sigma^{\prime}_c }}{{m^{\prime}}}\left( {D_p^2 - s^{\prime}} \right) \hfill \\ p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_p^2 p_{r_p } + E^{\prime}\left( {1 + \nu^{\prime}} \right)\left( {r_1^2 - r_p^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_p^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_p^2 } \right]}} \hfill \\ \end{array} \right.$$

(49)

where $D_p = \left( {\frac{{m^{\prime}}}{2}{\text{ln}}\frac{r_p }{{r_0 }} + \sqrt {{p_i \frac{{m^{\prime}}}{{\sigma^{\prime}_c }} + s^{\prime}}} } \right)$, $p_{r_p }$ is the radial stress at $r = r_p$.

1.3 State C

The boundary conditions for State C are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(50)

Given that $\varepsilon_\theta^p \left| {_{r = r_1 } } \right.$ is nonzero, Eq. (18) is inapplicable in this case. By substituting Eqs. (15) and (16) into Eq. (3), the radial displacement $u_{r_1 }$ at r = r₁ can be expressed as

$$u_{r_1 } = r_1 \left\{ {C_1 r_1^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right) + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\}$$

(51)

where $D_1 = \left( {\frac{{m^{\prime}}}{2}{\text{ln}}\frac{r_1 }{{r_0 }} + \sqrt {{p_i \frac{{m^{\prime}}}{{\sigma^{\prime}_c }} + s^{\prime}}} } \right)$, C₁ is the undetermined coefficient.

For the UZ, Eq. (12) is used to obtain $u_{r_1 }$ as

$$u_{r_1 } = \frac{1}{2G}\left( {p_0 - p_{r_1 } } \right)r_1$$

(52)

By combining Eqs. (51) and (52), the undetermined coefficient can be obtained by

$$C_1 = r_1^{K^{\prime}_\psi + 1} \left\{ {\frac{1}{2G}\left( {p_0 - p_{r_1 } } \right) - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right)} \right\}$$

(53)

By substituting Eq. (53) into Eq. (16) and considering Eqs. (3) and (15), the radial displacement at r = r₀ can be written as

$$u_{r_0 } = r_0 \left\{ {C_1 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(54)

The radial stresses $p_{r_1 }$ can be expressed as

$$p_{r_1 } = \frac{{\sigma^{\prime}_c }}{{m^{\prime}}}\left[ {\left( {\frac{{m^{\prime}}}{2}{\text{ln}}\frac{r_1 }{{r_0 }} + \sqrt {{p_i \frac{{m^{\prime}}}{{\sigma^{\prime}_c }} + s^{\prime}}} } \right)^2 - s^{\prime}} \right]$$

(55)

1.4 State D

The boundary conditions for State D are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \left( {\sigma_r + \sigma_\theta } \right)\left| {_{r = r_p - {\text{d}}r} } \right. = \left( {\sigma_r + \sigma_\theta } \right)\left| {_{r = r_p + {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_p + {\text{d}}r} } \right. = u_r \left| {_{r = r_p - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(56)

Based on Eq. (18), the radial displacement $u_{r_1 }$ can be written as

$$u_{r_1 } = \frac{m\sigma_c r_1 }{{4G\left( {K_\psi + 1} \right)}}\left[ {\left( {A_1 + \ln \frac{r_p }{{r_1 }}} \right)\left( {\frac{r_p }{{r_1 }}} \right)^{K_\psi + 1} } \right] + \frac{\sigma_c r_1 }{{2mG}}\left[ {\left( {1 - 2\nu } \right)\left( {D_2^2 - s} \right) + \nu mD_2 } \right]$$

(57)

where $A_1 = 2\sqrt {{\frac{{p_{r_1 } }}{m\sigma_c } + \frac{s}{m^2 }}} - \frac{1}{K_\psi + 1} + \nu$, $D_2 = \sqrt {{p_{r_1 } \frac{m}{\sigma_c } + s}}$.

By combining Eqs. (51) and (54), the undetermined coefficient $C_2$ can be obtained by

$$C_2 = r_1^{K^{\prime}_\psi + 1} \left\{ \begin{array}{l} \frac{m\sigma_c r_1 }{{4G\left( {K_\psi + 1} \right)}}\left[ {\left( {A_1 + \ln \frac{r_p }{{r_1 }}} \right)\left( {\frac{r_p }{{r_1 }}} \right)^{K_\psi + 1} } \right] + \frac{\sigma_c r_1 }{{2mG}}\left[ {\left( {1 - 2\nu } \right)\left( {D_2^2 - s} \right) + \nu mD_2 } \right] \hfill \\ - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right) \hfill \\ \end{array} \right\}$$

(58)

The radial displacement at the tunnel boundary can be written as

$$u_{r_0 } = r_0 \left\{ {C_2 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(59)

The variables $p_{r_p }$, $p_{r_1 }$ and $r_p$ in Eq. (59) can be obtained by

$$\left\{ \begin{array}{l} p_{r_1 } = \frac{{\sigma^{\prime}_c }}{{m^{\prime}}}\left( {D_1^2 - s^{\prime}} \right) \hfill \\ p_{r_p } = \frac{\sigma_c }{m}\left[ {\left( {\sqrt {{\frac{{mp_{r_1 } }}{\sigma_c } + s}} + \frac{m}{2}{\text{ln}}\frac{r_p }{{r_1 }}} \right)^2 - s} \right] \hfill \\ 2\frac{\sigma_c }{m}\left( {D_3^2 - s} \right) + \sigma_c D_3 = 2p_0 \hfill \\ \end{array} \right.$$

(60)

where $D_3 = \left( {\frac{m}{2}{\text{ln}}\frac{r_p }{{r_1 }} + \sqrt {{p_{r_1 } \frac{m}{\sigma_c } + s}} } \right)$.

Appendix 2: Solutions for Different Forms

2.1 Form 1

The boundary conditions for Form 1 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_b + {\text{d}}r} } \right. = u_r \left| {_{r = r_b - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(61)

By referring to Eq. (20), the tunnel wall displacement can be given by

$$u_{r_0 } = \frac{{\left( {1 + \nu^{\prime}} \right)r_0 }}{{\left( {r_b^2 - r_0^2 } \right)E^{\prime}_c }}\left[ {\left( {p_{r_b } + p_i } \right)r_b^2 + \left( {1 - 2\nu^{\prime}} \right)\left( {p_{r_b } r_b^2 - p_i r_0^2 } \right)} \right] - u_0$$

(62)

where $p_{r_b }$ is the radial stress at $r = r_b$ which is given by

$$\left\{ \begin{array}{l} p_{r_b } = \frac{{2\left( {1 - \nu^{\prime}} \right)\left[ {p_{r_1 } r_1^2 + \alpha p_i r_0^2 } \right]}}{{\alpha \left[ {\left( {1 - 2\nu^{\prime}} \right)r_b^2 + r_0^2 } \right] + \left( {1 - 2\nu^{\prime}} \right)r_b^2 + r_1^2 }} \hfill \\ p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_b^2 p_{r_b } + E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_b^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_b^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_b^2 } \right]}} \hfill \\ \end{array} \right.$$

(63)

where $\alpha = \frac{{E^{\prime}\left( {r_1^2 - r_b^2 } \right)}}{{E^{\prime}_c \left( {r_b^2 - r_0^2 } \right)}}$, $E^{\prime}_c = \frac{E_b A_b }{{S_c S_l }} + E^{\prime}$.

2.2 Form 2

The boundary conditions for Form 2 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(64)

By referring to Eq. (20), the tunnel wall displacement can be given by

$$u_{r_0 } = \frac{{\left( {1 + \nu^{\prime}} \right)r_0 }}{{\left( {r_1^2 - r_0^2 } \right)E^{\prime}_c }}\left[ {\left( {p_{r_1 } + p_i } \right)r_1^2 + \left( {1 - 2\nu^{\prime}} \right)\left( {p_{r_1 } r_1^2 - p_i r_0^2 } \right)} \right] - u_0$$

(65)

where $p_{r_b }$ is the radial stress at $r = r_b$ which is given by

$$\left\{ \begin{array}{l} p_{r_1 } = \frac{{2\left( {1 - \nu^{\prime}} \right)\left[ {p_{r_b } r_b^2 + \beta p_i r_0^2 } \right]}}{{\beta \left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_0^2 } \right] + \left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_b^2 }} \hfill \\ p_{r_b } = \frac{{2E\left( {1 - \nu } \right)r_1^2 p_{r_1 } + E_c \left( {r_b^2 - r_1^2 } \right)p_0 }}{{E_c \left( {r_b^2 - r_1^2 } \right) + E\left[ {\left( {1 - 2\nu } \right)r_b^2 + r_1^2 } \right]}} \hfill \\ \end{array} \right.$$

(66)

where $\beta = \frac{{E_c \left( {r_b^2 - r_1^2 } \right)}}{{E^{\prime}_c \left( {r_1^2 - r_0^2 } \right)}}$, $E_c = \frac{E_b A_b }{{S_c S_l }} + E$.

2.3 Form 3

The boundary conditions for Form 3 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(67)

By referred to Eq. (48), the tunnel wall displacement is given by

$$u_{r_0 } = \frac{{m^{\prime}\sigma^{\prime}_c r_0 }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_p }{{r_0 }}} \right)\left( {\frac{r_p }{{r_0 }}} \right)^{K^{\prime}_\psi + 1} + \frac{{\sigma^{\prime}_c r_0 }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_0^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_0 } \right] - u_0$$

(68)

where $G^{\prime}_c = \frac{{E^{\prime}_c }}{{2\left( {1 + \nu^{\prime}} \right)}}$.

The plastic radius $r_p$ is given by

$$\left\{ \begin{array}{l} p_{r_b } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_b + \xi \left( {r_b } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_b } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ r_p = r_1 \left[ {1 - \frac{{2\left( {p_{r_1 } - p_{r_p } } \right)}}{{\sqrt {{m^{\prime}\sigma^{\prime}_c p_{r_1 } + s^{\prime}\sigma^{\prime2}_c}} }}} \right]^{0.5} \hfill \\ p_{r_p } = \frac{{\sigma^{\prime}_c }}{{m^{\prime}}}\left( {D_p^2 - s^{\prime}} \right) \hfill \\ p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_p^2 p_{r_p } + E^{\prime}\left( {1 + \nu^{\prime}} \right)\left( {r_1^2 - r_p^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_p^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_p^2 } \right]}} \hfill \\ \end{array} \right.$$

(69)

2.4 Form 4

The boundary conditions for Form 4 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(70)

The tunnel wall displacement is given by

$$u_{r_0 } = \frac{{m^{\prime}\sigma^{\prime}_c r_0 }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_p }{{r_0 }}} \right)\left( {\frac{r_p }{{r_0 }}} \right)^{K^{\prime}_\psi + 1} + \frac{{\sigma^{\prime}_c r_0 }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_0^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_0 } \right] - u_0$$

(71)

The plastic radius $r_p$ is given by

$$\left\{ \begin{array}{l} p_{r_p } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_p + \xi \left( {r_p } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_p } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ r_p = r_b \left[ {1 - \frac{{2\left( {p_{r_b } - p_{r_p } } \right)}}{{\sqrt {{m^{\prime}\sigma^{\prime}_c p_{r_b } + s^{\prime}\sigma^{\prime2}_c}} }}} \right]^{0.5} \hfill \\ p_{r_b } = \frac{{p_{r_1 } r_1^2 \left( {r_b^2 - r_p^2 } \right) + p_{r_p } r_p^2 \left( {r_1^2 - r_b^2 } \right)}}{{\left( {r_1^2 - r_p^2 } \right)r_b^2 }} \hfill \\ p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_b^2 p_{r_b } + E^{\prime}\left( {1 + \nu^{\prime}} \right)\left( {r_1^2 - r_b^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_b^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_b^2 } \right]}} \hfill \\ \end{array} \right.$$

(72)

2.5 Form 5

The boundary conditions for Form 5 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(73)

The tunnel wall displacement is given by

$$u_{r_0 } = \frac{{m^{\prime}\sigma^{\prime}_c r_0 }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_p }{{r_0 }}} \right)\left( {\frac{r_p }{{r_0 }}} \right)^{K^{\prime}_\psi + 1} + \frac{{\sigma^{\prime}_c r_0 }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_0^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_0 } \right] - u_0$$

(74)

The plastic radius $r_p$ is given by

$$\left\{ \begin{array}{l} p_{r_p } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_p + \xi \left( {r_p } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_p } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ r_p = r_1 \left[ {1 - \frac{{2\left( {p_{r_1 } - p_{r_p } } \right)}}{{\sqrt {{m^{\prime}\sigma^{\prime}_c p_{r_1 } + s^{\prime}\sigma^{\prime2}_c}} }}} \right]^{0.5} \hfill \\ p_{r_b } = p_0 - \frac{r_1^2 }{{r_b^2 }}\left( {p_0 - p_{r_1 } } \right) \hfill \\ p_{r_1 } = \frac{{\eta p_{r_b } r_b^2 \left( {2 - 2\nu } \right) + p_{r_p } r_p^2 \left( {2 - 2\nu^{\prime}} \right)}}{{\eta r_b^2 + r_p^2 + \left( {\eta + 1 - 2\nu - 2\nu^{\prime}} \right)r_1^2 }} \hfill \\ \end{array} \right.$$

(75)

where $\eta = \frac{{G^{\prime}_c \left( {r_1^2 - r_p^2 } \right)}}{{G_c \left( {r_b^2 - r_1^2 } \right)}}$, $G_c = \frac{1 + \nu }{{2E_c }}$.

2.6 Form 6

The boundary conditions for Form 6 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(76)

The tunnel wall displacement is given by

$$u_{r_0 } = r_0 \left\{ {C_6 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(77)

with

$$C_6 = r_1^{K^{\prime}_\psi + 1} \left\{ {\frac{1}{2G}\left( {p_0 - p_{r_1 } } \right) - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_b^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_b } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A^{\prime}_b + \ln \frac{r_1 }{{r_b }}} \right)} \right\}$$

(78)

where $A^{\prime}_b = 2\sqrt {{\frac{{p_{r_b } }}{{m^{\prime}\sigma^{\prime}_c }} + \frac{{s^{\prime}}}{{m^{\prime2} }}}} - \frac{1}{{K^{\prime}_\psi + 1}} + \nu^{\prime}$, $D_b = \left( {\frac{{m^{\prime}}}{2}{\text{ln}}\frac{r_1 }{{r_b }} + \sqrt {{p_{r_b } \frac{{m^{\prime}}}{{\sigma^{\prime}_c }} + s^{\prime}}} } \right)$.

The variables $p_{r_1 }$ and $p_{r_b }$ are given by

$$\left\{ \begin{array}{l} p_{r_b } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_b + \xi \left( {r_b } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_b } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ p_{r_1 } = \frac{{2E\left( {1 - \nu^{\prime2} } \right)r_b^2 p_{r_b } + E^{\prime}\left( {1 + \nu^{\prime}} \right)\left( {r_1^2 - r_b^2 } \right)p_0 }}{{E^{\prime}\left( {1 + \nu } \right)\left( {r_1^2 - r_b^2 } \right) + E\left( {1 + \nu^{\prime}} \right)\left[ {\left( {1 - 2\nu^{\prime}} \right)r_1^2 + r_b^2 } \right]}} \hfill \\ \end{array} \right.$$

(79)

2.7 Form 7

The boundary conditions for Form 7 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(80)

The tunnel wall displacement is given by

$$u_{r_0 } = r_0 \left\{ {C_7 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(81)

with

$$C_7 = r_1^{K^{\prime}_\psi + 1} \left\{ {\frac{1}{2G_c }\left( {p_0 - p_{r_1 } } \right) - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right)} \right\}$$

(82)

The variables $p_{r_1 }$ and $p_{r_b }$ are given by

$$\left\{ \begin{array}{l} p_{r_1 } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_1 + \xi \left( {r_1 } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_1 } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ p_{r_b } = \frac{{2E\left( {1 - \nu } \right)r_1^2 p_{r_1 } + E_c \left( {r_b^2 - r_1^2 } \right)p_0 }}{{E_c \left( {r_b^2 - r_1^2 } \right) + E\left[ {\left( {1 - 2\nu } \right)r_b^2 + r_1^2 } \right]}} \hfill \\ \end{array} \right.$$

(83)

2.8 Form 8

The boundary conditions for Form 8 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_p + {\text{d}}r} } \right. = u_r \left| {_{r = r_p - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(84)

The radial displacement at the tunnel boundary can be expressed as

$$u_{r_0 } = r_0 \left\{ {C_8 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(85)

with

$$C_8 = r_1^{K^{\prime}_\psi + 1} \left\{ \begin{array}{l} \frac{m\sigma_c r_1 }{{4G\left( {K_\psi + 1} \right)}}\left[ {\left( {A_1 + \ln \frac{r_p }{{r_1 }}} \right)\left( {\frac{r_p }{{r_1 }}} \right)^{K_\psi + 1} } \right] + \frac{\sigma_c r_1 }{{2mG}}\left[ {\left( {1 - 2\nu } \right)\left( {D_2^2 - s} \right) + \nu mD_2 } \right] \hfill \\ - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}}}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_b^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_b } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}\left( {K^{\prime}_\psi + 1} \right)}}\left( {A^{\prime}_b + \ln \frac{r_1 }{{r_b }}} \right) \hfill \\ \end{array} \right\}$$

(86)

The variables $p_{r_1 }$, $p_{r_p }$, $p_{r_b }$ and $r_p$ are given by

$$\left\{ \begin{array}{l} p_{r_b } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_b + \xi \left( {r_b } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_b } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ p_{r_1 } = \frac{{\sigma^{\prime}_c }}{{m^{\prime}}}\left( {D_b^2 - s^{\prime}} \right) \hfill \\ p_{r_p } = \frac{\sigma_c }{m}\left[ {\left( {\sqrt {{\frac{{mp_{r_b } }}{\sigma_c } + s}} + \frac{m}{2}{\text{ln}}\frac{r_p }{{r_b }}} \right)^2 - s} \right] \hfill \\ 2\frac{\sigma_c }{m}\left( {D_3^2 - s} \right) + \sigma_c D_3 = 2p_0 \hfill \\ \end{array} \right.$$

(87)

2.9 Form 9

The boundary conditions for Form 9 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_p + {\text{d}}r} } \right. = u_r \left| {_{r = r_p - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(88)

The radial displacement at the tunnel boundary is written as

$$u_{r_0 } = r_0 \left\{ {C_9 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(89)

with

$$C_9 = r_1^{K^{\prime}_\psi + 1} \left\{ \begin{array}{l} \frac{m\sigma_c r_1 }{{4G_c \left( {K_\psi + 1} \right)}}\left[ {\left( {A_1 + \ln \frac{r_b }{{r_1 }}} \right)\left( {\frac{r_b }{{r_1 }}} \right)^{K_\psi + 1} } \right] + \frac{\sigma_c r_1 }{{2mG_c }}\left[ {\left( {1 - 2\nu } \right)\left( {D_9^2 - s} \right) + \nu mD_9 } \right] \hfill \\ - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right) \hfill \\ \end{array} \right\}$$

(90)

where $D_9 = \left( {\frac{m}{2}{\text{ln}}\frac{r_1 }{{r_b }} + \sqrt {{p_{r_b } \frac{m}{\sigma_c } + s}} } \right)$.

The variables $p_{r_1 }$, $p_{r_p }$, $p_{r_b }$ and $r_p$ are given by

$$\left\{ \begin{array}{l} p_{r_1 } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_1 + \xi \left( {r_1 } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_1 } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ p_{r_b } = \frac{{2E\left( {1 - \nu } \right)r_1^2 p_{r_1 } + E_c \left( {r_b^2 - r_1^2 } \right)p_0 }}{{E_c \left( {r_b^2 - r_1^2 } \right) + E\left[ {\left( {1 - 2\nu } \right)r_b^2 + r_1^2 } \right]}} \hfill \\ p_{r_p } = p_{r_b } + \frac{m\sigma_c }{4}\left\{ {\left[ {\ln r_p + \xi \left( {r_p } \right)} \right]^2 - \left[ {\ln r_b + \xi \left( {r_b } \right)} \right]^2 } \right\} - \frac{{f\left( {r_p } \right) - f\left( {r_b } \right)}}{m\sigma_c } \hfill \\ 2\frac{\sigma_c }{m}\left( {D_3^2 - s} \right) + \sigma_c D_3 = 2p_0 \hfill \\ \end{array} \right.$$

(91)

2.10 Form 10

The boundary conditions for Form 10 are given by

$$\left\{ \begin{array}{l} \sigma_r \left| {_{r = r_0 } } \right. = p_i \hfill \\ \sigma_r \left| {_{r = \infty } } \right. = p_0 \hfill \\ \sigma_r \left| {_{r = r_b + {\text{d}}r} } \right. = \sigma_r \left| {_{r_b - {\text{d}}r} = p_{r_b } } \right. \hfill \\ \sigma_r \left| {_{r = r_p + {\text{d}}r} } \right. = \sigma_r \left| {_{r_p - {\text{d}}r} = p_{r_p } } \right. \hfill \\ u_r \left| {_{r = r_1 + {\text{d}}r} } \right. = u_r \left| {_{r = r_1 - {\text{d}}r} } \right. \hfill \\ u_r \left| {_{r = r_p + {\text{d}}r} } \right. = u_r \left| {_{r = r_p - {\text{d}}r} } \right. \hfill \\ \end{array} \right.$$

(92)

The radial displacement at the tunnel boundary is written as

$$u_{r_0 } = r_0 \left\{ {C_9 r_0^{ - K^{\prime}_\psi - 1} - \frac{{m^{\prime}\sigma^{\prime}_c A_i }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}} + \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right]} \right\} - u_0$$

(93)

with

$$C_{10} = r_1^{K^{\prime}_\psi + 1} \left\{ \begin{array}{l} \frac{m\sigma_c r_1 }{{4G_c \left( {K_\psi + 1} \right)}}\left[ {\left( {A_1 + \ln \frac{r_p }{{r_1 }}} \right)\left( {\frac{r_p }{{r_1 }}} \right)^{K_\psi + 1} } \right] + \frac{\sigma_c r_1 }{{2mG_c }}\left[ {\left( {1 - 2\nu } \right)\left( {D_{10}^2 - s} \right) + \nu mD_{10} } \right] \hfill \\ - \frac{{\sigma^{\prime}_c }}{{2m^{\prime}G^{\prime}_c }}\left[ {\left( {1 - 2\nu^{\prime}} \right)\left( {D_1^2 - s^{\prime}} \right) + \nu^{\prime}m^{\prime}D_1 } \right] + \frac{{m^{\prime}\sigma^{\prime}_c }}{{4G^{\prime}_c \left( {K^{\prime}_\psi + 1} \right)}}\left( {A_i + \ln \frac{r_1 }{{r_0 }}} \right) \hfill \\ \end{array} \right\}$$

(94)

where $D_{10} = \left( {\frac{m}{2}{\text{ln}}\frac{r_1 }{{r_p }} + \sqrt {{p_{r_p } \frac{m}{\sigma_c } + s}} } \right)$.

The variables $p_{r_1 }$, $p_{r_p }$, $p_{r_b }$ and $r_p$ are given by

$$\left\{ \begin{array}{l} p_{r_1 } = p_i + \frac{{m^{\prime}\sigma^{\prime}_c }}{4}\left\{ {\left[ {\ln r_1 + \xi \left( {r_1 } \right)} \right]^2 - \left[ {\ln r_0 + \xi \left( {r_0 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_1 } \right) - f\left( {r_0 } \right)}}{{m^{\prime}\sigma^{\prime}_c }} \hfill \\ p_{r_b } = \frac{{2E\left( {1 - \nu } \right)r_1^2 p_{r_1 } + E_c \left( {r_b^2 - r_1^2 } \right)p_0 }}{{E_c \left( {r_b^2 - r_1^2 } \right) + E\left[ {\left( {1 - 2\nu } \right)r_b^2 + r_1^2 } \right]}} \hfill \\ p_{r_p } = p_{r_1 } + \frac{m\sigma_c }{4}\left\{ {\left[ {\ln r_p + \xi \left( {r_p } \right)} \right]^2 - \left[ {\ln r_1 + \xi \left( {r_1 } \right)} \right]^2 } \right\} - \frac{{f\left( {r_p } \right) - f\left( {r_1 } \right)}}{m\sigma_c } \hfill \\ 2\frac{\sigma_c }{m}\left( {D_3^2 - s} \right) + \sigma_c D_3 = 2\frac{{p_{r_b } r_b^2 - p_{r_p } r_p^2 }}{r_b^2 - r_p^2 } \hfill \\ \end{array} \right.$$

(95)