On Multi-Component Gas Migration in Single-Phase Systems

Abstract

The present work deals with diffusion of gases in fully saturated porous media. We test and validate the gas transport mechanism of dissolution and diffusion, implemented in the TH²M process class in the open-source finite-element software OpenGeoSys. We discuss the importance of gas diffusion for the integrity of the multi-barrier system. Furthermore, we present a multi-component mass balance equation implementation in Python, which serves as a reference for the two-component TH²M implementation and allows for a discussion of multi-component gas diffusion in liquids. We verify and validate the numerical implementations as follows: First, we come up with a set of numerical benchmarks in which solutions obtained by the two-component TH²M and multi-component implementations are compared. Thus, we show under which conditions predictions made by the TH²M model can be used for multi-component gas systems. Finally, the work is validated using a through diffusion experiment performed at Belgium’s Nuclear Research Centre SCK CEN and a sensitivity analysis is conducted based on the featured experiment. The results of this work illustrate that predictions by both the two- and four-component models match the laboratory findings very well. Therefore, we conclude that also the two-component implementation can reflect the multi-component processes well under the given constraints such as full saturation.

Highlights

• Numerical modelling of a laboratory scale gas diffusion experiment using Boom Clay samples.

• Validation of numerical implementation by comparison of experimental and numerical results.

• Extension of a two-component two-phase flow model towards a multi-component model including comparison of the two implementations.

• Sensitivity analysis identifies and quantifies the influence of key diffusion parameters, such as the Henry coefficient and diffusivity.

1 Introduction

A thorough understanding of the principles of gas transport in deep geological radioactive waste repositories is of high interest, in order to make predictions for the long-term integrity of the geotechnical and geological barrier system as well as radionuclide transport away from the repository (Levasseur et al. 2021). Gas is present in the repository at different stages of the lifetime: During the construction and operation phase, atmospheric air is introduced, creating aerobic conditions (Giroud 2018). This air remains in the system after the repository closure for a brief period depending on local hydro-chemical conditions, before the system will tend back to anaerobic conditions in the host rock and the repository (King et al. 2001). In the next phase, gas (mainly hydrogen H₂) can be generated due to the anaerobic corrosion of metallic components in the repository, such as the waste containers, metallic structural elements or metallic radioactive waste (Levasseur et al. 2022). In the last phase, after the failure of the radioactive waste canisters, radionuclides might be released, some of which take gaseous form (e.g. in case of $\textrm{C}^{14}$) and some of which dissolve in the pore liquid (Liang et al. 2021). By the time of the canister failure, formation water will likely have re-saturated the entire repository and host rock (Mohanty et al. 2000; Shaw 2015) and gaseous components exist in dissolved form.

In general, gas transport plays an important role for the safety of deep geological repositories. As shown in Fig. 1 (Marschall et al. 2005), gas transport in initially fully saturated host rock away from the repository takes place as a function of gas pressure or gas generation rate as well as the hydromechanical stress state of the host rock (Cuss 2014).

Fig. 1

Adapted from Marschall et al. (2005)

Gas transport mechanisms as a function of gas pressure, gas generation rate and stress state of the porous medium. The central two phase flow region represents the definition and derivation of the TH²M implementation (Grunwald et al. 2022).

From the left to the right in Fig. 1, at low gas pressures, gas transport takes place via the dissolution and diffusion of gas in interstitial water, with a minor contribution by advection of dissolved gas in the moving liquid phase. Diffusion is driven by concentration gradients which depend on the partial gas pressure and properties of the gas species, but it also depends on the mixture composition. In multi-component gas mixtures, concentration gradients of single components due to a non-constant gas composition can also drive a diffusive transport in the gaseous phase (Masum et al. 2012). If the gas production rate exceeds the capability of gas dissolution and diffusion to remove gas from the source, a distinct gas phase can form (Bourgeat et al. 2013; Ibtihel and Jaffré 2014) and gas transport takes place via visco-capillary two-phase flow in addition to the diffusion. Finally, if gas pressure continues to build up, it might eventually exceed the minimal principal stress and—depending on the cohesive strength of the material—distinct pathways might be created due to micro fissures and fracking of the rock (Gonzalez-Blanco et al. 2022). This process might alter the hydraulic properties of the material (Xu et al. 2013; Ziefle et al. 2022) and might impair the safety function of the geotechnical and geological barrier system (de La Vaissière et al. 2015). The role of gas transport in a radioactive waste repository in clayey host rock, characterized by low permeability, can be summarized as follows: Hydrogen is the main gas in the radioactive waste repository due to anoxic corrosion of steel. The solubility of hydrogen gas in water is low, as is the diffusion coefficient of gas in clay rock. This can be a safety issue due to the risk of rock fracture and consequent generation of pathways for solution migration if the gas pressure becomes too high due to insufficient removal of gas. Therefore, a good characterization of the dissolution and diffusion of gas is a necessity.

In this work, we focus on the gas dissolution and diffusion process in fully saturated media and validate the respective models which are implemented in the non-isothermal two-phase two-component implementation in deformable porous media (TH²M) (Grunwald et al. 2022) in the open-source finite-element software OpenGeoSys (OGS-6) (Bilke et al. 2019). Additionally, we introduce a multi-component numerical implementation as a simple, one-dimensional finite-volume scheme written in Python, serving as a reference for multi-component systems for the two-component TH²M implementation. Since the multi-component implementation is based on the component mass balance equation implemented in TH²M, it can also serve as test for future code developments in OGS-6. We test a superposition strategy, where multi-component gas diffusion in liquid can be reflected, even with the limitations of a binary mixture (i.e. one water component and one dissolved gaseous component) implementation. The comparison of binary and multi-component implementations is made using a series of numerical test cases. Finally, the diffusion models are calibrated and validated using a double through-diffusion experiment conducted at Belgium’s Nuclear Research Centre SCK CEN (Jacops et al. 2013, 2015). The results are discussed and a sensitivity study is performed. The objective of this work on the one hand is to study and interpret multi-component gas diffusion experiments and to validate the gas dissolution and diffusion process in numerical models. On the other hand, the wider perspective of this work is ultimately the application of the numerical models to repository-scale analyses.

2 Model Equations in the TH²M and Four-Component Formulations

The component mass balance equation as it is used by the TH²M implementation in OGS-6 was derived by Grunwald et al. (2022) and further discussed in Pitz et al. (2022). It considers a porous medium whose pore space is occupied by a liquid and a gaseous phase with $\alpha \in \{ \text {L, G} \}$, respectively. A water component and a gaseous component can be present in each phase with $\zeta \in \{ \text {W, C} \}$, respectively, where C can be substituted by any gas species. The partial differential equation (PDE) is originally implemented for a non-isothermal process in deformable porous media, but for the purpose of this work, the equation can be simplified by assuming incompressible solid grains, an isothermal process and zero deformation of the porous medium. The simplified equation hence reads (all symbols along with dimensions and units used in this work can be found in the appendix, Table 2):

$$\begin{aligned} 0= & {} \phi \left[ (1 - S_\textrm{L}) \frac{\text {d}\rho ^\mathrm {\zeta }_\textrm{GR}}{\text {d}t} + S_\textrm{L}\frac{\text {d}\rho ^\mathrm {\zeta }_\textrm{LR}}{\text {d}t} \right] + \phi (\rho ^\mathrm {\zeta }_\textrm{LR}- \rho ^\mathrm {\zeta }_\textrm{GR}) \frac{\text {d}S_\textrm{L}}{\text {d}t}\nonumber \\{} & {} + \,\textrm{div}\,\left( {\varvec{A}}^\mathrm {\zeta }+ {\varvec{J}}^\mathrm {\zeta }\right) , \end{aligned}$$

(1)

wherein t represents the time, $S_\textrm{L}$ represents the liquid saturation defined in the following section as a constitutive law, $\phi$ is the medium porosity and $\rho ^\mathrm {\zeta }_\textrm{GR}$ and $\rho ^\mathrm {\zeta }_\textrm{LR}$ represent the partial density of the component in the gaseous and liquid phase, respectively. ${\varvec{J}}^\mathrm {\zeta }= {\varvec{J}}^\mathrm {\zeta }_\textrm{L}+ {\varvec{J}}^\mathrm {\zeta }_\textrm{G}$ and ${\varvec{A}}^\mathrm {\zeta }= {\varvec{A}}^\mathrm {\zeta }_\textrm{L}+ {\varvec{A}}^\mathrm {\zeta }_\textrm{G}$ denote the diffusive and advective transport of component $\zeta$ in both fluid phases and they are defined in the following section by constitutive laws.

Equation (1) is implemented in OGS-6 for two components, namely the water component and a gaseous component. The gaseous component can be parametrized to represent either a specific type of gas or a gas mixture. While this approach proves to be efficient and accurate for many problems, there are some limitations to it when it comes to modelling multi-component systems featuring more than a single gas component. These limitations could include multi-component diffusion processes or gas pressure gradients created by the production of different species of gases. For this reason, the above PDE was additionally implemented in a finite-volume (FVM) numerical solving scheme considering two additional gaseous components next to the water component and the first gaseous component. This implementation will be called the four-component model henceforth. As opposed to the TH²M model, the four-component implementation disregards thermal and mechanical processes entirely. Instead, four monolithically coupled component mass balance equations following Eq. (1) are implemented. Evaluating results obtained by the two-component TH²M model and the reference four-component model allows for the discussion and testing of the application of the TH²M implementation in multi-component systems. In the four-component implementation, the liquid pressure $p_\textrm{LR}$ as well as the gaseous component partial pressure in the gaseous phase $p_\zeta$ are chosen as primary variables. In the TH²M implementation, the gaseous phase pressure $p_\textrm{GR}$ and the capillary pressure $p_\textrm{cap}$ are the primary variables describing the hydraulic process.

The constitutive laws implemented in the two models are almost identical with some slight differences due to the choice of primary variables. However, the physical conceptualization of the four-component model was adapted (or generalized for n components) from Grunwald et al. (2022) and, thus, the differences are small and are discussed in the following section. To differentiate between laws applied to gaseous components and laws applied to all components including the water component, we use two different indices: $\xi \in \{ \text {He, } \text {CH}_4, \text { A} \}$ represents the set of gaseous components helium, methane and air. $\zeta \in \{ \text {He, } \text {CH}_4, \text { A}, \text { W} \}$ represents the set of gaseous components as well as the water component. As the four-component formulation uses the partial gas pressures as well as the liquid phase pressure as main variables to describe the system, the capillary pressure resulting from the liquid and gas pressure differential in partially saturated media can be expressed as follows:

$$\begin{aligned} p_\textrm{cap}= p_\textrm{GR}- p_\textrm{LR}\,. \end{aligned}$$

(2)

In TH²M, the capillary pressure $p_\textrm{cap}$ is used as a primary variable and the liquid pressure $p_\textrm{LR}$ becomes a dependent variable. The partial density of component $\xi$ in the gas phase is given by the ideal gas law

$$\begin{aligned} \rho ^\xi _\text {GR} = \frac{p_\xi M^\xi }{RT} \,, \end{aligned}$$

(3)

with R and T as the universal gas constant and temperature, respectively, and $M^\xi$ as the component molar mass. For the water component, we can use an empirical vapour density as a function of capillary pressure and temperature (Kimball et al. 1976) to express the component density in the gaseous phase. This formulation already takes into account the Kelvin–Laplace correction of the effective vapour pressure/density for the curvature of the wetting phase in capillary spaces, formulated in terms of SI units:

$$\begin{aligned} \rho ^\textrm{W}_\textrm{GR}= 10^{-3} \frac{\textrm{kg}}{\textrm{m}^3} \cdot \exp \left( {19.819-4975.9 \textrm{K}/T}\right) \cdot \exp \left( -\frac{p_\textrm{cap}}{\rho _\textrm{LR}R T} \right) , \end{aligned}$$

(4)

where $\rho _\textrm{LR}$ represents the liquid density defined in Eq. (7). The resulting pressure of the gas phase is given by Dalton’s law which states that different gases in the air mixture do not interact and the resulting gas pressure is the sum of all partial pressures:

$$\begin{aligned} p_\textrm{GR}= \Sigma _\zeta p_\zeta . \end{aligned}$$

(5)

Likewise, we can invoke the same law to calculate the effective gas phase density

$$\begin{aligned} \rho _\textrm{GR}= \Sigma _\zeta \rho ^\mathrm {\zeta }_\textrm{GR}. \end{aligned}$$

(6)

The density of the liquid phase is given by a multi-linear function of liquid pressure and concentration of dissolved gases:

$$\begin{aligned} \rho _\textrm{LR}= \rho _\text {LR,ref} \left( 1+\beta _{p,\textrm{LR}}\left( p_\textrm{LR}-p_\text {LR,ref}\right) + \Sigma _\xi \beta _{\xi \text {,LR}} c^\xi _\text {L} \right) \,, \end{aligned}$$

(7)

where $\beta _{\xi \text {,LR}}$ represents the expansion of the liquid phase due to changes of the concentration of dissolved gaseous components, defined in Eq. (12). $c^\xi _\text {L}$ represents said component concentration defined in Eq. (9) and $\beta _{p,\textrm{LR}}$ is the liquid compressibility. $\rho _\text {LR,ref}$ and $p_\text {LR,ref}$ represent the reference liquid density and pressure as liquid properties. Finally, the partial densities of gaseous components in the liquid phase are governed by Henry’s law with the density of the dissolved component

$$\begin{aligned} \rho ^\xi _\text {LR}=\rho _\textrm{LR,ref} \beta _{\xi \text {,LR}} c^\xi _\text {L}, \end{aligned}$$

(8)

where the concentration of the dissolved component is

$$\begin{aligned} c^\xi _\text {L} = H^\xi p_\xi , \end{aligned}$$

(9)

with $H^\xi$ as the gas component-specific Henry coefficient. The density of the last component (water) in the liquid phase results from $\rho ^\textrm{W}_\textrm{LR}= \rho _\textrm{LR}- \Sigma _\xi \rho ^\xi _\text {LR}$. The mass fraction of component $\zeta$ in the liquid phase $x_{m,\textrm{L}}^\mathrm {\zeta }$ is given by:

$$\begin{aligned} x_{m,\textrm{L}}^\mathrm {\zeta }= \frac{\rho ^\mathrm {\zeta }_\textrm{LR}}{\rho _\textrm{LR}} \,. \end{aligned}$$

(10)

Thus, $\beta _{\xi \text {,LR}}$ can be defined as follows. In Eq. (10), the definition of mass fractions of dissolved gases in the liquid phase used by OGS is given. At the same time, the mass fractions can be related to the concentration of dissolved gas and its molar mass via (Watanabe and Iizuka 1985):

$$\begin{aligned} x^\xi _\text {m,L} = \frac{c^\xi _\text {L} M^\xi }{\rho _\textrm{LR}} \,. \end{aligned}$$

(11)

Hence, Eq. (11) with Eqs. (10) and (8) leads to the definition of $\beta _{\xi \text {,LR}}$ with:

$$\begin{aligned} \begin{aligned} \frac{c^\xi _\text {L} M^\xi }{\rho _\textrm{LR}}&= \frac{\rho _\textrm{LR,ref} \beta _{\xi \text {,LR}} c^\xi _\text {L}}{\rho _\textrm{LR}} \\ \Rightarrow \beta _{\xi \text {,LR}}&= \frac{M^\xi }{\rho _\textrm{LR,ref}}\\. \end{aligned} \end{aligned}$$

(12)

A component can be transported advectively in both phases $\alpha \in \{ \text {G,L}\}$, and advection is governed by Darcy’s law

$$\begin{aligned} {\varvec{A}}^\mathrm {\zeta }_{\alpha }= - \rho _\mathrm {\alpha R}^\mathrm {\zeta }\frac{{k^\textrm{rel}_\mathrm {\alpha }}{{\varvec{k}}_\textrm{S}}}{\mu _\mathrm {\alpha R}} \,\textrm{grad}\,p_\mathrm {\alpha R}, \end{aligned}$$

(13)

where ${{\varvec{k}}_\textrm{S}}$ represents the anisotropic intrinsic medium permeability tensor. The gas phase relative permeability $k^\text {rel}_\text {G}$ is assumed to be zero in this work and the liquid phase relative permeability is defined according to van Genuchten/Mualem (1976):

$$\begin{aligned} k^\text {rel}_\text {L}=\sqrt{S_\text {e}}\left( 1-\left( 1-S_\text {e}^{n/(n-1)}\right) \right) ^{(2n-2)/n} \,. \end{aligned}$$

(14)

$\mu _\mathrm {\alpha R}$ represents the viscosity of phase $\alpha$. The diffusion of a component in the liquid phase is driven by its mass fraction gradient, expressed by

$$\begin{aligned} {\varvec{J}}^\mathrm {\zeta }_\textrm{L}= & {} - \rho _\textrm{LR}{\varvec{D}}^\mathrm {\zeta }_\textrm{L}\,\textrm{grad}\,x_{m,\textrm{L}}^\mathrm {\zeta }= -\rho _\textrm{LR}{\varvec{D}}^\mathrm {\zeta }_\textrm{L}\left( \frac{\partial x_{m,\textrm{L}}^\mathrm {\zeta }}{\partial p_\textrm{LR}}\,\textrm{grad}\,p_\textrm{LR}\right. \nonumber \\{} & {} \left. + \Sigma _\zeta \frac{\partial x_{m,\textrm{L}}^\mathrm {\zeta }}{\partial p_\zeta }\,\textrm{grad}\,p_\zeta \right) . \end{aligned}$$

(15)

The effective diffusion coefficient in the liquid phase ${\varvec{D}}^\mathrm {\zeta }_\textrm{L}$ is treated as a constant component property and it is scaled by the liquid saturation and the porosity:

$$\begin{aligned} {\varvec{D}}^\mathrm {\zeta }_\textrm{L}= \phi S_\textrm{L}{\varvec{\textrm{I}}}D_\text {L}^\zeta \,, \end{aligned}$$

(16)

where $D_\text {L}^\zeta$ is the binary diffusion coefficient of component $\zeta$ in water. This seems reasonable because the liquid composition does not change significantly when gas components are dissolved. There is the constraint that the sum of mass-fraction-weighted diffusive mass fluxes must be equal to zero (Verros 2011):

$$\begin{aligned} 0 \overset{!}{=}\ \Sigma _\zeta \left( \rho _\textrm{LR}x_{m,\textrm{L}}^\mathrm {\zeta }{\varvec{j}}_\text {L}^\zeta \right) \,, \end{aligned}$$

(17)

wherein the diffusion velocity is related to the diffusive mass flux via the liquid phase density: ${\varvec{j}}_\text {L}^\zeta = \frac{{\varvec{J}}^\mathrm {\zeta }_\textrm{L}}{\rho _\textrm{LR}}$. In the four-component implementation, we achieve this by adding a correction velocity ${\varvec{j}}_\text {L}^\text {c}$ to the diffusion velocity in such a way that

$$\begin{aligned} \begin{aligned} 0&= \Sigma _\zeta \left( \rho _\textrm{LR}x_{m,\textrm{L}}^\mathrm {\zeta }\left( {\varvec{j}}_\text {L}^\zeta + {\varvec{j}}_\text {L}^\text {c} \right) \right) \\ \Leftrightarrow {\varvec{j}}_\text {L}^\text {c} \underbrace{\Sigma _\zeta x_{m,\textrm{L}}^\mathrm {\zeta }}_{=1}&= \Sigma _\zeta x_{m,\textrm{L}}^\mathrm {\zeta }{\varvec{j}}_\text {L}^\zeta \,, \\ \end{aligned} \end{aligned}$$

(18)

leading to the definition of the correction diffusive velocity as the sum of the mass-averaged diffusion velocities of all components. Adding this diffusion correction term in the diffusive mass flux definition Eq. (15) finally leads to:

$$\begin{aligned} {\varvec{J}}^\mathrm {\zeta }_\textrm{L}= - \rho _\textrm{LR}{\varvec{D}}^\mathrm {\zeta }_\textrm{L}\,\textrm{grad}\,x_{m,\textrm{L}}^\mathrm {\zeta }+ \rho _\textrm{LR}x_{m,\textrm{L}}^\mathrm {\zeta }\Sigma _\zeta {\varvec{D}}^\mathrm {\zeta }_\textrm{L}\,\textrm{grad}\,x_{m,\textrm{L}}^\mathrm {\zeta }\,, \end{aligned}$$

(19)

wherein the mass fraction gradient $x_{m,\textrm{L}}^\mathrm {\zeta }$ is expressed in terms of primary variables as follows:

$$\begin{aligned} \,\textrm{grad}\,x_{m,\textrm{L}}^\mathrm {\zeta }= \frac{\partial x_{m,\textrm{L}}^\mathrm {\zeta }}{\partial p_\textrm{LR}}\,\textrm{grad}\,p_\textrm{LR}+ \Sigma _\xi \left( \frac{\partial x_{m,\textrm{L}}^\mathrm {\zeta }}{\partial p_\xi } \,\textrm{grad}\,p_\xi \right) . \end{aligned}$$

(20)

The saturation in OGS-6 and the four-component implementation can be given according to different laws. Often, it is given as a function of capillary pressure (Van Genuchten 1980; Brooks and Corey 1964), but in this work, we consider the porous medium to be fully saturated at all times and hence, $S_\textrm{L}=1$. Accordingly, the corresponding time-derivative of the saturation in Eq. (1) vanishes as well as the term representing the component density $\rho ^\mathrm {\zeta }_\textrm{GR}$ in the gas phase and advection or diffusion in the gas phase ${\varvec{J}}^\mathrm {\zeta }_\textrm{G}$ and ${\varvec{A}}^\mathrm {\zeta }_\textrm{G}$.

3 Numerical Implementation

3.1 TH²M in OGS-6 (FEM)

The TH²M process model is implemented in the open-source numerical framework of OGS-6 (Grunwald et al. 2022; Bilke et al. 2019). The finite-element type used for the numerical simulations is quadrangular featuring linear shape functions for the primary variables $p_\textrm{GR}$ and $p_\textrm{cap}$. The finite elements are equidistant to facilitate the comparison with results obtained by the four-component implementation (see Sect. 3.2). The temporal dimension is discretized using the implicit Euler method with a fixed time step size, as fixing the time step size for the models in both implementations mitigates errors resulting from differing discretizations. The time increment is increased from 1.0e05 s in the beginning of the simulations to 1.0e07 s towards the end of the simulation for the numerical validation examples and 1.0 s to 1.0e05 s for the experimental simulations, respectively. This results in a linear equation system, which is solved using the stabilized bi-conjugate gradient method with a relative error tolerance of 1.0e-16. The Newton–Raphson scheme is used to iteratively solve the non-linear equation system with a convergence criterion of 1.0e-08 relative tolerance.

3.2 Four-Component Model in Python (FVM)

The four-component model is implemented from scratch as 1D finite-volume scheme with equidistant spatial discretization in Python (Van Rossum et al. 2009) using only Numpy as external library (Charles et al. 2020). The temporal dimension is discretized using the implicit Euler method with fixed time step sizes identical to the time steps used in the FEM model (Sect. 3.1). The resulting linear equation system is solved using the Numpy (Charles et al. 2020) linear solver based on the LAPACK routine _gesv (Anderson 1999). The non-linear solver is implemented as fixed-point iterations following the Picard method. The convergence criterion is given by a relative tolerance of 1.0e-08 with regard to the previous non-linear iteration.

4 Numerical Tests: Modelling Multi-Component Systems

The four-component implementation in Python can be tested for plausibility by assigning identical properties, initial conditions and boundary conditions to all three gaseous components and by multiplying any corresponding initial condition or boundary condition value in the TH²M model by three. Due to Dalton’s law, the three partial pressures (or Neumann gas production terms) should always add up to an equal value and the four-component model should compute the same result as the TH²M model, in which a single gaseous component is considered. Thus, this series of tests helps to cross-verify both the four-component implementation and the juxtaposition method introduced in Sect. 4.3.

Fig. 2

Quasi-1D beam for the plausibility tests. The top and bottom boundaries are always considered to be impermeable and at the left and right boundaries, Neumann and Dirichlet BCs can be applied

It should be noted that in the following tests, the FVM-Python code and the TH²M code were given the same equidistant meshes and time discretizations to minimize differences originating from the numerical solving scheme. However, the equidistant mesh is a limitation only for the FVM code and not for the FEM implementation in OGS-6 which can be considered the more powerful numerical method with regard to spatial discretization (Fig. 2).

4.1 Test #1: Plausibility

The first test is performed to cross-verify the two codes used in this work. A gas is injected into the quasi-one-dimensional bar from the left side by imposing a Dirichlet boundary condition with a constant gas phase pressure of 1.0 MPa. At the right boundary, the gas phase pressure is fixed at 100.0 Pa, which is also the value of the initial condition on the domain. This value is chosen to be low, because the gas pressure cannot be equal to or less than zero for numerical reasons. For all practical purposes, the initial gas pressure can be treated as zero pressure. The initial liquid pressure is 1.0 MPa and there are Dirichlet boundary conditions in place at the right and left boundary, fixing this value throughout the simulation.

Fig. 3

Comparison of results obtained by the TH²M model and by the four-component FVM implementation. All gas components have been parametrized as $\text {N}_2$

For this plausibility test, all three gaseous components in the four-component model were assigned properties identical to the gas component properties in the TH²M model ($\text {N}_2$ properties). The values of the Dirichlet boundary conditions and initial condition of each respective component are divided by three so that their sum adds up to the same value used in the TH²M model. Figure 3 shows the effective gas pressure and the liquid pressure profiles across the bar obtained by the two models. While a near-perfect agreement was achieved between the predicted gas phase pressure results, the liquid pressures predicted by the TH²M model are slightly lower than those predicted by the four-component model. However, the differences between the predictions are on the order of 1 to 10 Pa or about 0.01%. The reason for this is likely the liquid diffusion and the different correction for the total mass diffusion constraint in the two models. Thus it can be stated that slight differences in formulation lead to only negligible differences in this benchmark setup. Hence, this plausibility test provided the expected results and the two different implementations can, under the given circumstances, produce equivalent results.

4.2 Test #2: Multi-Component Gas Diffusion

This test is similar to the previous test with regard to the diffusion process. In this case however, the three gas components in the four-component formulation are parametrized as nitrogen, oxygen and hydrogen. The former two are used to describe air, whereas the latter is chosen because of its contrasting diffusive properties. The Dirichlet boundary conditions are chosen per component so that a gas mixture is created with 33% hydrogen, 14.74% oxygen and 52.26% nitrogen and their partial pressures adding up to 0.1013 MPa. In the TH²M model, the gas component is parametrized with average values of these three components based on the gas mixture with the volume fractions given above.

Fig. 4

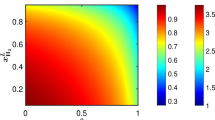
Comparison of results obtained by the TH²M model and by the four-component FVM implementation. The left plot shows the partial pressures calculated by the four-component model. The right plot shows resulting gaseous phase pressure profiles obtained by the four-component model (colorized) compared to profiles obtained by the TH²M model, which used average gas phase properties based on the component properties (black)

Figure 4 shows the result and comparison of this simulation. In the left plot, the partial component pressure profiles across the bar are plotted. It can be seen that the $\text {H}_2$ component is already at a steady state with a linear pressure profile after 5.0e07 s, whereas the concentration front of the other two components only arrives at the downstream boundary at this time. This effect is due to the high diffusivity of hydrogen, when compared with nitrogen or oxygen. From the viewpoint of the gas phase with a multi-component composition, the differing diffusivity of each constituting component leads to a slight dispersion. The plot on the right side shows this effect by the comparison of the gas phase pressures predicted by the two-component TH²M model and the four-component model. The dispersion of the pressure front can be seen by the fact that the gas phase pressure predicted by the four-component model is at some points in time and space higher or lower than the respective pressure predicted by the TH²M model. In general, the differences are small, but the results can be improved by applying the superposition strategy illustrated in the next test.

4.3 Test #3: Juxtaposition of Multiple TH²M Runs

In this test, the superposition strategy is tested, in which multiple simulation runs of the TH²M model are combined to simulate the partial pressure evolution per component. The resulting partial pressures may then be added in a post-processing step to obtain a prediction of the gas phase pressure evolution. Essentially, this strategy means modelling the transport of every individual component fully decoupled from the other components.

Fig. 5

Comparison of results obtained by multiple combined TH²M model runs (black) and by the four-component FVM implementation (colourized dots). One simulation for each gas component was performed in the TH²M model (left plot). The partial gas pressures were then summed up to obtain the effective gaseous phase pressure (right plot)

This strategy can be expected to perform well in fully saturated conditions as long as partial gas pressure gradients do not cause a liquid pressure gradient, which would in turn drive advective gas transport in the liquid phase. In partially saturated conditions, this approach is limited because the gas pressure and hence gas pressure gradients and gas advection depend equally on each component and must thus be modelled in a fully coupled way. This test is identical to the previous test with regard to initial and boundary conditions and component or phase properties. They only differ with regard to the modelling approach used for the TH²M model. It can be seen in the partial pressure plot (left side in Fig. 5) that the TH²M model now obtains good results for each individual component as well. Because the gas phase pressure is the sum of all partial pressures, these results are in very good agreement as well (right plot in Fig. 5). The superposition modelling approach proves to work well and improves the results slightly. However, in the next section, a laboratory experiment is modelled, in which gas injections occur from opposing boundaries. Thus, the superposition is not only helpful, but also necessary to capture the multi-component diffusion experiment. Overall, the presented test cases build a basis for the modelling in the following section and serve as numerical validation.

5 Model Application: Double Diffusion Experiment

The gas diffusion through a Boom Clay rock sample was experimentally tested in a fully liquid saturated double through-diffusion experiment conducted at SCK CEN (Jacops et al. 2015, 2021).

5.1 Experimental Setup

The experiment features a cylindrical sample whose faces are connected with a vessel each, and each vessel has a volume of 1.0 l. In one vessel, there are 0.468 l of water and helium gas, whereas in the other vessel, there are 0.472 l of water and methane gas. Both are pressurized at 1.0 MPa initially (Fig. 6). In the following, we will call the first and second vessels the ‘helium’ and ‘methane’ vessels, respectively. For the helium component, the helium vessel represents the upstream vessel and the methane vessel represents the downstream vessel and vice versa in case of methane. Because the gas phase pressure in the upstream vessel is known, the amount or concentration of dissolved gas in the respective vessel can be calculated via Henry’s law. Small gas phase samples can be taken from each vessel and the gas composition can be analysed using a gas chromatograph.

Fig. 6

(adapted from Jacops et al. (2015))

Experimental setup with time-dependent boundary conditions

Due to the experimental setup, there are two concentration gradients created in the sample, both of which drive solute gas diffusion in the liquid phase. Helium is transported from the helium vessel, through the clay core, to the methane vessel, and methane is transported in the opposite direction. As a consequence of the diffusive transport, each gas species arrives in the respective downstream vessel and its concentration in the water of the vessel increases. Following Henry’s law and assuming that the partial pressure of a species in the gas phase and its concentration in the liquid phase are always at an instant equilibrium, the partial pressure in the gas phase of the downstream vessel increases over the course of the experiment. Hence, the gas phase composition in both vessels changes over time and this process is measured using a gas chromatograph. The diffusion coefficient of the studied gas is then derived from the evolution of the concentration in the downstream reservoir (transient and steady states).

As a consequence of the experimental setup, there is no total gas phase or liquid phase pressure gradient created across the sample. Therefore, it can be assumed that gas transport will not take place via advection, but is only driven by diffusion. All Boom Clay samples used in this study are taken from the ON-Mol-1 borehole which was drilled in 1997, in the town of Mol, in the NE of Belgium (Lambert coordinates X (m) 200191.278 and Y (m) 211651.761). The cylindrical samples from the drilling were 100 mm both in diameter and in length. When installing the samples in the diffusion cell, the outer rim (10 mm) and the top and bottom part (35 mm) of the clay, which might have dried out during storage and/or could have been prone to oxidation during handling of the cores, were removed. Thus, the final clay core sample used in this work has a cylindrical shape with a length of 30 mm and a radius of 40 mm. It is installed in such a way that the two filters are next to the faces of the cylinder and the bedding of the clay is perpendicular to the axis of the cylinder (and the direction of gas transport through the sample). The total pressure in the two vessels is not constant. Although the change of gas pressure due to gas dissolution and diffusion away from the upstream vessel is expected to be negligible over the period of the experiment, the gas pressure decreases significantly on both vessels over time. This is due to the sampling of the gas phase for evaluation in the gas chromatograph, during each of which some gas is removed from the system and the total pressure decreases. Thus, the boundary conditions in both the upstream and downstream vessels are time dependent (cf. Fig. 6). Overall, the measurements of gas pressure and composition in each vessel were carried out over a total period of 72 days (Table 1).

5.2 Setup of the Numerical Model

Table 1 Material and fluid properties for the numerical model of the through-diffusion experiment.

The numerical model representing the experiment consists of a quasi-one-dimensional bar divided into 100 equidistant elements (101 nodes). The vessels, tubing or filters are not simulated, but only the clay sample itself is modelled in this work. Thus, the storage capacity in the filters, tubing and vessels is neglected and it is assumed that the liquid and partial gas pressures at the inlet boundary of the elements are always equal to the pressures measured in the respective vessels. It is furthermore assumed that any gas present in dissolved form at the inlet and outlet boundaries of the domain is in an equilibrium with the gas present in gaseous form in the respective vessel. The equilibrium condition is given by Henry’s law, given in Eq. (9). Finally, the measured gas concentrations in both vessels suggest that the concentration of each gas at the downstream side remains very low during the course of the experiment, because gas diffusion is a relatively slow transport process. Therefore, we assume that the partial gas pressure of each gas at its respective downstream boundary is equal to 100 Pa. This value is small in relation to the pressure in the upstream vessel. It is chosen for numerical reasons (assuming a pressure of 0.0 Pa would lead to numerical instabilities) and it is also the assumed initial uniform partial pressure of each gaseous component in the domain. Using a Dirichlet boundary condition at the downstream side conveniently allows the evaluation of the component mass flow rate across the boundary.

In the post-processing, the component mass flow rate is integrated over the time to calculate the total gas component mass which crossed the downstream boundary out of the clay sample $m^\zeta _\text {Vessel}$. Invoking Henry’s law and assuming that the equilibrium between the dissolved and gaseous particles is instantaneous and neglecting the volume of the tubing, the resulting partial gas pressure in the downstream vessel given by the equilibrium condition is calculated by:

$$\begin{aligned} \rho _\text {Vessel}^\zeta = \frac{m^\zeta _\text {Vessel}}{V_\text {Vessel}} = \phi _\text {L} \rho ^\mathrm {\zeta }_\textrm{LR}+ (1-\phi _\text {L})\rho ^\mathrm {\zeta }_\textrm{GR}\, \end{aligned}$$

(21)

where we interpret $\rho _\text {Vessel}^\zeta$ as the total effective density of the gas component in the downstream vessel and where $\phi _{\textrm{L}}$ represents the volume fraction in the vessel occupied by the liquid. The volume of the vessel $V_\text {Vessel}$ is always 1 l and the volume fraction of the liquid in the vessels is $\phi _\text {L} = 0.472$ for the methane vessel (downstream vessel for helium) as well as $\phi _\text {L} = 0.468$ for the helium vessel (downstream vessel for methane) After inserting the expressions Eqs. (8) and  (3) for the partial component densities in the liquid and gas phase and after some rearranging, we get the following expression for the resulting partial component pressure in the gas phase of the downstream vessel:

$$\begin{aligned} p^\zeta _\text {Vessel} = \frac{m^\zeta _\text {Vessel}}{V_\text {Vessel}\left( \phi _\text {L} M^\zeta H^\zeta + (1-\phi _\text {L}) \frac{M^\zeta }{RT}\right) }, \end{aligned}$$

(22)

where $m^\zeta _\text {Vessel}$ represents the accumulated component mass which was the output of the numerical model. Finally, the gas concentration is calculated by invoking Dalton’s law and by normalizing with regard to the experimental data and the time dependent gas pressure in the vessels (cf. Fig. 6), given in parts per million ppm:

$$\begin{aligned} c_\text {G,ppm}^\zeta (t)= {1.0e06\,.}\frac{p^\zeta _\text {Vessel}(t)}{p_\textrm{GR}(t)}. \end{aligned}$$

(23)

Because the OGS-6 TH²M implementation features two phases and two components (water and gas component), the two gas components of the double diffusion experiment could not be simulated in a single run. Instead, two simulations were performed and the results (partial gas pressures) were juxtaposed to get a representation of total gas pressure evolution in the sample and vessels (cf. Figs. 5 and  7). As it was shown in the previous Sect. 4.3, this strategy is justified and results in negligible errors as long as the considered sample is fully saturated (no advective transport in the gaseous phase) and no gas pressure gradients are imposed across the sample.

Fig. 7

Calculated and measured results for the through-diffusion experiment

5.3 Results of Laboratory Experiment Modelling

Figure 7 illustrates the results of the numerical modelling as well as the laboratory measurements. The plot on the left side shows the calculated gas mass diffusion rate for the helium and methane at the respective downstream boundaries. It can be seen that after some delay, the concentration front of solute gas arrives at the outlet and the gas mass diffusion rate increases. This delay is longer in case of methane than in the case of helium. It can be attributed to the lower diffusivity of the larger molecule (methane) as well as to the higher Henry coefficient, which increases the storage capacity of methane in the liquid. The higher storage coefficient explains well the delay of the peak mass diffusion rate of methane, when compared to the helium mass diffusion rate. In general, the mass diffusion rate values of methane are significantly higher than those of helium, despite its lower diffusion coefficient. This effect is due to the higher molar mass of methane, which means higher mass flux at equal particle flux. The higher Henry coefficient of methane also implies more dissolved gas at equal partial pressures. In general, the mass diffusion rate of both gases decreases proportionally to the decrease of the gas pressure in the upstream vessel, which is the driving force in this experiment.

At the right side of Fig. 7, the calculated gas concentrations in the respective downstream vessels are plotted and compared to the laboratory measurements. It can be seen that the fit of numerical and experimental data is generally very good. The delayed arrival of the methane at the outlet is captured both in the laboratory and in the simulation. It can also be seen that the line plots representing the numerical results exhibit a subtle “jiggle”. This is due to the pressure change in the downstream vessel, which affects the predicted partial pressure due to the post-processing (Eq. (23)).

Figure 8 shows a sensitivity analysis of the predicted methane concentration in the downstream vessel gas phase with regard to porosity, diffusion coefficient and Henry coefficient. Therein, the linear nature of Henry’s and Fick’s law can be observed in the sense that the linear variation of any of these three parameters results in a corresponding linearly increased or decreased predicted concentration. This linear behaviour is observed after the initial onset of concentration increase, during which storage plays a more dominant role. The rate of concentration increase in the downstream vessel will in theory change, once significant partial pressures in the downstream vessels are achieved, which would act as some back pressure and reduce the mass flux. The same holds for the decreasing partial gas pressure in the upstream vessel. In general, the given system seems to be most sensitive to the Henry coefficient. This is likely due to the fact that the Henry coefficient appears twice in the calculation of the dissolved gas fraction $x_{m,\textrm{L}}^\mathrm {\zeta }$. Taking into account that $\beta _\text {LR}^\zeta$ is proportional to $H^\zeta$, one can see from the partial solute density in the liquid Eq. (8) that the dependence of the component mass fraction is quadratic with regard to $H^\zeta$. This does however not introduce a non-linearity because the Henry coefficient is treated as a constant. If it were variable and dependent on the process variables, this would be different. This could for example be the case in non-isothermal settings, because the Henry coefficient is generally defined as temperature dependent, but in the given isothermal case, no such dependence is introduced.

The sensitivity analysis also demonstrates the ability of the numerical models to interpret this set of gas diffusion experiments. The results obtained using diffusivity and Henry coefficients from the literature show that the problem is well understood within the given constraints. However, if there is some uncertainty with regard to a host rock property (e.g. porosity, tortuosity or some form of heterogeneity), this study shows that numerical predictions can be sensitive to these features, which has to be taken into account in an integrity analysis.

Fig. 8

Sensitivity of the model to variation of porosity, diffusivity and Henry coefficient

Finally, the through-diffusion experiment was conducted using Boom Clay samples (borehole ON-Mol-1) with different pairs of gaseous components (Jacops et al. 2013) and, thus, some more results are depicted in Fig. 9. The featured gases are argon, xenon, neon and ethane and it can be seen that the numerical and experimental results generally agree well. Generally, potential fitting parameters such as component diffusivity in the liquid or the porosity of the sample were taken directly from the laboratory measurements or from literature values, respectively. The good agreement between numerical predictions based on literature values and the diffusion–advection transport equation and the experimental measurements illustrates firstly the performance of the experiment itself and the accuracy of the measurements. Secondly, it illustrates that the two-component two-phase TH²M implementation in OGS-6 is capable of reflecting the discussed gas diffusion processes in more complex multi-component systems.

Fig. 9

Calculated and measured results for the through-diffusion experiment with other gas species: ethane, xenon, neon and argon

6 Discussion and Conclusion

The TH²M implementation was derived based on the theory of porous media and a two-phase two-component formulation (Grunwald et al. 2022). Corresponding verification and validation work was so far mostly carried out for two-phase systems (Grunwald et al. 2022; Pitz et al. 2022, 2023) related to the second region in the Marschall gas transport concept (Fig. 1). With the present work, we extend the validity window towards the left region in Fig. 1, where gas transport occurs by gas dissolution and diffusion. Thus, we form a basis for the application of OGS-6 for the prediction of peak gas pressures in deep geological repositories in low-permeability host rock formations. By comparing results obtained by the two-component OGS-6 implementation to results obtained by a simple four-component implementation, we were able to illustrate the good performance of the modelling strategy allowing the application of the TH²M model in multi-component systems. The methodology consists of the juxtaposition of results originating from multiple model runs, each run for a given gas component. The juxtaposition proves to be a reliable method with the given constraints, foremost full saturation and no induced liquid pressure gradients. It remains to be a question for future work, whether a similar approach would lead to good results in partially saturated systems or in the presence of gas or liquid pressure gradients. At the same time, we present a set of constitutive equations illustrating how the existing TH²M implementation could be extended to a multi-component implementation—at least for the hydraulic part. Finally, the experimental and numerical results of the double through-diffusion experiment performed at SCK CEN (Jacops et al. 2013, 2021) show good agreement for a variety of gas components, thus increasing the confidence in predicted system behaviour in which gas transport by dissolution and diffusion is dominating. The effective diffusion coefficients providing the best numerical fit to the experimental results are very similar to—and only insignificantly adapted from—values used by previous numerical analyses of the experiment (Jacops et al. 2013). Therefore, good agreement between different numerical mode predictions is achieved. The featured through-diffusion experiment is a specific test case with a fully saturated sample and gas equilibrium in the reservoir. In the application to the repository safety case, it will be important to test the de-saturation of the clay by liquid displacement by the hydrogen gas itself, due to the limitation of its solubility and diffusion in the rock (Grunwald et al. 2023).

The validation work in this paper is therefore subject to specific constraints such as full liquid saturation, no total gas pressure gradient and no advection. Therefore, this work should be seen a step of model validation of gas diffusion experiments on the path towards more general analyses of gas transport. In light of this, further work should comprise the modelling of similar experimental through-diffusion setups as the present one, but with a focus on partial saturation. Future work will also focus on the application of this process to the large scale of a deep geological repository.

Appendix: Overview of Symbols

See Table 2.

Table 2 Explanation of symbols