1 Introduction

The rheological deformation of surrounding rock caused by excavating soft rock tunnels can lead to significant construction and safety challenges due to creep-induced damage (Xu et al. 2012; Kabwe et al. 2020a, b). Therefore, it is necessary to study the time-dependent deformation mechanisms of the soft rock surrounding rock caused by tunnel excavation (Manchao 2014; Wang and Cai 2022a, b).

The ultimate large deformation of soft rock is a creep–damage coupled problem (Li and Tang 2015; Wang and Cai 2020; Xia et al. 2021a, b). Inspired by the fundamental understanding of rock creep and damage mechanics, previous studies have mainly focused on the macroscale level using creep–damage constitutive models to reveal the rheological process of soft rock tunnels (Ping et al. 2016; Liu et al. 2017; Huang et al. 2020a, b; Li et al. 2022a, b, 2023). In addition, the different stages of long-term deformation of soft rocks were also studied from clay mineral slippage and disintegration (Fahimifar et al. 2010; Jiang et al. 2016; Liu et al. 2020a, b; Kovacevic et al. 2021; Maheshwari 2021; Cui et al. 2022). These results further demonstrate that the large deformation of soft rock tunnels is caused by the combined effects of damage and creep (Song et al. 2016; Yang et al. 2019; Kabwe et al. 2020a, b; Mu et al. 2020; Yu et al. 2020).

However, challenges remain in correlating the dissolution and slide of clay minerals at the mesoscale with crack propagation and coalescence at the macroscale. Long-term failure propagation in soft rock engineering is actually a multiscale issue (Li and Tang 2015; Xue et al. 2021). The mechanical properties and spatial orientations of rock joints could significantly influence tunnel excavation (Jia and Tang 2008; Deng et al. 2014). From a macroscopic perspective, joints may affect the local mineral grain flow and cause anisotropic deformation of the rock mass (Wang and Cai 2021a, b, 2022a). A multiscale analysis needs to be incorporated into the large deformation analysis of soft rock. Using a mesoscopic representative volume element (RVE), Tang et al. developed a theoretical model for simulating the trans-scale progressive failure of rock based on statistical and continuum damage mechanics (Li and Tang 2015). In addition, renormalization group theory (Xia et al. 2021a, b) and fractal geometry (Wei et al. 2019; Zhou et al. 2019) are commonly used to analyze meso-to-macro cascading in the phase-changing process, but they have limited capabilities of accurately predicting the deformation of the rocks surrounding the tunnel. Several attempts have been made to model the creep and time-dependent damage of soft rock from trans-scale modeling (Potyondy 2007; Li et al. 2017, 2018; Cui et al. 2019; Song et al. 2019; Guo et al. 2020; Wang and Cai 2021a, b; Xia et al. 2021a, b). However, the challenges of the computational efficiency and anisotropic nature of soft rock and rock joints need to be addressed before theoretical models can be implemented in engineering practice.

In the present study, a multiphase numerical model of soft rock was developed to investigate the creep-induced damage behavior of the soft rocks surrounding a tunnel after excavation through coupled meso/macroscale simulation. The anisotropic mechanical behavior of the rock due to joints was also considered. The numerical results of the developed model were validated by using the field monitoring data of a tunnel case study.

2 Methods

The discrete element method (DEM) can reproduce and characterize rock mechanical behavior. As one of the most widely used DEM software programs, Particle Flow Code (PFC) shows excellent performance in simulating the fabric features of rocks using multiple-grain models (Potyondy and Cundall 2004; Bahaaddini et al. 2013).

Rock deterioration is considered a micro-to-macro trans-scale process, where the accumulated internal mesoscale damage could lead to a macroscale strength loss. In this paper, we want to correlate mesoscopic damage to macroscopic large deformation. For rocks, microcracks initiate at the grain scale. The parallel bond model (PBM) implemented in PFC can simulate the cementation of spherical grains at contacts. Burger’s model adopted in PFC can mimic the sliding creep of grains. The bond damage and grain creep are termed mesoscale damage herein. The mesoscale damage initiated from the grain contact area is limited at the mesoscale (less than 1 mm). The grain assembly can represent rock and rock mass, which are referred to as the macroscale (1–10 cm) and the engineering scale (> 1 m), respectively.

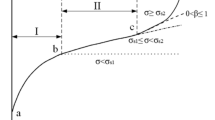
As shown in Fig. 1, the damage and deformation of the soft rock surrounding rock resulting from tunnel excavation can be studied through coupled meso/macroscale modeling. The mechanical properties of soft rock at the macroscale are characterized by bedrock strength, joint distribution, and tectonic stress, which are anisotropic in nature. The mechanical behavior of the rock at the mesoscale can be modeled by the skeleton and mineral bonding contents (Pinyol et al. 2007). In addition, the damage of the soft rock at the mesoscale can be divided into three phases: (1) initial phase before the excavation, (2) loading phase due to the excavation-induced stress redistribution, and (3) creep-induced damage and large deformation phase.

Fig. 1
figure 1

Coupled meso/macroscale modeling of damage and deformation of the soft rock surrounding rock resulting from tunnel excavation

Full size image

2.1 Modeling the Macroscale Damage and Deformation of the Surrounding Soft Rock Resulting from Tunnel Excavation

Figure 2 shows the macroscale modeling of the surrounding soft rock with consideration of the anisotropic state of the rock. The stress state of the soft rock surrounding the tunnel can be defined as:

Fig. 2
figure 2

Macroscale modeling of soft rock with consideration of the anisotropic state

Full size image
$$\begin{array}{c}{\sigma }_{ij}=\left[\begin{array}{ccc}{\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_{22}& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_{33}\end{array}\right].\end{array}$$
(1)

For hydrostatic conditions, the principal stresses of the surrounding rock can be described as:

$$\begin{array}{c}{\sigma }_{ii}=\left[\begin{array}{ccc}{\sigma }_{m}& & \\ & {\sigma }_{m}& \\ & & {\sigma }_{m}\end{array}\right],\end{array}$$
(2)

where \({\sigma }_{m}=\frac{1}{3}{I}_{1}=\frac{1}{3}\left({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}\right)\) is the average principal stress. The stress tensor comprises the tectonic and gravity stresses of the rock surrounding the tunnel, which is composed of hydrostatic and deviatoric stresses. That is,

$$\begin{array}{c}{\sigma }_{ij}={\delta }_{ij}{\sigma }_{m}+{s}_{kk},\end{array}$$
(3)

where \({s}_{kk}\) is the deviatoric stress tensor and \({\delta }_{ij}\) is the Kronecker delta (if \(i=j\), \({\delta }_{ij}\) = 1; if \(i\ne j,\) \({\delta }_{ij}\) = 0). The damage process of the soft rock surrounding the tunnel can be treated as an irreversible dissipation process. The thermodynamic potential function \(\psi\) (Helmholtz energy) of the surrounding rock can be expressed as a function of elastic strain (\({\varepsilon }^{e}\)) and internal variables, \({v}_{k}(k=\mathrm{1,2},3\dots , n)\), under isothermal conditions. That is,

$$\psi =\psi \left({\varepsilon }^{e},{v}_{k}\right),$$
(4a)
$$\sigma =\rho \frac{\partial \psi }{\partial {\varepsilon }^{e}}.$$
(4b)

The anisotropic damage characteristics of the rock can be defined using the isotropic hardening variable \({v}_{\mathrm{p}}\) for plastic deformation, the damage variable D for anisotropic damage, and the scalar variable \(\beta\) for the current state of damage. That is,

$$\begin{array}{c}{v}_{k}=\left\{{v}_{\mathrm{p}}, D,\beta \right\}.\end{array}$$
(5)

In an engineering case, the rock mass has initial damage from rock mass joints (Fig. 1). Based on the strain equivalence principle, the strain caused by stress acting on damaged material in the stressed state is equivalent to the strain caused by effective stress acting on undamaged material, and we obtain:

$$\begin{array}{c}\varepsilon =\frac{{\sigma }^{\prime}}{{E}_{0}}=\frac{\sigma }{{E}_{1}},\end{array}$$
(6)

where \({E}_{0}\) and \({E}_{1}\) are the elastic moduli of intact and damaged rock, respectively. The damage variable \(D\) can be introduced as the decay of \({E}_{0}\) (Xue et al. 2022),

$$\begin{array}{c}D=1-\frac{{E}_{1}}{{E}_{0}}.\end{array}$$
(7)

Based on the irreversible thermodynamic theory (Zhou and Zhu 2010), it is assumed that the plastic deformation and damage evolution of soft rock are mutually independent. Thus, the Helmholtz free energy function of the surrounding soft rock can be described as:

$$\begin{array}{c}\rho \psi \left({\varepsilon }^{e},{v}_{\rm p}, D,\beta \right)=\rho {\psi }^{e}\left({\varepsilon }_{ij}^{e},D\right)+\rho {\psi }^{p}\left({v}_{\rm p}\right)+\rho {\psi }^{d}\left(\beta \right).\end{array}$$
(8)

The term \(\rho {\psi }^{d}\left(\beta \right)\) can be expressed in a simple form using the internal variable \(\beta\), which represents damage accumulation and mesoscale damage evolution. Therefore, the damage potential function at the macroscale can be expressed as:

$$\begin{array}{c}{F}_{\mathrm{d}}\left({v}_{\mathrm{p}}, D,\beta \right)=0,\end{array}$$
(9)
$$\begin{array}{c}d\beta =d{\lambda }_{\mathrm{d}}\frac{\partial {F}_{\mathrm{d}}}{\partial \beta },\end{array}$$
(10)

where \({\lambda }_{\mathrm{d}}\) is the parameter denoting the damage consistency parameter. If \({F}_{\mathrm{d}}<0\), the soft rock is in the elastic stage, and the stress tensor can be defined as Eq. (4b). In the damage stage, according to the non-associated rule of orthogonal flow, we obtain:

$$\begin{array}{c}d{\varepsilon }_{ij}^{d}=d\lambda \frac{\partial Q}{\partial {\sigma }_{ij}},\end{array}$$
(11)

where Q denotes the damage yield function. \(\lambda\) is determined by the damage potential function \({F}_{\mathrm{d}}\) and the hardening parameter.

2.2 Modeling the Mesoscale Damage and Deformation of the Surrounding Soft Rock Resulting from Tunnel Excavation

To analyze the damage accumulation of soft rocks during tunnel excavation at the mesoscale, the following assumptions are made in this study:

  1. (1)

    The tunnel rock is composed of skeleton particles and cementations (Pinyol et al. 2007; Li and Wong 2016).

  2. (2)

    There are two types of bonding in soft rock, i.e., (1) strong bonding for tension, shear and torsion resistance and (2) weak bonding for creep resistance.

  3. (3)

    Strong bonding fails when the bearing capacity is exceeded. Soft rocks experience creep when the slippage and dissipation of weak bonding occurs (Liu et al. 2020a, b).

2.2.1 Initial Phase Before the Excavation

Before excavation, the rock surrounding the tunnel is subject to tectonic in situ stress \({\sigma }_{ij}\), which is a stable and inelastic state. It is assumed that the total stress (\({\sigma }_{ij}\)) can be expressed by the sum of the strong bonding stress (\({F}_{ij}\)) and weak bonding stress (\({f}_{ij}\)). That is,

$$\begin{array}{c}{\sigma }_{ij}={F}_{ij}+{f}_{ij}=2{f}_{ij}+\left({F}_{ij}-{f}_{ij}\right)=2{f}_{ij}+{\alpha }_{kl}*{F}_{ij},\end{array}$$
(12)

where \({\alpha }_{kl}*{F}_{ij}\) is the anisotropic stress, which is expressed as \({\beta }_{kl}*{f}_{ij}\). \({\alpha }_{kl}\) and \({\beta }_{kl}\) are tensors revealing anisotropy determined by the actual physical state of the rock surrounding the tunnel.

2.2.2 Loading Phase Due to Excavation-Induced Stress Redistribution

Due to tunnel excavation, the mechanical equilibrium of the surrounding rock is disturbed. As shown in Fig. 1, the cementations between grains play a role in resisting deformation caused by stress, preventing the relative shearing, deviation, and rotation of skeleton grains. The mesoscale damage can be described as the bonding failure of rock gains due to tension or shear, as shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of the mesoscale damage model

Full size image

The parallel bonded model (PBM) (Potyondy 2007; Xia et al. 2021a, b) is used for modeling the bonding failure of rock gains at the mesoscale mainly based on the binding characteristics of the rock gains, i.e., shear strength \({\sigma }_{c}\), tensile strength \({\tau }_{c}\), normal stiffness \({k}^{n}\), tangential stiffness \({k}^{s}\), and bonding radius \(R\). That is,

$$\begin{array}{c}\Delta {F}^{n}={k}^{n}A\Delta {U}^{n}, \Delta {F}^{s}=-{k}^{s}A\Delta {U}^{s},\end{array}$$
(13)
$$\begin{array}{c}\Delta {M}^{n}=-{k}^{s}J\Delta {\theta }^{n}, \Delta {M}^{s}=-{k}^{n}I\Delta {\theta }^{s},\end{array}$$
(14)

where \({F}^{n}\) and \({F}^{s}\) are the normal and tangential forces, respectively. \({M}^{n}\) and \({M}^{s}\) are the normal and tangential moments, respectively. \({U}^{n}\), \({U}^{s}, {\theta }^{n}\), and \({\theta }^{s}\) are the relative displacements and rotation angles in the normal and tangential directions, respectively. \(A\), \(I\), and \(J\) are the area, moment of inertia, and polar moment of the bonds section, respectively, which can be described as

$$\begin{array}{c}A=\pi {R}^{2},\end{array}$$
(15)
$$\begin{array}{c}I=\frac{1}{4}\pi {R}^{4},\end{array}$$
(16)
$$\begin{array}{c}J=\frac{1}{2}\pi {R}^{4}.\end{array}$$
(17)

The maximum tensile stress and shear stress on the grain surface can be calculated using the following equations:

$$\begin{array}{c}\sigma =\frac{{-F}^{n}}{A}+\frac{\left|{M}^{s}\right|R}{I},\end{array}$$
(18)
$$\begin{array}{c}\tau =\frac{{F}^{s}}{A}+\frac{\left|{M}^{n}\right|R}{J}.\end{array}$$
(19)

Mesoscopic damage to soft rock tunnels occurs when \(\sigma \ge {\sigma }_{\mathrm{c}}\) or \(\tau \ge {\tau }_{\mathrm{c}}\), as shown in Fig. 2. The values of \({\sigma }_{\mathrm{c}}\) and \({\tau }_{\mathrm{c}}\) determine the mechanical capacity of cementation, which can be obtained through a calibration process based on the peak strength of rock samples.

2.2.3 Creep-Induced Damage Phase Leading to Large Deformation

Clay minerals in soft rock may expand and disintegrate when exposed to water or constant loading. This long-term process can finally lead to the stress redistribution and damage accumulation of the rock surrounding the tunnel (Kontogianni et al. 2006; Tang et al. 2018; Xiong et al. 2020; Zhang et al. 2021). Because weak bonding is unable to carry tension, shear, and torsion, only the normal pressure is considered in the creep model. In this study, the creep behavior of soft rock is modeled using Burger’s model, which combines the characteristics of the Kelvin and Maxwell models (Fahimifar et al. 2010; Maheshwari 2021). Figure 4 shows the major components of Burger’s model. The details are shown in Table 1.

Fig. 4
figure 4

Burger’s creep model

Full size image
Table 1 Governing equations of the Maxwell model, Kelvin model and Burger’s model
Full size table

Figure 5 shows the creep–damage model for simulating the large deformation and viscoelasticity damage of the soft rock surrounding the tunnel. It is assumed that the strong bonding is linear elastic before brittle failure, where \({E}_{3}\) is the linear elastic modulus.

Fig. 5
figure 5

Diagram of the creep–damage model

Full size image

The governing equations of Burger’s model can be described as

$$\begin{array}{c}\sigma +{\alpha }_{1}\dot{\sigma }+{\alpha }_{2}\ddot{\sigma }={\beta }_{1}\dot{\varepsilon }+{\beta }_{2}\ddot{\varepsilon },\end{array}$$
(20)

where

$$\begin{array}{c}{\alpha }_{1}=\frac{{\eta }_{1}+{\eta }_{2}}{{E}_{1}}+\frac{{\eta }_{2}}{{E}_{2}},\end{array}$$
(21a)
$$\begin{array}{c}{\alpha }_{2}=\frac{{\eta }_{1}{\eta }_{2}}{{E}_{1}{E}_{2}},\end{array}$$
(21b)
$$\begin{array}{c}{\beta }_{1}={\eta }_{2},\end{array}$$
(21c)
$$\begin{array}{c}{\beta }_{2}=\frac{{\eta }_{1}{\eta }_{2}}{{E}_{1}}.\end{array}$$
(21d)

For a parallel connection, as shown in Fig. 5, the strain (\({\varepsilon }_{\mathrm{c}}\)) and stress (\({\sigma }_{\mathrm{c}}\)) of the coupled creep–damage model can be described as:

$$\begin{array}{c}{\varepsilon }_{\mathrm{c}}=\varepsilon ={\varepsilon }_{3},\end{array}$$
(22)
$$\begin{array}{c}{\sigma }_{\mathrm{c}}={\sigma }_{3}+\sigma ,\end{array}$$
(23)
$$\begin{array}{c}{\sigma }_{3}={E}_{3}{\varepsilon }_{3}.\end{array}$$
(24)

where \({\varepsilon }_{3}\) and \({\sigma }_{3}\) are the strain and stress of the damage model. By combining Eqs. (20)–(24), the coupled creep–damage model can be derived as:

$$\begin{array}{c}{\sigma }_{\mathrm{c}}+{\alpha }_{1}\dot{{\sigma }_{\mathrm{c}}}+{\alpha }_{2}\ddot{{\sigma }_{\mathrm{c}}}={E}_{3}{\varepsilon }_{3}+\left({\beta }_{1}+{\alpha }_{1}{E}_{3}\right)\dot{{\varepsilon }_{3}}+\left({\beta }_{2}+{\alpha }_{2}{E}_{3}\right)\ddot{{\varepsilon }_{3}}.\end{array}$$
(25)

At the initial phase (\(t\) = 0, \(\sigma ={\sigma }_{0}\)), Eq. (24) becomes

$$\begin{array}{c}\ddot{{\varepsilon }_{\mathrm{c}}}+\left(\frac{{\beta }_{1}+{\alpha }_{1}{E}_{3}}{{\beta }_{2}+{\alpha }_{2}{E}_{3}}\right)\dot{{\varepsilon }_{3}}+\left(\frac{{E}_{3}}{{\beta }_{2}+{\alpha }_{2}{E}_{3}}\right){\varepsilon }_{\mathrm{c}}-\frac{{\sigma }_{0}}{{\beta }_{2}+{\alpha }_{2}{E}_{3}}=0.\end{array}$$
(26)

In addition, the initial conditions of strain, stress, and creep rate can be described as:

$$\begin{array}{c}{\varepsilon }_{\mathrm{c}}=\frac{\sigma }{{E}_{1}}=\frac{{\sigma }_{3}}{{E}_{3}},\end{array}$$
(27a)
$$\begin{array}{c}{\sigma }_{0}={\sigma }_{3}+\sigma ,\end{array}$$
(27b)
$$\begin{array}{c}{\varepsilon }_{\mathrm{c}}=\frac{{\sigma }_{0}}{{E}_{1}+{E}_{3}},\end{array}$$
(28)
$$\begin{array}{c}\dot{{\varepsilon }_{\mathrm{c}}}=\frac{\sigma }{{\eta }_{1}}+\frac{\sigma }{{\eta }_{2}}=\frac{\left({\eta }_{1}+{\eta }_{2}\right){E}_{1}{\sigma }_{0}}{\left({E}_{1}+{E}_{3}\right){\eta }_{1}{\eta }_{2}}.\end{array}$$
(29)

Equation (26) can be rewritten as

$$\begin{array}{c}\ddot{{\varepsilon }_{\mathrm{c}}}+A\dot{{\varepsilon }_{\mathrm{c}}}+B{\varepsilon }_{\mathrm{c}}=C,\end{array}$$
(30)

where A, B and C are parameters related to the properties of the soft rock. By solving the second-order nonhomogeneous linear Eq. (30), the roots of the eigen-equation (i.e., \({\lambda }_{1}\) and \({\lambda }_{2}\)) can be obtained as:

$$\begin{array}{c}{\lambda }_{\mathrm{1,2}}=\frac{A\pm \sqrt{{A}^{2}-4B}}{2}=\frac{-\left[\frac{\left({\eta }_{1}+{\eta }_{2}\right){E}_{1}{E}_{3}}{\left({E}_{1}+{E}_{3}\right){\eta }_{1}{\eta }_{2}}+\frac{{E}_{1}}{{\eta }_{1}}\right]\pm \sqrt{[{\frac{\left({\eta }_{1}+{\eta }_{2}\right){E}_{1}{E}_{3}}{\left({E}_{1}+{E}_{3}\right){\eta }_{1}{\eta }_{2}}]}^{2}-4\frac{{E}_{1}{{E}_{2}E}_{3}}{{\eta }_{1}{\eta }_{2}\left({E}_{1}+{E}_{3}\right)}}}{2}.\end{array}$$
(31)

Then, the large deformation of the soft rock (\({\varepsilon }_{\mathrm{c}}\)) can be obtained as:

$$\begin{array}{c}{\varepsilon }_{\mathrm{c}}={C}_{1}{e}^{{\lambda }_{1}t}+{C}_{2}{e}^{{\lambda }_{2}t}+\frac{{\sigma }_{0}}{{E}_{3}}.\end{array}$$
(32)

The coefficients of \({C}_{1}\) and \({C}_{2}\) in Eq. (31) can be calculated when substituting Eqs. (27)–(29) into (30), and we obtain:

$$\begin{array}{c}{C}_{1}=\frac{\left({\eta }_{1}+{\eta }_{2}\right){E}_{1}{E}_{3}{\sigma }_{0}+{\lambda }_{2}{E}_{1}{\eta }_{1}{\eta }_{2}{\sigma }_{0}}{\left({\lambda }_{1}-{\lambda }_{2}\right)\left({E}_{1}+{E}_{3}\right){\eta }_{1}{\eta }_{2}{E}_{3}},\end{array}$$
(33)
$$\begin{array}{c}{C}_{2}=\frac{\left({\eta }_{1}+{\eta }_{2}\right){E}_{1}{E}_{3}{\sigma }_{0}+{\lambda }_{1}{E}_{1}{\eta }_{1}{\eta }_{2}{\sigma }_{0}}{\left({\lambda }_{2}-{\lambda }_{1}\right)\left({E}_{1}+{E}_{3}\right){\eta }_{1}{\eta }_{2}{E}_{3}}.\end{array}$$
(34)

2.3 Coupled Meso/Macroscale Modeling of Damage and Deformation of the Surrounding Rock Resulting from Tunnel Excavation

The coupled meso/macroscale process resulting in the large deformation of soft rock can be described as:

$$\begin{array}{c}d{\varepsilon }_{ij}={d\varepsilon }_{ij}^{e}+{d\varepsilon }_{ij}^{d}+{d\varepsilon }_{ij}^{cd},\end{array}$$
(35)

where \({\varepsilon }_{ij}^{e}={D}_{ijkl}{\sigma }_{ij}\), \(d{\varepsilon }_{ij}^{d}=d\lambda \frac{\partial Q}{\partial {\sigma }_{ij}}\) and \({d\varepsilon }_{ij}^{cd}=\dot{{\varepsilon }_{\mathrm{c}}}\). By considering the anisotropic mechanical behavior of the soft rock, Eq. (32) can be written as:

$$\begin{array}{c}{\varepsilon }_{ij}=F\left({\sigma }_{ij},t\right),\end{array}$$
(36)

where \({\sigma }_{ij}\) represents the anisotropic mechanical behavior of the rock due to the tectonic stress condition at the macroscale. That is,

$$\begin{array}{c}{\sigma }_{ij}=\left\{\begin{array}{c}{\delta }_{ij}{\sigma }_{m}+{s}_{kk}, \left({\text{non-hydrostatic state}}\right)\\ {\delta }_{ij}{\sigma }_{m}, \left({\text{hydrostatic state}}\right)\end{array}\right..\end{array}$$
(37)

Substituting Eq. (12) into Eq. (36), the multiscale coupled damage–creep model of soft rock surrounding a tunnel can be obtained,

$$\begin{array}{c}{\varepsilon }_{ij}=F\left({\sigma }_{ij}-{\alpha }_{kl}{F}_{ij},t\right)+{F}^{^{\prime}}\left({\alpha }_{kl}{F}_{ij},t\right).\end{array}$$
(38)

As shown in Fig. 6, Eq. (38) can be solved using the DEM based on a previously developed cell model that correlates the mesoscale structure and mechanical properties of soft rock (Li and Wong 2016; Xia et al. 2021a, b). The blue and green particles represent the normal and creep grains, respectively. It is assumed that there is a relatively strong bonding between the blue particles, whereas the bonding strength between green particles is relatively weak. The particles in the representative elementary volume (REV) are randomly arranged. In the numerical calculation, grain movement is determined by the model's boundary conditions and the mechanical evolution of bonding. Between two grains, the most common stress states are compressive or tensile forces applied to the normal direction of the bonding surface. The deformation between grains involves instantaneous and rheological deformation. The PBM mimicking strong bonding has five components (\({k}_{\rm n}\), \({k}_{\mathrm{s}}\), \({\overline{k} }_{\rm n}\), \({\overline{k} }_{\mathrm{s}}\) and \({\sigma }_{\mathrm{c}}\)). PBM deformation is determined by the normal (\({k}_{\rm n}\), \({\overline{k} }_{\rm n}\)) and shear (\({k}_{\mathrm{s}}\), \({\overline{k} }_{\mathrm{s}}\)) stiffnesses of springs. The damage is determined by the strength component \({\sigma }_{\rm c}\), which complies with the threshold shown in Fig. 3. The Burger’s model simulates weak bonding by four components (\({E}_{1}\), \({E}_{2}\), \({\eta }_{1}\) and \({\eta }_{2}\)). Weak bonding creep appears in the dashpot component (\({\eta }_{1}\), \({\eta }_{2}\)) when a normal stress is applied. \({E}_{1}\) and \({E}_{2}\) are elastic springs herein.

Fig. 6
figure 6

Coupled meso/macroscale modeling using DEM

Full size image

2.4 Modeling of the Long-Term Deformation of a Tunnel

2.4.1 Project Description

The soft rock tunnel selected in this study is located in northwest China with a total length of approximately 15 km and a maximum buried depth of 638 m (Chen et al. 2020; Zhang et al. 2020; Sun et al. 2021; Liu et al. 2022). Due to the instability of soft rock with a uniaxial saturated compressive strength of less than 30 MPa, collapses often occur. The tunnel faces show the soft rock surrounding the tunnel and bedding joints (Fig. 7) (Zhang et al. 2020). The inclination angle of the main joints of the surrounding rock is approximately 30°–85°, while the thickness between the joint surfaces is approximately 5–30 cm. Based on the X-ray diffraction tests, the main mineral components of the rock are clay and quartz. The average uniaxial strength of the rock samples is 29.6 MPa, while the average strength under water saturation for 24 h is 12.7 MPa. In addition, the tectonic stress measured by the original hydraulic fracturing shows that the maximum and minimum horizontal principal stresses are 20 and 14 MPa, respectively (Zhang et al. 2020). The deformation of the surrounding soft rock after excavation is relatively large, with the convergent deformation exceeding 1 m.

Fig. 7
figure 7

Tunnel faces showing the soft rock surrounding the tunnel and bedding joints. a Deformation of the tunnel surrounding rock in the left corner, b deformation of the left tunnel surrounding rock (Zhang et al. 2020), c BLSS 3D laser scanner used in rock mass deformation monitoring, and d Leica TCA2003 Total Station used for monitoring displacement of three points

Full size image

A total station and 3D laser scanner were used to monitor the section of the No. 2 inclined shaft of the tunnel. The deformation of the surrounding rock mass was measured by a BLSS 3D laser scanner. The 3D spatial deformation was calculated by distance, angle, and inclination correction, which was recorded by a laser distance sensor, position feedback encoder and inclination sensor, respectively. The measuring accuracy of the BLSS 3D laser scanner is 0.7 mm in a 10-m range. The final deformation is shown in Fig. 7a, b.

The monitored displacement of points “A”, “B”, and “C” was measured by a Leica TCA2003 total station. When measuring, the reference point is set up at a stable place, and reflective sheet targets are attached to the top of the vault. Three measurements were taken at each point for the average, which was continuously monitored for 25 days during the excavation. The monitoring results of the tunnel section investigated are presented in Fig. 8. The measuring range and accuracy of the Leica TCA2003 total station are 1000 and 0.1 mm, respectively.

Fig. 8
figure 8

Time-dependent displacement at monitoring points “A”, “B” and “C” in tunnel section “XK0 + 060 − XK0 + 250”

Full size image

2.4.2 Model Setup and Calibration

The numerical modeling process involves the following five steps:

  1. (1)

    Define the simulation domain of the grain model

As shown in Fig. 9a, the size of the research domain is 60 m (width) \(\times\) 60 m (height) \(\times\) 10 m (length), considering the size of the tunnel. “A”, “B”, and “C” are the three monitoring points in the tunnel face.

  1. (B)

    Distribute the grain particles into the simulation domain

Fig. 9
figure 9figure 9figure 9

Numerical solution. a Defining the simulation domain. “A”, “B” and “C” are three monitoring points. b Distribution of grain particles within the simulation domain. c Tectonic stresses applied to the domain. d Combined finite and discrete element approach. e Initial joints applied to the tunnel surrounding rock

Full size image

As shown in Fig. 9b, the grains are uniformly distributed between the boundaries of the domain, and the mechanical system is iterated until equilibrium is reached, in which fine particles are distributed in the tunnel zone (Gutierrez-Ch et al. 2022). Considering the modeling convenience, the fine particle zone is selected in a square region. The density and modulus of the grain assembly are 2500 kg/m3 and 600 MPa, respectively, based on the rock samples obtained from the tunnel.

  1. (C)

    Tectonic stresses applied to the domain

As shown in Fig. 9c, the tectonic stresses according to the in situ stress condition are applied to the simulation domain based on the servo method (Lin et al. 2022). The stress is calculated based on the overall contact force between grains and walls, while the velocity of walls is controlled by FISh (a computer coding language commonly used for DEM) until the dynamic stress balance is reached. The in situ stress is determined based on the field measurement results, i.e., the maximum, intermediate and minimum principal stresses are 20, 14 and 14 MPa, respectively.

  1. (D)

    Combined finite and discrete element approach

In the numerical simulation, the model length is usually set to nearly eight times the tunnel diameter to avoid boundary effects. However, limited by computing efficiency, the DEM grain-based model cannot meet all the requirements. Thus, as shown in Fig. 9d, a combined DEM–FEM approach (Huang et al. 2020a, b; Wang et al. 2020) was used in this paper for modeling the continuous deformation in the inner zone and expanding the simulation range. The inner FEM zone is used for the support material. In the DEM–FEM coupled zone, the calculated unbalanced force of grains will be attributed to the adjacent FEM nodes. This will cause a velocity alteration of FEM nodes, which will be assigned to the adjacent grains. The above coupling process is completed in each timestep. Before the model implementation, bonding models were added, and it is assumed that the cemented grains form a stable system. The bonding strength between the grain particles was calibrated based on the average strength of the intact rock mass (i.e., approximately 30 MPa). It is important to note that the already existing rock support could influence the initial equilibrium. After excavation, the support element was applied with a null modulus. The real lining structure is installed instantly after Day 1 when creep deformation begins.

  1. (E)

    Application of initial joints and boundary conditions

As shown in Fig. 9e, the deformation due to excavation can be modeled using the commercial DEM software Particle Flow Code (PFC). The modeling process of the joints is realized by using the smooth joint model in PFC, which can provide relative sliding friction (Hu et al. 2018). After the application of joints, the initial equilibrium before excavation was obtained under the boundary conditions shown in Fig. 9e. After excavation, the displacements at monitoring points “A”, “B” and “C” were numerically predicted.

When a mesoscale modeling approach is used to model the mechanical response of rocks, the mechanical parameters of grain elements as well as bonding elements need to be well calibrated (see Fig. 10). In this paper, the calibration process is complex for considering joints and creep conditions. Typically, the strength and elastic modulus of rock are determined by a ‘trial and error’ process (Coetzee 2017). In this paper, we calibrate the creep, strength, and joint parameters in the order shown in Fig. 10, which is presented in Table 2. The trials involved were repeated three times under different random seeds.

Fig. 10
figure 10

Numerical parameters need to be determined at different modeling scales and scenarios, including (1) static mechanical property and creep property calibration in rock samples; (2) verification of the calibrated model at the engineering scale; and (3) back-analysis for obtaining the mechanical properties of joints

Full size image
Table 2 Mechanical and physical properties used in mesoscopic scale analysis
Full size table

Based on field investigation, the basic rock properties are obtained from (Zhang et al. 2020), and the time-dependent creep test results are collected from (Tao et al. 2020). The mesoscale parameters presented in Table 2 are determined according to the following steps:

  1. (1)

    General parameters adopted in the DEM modeling

In the grain-based model, we need to consider calculation accuracy and efficiency. According to a previous study, when L/R (where L is the model length and R is the mean grain radius) is greater than 68, the properties of the material are nearly constant (Li et al. 2014; Cheng and Wong 2020). Previous studies have shown that in a DEM system, the number of mesoscale elements can meet the requirements of accuracy and calculation efficiency when greater than 15,000 (Lin et al. 2022). In the rock sample and rock mass calibration, we choose an L/R value greater than 100 in this paper. A total of 31,516 grains were used in the simulation based on convergence analysis. The damping coefficient is set to a default value of 0.5 to dissipate kinetic energy.

  1. (B)

    Loading test calibration

Static mechanical properties were calibrated prior to the creep deformation parameters. The loading test is the most commonly adopted method to characterize the elastic modulus and strength of rock samples. We conducted numerical tests to obtain reasonable bonding strength and stiffness. The calibration results are shown in Fig. 11a, where we find that the mechanical properties are well-calibrated compared to the real rock parameters. We compared the detailed mechanical properties of the rock samples in Table 3.

Fig. 11
figure 11

Calibration results. a Uniaxial loading stress‒strain curves of intact rock samples, b, c strain curves of creep test, d uniaxial loading stress–strain curves of intact rock mass, and e uniaxial loading stress‒strain curves of jointed rock mass

Full size image
Table 3 Mechanical properties of the rock sample in the calibrated and experimental results
Full size table
  1. (C)

    Creep test calibration

Because of the rheological deforming scenario discussed in this paper, we need to consider two kinds of contacts as bonding. The ratio of PBM to Burger’s model and their parameters will affect the final creep behavior of the rock. In this stage, the bonding strength is applied to a high value (tensile strength = 200 MPa, cohesive strength = 400 MPa), which will not damage the creep tests. The calibration process is finished by changing the parameter values after the ‘trial and error’ process.

The creep tests were carried out at 12, 24 and 36 MPa stresses (see Fig. 11). During the creep simulation process, we found that the results were reasonable when equating \(5\times {10}^{5}\) steps to a real 24 h in the laboratory. We keep the same treatment in this paper in regard to the conversion of timesteps to real time. In the calibrated sample, creep grains make up 18.7% of the total grains, which are randomly distributed in the particle assemblage. The final calibration results are presented in Fig. 11b, c, where we can compare the creep curves. The detailed calibration error is shown in Table 4, and the mean error of creep strain in different loading forces is less than 5%.

Table 4 Creep deformation under different normal stresses
Full size table
  1. (D)

    Verification on the engineering scale

According to the mentioned conclusion, when the model size to grain size ratio is larger than 68, the mechanical behavior of the DEM model is constant. It is necessary to verify this conclusion to promote mesoscale parameters to an engineering scale. Therefore, we conducted an engineering scale (15 m \(\times\) 15 m \(\times\) 30 m) uniaxial loading test via the DEM. We find that when the model size to grain size ratio is fixed, the strength and elastic modulus of the rock are also nearly constant (see Fig. 11d).

  1. (E)

    Bedding joint parameter calibration for rock mass

After rock sample calibration, we need to further determine the rock mass properties, where the joints are considered. Numerical back-analysis is a powerful method that can be used as a complementary technique to in situ or laboratory experiments to determine mechanical properties (Fakhimi et al. 2004; Li et al. 2022a, b). In situ failure, movement or convergence can be used to back-calculate the physical properties of rock joints. In this paper, the following steps were used for back-analysis:

  1. A.

    Strength of 29.6 MPa and elastic modulus of 7.6 GPa were used as determined from the laboratory loading test.

  2. B.

    A joint angle of 45 \(^\circ\) and a spacing of 15 m were assumed. The value of angle and space was justified based on field mapping.

  3. C.

    Reasonable values for joint roughness, joint cohesive strength, and friction coefficients based on the results of in situ tests and engineering judgment were assumed. We modified these parameters until there was good agreement between the numerical and measured in situ failures. After the back-analysis process, we obtained a reasonable rock mass numerical mechanical property compared with the rock mass property (E = 0.6 GPa, \({\sigma }_{\mathrm{c}i}\)=7.4 MPa) obtained from field investigation (Zhang et al. 2020).

3 Results and Discussion

3.1 Comparison Between the Predicted Displacement and Monitoring Data

Figure 12 shows the macroscopic deformation of the surrounding rock during the excavation. It shows that the predicted time-dependent displacements at “A”, “B” and “C” agree with the monitoring data reasonably well. In addition, the displacement at point “B” is larger than that at “A” and “C”. For example, on Day 25 after the excavation, the displacement at point “B” is more than twofold larger than that at point “C”. Furthermore, the maximum displacement surrounding the surface of the tunnel is approximately 526 mm, which could lead to tunnel damage.

Fig. 12
figure 12

Macroscopic deformation of the soft rock surrounding the tunnel during the excavation: a comparing the predicted time-dependent displacements at “A”, “B” and “C” with monitoring data, b displacement contour in the simulation domain and observed tunnel surface extrusion in the field

Full size image

3.2 The Asymmetrical Deformation of the Tunnel Face at Monitoring Points “B” and “C”

The deformation of the rocks surrounding the tunnel face is generally asymmetric due to the application of joints with different inclination angles (i.e., 30°, 45°, and 60°), and the asymmetric nature of the deformation becomes obvious at a joint inclination angle of 45° (Zhang et al. 2020). As shown in Fig. 13, the deformations at points “B” and “C” are symmetrical without initial joints, whereas the application of initial joints could lead to a significant difference in displacement between “B” and “C”. Under the joint inclination angle of 45°, the rock mass is prone to slide along the joint surface, which ultimately could lead to a large displacement on the left side of the tunnel.

Fig. 13
figure 13

The ultimate displacements at points “A”, “B” and “C” with or without initial joints

Full size image

Figure 14 demonstrates the movement of rock grains, which is captured from the initial equilibrium stage at cycle time step 10,000. The movement of rock grains demonstrates a symmetrical “X” shape, whereas the application of initial joints could result in the location of grains along the joints and two shearing zones. As monitoring point “B” is in one of the shearing zones, it has the largest displacement among the three measuring points.

Fig. 14
figure 14

Movement of grains with or without initial joints

Full size image

3.3 Mesoscopic Scale Damage and Deformation of the Surrounding Rock at Different Phases

As shown in Fig. 15, the large deformation of soft rock surrounding the tunnel is a gradual process. In the initial phase, the whole surrounding rock is stable. Due to the excavation-induced stress redistribution, the surrounding rock undergoes the loading phase, in which the weak bonds in the rock experience creep under excessive local stresses. As the deformation accumulates, creep-induced damage develops around the tunnel. The coupled creep–damage process ultimately causes large deformation of the surrounding rock of the tunnel. From Days 1–4, the excavation-caused stress concentration around the tunnel causes severe mesocrack accumulation; the creep-induced stable increase in crack number is captured thereafter.

Fig. 15
figure 15

The soft rock tunnel surrounding rock at different phases: a deformation maps and damage zones captured on different days, b counted crack numbers in the modeling process

Full size image

3.4 Model Sensitivity Analysis

Given the complexity of the scenario considered in this paper, we conducted a sensitivity analysis of the proposed model.

  1. (1)

    Effect of the change in tensile/cohesive strength on the final displacement

Figure 16 shows the predicted ultimate displacement at points “A”, “B” and “C” under different bonding strengths of cementations quantified by the mesoscopic tensile and cohesive strength of the rock grains. The initial values of the bonding characteristics (\({\sigma }_{\mathrm{c}}\) =30 MPa, \({\tau }_{\mathrm{c}}\) = 61 MPa) are obtained through the calibration process based on the peak strength of the rock samples. It shows that the decrease of the bonding tensile strength by 50% could increase the displacement at the top of the tunnel (point “A”) by 300% but have relatively little influence on the displacements at points “B” and “C”. However, the same proportional change in cohesive strength has a smaller effect on the final deformation. Thus, the final deformation is more sensitive to the tensile strength.

Fig. 16
figure 16

The predicted displacement at points “A”, “B” and “C” under different bonding strengths: a change in bond tensile strength and b change in bond cohesive strength

Full size image
  1. (B)

    Effect of the fraction of grains experiencing creep on the model mechanical responses

In this paper, we have coupled the damage and creep factors in a soft rock tunnel, and we also obtained a reasonable result. We refer to the grains that undergo creep as creep grains. We extended our discussion to some more scenarios with different creep grain ratios involving 18.7, 20.2, 21.7, 23.2 and 24.7% (Fig. 17). The rock strength, creep strain, and excavation deformation at three monitoring points “A” “B” and “C” are compared in Table 5 and Fig. 18 for sensitivity analysis. When the creep grain ratio rises to 24.7%, the error of the predicted deformation at the three monitoring points becomes large (greater than 10%). If this ratio continues to increase, the deformation prediction results obtained will differ significantly from the actual situation.

Fig. 17
figure 17

Time-dependent behavior under different ratios of creep grains: a creep curves of the rock sample under 24 MPa loading and b rheological displacement at the left point “B” of the tunnel

Full size image
Table 5 The influence of changing the creep grain ratio on the modeling results
Full size table
Fig. 18
figure 18

Comparison of the influence of changing the creep grain ratio on different modeling results

Full size image

In a time-dependent comparison, we conducted creep tests for laboratory-scale rock samples under 24 MPa stress. Figure 17 shows that the ultimate creep strain and deformation at the left side of tunnel monitor point “B” increase with increasing creep grain ratio. When the incremental creep grain ratio increases from 4.5 to 6.0%, the incremental deformation at the three monitoring points nearly doubles.

4 Conclusions

We implemented a damage-based, time-dependent modeling approach to reproduce the entire evolution of a large-deformation soft rock tunnel. By incorporating the coupled meso/macroscale deformation process of the rock into the model, the predicted time-dependent displacements of the tunnel face agree reasonably well with the monitoring data.

The model is able to reproduce both instantaneous damage patterns of brittle failure and time-delayed creep deforming patterns. Tunnel excavation strongly affects the initial stability of the surrounding rock mass, and brittle damage accumulated in mineral clusters leads to severe instantaneous deformation, which becomes less important in the creep evolution stage.

The application of the theoretical model to engineering cases provided the opportunity to investigate the evolution mechanisms of large deformation. As an emerging property, the model simulates a wider range of scenarios with different rock static and creep parameters. The final deformation is characterized by a high sensitivity to the value of mesoscale modeling parameters.