1 Introduction

Extensive research has been conducted on the strength of hard rock pillars. Owing to its simplicity, empirical strength formulae are popular and it is used extensively by practicing rock engineers to design layouts. A number of the historic pillar strength studies and formulae are summarised in Martin and Maybee (2000). Examples are also given in Gonzalez-Nicieza et al. (2006) and Esterhuizen et al. (2011). These formulae are based on observed pillar failures and typically takes the form of either a power- or linear-type equation. These equations have been used to predict pillar strengths for a wide range of pillar shapes and rock mass strengths. The pillar strength is mostly dependent on some rock mass strength parameters and the width and height of the pillar. A significant drawback of this approach is that the pillar strength estimates are empirical and the results should not be extrapolated beyond the range of the data which were used to derive it. For example, the use of the Canadian Hedley and Grant (1972) formula in South African platinum mines, where there is occasionally a weak clay layer present in the pillars, has led to spectacular mine-wide collapses (Malan and Napier 2011). It is therefore important to also consider the mode of failure of the pillars. This was highlighted by Esterhuizen et al. (2019) who presented a case study in which tall, slender (18 m high, 9 m wide) pillars collapsed at a limestone mine in Pennsylvania. The large angular discontinuities in the pillars contributed to the collapse and these were not accounted for when the pillar strength was estimated. A further drawback is that the empirical strength equations does not consider the possible time-dependent failure of the pillars. Martin and Maybee (2000) mention that: “Observations of pillar failures in Canadian hard-rock mines indicate that the dominant mode of failure is progressive slabbing and spalling”. The time-dependent nature of this progressive slabbing was not quantified in the study, however, and further work is required.

In terms of coal mining, Van der Merwe (2003, 2004, 2016) describes observations made on the progressive weakening of coal pillars from the edges towards the core of the pillar. He noted that at some stage the remaining pillar core will be too small to handle the imposed load and it will fail completely. The time of failure can possibly be predicted by investigating the rate of scaling for different areas and seams. The rate of scaling was studied by comparing the actual life spans to the predicted time of failure for pillars in a database of failed pillars. Van der Merwe (2003) indicated that the scaling rate has an inverse relationship to time and a direct relationship to the mining height. The pillar data indicated a relationship between the scaling rate and the mining height over time \(\left(h/T\right)\). Based on the data, he proposed the following empirical equation to determine the rate of scaling, \(R\), for coal pillars:

$$R=m{\left[\frac{h}{T}\right]}^{x},$$
(1)

where \(x\) and \(m\) are dimensionless constants. Van der Merwe (2016) published calibrated values for these parameters based on an extended database, namely \(x=0.7549\) and \(m=0.1799\).

Numerical modelling to simulate time-dependent pillar failure is an alternative method to study the time-dependent behaviour. Napier and Malan (2012) simulated the time-dependent crush pillar behaviour in South African platinum mines using a limit equilibrium model. This model is explored further in this current paper using underground data from a hard rock bord and pillar mine. An example of the complex modelling of time-dependent pillar scaling is given in the paper by Sainoki and Mitri (2017). A non-linear rheological constitutive model is used in the code. The numerical study considered pillar failure occurring over a long period of time. The objective of the study was to determine the risk of surface subsidence caused by the eventual collapse of the pillars. The simulated damage in the pillar is shown in the paper and it illustrates that the depth of scaling increases with time. This clearly demonstrates the value of these models, but a major drawback is that the complex constitutive models are difficult to calibrate. A numerical modelling study was also conducted by Wang and Cai (2021) to investigate the time-dependent deformation of pillars. A grain-based time to failure model (GBM-TtoF) was used to study the time-dependent deformation of a pillar. To govern the creep deformation of the grains in the model, a Burgers creep model was adopted (Aydan et al. 2013).This model is also complex and, although the expected behaviour can be simulated, the constitutive model is difficult to calibrate.

In summary, very little work has been done on the time-dependent scaling of hard rock pillars in the past. Although hard rock pillars are not intuitively associated with time-dependent scaling, the authors collected underground data from a manganese mine (described in Sect. 2), where this pillar behaviour was observed in some of the old mining areas (Fig. 1). The ongoing scaling of the pillar after the application of the thin spray-on liner is considered as evidence that the scaling occurs in a time-dependent fashion. This behaviour may affect the long-term stability of sections of the mine and it should be quantified. The key objective of the paper was therefore an attempt to simulate the time-dependent scaling of pillars in a hard rock bord and pillar mine and to compare the numerical results with field observations.

Fig. 1
figure 1

Time-dependent scaling of a manganese pillar in a hard rock bord and pillar mine in South Africa. The pillar was covered with thin spray-on liner to prevent the scaling, but the ongoing failure destroyed the liner and the scaling continued

Full size image

2 Underground Observations of Pillar Behaviour

The manganese mining operations in the Kalahari region (Northern Cape Province) of South Africa is a major contributor to the economy of the country. The Kalahari Manganese Field is approximately 2.2 Ga years old and is the world’s premier land-based manganese ore reserve. The deposit contains an estimated 150 Mt of manganese ore reserves (Beukes et al. 2016). The manganese ore is found as shallow tabular deposits and it is exploited using both open cast and underground bord and pillar mining operations.

In terms of rock engineering designs, there is uncertainty regarding the strength of the manganese pillars, and it is not clear if the current bord and pillar layouts are optimised for maximum, safe extraction. There is almost no empirical data on the strength of the pillars. The Hedley and Grant pillar strength formula, with a typical rock mass strength parameter of K = 133 MPa, is currently used to design these pillars at most of the operations. There is no scientific justification to use this formula and the generally accepted value of K = 133 MPa needs further verification. The strength of intact manganese laboratory-sized specimens is exceptionally large and uniaxial compressive strength values exceeding 400 MPa have been recorded. A lower average value of 280 MPa is quoted in some reports from the mines.

In spite of the large intact rock strength, underground studies by the authors indicated that the pillar behaviour is mostly controlled by the joint sets and the spacing of the joints in the manganese ore. Typically, in the high-grade areas, very few joints are present and these joints are widely spaced. The pillars appear solid, even for pillars with a w:h ratio of less than 1.5 (typically 7 m wide, 5.5 m high). In other areas, there are a number of intersecting joint sets with some of the joints at a very small spacing (< 10 cm). These pillars are characterised by intensive scaling. The differences in pillar behaviour are illustrated in Fig. 2. The rock mass rating clearly controls the pillar behaviour and a power-law strength formula with a single “calibrated” rock mass strength value does not cater for this.

Fig. 2
figure 2

Different manganese pillar behaviours caused by the number of joint sets and the spacing of the joints

Full size image

To study the time-dependent pillar scaling, the authors established a number of monitoring stations (Fig. 3). A problem with the quantitative monitoring of time-dependent pillar scaling is that stable reference points are required. Distance measurements from stable reference points to particular points on the pillar sidewalls should be recorded over a period of time. As the pillar sidewalls are subjected to scaling, however, it is difficult to ensure that the measurements are conducted between the same positions on the pillar and the reference points. As a first attempt to overcome this problem, large crosses were painted on the sidewalls of the pillars, as well as the pillars adjacent to the pillar being monitored (Fig. 4). The distance between the crosses of opposing pillar sidewalls was recorded using a laser distance meter (Fig. 5). If parts of a cross are lost owing to scaling, the centre position can still be estimated from the remaining portions of the lines. If both pillars scale, the scaling distance will then be simply estimated to be half the increase in measured distance. Although rather crude, this method proved useful to indicate that no scaling occurred during a 3-month monitoring period for all the pillar stations. This indicated that the measurement period was too short to record any time-dependent scaling. It seems as if the bulk of the scaling occur very soon after the pillar has formed and then the rate of scaling decreases with time. The pillars typically assumed an “hourglass” shape.

Fig. 3
figure 3

Layout of a bord and pillar manganese mine and the areas where monitoring was conducted. Areas 1, 2 and 3 were in the low-grade area, with a high joint density, and Areas 4 and 5 were in the high-grade areas

Full size image
Fig. 4
figure 4

A measurement cross painted on a manganese pillar. The photograph on the left was taken on 6 May 2021 and the photograph on the right on 18 August 2021. The lines were still pristine on the second date and no scaling occurred during this 3-month period

Full size image
Fig. 5
figure 5

A plan view of the pillars illustrating the measurements between the reference crosses painted on adjacent pillars

Full size image

As an alternative, another type of measurement was conducted. This was the estimated distance that the pillars have already scaled. The original position of the pillar edge against the hanging wall could be easily identified and the distance from this position to the maximum scaling depth was measured as illustrated in Fig. 6. In many cases, the scaling resulted in the pillar assuming an “hourglass” shape. Van der Merwe (2004) also found this to be the most common shape formed by the time-dependent scaling of coal pillars. The measured scaling distance for the various pillars monitored is given in Table 1. Rock mass ratings (RMR) were done on the selected pillars, but these values should be viewed as approximations only, as drill cores for each pillar was not available to do RQD ratings. The RQD was estimated along a horizontal line on the pillar edges, so it is essentially the vertical joint spacing. It was nevertheless very valuable to compare the rock mass quality of pillars in different areas.

Fig. 6
figure 6

Measurement (left) of the maximum scaling distance for pillars with an “hourglass” shape (right)

Full size image
Table 1 Measured scaling distance for the various pillars studied
Full size table

The area with the lowest pillar rock mass rating (Area 1) has the largest scaling distance. Values as large as 2 m were measured with an average value of 0.8 m. The areas of the pillars have been substantially reduced as a result and this increases the stress on the pillars and reduces the factor of safety. The pillars in Area 1 were cut during the period from March to June 2018, whereas the pillars in Areas 2 and 3 were only cut during January and February 2021, respectively. As a first crude estimate of the scaling rate of the pillars with a low rock mass rating (RMR < 50), it appears that 0.5 m of scaling occurs during the first 3 months after the pillar is formed and then another 0.3 m occurs during the next 3 years. As the time-dependent scaling is such a slow process, it explains why no prominent scaling was recorded by the authors during the short 3-month monitoring period. For the pillars with a higher rock mass rating (Areas 4 and 5), some “scaling” was also recorded based on the measurement methodology shown in Fig. 6. These pillar sidewalls appeared solid, however, and this value may simply reflect blast damage. There is also no time-dependent scaling for pillars with a high rock mass rating (RMR > 60) as the scaling distance is approximately similar for pillars of different ages.

The simulation of time-dependent pillar failure in bord and pillar layouts is a difficult numerical modelling problem. It should be noted that codes based on the finite element method (FEM) or distinct element method (DEM) can simulate the pillar scaling illustrated in Fig. 6 if an appropriate time-dependent constitutive model is used. Some examples illustrating these approaches are described in the introduction of this paper. In contrast, a displacement discontinuity boundary element approach was used for this study owing to the advantages described below. A large area needs to be simulated to accurately model the stress acting on the pillars. In these large models, it is often not practical to include the failure of pillars owing to constraints in the codes, such as the requirement of small element sizes to accurately represent the depth of failure in the pillar sidewalls. Furthermore, in hard rock bord and pillar mines, the pillar cutting is typically poor and the resulting pillar shapes are irregular. Building an accurate geometry of the layout and the irregular pillar shapes is a daunting task. As a result, three-dimensional finite element or finite difference models are seldom used to simulate bord and pillar layouts on a large scale. These codes are nevertheless valuable to simulate the failure of a single pillar and to study the detailed failure mechanisms (e.g. Sainoki and Mitri 2017). In contrast, displacement discontinuities boundary element (DD) models (e.g. Crouch and Starfield 1983; Brand and Bray 1978) overcome the problem of building the large-scale models with many pillars, but it is typically impossible for most of these codes to simulate the failure of the pillars. This problem can be circumvented by using a limit equilibrium model in a displacement discontinuity code and this is described in the next section.

The TEXAN code used in this study is a displacement discontinuity code and it was developed specifically to simulate a large number of small pillars in tabular layouts (Napier and Malan 2007). Owing to the restrictions on the number of elements that can be practically solved in TEXAN, smaller areas were simulated in detail and one of these areas are shown below. To simplify the digitising of the outlines and the meshing procedure, the pillar outlines were approximated by using straight line segments. The mined areas were covered using a triangular mesh. In terms of element sizes, the centroids of adjacent triangular elements are spaced approximately 1.5 m apart. The pillars of interest also had to be covered with a triangular mesh to enable the calculation of the APS in these pillars. Not all the pillars had to be meshed as the nature of the displacement discontinuity codes is such that any area not covered by elements is considered as solid rock material. Regarding element size, it is known that when using displacement discontinuity boundary element modelling, the average pillar stress (APS) is affected by the element size. This was explored by Napier and Malan (2011). For known analytical solutions of APS, it was found that the simulated APS approximates the analytical values closely if the element size tends to zero. Small element sizes are therefore needed for these simulations. For the purposes of this study, the 1.5 m sizes were considered adequate. The APS values for the pillars of interest were estimated using numerical modelling. These values are given in Table 1.

The parameters used for the initial simulations to determine the pillar APS values are given in Table 2. The only parameter that is different for the five areas is the depth below surface. The dip of the reef is small in this particular area (≈ 7°) and it was therefore simulated with no dip in the models for simplicity. Some uncertainty exists regarding the correct average density of the overburden and this will have an effect on the simulated APS values. This was assumed to be 3000 kg/m3 and the virgin stress k-ratio was assumed to be unity in both horizontal directions. The boundary element modelling used in this study implicitly assumes that the rock is homogenous, elastic, and isotropic. Figure 7 illustrates the simplified geometry of Area 1 used to simulate the APS values of the pillars in this area.

Table 2 Parameters used in the TEXAN code for the elastic models with rigid pillars
Full size table
Fig. 7
figure 7

Simplified geometry of Area 1 simulated with the TEXAN code. The three pillars of interest (N3_1, N3_2 and N3_9) are highlighted by the blue fill colour

Full size image

3 A Time-Dependent Limit Equilibrium Model to Simulate the Observed Behaviour

Napier and Malan (2014, 2018) describe a time-dependent limit equilibrium model to simulate the time-dependent response of the rock mass in deep gold mines. This model was explored to simulate time-dependent pillar scaling in general and the observations made regarding the manganese pillars described above.

Consider a pillar with two adjacent mined bords as illustrated in Fig. 8. The results presented here are essentially for the plane strain case of a strip pillar. The pillar is fractured on its edges and it has a solid intact core. The force equilibrium of a thin section of rock in the fractured portion of the pillar is also indicated in the figure and it is assumed that this section is in limit equilibrium. The reef normal stress is depicted by \({\sigma }_{n}\) and the reef-parallel stress by \({\sigma }_{s}\). The mining height is \(H\).

Fig. 8
figure 8

Force equilibrium of a slice of rock in a pillar

Full size image

At the contact with the hanging wall and footwall, there is a parting present. The friction angle on these interfaces are given by \(\phi\) and the coefficient of friction is \({\mu }_{I}=tan\phi\). This is one of the drawbacks of this simplified limit equilibrium model as it assumes a symmetrical model with the same friction on both contacts. The edges of the pillar will fail if the stress exceeds the rock strength. For high stress levels, the pillar may be completely fractured. Alternatively, at lower stresses, the core of the pillar may still be intact.

For this basic model, it is assumed that the material is unconfined at the edge of the pillar. For the thin section of rock to be in equilibrium, it is required that:

$$H{\sigma }_{s}\left(x+\Delta x\right)=H{\sigma }_{s}\left(x\right)+2\tau \Delta x.$$
(2)

This can be written in the form of a differential equation if the width of the slice tends to zero:

$$\underset{\Delta x\to 0}{\mathrm{lim}}\frac{{\sigma }_{s}\left(x+\Delta x\right)-{\sigma }_{s}\left(x\right)}{\Delta x}=\frac{2\tau }{H}=\frac{d{\sigma }_{s}}{\mathrm{d}x}.$$
(3)

The following assumptions are made to solve this equation. As indicated in the diagram, \(\tau\) is related to the normal stress \({\sigma }_{n}\) by the following frictional condition:

$$\tau ={\mu }_{I}{\sigma }_{n}=\mathrm{tan}\phi \left({\sigma }_{n}\right),$$
(4)

where \(\phi\) is the friction angle on the interface. A failure relationship is also assumed to relate the reef normal stress, \({\sigma }_{n}\), to the reef-parallel stress, \({\sigma }_{s}\), and this is given by:

$${\sigma }_{n}=m{\sigma }_{s}+S,$$
(5)

where \(S\) and \(m\) are specified strength constants. Once failure occurs, \(S\) can be considered as the strength of the failed pillar material and \(m\) is a slope parameter. Inserting Eqs. (4) and (5) into Eq. (3) gives:

$$\frac{\mathrm{d}{\sigma }_{s}}{\mathrm{d}x}=\frac{2\mathrm{tan}\phi }{H}\left(m{\sigma }_{s}+S\right)$$
(6)

Integration of Eq. (6) and by considering that at \(x=0\), it is known that \({\sigma }_{s}=0\), and gives the solution as:

$$\frac{\mathrm{ln}\left(m{\sigma }_{s}+S\right)}{m}=\frac{2x\mathrm{tan}\phi }{H}+\frac{\mathrm{ln}\left(S\right)}{m}.$$
(7)

This can be simplified to

$$\frac{m{\sigma }_{s}+S}{S}={{e}}^{2mx\mathrm{tan}\phi /H},$$
(8)

and from this the solution of the reef-parallel stress follows as:

$${\upsigma }_{\mathrm{s}}=\frac{\mathrm{S}}{\mathrm{m}}\left({{e}}^{2\mathrm{mxtan\phi }/\mathrm{H}}-1\right).$$
(9)

Substituting Eq. (9) into Eq. (5) gives:

$${\upsigma }_{\mathrm{n}}=\mathrm{S}{{e}}^{2\mathrm{mxtan\phi }/\mathrm{H}}.$$
(10)

Equation (10) predicts that for this simple limit equilibrium model, the normal stress increases exponentially away from the pillar edge. It should be noted that when assigning parameter values, it is a requirement that \(S>0;\) otherwise, \({\sigma }_{n}=0\) for all values of \(x\). A valid solution can also be determined, even if \(S=0\), provided a confining stress is applied at \(x=0\).

For practical implementation of this model in TEXAN, different values of the parameters \(S\) and \(m\) are adopted for intact and failed material. The current model in TEXAN provides the option to use three strength envelopes having the form of Eq. (5) (Napier and Malan 2018).

  1. 1.

    The strength of the intact rock can be defined as an unconfined strength value \({S}^{0}\) and by a slope parameter \({m}^{0}\).

  2. 2.

    Once the material fails, a strength drop is assumed to occur immediately to an initial limit strength envelope defined by intercept and slope parameters \({S}^{c}\) and \({m}^{c},\) respectively.

  3. 3.

    Once the material has failed, the strength can decay in a time-dependent manner to a residual strength envelope specified by parameters \({S}^{f}\) and \({m}^{f}\).

These strength envelopes are illustrated in Fig. 9. The initial strength drop does not occur if \({S}^{0}={S}^{c}\) and \({m}^{0}={m}^{c}\). Similarly, no time-dependent strength decay occurs if \({S}^{c}={S}^{f}\) and \({m}^{c}={m}^{f}\).

Fig. 9
figure 9

Different reef strength envelopes adopted for the time-dependent limit equilibrium model

Full size image

The transition between the initial limit strength and the residual limit strength envelopes is assumed to be governed by a strength decay function \(F(\tau )\) that depends on the elapsed time \(\tau =t-T(x)\) between the current time t and the initial time of failure, \(T(x)\), at point \(x\). The model assumes the following (Napier and Malan 2018):

$$S\left(t\right)={S}^{f}+F\left(t-T\left(x\right)\right)\left({S}^{c}-{S}^{f}\right),$$
(11)
$$m\left(t\right)={m}^{f}+F\left(t-T\left(x\right)\right)\left({m}^{c}-{m}^{f}\right).$$
(12)

It is assumed that \(F(\tau )=1\) if \(\tau <0\) and that \(F(\tau )\) is a simple exponential function of the form:

$$F\left(\tau \right)={\left(\frac{1}{2}\right)}^{\frac{\tau }{\lambda }}={e}^{-\alpha \tau },$$
(13)

when \(\tau \ge 0\). \(\lambda\) is a half-life parameter. For Eq. (13):

$$\mathrm{ln}{\left(\frac{1}{2}\right)}^{\frac{\tau }{\lambda }}=\mathrm{ln}\left({e}^{-\alpha \tau }\right),$$
(14)

which is:

$$\frac{\tau }{\lambda }\mathrm{ln}\left(\frac{1}{2}\right)=-\alpha \tau .$$
(15)

This can be simplified to give the exponential decay exponent as:

$$\lambda =\frac{\mathrm{ln}\left(2\right)}{\alpha }.$$
(16)

This choice of exponential decay model for the rock is supported by the work presented in Malan and Napier (2018). They recorded and simulated time-dependent closure profiles in gold mine stopes. Exponential decay is also very common in nature of which the well-known example is radioactivity.

To obtain some insight into the model, Eq. (11) was plotted using the parameters \({S}^{f}=5\mathrm{ MPa}\) and \({S}^{0}=50\mathrm{ MPa},\) where \(t\) is in months. It was assumed that \(T\left(x\right)=0\). Figure 10 illustrates \(\mathrm{S}\left(t\right)\) against \(t\) (months). The effect of the half-life parameter (strength decay) is illustrated. This indicates that as the half-life parameter increases, the parameter \(S\left(\mathrm{t}\right)\) will be larger over the short term than for a smaller half-life value. A larger half-life value therefore leads to a slower reduction in strength and a slower rate of scaling when considering Fig. 10.

Fig. 10
figure 10

The time-dependent reduction in the value of the “intercept” parameter for different values of half-life

Full size image

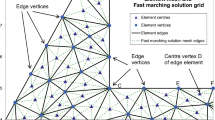
It should be noted that the model described above is for the assumed one-dimensional variation of the limit stress as a function of the distance to edge of the pillar. The more general case of stress variation in two-dimensional tabular layout geometries is described in Napier and Malan (2021) and the TEXAN code uses a special fast marching solution technique to determine the seam-parallel gradient direction in the case of general pillar shapes that are tessellated using unstructured triangular element meshes.

4 Simulation of Pillar Scaling Using the Limit Equilibrium Model

The scaling of the pillars in the different geotechnical areas was simulated using the limit equilibrium model described above. For the preliminary simulations, no time-dependent scaling was included. A key objective of this modelling was to understand if a preliminary calibration of the limit equilibrium model can simulate the distinctly different pillar behaviours in the different geotechnical areas. Similar to other inelastic models, the limit equilibrium model in TEXAN requires a large number of parameters to be calibrated and these are listed in Table 3. The number of parameters increases further if time-dependent behaviour is considered and this is discussed in the next section.

Table 3 Parameters used for the limit equilibrium model
Full size table

A preliminary calibration of the parameters was done as follows: Napier and Malan (2021) studied an experimental pillar mining section with a number of intact and failed pillars in a platinum mine. They conducted a number of simulations with different parameters until a good fit with the underground observations was obtained. These parameters were used as a starting point in this current study, except for specifying the much larger reef height of 5.5 m for the manganese pillars. These preliminary parameters gave surprisingly good results for the areas with significant scaling (e.g. Area 1 and 6) and then as a next step, for Areas 4 and 5, the intact strength intercept, \({S}_{0}\), was increased until the absence of scaling observed underground was also reflected in the model. The failed and intact pillars are shown in Figs. 11 and 12. This is correct as the model reflect the extensive scaling in Area 1 and the intact pillars in Area 4. The only difference in the calibrated values was that \({S}_{0}\) = 60 MPa was used for the areas with signficiant scaling and \({S}_{0}\) = 85 MPa was used for the areas with no scaling (Table 3). This seems intuitively correct as the spacing of the joint sets will affect the intact rock mass strength and a closer joint spacing will result in a lower strength. These models illustrate qualitatively the value of this limit equilibrium model, but it also highlights the difficulty of calibration of the parameters. If, for example, the slope and residual strength parameters are modified, a different intact strength intercept value will be required to match the observations. Additional work to calibrate the parameters will have to be done in future. This will require an in-depth investigation and is beyond the scope of this current study.

Fig. 11
figure 11

Simulation of the pillars using the limit equilibrium model in TEXAN for Area 1. Only the pillars of interest are shown in this plot. The red dots are the collocation points of the failed elements and the grey dots are the collocation points of the intact elements

Full size image
Fig. 12
figure 12

Simulation of the pillars using the limit equilibrium model in TEXAN for Area 4. Only the pillars of interest are shown in this plot and the grey dots are the collocation points of the intact elements

Full size image

5 Simulation of Time-Dependent Pillar Scaling

As an initial geometry to test the time-dependent limit equilibrium model, a small idealised layout consisting of twenty-five pillars was simulated (Fig. 13). The standard pillar and bord dimensions at the mine were used. Three different types of simulations using the idealised layout were conducted. For the first set of simulations, no immediate strength drop was assumed and therefore \({S}^{0}={S}^{c}\) and \({m}^{0}={m}^{c}\) (see Fig. 9). This was used to illustrate the effect of the half-life parameter on the time-dependent fracturing of the pillars. For the second set of simulations, an immediate strength drop of 40 MPa after failure was assumed in an attempt to better simulate the higher rate of scaling early in the life of the pillars. For the third set of simulations, the limit equilibrium parameters were modified in an attempt to fit the rate of scaling observed underground. Small triangular elements were used for these models and each 7 m × 7 m pillar contained 574 elements. This is an average element size of 0.085 m2. The large number of elements and the required time steps for the time-dependent model resulted in very long run times.

Fig. 13
figure 13

The simple idealised pillar geometry used to test the time-dependent limit equilibrium model

Full size image

The parameters in Table 4 were adopted for the first set of simulations. The time-dependent limit equilibrium model resulted in the gradual failure of the pillars. This is illustrated in Fig. 14 for pillar A (see Fig. 13). The larger half-life values resulted in a slower rate of “scaling” of the pillar. Of significance is that after a period of time, the rate of scaling becomes very slow and this qualitatively agrees with the limited data collected underground.

Table 4 Parameters used for the time-dependent limit equilibrium model with no immediate strength drop
Full size table
Fig. 14
figure 14

Progressive failure of the pillar A for different values of λ. The fraction of the pillar that failed was simply the number of failed elements divided by the total number of elements in the pillar

Full size image

For the second set of simulations, an immediate strength drop was used to simulate the more rapid scaling of the pillars immediately after they are formed. This may be blasting damage and nearby blasting, as the faces move away, and may cause the blocky scaling to dislodge from the pillars (Fig. 15). An arbitrary strength drop of 40 MPa was used. The parameter values were therefore similar to those in Table 4, except that \({S}^{c}=10\mathrm{ MPa}\).

Fig. 15
figure 15

Progressive failure of the pillar A for different values of λ. For this simulation, there was an immediate strength drop of 40 MPa

Full size image

From the data of scaling distance presented in Table 1, the fraction of each pillar which was failed was calculated. The standard planned pillar size of 7 m × 7 m was used for this calculation, so it is only an estimation. The data is illustrated in Fig. 16 (blue dots) and plotted as a function of the age of the pillar. Only the approximate age of the pillars was known and therefore the data seems to be stacked in columns. There is no clear trend in the data, except that it seems that the amount of pillar scaling does increase with time. A numerical solution of the progressive failure of a pillar was fitted to this data using a trial and error approach. A number of parameters were tested. The best fit parameters are given in Table 5. Note that the model with the initial strength drop seems to be at least a reasonable approximation of the data. As future work, additional data needs to be collected from underground to obtain a better understanding of the rate of scaling. This can then be simulated as further verification of the model.

Fig. 16
figure 16

Progressive failure of the pillars as a function of time

Full size image
Table 5 Parameters used to obtain the numerical modelling results illustrated in Fig. 16
Full size table

6 Conclusions

A limit equilibrium model to simulate the time-dependent scaling of hard rock pillars in bord and pillar layouts is proposed in this study. A case study of pillar scaling in a manganese mine is presented. Extensive scaling is observed for pillars in areas where there are many intersecting joint sets with a small spacing between the joints. It appears that the scaling occurs in a time-dependent fashion. Evidence for this is the ongoing deterioration of pillars in old areas, even after they were reinforced with thin spray-on liners.

Monitoring of selected pillars were conducted in an attempt to quantify the rate of time-dependent scaling. Contrary to expectations, almost no additional scaling was recorded for the pillars during a 3-month monitoring period. The existing extent of scaling for pillars of different ages could be measured and it seems as if most of the scaling occurred soon after the pillars are formed. Only a limited amount of additional time-dependent scaling seems to occur after this.

Numerical simulations of the time-dependent scaling were conducted using the TEXAN displacement discontinuity code. It allows for the use of a limit equilibrium constitutive model to simulate on-reef failure. An exponential decay of the failed rock mass strength at the edges of the pillars resulted in simulated time-dependent failure that is qualitatively similar to the underground observations. The value of this model is that mine-scale simulations can easily be conducted and the time-dependent failure of the pillars can now be included in these studies. The long-term stability of old mining sections can therefore be investigated.

This work focused on hard rock pillars, but this model can also be used for coal mines to simulate the progressive weakening of coal pillars. The necessary calibration of the limit equilibrium model for the coal pillars will have to be conducted, however.

Although this model gave encouraging results, further work is required and this is listed below:

  • A more precise calibration of the limit equilibrium model is required. This should possibly involve laboratory work to determine rock strengths and friction angles of the manganese ore. A physical model in the laboratory may be valuable to test the applicability of this constitutive model and to gain an improved understanding of the various parameters.

  • It is not clear if the limit equilibrium model is a good approximation of the pillar failure mechanism at the manganese mines. The failure is controlled by the various intersecting joint sets and these form small blocks that facilitate the scaling. This mechanism should be simulated using a distinct element code and the results should be compared to those provided by a limit equilibrium model in a displacement discontinuity code.

  • Underground monitoring of the time-dependent scaling of the pillars should be conducted over a longer period of time. Regular monitoring should be conducted, especially when the new pillars are still close to the face, to determine if the nearby blasting contributes to the scaling. From this data, the rate of scaling can hopefully be more accurately determined.