Anisotropic Poroelastic Modelling of Depletion-Induced Pore Pressure Changes in Valhall Overburden

Abstract

Stress and pore pressure changes due to depletion of or injection into a reservoir are key elements in stability analysis of overburden shales. However, the undrained pore pressure response in shales is often neglected but needs to be considered because of their low permeability. Due to the anisotropic nature of shales, the orientation of both rock and stresses should be considered. To account for misalignment of the medium and the stress tensor, we used anisotropic poroelasticity theory to derive an angle-dependent expression for the pore pressure changes in transversely isotropic media under true-triaxial stress conditions. We experimentally estimated poroelastic pore pressure parameters of a shale from the Lista formation at the Valhall field. We combined the experimental results with finite element modelling to estimate the pore pressure development in the Valhall overburden over a period of nearly 40 years. The results indicate non-negligible pore pressure changes several hundred meters above the reservoir, as well as significant differences between pore pressure and effective stress estimates obtained using isotropic and anisotropic pore pressure parameters. We formulate a simple model approximating the undrained pore pressure response in low permeable overburden. Our results suggest that in the proximity of the reservoir the amplitude of the undrained pore pressure changes may be comparable to effective stresses. Combined with the findings of joint analysis of locations of casing deformation and total and effective stresses, the results suggest that pore pressure modelling may become an important element of casing collapse and caprock failure risk analysis and mitigation.

Highlights

• We propose a workflow for pore pressure change modelling in shales based on the anisotropic poroelasticity theory,

• Modeling of Valhall oil field overburden indicates significant pore pressure changes a few hundred meters above the producing reservoir,

• Pore pressure changes predicted using anisotropic and isotropic poroelastic parameters differ significantly in magnitude and spatial distribution,

• Pore pressure changes in anisotropic shales can be approximated with the use of a single poroelastic parameter and vertical stress changes,

• Results suggest that the undrained pore response modelling could become a useful tool for casing collapse risk analysis and mitigation.

1 Introduction

In a typical geological storage or petroleum system, fluids in the reservoir are prevented from migrating toward the surface by low permeability cap rocks, such as shales (e.g., Magoon and Dow 1994). Low permeability of sealing formations hinders upward fluid movement, and, therefore, limits direct diffusive pore pressure equilibration. Pressurization or depletion of a reservoir changes the pore pressure, and hence the effective stresses in the reservoir itself, and the reservoir deformation consequently changes the stresses in its surroundings (e.g.,Geertsma 1973; Hall et al. 2002; Kenter et al. 2004; de Gennaro et al. 2008; Herwanger and Koutsabeloulis 2011). This may result in pore pressure changes in the reservoir’s low-permeability surroundings caused by their undrained response to the stress changes. Undrained pore pressure responses have been studied and quantified using empirical parameters for several decades (e.g.,Skempton 1954; Henkel 1960; Henkel and Wade 1966; Janbu et al. 1988). They are also consistent with fundamental poroelasticity theory (e.g., Biot 1941, Detournay and Cheng 1993, Fjær et al. 2021).

In this paper we will focus on pore pressure changes in overburden shales. This broad class of sediments is usually characterized by permeabilities in the nano-Darcy range (e.g.,Howard 1991; Best and Katsube 1995; Schlömer and Krooss 1997; Katsube 2000; Goral et al. 2020) and commonly exhibits transversely isotropic behavior (i.e., physical properties symmetric about an axis normal to a plane of isotropy), both in terms of their seismic (e.g.,Levin 1979; White et al. 1983; Banik 1984; Brocher and Christensen 1990; Johnston and Christensen 1995) and poroelastic static properties (e.g.,Holt et al. 2018a, 2018b; Duda et al. 2021; Soldal et al. 2021). Although increasingly studied under laboratory conditions, the impact of the poroelastic anisotropy of shales on reservoir-scale geomechanical modelling remains largely unknown. It may prove to be an important factor for modelling the safety of CO₂ storage and hydrocarbon production in circumstances, where stresses are commonly found to approach the upper crust’s strength limits (Townend and Zoback 2000) and even small effective stress changes may activate faults (Nicholson and Wesson 1990; McGarr et al. 2002; Ellsworth 2013).

The aim of this study is to show the importance of the anisotropic undrained pore pressure response in modelling the development of effective stress, caused by reservoir depletion or pressurization, in low permeability rocks, and to offer a method to approximate the undrained pore pressure response in anisotropic low permeability overburden using limited number of input parameters. To achieve that aim, we model pore pressure changes in the overburden of the Valhall field located in the Norwegian sector of the North Sea. First, we use anisotropic poroelasticity theory (Thompson and Willis 1991; Cheng 1997) to establish a link between changes in a fully three-dimensional stress state, anisotropic pore pressure parameters, and the angular relationship between the principal directions of their corresponding tensors. Then, we analyze results of laboratory experiments that provide a set of poroelastic pore pressure parameters of an overburden shale cored from the Lista formation directly above a hydrocarbon reservoir at the Valhall field. Next, we use the Valhall reservoir and overburden geometry, and corresponding finite-element stress modelling results provided by the field operator (AkerBP), to approximate the pore pressure and the effective stress changes in the proximity of the reservoir over a period of nearly 40 years (1982–2020). Finally, we compare predictions made using anisotropic and isotropic pore pressure coefficients with approximated results obtained solely with a single poroelastic pore pressure parameter (describing pore pressure response to changing stress along symmetry axis of the medium) and vertical stress change.

2 Theory

Skempton (1954) derived Eq. (1) to describe the pore pressure changes in soils tested in undrained conditions:

$$\Delta p_{\text{f}} = B_{\text{S}} \left[ {\Delta \sigma_{{\text{RAD}}} + A_{\text{S}} \left( {\Delta \sigma_{{\text{AX}}} - \Delta \sigma_{{\text{RAD}}} } \right)} \right],$$

(1)

where $p_{\text{f}}$ is pore pressure, $B_{\text{S}}$ and $A_{\text{S}}$ are Skempton’s pore pressure parameters, and $\sigma_{{\text{AX}}}$ and $\sigma_{{\text{RAD}}}$ are axial and radial (in relation to the geometry of a cylindrical sample and its orientation in an experimental setup) stresses. Skempton (1954) assumed that deviations of $A_S$ from 1/3 (the value given by isotropic linear elasticity) are caused by deviations from a strictly elastic material deformation. Cheng (1997) demonstrated that Skempton’s parameters can also be derived from anisotropic poroelasticity. Holt et al. (2017) applied this approach for vertically transversely isotropic (VTI) shales and proved experimentally that the value of $A_S$ depends on the angle $\theta$ between the direction of axial stress applied to a sample and the symmetry axis of a transversely isotropic medium. Here, the pore pressure parameters $B_S$ and $A_S$ are expressed in terms of poroelastic constants, $B_{11}$ and $B_{33}$(defined in the Appendix A), describing the properties of the medium within the symmetry plane and along the symmetry axis, respectively:

$$B_{\text{S}} = \frac{{2B_{11} + B_{33} }}{3},$$

(2)

$$A_{\text{S}} = \frac{{B_{11} \sin^2 \theta + B_{33} \cos^2 \theta }}{3B_S }.$$

(3)

In our work, we use the poroelastic pore pressure parameters from the tensor ${\varvec{B}}$ and the stress change tensor $\Delta {\varvec{\sigma}}$ (Eqs. 4 and 5), to describe the impact of all three principal stress changes on the undrained pore pressure response in transversely isotropic shales. The tensors of transversely isotropic poroelastic pore pressure parameters and stress changes along their respective principal directions are

$${\varvec{B}} = \left[ {\begin{array}{*{20}c} {B_{11} } & 0 & 0 \\ 0 & {B_{11} } & 0 \\ 0 & 0 & {B_{33} } \\ \end{array} } \right],$$

(4)

$$\Delta {\varvec{\sigma}} = \left[ {\begin{array}{*{20}c} {\Delta \sigma_{11} } & 0 & 0 \\ 0 & {\Delta \sigma_{22} } & 0 \\ 0 & 0 & {\Delta \sigma_{33} } \\ \end{array} } \right]$$

(5)

The above stress change tensor is defined as a difference between the final and the initial principal stress tensors:

$$\Delta {\varvec{\sigma}} = {\varvec{\sigma}}^{{\text{final}}} - {\varvec{\sigma}}^{{\text{initial}}}$$

(6)

The relationship between the two tensors is given by Cheng (1997)

$$\Delta p_f = \frac{1}{3}B_{ij} \Delta \sigma_{ij}$$

(7)

Equation (7) assumes that the tensors ${\varvec{B}}$ and ${\varvec{\sigma}}$ share the same axes. However, in the reality these tensors may be misaligned, and require rotation to align them. During modeling, we estimate the orientation of the material’s principal directions (coinciding with the principal directions of the poroelastic tensor ${\varvec{B}}$) from the geometry of the layering and compare it with the orientation of the principal stresses. For that purpose, we assume that the symmetry axis of the medium (rock) at a given location is normal to the interface defined in the geomechanical model. Principal stresses, their magnitude and directions, are estimated by computing eigenvectors and eigenvalues of an arbitrarily oriented stress tensor. In most available software packages (including Python’s NumPy library that we used) eigenvalues are then arranged along the diagonal of the tensor in ascending order according to their values, i.e., $\sigma_{33}^S$ and $\vec{S}_3$ describe the largest of the principal stresses.

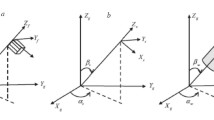
We describe the spatial orientation of the principal directions of the two tensors by defining their frames in the coordinates of an external geo-reference system XYZ (easting, northing and depth) composed of unit vectors: ${\varvec{M}}$ for medium properties and ${\varvec{S}}$ for stresses (Fig. 1):

$${\varvec{M}} = \left\{ {\vec{M}_1 ,\vec{M}_2 ,\vec{M}_3 } \right\} = \left\{ {\left[ {m_{11} ,m_{12} ,m_{13} } \right],\left[ {m_{21} ,m_{22} ,m_{23} } \right],\left[ {m_{31} ,m_{32} ,m_{33} } \right]} \right\},$$

(8)

$${\varvec{S}} = \left\{ {\vec{S}_1 ,\vec{S}_2 ,\vec{S}_3 } \right\} = \left\{ {\left[ {s_{11} ,s_{12} ,s_{13} } \right],\left[ {s_{21} ,s_{22} ,s_{23} } \right],\left[ {s_{31} ,s_{32} ,s_{33} } \right]} \right\}.$$

(9)

Fig. 1

Orientation of the medium (frame ${\varvec{M}}$) and the principal stress tensor (frame ${\varvec{S}}$), relative to the geo-reference system (XYZ). The rotation angles α (rotation around $\vec{S}_3$) and β (around $\vec{n}$) are needed to move the stress tensor frame ${\varvec{S}}$ to the orientation of the medium, ${\varvec{M}}$. Planes $\vec{S}_1 - \vec{S}_2$and $\vec{M}_1 - \vec{M}_2$ are marked for better visualization of the vector orientations

In the case of a vertically transversely isotropic medium, the orientation of vectors $\vec{M}_1$ and $\vec{M}_2$ is arbitrary and serves only to define their shared isotropic plane. If the symmetry class of the medium was to be modified, e.g., to orthorhombic or monoclinic due to creation of cracks, all symmetry axes would need to be defined more thoroughly.

The next step is to rotate the stress tensor frame ${\varvec{S}}$ to the orientation of the medium frame ${\varvec{M}}$ using Euler passive rotations according to the right-hand convention. First, we rotate the stress tensor frame around vector $\vec{S}_3$ by angle $\alpha$ (Fig. 1b), so that vector $\vec{S}_1$ coincides with the so-called lines of nodes $\vec{n}$ given by the following equation:

$$\vec{n} = \vec{S}_3 \times \vec{M}_3 .$$

(10)

Then, we rotate the stress frame around $\vec{n}$ by angle $\beta$ (Fig. 1c). The rotation angles are given by a dot-product of the pair of vectors they relate which yield

$$\alpha_V = \cos^{ - 1} \left( {\frac{{\vec{S}_1 \cdot \vec{n}}}{{\left| {\vec{n}} \right|}}} \right),$$

(11)

$$\beta_V = \cos^{ - 1} \left( {\vec{S}_3 \cdot \vec{M}_3 } \right).$$

(12)

The rotation angles are confined to − 180° < $\alpha$ < 180° and 0 < $\beta$ < 180°. If the initial stress tensor has a frame aligned with the external coordinate system (i.e., $s_{ij}$ = $\delta_{ij}^{{\text{Kronecker}}}$), the expressions for the rotation angles simplify to

$$\alpha_V = \cos^{ - 1} \left( {\frac{{m_{32} }}{{\sqrt {1 - m_{33}^2 } }}} \right),$$

(13)

$$\beta_V = \cos^{ - 1} \left( {m_{33} } \right).$$

(14)

This step can yield angles representing rotations around the actual rotation axes, as well as around their negative vectors (e.g., $\vec{S}_3$ and − $\vec{S}_3$). This may be verified by the cross-product of the rotated and objective vectors (e.g., $\vec{S}_1$ rotated by $\alpha$ to $\vec{n}$) scaled by product of their magnitudes, and eventually corrected by multiplying the rotation angle by -1, as shown for angle $\alpha_V$ in the following equation:

$$\alpha = \left\{ {\begin{array}{*{20}c} {\alpha_V \quad \;\;{\text{if}}\quad \;\frac{{\vec{S}_1 \times \vec{n}}}{{\left| {\vec{S}_1 } \right|\left| {\vec{n}} \right|\sin \alpha_V }} = \vec{S}_3 ,} \\ { - \alpha_V \quad \;\;{\text{if}}\quad \;\frac{{\vec{S}_1 \times \vec{n}}}{{\left| {\vec{S}_1 } \right|\left| {\vec{n}} \right|\sin \alpha_V }} = - \vec{S}_3 .} \\ \end{array} } \right.$$

(15)

To avoid problems related to the number precision limitations, we correct the rotations angles according to the sign of the expression (15), rather than its exact value—assuming $\vec{S}_3$ = [0,0,1], as in Eqs. (13) and (14), the conditions become

$$\alpha = \left\{ {\begin{array}{*{20}c} {\;\;\alpha_V \quad \;\;{\text{if}}\quad \;\frac{{m_{31} }}{\sin \alpha_V } > 0,} \\ { - \alpha_V \quad \;\;{\text{if}}\quad \;\frac{{m_{31} }}{\sin \alpha_V } < 0.} \\ \end{array} } \right.$$

(16)

Mathematically, the frame rotations are expressed by rotation matrices:

$${\varvec{R}}_3 \left( \alpha \right) = \left[ {\begin{array}{*{20}c} {\cos \alpha } & { - \sin \alpha } & 0 \\ {\sin \alpha } & {\cos \alpha } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],$$

(17)

$${\varvec{R}}_1 \left( \beta \right) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \beta } & { - \sin \beta } \\ 0 & {\sin \beta } & {\cos \beta } \\ \end{array} } \right].$$

(18)

For this type of rotation, the cumulative intrinsic ("moving body") rotation matrix is

$${\varvec{R}}\left( {\alpha ,\beta } \right) = {\varvec{R}}_1 \left( \beta \right)^T {\varvec{R}}_3 \left( \alpha \right)^T = \left[ {\begin{array}{*{20}c} {\cos \alpha } & {\sin \alpha } & 0 \\ { - \sin \alpha \cos \beta } & {\cos \alpha \cos \beta } & {\sin \beta } \\ {\sin \alpha \sin \beta } & { - \cos \alpha \sin \beta } & {\cos \beta } \\ \end{array} } \right].$$

(19)

Then, we are ready to rotate the principal stress tensor (${\varvec{\sigma}}^S$) into the medium frame (${\varvec{\sigma}}^M$):

$${\varvec{\sigma}}^M = {\varvec{R}}\left( {\alpha ,\beta } \right){\varvec{\sigma}}^{\varvec{S}} {\varvec{R}}\left( {\alpha ,\beta } \right)^T .$$

(20)

Now, we rotate stress tensors representing the stress state before and after the change in stress (caused by fluid injection or drainage operation) was introduced. The angles $\alpha$ and $\beta$ need to be estimated separately for the two stress tensors to account for potential stress state rotation.

Such changes of the principal stress directions in the reservoir and its overburden may be caused by depletion- or injection-related arching effects (e.g., Geertsma 1973; Segall and Fitzgerald 1998; Rudnicki 1999; Fjær et al. 2021). This is of relevance for soft, strongly compacting reservoirs (such as Ekofisk or Valhall) having quite non-uniform spatial patterns (Kristiansen and Plischke 2010). Principal stress rotation can be also caused by stress concentrations and re-alignment in proximity of faults and fractures during hydrocarbon production (e.g., Zoback 2007; Han et al. 2015), response to high-rate injections (e.g., Martínez-Garzón et al. 2013, 2014, Schoenball et al. 2014, Ziegler et al. 2017) or large earthquakes (e.g., Hardebeck and Hauksson 2001; Bohnhoff et al. 2006; Ickrathet al. 2015).

An alternative approach would be to use geo-referenced stress tensor (stresses measured along the external X, Y and Z directions) instead of principal stress tensor as the starting points of the rotation procedure. In this case, the initial stress tensors have nine non-zero elements. On the other hand, the orientation of the tensor frames is identical, and hence only one set of rotation angles is needed to rotate both the initial and the final stress tensors.

Finally, we can insert the expression for stresses obtained in Eq. (20) into Eq. (7):

$$\Delta p_{\text{f}} = \frac{1}{3}B_{ij} \left( {\sigma_{ij}^{M,{\text{final}}} - \sigma_{ij}^{M,{\text{initial}}} } \right).$$

(21)

For a transversely isotropic elastic medium with the stress tensor initially aligned with its constant principal stress directions (i.e., not changing during loading or unloading, as in typical laboratory conditions), Eq. (21) takes the form:

$$\begin{gathered} \Delta p_f = \frac{1}{3}\left( {\Delta \sigma_{11}^S } \right.\left[ {2B_{11}^M + B_{33}^M } \right] \\ + \left[ {\Delta \sigma_{33}^S - \Delta \sigma_{11}^S } \right]\left[ {B_{11}^M \sin^2 \beta + B_{33}^M \cos^2 \beta } \right] \\ + \left[ {\Delta \sigma_{22}^S - \Delta \sigma_{11}^S } \right]\left. {\left[ {B_{11}^M \sin^2 \alpha + B_{33}^M \cos^2 \alpha + \left\{ {B_{11}^M - B_{33}^M } \right\}\cos^2 \alpha \cos^2 \beta } \right]} \right). \\ \end{gathered}$$

(22)

Alternatively, Eq. (22) can be expressed in terms of Skempton-like parameters:

$$\Delta p_f = \overline{B}\left( {\Delta \sigma_{11}^S + A_{3 - 1} \left[ {\Delta \sigma_{33}^S - \Delta \sigma_{11}^S } \right] + A_{2 - 1} \left[ {\Delta \sigma_{22}^S - \Delta \sigma_{11}^S } \right]} \right),$$

(23)

where $\overline{B}$, $A_{3 - 1}$ and $A_{2 - 1}$ are defined as

$$\overline{B} = \frac{{2B_{11}^M + B_{33}^M }}{3},$$

(24)

$$A_{3 - 1} = \frac{{B_{11}^M \sin^2 \beta + B_{33}^M \cos^2 \beta }}{{3\overline{B}}},$$

(25)

$$A_{2 - 1} = \frac{{B_{11}^M \sin^2 \alpha + B_{33}^M \cos^2 \alpha + \left( {B_{11}^M - B_{33}^M } \right)\cos^2 \alpha \cos^2 \beta }}{{3\overline{B}}}.$$

(26)

Here, parameter $A_{3 - 1}$ is equivalent to $A_S$ from Eq. (3), whereas parameter $A_{2 - 1}$ is an expansion to Skempton (1954), capturing the impact of the third principal stress (when elasticity is assumed). These Skempton-like parameters allow us to maintain the clarity of the original Eq. (1) and may serve as a useful tool to describe the impact of the shear stress changes on the undrained pore pressure response. The impact of $\Delta \sigma_{33}^S - \Delta \sigma_{11}^S$, controlled by parameter $A_{3 - 1}$, depends only on $\beta$, i.e., the angle between the direction of the principal stress $\sigma_{33}^S$ ($\vec{S}_3$) and the symmetry axis of the medium ($\vec{M}_3$). The angle-dependence of the impact of $\Delta \sigma_{22}^S - \Delta \sigma_{11}^S$ on the undrained pore pressure response, scaled by $A_{2 - 1}$, is more nuanced and depends on both $\alpha$ and $\beta$.

Once the pore pressure parameters have been estimated from experimental data, the undrained pore pressure response obtained with Eq. (22) can be compared with results given by Eq. (1) under assumption of linear isotropy of the medium, i.e., with $A$ = 1/3. Proper identification of the symmetry class of the medium and determination of the pore pressure parameters can have a large impact on the estimation of the Terzaghi effective stresses $\sigma^{\prime}_{ii}$ (commonly used in the context of rock failure):

$$\sigma^{\prime}_{ii} = \sigma_{ii} - p_f .$$

(27)

Here, pore pressure shifts the stress state described using a Mohr circle without changing its radius. In the case of stress changes different from hydrostatic ($\Delta \sigma_{11}^M$ = $\Delta \sigma_{22}^M$ = $\Delta \sigma_{33}^M$), the undrained pore pressure response in anisotropic media can be significantly different from that predicted using the isotropic Skempton’s parameter. Consequently, the distance between the Mohr circle and a potential failure envelope can be smaller than anticipated, as shown schematically in Fig. 2 (for more details see Duda et al. 2022). This can strongly affect stability assessment of media of interest and in a field scenario can potentially lead to increased problems during drilling and with the integrity of existing wells, or to fault reactivation. Alternatively, an overestimation of $\Delta p_f$ may give a narrower acceptable mud weight window, and, therefore, rule out some reasonable well-planning scenarios.

Fig. 2

Mohr circle predicted by the anisotropic (blue) and the isotropic (brown) pore pressure parameters for Lista overburden shale loaded with 2 MPa in the direction along the symmetry axis and unloaded by 1 MPa along the symmetry place direction. The applied stress path (constant mean stress) is consistent with predictions given for the overburden by Geertsma (1973)

3 Experiments

The material used in this study originates from a borehole drilled at the Valhall oilfield. The reddish-brown shale was cored at measured depths of 2890–2900 m in the Lista formation, several meters above the chalk reservoir itself (for more details on the stratigraphy of the field, see, e.g., Kristiansen 2007).

Initially, the core was stored in the original core liner with oil-base drilling mud, and then cut into 1 m sections and placed into a cylinder filled with base-oil and sealed with end caps. Once it arrived to our laboratory, the drilling fluid was wiped off and the core was stored in Marcol-82 (chemically inert purified mixture of liquid saturated hydrocarbons) in a closed container to avoid any changes to its water content (Ewy 2015, 2018; Wild et al. 2017; Giger et al. 2018). The chemical composition of the pore fluid was determined to avoid artifacts associated with osmotic effects during experiments (Mazurek et al. 2015). A cylindrical sample of 38.1 mm in diameter and 50 mm in length was placed inside an oedometer and compressed axially while collecting the effluent in syringes from the end pistons. Axial stress exerted on the sample was held at 10 MPa for 5 days and at 15 MPa for another 10 days—this allowed us to collect approximately 1.5 ml of the pore fluid which was sent to the Institute of Geological Sciences at the University of Bern, Switzerland for ion chromatography and inductively coupled plasma-optical emission spectrometry analysis to quantify its ionic content. The results of these analyses served as a basis for the preparation of a brine compatible with the pore fluid in its physical and chemical properties, which we used as an analogue fluid in the pore pressure lines in our main experiment.

The porosity of the rock was determined to be 31%. To estimate this value we selected a sample of the core neighboring the location of the plug used in the triaxial test, weighed it and estimated its volume (using Archimedes principle). Then, the sample was heated to 105 ℃ for 15 days. Finally, the sample was weighed again, and its porosity was estimated from the weight loss (associated with water content loss) under assumption of full water saturation prior to heating. Assuming a homogenous porosity distribution in the section of the core we had chosen for testing, the cylindrical sample of 25.5 mm in diameter and 51.6 mm in length used in the triaxial test contained approximately 8.1 ml of pore fluid. The sample was drilled perpendicularly to the bedding, i.e., the lamination-related symmetry axis of the medium ($\vec{M}_3$) was parallel to the geometrical long axis of the sample. During coring and end-grinding the sample was kept oil wet with Marcol-82, which was used as a circulation and cooling fluid, to avoid any changes to the pore fluid content. The sample was installed inside a Viton sleeve with radial drains to allow drainage along the sides of the plug, and hence to increase the consolidation rate and in consequence shorten the duration of the experiment.

The test was conducted using a triaxial apparatus consisting of a load frame and pressure vessel (for more details, see Bakk et al. 2020). In the pressure vessel the sample was exposed to an isotropic external pressure exerted by fluid, and an axial differential stress was applied with an axial actuator. The pore pressure was controlled using a hydraulic servo-controlled pressure intensifier and pore fluid lines were connected to both end-pistons. The pore pressure measurements were taken outside the pressure cell near the in- and outlets of the pore fluid lines. The estimated dead volume of the pore fluid system was significantly lower than the estimated pore volume (0.7 and. 8.1 ml, respectively), which gives us confidence in the measured values of pore pressure change. Axial strain was measured with a set of three evenly azimuthally distributed linear variable differential transformers (LVDTs). Radial strain was measured in two orthogonal directions using strain-gauged extensometers (cantilevers) in contact with the sample at its mid-height through metal pins penetrating the sleeve. The reported values of strains are the averages of the values given by the set of sensors measuring deformation in corresponding directions. Temperature was measured inside the pressure cell during the entire experiment to check for temperature variations that would impact the observed pore pressure changes.

After instrumentation and after the sample was installed in the pressure vessel, a nominal confining pressure of 2 MPa was established. The analog brine was introduced and about 60 ml was passed along the sample through the side drains, while confining pressure was automatically adjusted by the control system to maintain the isochoric boundary condition. Then, the back pressure in the pore pressure line was increased to 2 MPa and approximately 30 ml of the analog brine was flowed along the sample to ensure removal of any trapped air. During this saturation stage (24 h), the confining pressure increased to 29.2 MPa, while pore pressure was kept at 2 MPa. After approx. 4 days the estimated in-situ stress and pore pressure were established (total stresses of 49.8 MPa in radial and 54.4 MPa in axial directions,, and a pore pressure of 44.4 MPa). The sample was left for 6 days to consolidate. This resulted in a swelling of − 7 millistrain radially and − 8 millistrain axially. The estimates of initial in-situ conditions were provided by the operating company.

During this initial stage of the experiment, we determined the allowable axial strain rate from the consolidation coefficient (Head and Epps 2011). Once the system stabilized at the initial in-situ stress and pore pressure levels, four low-amplitude axial stress (1 MPa) and one confining pressure (3 MPa) undrained unloading–reloading cycles were carried out to ensure proper positioning and alignment of the sample inside the cell and to investigate possible stress-dependence of the amplitude of the pore pressure response.

The main undrained part of the experiment consisted of four further unloading–reloading cycles (Fig. 3).

Fig. 3

Main undrained part of the multistage stress loading–unloading experiment carried out on a cylindrical plug of the Valhall overburden shale drilled perpendicularly to bedding (β  = 0, see Fig. 1)

Unloading the sample starting from the maximum stress level experienced in the experiment allowed us to keep shear stresses low and to avoid effects, such as microfracture closure, hence limiting the extent of non-elastic and non-linear deformation which could occur during virgin loading. The moduli measured during such an unloading–reloading cycle are also closer to the elastic moduli than in the case of a loading–unloading cycle. The amplitude of the axial stress changes (in the experimental context, $\Delta \sigma_{AX}$ is equivalent to $\Delta \sigma_{33}^S$) was 3 MPa and the radial stress ($\Delta \sigma_{RAD}$ equivalent to $\Delta \sigma_{11}^S$) followed specific stress paths:

$$\kappa = \frac{{\Delta \sigma_{11}^S }}{{\Delta \sigma_{33}^S }},$$

(28)

starting with so-called a “triaxial” cycle ($\kappa$ = 0, time interval approx. 352–358 h), followed by an “isotropic” cycle ($\kappa$ = 1, 360–368 h), a “K₀” stress path cycle ($\kappa$ = 0.87, adjusted to yield no radial strain, 378–386 h) and a “constant mean stress” ($\kappa$ = – 0.5, 400–408 h) stress path. The last cycle had a slightly lower amplitude axial stress change to keep it above the confining pressure (the exact measured stress and pore pressure values are given in Table 1 in the Appendix B)—in the case of the confining pressure higher than the axial stress, the confining fluid would be able to push the axial piston away from the upper surface of the sample. After every undrained cycle the valve connecting the pore fluid intensifier and the pore fluid system inside of the cell was opened, and the pore pressure was brought back to its initial in-situ value, and the sample re-consolidated. Further analysis of the data was carried out using the stress and pore pressure measurements taken directly before the initiation of the unloading and 1000 s after its completion (to let the pore pressure equilibrate).

As the sample was drilled perpendicularly to the bedding ($\beta$ = 0) and radial stress is always isotropic (i.e., $\sigma_{11}^S$ = $\sigma_{22}^S$ and $\Delta \sigma_{11}^S$ = $\Delta \sigma_{22}^S$), Eq. (22) simplifies to

$$\Delta p_f = \frac{1}{3}\left( {2\Delta \sigma_{11}^S B_{11}^M + \Delta \sigma_{33}^S B_{33}^M } \right),$$

(29)

or alternatively

$$\frac{\Delta p_f }{{\Delta \sigma_{33}^S }} = \frac{1}{3}\left( {2\kappa B_{11}^M + B_{33}^M } \right).$$

(30)

The use of four different stress paths allowed us to verify the expected linearity of the experimental results in the $\Delta p_f /\Delta \sigma_{33}$—$\kappa$ space (Fig. 4) and strengthen our trust in the obtained poroelastic pore pressure parameters values.

Fig. 4

Change in pore pressure normalized by axial stress change vs. stress path parameter for the Valhall overburden shale sample drilled perpendicularly to the bedding (β  = 0, see Fig. 1)

To estimate the values of the anisotropic pore pressure coefficients $B_{11}$ and $B_{33}$ we solved a set of four linear Eqs. (29), one for each of the unloading stages, numerically. This yielded $B_{11}$ = 0.53 and $B_{33}$ = 1.51, or alternatively $B_S$ = 0.86 and $A_S \left( {\beta = 0} \right)$ = 0.59 from Eqs. (2) and (3). The experimental results yield the poroelastic coefficient $B_{33}$ almost three times larger than $B_{11}$—such a high degree of anisotropy indicates large contrast in rock compliance to loading applied along and perpendicular to the symmetry axis. It also signals the dominant role of $B_{33}$ in the pore pressure response in horizontally or near-horizontally layered Lista shale.

For the purposes of our overburden response modelling, we simply assume that these experimentally estimated properties are representative for the entire volume of the Valhall overburden.

We used $B_{11}$ and $B_{33}$ together with Eqs. (25) and (26) to visualize the angle dependence of coefficients $A_{3 - 1}$ (Fig. 5, left) and $A_{2 - 1}$ (Fig. 5, right) which control the impact of shear stresses on the pore pressure response. The values of both parameters vary between 0.21 ($B_{11} /3\overline{B}$) and 0.59 ($B_{33} /3\overline{B}$), deviating significantly from 1/3 (their values predicted by isotropic linear elasticity). This confirms previous observations made on shales by Holt et al. (2018a), Holt et al. (2018b) and Soldal et al. (2021).

Fig. 5

Angle-dependency of parameters $A_{3 - 1} (\beta )$ and $A_{2 - 1} (\alpha ,\beta )$ which describe the impact of shear stresses on the undrained pore pressure response in the Valhall overburden shale (for angles definition, see Fig. 1)

4 Modeling

We combine our estimated poroelastic pore pressure parameters for the Lista shale with Valhall field geometry and stress state evolution modelling results provided by the field operator, AkerBP, to model the undrained pore pressure response to reservoir depletion. The decrease in reservoir pore pressure is non-uniform, and locally reaches as much as 28 MPa (Kristiansen 2020). In the layer of model nodes directly above the reservoir (the bottom part of the Lista formation, on average 8.9 m above the first layer of nodes in the reservoir) the average stress paths $\kappa$, Eq. (28), computed for all points with $\Delta \sigma_{33}^M$ > 0.1 MPa were 0.38 and 0.39 for $\sigma_{11}^M$ and $\sigma_{22}^M$, respectively, with standard deviations of 1.11 and 1.13. This variety of estimated stress paths suggests a wide range of possible stress-induced pore pressure changes, as previously shown in Fig. 4 (where the sampled stress paths had the average of 0.34 and the standard deviation of 0.72).

The geomechanical model of the reservoir overburden consists of 50 layers. Each layer above the reservoir consists of nodes for which the vertical projection forms a 50 × 50 m regular grid d (outside the central part of the model the lateral distance between neighboring points increases). The vertical distance between the layers is variable (although it remains comparable to the lateral distance between nodes) and is adjusted, so that the model layers resemble the geological 3D structure of the layers and features in the subsurface. The model accounts for the anisotropy of mechanical properties in the overburden by assigning different horizontal and vertical undrained elastic parameters (in total: two Young’s moduli, two Poisson’s ratios and a single shear modulus) in the layers above the reservoir. The values of the elastic moduli in the overburden were estimated by the field operator with the use of correlations relating measurements of in-situ sonic velocity measurements with static stiffnesses determined through laboratory testing (Kristiansen 1998). In the newer iterations of geomechanical modelling, the properties of both the reservoir and the overburden were updated to provide maximum fit of the modelling results to compaction and subsidence history combined with the information on the volumes produced from the reservoir. We base our analysis on a recent geomechanical model which has not been yet described in the literature.

We assume that the orientation of the symmetry axis of the medium ($\vec{M}_3$) at every model node coincides with the vector normal to the corresponding model layer at given point. Hence, the normal can be estimated for each of the nodes by comparing its position with the location of two out of four of its nearest neighbors from the same layer (Fig. 6a–d), chosen such that the three considered points form a right angle. The normal vector is determined for the point in the vertex of the angle as the dot-product of the vectors forming the angle. With this method we obtain four normal vectors at each point (one for each of valid neighbor pairs)—their averaged coordinates are used to describe a representative normal vector for the surface (Fig. 6e).

Fig. 6

Estimation of the surface normal at given point by comparing its position with the location of its two nearest neighbors—the dot-product of the vectors forming the right angle gives the parameters of the normal vector. For each point of the model four variants (a–d) are estimated and then averaged (e)

Statistical comparison between the four estimated normal-vector variants showed no significant differences, and hence their average should be a good representation of the local orientation of the medium. As the stresses we rotate are initially oriented along the directions of the external coordinate system, the orientation of the rock symmetry axis is sufficient to estimate the angles $\alpha$ and $\beta$ using Eqs. (13) and (14).

Rotation angles between the external (or geo-reference) coordinates system XYZ (i.e., $S$ = ([1,0,0], [0,1,0], [0,0,1])) and the orientation of the medium estimated for the surface corresponding to the top of the Tor formation (reservoir rocks) are shown in Fig. 7. As the initial stress tensor does not represent principal stresses (i.e., it contains non-diagonal stress tensor elements) and the principal stress directions change due to the depletion, Eqs. (22) and (23) take a more complex form. Hence, the rotation angles do not give full insight into the impact of the particular principal stresses on the undrained pore pressure response. Referring to their definitions shown in Fig. 1, the angles displayed in Fig. 7a tell us about the rotation of the stress frame around the vertical axis. The rotation by the angle $\alpha$ moves $\vec{S}_1$ (which represents direction of $\sigma_{11}^S$) into the assumed material symmetry plane. It, therefore, depends mostly on the local dipping direction. The use of a cyclic color scale is necessary as rotations of 180 or -180 degrees give the same result. The rotation angles shown in Fig. 7b are more intuitive, as $\beta$ is the angle between the vertical axis, Z (or $\vec{S}_3$), and the symmetry axis of the material $\vec{M}_3$ Thus, near-zero angles indicate a nearly flat surface, whereas large angles mark steep slopes or faults intersecting model surfaces and creating local discontinuities.

Fig. 7

Top view of the distribution of the rotation angles α (a) and β (b) on the upper surface of the Tor formation (for angles definition, see Fig. 1). The easting direction corresponds to X direction and the northing direction to Y direction in Fig. 1a

We model the undrained pore pressure response to the stress state changes that took place between 1982 (start of the hydrocarbon production in Valhall) and 2020. Using stress tensors aligned with the external frame XYZ allows us to account for the stress rotations caused by the reservoir depletion without having to estimate rotation angles separately for the two stress states.

The pore pressure changes were first estimated with the use of the anisotropic poroelastic tensor ${\varvec{B}}$ (Eq. 4) representing the vertically transversely isotropic shale. They were later re-estimated using the same input stress changes, but with the isotropic Skempton’s parameter $B_S$ = 0.86 and $A_S$ = 1/3 (Eqs. 2 and 3). Estimation of pore pressure changes based on stresses from the geomechanical model computed with anisotropic elastic moduli and the isotropic pore pressure parameters is meant to quantify the consequences of neglecting the anisotropic character of the undrained pore pressure response. A fully isotropic case (i.e., isotropic geomechanical model and isotropic poroelastic pore pressure parameters) was not considered, because no up-to-date isotropic geomechanical model of the Valhall field was available.

The distribution of $\Delta p_f$ given by the anisotropic tensor in the layer directly above the reservoir (corresponding to the Lista formation) is shown in Fig. 8a. The undrained pore pressure changes show a rather complex pattern above the central part of the reservoir (zone U, 522–528 km easting and 6234–6240 km northing) with amplitudes within this layer reaching − 7.2 MPa in the negative and 6.2 MPa in the positive direction. For comparison, the minimum principal stress change ranged from − 8.3 to 4.8 MPa, the intermediate from −6.0 to 6.0 MPa and the maximum from − 8.6 to 9.7 MPa in the same area.

Fig. 8

Top view of undrained pore pressure response predicted using transversely isotropic poroelastic tensor B in the layer directly above the reservoir (a), and the difference between pore-pressure predictions made using the anisotropic and isotropic tensors B (b). In both cases, stress changes were estimated with the use of transversely isotropic geomechanical model of the overburden. P1 and P2 mark the end points of the vertical cross sections (Fig. 9). Rectangle U marks the boundaries of a part of the model above the central part of the reservoir chosen for further analysis (Figs. 10, 11, 12, 13, 14). The color scale range was limited in both plots to better visualize the dominating low-magnitude pore pressure changes and differences

The difference between the anisotropic and the isotropic pore pressure estimates is shown in Fig. 8b. Above the central part of the reservoir (zone U), the maximum difference between the two solutions within this model layer is 2.0 MPa. As indicated by the similarity of the features in both plots in this figure, the directions of the pore pressure changes given by the anisotropic and isotropic solutions agree for most of the points on the surface. The undrained pore pressure response given by the anisotropic tensor has generally higher amplitudes, regardless of the polarity of the pore pressure changes.

To investigate the vertical extent of the undrained pore pressure response we interpolated the modelled pore pressure changes in individual layers of nodes onto the P1–P2 cross section marked in Fig. 8. This cross section (Fig. 9), passing through a zone of large pore pressure increase, shows that the pattern of pore pressure changes observed in the layer of nodes directly above the reservoir (Fig. 8) does not change significantly with the distance from the reservoir. The magnitude of the undrained response given by the anisotropic poroelastic tensor ${\varvec{B}}$ decreases gradually with distance from the reservoir but remains larger than 1 MPa up to 340 m above its top surface (this maximum vertical extent of at least 1 MPa change is observed at X = 5230 m). The isotropic prediction gives a maximum vertical extent of at least 1 MPa pore pressure change of only 210 m above the reservoir.

Fig. 9

Cross section between points P1 and P2 (Fig. 8) through the modelled undrained pore pressure response predicted using the transversely isotropic poroelastic tensor B (a) and the difference between solutions given by the anisotropic tensor B and the isotropic parameter B_S (b). Dotted lines in (a) delineate areas, where the absolute values of the pore pressure changes predicted using the anisotropic tensor B are larger than 1 MPa. The dotted line in (b) illustrates the percentage difference between the two solutions computed along a vertical profile at X = 5230 m (thick solid line)

The difference between the anisotropic and the isotropic predictions (Fig. 9b) follows the same pattern of distribution as in the layer shown in Fig. 8, mimicking the features observed in Fig. 9a. The largest absolute differences are observed closest to the reservoir, where the stress changes were largest. To study the differences in more detail, we computed the relative difference profile for a vertical column at X = 5230 m, where the vertical extent of significant pore pressure changes (> 1 MPa) was the largest. The relative difference between the two solutions initially increases vertically upward, reaching its maximum of 48% at a depth of 2210 m, roughly 270 m above the reservoir. The relative difference remains above 40% for the next 360 m of the column. Despite these large percentage changes, the inclusion of the poroelastic anisotropy should not have much impact on pore pressure predictions in the part of the overburden further away the reservoir, as the corresponding absolute magnitude of the undrained pore pressure change given by both of the two predictions is small. In the case of isotropic geomechanical model of the overburden and isotropic poroelastic pore pressure parameters, the expected differences in predicted undrained pore pressure responses are significantly larger (Holt et al. 2022).

Next, we use Eq. (27) to investigate the impact of the undrained pore pressure changes on the horizontal effective stress $\sigma^{\prime}_{XX}$ in the zone U in the layer directly above the reservoir, as shown in Fig. 10. Both normal horizontal stresses changes, $\Delta \sigma_{XX}$ oriented along easting direction and $\Delta \sigma_{YY}$ oriented along northing direction, have similar spatial distributions and amplitudes, and hence we show only one of the two modelled stress change maps. The distribution pattern of total horizontal stress changes (Fig. 10a) qualitatively reflects the distribution of the undrained pore pressure changes shown in Fig. 8a. However, in some areas of the analyzed zone U the amplitude of the undrained pore pressure response is larger than the amplitude of the normal horizontal stress changes, causing a change of sign of the effective stress change. Hence, the distribution of the modelled effective stress changes does not resemble the distribution of changes of the two components of effective stress (total stress and pore pressure), both in terms of changes direction and magnitude.

Fig. 10

Map of the horizontal (parallel to easting direction) stress change distribution within zone U. The maps display total (a) and effective (b) stress changes between years 1982 and 2020 in the layer directly above the reservoir. The horizontal effective stress was computed using pore pressure changes given using the transversely isotropic poroelastic tensor (VTI). The color scale range was limited to better visualize the effective stress changes (b) of relatively lower amplitudes in comparison with the total stress changes (a). The polygons F1, F2, and F3 indicate examples of zones with significant differences between maps (a) and (b)

This non-uniformity is expressed by displacement or disappearance of the features dominating the total horizontal stress change in the effective stress change map (Fig. 10b), e.g., strong reduction of absolute value in the local minimum F1, change of sign in the eastern part of the total stress increase ridge F3 or change of sign and significant increase in change magnitude at F2. The extrema of the changes shift from − 5.76 and 6.50 MPa in the total horizontal stress $\sigma_{XX}$ to − 2.75 and 5.26 MPa in the effective horizontal stress $\sigma^{\prime}_{XX}$. In the case of the horizontal stress oriented along the northing direction, $\sigma_{YY}$, the extreme values change from − 5.31 and 5.33 MPa to − 2.15 and 4.02 MPa. The effective stresses estimated with the use of the isotropic poroelastic pore pressure parameters yield similar distribution of effective stress changes but with significantly lower amplitudes; these changes are between − 2.04 MPa and 3.31 MPa for $\Delta \sigma^{\prime,\,{\text{ISO}}}_{XX}$ and between − 1.50 MPa and 2.27 MPa for $\Delta \sigma^{\prime,\,{\text{ISO}}}_{YY}$.

To further explore the impact from the symmetry class of the pore pressure parameters on the geomechanical modelling results, we estimated the minimum effective principal stress (oriented predominantly horizontally, used to determine Mohr’s circles, as in Fig. 2) using both isotropic and transversely isotropic poroelastic pore pressure parameters (Fig. 11). Both isotropic and VTI symmetries generally yield similar patterns in minimum effective principal stress distribution (as expected from our analyses of Figs. 8 and 9). The average value of the predicted minimum effective principal stresses within zone U is 4.08 MPa for the anisotropic and 4.01 MPa for the isotropic solutions. Their standard deviations over zone U are 0.65 and 0.50 MPa, respectively. This is reflected by the more abrupt stress changes seen in Fig. 11a. Moreover, changes in the amplitude relationships between some adjacent extrema are observed. One such change is seen when comparing two low effective stress valleys located between F4 and F5. There, the effective stress in the western minimum decreases and the amplitude of the eastern minimum increases when moving from the anisotropic to the isotropic pore pressure response.

Fig. 11

Map of the minimum effective principal stress distribution within zone U. The maps display stresses in year 2020 in the layer directly above the reservoir computed using pore pressure values from year 1982 updated with changes given using the transversely isotropic poroelastic tensor B (a) and the corresponding isotropic tensor (b). The polygons F4 and F5 indicate examples of zones with significant differences between maps (a) and (b)

The comparison of the total and the effective vertical stress changes does not reveal such significant differences between the two stress distributions and amplitudes as in the case of the horizontal stresses. To extend our analysis to the entire examined volume, we show the comparison of total stress changes and pore pressure changes in the corresponding nodes of the model in Fig. 12. The distributions of the clouds of points (over 113 000 points each) were approximated with the use of linear trend lines and the quality of the fits was assessed with the regression parameter $R^2$(i.e., coefficient of determination, here describing the proportion of the variance of $\Delta p_f$ explained by the variance of corresponding $\Delta \sigma_{ij}$).

Fig. 12

Comparison of the normal stress changes (defined along the geographical easting direction) of and the undrained pore pressure response (estimated with the use of transversely isotropic VTI poroelastic parameters) in corresponding nodes of the model. The box contains equations for the linear trend lines and their linear regression coefficients R²

In all three cases, the intercept of the linear trend lines is very small (as expected from Eq. 23), and, therefore, can be treated as negligible. In the case of the vertical total stress changes, the slope of the $\Delta \sigma_{ij}$–$\Delta p_f$ trend line is 0.65—the inverse of this value is 1.53, approximately equal to $B_{33}$ (= 1.51). No such relationships are observed for horizontal stress changes and the other pore pressure parameters. At the same time, the parameter $R^2$ for the trend line relating the total vertical stress changes with the values of the undrained pore pressure response is 0.97, suggesting clear linear correlation between the two variables. In the cases of the horizontal stress changes $\Delta \sigma_{XX}$ and $\Delta \sigma_{YY}$, the value of the parameter $R^2$ is 0.74 and 0.79, respectively. In the case of the pore pressure changes estimated with the use of the isotropic poroelastic pore pressure parameters, the parameter $R^2$ is between 0.85 and 0.90 for all three considered normal stress changes. No direct relationships between the estimated value of the slope parameter and the values of the pore pressure parameters is observed in the isotropic poroelastic case.

Encouraged by the high value of the $R^2$ factor for $\Delta \sigma_{ZZ}$ we approximated and showed (Fig. 13) the undrained pore pressure changes with the total vertical stress changes and its corresponding slope value:

$$\Delta p_{\text{f}} = \frac{1}{{B_{33} }}\Delta \sigma_{ZZ} \approx 0.66\Delta \sigma_{ZZ} .$$

(31)

Fig.13

Comparison of the undrained pore pressure response estimated with the use of transversely isotropic (VTI) poroelastic parameters with the undrained pore pressure response approximated with Eq. (31) in the zone U in the layer directly above the reservoir. The dimension of bins used to count the points was 0.1 by 0.1 MPa. Dashed lines contour area within which the difference between the modelled and the approximated values of the undrained pore pressure changes is smaller than 1 MPa

We compared these predictions with the response computed with the use of the anisotropic poroelastic pore pressure parameters (Eq. 22) in the entire model and in the zone U in the layer directly above the reservoir, where the pore pressure changes are expected to be largest. We supplemented the scatter plot with the number of points falling within a bin of 0.1 by 0.1 MPa expressed by the color of the individual points, which revealed high density of points directly on and in the direct proximity of the $\Delta p_f (\Delta \sigma_{ZZ} )$ = $\Delta p_f^{VTI}$ line.

To assess the quality of the pore pressure change approximation quantitatively, we computed the difference between the two models, i.e., $\Delta p_f^{VTI}$–$\Delta p_f (\Delta \sigma_{ZZ} )$. Standard deviations of prediction differences in the entire model and in the zone U in the layer directly above the reservoir are 0.11 and 0.25 MPa, respectively. This means that approximately 68.2% of the pore pressure change differences have magnitudes lower than these values. Standard deviations of prediction differences between isotropic and anisotropic pore pressure estimates, i.e., $\Delta p_f^{VTI}$–$\Delta p_f^{VTI}$, in the same data volumes are 0.14 and 0.33 MPa, respectively.

To complement the analysis of the effective stresses, we projected the reported casing deformation locations onto the maps of pore pressure changes (Fig. 14a) and total vertical stress (Fig. 14b) in the zone U. We consider projecting to be a valid mean to visualize the locations of the casing deformation incidents, as both the undrained pore pressure response and stress change distributions are not varying much vertically within the relevant interval (as shown for the pore pressure response in Fig. 9). Moreover, we cross-plot the horizontal and vertical effective stress changes at known casing deformation locations, and to add some context and to present general data trends we supplement them with estimated values of these parameters in the entire zone U (Fig. 14c). To explore the relationship between the location, the stress and pressure changes and casing deformation depths, the casing collapse points were colored according to their vertical distance to the top of the reservoir. Combined analysis of the predicted pore pressure changes (Fig. 14a) and the total vertical stress (Fig. 14b) distributions indicates that a substantial number of the reported casing deformations were located in places characterized with rapid lateral changes of both parameters.

Fig. 14

Map of the undrained pore pressure response computed with the use of anisotropic poroelastic parameters (a) and total vertical stress distribution within zone U in year 2020 (b), supplemented with cross-plot of horizontal and vertical effective stress changes in the same area in the layer directly above the reservoir (c). Both the maps and the cross-plot were overlaid with points marking the location of vertical projections (a, b) and the values of corresponding parameters at the location (c) of known casing deformations. The filling color of the casing failure points (a–c) indicates the height above the top reservoir surface at which casing deformation was registered and it was clipped to 340 m, although point 21 is located 753 m above the reservoir surface. The size of bins used to count the points in (c) was 0.1 by 0.1 MPa

The first analyzed cluster of points is situated directly above the central part of the reservoir (points 8, 9, 10, 12 and 19). Although located relatively close to each other, these casing deformation points are not grouped together in the effective stress changes cross-plot (Fig. 14c)—they are distributed roughly along a line connecting points 10 and 19 in the order resembling their geographical distribution. This alignment is not reproduced in corresponding cross-plots obtained with isotropic pore pressure parameters, nor obtained with total stresses changes.

Points in the next group, located above the north-eastern flank of the reservoir (2, 15, 17, 20 and 21) follow transition lines between zones of positive and negative pore pressure changes (which reflect well changes in the total vertical stress changes, as discussed before). This group is not aligned in the effective stress cross-plot; however, these points seem to be on average located further away from the reservoir (average height above the reservoir surface of 280 m) than the rest of the analyzed points (99 m). Points grouped above the south-western flank of the reservoir (1, 3, 5, 7 and 11) form a rather loose cluster with positive values of the vertical and negative values of horizontal effective stress changes (except for point 3). Points 6 and 18, although spatially belonging to the clusters above the flanks of the reservoir, are characterized with higher predicted magnitude of vertical effective stress and pore pressure changes, as well as with larger decreases in the horizontal effective stress.

Points 4, 14 and 16 located above the edges of the central part of the dome along the NNW–SSE reservoir axis, while characterized with relatively large drops in pore pressure and low values of total vertical stress, form a group with anomalously high values of horizontal effective stress increment and vertical effective stress decrease in the effective stress cross-plot. Points 13 and 22, although located roughly along the same axis, do not show such extreme effective stress changes.

5 Discussion

The results of the undrained experiment we carried out on the Lista overburden shale (Fig. 3) indicate a very consistent behavior of the rock within its elastic deformation range in assumed in-situ stress and pore pressure conditions and yielded $B_{11}$ = 0.53 and $B_{33}$ = 1.51, or alternatively $B_S$ = 0.86 and $A_S = A_{3 - 1} (\beta = 0)$ = 0.59.

Experimental results reported by Holt et al. (2018a), Holt et al. (2018b), Duda et al. (2021) and Soldal et al. (2021) confirm the anisotropic angle-dependent character of the undrained pore pressure response and the transverse isotropy of various shales. Encouraged by these results, we took a next step toward better description of the anisotropic pore pressure changes and extended Eqs. (1)–(3), which are limited to isotropic horizontal stress changes, to obtain Eq. (22) which includes the entire stress tensor needed in a field modelling scenario. We also defined an additional Skempton-like pore pressure parameter $A_{2 - 1}$, Eq. (26), capturing the impact of the intermediate principal stress. In our test we measured $A_{2 - 1} (\alpha = 0,\beta = 0)$ = 0.21 (Fig. 5), which confirmed the observations in the aforementioned literature indicating that for shales the pore pressure parameters expressing the influence of shear stress changes within the elastic deformation range generally differ significantly from 1/3, the value expected under the assumption of linear elastic isotropy of the material (Skempton 1954).

An apparent limitation of our experimental study arises from using a triaxial apparatus with isotropic horizontal stresses and horizontal stress changes, contrary to a true-triaxial setup, where the effect of changing the principal stresses individually may be investigated. Application of anisotropic horizontal stresses may have revealed lower symmetries of the medium. However, from the point of view of the anisotropic poroelasticity (Thompson and Willis 1991; Cheng 1997), a single undrained triaxial experiment suffices to fully describe pore pressure changes in a transversely isotropic material characterized by a single symmetry plane and a symmetry axis oriented along $\sigma_{AX}$. Moreover, in the case of both historical and current stresses modelled in the Valhall overburden, the horizontal stresses are statistically nearly identical (analysis of all model nodes in the overburden yields mean value of the ratio between $\sigma_X$ and $\sigma_Y$ of 1.0 and standard deviations of $\sigma_X$ and $\sigma_Y$ of 0.010 and 0.009, respectively), as reported by, e.g., Kristiansen (1998). Hence, the modelled settings are expected to be equivalent to the experimental conditions. Intermediate stress estimates are usually burdened with large uncertainties, as the determination of the maximum horizontal stress under field conditions still remains a challenge (e.g., Zoback 2007; Fjær et al. 2021), and, therefore, the potentially small differences between the horizontal true-triaxial in-situ stresses, even if achieved, would still be uncertain and probably of smaller importance.

Second, the somewhat subjective duration of the assumed post-unloading stabilization period (1000 s) can be also questioned. Although apparently random, it was an observation-based compromise between giving the system enough time for pressure equilibration (the gradient of the pore pressure changes decreases significantly within this interval) and not allowing the time-delayed deformation (e.g., creep) of the shale to impact the measurement results. A nearly perfectly linear behavior is observed in the $\Delta p_f /\Delta \sigma_{33}$—$\kappa$ plot (Fig. 4), as predicted from anisotropic poroelasticity in Eq. (30). Supported by a negligible onset of permanent deformation after each of the unloading–reloading cycles (Fig. 3), it indicates excellent measurement precision and an only marginal impact of changes in the values of the poroelastic pore pressure parameters due to non-elastic effects (Duda et al. 2021) on the pore pressure changes within the chosen stress range and stabilization interval.

The assumption about the large-scale undrained behavior of the overburden shales can be addressed through classical consolidation theory. As outlined by Biot (1941), if the integrity of the cap rock is not compromised, the sealing ability should maintain the undrained pore pressure response on a time-scale given by consolidation. One can estimate the time to reach pore pressure equilibrium with the surroundings given by diffusive behavior $t_D$ using a simplified description presented by Fjær et al. (2021):

$$t_D \approx \frac{l_D^2 }{{C_D }}.$$

(32)

where $l_D$ is a characteristic diffusion length and $C_D$ is a diffusion coefficient controlled primarily by permeability, but also by porosity, and rock and pore fluid stiffnesses. In Valhall, the reservoir prior to production was highly over-pressurized (Pattillo et al., 1998) and the overburden pore pressure remains abnormally high for around 2000 m above the reservoir (Fjær et al. 2021). The geological age of the reservoir is around 20 million years (Kristiansen and Sandberg 2018), which means that in-situ effective $C_D$ of the overburden must have been 0.2 m²/year or lower. If we assume that this estimate of the diffusion coefficient is representative for the direct overburden of the reservoir now, the approximate time to equilibrate the pore pressure 10 m above the reservoir given by Eq. (32) is 500 years. The diffusion coefficient based on laboratory data is about 10 times larger (permeability was estimated to be of around 5 nanoDarcy), which reduces the consolidation time to approximately 40 years. However, if we further assume that this value of diffusion coefficient is representative for the first 100 m of the cap rock above the reservoir, the equilibration at that distance would be 4000 years. All these estimates are uncertain, but since the stress altered volume stretches hundreds of meters above the reservoir, the assumption of undrained overburden response in the course of reservoir lifetime appears realistic. Fluid flow between the reservoir and the cap rock may still occur along faults or fractures activated or opened in the result of changes in reservoir pore pressure (depletion or injection), but in low-permeability formations it would be spatially limited to these features and their proximity.

In the numerical part of our study, we combined the pore pressure parameters given by the laboratory experiments with the results of finite element stress modelling of the Valhall field and estimated the undrained pore pressure response in the entire overburden. The resultant pore pressure changes directly above the central part of the reservoir (Fig. 8a, zone U) were of several MPa in magnitude, reaching absolute amplitudes as high as 7.2 MPa. The modelled pore pressure development remained significant for several hundred meters above the reservoir top surface, exceeding 1 MPa as far as 340 m above the chalk reservoir-overburden shale interface (Fig. 9). Moreover, the impact of the undrained pore pressure response on the effective stress values is far from negligible—in Fig. 10, we show that effective horizontal stress changes differ from total horizontal stress changes not only in magnitude, but also in the direction of changes and their distribution. Considering the large rock volume experiencing substantial pore pressure alteration, the commonly near-failure stress conditions in the upper crust (Townend and Zoback 2000), and the unquestionable presence of pre-existing faults and fractures in the subsurface around the reservoir, we conclude that the undrained pore pressure response should be accounted for in the assessment of the stability of the reservoir's surroundings, during production and injection operations. In our opinion, the magnitude and range of the modelled undrained pore pressure changes and their resultant impact on the effective stresses (directly in shales and also indirectly in layers around them) make them a good candidate to explain some of the instabilities and microseismic events reported at considerable distances from injection locations (e.g., Verdon et al. 2011; Rutqvist 2012; Vasco et al. 2018, Williams-Stroud et al. 2020 and references therein), as well as events recorded at depths of 2300–2350 m, i.e., above the reservoir, during a short passive monitoring campaign at Valhall in 1998 (Dyer et al. 1999; Kristiansen et al. 2000; Zoback and Zinke 2002). Until now, these have been explained mainly as caused either by fluid migration through systems of discontinuities and cracks or by injection-induced stress transfer.

To explore the consequences of disregarding the anisotropic character of the pore pressure changes, we compared the modelling results we obtained with anisotropic parameters and with their isotropic counterparts, estimated only from the isotropic unloading-loading undrained experimental cycle (i.e., $\kappa$ = 1, yielding $B_S$ = 0.86 and $A_S$ = 1/3). The comparisons, shown in Figs. 8b and 9b, indicate that for the two solutions the general large-scale trends are somehow similar and that the anisotropic pore pressure response tends to have higher absolute amplitudes. In consequence, the undrained pore pressure changes predicted with the anisotropic pore pressure parameters not only have larger relative impact on the value of effective stresses, but also may potentially exert non-negligible influence on the subsurface at distances larger than initially expected. The differences between the isotropic and anisotropic solutions transferred to the effective stress analysis (Fig. 11) are also expressed in terms of the larger standard deviation (quantifying the deviance of the observed values given by a model from their global mean value.) of the effective stresses changes given by the anisotropic solution. In the case of the minimum principal stress changes $\Delta \sigma^{\prime}_{\min }$ in the zone U, standard deviation increases from 0.50 MPa for the isotropic approach to 0.65 MPa when the anisotropic character of shales is accounted for. These standard deviations describe large populations of points; however, our interest lies predominantly in the points characterized with the largest pressure changes, where differences between the isotropic and anisotropic results are significantly larger. Changes in amplitude between neighboring local extrema of effective stress are also observed when going from isotropic to anisotropic estimates. This indicates that the zones with the lowest effective stresses in anisotropic overburden (i.e., potentially closest to caprock failure or to fault reactivation) may not be identified if poroelastic anisotropy is not accounted for.

In the direct proximity of the reservoir, effective stresses are relatively low (in the zone U the average predicted minimum effective principal stress is just above 4 MPa, Fig. 11) and quantitatively comparable with effective stress changes (Fig. 10b). This emphasizes that even small differences in the undrained pore pressure response prediction, let alone differences in the predicted direction of pore pressure change, may have significant implications for overburden stability and integrity assessment (as shown in Fig. 2) and drilling operations design (due to a narrowing mud window). The consequences of the anisotropic undrained pore pressure changes for the borehole wall stability were recently theoretically explored by Raaen et al. (2019) and successfully identified in field observations by Asaka and Holt (2021).

Higher amplitude of the pore pressure changes predicted with the anisotropic pore pressure parameters (regardless of the polarity of the pore pressure changes) suggests a relatively large impact of $B_{33}$, the parameter capturing the properties of the medium along its symmetry axis, which is significantly higher than the isotropic parameter $B_S$. Moreover, statistical analysis of principal stress directions in zone U in the areas with pore pressure increase shows that the maximum principal stress in these nodes is predominantly vertical, even after depletion. In the modelling results corresponding to year 2020, the vertical component of the direction unit vector of the maximum principal stress ($s_{i3}$) is larger than 0.95 in 91% of such points. This is true only for 58% of points in the areas with negative pore pressure changes, indicating a less vertical orientation of the maximum principal stress in these zones. It also signals the impact of stress field orientation and the poroelastic anisotropy of shales on the direction and magnitude of the undrained pore pressure response.

This makes it impossible to simply correct the pore pressure changes obtained with the isotropic pore pressure parameters to make them fit the anisotropic predictions. For example, the use of a scalar scaling factor (i.e., multiplication of Skempton’s $B_S$ or of the isotropic pore pressure change predictions by a constant) could locally adjust the amplitude but would not affect the distribution of zones with pore pressure increase or decrease, as this operation takes no account for the causes of differences in behavior between the isotropic and anisotropic media in non-hydrostatic stress conditions.

On the other hand, the observed correlation between the vertical stress changes and the undrained pore pressure changes estimated with the use of the anisotropic poroelastic pore pressure parameters (shown in Fig. 12) emerges from both geometry and properties of the modelled medium and the amplitude and direction of the on-going stress changes. First, as already mentioned before, the deviation of the bedding normal from the vertical direction is small in a substantial part of the model. Second, the value of the poroelastic parameter $B_{33}$ expressing the impact of the stress changes along the direction normal to the bedding (along symmetry axis) in Lista shale is significantly larger than the value of $B_{11}$ expressing the impact of the stress changes along the bedding (in symmetry plane). It is worth noting that the ratio of these two parameters is mostly a function of elastic stiffness anisotropy, as described more in detail in Appendix A. Finally, the total vertical stress changes are generally larger in comparison with horizontal stress changes.

This combination of factors allows us to approximate the distribution of the undrained pore pressure changes in transversely isotropic shales with the use of the total vertical stress changes $\Delta \sigma_{ZZ}$ and parameter $B_{33}$ only. While requiring less input information than the isotropic undrained pore pressure response model, this approximation yields pore pressure changes closer to the most physically accurate transversely anisotropic model. Moreover, it does not require information on the geometry of the model and hence is significantly less complicated and time-consuming than modelling of the undrained pore pressure changes with the use of the poroelastic ${\varvec{B}}$ and stress ${\varvec{\sigma}}$ tensors and rotation angles $\alpha$ and $\beta$. This may have practical implications not only for geomechanical modelling, but also for experimental practices, as these results indicate that in the case of time-limited undrained tests carried out on overburden shales it may be beneficial to substitute a rather standard hydrostatic cycle (the so-called “Skempton test”) with an undrained uniaxial stress cycle providing information on $B_{33}$. However, we consider measuring directly both Skempton’s $B_S$ (in an hydrostatic cycle) and $B_{33}$ (in an uniaxial cycle) to be the best option, as it makes it possible to estimate the entire poroelastic tensor ${\varvec{B}}$ (Eq. 2).

Nevertheless, one should have in mind that although apparently successful above the central part of Valhall reservoir, this approximation may produce larger errors for reservoirs with less dominant vertical stress changes and more complex geometries. For other overburden shales, less pronounced dominance of the poroelastic pore pressure parameters $B_{33}$ over its in-plane counterpart $B_{11}$ may also play a role in decreasing the quality of approximation. However, the comparison of Lista shale with other overburden shales described by Holt et al. (2017, 2018a, b), Lozovyi and Bauer (2019), Soldal et al. (2021) and Duda et al. (2022) suggests that Lista’s pore pressure parameters lie within a range typical for relatively soft caprock shales (in terms of static moduli and strength). In the case of Lista shale, parameter $B_{11}$ = 0.53, parameter $B_{33}$ = 1.51 and the ratio between them $B_{11}$/$B_{33}$ = 0.35. In the case of the other five considered shales, the mean values of the poroelastic pore pressure parameters are: $B_{11}$ = 0.52, $B_{33}$ = 1.37, $B_{11}$/$B_{33}$ = 0.38, and their corresponding standard deviations are 0.10, 0.18 and 0.09, respectively.

The main uncertainties in our approach result from the assumption that the properties of the Lista shale are representative for the entire overburden of the reservoir. Although the values of the pore pressure parameters seem to be close to the values experimentally measured in other North Sea overburden shales, the modelling results do not include any effects that would be caused by the natural variation of these parameters and the potential presence of inter-bedded permeable formations exhibiting drained behavior. Nor at this stage do we consider the impact of plastic deformation (reported by Duda et al. 2021). In this modeling scenario, we register stress changes larger than the 3 MPa that we applied in the laboratory. We might, therefore, expect a larger influence of non-elastic effects on the pore pressure evolution than we observed experimentally. We also neglect the influence of the gas cloud, which is apparent in the seismic data, above the Valhall reservoir (e.g., Lewis et al. 2003; Whaley 2009), which could significantly affect the mechanical properties of the overburden and its poroelastic pore pressure parameters sensitive to the fluid properties, i.e., $\overline{B}$ (parameters $A_{3 - 1}$ and $A_{2 - 1}$ are measures of anisotropy of the medium and do not depend on fluid properties, as can be concluded from Eqs. 24–26, Appendix A and Cheng 1997). However, including these factors in the analysis would require very detailed information on the overburden rocks, such as local relative saturations and deformation modes (elastic or plastic), that is not available for our case, nor in most other field cases.

To extend our analysis to the impact of the stress and pore pressure changes on casing integrity in boreholes located above and around a depleting reservoir, we need to define the most probable scenarios responsible for casing deformations. In the first scenario, casing collapses due to large pressure contrast between the inside of the casing and pore pressure in the surrounding formation. Although this scenario fits best into our analysis (as we focus on pore pressure changes in the overburden), such situations are expected to be extremely rare. Other scenarios assume that casing shear deformation is the result of slip on bedding planes, lithological interfaces or fault planes (Dusseault et al. 2001; Bruno 2002; Ewy 2021), which in shales would not necessarily cause seismic events. Displacement along such surfaces may take place when shear stress along the slip surface increases or effective stress normal to the slip plane drops (or the combination of the two).

The distribution of the shear stresses in the reservoir overburden is difficult to predict accurately due to strong influence of local discontinuities and heterogeneities. However, it can be approximated using maps of vertical total stress, where the zones characterized with rapid lateral variability caused by reservoir compaction are expected to have the largest shear stress values. Modelling results presented in Fig. 14b indicate that most of the 22 registered cases of casing deformation were located in the zones with large lateral gradients of total vertical stresses, where bending and flexing of casing become probable (Ewy 2021). To facilitate the shear slip along the plane, the effective stress normal to the slip surface should be low. In the case of slipping on bedding planes or lithological interface, this normal stress can be approximated by vertical effective stress (under assumption of nearly horizontal orientation of these surfaces). In the case of slipping on fault surface, the normal effective stress depends strongly on the orientation of the fault plane, but generally it can be approximated with horizontal effective stresses. In both cases, an increase of pore pressure would push the subsurface closer toward shear slip (Fig. 2). This becomes particularly important if pore pressure changes are of amplitude similar or larger than total stress changes. This is observed in Valhall overburden for the undrained pore pressure response predicted with the anisotropic pore pressure parameters, which in general yielded larger amplitudes of pore pressure changes than their isotropic counterparts (Fig. 12). This observation suggests that some of the casing deformations incidences assumed to be facilitated by the presence of permeable fractures, could be explained by pore pressure change caused by stress state alteration in low permeability shales.

We used the undrained pore pressure response estimated with the use of anisotropic poroelastic pore pressure parameters to evaluate changes in the effective stresses (Fig. 14c) with the intent to identify casing deformation mechanisms promoted by such changes at known casing deformation locations. In the light of the previous paragraph, we may point two pairs of registered casing deformations at which locations the modelled effective stresses changes could facilitate shear slip. In the case of points 4 and 16, relatively large decrease of the vertical effective stress could create conditions favorable for the slip along bedding planes or geological interfaces. The second pair consists of points 6 and 18, located on the opposite end of the effective stress cross-plot shown in Fig. 14c. These two points are characterized with relatively large increase of the vertical and relatively large decrease of the horizontal effective stress, which combined promote shear slip along near vertically oriented fault or fractures. It is worth noting that if no pore pressure changes are assumed, both total stresses gain in value at the casing deformation locations. Nevertheless, without more detailed observations from the inside of the analyzed boreholes and information on the location and orientation of discontinuities, we can only indicate promoted mechanisms, but not determine them unequivocally.

An additional observation which may indicate that the predictions of stresses and resultant pore pressure changes recreate actual trends in the overburden is the correlation between spatial distribution of the points located above the central part of the reservoir (8, 9, 10, 12 and 19) and their distribution in the effective stress cross-plot (Fig. 14c). This correlation between the plots indicates gradual transition from one stress change regime to another along NNW–SSE reservoir axis.

6 Conclusions

Estimation of effective stresses is imperative for assessing the stability of reservoir overburdens and the integrity of boreholes, as even small perturbations in the near-failure or stress-concentration regions may lead to fault activation or rock failure. One of the key factors influencing the effective stress is pore pressure, which in low-permeability media, such as shales, changes in an undrained response to modification of the stress state. This undrained pore pressure response seems to be neglected in many studies, probably guided by an intuition that there will be negligible pore pressure response associated with fluid flow in the low-permeability shale over the lifetime of a reservoir.

In this paper, we propose an expression for the undrained pore pressure change which takes into account the impact of the anisotropic properties of a medium, all stress tensor elements, and the misalignment of the stress tensor frame with the frame of the medium. Although overcoming most of the shortcomings of commonly used stress-based expressions, it does not include the impact of plastic deformation on the undrained pore pressure response.

A triaxial loading apparatus allowed us to estimate the anisotropic poroelastic pore pressure parameters of an overburden shale extracted from the Lista formation directly above the chalk reservoir in the Valhall field. The experimental results indicate that the values of the pore pressure parameters in Lista shale are generally far from those expected in an isotropic medium, supporting the expected anisotropic (transversely isotropic) nature of this material.

We combined our estimates of the pore pressure parameters with the geometry of the subsurface and the results of finite element stress field evolution modelling in the Valhall reservoir overburden to compare the undrained pore pressure responses given by the anisotropic and isotropic pore pressure parameters. The undrained pore pressure response given by the anisotropic tensor has generally higher absolute amplitudes, with the largest discrepancies observed in the areas with the largest pore pressure changes. The comparison reveals differences not only in the magnitude but also in the spatial distribution of the pore pressure and effective stress changes in both horizontal and vertical directions, highlighting the importance of accounting for poroelastic anisotropy in overburden shale behavior modelling.

Experimental observations and correlations observed in the modelled data allowed us to formulate a method to accurately approximate the undrained pore pressure response in anisotropic overburden shales using merely estimated vertical stress changes and a single parameter describing rock poroelastic properties along its symmetry axis.

Finally, the joint analysis of the locations of known casing deformation incidents and modelled total and effective stresses indicates correlation between casing failures and areas with rapid lateral changes of total vertical stress. At the analyzed casing deformation locations, the predicted undrained pore pressure changes have magnitudes comparable to the total stress changes. Moreover, we observed correlation between the spatial distribution of such casing failures and their locations in the modelled effective stress cross-plots which may indicate that we recreated an actual transition between stress change regimes. This makes us believe that the undrained pore response modelling could become a useful tool for casing collapse risk analysis and mitigation.

Appendices

Appendix A

Using the framework given by Cheng (1997), the poroelastic pore pressure parameters can be defined as

$$B_{11} = \frac{{3M \cdot \left( {C_{33} \alpha_{11} - C_{13} \alpha_{33} } \right)}}{{2C_{33} \left( {C_{11} - C_{66} } \right) - 2C_{13}^2 }},$$

(33)

$$B_{33} = \frac{{3M\left( {2\left[ {C_{11} - C_{66} } \right]\alpha_{33} - 2{\mkern 1mu} C_{13} {\mkern 1mu} \alpha_{11} } \right)}}{{2C_{33} \left( {C_{11} - C_{66} } \right) - 2{\mkern 1mu} C_{13}^2 }}.$$

(34)

where $\alpha_{11}$ and $\alpha_{33}$ are anisotropic Biot’s parameters, different from the effective stress parameter assumed to be equal 1 in Eq. (27) (as we consider effective stresses mostly in the failure-related context, we assumed that this parameter is very close to 1, as indicated by empirical evidence in the literature). The stiffness parameters $C_{ij}$ can be expressed with Young’s moduli and Poisson’s ratios (Bower 2010):

$$\begin{aligned} C_{33} &= E_V (1 - \nu_{_{HH} }^2 )\Lambda , \\ C_{11} &= E_H (1 - \nu_{HV} \nu_{VH} )\Lambda , \\ C_{66} &= E_H /2(1 + \nu_{HH} ), \\ C_{13} &= E_H \nu_{VH} (1 + \nu_{HH} )\Lambda , \\ \Lambda &= \left( {1 - \nu_{_{HH} }^2 - 2\nu_{HV} \nu_{VH} - 2\nu_{HV} \nu_{VH} \nu_{HH} } \right)^{ - 1} . \\ \end{aligned}$$

(35)

The ratio between the two poroelastic parameters is

$$\frac{{B_{33} }}{{B_{11} }} = \frac{{2{\mkern 1mu} C_{13} {\mkern 1mu} \alpha_{11} - 2\left( {C_{11} - C_{66} } \right)\alpha_{33} }}{{C_{13} {\mkern 1mu} \alpha_{33} - C_{33} {\mkern 1mu} \alpha_{11} }}$$

(36)

Using the correlations between the stiffness parameters estimated by Sayers and den Boer (2018) and Asaka et al. (2021), we can assume that the values of $C_{13}$ and $C_{66}$ are small in comparison with $C_{11}$ and $C_{33}$. Hence, the latter two stiffness parameters dominate the final values of $B_{11}$ and $B_{33}$, and of the ratio between them.

Appendix B

See Table 1.

Table 1 Stress and pore pressure changes during the undrained unloading stages of the triaxial experiment carried out on Lista overburden shale from Valhall field shown in Fig. 3