Dynamic Split Tensile Strength of Basalt, Granite, Marble and Sandstone: Strain Rate Dependency and Fragmentation

Abstract

The aim of this study is to understand the strength behaviour and fragment size of rocks during indirect, quasi-static and dynamic tensile tests. Four rocks with different lithological characteristics, namely: basalt, granite, sandstone, and marble were selected for this study. Brazilian disc experiments were performed over a range of strain rates from ~ 10^–5 /s to 2.7 × 10¹ /s using a hydraulic loading frame and a split Hopkinson bar. Over the range of strain rates, our measurements of dynamic strength increase are in good agreement with the universal theoretical scaling relationship of (Kimberley et al., Acta Mater 61:3509–3521, 2013). Dynamic fragmentation during split tension mode failure has received little attention, and in the present study, we determine the fragment size distribution based on the experimentally fragmented specimens. The fragments fall into two distinct groups based on the nature of failure: coarser primary fragments, and finer secondary fragments. The degree of fragmentation is assessed in terms of characteristic strain rate and is compared with existing theoretical tensile fragmentation models. The average size of the secondary fragments has a strong strain rate dependency over the entire testing range, while the primary fragment size is less sensitive at lower strain rates. Marble and sandstone are found to generate more pulverised secondary debris when compared to basalt and granite. Furthermore, the mean fragment sizes of primary and secondary fragments are well described by a power-law function of strain rate.

Highlights

• Dynamic tensile strength of the rocks are experimentally observed to obey the universal theoretical scaling relationship proposed by Kimberley et al.

• Dilatancy occurred directly from the start of loading for saturated coal due to regional overpressure.

• Primary (coarse) and secondary (fine) fragments size generated from the split tensile tests are represented by a power-law function of strain rate.

• The mean fragment size of primary fragments is less sensitive to strain rate, while the secondary fragments have a strong strain rate dependency.

1 Introduction

The tensile behaviour of rock is a vital aspect of the overall dynamic characteristics of rocks. Rocks can be subjected to dynamic loading during various events such as drilling, blasting, earthquake, landslide, and impact cratering (Kenkmann et al. 2014; Zhou et al. 2014; Zhu et al. 2015). Dynamic fracturing is a complicated process, dependent on the mechanical properties of rock, microstructural features, and the type of loading. Rocks are generally weak in tension, where the uniaxial tensile strength is typically ~ 1/10th of the uniaxial compressive strength of the rock (Aadnøy and Looyeh 2019; Hoek 1966). Furthermore, the dynamic tensile behaviour of rocks, including fragmentation, can be different from the dynamic compressive behaviour at varying levels of strain rate dependencies; the different failure mechanism of rocks in compression and tension leads to different stress–strain characteristics. Moreover, the tensile strength of rocks has been found to be more sensitive to strain rate than the compressive strength (Heard et al. 2018). Several methods are available to characterise the dynamic tensile response of rocks at high strain rates. Among the various methods, the Hopkinson pressure bar has been the most popular method for investigating the tensile dynamic behaviour of rocks, either in pure tension mode (direct tension) or Brazilian test (indirect tension) mode. Previous work related to the Brazilian method of testing rocks using a split Hopkinson pressure bar (SHPB) has shown satisfactory performance (Wang et al. 2004; Zhu et al. 2015), with the advantages of easy specimen preparation, simple operation and good repeatability. In 2012, the International Society for Rock Mechanics (ISRM) recommended Brazilian disc tests as an appropriate method for determining tensile strength under dynamic loading (Zhou et al. 2012). A more detailed review of the dynamic tensile characterisation of rocks is available in Zhang and Zhao (2014) and Heard et al. (2018).

Dynamic effects on the strength of the rocks are commonly represented by the ‘Dynamic Increase Factor’ (DIF, describing the relative enhancement of dynamic strength with respect to the static strength). Over the past few decades, research into the dynamic behaviour of rocks has led to the development of several DIF curves (Liu et al. 2018). Several empirical equations relating the dynamic strength and static strength of the rock to the strain rate are available in the literature (Zhang and Zhao 2014); some of the relevant equations to the present study are listed below:

Granite: t (Masuda et al. 1987).

Sandstone: ${\sigma }_{dyn} =\mathrm{ A}+\mathrm{B log} (\dot{\varepsilon })+ C\mathrm{ log}{ (\dot{\varepsilon })}^{2}+D\mathrm{ log}{ (\dot{\varepsilon })}^{3}$ (Singh et al. 1989).

Marble: ${\sigma }_{dyn} = {e}^{C\dot{\varepsilon }}{\sigma }_{sta},$ (Liu 1980). where $\dot{\varepsilon }$ is the strain rate and ${\sigma }_{dyn}$ and ${\sigma }_{sta}$ are the dynamic and static strength of the rocks, respectively.

The empirical equations or the DIF curves as a function of strain rate or loading rate are generally case specific, which depend on the rock type and the nature of the testing method; hence, their applicability is limited. Kimberley et al. (2013) developed a theoretical universal rate-dependent scaling relationship for the compressive strength of brittle materials incorporating micro-mechanical behaviour. The micro-crack interaction associated with the flaws and their rate dependence is explained in Paliwal and Ramesh (2008) and Kimberley and Ramesh (2011). The flaws distributed in the material play a significant role in governing the strength of the material. The developed scaling relationship captures the insensitivity of strength to strain rate at low strain rates and the strong dependency at higher strain rates. Kimberley et al. (2013) also showed that their scaling relationship could predict the material’s tensile strength by varying some material parameters. However, the model’s validity at high-rate tensile failure is not yet proven. Li et al. (2018c) extended the Kimberley model for tensile conditions by incorporating the effects of microscale heterogeneity using the Grain-Based Discrete Element Method (GB-DEM) and developed a function without altering the basic form. The DIF curves for granite increased linearly with strain rate until intermediate strain rate and then drastically increased at higher strain rates. For a general case, Li et al. (2018a, 2018b, 2018c) recommended DIF curves in the form of a stretched Kimberley function. Additional details of the Kimberley and Li et al. model are presented later in the discussion section in conjunction with our experimental results.

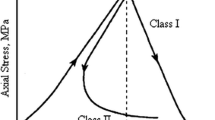
During dynamic tensile failure, micro-cracks (mode I) develop from arbitrarily oriented flaws (Griffith 1921). These cracks propagate under the influence of mechanical loading and coalesce to form larger cracks. The cracks increase in size, coalesce to form multiple cracks and manifest themselves into a network of visible fractures, leading to rock debris and fragmentation (Fig. 1). Estimation of the particle size during fragmentation can offer insights into various physical phenomena. Some of the examples are: (1) the fragment size provides a critical observation of the fracture mechanics of faults generated by co-seismic activity, where co-seismic loading leads to rock pulverisation. (Aben et al. 2016; Dor et al. 2006); (2) average rock fragment size is generally used as an index in selecting and optimum usage of explosives in the mining industry (Cho and Kaneko 2004); (3) The tensile fragments (spall) of impact craters account for a significant amount of the ejecta; nearly 50% of the ejected volume was observed in the experimental work of Dufresne et al. (2013). Also, the degree of fragmentation is known to vary in different zones of an impact crater (Melosh 1989; Kenkmann et al. 2014). Therefore, the determination of tensile strength and characterisation of tensile fragments over varying strain rates has important applications in impact crater studies.

Fig. 1

An illustration of crack initiation, propagation and fragmentation process

Early studies on fragmentation were pioneered by Nevill Mott, who invented a theory based on an expanding cylindrical shell. The average fragment size was subsequently predicted using statistical models (Mott 1947). Since then, dynamic fragment characterisation has been a subject of considerable research interest, and researchers have used a variety of statistical distributions in evaluating average fragment size. Some of the common statistical distributions used are: exponential (Grady and Kipp 1985), log-normal (Ishii and Matsushita 1992), power-law (Oddershede et al. 1993), Weibull (Brown and Wohletz 1995), Swebrec (Ouchterlony 2005) and Gilvarry (Sil'vestrov 2004). Another group of researchers have developed models based on principles of energy balance (Glenn and Chudnovsky 1986; Grady 1982; Yew and Taylor 1994). According to energy-based fragment size models, the fragment size is governed by the balance between externally imparted energy and internally developed energy on the surfaces of the fragments. Several numerical models were also developed to include the effect of stress waves (Drugan 2001; Levy and Molinari 2010; Miller et al. 1999; Zhou et al. 2006). The above listed theoretical and computational models are derived from 1D tensile loading expanding ring experiments (or numerical simulations), where the specimen is stretched uniformly under high strain rate.

Experimental studies of dynamic tensile fracturing commonly use spallation techniques (Grady 1988, 2006). The Split Hopkinson Tension Bar (SHTB) is a reliable apparatus for dynamically characterising brittle materials under tensile loading. Griffith et al. (2018) used a SHPB facility to generate tensile radial stress in the rock specimen using expanding cylinder theory. Their experiments suggested that the fragmentation process has a strong strain rate dependency, and the transition from fragments to pulverisation occurs at a strain rate in the order of 10² /s.

The split tensile test (Brazilian test) is generally not considered favourable for fragmentation studies, as the indirect tension test usually initiates and propagates a single fracture. Such fracture behaviour is often observed during quasi-static loading. However, at higher strain rates, a complex stress interaction takes place within the rock specimen leading to multiple fragments and the mass percentage of the fragments are found to increase (Zhu et al. 2020) and becomes more relevant for fragmentation study. Fragments resulting from the dynamic split tension tests are generally of two different sizes: coarse sized fragments (mostly semi-disc type) from the primary fractures and finer debris from secondary fractures (Cai 2013). A schematic diagram of primary and secondary fragments generated from a SHPB Brazilian test is shown in Fig. 2. The secondary fractures play a significant role in the dynamic fragmentation process, which is often overlooked in fragment analysis. Very little information is available in the existing literature (Li et al. 2018a; Zhu et al. 2020) on the dynamic fragmentation during high-rate Brazilian tests, and there are no details concerning the size distribution of fragments. Therefore, there is a need for in-depth analysis and characterisation of dynamic strength and fragmentation in split tensile test mode.

Fig. 2

A Schematic representation of typical fragmentation process during dynamic Brazilian test (figure adapted from Zhu et al., 2020)

In this study, using dynamic Brazilian disc testing, the tensile strength of rocks of different lithologies is investigated using SHPB at an intermediate strain rate range (10⁰–10² /s). We discuss the DIF associated with strain rate and the applicability of the universal theoretical scaling relationship of strength. Additionally, fragment size distributions of the experimental products (primary and secondary fragments) are measured, and the strain rate dependency of the fragment sizes are systematically quantified. Finally, the experimental results are compared with the existing theoretical models on dynamic fragmentation, and the acceptability of such models for split tensile fragments are discussed.

2 Experimental Details

2.1 SHPB Test Apparatus and Working Principles

The dynamic split tensile tests were carried out using a split Hopkinson pressure bar (SHPB) facility at the Geology Department, Albert-Ludwigs Universität Freiburg, Germany. The SHPB consists of three 50 mm diameter bars made of Titanium alloy (E_B = 110 GPa, ρ_B = 4.43 g/cc); they are termed the striker bar, incident bar, and transmission bar. A striker bar of length 250 mm is housed inside a barrel connected to a pressure vessel. The length of the incident and transmitted bars were designed (equal to 2500 mm) to avoid wave reflections during the test time. The end of the transmitted bar is made to pass through a momentum trap system, where the bar's movement is arrested. To achieve 'dynamic force equilibrium’, it is necessary to use a pulse shaper between the striker and incident bar, which results in slowly rising incident pulse and avoids wave dispersion effects in brittle materials (Frew et al. 2002; Zhang and Zhao 2014). In our study, we have used aluminium foam of 10 mm thickness and 90% porosity as a pulse shaper. The aluminium foam was pre-hit at a striker velocity of ~ 10 m/s resulting in a final thickness of ~ 7.5 mm (Rae et al. 2022, 2020; Zwiessler et al. 2017). The pre-hit aluminium foam ensures a uniform contact between the bar and pulse shaper. The schematic diagram of the SHPB bar is shown in Fig. 3a.

Fig. 3

a Schematic diagram of a split Hopkinson pressure bar, b Wave propagation of stress pulse in the specimen and c top view of the flattened Brazilian disc before mounting

The cylindrical rock specimen is placed between the incident and transmitted bar. The compressed gas released from the pressure vessel accelerates the striker bar, which in turn strikes the incident bar via the pulse shaper. A compressive elastic wave generated in the incident bar travels towards the rock specimen. Due to the change in material impedance at the bar–specimen interface, part of the compressive wave is reflected, while the remaining part of the wave is transmitted through the specimen into the transmission bar. During this process, the specimen must be uniformly compressed and undergo homogeneous deformation in compression. In the case of the Brazilian test, the ‘dynamic force equilibrium’ condition is satisfied when the forces at the ends of the bars are equal during the test time of the experiment. In addition to dynamic force equilibrium, dynamic Brazilian disc tests should ensure that crack initiates at the centre of the specimen.

During the dynamic Brazilian tests, the compressional waves generated from the incident bar transmits semi-radially into the cylindrical specimen (refer Fig. 3b). The compressional waves get reflected as a tensile stress pulse at the cylindrical free surface and reach the diametrical line of the specimen. Zhou et al. (2014) observed the stress pulses with incident angle (β) greater than 45° encounters multiple reflections, which lead to energy loss and further weaken the tensile stress wave. It was concluded through experimental and numerical investigation, the stress pulse with angle β ~ 30° reach the centre of the specimen with minimum reflections. With superpositions of additional tensile stress pulse from both sides, the centre of the specimen becomes the most vulnerable point in the specimen for a tensile failure.

The response of the rock specimen is determined using wave propagation theory (Kolsky 1963). The axial stress waves induced in the incident and the transmission bars are recorded using strain gauges mounted on the respective bars; consequently, three strain measurements were made: (i) incident, ε_i (ii) reflected, ε_r and (iii) transmitted, ε_t. A digital oscilloscope records the voltage signals at a sampling rate of 1.25 MHz. The noise in the strain signals are filtered, and Pochhammer-Chree dispersion correction (see Chen and Song (2011) and Rigby et al. (2018) for further details) is applied after that. The force accumulated on the incident (F₁) and transmitted (F₂) bar ends are evaluated using Eqs. 1 and 2:

$$F_{1} { } = {\text{ E}}_{{\text{B}}} {\text{A}}_{B} \left[ {\varepsilon_{i} \left( {\text{t}} \right) + \varepsilon_{r} \left( {\text{t}} \right)} \right]$$

(1)

$$F_{2} = {\text{E}}_{B} {\text{A}}_{B} \left[ {\varepsilon_{t} \left( {\text{t}} \right)} \right]$$

(2)

$${\text{A}}_{B} = \frac{{\pi { }D_{B}^{2} }}{4},$$

where A_B is the cross-sectional area of the bar, E_B is the elastic modulus of the pressure bar, and D_B is the diameter of the SHPB bar.

For the rock specimen is in the state of dynamic force equilibrium, we have:

$$F_{1} { } = { }F_{2} .$$

(3)

The dynamic split tensile strength of the rock specimen can be determined using either the peak load generated on the incident end or the transmitted end of the specimen (Jin et al. 2017). Ideally, with the assumption of force equilibrium, both the values should yield the same tensile strength values. Perfect dynamic equilibrium is not always possible, and considering the experimental errors, we use the average value as the dynamic tensile stress, ${\upsigma }_{\mathrm{t}}\left(\mathrm{t}\right)$:

$$\sigma_{{\text{t}}} \left( {\text{t}} \right) = { }\frac{{\left( {2F_{1} } \right)}}{{\pi {\text{D}}_{S} {\text{T}}}}{ }or{ }\frac{{\left( {2F_{2} } \right)}}{{\pi {\text{D}}_{S} {\text{T}}}}{ } \Rightarrow \frac{{2E_{B} {\text{A}}_{B} }}{{\pi D_{S} T}}\left[ {\varepsilon_{{\text{i}}} \left( {\text{t}} \right) + \varepsilon_{{\text{r}}} \left( {\text{t}} \right)} \right]{ }or\;\frac{{2E_{B} {\text{A}}_{B} }}{{\pi D_{S} T}}\left[ {\varepsilon_{t} \left( {\text{t}} \right)} \right]$$

$$\sigma_{{\text{t}}} \left( {\text{t}} \right)_{avg.} = \frac{{\left( {F_{1} + F_{2} } \right)}}{{\pi {\text{D}}_{S} {\text{T}}}} = \frac{{E_{B} {\text{A}}_{B} }}{{\pi D_{S} T}} \left[ {\varepsilon_{{\text{i}}} \left( {\text{t}} \right) + \varepsilon_{{\text{r}}} \left( {\text{t}} \right) + \varepsilon_{t} \left( {\text{t}} \right)} \right],$$

(4)

where D_S and T are the diameter and thickness of the cylindrical disc of the rock specimen.

2.2 Rock Specimen Preparation

In the present study, we investigate four different types of rocks of igneous, sedimentary and metamorphic origin. Samples of basalt, granite (igneous), sandstone (sedimentary) and marble (metamorphic) with densities of 2.90, 2.62, 2.04 and 2.70 g/cm³, respectively, were collected from different lithostratigraphic units: fine-grained basalt was collected from Hegau, Germany (referred hereafter as ‘HeBa’); pale pink, coarse-grained granite was collected from Malsburg, Germany (MaGr); fine-grained, porous sandstone was collected from Seeberg, Germany (SeSa); and lastly, calcite dominated marble was acquired from Carrara region, Italy (CaMa). Quasi-static mechanical properties of the rocks were carried out using a FORM + TEST Alpha 2–3000 hydraulic loading frame. With a minimum of three specimens per rock type, stress-controlled quasi-static Brazilian tests were performed with loading rates from 0.05 to 0.15 kN/s. The physical and mechanical properties of the rocks used in the present study are summarised in Table 1.

Table 1 Physical and mechanical properties of the investigated rocks

The Brazilian disc specimens were prepared according to the recommended ISRM standards (Zhou et al. 2012) for SHPB testing. Uniform, representative, cylindrical specimens of diameter 41 ± 0.25 mm were drill-cored from large blocks of each lithology. According to the ISRM recommendation, hard rock specimens or small diameter specimens should be prepared with a 1:1 slenderness ratio; soft rock specimens or large diameter specimens should be prepared with a slenderness ratio of 0.5:1 (Mishra et al. 2020). In the present study, all four types of rocks were prepared with two sets of length to diameter ratios, 0.5:1 and 1:1. The diametrical surfaces of the specimens were made flat, such that the surfaces are perpendicular to the loading axis. A total of 40 cylindrical specimens were prepared: 10 HeBa, 10 MaGr, 12 SeSa and 8 CaMa. The specimens were labelled after their rock type in sequential order.

Additional modifications were made to the cylindrical specimens to facilitate the dynamic force equilibrium and centrally initiated crack conditions. To prevent compressive stress concentration and failure at the loading ends (between the specimen and the bar), cylindrical specimens are recommended to have a flattened end (Rodríguez et al. 1994; Wang et al. 2004, 2006, 2009). The two cylindrical faces of the specimen in contact with the bars were trimmed and flattened, such that the flat ends are parallel to each other. The loading from the bar onto the specimen is thus distributed over the flattened area. The width of the flat portion is governed by the loading angle, 2α (shown in Fig. 3c). In the theoretical and experimental studies of Wang et al. (2004), flattened disc specimens with a loading angle of 20° are more likely to produce a central crack initiation. All the specimens in the present study were flattened as per Wang et al.’s (2004) recommendation. The expression for determining the tensile strength of a flattened Brazilian disc specimen is equivalent to a circular specimen, with an additional co-efficient. Wang et al.'s (2004) performed a rigorous stress analysis using an ANSYS numerical tool to determine the co-efficient value (= 0.95) for a loading angle of 20˚. The final expression for determining the tensile stress of the flattened Brazilian disc is given below (Wang et al. 2006):

$$\sigma_{t} \left( {\text{t}} \right)_{avg.} = { }\frac{{0.95\left( {F_{1} + F_{2} } \right)}}{{\pi D_{s} T}}$$

(5)

2.3 Analysis and Data Processing

2.3.1 Force Equilibrium and Validation

As mentioned in Sect. 2.1, the prerequisites for SHPB testing of the Brazilian disc are the ‘dynamic force equilibrium’ and ‘central crack initiation’ in the rock specimen. The signals recorded by the strain gauges on the incident and transmitted bar are processed, and the forces developed at the end of the bars are evaluated using Eq. 1 and Eq. 2. Figure 4a shows typical incident and reflected signals, with the corresponding forces generated at the bar ends. The forces at each end of the rock specimen remain approximately equal throughout the test time of the experiment, which suggests the rock specimen remained in the state of equilibrium before failure. Hence, the dynamic force equilibrium is satisfied.

Fig. 4

a Dynamic force evaluated at the ends of the specimen, b Raw voltage signal recorded from the left and right electric paint circuit

Furthermore, it is important to ensure that the crack originates at the centre of the rock specimen. Generally, a high-speed camera is used to monitor the crack propagation and the subsequent fracture process (Jin et al. 2017; Li et al. 2018b). Alternatively, multiple strain gauges can be placed on rock specimens for the same purpose (Wang et al. 2016; Zhou et al. 2014); however, the specimen dimensions in this study are too small to mount multiple strain gauges. Instead, a simpler and cost-effective method was employed based on the electric potential drop method to prove the hypotheses: (i) crack originates from the centre and (ii) crack propagates in the opposite direction (see definition in Fig. 4b). Interconnected electric circuits in the form of grids are painted on the surface of the rock specimen using electrically conductive paint (Bare Conductive, London, UK). Two such mirror image circuits are marked on the incident (left), and the transmitted (right) ends of the rock specimen, as shown in Fig. 4b (inset figure). A Wheatstone bridge balances the two legs of the circuit. The circuits are activated by passing a constant current through them, and the electric potential across the circuits is continuously monitored via a signal amplifier. Figure 4b shows the voltage–time signal recorded from the left and right circuits. It can be observed that the two signals have synchronised start and ending time. Each circuit signal has three distinct voltage drops (the regions are highlighted inside grey boxes); this suggests that cracks have originated from the centre (see graphical representation of hypothesis in Fig. 4b), and thus proves the hypothesis-i. The centrally originated crack is believed to travel in the opposite direction towards the ends of the bars. The large-sized fragmented specimen collected from the SHPB test was observed to be split into two halves (semi-disk shaped) by sequentially disconnecting the three grids of the left (or right) circuits along the centre of the specimen, which implies that hypothesis-ii is true. Also, we observe in Fig. 4a, the sectional voltage amplitudes (voltage difference between the two successive jumps) at the three locations are different; the possible reason could be that the propagating cracks are travelling at different velocities in the opposite direction. Overall, it implies that the specimen has failed in tension mode.

2.3.2 Determination of Strain Rate

Measurement of strain rate during the deformation is an important aspect of dynamic testing. During a traditional compressional SHPB testing, the strain rate is normally calculated from the strain signals measured on the incident, and transmitted bar or an approximate value is deduced from the velocity of the striker bar and length of the specimen (Rae et al. 2020; Shin and Kim 2019). Because of the non-uniform stress state in the Brazilian disk specimen, both methods will not yield a representative tensile strain rate. Thus, in the present study, an additional strain gauge was placed on the specimen surface to determine the strain rate up to the point of failure. In all our test specimens, a strain gauge (HBM, 1-LY66-6/120) was mounted on the centre of the rock specimen surface using an HBM X60 adhesive, such that the loading axis is perpendicular to the gauge axis and measures tensile strain. A schematic diagram of the strain gauge mounted flattened Brazilian specimen is shown in Fig. 3c.

A typical strain gauge signal recorded from MaGr02 is shown in Fig. 5a; the strain signal values are normalised (between 0 and 1) and plotted along with the tensile stress. The strain remains at zero until the stress signal experiences a sudden rise. At this point, the strain begins to rise gradually before abruptly increasing, and the signal is cut off. The abrupt increase of strain indicates that the fracture is growing in the specimen. Figure 5b shows this failure stage during the time interval from 0.1 to 0.275 ms. The failure initiation can be more clearly identified using the first derivative of strain signals, shown in Fig. 5b. The material deformation starts when the initial perturbation happens in the strain rate signal history, and the end of the failure is when the 'ε' signal shows an abrupt increase (Griffith et al. 2018). The strain rate is determined by taking the slope representative plotsof the strain curve over this macroscopic failure period (from point A–B in Fig. 5b). Figure 6 shows of tensile stress and strain history from each of the four different rock types (the region over which strain rate is determined is highlighted in the grey colour band). In all the test cases, the end of the failure zone is observed in the close vicinity of peak stress.

Fig. 5

a A typical plot of normalised strain and normalised stress versus time of a granite specimen (MaGr02), b an extract of the strain and strain rate between 0.1 and 0.275 ms

3 Experimental Results and Discussion

3.1 Dynamic Split Tensile Strength and its Strain Rate Dependency

Based on the methods described in Sect. 2.3, the tensile strength of the rock specimens and the strain rate of each experiment were evaluated. Table 2 lists the strain rates and corresponding split tensile strength values for all the test cases; the experimental uncertainty of stress and strain rate are also indicated. In the present experimental series, the quasi-static Brazilian tests were performed at strain rates ranging from 10^–5 /s to 10^–3 /s and the strain rates in the dynamic Brazilian tests ranged from 4 × 10^–1 /s to 2.7 × 10¹ /s. Figure 7 shows the variation of tensile strength with the strain rate under quasi-static and dynamic conditions for all lithologies. Overall, the dynamic tensile strength of the rocks is higher than the quasi-static tensile strength (1.5 to 5 times), and there is a strong dependency of tensile strength on strain rate.

Table 2 Dynamic split tensile strength and strain rate generated in different test specimens

The strain rate dependency of the dynamic split tensile strength of the four different rocks is shown in Fig. 7. In absolute terms, the quasi-static strength of the rocks is highest for basalt, followed by granite, marble and sandstone. Correspondingly, we see similar behaviours among the test specimens under dynamic loading. The sedimentary rocks like sandstones have relatively high heterogeneities (inherent flaws, micro-cracks, weak bedding planes) compared to igneous (basalt, granite) and metamorphic (marble) rocks, which significantly influences the strength of the rocks. Studies have shown that micro-cracks originating from the microscopic flaws significantly influence the dynamic strength of the material (Daphalapurkar et al. 2011).

Fig. 6

Tensile stress and strain against time for: a HeBa02, b MaGr05, c SeSa03, and d CaMa02

The increase in the dynamic tensile strength can be better understood using DIF, the dynamic strength normalised by the quasi-static strength of the material. Generally, power laws are used to fit the DIF (σ_t/σ_o) as a function of strain rate or loading rate (Doan and d’Hour 2012; Grady and Lipkin 1980; Lankford 1981). However, Kimberley et al. (2013) developed a universal rate-dependent theoretical scaling relationship incorporating the material’s microstructural properties. The interaction of pre-existing flaws and dynamics of the micro-crack growth have been shown to be important in describing the strength of the brittle materials. The model describes characteristic strength (σ_o) and characteristic strain rate (${\dot{\varepsilon }}_{o}$) by incorporating mechanical (Young’s modulus (E), fracture toughness (${K}_{IC})$, limiting crack speed (${c}_{d}$)) and microstructural (flaw size ($\overline{s })$, flaw density ($\eta )$) parameters. The functional form of characteristic stress and characteristic strain rate is shown in Eq. 6, as described in the original work of Kimberley et al. (2013).

$$\sigma_{0} = \alpha \frac{{K_{IC} }}{{\overline{s}\eta^{1/4} }};\dot{\varepsilon }_{0} = \alpha \frac{{c_{d} K_{IC} \eta^{1/4} }}{{\overline{s}E}}.$$

(6)

The characteristic stress is related to the stress required to generate a crack, thereby bridging the inherent flaws in the material; the value of α is chosen such that the characteristic stress value is equal to the quasi-static compressive strength. The characteristic strain rate is the critical strain rate at which the strength of the rock is double the quasi-static strength (DIF = 2). The universal theoretical scaling relationship in terms of characteristic strength and characteristic strain rate is shown in Eq. 7 (Kimberley et al. 2013):

$$\frac{{\sigma_{t} }}{{\sigma_{o} }} = 1 + \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{o} }}} \right)^{2/3} .$$

(7)

Kimberley et al. (2013) state that their theoretical model matches the behaviour of brittle materials (ceramics and geological materials) at both compression and tensile conditions. With regard to the compressional behaviour, their model has been verified, but very limited data were available in tension to make a detailed assessment. Hogan et al. (2015) explored Kimberley's relation in tension condition by fitting their indirect tension experimental data (using Brazilian disc technique) on meteorite samples at low strain rates.

Li et al. (2018c) questioned the validity of the Kimberley model, in particular to tension loading. Li et al. (2018c) developed a model similar to the Kimberley model based on the numerical simulation (DEM) and recommended a more fundamental form (shown in Eq. 8) for DIF. In the proposed equation, the exponent term, increase rate parameter (β), is a free parameter that can vary between 0 and 1. The increase rate parameter indicates the strain rate sensitivity; the higher the value, the more sensitive the rock to strain rate effects. Theoretically, the value of β is dependent on the type of the test (tension/compression) and the inherent material properties like crack density, wave velocity and the other heterogeneity characteristic of the rock. A review of the experimental data in dynamic tension (direct and indirect) along with the regression results is presented in Li et al. (2018a); the β value is found to vary from 0.35 to 0.63.

$$\frac{{\sigma_{t} }}{{\sigma_{o} }} = 1 + \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{o} }}} \right)^{\beta } .$$

(8)

In the present experimental series, the characteristic stress and characteristic strain rate for individual rocks values are obtained by non-linear least-square fitting (Eq. 8) to the experimental data set of each rock. The dependent variable's regression values and characteristic values are shown in the table in Fig. 7. For the rocks under investigation in Brazilian tests, β is found to vary from 0.54 to 0.71. With β being a free parameter, the characteristic strain rate ($\dot{{\varepsilon }_{o}})$ of the investigated rocks in tension are determined to be: Basalt = 1.32 ± 0.96 /s; Granite = 2.09 ± 1.63 /s; Sandstone: 1.49 ± 0.68 /s; Marble = 2.83 ± 2.50 /s. And the characteristic stress (${\sigma }_{o})$ of the investigated rocks are: Basalt = 15.03 ± 2.56 MPa; Granite = 8.16 ± 2.00 MPa; Sandstone: 4.38 ± 0.60 MPa; Marble = 6.72 ± 1.85 MPa. These characteristic values indicate the relative dynamic strength of the investigated rocks compared to their quasi-static strength.

Fig. 7

Variation of tensile strength with strain rate for the investigated rocks: Basalt, Granite, Sandstone and Marble

Kimberley’s theoretical model is available in the normalised form (dynamic strength/quasi-static strength); The experimentally observed results from the present study are graphically compared in the similar normalised form and compared with the theoretical model in Fig. 8. The tensile strength and strain rate listed in Table 2 are normalised against their corresponding rock’s characteristic value. Considering the experimental uncertainty, a β value of 0.583 ± 0.012 (within 2 standard deviation errors), close to the value of 2/3 suggested by Kimberley et al. (2013) Consequently, we have repeated the curve fitting procedure with β = 2/3 to determine the definitive characteristic strain rate. The revised characteristic strain rate values for the rocks are: Basalt = 2.40 ± 0.68 /s; Granite = 2.52 ± 1.01 /s; Sandstone: 2.61 ± 0.56 /s; Marble = 2.39 ± 1.15 /s. Furthermore, the flaw density and flaw size for the specific rock type can be technically determined using the characteristic values in Eq. 6.

Fig. 8

Normalised tensile strength data from the present experimental series is compared with the strength model of Kimberley et al. (2013)

The previous study from our research group (Rae et al. 2020, 2022; Zwiessler et al. 2017) have used the same rock types, Malsburg Granite, Seeberger Sandstone and Carrara Marble for compressive SHPB experiments and have determined the characteristic strain rate values. Since the results are available for rocks with the same lithologies in compression, comparing the characteristic strain rate among compression and tension experiments is interesting. The characteristic strain rate of Malsburg Granite, Seeberger Sandstone and Carrara Marble in compression was found to be 217 ± 95 /s, 322 ± 92 /s and 144 ± 33 /s, respectively (Rae et al. 2020, 2022). The ratio of the characteristic strain rate in compression to the characteristic strain rate tension for the rock types are: MaGr =  ~ 86; SeSa =  ~ 123; CaMa =  ~ 60; we observe that there is no definitive ratio among them, and they do not overlap as well.

3.2 Dynamic Fragmentation

A typical dynamic Brazilian test performed using SHPB will result in four different types of fragments (Zhu et al. 2020): Type I—semi-disc, Type II—section fragments, Type III—small-sized fragments and Type IV—debris/powder (see Fig. 2). Type I and Type II are coarse sized fragments that are primarily caused due to tension failure. Type I fragments are mostly two large-sized semi-circular disc-shaped fragments. Type II fragments are flake-like split fragments emerging from tensile failure. Type III fragments are small-sized section fragments due to shear failure, generally appear close to the bar ends (Dai et al. 2010); Type IV fragments are mostly in the pulverised state, generated around the shear and tensile fracture surfaces. In the present study, Type I and Type II fragments are categorised as coarse fragments (primary), and they are mainly bounded by tensile fractures (mode I). Type III and IV fragments are finer particle fragments (secondary) resulting from different kinds of failure modes, possibly to a greater extent by shear failure. Therefore, secondary finer fragments cannot, in themselves, be classified under specific failure modes. The fragment morphology of different rocks (HeBa, MaGr, SeSa, and CaMa) at different strain rates with the four fragment types are highlighted in Fig. 9.

Fig. 9

Fragment morphology of Basalt (HeBa), Granite (MaGr), Sandstone (SeSa), Marble (CaMa) after dynamic Brazilian failure

Particle size distributions were measured for all the fragmented specimens collected after failure using sieves. Standard sieves with square apertures of 16, 6.3, 2, 1, 0.63, 0.4 and 0.2 mm were used, and particles finer than 0.2 mm were collected in a pan. Several distribution functions have been used to fit the size distribution of the fragments generated from high dynamic events: power law, log-normal, Weibull, Gilvarry, Swebrec; the most popular is Weibull distribution for impact fragmentation (Cheong et al. 2004). ISO standards (ISO 9276–3:2008) recommend Rosin–Rammler (Weibull) distribution and Gates–Gaudin–Schuhmann (bilogarthimic) distribution for the extreme value analysis of the coarse and fine particles, respectively. Sanchidrián et al. (2014) have performed a detailed fragment analysis on high strain deformed rocks and have recommended Grady, Weibull and Swebrec functions as an ideal choice for coarse fragments, and bi-component distribution like bi-modal Weibull and Grady are preferred for fine fragments.

Figure 10 presents the Fragment Size Distribution (FSD) data and fitted cumulative Weibull distributions for basalt, granite, sandstone and marble at different strain rates. The goodness-of-fit is largely considered to be extremely good for all the test cases, except for a few test cases of granite at higher strain rates (24.42 /s and 27.14 /s). In the FSDs, the weight of fragments retained on each of the sieves has been expressed as the percentage of the total weight of the specimen and subsequently, the cumulative weight of the fragments smaller than size ‘D’, P(< D) is determined. For all the test cases, the passing weight percentage of the fragments increases with strain rate at all particle sizes. The majority of the fragments (more than 60%, as shown in the inset Fig. 10) were found to retain on the sieves having larger aperture sizes (16 mm and 6.3 mm); these fragments were shaped to fit the characteristics of Type I and Type-II fragments. Therefore, a 6.3 mm sieve was used to segregate primary and secondary fragments; particles retained on the 6.3 mm sieve are primary fragments, and the rest of the particles passing through the 6.3 mm sieve are secondary fragments.

Fig. 10

Fragment size distributions for the rocks: a Basalt, b Granite, c Sandstone, and d Marble

3.2.1 Measurement of Primary Fragments

The primary fracture fragments of the rocks splitting into two half-disc geometries (Type-I) and angular flaky fragments along the loading direction (Type II) are shown in Fig. 9, under primary fragments. At low strain rate conditions, the cylindrical specimen generally splits into two halves and as the strain rate increases, the discs are severely damaged (resulting in fractural debris). A cumulative fragment size distribution for each rock type is fitted to the sieve analysis data using the two-parameter Weibull distribution. The cumulative density function of Weibull distribution is expressed as:

$$P\left( { < D} \right) = 1 - \exp \left[ { - \frac{D}{{S_{o}^{p} }}} \right]^{{n_{p} }} ,$$

(9)

where P(< D) is the cumulative weight percent of all the fragments smaller than particle size (D); n_p and ${S}_{o}^{p}$ are fitting parameters.

The parameter ‘${S}_{o}^{p}$’ is the scale factor, interpreted as a characteristic dimension of the fragments or maximum diameter (Wu et al. 2009) of the fragments over the accumulated range. The parameter ‘n_p’ is the shape factor representing the fragment size distribution range; it is also referred to as the Weibull modulus (or uniformity index). The Weibull parameters derived from the experimental sieve data are shown in Fig. 10. As the distribution is mostly dominated by Type I and Type II fragments, the characteristic size (${S}_{o}^{p})$ and uniformity index (n_p) represent the features of coarse sized primary fragments.

The primary characteristic fragment size (${S}_{o}^{p}$) is plotted as a function of strain rate for rocks HeBa, MaGr, SeSa and CaMa in Fig. 11i a–d. For a comprehensive understanding, the characteristic fragment size for each of the rocks is plotted along with the characteristic values of the theoretical models derived for the respective rock type. For comparison with the experimental data, the following average fracture toughness (K_IC) values are chosen for the theoretical model (Atkinson and Meredith 1987): K_{IC_Basalt} = 2.58 MPa m^0.5, K_{IC_Granite} = 1.73 MPa m^0.5, K_{IC_sandstone} = 0.9 MPa m^0.5 and K_{IC_marble} = 1.16 MPa m^0.5. The elastic wave speed is obtained theoretically from young's modulus and density of the rock: c = sqrt (E_s/ρ). A review of the existing theoretical models is available in Li et al. (2018a); the popular model includes Grady model, GC model, YT model, Zhou et al. model, and YTGC model. The expression for characteristic fragment size proposed in the theoretical models are summarised below (Eq. 10–13):

Fig. 11

i Dependency of characteristic fragment size on strain rate in rocks: a Basalt, b Granite, c Sandstone, and d Marble; ii Uniformity index as a function strain rates for primary fragments

Grady model (Grady 1982):

$$S_{Grady} = \left( {\frac{{\sqrt {12} K_{IC} }}{{\rho c\dot{\varepsilon }}}} \right)^{\frac{2}{3}} .$$

(10)

GC model (Glenn and Chudnovsky 1986):

$$S_{GC} = 2 \sqrt {\frac{\alpha }{3}} sinh\frac{\varphi }{3},$$

(11)

$$where\;\varphi = sinh^{ - 1} \left( {\beta \left( {\frac{3}{\alpha }} \right)^{\frac{3}{2}} } \right), \alpha = 12 \left( {\frac{{\sigma_{c} }}{{\rho c\dot{\varepsilon }}}} \right) \;and \beta = 12 \left( {\frac{{K_{IC} }}{{\rho c\dot{\varepsilon }}}} \right)^{2}$$

YT model (Yew and Taylor 1994):

$$S_{YT} = \left( {\frac{{\sqrt 3 K_{IC} }}{{\rho c\dot{\varepsilon }}}} \right)^{\frac{2}{3}} .$$

(12)

Zhou et al. model (Zhou et al. 2006):

$$S_{Zhou} = \frac{{4.5 S_{o} }}{{\left( {1 + 0.77\left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{o} }}} \right)^{\frac{1}{4}} + 5.4\left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{o} }}} \right)^{\frac{3}{4}} } \right)}},$$

(13)

where $S_{o} = \frac{{K_{IC}^{2} }}{{\sigma_{c}^{2} }}$ and $\dot{\varepsilon }_{o} = \frac{{c\sigma_{c}^{3} }}{{E_{s} K_{IC}^{2} }}$

YTGC model (Jan Stránský 2010):

$$S_{YTGC} = \left( {\frac{{2K_{IC} }}{{\rho \sigma_{c} \dot{\varepsilon }}}} \right)^{\frac{1}{2}} .$$

(14)

Figure 11i compares the characteristic size of fragments from the present experiments to the various fragmentation models listed above. The Grady model has been considered to overestimate the characteristic size, particularly at a lower strain rate (Griffith et al. 2018). In the present study, characteristic values at lower strain rates (1–10/s) show no significant difference in the characteristic values but slightly decrease as the strain rate increase. Such behaviour is described in the GC model; however, the GC model tends to over predict the present experimental results. At intermediate strain rates (10–27/s), the measured values are more closely matched by the Zhou et al. model than the GC model, except for the porous SeSa. The characteristic dimension of the SeSa is much lower than the Zhou et al. model predicts. As discussed earlier, the sandstone rock is highly porous, and the crack branching process is quite active from the other three rock types. Even at low impact experiments, the dominant fragments of sandstone were observed to be barely intact, which indicates the rock has probably undergone an early shear failure fracture at a lower strain rate.

The shape factor or uniformity index (n_p) represents the homogeneity of the fragment size distribution; a higher value corresponds to a homogeneous set with uniform fragment size, whereas a lower value represents a heterogeneous set with a wide distribution of fragment size (Lu et al. 2008). The influence of strain rate on the uniformity index (n_p) is shown as a scatter plot in Fig. 11ii. The n_p value of the fragment size distribution is rate-dependent and decreases with an increase in strain rate. The trend of the index values with respect to the strain rate suggests that beyond a transitional strain rate, the index value remains constant. The transition strain rate is defined as strain rate range over which the dynamic strength becomes significantly different from the quasi‐static strength. It is evident from Fig. 11i (characteristic fragment size plotted against strain rate), the fragment size remains constant at lower strain rates (in the quasi-static regime) and begins to decrease with increase in strain rate (dynamic effects begins to dominate). Given the limited number of experiments, the exact value of the transitional strain rate was not determined; the strain rate range over which the dynamic effects significantly influence the fragmentation process in the investigated rocks (basalt, granite, marble) is between ~ 10 and 15 /s (and for sandstone the values is ~ 5/s). Interestingly, around the zone of this transitional strain rate, the trend of the uniformity index changes. As seen in Fig. 11ii, over the lower strain rate range (0–15/s) the uniformity index (np) values are very high (indicates homogeneous fragments) and decreases with increase in the strain rate (becomes heterogenous). The transitional strain rate for sandstone (SeSa) could be much less than 10 /s. Additional experimental data are required beyond transitional strain rates for further understanding. Unfortunately, the present experimental setup is difficult to attain high strain rates in the Brazilian test mode.

The statistical properties of Weibull distribution for primary (coarse) fragments are also derived using the formula: (i) mean, $\mu_{p - mean} = S_{0}^{p}\Gamma \left( {1 + 1/n_{p} } \right)$ and (ii) variance, $\sigma_{p}^{2} = S_{0}^{p2}\Gamma \left( {1 + 2/n_{p} } \right) - \mu_{{p - {\text{mean}}}}^{2}$, where Γ is the gamma function. The mean of the fitted Weibull CDF is interpreted as the 'Mean particle size, μ_p-mean’ of the primary fragments, which are moderately lower than the characteristic size values.

3.2.2 Measurement of Secondary Fragments.

The secondary fragments involve complex fracture processes with different failure modes, possibly dominated by the shear cracks; furthermore, these cracks branch out leading to fine fragments (Momber 2000). In the previous section, for coarse-grained particle fragments, Weibull distribution CDF was found to represent the experimental data well. However, if the analysis is focused on the finer portion of the fragments, i.e. when the size of the fragments is very small when compared to characteristic size (D <  < S_o), Weibull CDF (Eq. 9) gets reduced to (Momber 2000; Turcotte 1986; Wu et al. 2009) the form shown in Eq. 15. Where S(< D) is the cumulative weight percent of all the fine fragments, $S_{o}^{s}$ and $n_{s}$ are shape and scale factors, respectively, for the secondary fragments.

$$S\left( { < D} \right)\% = \left( {\frac{D}{{S_{0}^{s*} }}} \right)^{{n_{s} }} .$$

(15)

It is interesting to observe that the reduced form of Weibull CDF distribution is similar to the Gates-Gaudin-Schuhmann distribution (Macı́as-Garcı́a et al. 2004; Turcotte 1986). Equation 15 is further transformed into a linearised function by applying natural logarithm, which yields:

$$ln{ }\frac{{S\left( { < D} \right)}}{100} = ln\left( { - \frac{D}{{S_{o}^{s} }}} \right)^{{n_{s} }}$$

(16)

$$l_{n} \frac{{S\left( { < D} \right)}}{100} = n_{s} \cdot \ln D - n_{s} \cdot \ln S_{0}^{s}$$

(17)

Equation 17 is in the linear form y = m (x) + C, which can be graphically represented with ln (S < D)/100 as the y-axis and ln (D) as the x-axis. The slope of the linear fit data gives us the shape factor, ‘n_s’ and the characteristic size for secondary fragments, ${S}_{o}^{s}$ is obtained from the y-intercept. It is important to note that S(< D) is the cumulative weight percent of all secondary fragments, passing through 6.3 mm and retained on 2 mm and below sieve sizes, viz., the primary fragments are removed in the analysis. The graphical natural log–log plots of secondary fragments for basalt, granite, sandstone and marble rocks are shown in Fig. 12. The individually derived parameters of the distribution at varying strain rates are mentioned in Fig. 12(inset table); the co-efficient of determination (R²) values is greater than 0.970. When compared to primary fragments, the uniformity index (n_s) value does not vary much with the increase in the strain rate, meaning the distributions have a similar D value (also called the fractal dimension, D = 3–n_s). The average D values for the basalt, granite, sandstone, and marble is 2.103, 2.239, 2.829, and 2.730, respectively, which indicates that the fragment size distributions are self-similar.

Fig. 12

Grain size distribution of the secondary fracture debris for a Basalt, b Granite, c Sandstone, and d Marble

Similar to primary fragments, the statistical properties of Gates–Gaudin–Schuhmann distribution for secondary (fine) fragments are evaluated using: (i) mean, μ_s-mean = (${S}_{o}^{p}$ n_s) / (1 + n_s) and (ii) variance, ${\sigma }_{s}^{2}$ = ${{S}_{o}^{p}}^{2}$ [n_s/(n_s + 2) – n_s²/(n_s + 1)²].

3.2.3 Normalisation of Fragment Size

Dynamic fragmentation of rocks is commonly treated as a statistical process, which depends on mechanical loading parameters (strain rate, testing method) and inherent rock properties (density, modulus, mineralogical composition, microstructural features, etc.). It would be convenient to represent the fragmented products in a dimensionless quantity. In this section, the strain rate ($\dot{\varepsilon })$ and the mean fragment size (μ_p-mean and μ_s-mean) are normalised over characteristic strain rate (${\dot{\varepsilon }}_{o})$ and characteristic length (L_o), respectively. The characteristic length, L_o is the representative scale of the system used for comparing experimental data with similar conditions. In the present study, it is the distance travelled by the stress waves over the characteristic time (t_o), which is given by the expression (Camacho and Ortiz 1996; Li et al. 2018a):

$$t_{o} = { }\frac{{K_{IC}^{2} }}{{c_{p} \sigma_{t}^{2} }}$$

(18)

$$L_{o} = c_{p} .t_{o} \to \frac{{K_{IC}^{2} }}{{\sigma_{t}^{2} }},$$

(19)

where σ_t is the quasi-static tensile strength, and c_p is the P-wave velocity of the rock.

The reference values of K_IC used in Eq. 19 are mentioned in Sect. 3.2.1. The characteristic values of length, stress and strain rate for all the four rock types are summarised in Table 3.

Table 3 The estimated characteristic parameters for different rocks

From Sect.3.2.1, of the many theoretical fragmentation models, the most relevant models for primary fragments are Grady (1982), Glenn and Chudnovsky (1986) and Zhou et al. (2006) models. To compare the experimental results with the existing theoretical models, the average fragment size needs to be appropriately normalised. The expression for normalised mean fragment size as per the theoretical model of Grady (1982), Glenn and Chudnovsky (1986) and Zhou et al. (2006) with the normalised strain rate are listed in Eq. 20-Eq. 22 (Levy and Molinari 2010):

$$\overline{S}_{Grady} = \left( {\frac{24}{{\overline{{\dot{\varepsilon }}}^{2} }}} \right)^{\frac{1}{2}}$$

(20)

$$\overline{S}_{GC} = { }\frac{4}{{\overline{{\dot{\varepsilon }}} }}\sinh \left( {\frac{1}{3}{ }sinh^{ - 1} \left( {\frac{3}{2}\overline{{\dot{\varepsilon }}} } \right)} \right)$$

(21)

$$\overline{S}_{zhou} = \frac{4.5}{{1 + 4.5\overline{\dot{\varepsilon }}^{2/3} }},$$

(22)

where$\overline{{\dot{\varepsilon }}} = \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{o} }}{ };\overline{{S{ }}} = \frac{{S_{o} }}{{L_{o} }}.$

The fragment size (primary and secondary) for different rocks from the present study are summarised in Fig. 13a. A simple power-law is commonly used for the size distribution of the fragments. The power-law fits very well with the experimental data; Fig. 13a shows that the normalised mean particle size of primary fragments gradually decreases with the strain rate and remains flat at the intermediate strain rate ($\dot{\varepsilon }$ > 10¹) onwards. In the case of secondary fragments, the mean fragment size begins to flatten at a lower strain rate (10⁰ < $\dot{\varepsilon }$  < 10¹) onwards.

Fig. 13

a An overview plot of normalised mean particle size (primary and secondary) versus normalised strain rate; b A comparison of normalised mean particle size with different fragmentation models in log–log scale

The fragmentation results of the present study for mean particle size of primary fragments are compared with the theoretical models in the non-dimensional log–log plot in Fig. 13b. Although none of these theoretical models predicts the exact experimental fragment size, the trend of the experimental data is more similar to the Glenn and Chudnovsky (GC) model than the Grady model. However, the fragment size magnitude from experiments is three times lower than the GC model. Moreover, the strain rate sensitivity in GC models appears to begin at low strain rates (10⁰ < $\dot{\varepsilon }$  < 10¹). In contrast, in the present experiments, the size of the fragments begins to decrease at an intermediate strain rate onwards ($\dot{\varepsilon }$ > 10¹). A global power-law relation defining the rate dependency of the mean particle size of primary (${\overline{S} }_{p})$ and secondary (${\overline{S} }_{s})$ fragments from the experiments are given as:

$$\overline{S}_{p} = { }0.69 \pm 0.03{ }\overline{{\dot{\varepsilon }}} { }^{{ - 0.019{ } \pm 0.031}} { };{ }\overline{S}_{s} = { }0.125 \pm 0.01{ }\overline{{\dot{\varepsilon }}} { }^{{ - 0.513{ } \pm { }0.013}}$$

(23)

No specific model is available to compare the secondary finer debris, and the present experimental data cannot be directly compared with the existing theoretical models. But for completeness, the experimental results of secondary fragments are cautiously correlated in the same plot adjacent to primary fragments. The power law for secondary fragments appears to decrease linearly at low to intermediate strain rates. The secondary fragment sizes are significantly lower (~ an order of magnitude) than the primary fragment size. The power law for primary fragments of dynamic Brazilian tests is nearly entirely independent of strain rate. However, there are signs of a decrease in the fragment size at an intermediate strain rate. Additional investigation at a higher strain rate will determine any significant effect of strain rates on the fragment size thereafter.

4 Summary and Conclusion

In this study, 40 dynamic Brazilian experiments are performed to determine the tensile strength and fragment size at low to intermediate strain rates (in the range of 10⁰ to 2.7 × 10¹ /s). Four different rock lithologies are considered in the present study, of which two are igneous rocks (basalt and granite), and the other two belong to sedimentary (sandstone) and metamorphic type (marble), respectively. We demonstrate that reliable strain rate measurements are possible using a centrally mounted strain gauge in the flattened Brazilian rock specimens. The experimental results show that the split tensile strength of the rock is dependent on strain rate, more specifically, the characteristic strain rate. The average characteristic strain rate in tension for basalt, granite, sandstone and marble are found to be 2.40 ± 0.68, 2.52 ± 1.0, 2.61 ± 0.56 and 2.39 ± 1.15, respectively. Moreover, the characteristic strain rate in tension is found to be approximately 1 to 2 orders of magnitude lower than the characteristic value of the same rock in compression. The split tensile strength of rocks in a unified form expressed in terms of characteristic strain rate and characteristic stress has a rate of increase exponent factor of 0.583 ± 0.012. Considering the influence of rock's inhomogeneity and non-linear behaviour, the experimental results of the split tensile test are very much in accordance with the universal theoretical scaling model, as predicted by Kimberley et al. (2013).

The study showed that fragmentation in split tension mode is important in understanding various phenomena, in which indirect tension failure occurs. The fragment size distribution is determined for two classes of fragments, namely, coarser primary fragment (particle size > 6.3 mm) and finer secondary fragment (particle size < 6.3 mm). A power-law function of strain rate describes the mean fragment sizes of rocks in the primary and secondary assembly. The experimental results do not correspond to any of the existing theoretical models, but the mean particle size of the primary fragment is found to behave similarly to Glenn and Chudnovsky’s model at lower strain rates, where fragment size remains nearly constant up to the transitional strain rate and decrease after that. It can be experimentally stated that the theoretical models are partially successful in predicting the dominant fragment size in the dynamic split tension mode. Regarding secondary fragments, the finer fragment size appears to follow a linear decreasing trend in the log–log plot, and the fragment size values are lower by an order magnitude than the primary fragment size. In addition, it is important to note that the secondary fragments from the experiments are a major by-product and have a significant role in tensile fragmentation, particularly at an intermediate strain rate.