Skip to main content
SpringerLink
Log in

Numerical Modeling of Stand-Up Time of Tunnels Considering Time-Dependent Deformation of Jointed Rock Masses

  • Original Paper
  • Published:
Rock Mechanics and Rock Engineering Aims and scope Submit manuscript

Abstract

The mechanical responses of tunnels are time-dependent due to creep deformation of rock masses, which can result in large deformations on tunnel walls over time and influence excavation stability. This study investigates time-dependent deformation behaviors of tunnels excavated in jointed rock masses. The creep deformations of both rock and joints are considered using a creep model for jointed rock masses implemented in a distinct-element method code. Simulations of the time-dependent deformation behavior of tunnels are conducted using two-dimensional plane strain models based on the convergence-confinement analysis method. The weakening of the rock mass in a cross-section in an excavated tunnel due to time-dependent deformation of rock mass is simulated using the internal pressure reduction method. Stand-up times of tunnels excavated in jointed rock masses with different rock mass qualities and unsupported roof spans are simulated. The simulation results agree with field data, which validates the effectiveness of the analysis approach used. The analysis approach provides a useful tool for improving the understanding of time-dependent deformation behavior of tunnels.

Highlights

  • Time-dependent deformation of rock mass near the tunnel face is simulated using a creep model for jointed rock mass implemented in UDEC.

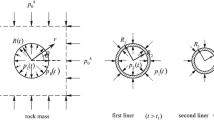
  • The weakening of face-effect due to time-dependent deformation of rock mass can be analyzed using the convergence-confinement and the internal pressure reduction methods.

  • Stand-up times of unsupported tunnels in joined rock masses are simulated.

  • The simulated stand-up times agree with Bieniawski’s field data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

References

  • Abdollahi MS, Najafi M, Bafghi AY, Marji MF (2019) A 3D numerical model to determine suitable reinforcement strategies for passing TBM through a fault zone, a case study: Safaroud water transmission tunnel Iran. Tunn Undergr Space Technol 88:186–199

    Article  Google Scholar 

  • Aftes (1976) Recommandations relatives à la méthode convergence-confinement. Tunnels et Ouvrages souterrains

  • Alejano L, Alonso E, Rodriguez-Dono A, Fernandez-Manin G (2010) Application of the convergence-confinement method to tunnels in rock masses exhibiting Hoek–Brown strain-softening behaviour. Int J Rock Mech Min Sci 1997(47):150–160

    Article  Google Scholar 

  • Barla G, Bonini M, Debernardi D (2010) Time dependent deformations in squeezing tunnels. ISSMGE Int J Geoeng Case Hist 2:40–65

    Google Scholar 

  • Barla G, Debernardi D, Sterpi D (2012) Time-dependent modeling of tunnels in squeezing conditions. Int J Geomech 12:697–710

    Article  Google Scholar 

  • Barton N (1978) Recent experiences with the Q-system of tunnel support design.

  • Barton N (1995) The influence of joint properties in modelling jointed rock masses. In: 8th ISRM congress, 1995. OnePetro

  • Bieniawski ZT (1989) Engineering rock mass classifications: a complete manual for engineers and geologists in mining, civil, and petroleum engineering. Wiley

    Google Scholar 

  • Bieniawski Z (1990) Tunnel design by rock mass classifications. Pennsylvania State Univ University Park Dept of Mineral Engineering

  • Brown ET, Bray JW, Ladanyi B, Hoek E (1983) Ground response curves for rock tunnels. J Geotech Eng 109:15–39

    Article  Google Scholar 

  • Cai M (2008) Influence of stress path on tunnel excavation response—numerical tool selection and modeling strategy. Tunn Undergr Space Technol 23:618–628

    Article  Google Scholar 

  • Cai M (2011) Rock mass characterization and rock property variability considerations for tunnel and cavern design. Rock Mech Rock Eng 44:379–399

    Article  Google Scholar 

  • Cai M, Kaiser P, Uno H, Tasaka Y, Minami M (2004) Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int J Rock Mech Min Sci 41:3–19

    Article  Google Scholar 

  • Cai M, Kaiser P, Tasaka Y, Minami M (2007) Determination of residual strength parameters of jointed rock masses using the GSI system. Int J Rock Mech Min Sci 44:247–265

    Article  Google Scholar 

  • Carranza-Torres C (2009) Analytical and numerical study of the mechanics of rockbolt reinforcement around tunnels in rock masses. Rock Mech Rock Eng 42:175–228

    Article  Google Scholar 

  • Carranza-Torres C, Fairhurst C (2000) Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek–Brown failure criterion. Tunn Undergr Space Technol 15:187–213

    Article  Google Scholar 

  • Eberhardt E (2001) Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face. Int J Rock Mech Min Sci 38:499–518

    Article  Google Scholar 

  • Estébanez E, Lage A (2018) Analytical formulation of stand-up time based on 1989 Beniawski's chart. In: ISRM European Rock Mechanics Symposium-EUROCK 2018, OnePetro

  • Fahimifar A, Tehrani FM, Hedayat A, Vakilzadeh A (2010) Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field. Tunn Undergr Space Technol 25:297–304

    Article  Google Scholar 

  • Guan Z, Jiang Y, Tanabashi Y, Huang H (2008) A new rheological model and its application in mountain tunnelling. Tunn Undergr Space Technol 23:292–299

    Article  Google Scholar 

  • Herget G (1987) Stress assumptions for underground excavations in the Canadian Shield. Int J Rock Mech Min Sci Geomech Abstr 24:95–97

    Article  Google Scholar 

  • Itasca (2015) UDEC (universal distinct element code), version 6.0. Minneapolis Itasca

  • Kabwe E, Karakus M, Chanda EK (2020a) Isotropic damage constitutive model for time-dependent behaviour of tunnels in squeezing ground. Comput Geotech 127:103738

    Article  Google Scholar 

  • Kabwe E, Karakus M, Chanda EK (2020b) Time-dependent solution for non-circular tunnels considering the elasto-viscoplastic rockmass. Int J Rock Mech Min Sci 133:104395

    Article  Google Scholar 

  • Kontogianni V, Psimoulis P, Stiros S (2006) What is the contribution of time-dependent deformation in tunnel convergence? Eng Geol 82:264–267

    Article  Google Scholar 

  • Kuesel TR, King EH, Bickel JO (2012) Tunnel engineering handbook. Springer Science & Business Media

    Google Scholar 

  • Lauffer H (1958) Gebirgsklassifizierung für den Stollenbau: Geology Bauwesen, v. 24

  • Lauffer H (1988) Zur Gebirgsklassifizierung Bei Fraesvortrieben. Felsbau 6:137–149

    Google Scholar 

  • Malan DF (1998) Investigation into the identification and modelling of time-dependent behaviour of deep level excavations in hard rock

  • Manh HT, Sulem J, Subrin D, Billaux D (2015) Anisotropic time-dependent modeling of tunnel excavation in squeezing ground. Rock Mech Rock Eng 48:2301–2317

    Article  Google Scholar 

  • Martin C, Kaiser P, Mccreath D (1999) Hoek-Brown parameters for predicting the depth of brittle failure around tunnels. Can Geotech J 36:136–151

    Article  Google Scholar 

  • Nguyen V-M, Nguyen Q-P (2015) Analytical solution for estimating the stand-up time of the rock mass surrounding tunnel. Tunn Undergr Space Technol 47:10–15

    Article  Google Scholar 

  • Pan Y-W, Dong J-J (1991) Time-dependent tunnel convergence—I. Formulation of the model. Int J Rock Mech Min Sci Geomech Abstr 28:469–475

    Article  Google Scholar 

  • Panet M, Guellec P (1974) Contribution à l'étude du soutènement d'un tunnel à l'arrière du front de taille. Progres en mecanique des roches-comptes rendus du 3eme congres de la societe internationale de mecanique des roches, Denver 1974

  • Panet M, Sulem J (2022) Convergence-confinement method for tunnel design. Springer

    Book  Google Scholar 

  • Panet M, Givet P, Guilloux A, Duc J, Piraud J, Wong H (2001) The convergence–confinement method. Press ENPC

    Google Scholar 

  • Ramamurthy T (2007) A realistic approach to estimate stand-up time. In: 11th ISRM Congress, 2007. OnePetro

  • Read R, Chandler N, Dzik E (1998) In situ strength criteria for tunnel design in highly-stressed rock masses. Int J Rock Mech Min Sci 35:261–278

    Article  Google Scholar 

  • Sainoki A, Tabata S, Mitri HS, Fukuda D, Kodama J-I (2017) Time-dependent tunnel deformations in homogeneous and heterogeneous weak rock formations. Comput Geotech 92:186–200

    Article  Google Scholar 

  • Sakurai S (1978) Approximate time-dependent analysis of tunnel support structure considering progress of tunnel face. Int J Numer Anal Meth Geomech 2:159–175

    Article  Google Scholar 

  • Sakurai S (1997) Strength parameters of rocks determined from back analysis of measured displacements. In: First Asian Rock Mechanics Symposium. ISRM, Seoul, pp 95–99

  • Sharifzadeh M, Tarifard A, Moridi MA (2013) Time-dependent behavior of tunnel lining in weak rock mass based on displacement back analysis method. Tunn Undergr Space Technol 38:348–356

    Article  Google Scholar 

  • Shen B, Barton N (1997) The disturbed zone around tunnels in jointed rock masses. Int J Rock Mech Min Sci 34:117–126

    Article  Google Scholar 

  • Sulem J, Panet M, Guenot A (1987) An analytical solution for time-dependent displacements in a circular tunnel. Int J Rock Mech Min Sci Geomech Abstr 24:155–164

    Article  Google Scholar 

  • Unlu T, Gercek H (2003) Effect of Poisson’s ratio on the normalized radial displacements occurring around the face of a circular tunnel. Tunn Undergr Space Technol 18:547–553

    Article  Google Scholar 

  • Vlachopoulos N, Diederichs M (2009) Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels. Rock Mech Rock Eng 42:131–146

    Article  Google Scholar 

  • Vlachopoulos N, Diederichs MS (2014) Appropriate uses and practical limitations of 2D numerical analysis of tunnels and tunnel support response. Geotech Geol Eng 32:469–488

    Article  Google Scholar 

  • Wang M, Cai M (2020a) A grain-based time-to-failure creep model for brittle rocks. Comput Geotech 119:103344

    Article  Google Scholar 

  • Wang M, Cai M (2020b) Modeling time-dependent deformation of rock joint. In: 54th US Rock Mechanics/Geomechanics Symposium. OnePetro

  • Wang M, Cai M (2021a) Numerical modeling of time-dependent spalling of rock pillars. Int J Rock Mech Min Sci 141:104725

    Article  Google Scholar 

  • Wang M, Cai M (2021b) A simplified model for time-dependent deformation of rock joints. Rock Mech Rock Eng 54:1779–1797

    Article  Google Scholar 

  • Wang M, Cai M (2021c) Simulation of time-dependent deformation of brittle rock pillars using a grain-based time-to-failure model. In: 55th US Rock Mechanics/Geomechanics Symposium. OnePetro

  • Wang M, Cai M (2022) Modeling of time-dependent deformation of jointed rock mass. Rock Mech Rock Eng.https://doi.org/10.1007/s00603-021-02750-2

  • Xu G, He C, Yang Q, Wang B (2019) Progressive failure process of secondary lining of a tunnel under creep effect of surrounding rock. Tunn Undergr Space Technol 90:76–98

    Article  Google Scholar 

  • Zhang L, Liu Y, Yang Q (2016) Study on time-dependent behavior and stability assessment of deep-buried tunnels based on internal state variable theory. Tunn Undergr Space Technol 51:164–174

    Article  Google Scholar 

Download references

Acknowledgements

This work was financially supported by NSERC (Natural Science and Engineering Research Council of Canada, RGPIN-2016-04052, ALLRP 560390-20), the China Scholarship Council (Grant No. CSC201806370225), and MIRARCO of Laurentian University.

Author information

Authors and Affiliations

  1. Bharti School of Engineering and Computer Science, Laurentian University, Sudbury, ON, Canada

    Mingzheng Wang & Ming Cai

  2. MIRARCO-Mining Innovation, Laurentian University, Sudbury, ON, Canada

    Ming Cai

  3. Key Laboratory of Ministry of Education for Safe Mining of Deep Metal Mines, Northeastern University, Shenyang, China

    Ming Cai

Authors
  1. Mingzheng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ming Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ming Cai.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, M., Cai, M. Numerical Modeling of Stand-Up Time of Tunnels Considering Time-Dependent Deformation of Jointed Rock Masses. Rock Mech Rock Eng 55, 4305–4328 (2022). https://doi.org/10.1007/s00603-022-02871-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00603-022-02871-2

Keywords

Search

Navigation