Simplified Seismic Modelling of Fractured Rock: How Effective is the Localised Effective Medium Compared to Explicit Representation of Individual Fractures

Abstract

Seismic waves can be an effective probe to retrieve fracture properties particularly when measurements are coupled with forward and inverse modelling. These seismic models then need an appropriate representation of the fracturing. The fractures can be modelled either explicitly, considering zero thickness frictional slip surfaces, or by considering an effective medium which incorporates the effect of the fractures into the properties of the medium, creating anisotropy in the wave velocities. In this work, we use a third approach which is a hybrid of the previous two. The area surrounding the predefined fracture is treated as an effective medium and the rest of the medium is made homogeneous and isotropic, creating a Localised Effective Medium (LEM). LEM can be as accurate as the explicit but more efficient in run-time. We have shown that the LEM model can closely match an explicit model in reproducing waveforms recorded in a laboratory experiment, for wave propagating parallel and perpendicular to the fractures. The LEM model performs close to the explicit model when the wavelength is much larger than the element size and larger than the fracture spacing. By the definition of the LEM model, we expect that as the LEM layer becomes coarser the model will start approaching the effective medium result. However, what are the limitations of the LEM and is there a balance between the stiffness, the frequency and the thickness, where the LEM performs close to an explicit model or approaches the effective medium model? To define the limits of the LEM we experiment varying fracture stiffness and source frequency. We then compare for each frequency and stiffness the explicit and effective medium with five models of LEM with different thickness. Finally, we conclude that the thick LEM layers with lower resolution perform the same as the thinner and finer resolution LEM layers for lower frequencies and higher fracture stiffness.

1 Introduction

Seismic waves can give information about fractures. The discontinuity in the rock mass created by the fracture affects seismic wave propagation (e.g., Schoenberg 1980). Part of the energy of the wave is reflected back and the transmitted wave is attenuated. The energy loss and attenuation depends on the geometry and the mechanical properties of the fracture and is frequency dependent. As a result the recorded waveform carries information about the fractures and can be used as a diagnostic tool (e.g., Schoenberg 1980; Coates and Schoenberg 1995; Crampin 1981; Majer et al. 1988; Pyrak-Nolte et al. 1990). Using numerical models to simulate the wave propagation in the rock mass and compare the full waveform with recorded experimental waveforms allows us to both improve the model and to improve interpretation of the fractures (e.g., Schoenberg 1980; Coates and Schoenberg 1995; Hildyard 2007; Pyrak-Nolte et al. 1990; Perino et al. 2010; Vlastos et al. 2003).

There are two main methods for representing fractures in numerical models. The first one uses displacement discontinuities to express each fracture explicitly in a background medium (e.g., Schoenberg 1980; Pyrak-Nolte et al. 1990; Hildyard 2007) and the second is the effective medium (EM) where the effect of the fractures is expressed in the compliance matrix of the medium potentially producing anisotropic material behaviour (e.g., Crampin 1981; Hudson 1981). Previous studies on the displacement discontinuity representation have shown that it can successfully predict the effect of the fractures, on the waveforms, in terms of phase velocity, frequency contents, and wave shape (e.g., Hildyard 2007; Parastatidis et al. 2017; Parastatidis 2019; Pyrak-Nolte et al. 1990; Chichinina et al. 2009a, b; Blum et al. 2011). Similarly, studies for the EM have proven that the models can predict the wave velocities (e.g., Rathore et al. 1995; Tillotson et al. 2011, 2014), but there are several restrictions on matching the frequency contents and amplitude of the waveforms due to the fracture size (e.g., Schubnel and Gueguen 2003; Schubnel et al. 2003; Shuai et al. 2018). Both models are successfully applied on different problems each one. However, the major debate is accuracy versus computational time.

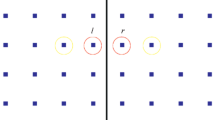
A third approach which can bridge the gap between EM and explicit fractures is a hybrid of the two methods called the‘localised effective medium’ (LEM). LEM has modelling features from both EM and explicit model, even though LEM does not implement a displacement discontinuity, it expresses each fracture explicitly as a zone with effective medium characteristics. The major difference between EM and LEM is that, in the case of EM the stiffness matrix represents the sum of all the fracture areas in the modelled volume. LEM uses the same compliance matrix as the EM. In contrast, the LEM solves for the five constant effective medium moduli only locally to the fracture positions. The fracture is represented as a zone with material properties of an EM the stiffness matrix which is calculated separately for each zone (Coates and Schoenberg 1995; Wu et al. 2005; Vlastos et al. 2003; Zhang and Gao 2009; Li et al. 2010) as presented in Fig. 1. This model can be considered a hybrid between the displacement discontinuity and effective medium models, as it introduces explicit fracture regions in the format of effective medium zones into the homogeneous isotropic background medium. This highlights the extra flexibility of this model as it can perform either close to the explicit model or close to the EM model depending on the the density of fractures and the resolution of the model.

Fig. 1

The zones surrounding the predefined fracture positions are anisotropic while the rest are the background medium (as modified from Parastatidis (2019)). The finer the mesh of the model the thinner the LEM layer and the closer to the explicit model

Experiments have also been done to validate the localised effective medium model. Groenenboom and Falk (2000), used data from a triaxial laboratory experiment and a numerical model based on a localised effective medium in order to examine scattering phenomena like guided waves and concluded that diffracted arrival times can be used to determine the size of the fractures. Fang et al. (2014) used the fracture transfer function from surface seismic scattered waves to detect fracture direction, to model laboratory measurements for parallel fractures in different azimuths.

There has been a significant amount of work at a purely theoretical level for the localised effective medium model examining velocity, transmission coefficient and scattering attenuation. Vlastos et al. (2003) compared theoretical travel times with the synthetic waveforms of the localised effective medium model for three cases to validate the method. The first case concentrates, on different spatial distributions, which produce different wave field characteristics and shows the importance of spatial distribution. The second case studies the effect of fracture length variation where high clustering results in increasing local fracture densities causing energy trapping. The last case examines how fractures with a fractal distribution of size affects the wave field and concludes that frequency-dependent seismic scattering depends on spatial distribution. A study for scattering attenuation for different stages of fracture growth was made by Vlastos et al. (2007) using a localised effective medium. Synthetic seismograms generated for each stage of the fracture growth computing multiple scattering attenuation as a function of frequency and they concluded that scattering attenuation is strongly frequency dependent. Using this method of scattering attenuation the fracture properties can be characterised and dominant scale lengths of the fractures identified. Li et al. (2010) introduced a viscoelastic medium model with equally spaced parallel joints, creating a new localised effective medium model using the assumption of a virtual wave source. Comparing velocities with the displacement discontinuity model, Li et al. (2010) showed that the virtual wave source model is equally as good as displacement discontinuity model results with the new model accurately predicting the transmission coefficient. Synthetic waveforms for displacement discontinuity and localised effective medium numerical models have been compared for numerical experiments on propagation in single and multiple parallel fractures by Zhang and Gao (2009), where they concluded that both models agree well.

Previous work on modelling the wave propagation in a medium with parallel fractures, to match experimental waveforms, has shown that the explicit representation of fractures agrees with experiment data when the fracture stiffness is stress dependent (e.g., Hildyard 2001, 2007; Parastatidis et al. 2017; Parastatidis 2019; Pyrak-Nolte et al. 1990) in which, the fracture stiffness takes different values across the same fracture based on the background stress state, areas with higher stress have higher fracture stiffness and vice versa (e.g., Bandis et al. 1983; Hildyard 2007). Finite difference modelling code WAVE3D (Hildyard et al. 1995) was used to examine three different approaches to fracture representation—explicit representation of discontinuities, a transversely isotropic effective medium, and a localised effective medium—in order to define the limitations and the applicability of each model. In addition the stress state of the medium can lead to a non-uniform fracture stiffness and modify waveforms. Introducing stress dependent fracture stiffness to the previous models showed that the explicit and the LEM model can closely approach waveforms recorded in a laboratory experiment for high frequencies with multiple parallel fractures (Hildyard 2007, 2001; Parastatidis et al. 2017; Parastatidis 2019). A further step is to examine the performance of LEM for parallel fractures and how its behaviour changes along with the changes in of the cracks per unit length. It is also necessary to examine the performance of the three approaches in fracture networks with more complex fracture networks on various angles and fracture surfaces with complex geometries closer to real rock fractures. However, at this stage to simplify our models, we use parallel fractures and examine the wave propagation parallel and perpendicular to the fractures using uniform fracture stiffness.

In this study we examine how flexible the LEM approach is, by comparing the waveforms of an explicit case with parallel fractures, the EM approach and five cases for the LEM with different cracks per unit length and different thicknesses of the effective medium layers. Next, we compare the waveforms from the three approaches, scaling the element size and the stiffness and the frequency of the models from mm to m. The next part describes the numerical implementations of each of the three approaches for fracture representations. We then describe the logic behind the series of numerical models we have run to validate the flexibility of the LEM against the explicit and EM models, and present how the waveforms from the LEM models correlates with the explicit and EM. We finally discuss the results from the models and we conclude that for lower source frequencies and high fracture stiffness the LEM will perform equivalently good even for the thick LEM layer.

2 Methodology

The numerical implementation of explicit fractures based on the displacement discontinuity model is presented in Fig. 2. Some variables are continuous and some have to be calculated independently for the different positions of the upper and the lower fracture surface. It is clear from the definition of the displacement discontinuity model that the normal stress on the upper $^{u}$ surface of the fracture $\sigma _{22}^{u}$ is equal to the normal stress on the lower $^{l}$ surface of the fracture $\sigma _{22}^{l}$ since the stress is continuous. The stress $\sigma _{11}^{u}, \sigma _{11}^{l}$ and velocity $u_{1}^{u}, u_{1}^{l}$ are discontinuous and have dual values. The values of normal and shear displacement can be calculated, assuming that they are coupled to the normal and shear stress with the normal $K_{n}$ and shear $K_{s}$ stiffness values, respectively. A full description of the numerical implementation of the displacement discontinuity model with equations is presented in Hildyard (2001). Implementation and equations for 3D can be found in Hildyard and Young (2002).

Fig. 2

Variable positions in a two dimension fracture in staggered grid modified from Hildyard (2001). In a staggered grid each variable is calculated at a different position in space. The X indicates position of $\sigma _{11}$, O indicates positions of velocity $u_{1}$, $\Delta$ indicates positions $\sigma _{12}$ and the forth position is for velocity $u_{2}$. The two fracture surfaces are coincident in space. Across the fracture surfaces we have an upper and lower value of $\sigma _{22}^{u}$, $\sigma _{22}^{l}$, $\sigma _{11}^{u}$, $\sigma _{11}^{l}$, $u_{1}^{u}$ and $u_{1}^{l}$. Since normal stress is continuous $\sigma _{22}^{u}$ $=\sigma _{22}^{l}$ $=\sigma _{22}$ but $\sigma _{11}$ and $u_{1}$ have dual values and will be calculated independently

EM theory uses five elastic constants to apply the effect of a single set of parallel fractures in the medium. The stiffness matrix C has a general representation of these five elastic constants. We use the Coates and Schoenberg (1995) approach for an effective medium, linking cracks per unit length (1/L) and crack stiffness (Kn, Ks) with elastic constants. For the EM, the cracks per unit length is calculated taking into account the total number of fractures and the total volume of the studied area. The stiffness matrix C for the EM and LEM is given by

$$\begin{aligned} C= & {} \begin{bmatrix} (\lambda + 2\mu )(1-r^{2}\delta _N) &{} \lambda (1-r\delta _N) &{} \lambda (1-\delta _N) &{} 0 &{} 0 &{} 0 \\ \lambda (1-r\delta _N) &{} (\lambda + 2\mu )(1-r^{2}\delta _N) &{} \lambda (1-\delta _N) &{} 0 &{} 0 &{} 0 \\ \lambda (1-\delta _N) &{} \lambda (1-\delta _N) &{} (\lambda + 2\mu )(1-\delta _N) &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \mu (1-\delta _T) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \mu (1-\delta _T) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \mu \end{bmatrix}, \end{aligned}$$

(1)

$$\begin{aligned}&\begin{aligned} r&=\frac{\lambda }{\lambda + 2\mu }=\frac{\nu }{1-\nu } ,\\ \\ \delta _{T}&=\frac{K_{s}^{-1} \mu }{L + K_{s}^{-1}\mu } ,\\ \\ \delta _{N}&=\frac{K_{n}^{-1}(\lambda +2\mu )}{L + K_{n}^{-1}(\lambda +2\mu )} , \end{aligned} \end{aligned}$$

(2)

where $\lambda$ is Lamé’s first parameter, $\mu$ is the shear modulus (Lamé’s second parameter), $\nu$ is Poisson’s ratio and 1/L is the cracks per unit length. On the other hand, the LEM applies the stiffness matrix (eq. 1) locally to the fracture. Therefore, the quantity cracks per unit length is given by

$$\begin{aligned} \frac{1}{L}=\frac{A\times B}{A\times B \times h}=\frac{1}{h} , \end{aligned}$$

(3)

where A and B are the length and width of the fracture and h is the thickness of the LEM layer. Usually h is equal to the element size $\Delta$x to provide maximum discreteness. However, various values of thicker h are also considered to examine the flexibility of this model.

From the definition of the implementation of the LEM, it is clear that the finer the mesh of the models and the thinner the LEM layer, the closer it is to the explicit model. Previous work on modelling a laboratory experiment (Pyrak-Nolte et al. 1990; Parastatidis et al. 2017) with multiple parallel fractures has shown that the LEM model performs close to the explicit model and the real data for waves propagating parallel and perpendicular to the fractures. For fracture networks with various angles (Parastatidis 2019) other than parallel, the explicit model and LEM have a comparable response as the ratio between wavelength and fracture diameter is equal to or higher than 2. Both studies (Parastatidis et al. 2017; Parastatidis 2019) concluded that the LEM model and the explicit model are in agreement when the wavelength is much larger than the element size (following the rule for dispersion) and at least two times larger than the fracture spacing. The question then is how the thickness of the LEM layer changes the result, and whether there is a balance between stiffness, frequency and LEM thickness, where the LEM performs close to the explicit model or is approaching the EM model.

3 Models and Results

To better understand the flexibility of the LEM, a set of numerical experiments with various LEM thickness and for different source frequencies and fracture stiffness were designed. In order to maximise computational efficiency and the parameter space to search, the models are relatively small in terms of size. The element size is 0.5 mm and the size of the model is 120 elements on each side, giving a model with 1.7 million elements. The block has been cut through by five parallel fractures with 5 mm spacing. The material properties are from an experiment by Pyrak-Nolte et al. (1990), which is laminated steel (see Table 1). The source is a plane wave double ricker wavelet, the area the source is applied to is a 10 mm$\times$10 mm square and we use five different source frequencies. The dominant frequencies of the sources and the wavelength $\lambda$ are summarised in Table 2, where the wavelengths avoid numerical dispersion ( $\lambda$ $\ge$ 10 $\Delta$x) and the largest wavelength (19.30 mm) for the lowest frequency is almost four times larger than the fracture spacing. Three values for ${K_{n}}$ and ${K_{s}}$ have been applied for the fracture stiffness of the explicit case and for the stiffness matrix of the EM and LEM models (Table 3). The first values for fracture stiffness are the same as the values calculated for the Pyrak-Nolte et al. (1990) experiment. The second and the third stiffness values are the minimum and maximum stiffness values calculated on the stress dependent case when modelling the same experiment (Parastatidis et al. 2017; Parastatidis 2019).

Table 1 Material properties of laminated steel sample (Pyrak-Nolte et al. 1990)

Table 2 The five frequencies used in the models and the wavelength $\lambda$ in mm based on the P-wave velocity (6022 m/s)

Table 3 The three cases for fracture stiffness ($K_{n}$ and $K_{s}$) used in the models to evaluate the performance of LEM against the explicit and EM models

Table 4 The five sub-cases for LEM thickness and the calculated 1/L m$^{-1}$ used in the models to evaluate the performance of LEM against the explicit and EM models

Fig. 3

Snapshots from P-wave propagation perpendicular (right) and parallel (left) to fractures at $t = 6.7$ $\mu$s a EM model, b explicit and c localised effective medium 1/L = 2000 m$^{-1}$, d localised effective medium 1/L = 1000 m$^{-1}$, e localised effective medium 1/L = 667 m$^{-1}$, f localised effective medium 1/L = 500 m$^{-1}$, g localised effective medium 1/L = 400 mv. (Red represents the peak amplitude, and all snapshots are on the same scale) the image has been modified from Parastatidis (2019)

The acquisition is aligned perpendicular and parallel to the fractures. This creates in total fifteen cases (five source frequencies and 3 sets of fracture stiffness) for parallel and fifteen for perpendicular propagation. There are then seven different implementation of these models. The explicit model, EM model, and five sub-cases of the LEM model, resulting in 105 models for parallel and 105 models for perpendicular propagation. These five sub-cases vary the thickness of the LEM layer around a fracture (Table 4). As the thickness of the LEM layers increase by 0.5 mm each time, the spacing between the lower surface of one LEM layer and the upper surface of the next LEM layer decreases by 0.5 mm, respectively. The thickness of the LEM layer surrounding the fracture affects the cracks per unit length parameter (1/L) of the LEM model. Figure 3 shows snapshots of the wavefield propagating through LEM models with the values of 1/L given in Table 4, plus the explicit fracture and EM cases.

3.1 Wave Propagation Parallel to Fractures

In this section we examine wave propagation parallel to the fractures. First, we examine the fractures with stiffness with ${K_{n}}$ = 60000 GPa/m. In general, as the frequency of the source gets lower, the different thickness LEM models start to produce the same results. More specifically, in Fig. 4a the higher 1/L, the higher the attenuation and the closer to the explicit model for the highest frequency. As shown in Fig. 4c the cross-correlation coefficient between explicit and LEM models increases as the 1/L goes higher and gets maximum values for lower frequencies. On the other hand, as the cracks per unit length parameter decreases and, the thickness of the LEM layers increases, the waveform has lower attenuation and is close to the EM model (Fig. 4d). When the frequency and the cracks per unit length are at their highest values (Fig. 4a) it is possible that the fractures above and below the source point (Fig. 3) create reflections at time 13 $\mu$s and 16 $\mu$s. However, when 1/L gets below 667 m$^{-1}$ these reflections become smoother in frequency and amplitude. It seems that all of the five LEM cases have captured some of the complexity that the waveform of the explicit model has. In the next step where the frequency of the source is 0.5 MHz (Fig. 4c), all of the LEM cases which did not previously match with the explicit one, approach the second case (1/L = 1000 m$^{-1}$) to perform the same as the first case (1/L = 2000 m$^{-1}$), increasing the correlation coefficient from 0.85 to 0.94 (Fig. 4c). Reducing the source frequency further (Fig. 4b), more LEM cases with lower 1/L value start to perform in a similar manner. The correlation coefficient increasing gradually above 0.9 for all the five LEM cases when source frequency is 0.31 MHz . In Fig. 4c for the first three LEM models the correlation coefficient is above 0.9 with time shifting lower than 0.1 $\mu$s. In Fig. 4c four of the LEM models have correlation coefficient above 0.9. As a result, a first conclusion concerning wave propagation parallel to the fractures is that the LEM can perform similar to the explicit model at lower frequencies when the wavelength is more than five times higher than the spacing of the LEM layers (Tables 3 and 4), no matter the thickness of the LEM layer and the 1/L value, but at high frequencies the LEM has to be thin and the 1/L value very high.

Fig. 4

Comparison of P-wave propagation parallel to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=60000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and maximum cross correlation coefficient for wave propagation parallel to fractures between explicit and LEM c, EM and LEM d versus the different LEM cracks per unit length and for the five different source frequencies. As the source frequency drops the LEM models approach the explicit making 1/L less important while for the high frequencies and low 1/L LEM lose the explicitness and perform close to EM (the image has been modified from Parastatidis (2019))

3.2 Wave Propagation Perpendicular to the Fractures

In this part, the source and receiver are aligned perpendicular to the fractures. As expected, the amplitude is significantly lower for all models compared to wave propagation parallel to the fractures.

Fig. 5

Comparison of the P-wave propagation perpendicular to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=60000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and the maximum cross correlation coefficient for wave propagation perpendicular to fractures between explicit and LEM (c), EM and LEM (d), versus the different LEM cracks per unit length and for the five different source frequencies. Similar to the waveforms propagating parallel to the fractures when the source frequency drops the LEM models approach the explicit making 1/L. But in this case the wave attenuation is higher and only the LEM models with high 1/L match the explicit even for low frequencies (the image has been modified from Parastatidis (2019))

In contrast to the previous section, the waveforms from the last four LEM cases are a lot different from the first and the explicit one for ${K_{n}}$=60000 GPa/m. This is due to the lower 1/L values which do not create as strong reflection surfaces as the first model. More energy of the wave passes through the thicker LEM layers resulting in waveforms with up to ten times higher amplitude (Fig. 5a LEM 1/L = 400 m$^{-1}$). Moreover, the first arrival is different in all of the models (Fig. 5a, c). The dominant period of the waveforms for the last three models is similar to the EM model and only the first LEM model has the same first arrival and dominant period as the explicit model (Fig. 5c). The EM model has higher amplitude and later first arrival. When the frequency of the source goes below 0.42 MHz (Fig. 5c), the LEM model with half the 1/L value (1/L = 1000 m$^{-1}$) and double the thickness of the LEM layers compared to the original case (1/L = 2000 m$^{-1}$) starts to look closer to the explicit model in first arrival and dominant period (Fig. 5c). The amplitude is lower than in the previous frequencies (Fig. 5a) but not as low as with the explicit model. As in the previous case with wave propagation parallel to the fractures, the higher the frequency (0.63 MHz) and the lower the 1/L,(1/L = 400 $m^{-1}$) the closer to the EM model, with correlation coefficient close to 0.90 (Fig. 5d). Finally, for source frequency 0.36 MHz (Fig. 5c, d) the first two LEM models matching increase by 8%. The other three cases, even though they have the same dominant period and arrival time closer to the explicit, the amplitude is still higher than the other models.

3.3 Fracture Stiffness

Next, we investigate the effect of varying fracture stiffness. We are going to use two more values for fracture stiffness as shown in Table 3. The second case from Table 3 is similar to the previous case but with increased fracture stiffness from 60000 GPa/m to 100000 GPa/m. As expected, the higher the stiffness the less amplitude attenuation for the waveforms. The waveforms from the LEM models now start to correlate better with values between 8 and 28% higher than before (Figs. 4c and 6c) at even higher frequencies compared to the case with ${K_{n}}$=60000 GPa. However, as for the previous case with stiffness 60000 GPa/m, the lower the 1/L value, the closer to the EM model and the higher the amplitude of the direct wave, as maximum correlation values shows in Fig. 6c.

Fig. 6

Comparison of P-wave propagation parallel to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=100000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and maximum cross correlation coefficient for wave propagation parallel to fractures between explicit and LEM c, EM and LEM d versus the different LEM cracks per unit length and for the five different source frequencies. Similar to the case with fracture stiffness 60000 GPa/m for the low source frequency the LEM models approach the explicit while for the high frequencies and low 1/L LEM perform close to EM (the image has been modified from Parastatidis (2019))

As for wave propagation parallel to the fractures when increasing the normal stiffness to 100000 GPa/m, only the first case of LEM matches the explicit model, for the higher source frequency model. The other four cases are comparable to the EM model (Fig. 7c). When the frequency is reduced the second LEM model approaches the first and the explicit with the correlation coefficient increasing (Fig. 7c). The third LEM model (1/L = 667m$^{-1}$) tends to match the explicit model for frequency below 0.42 MHz (Fig. 7c), while for the same frequency the second case fully matches the explicit (with maximum correlation coefficient 0.96 and 0.87, respectively). As the source frequency gets lower all of the LEM models gets closer to the explicit model (Fig. 7c, b). Thus, the higher the normal stiffness and the lower the source frequency, the LEM performs close to the explicit model, (Fig. 7c) no matter the thickness and the 1/L value.

Fig. 7

Comparison of the P-wave propagation perpendicular to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=100000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and the maximum cross correlation coefficient for wave propagation perpendicular to fractures between explicit and LEM c, EM and LEM d, versus the different LEM cracks per unit length and for the five different source frequencies. The higher the stiffness the lower the attenuation and the LEM and explicit can match at higher frequencies (the image has been modified from Parastatidis (2019))

Finally, for the lower stiffness value 30000 GPa/m the first two LEM models start to perform similarly, for lower frequencies below 0.42 MHz (Fig. 8c, d). In Fig. 8c only the LEM with 1/L = 2000 $\mu$s value correlates to 0.94 with the explicit model and as the source frequency decreases, the second LEM model approaches the result of the explicit model (Fig. 8c). In contrast with the previous cases with higher normal stiffness, the models with lower 1/L value do not match the EM model as much for the high frequencies (Fig. 8d). When the source frequency gets even lower, the LEM models with lower 1/L (500 and 400 m$^{-1}$) tend to mimic the explicit and the first LEM model, with maximum correlation values 0.90 and 0.86, respectively, performing better than in Fig. 8c, b.

Fig. 8

Comparison of P-wave propagation parallel to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=30000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and maximum cross correlation coefficient for wave propagation parallel to fractures between explicit and LEM (c), EM and LEM (d) versus the different LEM cracks per unit length and for the five different source frequencies. For low fracture stiffness values and high source frequency the LEM is closer to EM than the explicit (the image has been modified from Parastatidis (2019))

Finally, a lower stiffness of 30000 GPa/m is used as in the previous section for wave propagation parallel to the fractures (Fig. 7a). In the previous cases with higher stiffness and high frequencies, the last three models match each other (Fig. 9a, c). However, in the case where the stiffness is low, none of them is equal to the other two. In order for the second LEM model ((1/L = 1000m$^{-1}$) to start to match the first and the explicit with correlation coefficient above 0.8 (Fig. 9c), the source frequency has to drop below 0.31 MHz (Fig. 9b). For wave propagation perpendicular to the fractures, it is harder to match the waveforms of the five LEM models. As the 1/L value reduces and the thickness of the LEM layers increases, the LEM becomes a smoother reflector allowing more energy of the wave to pass through for high frequencies creating this mismatch. For the four LEM cases with 1/L between 1000 and 400 $m^{-1}$ the correlation coefficient between explicit and LEM models never reaches a value above 0.90 even for the lower frequency (Fig. 9c). In contrast the correlation is higher between EM and LEM models especially for the higher frequencies (Fig. 9d). When the frequency is low, the wavelength is high relative to the fracture spacing, and when the stiffness is high the LEM models start to match.

Fig. 9

Comparison of the P-wave propagation perpendicular to the fractures for the Explicit, EM and the 5 cases of LEM, with ${K_{n}}$=30000 GPa/m and with source frequencies of a 0.63 MHz and b 0.31 MHz and the maximum cross correlation coefficient for wave propagation perpendicular to fractures between explicit and LEM (c), EM and LEM (d), versus the different LEM cracks per unit length and for the five different source frequencies. The low fracture stiffness values makes almost impossible the LEM with 1/L lower than 2000 $m^{-1}$ to match either the explicit or the EM models (the image has been modified from Parastatidis (2019))

To sum up, for wave propagation parallel to the fractures, for high stiffness and higher frequencies the LEM models with 1/L = 667 m$^{-1}$ and above perform closer to the explicit model and the models below that 1/L value are closer to the EM model. However, when the stiffness is low and the source frequency is also low (with wavelength more than six times the spacing between LEM layers, as in Tables 4 and 2), the LEM model with 1/L = 500 m$^{-1}$ and 400 m$^{-1}$ is closer to the explicit model and not to the EM model.

3.4 Scaling the Models to Larger Size

From the previous work described above, we concluded that when increasing the thickness of the LEM model and decreasing the 1/L value, the model loses the ability to match with the explicit fracture model for high frequencies, but as the frequency drops the model finally tends to match the explicit model. As explained in Sect. 2 the maximum 1/L value depends on the element size when using the thinner LEM option (equation 3). Now we examine how the LEM model works when the element size is larger than the previous models by scaling the previous experiment by a factor of ten for three cases. In the first case, the element size is the same as in the previous models 0.5 mm and 1/L = 2000 m$^{-1}$ (Fig. 10a, b) the second is 5 mm and 1/L = 200 m$^{-1}$ (Fig. 10c, d) and finally 50 mm and 1/L = 20 m$^{-1}$ (Fig. 10e, f) (Table 5). In this stage, we use only one value for normal stiffness and one source frequency per model which is scaled by a factor of ten and we examine the wave propagation parallel and perpendicular to the fractures. For all three cases, the maximum frequency for the source has been used, as calculated using the method described previously, to avoid dispersion.

Table 5 Scaling the experiment for larger element size to test the performance of the LEM model for larger element size and lower 1/L value

The first conclusion related to these models concerns wave shape. In all three scaled cases, the wave shape is the same for both parallel (Fig. 10a, c, e) and perpendicular (Fig. 10b, d, f) to the fractures propagation. When comparing the explicit model (red waveform) with the LEM model for the smallest element size 0.5 mm and 1/L = 2000 m$^{-1}$, both parallel (Fig. 10a) and perpendicular (Fig. 10b), look identical. As the size increases to 5 mm with 1/L = 200 m$^{-1}$ (Fig. 10c, d) and 50 mm with 1/L = 20 m$^{-1}$ (Fig. 10c, d) the LEM models mimic the explicit models. While we expect this result from the laws of scaling, this leads to the conclusion that it is the alternation of the LEM layer and homogeneous isotropic layers in between that creates an “explicitness” of the LEM model and not the actual value of the 1/L. However, the rule for matching the explicit model with the LEM with a low 1/L value was to use the highest frequency source with the highest possible 1/L value with as thin as possible LEM layers. As shown in a previous section, when the LEM layer is thicker than the element size and lower 1/L values for high frequencies are used, the models perform differently when the frequency goes lower.

Fig. 10

Comparison of P-wave propagation parallel and perpendicular to the fractures for the Explicit, EM and the LEM a, b the element size is 0.5mm and 1/L = 2000$m^{-1}$, c, d element size is 5mm and 1/L = 200$m^{-1}$ and e, f element size is 50mm and 1/L = 20$m^{-1}$ the explicit model consists of 5 fractures. It is clear from the waveforms that there is a linear connection between element size, maximum 1/L and maximum source frequency

4 Discussion

Based on previous studies (e.g., Hildyard 2007; Parastatidis et al. 2017; Parastatidis 2019; Chichinina et al. 2009b; Mollhoff and Bean 2009) the explicit model is an accurate approach when comparing waveforms from model versus real experiment or field data. However, the explicit model requires a specific resolution based on actual fracture sizes and fracture positions. The LEM model can be as accurate as the explicit model but if the required frequencies allow, it can be lower resolution and hence have lower needs on memory and run-time. LEM can be as accurate as the explicit model but with lower needs on memory and run-time. In this study we tested the limits of the LEM model by changing the layer thickness and as a consequence the value of 1/L for various frequencies and fracture stiffness. Vlastos et al. (2007) concluded that for the LEM model the scattering attenuation is frequency dependent. Similarly, the explicit model is frequency dependent too (e.g., Pyrak-Nolte et al. 1990). The two models produce similar results, as shown in previous work Parastatidis et al. (2017) and Parastatidis (2019), when the LEM layers are as thick as the element size and 1/L is at its maximum value (see Sect. 2). The question then is, how thin the LEM layers has to be in order to produce comparable results to the explicit model and what are the frequency and stiffness limits.

It is clear from the Figs. 4 to 10 that as the frequency goes lower and stiffness higher, the value of 1/L is less important to match the explicit and LEM models. On the other hand, as the frequency increases the models with lower 1/L start to behave like the EM model. As the 1/L decreases the thickness of the LEM layers increases and as a result the spacing between the LEM layers is reduced (see Table 4). Cai and Zhao (2000) studied the effects of multiple parallel explicit fractures on wave attenuation as a function of spacing and number of fractures and show that the dependence of the transmission coefficient on the number of fractures and the fracture spacing is controlled by $\xi =\frac{\Delta x}{\lambda }$ the ratio of fracture spacing ($\Delta$x) to wavelength ($\lambda$). The transmission coefficient $|T_{1}|$ of the P-wave for a single fracture is as follows:

$$\begin{aligned} |T_{1}|=\Bigg [\frac{4\big (\frac{k}{z}\big )^2}{4\big (\frac{k}{z}\big )^2 +\omega ^2}\Bigg ]^{1/2} , \end{aligned}$$

(4)

where k is the normal stiffness, $\omega$ is the angular velocity and $z=\rho V_{P}$ is the seismic impedance for given density $\rho$ and P-wave velocity $V_{P}$. For N number of fractures the transmission coefficient is $|T_{N}|=|T_{1}|^{N}$ (Cai and Zhao 2000; Pyrak-Nolte et al. 1990). However this is only a simple approximation and it doesn’t consider multiple reflections and waveform conversions which is something expected to happen in the explicit and the very thin LEM models. Figure 11 summarises $|T_{5}|$ as a function of $\xi$ for the three stiffness values used in the models and five fracture spacing values (see Table 4). Based on the calculation in Fig. 11 it is expected that the $|T_{5}|$ will be almost double for higher stiffness value (100000 GPa/m) and close to zero for the lower one (30000 GPa/m). Table 6 summarises the upper and lower limits of $|T_{5}|$ for each of the stiffness value. From table 6 it is concluded that for explicit fractures $|T_{5}|$ will be the same for the same frequency and different fracture spacing (e.g., for $\xi$=0.16, $\Delta x$=3 mm, $\lambda$=19 mm and K$_{n}$=60000 GPa/m $|T_{5}|$=3.15 and for $\xi$=0.26 $\Delta x$=5 mm, $\lambda$=19 mm and K$_{n}$=60000 GPa/m $|T_{5}|$=3.15) creating a frequency dependence of fracture spacing and $|T_{5}|$. However, the LEM models with 1/L other than the maximum (2000 $m^{-1}$) do not behave like that. Based on the models presented above, when the LEM layer starts to become thicker the model starts losing its frequency dependence for high frequencies, behaving closer to the EM model which is frequency independent. Comparing the wavelenght of the source and the thickness of the LEM with higher correlation to explicit model we could come with a rule that the LEM is frequency dependent as long as the wavelength of the source is 19 times higher than the LEM layer thickness for wave propagation perpendicular to the fractures; however, this rule might needs further testing. For example the LEM with 1/L = 2000 and 1000 $m^{-1}$ (thickness is 0.5 and 1 mm, respectively) reaches maximum correlation (0.89 to 0.99) with the explicit model when the source frequency is lower than 0.625 MHz ($\lambda$=9.64 mm) for the first and 0.312 MHz ($\lambda$=19.30 mm) for the second for all the different values of stiffness. Lower frequencies with 19 times higher wavelength from the other LEM models need to be tested to confirm the above statement. Finally, transmission coefficient $|T_{N}|$ of the LEM needs to be tested as a function of layer spacing and layer thickness, in order to test if there is any relationship similar to the one for the explicit model.

Fig. 11

Magnitude of transmission coefficient for 5 fractures $|T_{5}|$ as a function of $\xi$ for different values of normal stiffness $K_{n}$ and fracture spacing $\Delta x$ (the image has been modified from Parastatidis (2019))

Table 6 $|T_{5}|$ values for the upper and lower xi limit for each stiffness value

5 Conclusions

We have tested the performance of the LEM against the explicit fracture model and EM for different LEM layer thickness and for various frequencies and fracture stiffness. For high frequencies the LEM layer needs to be as thin as possible to operate similar to the explicit fracture model rather than close to the EM.

The models were scaled up for larger element size and lower frequencies, showing that there is a linear relationship between frequency, stiffness and element size.

The conclusions made from the LEM tests and the complex fracture models are as follows:

• The thickness of the LEM layer is important when the frequency is high, and the normal stiffness is low.

• The LEM thickness has to be as thin as 19 times the wavelength when the model is operating at its lowest possible stiffness, but when the source wavelength is about half the maximum, the LEM can be flexible in terms of thickness.

• As a result, when the frequency is high the LEM models with thick layers tend to perform similar to the EM model, and when the frequency is lower the thick LEM layer performs similar to the thinner one and the explicit model with a correlation coefficient above 0.9.

• Using a larger element size and, as a result lower 1/L value, has no impact on the waveform when using the suggested maximum frequency, creating a linear relationship between element size, maximum frequency, 1/L and stiffness. The scaling of the model leads to the conclusion that heterogeneity created by the alternation between LEM layer and homogeneous material is the one that creates an effect on the waveform similar to the explicit model.

Based on the above conclusions we could use a fine or coarser LEM model according to the needs on waveform frequencies and accuracy each time, reducing the run-time and cost compared to explicit model. However, further work needs to be done on that direction to test the performance of LEM versus explicit model on fractures with complex geometries and various propagation angles, other than uniform stiffness and parallel or perpendicular to the fractures.