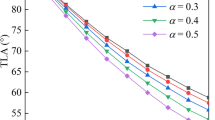
Abstract
The brittle fracture behavior of rocks under mixed-mode loading is important in rock engineering. First, a new configuration called the notched deep beam (NDB) specimen was introduced for the fracture testing of rock materials under mixed-mode I/II loading, and a series of finite element analyses were performed to calibrate the dimensionless fracture parameters (i.e., Y I, Y II and \(T^{*}\)). The results showed that an NDB specimen subjected to three-point bending is able to generate pure mode I loading, pure mode II loading, and any mixed-mode loading in between. Then, several NDB specimens made of sandstone were used to investigate the brittle fracture behavior of rock under mixed-mode I/II loading. The fracture surfaces were theoretically described using a statistical method, and the results indicated that all the fracture surfaces generated under different mixed-mode loading were statistically identical; to some extent, these results experimentally showed that only tensile fracture occurs under mixed-mode I/II loading. The obtained fracture strengths were then analyzed using several brittle fracture criteria. The empirical criterion, maximum energy release rate criterion, generalized maximum tangential stress (GMTS) criterion, and improved R-criterion accurately predicted the fracture strength envelope of the sandstone. Finally, based on the concepts of point stress and mean stress, the micro-crack zones (MCZs) under different mixed-mode loading were theoretically estimated based on the MTS and GMTS criteria. The critical radius of MCZ in the crack propagation direction was not a constant for all mixed-mode loading conditions regardless of whether the T-stress was considered. This result suggests that the size of the core region used to predict the crack initiation direction and fracture strength based on the GMTS criterion should be chosen more carefully.















Similar content being viewed by others
Abbreviations
- a :
-
Crack length
- B :
-
Thickness of an NDB specimen
- C :
-
= 1/(2π) for the PS case, = 2/π for the MS case
- d :
-
Half-distance between the two bottom supports for an NDB specimen
- E :
-
Young’s modulus of elasticity
- f 1, f 2 :
-
Parameters related to the scale of the micro-crack zone
- G :
-
Energy release rate
- G c :
-
Critical energy release rate
- h 1, h 2, h 3, h 4 :
-
Heights corresponding to the four vertexes of a grid cell on the surface
- K I :
-
Mode I stress intensity factor
- K Ic :
-
Mode I fracture toughness
- K II :
-
Mode II stress intensity factor
- K IIc :
-
Mode II fracture toughness
- L :
-
Length of an NDB specimen
- P :
-
Applied load in an NDB three-point bending test
- P cr :
-
Peak load in an NDB three-point bending test
- r, ϑ :
-
Polar coordinates at the crack tip
- r 0 :
-
Critical radius of the core region in the crack propagation direction
- r c :
-
Radius of the core region
- R II,I :
-
Fracture toughness ratio
- r p :
-
Elastic–plastic boundary radius
- r pc :
-
Critical elastic–plastic boundary radius
- S :
-
Strain energy density factor
- S c :
-
Critical strain energy density factor
- T :
-
Nonsingular stress term
- \(T^{*}\) :
-
Nondimensional nonsingular stress term
- W :
-
Width of an NDB specimen
- Y I :
-
Nondimensional mode I stress intensity factor
- Y II :
-
Nondimensional mode II stress intensity factor
- α :
-
Crack inclination angle for an NDB specimen
- β I, β II :
-
Empirical parameters of the empirical criterion
- δ :
-
Scale of each grid cell
- η I, η II :
-
Parameters of the loading mode mixity
- κ :
-
= 3 − 4ν for the plane strain case, = (3 − ν)/(1 + ν) for the plane stress case
- ν :
-
Poisson’s ratio
- μ :
-
Shear modulus
- ξ :
-
= 2(1 − 2\(\nu^{*}\) )/3; \(\nu^{*}\) = ν for the plane strain case, \(\nu^{*}\) = 0 for the plane stress case
- σ rr , σ ϑϑ , σ rϑ :
-
Stress components in polar coordinates
- σ t :
-
Tensile strength of a given material
- σ xx , σ yy , σ xy :
-
Stress components in Cartesian coordinates
- σ ϑϑc :
-
Critical tangential stress
References
Ai T, Zhang R, Zhou HW, Pei JL (2014) Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl Surf Sci 314:610–621. doi:10.1016/j.apsusc.2014.06.152
Aliha MRM, Ayatollahi MR (2011) Mixed mode I/II brittle fracture evaluation of marble using SCB specimen. Procedia Eng 10:311–318. doi:10.1016/j.proeng.2011.04.054
Aliha MRM, Hosseinpour GR, Ayatollahi MR (2013) Application of cracked triangular specimen subjected to three-point bending for investigating fracture behavior of rock materials. Rock Mech Rock Eng 46:1023–1034. doi:10.1007/s00603-012-0325-z
Atkinson C, Smelser RE, Sanchez J (1982) Combined mode fracture via the cracked Brazilian disk test. Int J Fract 18:279–291. doi:10.1007/BF00015688
Awaji H, Sato S (1978) Combined mode fracture toughness measurement by the disk test. J Eng Mater Technol 100:175–182. doi:10.1115/1.3443468
Ayatollahi MR, Aliha MRM (2007a) Fracture toughness study for a brittle rock subjected to mixed mode I/II loading. Int J Rock Mech Min Sci 44:617–624. doi:10.1016/j.ijrmms.2006.10.001
Ayatollahi MR, Aliha MRM (2007b) Wide range data for crack tip parameters in two disc-type specimens under mixed mode loading. Comput Mater Sci 38:660–670. doi:10.1016/j.commatsci.2006.04.008
Ayatollahi MR, Aliha MRM, Hassani MM (2006) Mixed mode brittle fracture in PMMA—an experimental study using SCB specimens. Mater Sci Eng, A 417:348–356. doi:10.1016/j.msea.2005.11.002
Babadagli T, Develi K (2003) Fractal characteristics of rocks fractured under tension. Theor Appl Fract Mech 39:73–88. doi:10.1016/S0167-8442(02)00139-8
Backers T (2005) Fracture toughness determination and micromechanics of rock under mode I and mode II loading. Doctoral Thesis, University of Potsdam
Backers T, Stephansson O (2012) ISRM suggested method for the determination of mode II fracture toughness. Rock Mech Rock Eng 45:1011–1022. doi:10.1007/s00603-012-0271-9
Balzani C, Wagner W, Wilckens D, Degenhardt R, Büsing S, Reimerdes H-G (2012) Adhesive joints in composite laminates—a combined numerical/experimental estimate of critical energy release rates. Int J Adhes Adhes 32:23–38. doi:10.1016/j.ijadhadh.2011.09.002
Carpinteri A, Cornetti P, Pugno N, Sapora A, Taylor D (2009) Generalized fracture toughness for specimens with re-entrant corners: experiments vs. theoretical predictions. Struct Eng Mech 32:609–620
Chang S-H, Lee C-I, Jeon S (2002) Measurement of rock fracture toughness under modes I and II and mixed-mode conditions by using disc-type specimens. Eng Geol 66:79–97. doi:10.1016/S0013-7952(02)00033-9
Chong KP, Kuruppu MD (1984) New specimen for fracture toughness determination for rock and other materials. Int J Fract 26:R59–R62. doi:10.1007/BF01157555
Dai F, Chen R, Xia K (2010) A semi-circular bend technique for determining dynamic fracture toughness. Exp Mech 50:783–791. doi:10.1007/s11340-009-9273-2
Dai F, Wei MD, Xu NW, Ma Y, Yang DS (2014) Numerical assessment of the progressive rock fracture mechanism of cracked chevron notched Brazilian disc specimens. Rock Mech Rock Eng 48:463–479. doi:10.1007/s00603-014-0587-8
Erdogan F, Sih GC (1963) On the crack extension in plates under plane loading and transverse shear. J Fluids Eng 85:519–525. doi:10.1115/1.3656897
Fowell RJ (1995) Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens. Int J Rock Mech Min Sci 32:57–64
Funatsu T, Shimizu N, Kuruppu M, Matsui K (2014) Evaluation of mode I fracture toughness assisted by the numerical determination of K-resistance. Rock Mech Rock Eng 48:143–157. doi:10.1007/s00603-014-0550-8
Hasanpour R, Choupani N (2009) Rock fracture characterization using the modified Arcan test specimen. Int J Rock Mech Min Sci 46:346–354. doi:10.1016/j.ijrmms.2008.07.004
Hussain MA, Pu SL, Underwood J (1974) Strain energy release rate for a crack under combined mode I and mode II. Fract Anal 560:2–28. doi:10.1520/STP33130S
Kfouri AP, Brown MW (1995) Fracture criterion for cracks under mixed-mode loading. Fatigue Fract Eng Mater Struct 18:959–969. doi:10.1111/j.1460-2695.1995.tb00920.x
Khan SMA, Khraisheh MK (2000) Analysis of mixed mode crack initiation angles under various loading conditions. Eng Fract Mech 67:397–419. doi:10.1016/S0013-7944(00)00068-0
Khan SMA, Khraisheh MK (2004) A new criterion for mixed mode fracture initiation based on the crack tip plastic core region. Int J Plast 20:55–84. doi:10.1016/s0749-6419(03)00011-1
Kong XM, Schlüter N, Dahl W (1995) Effect of triaxial stress on mixed-mode fracture. Eng Fract Mech 52:379–388. doi:10.1016/0013-7944(94)00228-A
Kuruppu MD (1997) Fracture toughness measurement using chevron notched semi-circular bend specimen. Int J Fract 86:L33–L38
Leguillon D (2002) Strength or toughness? A criterion for crack onset at a notch. Eur J Mech A Solids 21:61–72. doi:10.1016/S0997-7538(01)01184-6
Lim IL, Johnston IW, Choi SK, Boland JN (1994) Fracture testing of a soft rock with semi-circular specimens under three-point bending. Part 2—mixed-mode. Int J Rock Mech Min Sci 31:199–212. doi:10.1016/0148-9062(94)90464-2
Luo L, Wang QZ (2009) Concurrent measurement of tensile strength and fracture toughness of quasi-brittle materials using U-notched beams: theoretical analysis. Eng Mech 26:244–250
Mróz KP, Mróz Z (2010) On crack path evolution rules. Eng Fract Mech 77:1781–1807. doi:10.1016/j.engfracmech.2010.03.038
Nuismer RJ (1975) An energy release rate criterion for mixed mode fracture. Int J Fract 11:245–250. doi:10.1007/BF00038891
Palaniswamy K, Knauss WG (1972) Propagation of a crack under general, in-plane tension. Int J Fract 8:114–117. doi:10.1007/BF00185207
Rao Q, Sun Z, Stephansson O, Li C, Stillborg B (2003) Shear fracture (mode II) of brittle rock. Int J Rock Mech Min Sci 40:355–375. doi:10.1016/S1365-1609(03)00003-0
Ren L, Zhu Z, Wang M, Zheng T, Ai T (2013a) Mixed-mode elastic-plastic fractures: improved R-criterion. J Eng Mech 140:04014033
Ren L, Zhu Z, Yang Q, Ai T (2013b) Investigation on the applicability of several fracture criteria to the mixed mode brittle fractures. Adv Mech Eng 5:545108. doi:10.1155/2013/545108
Ren L, Xie LZ, Li CB, Wang J (2014) Compressive fracture of brittle geomaterial: fractal features of compression-induced fracture surfaces and failure mechanism. Adv Mater Sci Eng 2014:814504. doi:10.1155/2014/814504
Ren L, Xie LZ, Xie H, Ai T, He B (2016) Mixed-mode fracture behavior and related surface topography feature of a typical sandstone. Rock Mech Rock Eng 49:3137–3153. doi:10.1007/s00603-016-0959-3
Ritchie RO, Knott JF, Rice JR (1973) On the relationship between critical tensile stress and fracture toughness in mild steel. J Mech Phys Solids 21:395–410. doi:10.1016/0022-5096(73)90008-2
Schmidt RA (1980) Microcrack model and its significance to hydraulic fracturing and fracture toughness testing. In: 21st US symposium on rock mechanics (USRMS), American Rock Mechanics Association, Rolla, Missouri, pp 581–590
Seweryn A (1998) A non-local stress and strain energy release rate mixed mode fracture initiation and propagation criteria. Eng Fract Mech 59:737–760. doi:10.1016/S0013-7944(97)00175-6
Sheity DK, Rosenfield AR, Duckworth WH (1985) Fracture toughness of ceramics measured by a chevron-notch diametral-compression test. J Am Ceram Soc 68:C325–C327. doi:10.1111/j.1151-2916.1985.tb10135.x
Sih GC (1974) Strain-energy-density factor applied to mixed mode crack problems. Int J Fract 10:305–321. doi:10.1007/BF00035493
Smith DJ, Ayatollahi MR, Pavier MJ (2006) On the consequences of T-stress in elastic brittle fracture. Proc Natl Acad Sci USA 462:2415–2437. doi:10.1098/rspa.2005.1639
Susmel L, Taylor D (2008) The theory of critical distances to predict static strength of notched brittle components subjected to mixed-mode loading. Eng Fract Mech 75:534–550. doi:10.1016/j.engfracmech.2007.03.035
Swartz SE, Taha NM (1990) Mixed mode crack propagation and fracture in concrete. Eng Fract Mech 35:137–144. doi:10.1016/0013-7944(90)90191-I
Theocaris PS, Andrianopoulos NP (1983) Failure theories for glassy polymers: the T-criterion for various yield loci. Pure Appl Chem 55:845–852. doi:10.1351/pac198355050845
Wang QZ, Feng F, Ni M, Gou XP (2011) Measurement of mode I and mode II rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar. Eng Fract Mech 78:2455–2469. doi:10.1016/j.engfracmech.2011.06.004
Wang J, Ren L, Xie LZ, Xie HP, Ai T (2016) Maximum mean principal stress criterion for three-dimensional brittle fracture. Int J Solids Struct 102–103:142–154. doi:10.1016/j.ijsolstr.2016.10.009
Whitcomb JD (1986) Parametric analytical study of instability-related delamination growth. Compos Sci Technol 25:19–48. doi:10.1016/0266-3538(86)90019-9
Williams ML (1957) On the stress distribution at the base of a stationary crack. J Appl Mech 24:109–114
Wu C-H (1978) Fracture under combined loads by maximum-energy-release-rate criterion. J Appl Mech 45:553–558. doi:10.1115/1.3424360
Yehia NAB, Shephard MS (1987) The NT-criterion for predicting crack growth increments. Eng Fract Mech 26:371–382. doi:10.1016/0013-7944(87)90019-1
Zhang X, Jeffrey RG, Bunger AP, Thiercelin M (2011) Initiation and growth of a hydraulic fracture from a circular wellbore. Int J Rock Mech Min Sci 48:984–995. doi:10.1016/j.ijrmms.2011.06.005
Zhang R, Ai T, Li H, Zhang Z, Liu J (2013) 3D reconstruction method and connectivity rules of fracture networks generated under different mining layouts. Int J Rock Mech Min Sci 23:863–871. doi:10.1016/j.ijmst.2013.10.013
Zhang R, Ai T, Zhou HW, Ju Y, Zhang ZT (2015) Fractal and volume characteristics of 3D mining-induced fractures under typical mining layouts. Environ Earth Sci 73:6069–6080. doi:10.1007/s12665-015-4376-9
Zhao Y (1990) Elliptic rule criterion for mixed mode crack propagation. Eng Fract Mech 37:283–292. doi:10.1016/0013-7944(90)90041-E
Zhou HW, Xie H (2003) Direct estimation of the fractal dimensions of a fracture surface of rock. Surf Rev Lett 10:751–762. doi:10.1142/S0218625X03005591
Acknowledgements
The authors express their sincere gratitude to all the anonymous reviewers for their comments devoted to improving the quality of our paper. This paper was financially supported by the Major State Research Projects (2016YFC0600702) and Provincial Science and Technology Support Project of Sichuan Province (2015JY0280).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Luo, Y., Ren, L., Xie, L.Z. et al. Fracture Behavior Investigation of a Typical Sandstone Under Mixed-Mode I/II Loading Using the Notched Deep Beam Bending Method. Rock Mech Rock Eng 50, 1987–2005 (2017). https://doi.org/10.1007/s00603-017-1227-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-017-1227-x