Abstract
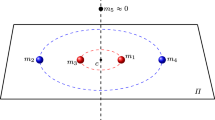
The aim of this paper is to study the motion of a \(2+n\)-body problem where two equal masses are assumed to be fixed. We assume that the value of each fixed mass is equal to \(M>0\) and the remaining n moving particles have equal masses \(m>0\). According to Newton’s second law and the universal gravitation law, the n particles move under the interaction of each other and the affection of the two fixed particles. Also, this motion has a natural variational structure. Under the simple choreography constraint, we show that the Lagrangian action functional attains its absolute minimum on a uniform circular motion.
Similar content being viewed by others
References
A. Ambrosetti, V. Coti-Zelati, Periodic Solutions for Singular Lagrangian Systems (Springer, Boston, 1993)
A. Ambrosetti, V. Coti-Zelati, Non-collision periodic solutions for a class of symmetric 3-body type problems. Topol. Methods Nonlinear Anal. 3(2), 197–207 (1994)
A. Bahri, P.H. Rabinowitz, A minimax method for a class of Hamiltonian systems with singular potentials. J. Funct. Anal. 82(2), 412–428 (1989)
V. Barutello, S. Terracini, Action minimizing orbits in the n-body problem with simple choreography constraint. Nonlinearity 17(6), 2015–2039 (2004)
V. Benci, G. Giannoni, Periodic solutions of prescribed energy for a class of Hamiltonian systems with singular potentials. J. Differ. Equ. 82(1), 60–70 (1989)
S.V. Bolotin, Nonintegrability of the problem of n centers for \(n>2\). (Russian) Vestnik Moskov. Univ. Ser. I Mat. Mekh 3, 65–68 (1984)
S.V. Bolotin, P. Negrini, Regularization and topological entropy for the spatial n-center problem. Ergodic Theory Dyn. Syst. 21(2), 383–399 (2001)
S.V. Bolotin, P. Negrini, Chaotic behavior in the 3-center problem. J. Differ. Equ. 190(2), 539–558 (2003)
R. Castelli, On the variational approach to the one and N-centre problem with weak forces, Ph.D Thesis, University of Milano-Bicocca (2009)
R. Castelli, Topologically distinct collision-free periodic solutions for the N-center problem. Arch. Ration. Mech. Anal. 223(2), 941–975 (2017)
A. Chenciner, R. Montgomery, A remarkable periodic solution of the three-body problem in the case of equal masses. Ann. Math. 152(3), 881–901 (2000)
V. Coti-Zelati, Periodic solutions of N-body type problems. IHP Anal non linéaire 7, 477–492 (1990)
M. Degiovanni, F. Giannoni, Dynamical systems with Newtonian type potentials. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 15, 467–494 (1988)
C. Marchal, How the method of minimization of action avoids singularities. Celest. Mech. Dyn. Astronom. 83, 325–353 (2002)
D.L. Ferrario, S. Terracini, On the existence of collisionless equivariant minimizers for the classical n-body problem. Invent. Math. 155(2), 305–362 (2004)
W. Gordon, Conservative dynamical systems involving strong forces. Trans. Am. Math. Soc. 204, 113–135 (1975)
W. Gordon, A minimizing property of Keplerian orbits. Am. J. Math. 99(5), 961–971 (1977)
M. Klein, A. Knauf, Classical Planar Scattering by Coulombic Potentials Lecture Notes in Physics. (Springer, Berlin, 1992)
A. Knauf, The n-centre problem of celestial mechanics for large energies. J. Eur. Math. Soc. 4(1), 1–114 (2002)
Y. Long, S. Zhang, Geometric characterizations for variational minimization solutions of the 3-body problem. Acta Math. Sin. (Engl. Ser.) 16(4), 579–592 (2000)
Y. Long, S. Zhang, Geometric characterization for variational minimization solutions of the 3-body problem with fixed energy. J. Differ. Equ. 160(2), 422–438 (2000)
R.S. Palais, The principle of symmetric criticality. Commun. Math. Phys. 69(1), 19–30 (1979)
E. Serra, S. Terracini, Collisionless periodic solutions to some three-body problems. Arch. Ration. Mech. Anal. 120(4), 305–325 (1992)
M. Shibayama, Minimizing periodic orbits with regularizable collisions in the n-body problem. Arch. Ration. Mech. Anal. 199(3), 821–841 (2011)
X. Wang, S. He, Lagrangian actions on 3-body problems with two fixed centers. Bound. Value Probl. 2012, 28 (2012)
Z. Wang, S. Zhang, New periodic solutions for Newtonian n-body problems with dihedral group symmetry and topological constraints. Arch. Ration. Mech. Anal. 219(3), 1185–1206 (2016)
S. Zhang, Q. Zhou, Variational methods for the choreography solution to the three-body problem. Sci. China Ser. A 45(5), 594–597 (2002)
Acknowledgements
The first author was supported by The Youth Fund of Mianyang Normal University and Project of Sichuan Education Department, and the second author was supported by the National Natural Science Foundation of China (11601045) and China Scholarship Council. Part of this work was done when the second author was visiting University of Minnesota. He thanks the School of Mathematics and Professor Richard Moeckel for their hospitality and support.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhao, F., Wang, Z. Action Minimizing Orbits in the 2-Center Problems with Simple Choreography Constraint. Few-Body Syst 63, 78 (2022). https://doi.org/10.1007/s00601-022-01779-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00601-022-01779-5