A novel capacitive mass sensor using an open-loop controlled microcantilever

Abstract

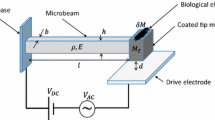
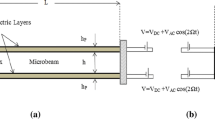
This article presents a method for quantitative estimation of the mass of an entity attached to the surface of an electrostatically actuated clamped-free microbeam implemented as a mass sensor. For this investigation, the microbeam is modeled as a Euler–Bernoulli beam taking into account the effects of electrostatic nonlinearity, viscous energy dissipation together with the effect of the fringing field capacitance. A modal superposition technique is used to simulate the dynamic response of the microcantilever. The dynamic pull-in voltage of microcantilever is evaluated using a developed modal. The present dynamic pull-in voltage results are compared with the existing results and on the basis of comparison, the accuracy of the developed model is ascertained. For mass quantification, firstly, an input shaping technique is employed to stabilize the microbeam at the specified position and then voltage perturbation is induced to make the system sensitive to inertial change. A parasitic mass expressed as a fraction of the total mass of the beam is then added resulting in an increase in the amplitude of vibration and hence an alteration in the capacitance. An empirical relation between the added mass and the change in capacitance is proposed.

Appendix

The following analytical modal analysis is given for the linear transverse vibrations of an undamped Euler–Bernoulli beam with clamped–free boundary conditions and a tip mass rigidly attached at the free end.

1.1 Boundary value problem

The governing equation of motion for undamped free vibrations of a uniform Euler–Bernoulli beam can be obtained as (Meirovitch 2010)

$$\begin{aligned} \hat{E}\hat{I}\frac{{{\partial ^4}\hat{w}(\hat{x},\hat{t})}}{{\partial {{\hat{x}}^4}}} + \hat{\rho }\hat{b}\hat{h}\frac{{{\partial ^2}\hat{w}(\hat{x},\hat{t})}}{{\partial {{\hat{t}}^2}}} = 0. \end{aligned}$$

(A.1)

The clamped–free boundary conditions with a tip mass attachment can be expressed as

$$\begin{aligned} \begin{array}{l} \displaystyle {\left. {\hat{w}} \right| _{\left( {0,\hat{t}} \right) }} = 0,\qquad {\left. {\frac{{\partial \hat{w}}}{{\partial \hat{x}}}} \right| _{(0,\hat{t})}} = 0, \displaystyle \\ {\left. {\hat{E}\hat{I}\frac{{{\partial ^2}\hat{w}}}{{\partial {{\hat{x}}^2}}}} \right| _{(\hat{L},\hat{t})}} = 0, \qquad {\left. {\hat{E}\hat{I}\frac{{{\partial ^3}\hat{w}}}{{\partial {{\hat{x}}^3}}} - {{\hat{M}}_a}\frac{{{\partial ^2}\hat{w}}}{{\partial {{\hat{t}}^2}}}} \right| _{\left( {\hat{L},\hat{t}} \right) }} = 0. \end{array} \end{aligned}$$

(A.2)

Equations A.1–A.2 define the boundary-value problem for the transverse vibrations of a cantilevered uniform Euler–Bernoulli beam with a tip mass attachment.

1.2 Solution using the method of separation of variables

The method of separation of variables (Greenberg 1998) can be used to solve Eq. A.1 by separating the spatial and temporal functions as

$$\begin{aligned} \hat{w}(\hat{x},\hat{t}) = \phi (\hat{x})\eta (\hat{t}), \end{aligned}$$

(A.3)

substitution of Eq. A.3 into Eq. A.1, yields

$$\begin{aligned} \frac{{\hat{E}\hat{I}}}{{\hat{\rho }\hat{b}\hat{h}}}\frac{1}{{\phi \left( {\hat{x}} \right) }}\frac{{{d^4}\phi \left( {\hat{x}} \right) }}{{d{{\hat{x}}^4}}} = - \frac{1}{{\eta \left( {\hat{t}} \right) }}\frac{{{d^2}\eta \left( {\hat{t}} \right) }}{{d{{\hat{t}}^2}}}. \end{aligned}$$

(A.4)

The left side of the Eq. A.4 relies on $\hat{x}$ alone, while the right side is based on $\hat{t}$ alone. Since $\hat{x}$ and $\hat{t}$ are independent variables, the traditional reason for the separation of variables states that both sides of the Eq. A.4 must be equal to the same constant:

$$\begin{aligned} \frac{{\hat{E}\hat{I}}}{{\hat{\rho }\hat{b}\hat{h}}}\frac{1}{{\phi \left( {\hat{x}} \right) }}\frac{{{d^4}\phi \left( {\hat{x}} \right) }}{{d{{\hat{x}}^4}}} = - \frac{1}{{\eta \left( {\hat{t}} \right) }}\frac{{{d^2}\eta \left( {\hat{t}} \right) }}{{d{{\hat{t}}^2}}} = \gamma \end{aligned}$$

(A.5)

yielding

$$\begin{aligned}&\frac{{{d^4}\phi \left( {\hat{x}} \right) }}{{d{{\hat{x}}^4}}} - \gamma \frac{{\hat{\rho }\hat{b}\hat{h}}}{{\hat{E}\hat{I}}}\phi \left( {\hat{x}} \right) = 0. \end{aligned}$$

(A.6)

$$\begin{aligned}&\frac{{{d^2}\eta \left( {\hat{t}} \right) }}{{d{{\hat{t}}^2}}} + \gamma \eta \left( {\hat{t}} \right) = 0. \end{aligned}$$

(A.7)

The positive constant $\gamma$ can be represented as the square of another constant: $\gamma =\omega ^2$. The solution forms of Eqs. A.6, and A.7 are then

$$\begin{aligned}&\phi \left( {\hat{x}} \right) = A\cos \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) + B\cosh \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) + C\sin \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) \\&\qquad + D\sinh \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) \end{aligned}$$

(A.8)

$$\begin{aligned}&\eta \left( {\hat{t}} \right) = E\cos \omega \hat{t} + F\sin \omega \hat{t} \end{aligned}$$

(A.9)

where A, B, C, D, E, and F are unknown constants and

$$\begin{aligned} {\lambda ^4} = {\omega ^2}\frac{{\hat{\rho }\hat{b}\hat{h}{{\hat{L}}^4}}}{{\hat{E}\hat{I}}} \end{aligned}$$

(A.10)

Equation A.3 can be employed in Eq. A.2 to obtain following boundary conditions

$$\begin{aligned}&\phi (0) = 0,\qquad {\left. {\frac{{d{\phi _i}(\hat{x})}}{{d\hat{x}}}} \right| _{\hat{x} = o}} = 0 \end{aligned}$$

(A.11)

$$\begin{aligned}&{\left. {\hat{E}\hat{I}\frac{{{d^2}{\phi _i}(\hat{x})}}{{d{{\hat{x}}^2}}}} \right| _{\hat{x} = \hat{L}}} = 0, \\&\qquad {\left. {\left[ {\hat{E}\hat{I}\frac{{{d^3}{\phi _i}(\hat{x})}}{{d{{\hat{x}}^3}}} + {\omega ^2}{{\hat{M}}_a}{\phi _i}(\hat{x})} \right] } \right| _{\hat{x} = \hat{L}}} = 0 \end{aligned}$$

(A.12)

The spatial form of boundary conditions, Eqs. A.11 and A.12, should then be employed to find the values of $\lambda$ which give the non-trivial ${\phi _i}(\hat{x})$. This process is referred to as the differential eigenvalue problem and is next covered.

1.3 Differential Eigenvalue problem

Substituting Eq. A.8 in Eq. A.11 yields

$$\begin{aligned} A + B&= {} 0 \end{aligned}$$

(A.13)

$$\begin{aligned} C + D&= 0 \end{aligned}$$

(A.14)

Equation A.8 then becomes

$$\begin{aligned} \phi \left( {\hat{x}} \right)&= A\left[ {\cos \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) - \cosh \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) } \right] \\&+ C\left[ {\sin \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) - \sinh \left( {\frac{\lambda }{{\hat{L}}}\hat{x}} \right) } \right] \end{aligned}$$

(A.15)

Hence the unknown constants are A and C only. Using Eq. A.15 in the remaining two boundary conditions given by Eq. A.12 gives

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {\cos \lambda + \cosh \lambda }&{\sin \lambda + \sinh \lambda }\\ {\sin \lambda - \sinh \lambda + \frac{{\lambda {{\hat{M}}_a}}}{{\hat{\rho }\hat{b}\hat{h}\hat{L}}}(\cos \lambda - \cosh \lambda )}&{ - \cos \lambda - \cosh \lambda + \frac{{\lambda {{\hat{M}}_a}}}{{\hat{\rho }\hat{b}\hat{h}\hat{L}}}(\sin \lambda - \sinh \lambda )} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} A\\ C \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right\} \end{aligned}$$

(A.16)

The coefficient matrix in Eq. A.16 has to be singular in order to obtain non-trivial values of A and C (hence non-trivial ${\phi _i}(\hat{x})$). Setting the determinant of the above coefficient matrix gives the characteristic equation of the differential eigenvalue problem as

$$\begin{aligned} 1 + \cos \lambda \cosh \lambda + \lambda \frac{{{{\hat{M}}_a}}}{{\hat{\rho }\hat{b}\hat{h}\hat{L}}}(\cos \lambda \sinh \lambda - \sin \lambda \cosh \lambda ) = 0 \end{aligned}$$

(A.17)

For the given system parameters $\hat{\rho }$, $\hat{b}$, $\hat{h}$, $\hat{L}$, and $\hat{M}_a$, one can solve for the roots of Eq. A.17, which are the eigenvalues of the system. The eigenvalue of the $i^th$ vibration mode is denoted here as $\lambda _i$, and it is associated with the $i^th$ eigenfunction denoted by ${\phi _i}(\hat{x})$ is obtained using second row of Eq. A.16 in Eq. A.15 to keep only a single modal constant

$$\begin{aligned} {\phi _i}\left( {\hat{x}} \right)&= A_i\left[ \left( {\cos \left( {\frac{{{\lambda _i}}}{{\hat{L}}}\hat{x}} \right) - \cosh \left( {\frac{{{\lambda _i}}}{{\hat{L}}}\hat{x}} \right) } \right) \right. \\&\left. + \left( \frac{{\sin {\lambda _i} - \sinh {\lambda _i} + {\lambda _i}\frac{{{{\hat{M}}_a}}}{{\hat{\rho }\hat{b}\hat{h}\hat{L}}}(\cos {\lambda _i} - \cosh {\lambda _i})}}{\cos {\lambda _i} + \cosh {\lambda _i} - {\lambda _i}\frac{{{{\hat{M}}_a}}}{{\hat{\rho }\hat{b}\hat{h}\hat{L}}}(\sin {\lambda _i} - \sinh {\lambda _i})} \right) \left( \sin \left( {\frac{{{\lambda _i}}}{{\hat{L}}}\hat{x}} \right) \right. \right. \\&\left. \left. - \sinh \left( {\frac{{{\lambda _i}}}{{\hat{L}}}\hat{x}} \right) \right) \right] \end{aligned}$$

(A.18)

Using Eq. into Eq. A.18, the nondimensional form of Eq. A.18 is obtained as

$$\begin{aligned} {\phi _i}\left( x \right)&= {A_i}\left[ \left( {\cos \left( {{\lambda _i}x} \right) - \cosh \left( {{\lambda _i}x} \right) } \right) \right. \\&\left. + \left( {\frac{{\sin {\lambda _i} - \sinh {\lambda _i} + {\lambda _i}\kappa (\cos {\lambda _i} - \cosh {\lambda _i})}}{{\cos {\lambda _i} + \cosh {\lambda _i} - {\lambda _i}\kappa (\sin {\lambda _i} - \sinh {\lambda _i})}}} \right) \left( \sin \left( {{\lambda _i}x} \right) \right. \right. \\&\left. \left. - \sinh \left( {{\lambda _i}x} \right) \right) \right] \end{aligned}$$

(A.19)

On defining a new constant $\beta _i$ as

$$\begin{aligned} {\beta _i} = \frac{{\sin {\lambda _i} - \sinh {\lambda _i} + {\lambda _i}\kappa (\cos {\lambda _i} - \cosh {\lambda _i})}}{{\cos {\lambda _i} + \cosh {\lambda _i} - {\lambda _i}\kappa (\sin {\lambda _i} - \sinh {\lambda _i})}}, \end{aligned}$$

(A.20)

Eq. A.20 is written as

$$\begin{aligned} {\phi _i}\left( x \right)&= {A_i}[ \left( {\cos \left( {{\lambda _i}x} \right) - \cosh \left( {{\lambda _i}x} \right) } \right) \\&+ {\beta _i}\left( {\sin \left( {{\lambda _i}x} \right) - \sinh \left( {{\lambda _i}x} \right) } \right) ]. \end{aligned}$$

(A.21)