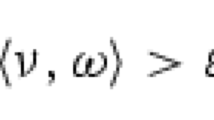Inverse mean curvature flow of rotationally symmetric hypersurfaces

Abstract

We prove that the Inverse Mean Curvature Flow of a non-star-shaped, mean-convex embedded sphere in $\mathbb {R}^{n+1}$ with symmetry about an axis and sufficiently long, thick necks exists for all time and homothetically converges to a round sphere as $t \rightarrow \infty$. Our approach is based on a localized version of the parabolic maximum principle. We also present two applications of this result. The first is an extension of the Minkowski inequality to the corresponding non-star-shaped, mean-convex domains in $\mathbb {R}^{n+1}$. The second is a connection between IMCF and minimal surface theory. Based on previous work by Meeks and Yau (Math Z 179:151–168, 1982) and using foliations by IMCF, we establish embeddedness of the solution to Plateau’s problem and a finiteness property of stable immersed minimal disks for certain Jordan curves in $\mathbb {R}^{3}$.

A Appendices

1.1 A.1 Non-cylindrical maximum principle

We recall Theorem 4.4:

Theorem A.1

Let $F: N^{n} \times [0,T) \rightarrow \mathbb {R}^{n+1}$ be a solution of the Inverse Mean Curvature Flow (1.1) over a closed manifold N. For a domain $U \subset N \times [0,T)$ and $f \in C^{2,1}(U) \cap C(\overline{U})$, suppose for a smooth vector field $\eta$ over U we have

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta \right) f \le \langle \eta , \nabla f \rangle . \end{aligned}$$

(Resp. $\ge$ at a minimum) Here $\Delta$ and $\nabla$ are the Laplacian and gradient operators over $N_{t}$, respectively. Then

$$\begin{aligned} \sup _{U} f \le \sup _{\partial _{P} U} f \end{aligned}$$

(Resp. $\inf _{U} f \ge \inf _{\partial _{P} U} f$). Furthermore, suppose that f has a positive supremum over U and that each $(x_{0},t_{0}) \in \partial _{P} U {\setminus } \tilde{\partial }_P U$ is a limit point of $U \cap \{ t < t_{0} \}$. Then

$$\begin{aligned} \sup _{U} f \le \sup _{\tilde{\partial }_{P} U} f \end{aligned}$$

(A.61)

(Resp. $\inf _{U} f \ge \inf _{\tilde{\partial }_{P} U} f$ for a positive minimum).

Proof of Theorem 4.4

For the first part, we follow the proof in the Appendix of [6]. For a given smooth vector field $\eta$ over U we have by hypothesis

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta \right) f \le \langle \eta , \nabla f \rangle . \end{aligned}$$

We argue by contradiction: define the function $\tilde{f}(x,t)=f(x,t)- \epsilon t$ for some $\epsilon >0$. Then

$$\begin{aligned} \partial _{t} \tilde{f}= \partial _{t} f- \epsilon , \quad \partial _{i} \tilde{f} = \partial _{i} f, \quad \partial _{ij} \tilde{f} = \partial _{ij} f. \end{aligned}$$

The operator over $\tilde{f}$ must then obey

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla \right) \tilde{f} < 0. \end{aligned}$$

(A.62)

On the other hand, at any interior maximum $(x_{0},t_{0}) \in U$ of $\tilde{f}$, the criteria for a local maximum dictate that at $(x_{0},t_{0})$

$$\begin{aligned} \partial _{t} \tilde{f} \ge 0, \quad \partial _{i} \tilde{f}=0, \quad \partial _{ij} \tilde{f} \le 0, \end{aligned}$$

where the last inequality is in the operator-theoretic sense for the symmetric matrix $\partial _{ij} \tilde{f}$. Writing

$$\begin{aligned} \Delta \tilde{f}= g^{ij} (\partial _{ij} \tilde{f} - \Gamma ^{k}_{ij} \partial _{k} \tilde{f}), \quad \nabla \tilde{f} = g^{ij} \partial _{j} \tilde{f} \partial _{i} \vec {F} \end{aligned}$$

in view of the positivity of $g_{ij}$, we see $\Delta \tilde{f} \le 0$ and $\nabla f=0$. Hence

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla \right) \tilde{f}(x_{0},t_{0}) \ge 0, \end{aligned}$$

contradicting (A.62). So $\tilde{f}$ has no interior maximum and thus

$$\begin{aligned} \sup _{U} f - \epsilon T \le \sup _{U} \tilde{f} \le \sup _{\partial _{P} U} f. \end{aligned}$$

Then $\sup _{U} f \le \sup _{\partial _{P} U} f + \epsilon T$. For $T< \infty$, letting $\epsilon \rightarrow 0$ yields the result. To prove the statement for the infimum, take $\tilde{f}=f- \epsilon t$, $\epsilon >0$, and repeat this argument for a minimum.

For the second part, we show $\sup _{U} f \le \sup _{\tilde{\partial }_{P} U} f$ if $\sup _{U} f > 0$. Define $Z= \partial _{P} U {\setminus } \tilde{\partial }_{P} U$, and for each $t \in [0,T)$ let $Z_{t}= Z \cap \{ t \}$ be the cross sections of Z. We argue by contradiction: suppose (A.61) does not hold. Then the maximum of f does not occur on $\partial _{\tilde{P}} U$ nor does it occur at an interior point of U, so it must occur on the set Z. Call $Z_{\max }$ the union of $Z_{t}$’s on which the maximum is achieved, and let $t_{*}>0$ be the first time at which $\sup _{U} f$ is achieved on $Z_{\max }$. Pick $\beta > 0$ such that

$$\begin{aligned} \sup _{U} f> \beta > \sup _{\partial _{P} U \setminus Z_{\max }} f, \end{aligned}$$

and define

$$\begin{aligned} Y_{\beta } = \{ (x,t) \in U| f(x,t) > \beta \}. \end{aligned}$$

$\overline{Y_{\beta }}$ must intersect $Z_{t_{*}}$. Consider $(x_{0},t_{*}) \in Z_{t_{*}} \cap \overline{Y_{\beta }}$. From the additional assumption in the proposition there is a sequence of points $(x_{n},t_{n}) \in U$ with $t_{n} < t_{*}$ converging to $(x_{0},t_{*})$. By continuity of f, $f(x_{n},t_{n}) > \beta$ for large enough n. This means that the set

$$\begin{aligned} X_{\beta }=\{ t < t_{*} \} \cap Y_{\beta } \end{aligned}$$

(A.63)

is nonempty and open. By openness, we pick a time $t_{1} < t_{*}$ so that the set $X_{\beta } \cap \{ t \le t_{1} \} \ne \varnothing$.

Fig. 6

The cutoff function $\phi$ is 1 for times less than $t_{1}$ and 0 for times greater than $t_{2}$. This guarantees that the supremum of $\phi f$ occurs at an interior point of $X_{\beta }'$

Fix a time $t_{2} \in (t_{1},t_{*})$ and choose a cutoff function $\phi : [0,T] \rightarrow [0,1]$ such that $\phi (t)=1$ when $t \in [0,t_{1}]$, $\phi '(t) < 0$ when $t \in (t_{1}, t_{2})$, and $\phi (t)=0$ when $t \in [t_{2},T]$, see Fig. 6. Since $(\phi f) (x, t_{1})= f(x, t_{1}) > \beta$ for $(x,t_{1}) \in X_{\beta }$, we know $\sup _{U} \phi f> \beta >0$.

We calculate

$$\begin{aligned} \partial _{t} (\phi f) = \phi \partial _{t} f + \phi ' f, \quad \Delta \phi f = \phi \Delta f, \quad \nabla (\phi f) = \phi \nabla f, \end{aligned}$$

so

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla \right) (\phi f) = \phi \left( \partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla \right) f + \phi ' f. \end{aligned}$$

(A.64)

By hypothesis we have $(\partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla ) f (x,t) \le 0$ and $\phi ' \le 0$. Since $\sup _{U} \phi f > 0$, any interior point $(x_{0},t_{0}) \in U$ at which $\phi f$ achieves this supremum would need to satisfy

$$\begin{aligned} \left( \partial _{t} - \frac{1}{H^{2}} \Delta - \eta \cdot \nabla \right) (\phi f) (x_{0},t_{0}) < 0. \end{aligned}$$

By the same argument used for the first part of Theorem 4.4, this is impossible, and so $\sup _{U} (\phi f) = \sup _{\partial _{P} U} (\phi f)$. However, $\sup _{\partial _{P} U {\setminus } Z_{\max }} \phi f \le \sup _{\partial _{P} U {\setminus } Z_{\max }} f < \beta$ by hypothesis, and $\phi f|_{Z_{\max }} \equiv 0$ as $\phi =0$ on $[t_{*},T)$. This would altogether yield

$$\begin{aligned} \sup _{\partial _{P} U} \phi f< \beta < \sup _{U} \phi f, \end{aligned}$$

contradicting the first part of the non-cylindrical maximum principle. Conclude then that

$$\begin{aligned} f(x,t) \le \sup _{\tilde{\partial }_{P}U} f \end{aligned}$$

on U. The statement may be shown for a minimum by choosing $\beta >0$ with $\inf _{U} f< \beta < \inf _{\partial _{P} U {\setminus } Z_{\max }} f$.

Remark A.2

The version of this principle used in [6, 21] does not include the hypothesis that U approaches $Z_{t_{*}}$ from below in time. However, if U only touches $Z_{t_{*}}$ from above in time, $Y_{\beta } \cap \{ t < t_{*}\}$ may be empty. The corresponding cutoff function would then need to be chosen to increase with t, so that the last term in (A.64) is possibly non-negative. Therefore, this additional hypothesis seems to be necessary.

1.2 A.2 Non-star-shaped admissible initial data

Proposition A.3

For any $n \ge 2$, there is an admissible surface $N_{0}^{n} \subset \mathbb {R}^{n+1}$ which is not star-shaped.

Proof

We will begin with an example of a non-star-shaped admissible surface which is of class $C^{2}$. Define the domain $E_{0} \subset \mathbb {R}^{n+1}$ by

$$\begin{aligned} E_{0}= \{ -10< x_{1}< 10 | (x_{2}^{2} + \cdots x_{n+1}^{2})^{\frac{1}{2}} < y(x_{1}) \}, \end{aligned}$$

(A.65)

where $y: (-10,10) \rightarrow \mathbb {R}^{+}$ is the even extension of the function

$$\begin{aligned} y(x) = {\left\{ \begin{array}{ll} \frac{3}{4} &{} x \in [0,8) \\ \frac{3}{4} + 2 (x-8)^{3} - \frac{11}{4}(x-8)^{4} + (x-8)^{5} &{} x \in [8,9) \\ \sqrt{1-(x-9)^{2}} &{} x \in [9,10), \end{array}\right. } \end{aligned}$$

(A.66)

across $x=0$. Direct computation shows that $y \in C^{2}((-10,10))$. One can also verify through either computing maxima or graphing that

$$\begin{aligned} \frac{3}{4} \le y(x) (1 + |y'(x)|^{2})^{\frac{1}{2}}\le & {} \frac{5}{4} \end{aligned}$$

(A.67)

$$\begin{aligned} \frac{y''(x)y(x)}{1+|y'(x)|^{2}}< & {} 1 , \end{aligned}$$

(A.68)

for each $x \in (-10,10)$. The left-hand side of (A.68) corresponds to the ratio $-\frac{k}{p}$ of the principal curvatures of $N_{0}$, and so this bound implies

$$\begin{aligned} \min _{N_{0}} H >0, \end{aligned}$$

(A.69)

The function in (A.67) corresponds to $p^{-1}$ on $N_{0}$, meaning

$$\begin{aligned} \frac{\max _{N_{0}} p}{\min _{N_{0}} p} < 2 \le n^{\frac{n}{2(n-1)}}, \quad n \ge 2, \end{aligned}$$

(A.70)

so altogether $N_{0}$ is mean-convex and admissible.

To demonstrate that $N_{0}$ is not star-shaped, it is sufficient to consider graph of the function y in the $x-y$ plane. In this plane, the line segment connecting (0, 0) to (9, 1), parametrized by $L(x)=\frac{1}{9}x$, satisfies

$$\begin{aligned} L(8) = \frac{8}{9} > \frac{3}{4}= y(8), \end{aligned}$$

meaning this segment must intersect the graph of y at another point by the intermediate value property. Furthermore, for any $x_{0} \le 0$ and $0 \le y_{0} < y(x_{0})$, the line segment connecting $(x_{0},y_{0})$ to (9, 1) satisfies

$$\begin{aligned} L_{(x_{0},y_{0})} (x) \ge L(x), \quad x \in [0,9], \end{aligned}$$

for the L(x) defined above. So $L_{(x_{0},y_{0})}(8) > \frac{3}{4}$, and once again by the intermediate value property this segment intersects the graph somewhere else. If we choose $x_{0} \ge 0$, $0 \le y_{0} < y(x_{0})$, the segment connecting $(x_{0},y_{0})$ to $(-9,1)$ must also intersect since y is even (Fig. 7).

Fig. 7

A graph of the function y(x) defined in (A.66). The admissible surface generated by y(x) is not star-shaped because of its long neck

For any $x_{0} \in E_{0}$, let $P \subset \mathbb {R}^{n+1}$ be the 2-plane containing $x_{0}$ and $X_{1}$ (if $x_{0}$ lies on this axis, let P be any 2-plane containing $X_{1}$). Choose Cartesian coordinates (x, y) on P so that x-axis is $X_{1}$ and the y-coordinate of $x_{0}$ is non-negative. Then either the line segment connecting $x_{0}$ to $(9,1) \in P$ or the line segment connecting $x_{0}$ to $(-9,1) \in P$ is not contained in $E_{0}$. Since these points lie on $N_{0}$, $N_{0}$ cannot be star-shaped with respect to $x_{0}$.

To conclude, we must show that $N_{0}$ is approximated in a $C^{2}$ sense by smooth rotationally symmetric hypersurfaces. For P as above, $N_{0} \cap P= \gamma$ is a closed plane curve parametrized over ${[0,1]}/{\mathbb {Z}} \simeq \mathbb {S}^{1}$ by

$$\begin{aligned} \gamma (t)= (x_{1}(t),x_{2}(t))= {\left\{ \begin{array}{ll} (10(4t-1), y(10(4t-1))) &{} 0 \le t \le \frac{1}{2}, \\ (10(3-4t), -y(10(3-4t)) &{} \frac{1}{2} \le t \le 1. \end{array}\right. } \end{aligned}$$

(A.71)

By convolving with a symmetric mollifier $\psi _{\epsilon }$ over $\mathbb {S}^{1}$, we obtain smooth functions $x^{\epsilon }_{1}(t)$ and $x^{\epsilon }_{2}(t)$ on $\mathbb {S}^{1}$ which are respectively even and odd about $t=\frac{1}{2}$. For $\epsilon$ small enough, the corresponding smooth curve $\gamma ^{\epsilon }(t)=(x^{\epsilon }_{1}(t),x^{\epsilon }_{2}(t))$ in P is uniformally convex over small intervals containing $t=0$ and $t=\frac{1}{2}$, and away from these intervals $x^{\epsilon }_{1}(t)$ and $x^{\epsilon }_{2}(t)$ converge in uniform $C^{2}$ topology to $x_{1}(t)$ and $x_{2}(t)$ as $\epsilon \rightarrow 0$. Then $\gamma _{\epsilon }$ is the cross section $N^{\epsilon }_{0} \cap P$ of a smooth, rotationally symmetric hypersurface $N^{\epsilon }_{0}$ which inherits properties (A.69) and (A.70) and fails to be star-shaped. $\square$