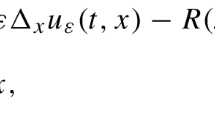Uniqueness of the viscosity solution of a constrained Hamilton–Jacobi equation

Abstract

In quantitative genetics, viscosity solutions of Hamilton–Jacobi equations appear naturally in the asymptotic limit of selection-mutation models when the population variance vanishes. They have to be solved together with an unknown function I(t) that arises as the counterpart of a non-negativity constraint on the solution at each time. Although the uniqueness of viscosity solutions is known for many variants of Hamilton–Jacobi equations, the uniqueness for this particular type of constrained problem was not resolved, except in a few particular cases. Here, we provide a general answer to the uniqueness problem, based on three main assumptions: convexity of the Hamiltonian function H(I, x, p) with respect to p, monotonicity of H with respect to I, and BV regularity of I(t).

Variational and viscosity solutions coincide (proof of Theorem 2)

Given $I \in BV(0,T)$, let V(t, x) denote the corresponding variational solution of (1.4). The purpose of this section is to show that V(t, x) is the unique locally Lipschitz viscosity solution of (1.1). This can be achieved by establishing comparison theorem, i.e. $u \le V$ (resp. $u \ge V$) for all locally Lipschitz viscosity sub-solution (resp. super-solution) of (1.1). While there are PDE proofs for such comparison results among continuous, but not necessarily Lipschitz, super and sub-solutions of (1.1), they are usually proved under slightly different conditions than (L1) - (L4). For instance, in [13] (see also [16, Appendix A]), it is assumed that the Hamiltonian H is uniformly Lipschitz in $x \in {\mathbb {R}}^d$. Henceforth, we will adopt techniques in convex analysis to prove the comparison between the variational solution with Lipschitz continuous super and sub-solutions of (1.1), under exactly the assumptions (L1) - (L4).

As the Hamiltonian is convex with respect to p, sub-solutions in the almost everywhere sense, and viscosity sub-solutions in particular, lie automatically below the variational solution [4, 11]. We include a proof here for the sake of completeness.

Proposition 12

Assume that u is locally Lipschitz, that $u(0,x) \le g(x)$ for all x, and that the following inequality holds for almost every $(t,x)\in (0,T)\times {\mathbb {R}}^d$,

$$\begin{aligned} \partial _t u(t,x) + H({I}(t),x,d_xu(t,x)) \le 0\quad a.e. \end{aligned}$$

(A.1)

Then, $u\le V$.

Proof

The proof is adapted from [11, Section 4.2]. A more direct proof can be found in [4, Section 9] but the latter assumes time continuity for H, which does not hold in the present case. A first observation is that (A.1) makes perfect sense as u is differentiable almost everywhere by Rademacher’s theorem. We shall establish that

$$\begin{aligned} u(t_2,\gamma (t_2)) - u(t_1,\gamma (t_1)) \le \int _{t_1}^{t_2} L({I}(s), \gamma (s), {\dot{\gamma }}(s))\, ds\, , \end{aligned}$$

(A.2)

for all curves $\gamma \in W^{1,\infty }$. Thus, the result will follow immediately by taking the infimum with respect to $\gamma$, since (2.1) of Lemma 9 says that any minimizer is indeed $W^{1,\infty }$.

To prove (A.2), we proceed by a density argument. The case of a linear curve $\gamma = x + (s-t_1) v$ is handled as follows: firstly, we deduce from (A.1) that

$$\begin{aligned} \partial _t u(t,x) + d_xu(t,x)\cdot v \le L({I}(t), x, v)\quad a.e. \end{aligned}$$

(A.3)

Secondly, by Fubini’s theorem one can find a sequence $x_n\rightarrow x$ such that (A.3) holds almost everywhere in the line $\{ (s,x_n+(s-t_1) v) \}$ for each n. Therefore, we can apply the chain rule to $u(s,x_n+(s-t_1) v)$, so as to obtain:

$$\begin{aligned} \dfrac{d}{ds}\left( u(s,x_n+(s-t_1) v)\right) \le L({I}(s), x_n+(s-t_1) v,v)\quad a.e. \end{aligned}$$

(A.4)

We deduce that (A.2) holds true for all linear curves by integrating (A.4) from $t_1$ to $t_2$ and taking the limit $n\rightarrow +\infty$.

Consequently, (A.2) holds true for any piecewise linear curve. The conclusion follows by a density argument of piecewise linear curves in the set of curves having bounded measurable derivatives. $\square$

It remains to show that viscosity super-solutions lie above the variational solution. For completeness’ sake, we give a definition of super-solution for time-measurable Hamiltonians. (See [12, 15] for various other equivalent definitions.)

Definition 13

(Viscosity super-solution) Let $\phi \in {\mathcal {C}}^1({\mathbb {R}}^d)$ be such that the minima of $u(t,\cdot ) - \phi$ are reached in a ball of radius R for all $t\in [0,T]$. Let ${\mathfrak {M}}(t)$ be the set of minimum points of $u(t,\cdot ) - \phi$, and $m(t) = \min u(t,\cdot ) - \phi$. Then, it is required that the following inequality holds true in the distributional sense:

$$\begin{aligned} m'(t) + \underset{y\in {\mathfrak {M}}(t)}{\sup } H({I}(t), y, d_x \phi (y)) \ge 0\quad \text {in}\; {\mathcal {D}}'(0,T)\, . \end{aligned}$$

(A.5)

Rather than directly invoking Definition 13, we will only use the following two consequences of it in our proofs.

Remark 3

In case I(t) is continuous, then ${\hat{H}}(t,x,p):= H(I(t),x,p)$ defines a continuous Hamiltonian. In that case, the above definition is consistent with the usual one for viscosity super-solution based on the notion of sub-differential [4, Definition 3.2]. Namely, $u \in C((0,T) \times {\mathbb {R}}^d)$ is a super-solution of (1.1) if, for each (t, x),

$$\begin{aligned} q + {\hat{H}}(t,x,p) \ge 0 \quad \text { for all }(q,p) \in D^{2,-}u(t,x), \end{aligned}$$

where the set of sub-differential, $D^{2,-}u(t,x)$, is the subset of ${\mathbb {R}} \times {\mathbb {R}}^d$ given by

$$\begin{aligned} D^{2,-}u(t,x)= \{(q,p) : \, (\forall \mu ,v )\quad u(t,x) - u(t-s\mu , x - sv) \le qs\mu + \langle p, sv\rangle + o(s)\}. \end{aligned}$$

Remark 4

Suppose that u is a viscosity super-solution of (1.1) for some I(t) in the sense of Definition 13, and that $I(t) \ge {\hat{I}}(t)$ for some continuous ${\hat{I}}(t)$, then by monotonicity of H in I, it can be verified that u is a super-solution of (1.1), with I(t) replaced by ${\hat{I}}(t)$, in the usual sense as in Remark 3. See [15] for details.

Proposition 14

Assume that u is a locally Lipschitz viscosity super-solution, in the sense of Definition 13, and that $u(0,x) \ge g(x)$ for all x. Then, $u\ge V$.

Proof

We follow the lines of [8] which is essentially based on convex analysis. We adapt their proof in our context for the sake of completeness. We will first prove the proposition in the special case of $I \in W^{1,\infty }(0,T)$. This assumption will be relaxed to $I \in BV(0,T)$ at the end of the proof.

Step #1 Finding the backward velocity: setting of the problem. The key is to find, for each (t, x), a particular direction ${\mathbf {v}}(t,x)$, such that the following inequality holds true:

$$\begin{aligned} d_+ u(t,x)(1,{\mathbf {v}}(t,x)) \ge L(I(t),x,{\mathbf {v}}(t,x))\, , \end{aligned}$$

(A.6)

where $d_+ u(t,x)(\mu ,v)$ is the one-sided directional differentiation in the direction $(\mu ,v)$:

$$\begin{aligned} d_+ u(t,x)(\mu ,v) = \limsup _{s\rightarrow 0+} \dfrac{u(t,x) - u(t-s\mu ,x-sv)}{s}\, . \end{aligned}$$

Fig. 1

Illustration of various shapes of cones as they may appear for a scalar function u (in opposition to the text where the domain of u is genuinely multi-dimensional). The regions shaded green correspond to (translated) hypograph $(z_i,u(z_i))+{\mathcal {H}}_{z_i}$, whereas the region shaded orange correspond to the (translated) contingent cones $(z_i,u(z_i)) +{\mathcal {T}}_{{{\,\mathrm{\mathbf {Epi}}\,}}u}(z_i,u(z_i))=(z_i,u(z_i))-{\mathcal {H}}_{z_i}$. Note that we have translated the vertices of the cones to the respective points $(z_i,u(z_i))$ for illustrative purposes

We can interpret (A.6) as follows: there exists an element which is common to the partial epigraph of $v \mapsto L(I(t),x, v)$:

$$\begin{aligned} {\mathcal {E}}_{t,x} = {{\,\mathrm{\mathbf {Epi}}\,}}_v (L(I(t),x,v)) = \left\{ (v,\ell ) \in {\mathbb {R}}^{d}\times {\mathbb {R}}: \ell \ge L(I(t),x,v) \right\} , \end{aligned}$$

and to the hypograph of $v \mapsto d_+ u(t,x)(1,v)$:

$$\begin{aligned} {{\,\mathrm{\mathbf {Hypo}}\,}}_v(d_+ u(t,x)(1,v)) = \left\{ (v,\ell ) \in {\mathbb {R}}^{d}\times {\mathbb {R}}: \ell \le d_+ u(t,x)(1,v) \right\} . \end{aligned}$$

For technical reason, we consider the full hypograph ${\mathcal {H}}_{t,x} = {{\,\mathrm{\mathbf {Hypo}}\,}}_{(\mu ,v)}(d_+u(t,x)(\mu ,v))$, taken with respect to variables $(\mu ,v) \in {\mathbb {R}} \times {\mathbb {R}}^d$. Precisely,

$$\begin{aligned} {\mathcal {H}}_{t,x} = \left\{ (\mu ,v,\ell ) \in {\mathbb {R}}\times {\mathbb {R}}^{d}\times {\mathbb {R}}: \ell \le \limsup _{s\rightarrow 0+} \dfrac{u(t,x) - u(t-s\mu ,x-sv)}{s} \right\} \, . \end{aligned}$$

(A.7)

In contrast with ${{\,\mathrm{\mathbf {Hypo}}\,}}_v(d_+ u(t,x)(1,v))$, ${\mathcal {H}}_{t,x}$ is a cone because the quantity in (A.7) is positively homogeneous with respect to $(\mu ,v)$. In fact, it coincides with the definition of a contingent cone, up to a change of sign. If $S\subset {\mathbb {R}}^{N}$ is a non-empty subset, and $z\in {\mathbb {R}}^{N}$, recall that the contingent cone of S at z, denoted by ${\mathcal {T}}_S (z)$, is defined as follows [3, Definition 3.2.1]:

$$\begin{aligned} w\in {\mathcal {T}}_S (z) \quad \Longleftrightarrow \quad \liminf _{s\rightarrow 0^+} \dfrac{\mathrm {dist}(z + s w,S)}{s} = 0\, . \end{aligned}$$

Then, we claim the following equivalence:

$$\begin{aligned} {\mathcal {H}}_{t,x} = - {\mathcal {T}}_{{{\,\mathrm{\mathbf {Epi}}\,}}u} (t,x,u(t,x))\, , \end{aligned}$$

(A.8)

where ${{\,\mathrm{\mathbf {Epi}}\,}}u = \{(t,x,\ell ):\, \ell \ge u(t,x)\}$. For the convenience of readers, the equivalence (A.8) is illustrated in Fig. 1 for a scalar function u. Now we show (A.8). Indeed, $(\mu ,v,\ell )$ belongs to $- {\mathcal {T}}_{{{\,\mathrm{\mathbf {Epi}}\,}}u}(t,x,u(t,x))$ if and only if there exist subsequences $s_n\rightarrow 0+$ and $(t_n,x_n,u_n)$ such that:

$$\begin{aligned} {\left\{ \begin{array}{ll} t - s_n \mu = t_n + o(s_n)\\ x - s_n v = x_n + o(s_n)\\ u(t,x) - s_n \ell = u_n + o(s_n) \end{array}\right. }\, \quad \text {and}\quad u_n \ge u(t_n, x_n)\, . \end{aligned}$$

The latter inequality is inherited from the choice $S = {{\,\mathrm{\mathbf {Epi}}\,}}u$. Reorganizing the terms, and using the Lipschitz continuity of u, we obtain:

$$\begin{aligned}&u(t,x) - s_n\ell \ge u(t-s_n \mu ,x-s_nv) + o(s_n)\, , \\&\dfrac{u(t,x) - u(t-s_n \mu ,x-s_nv)}{s_n} \ge \ell + o(1)\, . \end{aligned}$$

The latter is precisely (A.7). i.e. $(\mu ,v, \ell ) \in {\mathcal {H}}_{t,x}$ and this proves (A.8).

Summarizing, we are seeking a vector $v \in {\mathbb {R}}^d$ so that the element (1, v, L(I(t), x, v)) is common to ${\mathcal {H}}_{t,x}$ and to $\{1\}\times {\mathcal {E}}_{t,x}$. The latter is a convex set, but the former is not necessarily convex. Therefore, we are led to consider its convex closure ${{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x})$ in order to use the separation theorem. Next, we shall use the viability theory to remove the convex closure, exactly as in [8].

Step #2 Finding the backward velocity: the separation theorem. We wish to avoid separation of the two convex sets ${{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x})$ and $\{1\}\times {\mathcal {E}}_{t,x}$. We argue by contradiction. If the two sets are separated, then there exists a linear form $q\cdot + \langle p, \cdot \rangle$ such that (i) ${{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x})$ lies below the hyper-plane $\{(\mu ,v,\ell ): \ell = q\mu + \langle p, v \rangle \}$, and (ii) $\{1\}\times {\mathcal {E}}_{t,x}$ lies strictly above it [21]. We deduce from the latter condition (ii) that $q + \langle p, v \rangle \le L(I(t),x,v) - \delta$ for all $v\in {\mathbb {R}}^d$ and some $\delta >0$. This can be recast as $q + H(I(t),x,p) \le -\delta$ from the definition of the Legendre transform. On the other hand, we deduce from condition (i) that

$$\begin{aligned} \limsup _{s\rightarrow 0^+}\dfrac{u(t,x) - u(t-s\mu ,x-sv)}{s} = d_+u(t,x)(\mu ,v) \le q\mu + \langle p, v \rangle \, , \end{aligned}$$

for all $(\mu ,v)\in {\mathbb {R}}^{d+1}$. Consequently, (q, p) belongs to the subdifferential of u at (t, x). By applying the usual criterion of viscosity super-solutions for continuous Hamiltonian functions (see Remark 3), we find that $q + H(I(t),x,p) \ge 0$. This is a contradiction. Thus, the two convex sets are not separated, i.e.

$$\begin{aligned} (\forall t,x) \quad {{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x})\cap \left( \{1\}\times {\mathcal {E}}_{t,x}\right) \ne \emptyset \, . \end{aligned}$$

(A.9)

Step #3 Finding the backward velocity: the viability theorem. Note that (A.9) is equivalent to

$$\begin{aligned} (\forall t,x) \quad {{\,\mathrm{\overline{\mathrm {co}}}\,}}(-{\mathcal {T}}_{{{\,\mathrm{\mathbf {Epi}}\,}}u}(t,x,u(t,x)))\cap \left( \{1\}\times {\mathcal {E}}_{t,x}\right) \ne \emptyset \, . \end{aligned}$$

(A.10)

We wish to use the viability theorem [3, p. 85] (see also [8, Theorem 2.3]):

Theorem 15

(Viability) Suppose that $G:{\mathbb {R}}^N \rightsquigarrow {\mathbb {R}}^N$ is an upper semi-continuous set-valued map with compact convex values. Then for each closed set $S\subset {\mathbb {R}}^N$, the following statements are equivalent:

• (a)    $(\forall z\in S) \quad {\mathcal {T}}_S (z) \cap G(z) \ne \emptyset$;

• (b)    $(\forall z\in S) \quad \left( {{\,\mathrm{\overline{\mathrm {co}}}\,}}{\mathcal {T}}_S (z)\right) \cap G(z) \ne \emptyset$.

Further compactness estimate is required in order to apply Theorem 15. We claim that we can restrict (A.9) to a compact set:

$$\begin{aligned} {{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x}) \cap \left( \{1\}\times {\mathcal {E}}_{t,x} \right) \cap \left( \{1\}\times B(0,R_{ |x|})\times \left[ m,M\right] \right) \ne \emptyset \,, \end{aligned}$$

where for each $K>0$, $R_{K} = \max \{1, r_{K}\}$, with $r_K$ increasing in K such that

$$\begin{aligned} \Theta (r) > [u]_{\mathrm {Lip}(\overline{[0,T] \times B(0,K)})} (1 + r) + C_\Theta \quad \text { for all }r \ge r_K\,, \end{aligned}$$

(A.11)

(the choice of $r_K$ is possible due to the superlinear growth of $\Theta$), and m, M are respectively $m = \min L$, $M = \max L$ where both minimum and maximum are taken over the set $J\times \{x\}\times B(0,R_{|x|})$, where J is a compact set containing the values $\{I(t)\}_{t\in (0,T)}$.

To this end, consider the following two options: either the dual cone $({\mathcal {H}}_{t,x})^-$ is empty or non-empty. In the first case, it implies ${{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x}) = {\mathbb {R}}^d$, so that any element of ${\mathcal {E}}_{t,x}$ is appropriate. In particular,

$$\begin{aligned} (1, 0, L(I(t),x,0)) \in {{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x}) \cap \left( \{1\}\times {\mathcal {E}}_{t,x} \right) \cap \left( \{1\}\times B(0,1)\times \left[ m,M\right] \right) \,. \end{aligned}$$

(A.12)

In the second case, $({\mathcal {H}}_{t,x})^-$ is non-empty. Hence, there exists a linear form $q\cdot + \langle p, \cdot \rangle$ such that ${{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x})$ lies below the linear set $\{ q\mu + \langle p, v \rangle \}$ as in Step #2. Therefore, every common point $(1,v,\ell ) \in \overline{\mathrm{co}}({\mathcal {H}}_{t,x}) \cap (\{1\}\times {\mathcal {E}}_{t,x})$ (and there is at least one such point) must satisfy

$$\begin{aligned} L(I(t),x,v) \le \ell \le q + \langle p, v \rangle . \end{aligned}$$

By the facts that (i) L grows uniformly super-linearly (by (L3)), and (ii) (q, p) is bounded as it belongs to the subdifferential of the locally Lipschitz function u, i.e. $\max \{|q|, |p|\} \le [u]_{\mathrm {Lip}(\overline{(0,T) \times B(0,|x|)})}$, we deduce

$$\begin{aligned} \Theta (|v|) - C_\Theta \le L(I(t),x,v) \le \ell \le [u]_{\mathrm {Lip}(\overline{(0,T) \times B(0,|x|)})} (1 + |v|). \end{aligned}$$

By the choice of $r_K$ in (A.11), we must have $|v| < r_K$ with $K = |x|$, that is

$$\begin{aligned} {{\,\mathrm{\overline{\mathrm {co}}}\,}}({\mathcal {H}}_{t,x}) \cap \left( \{1\}\times {\mathcal {E}}_{t,x} \right) \cap \left( \{1\}\times B(0,r_{|x|})\times \left[ m,M\right] \right) \ne \emptyset \, . \end{aligned}$$

(A.13)

By (A.12) and (A.13), and our choice of $R_{|x|}:= \max \{1, r_{|x|} \}$, we find that

$$\begin{aligned} {{\,\mathrm{\overline{\mathrm {co}}}\,}}\left( - {\mathcal {T}}_{\{{{\,\mathrm{\mathbf {Epi}}\,}}u\}}(t,x,u(t,x))\right) \cap (-G(t,x)) = {{\,\mathrm{\overline{\mathrm {co}}}\,}}\left( {\mathcal {H}}_{t,x}\right) \cap (-G(t,x)) \ne \emptyset \,, \end{aligned}$$

where $G(t,x) = -\left( \{1\}\times {\mathcal {E}}_{t,x} \right) \cap \left( \{1\}\times B(0,R_{|x|})\times \left[ m,M\right] \right)$ is a continuous set-valued map with compact convex values. In order to apply the viability theorem to the closed subset $S = {{\,\mathrm{\mathbf {Epi}}\,}}u$, it remains to check that the statement (b) of Theorem 15, i.e.

$$\begin{aligned} \overline{\mathrm{co}} \left( {\mathcal {T}}_{{{\,\mathrm{\mathbf {Epi}}\,}}u}(t,x,U)\right) \cap G(t,x) \ne \emptyset \end{aligned}$$

holds for all $(t,x,U)\in {{\,\mathrm{\mathbf {Epi}}\,}}u$, and not only for points (t, x, u(t, x)) on the graph of u. This is immediate, as ${\mathcal {T}}_{\{{{\,\mathrm{\mathbf {Epi}}\,}}u\}}(t,x,U) = {\mathbb {R}}^{d+2}$ for $U>u(t,x)$.

Finally, all the assumptions of the viability theorem are met. As a consequence, we can remove the convex closure in (A.10), and thus in (A.9), so as to obtain:

$$\begin{aligned} (\forall t,x) \quad {\mathcal {H}}_{t,x} \cap \left( \{1\}\times {\mathcal {E}}_{t,x}\right) \ne \emptyset \, . \end{aligned}$$

In particular, for each (t, x) there exists a vector ${\mathbf {v}}(t,x)$ such that (A.6) holds true.

Step #4 Building the backward trajectory up to the initial time. Now that we are able to make a small step backward at each (t, x), let $\epsilon >0$ be given, and start from $(t_0,x_0)$. There exists $(s_0,v_0)$ such that

$$\begin{aligned} u(t_0,x_0) \ge s_0 L(I(t_0),x,v_0) + u(t_0-s_0,x_0 - s_0v_0) - \epsilon s_0\, . \end{aligned}$$

By choosing $s_0$ small enough, we can even replace the right-hand-side by:

$$\begin{aligned} u(t_0,x_0) \ge \int _{0}^{s_0} L(I(t_0-s),x_0-s v_0,v_0) \, ds + u(t_0-s_0,x_0 - s_0v_0) - 2 \epsilon s_0\, . \end{aligned}$$

(A.14)

In particular, we have

$$\begin{aligned} u(t_0,x_0) \ge \inf _{\gamma } \int _{t_0 - s_0}^{t_0} L(I(s'),\gamma (s'),{\dot{\gamma }}(s'))\, ds' + u(t_0 - s_0,\gamma (t_0 - s_0)) - 2 \epsilon s_0\, , \end{aligned}$$

where the infimum is taken over all $\gamma \in AC[0,t]$ such that $\gamma (t_0) = x_0$. As a result, the set

$$\begin{aligned} \Sigma = \left\{ \tau \in (0, t_0) : u(t_0,x_0) \ge \inf _{\gamma } \int _{\tau }^{t_0} L(I(s'),\gamma (s'),{\dot{\gamma }}(s'))\, ds' + u(\tau ,\gamma (\tau )) - 2 \epsilon (t_0-\tau ) \right\} \end{aligned}$$

is non-empty, and $\tau _*:= \inf \Sigma \in [0, t_0 - s_0]$ is well-defined. We wish to prove that $\tau _* = 0$. Suppose, for contradiction, that $\tau _* >0$. Then, the estimates obtained in Lemma 9 allows to extract a converging sequence $\{\gamma _n\}$ such that $\gamma _n$ is defined on the time span $(\tau _n,t)$, with $\tau _n\searrow \tau _*$, and $\{{\dot{\gamma }}_n\}$ is uniformly BV ${}^[$²${}^]$. Hence, we can pass to the limit ${\dot{\gamma }}_n \rightarrow {\dot{\gamma }}$ a.e. by Helly’s Selection Theorem, and then use Bounded Convergence Theorem to prove that

$$\begin{aligned} u(t_0,x_0) \ge \inf _\gamma \int _{\tau _*}^{t_0} L(I(s'),\gamma (s'),{\dot{\gamma }}(s'))\, ds' + u(\tau _*,\gamma (\tau _*)) - 2 \epsilon (t_0-\tau _*)\, . \end{aligned}$$

By applying again the single step backward as in (A.14) at $(\tau _*,\gamma (\tau _*))$, we can push our lower estimate to an earlier time $\tau _{**} \in (0,\tau _*)$, and obtain thoroughly a contradiction. Thus, $\tau _* = 0$ and

$$\begin{aligned} u(t_0,x_0) \ge \inf _{\gamma } \int _0^{t_0} L(I(s'), \gamma (s'), {\dot{\gamma }}(s'))\,ds' + g(\gamma (0)) - 2\epsilon t_0 = V(t_0,x_0) - 2\epsilon t_0. \end{aligned}$$

By letting $\epsilon \rightarrow 0$, we have established that $u\ge V$ in the case when $t\mapsto I(t)$ is Lipschitz continuous.

To conclude, it remains to remove the additional continuity assumption on I(t). Let $I \in BV(0,T)$. First of all, we approximate I(t) from below by a sequence of Lipschitz functions $I_k(t)\nearrow I(t)$ converging pointwise ${}^[$³${}^]$:

$$\begin{aligned} I_k(t) = \inf _{s>0} \left( I(s) + k |t-s|\right) \le I(t)\, . \end{aligned}$$

It follows from (H2) and Remark 4 that u is also a super-solution associated with $I_k(t)$. Hence we have

$$\begin{aligned} u \ge V_k \quad \text { in }(0,T) \times {\mathbb {R}}^d, \end{aligned}$$

(A.15)

where $V_k$ is the variational solution associated with $I_k$.

On the other hand, the compactness estimates on minimizing curves obtained in Lemma 9 combined with Lebesgue’s dominated convergence theorem guarantees that $V_k\nearrow V$. Thus, we may let $k \rightarrow \infty$ in (A.15) to deduce $u \ge V$. This completes the proof. $\square$