A mean curvature type flow with capillary boundary in a unit ball

Abstract

In this paper, we study a mean curvature type flow with capillary boundary in the unit ball. Our flow preserves the volume of the bounded domain enclosed by the hypersurface, and monotonically decreases an energy functional E. We show that it has the longtime existence and subconverges to spherical caps. As an application, we solve an isoperimetric problem for hypersurfaces with capillary boundary.

1 Introduction

In this paper, we are interested in a mean curvature type flow in the unit ball ${\mathbb {B}}^{n+1}\subset {\mathbb {R}}^{n+1}$ with capillary boundary. Roughly speaking, given a Riemannian manifold $N^{n+1}$ with a smooth boundary $\partial N$, a hypersurface with capillary boundary in N is an immersed hypersurface which intersects $\partial N$ at a constant contact angle $\theta \in (0,\pi )$.

For closed hypersurfaces, the mean curvature flow plays an important role in geometric analysis and has been extensively studied. One of classical results proved by Huisken [19] states that it contracts a closed convex hypersurface into a round point. Mean curvature type flows with a constraint play an important role in the study of isoperimetric problems. The following curve-shortening (and area-preserving) flow was studied by Gage [10]. Let $\gamma :{\mathbb {S}}^1\times [0,T)\rightarrow {\mathbb {R}}^2$ satisfy

$$\begin{aligned} \partial _t\gamma = \left( \kappa -\frac{2\pi }{L}\right) \nu , \end{aligned}$$

where $\kappa$ is the geodesic curvature of $\gamma$, L is the length of the curve at scale t, and $\nu$ is the outward unit normal vector of curve $\gamma (\cdot ,t)$. In a higher dimensional Euclidean space, Huisken introduced a non-local type mean curvature flow in [21]: Given a closed, connected hypersurface M, consider a family of embeddings $x:M\times [0,T)\rightarrow {\mathbb {R}}^{n+1}$ satisfies

$$\begin{aligned} \partial _tx= (c(t)-H)\nu , \end{aligned}$$

where $c(t):=\frac{\int _{M_t} H d\mu }{|M_t|}$ is the average of the mean curvature H of $M_t:=x(M,t)$ and $\nu$ is the unit outward normal vector field of $M_t$. Huisken proved that such a volume preserving flow converges to a round sphere if the initial hypersurface is uniformly convex. There has been a lot of work on such geometric flows. Here we just mention further [2] for studying such kind of flow in the case where the ambient space is Riemannian manifold and [30] for the extension to a general mixed volume preserving mean curvature flow. As one of applications, such a volume (or area)-preserving flow could be used to prove optimal geometric inequalities. In order to establish optimal geometric inequalities, there is another type mean curvature flow, which is first introduced by Guan and Li [16] inspired by the Minkowski formulas. A flow $x:M\times [0,T)\rightarrow {\mathbb {M}}^{n+1}_k$ satisfies

$$\begin{aligned} \partial _tx=(n\phi '(\rho )-Hu)\nu , \end{aligned}$$

where u is the support function of hypersurface $x(M,\cdot )$ and ${\mathbb {M}}^{n+1}_k$ is the space form with constant sectional curvature k and metric $ds^2:=d\rho ^2+\phi ^2(\rho )g_{_{{\mathbb {S}}^{n}}}$. This flow is also volume preserving and area decreasing by the Minkowski formulas. They obtained the longtime existence of this flow and proved that it smoothly converges to a round sphere if the initial hypersurface is star-shaped. As a result, this yields a flow proof of classical Alexandrov-Fenchel inequalities of quermassintegrals in convex geometry. Recently, they obtained that a similar phenomenon also holds for the general warped produced manifold in [17] jointed with Wang. For the methods which use a fully nonlinear flow to establish geometric inequalities, we refer also to [18]. Last but not least, we recommend the literature [4,5,6,7, 32] and references therein for extensions to general anisotropic and fully nonlinear curvature flows in various ambient spaces.

There has been a great interest in the investigation of hypersurfaces with non-empty boundaries in the last thirty years. For instance, Stahl [34] considered the mean curvature flow with free boundary in the Euclidean space, and he showed that the solution either has the longtime existence or the curvature and its derivatives blow up at the maximal time. Later, Marquardt [29] considered the inverse mean curvature flow for hypersurfaces with boundary perpendicular to a convex cone, and proved that it has the long time existence and converges to a piece of round sphere, if the initial hypersurface is star-shaped and strictly mean convex. Recently Lambert-Scheuer [25] studied the same flow as [29] but with the supporting hypersurface being a sphere instead of a cone. They proved that a convex hypersurface which is perpendicular to a sphere along the boundary converges to a flat disk in certain sense. As a nice geometric application of this flow they proved in [24] a Willmore type inequality. We also would like to mention the recent articles [33, 36] for a mean curvature type flow and a fully nonlinear inverse curvature type flow respectively in the unit ball with free boundary, where new geometric inequalities were proved as applications. For the study of a nonparametric mean curvature flow with free or capillary type boundaries, we refer to [3, 11, 20, 27].

Those results motivate us to consider the following mean curvature type flow for hypersurfaces with capillary boundary. To be more precise, let ${\varSigma }_0$ be a properly embedded compact smooth hypersurface in $\overline{{\mathbb {B}}}^{n+1} (n\ge 2)$ with capillary boundary $\partial {\varSigma }_0\subset {\mathbb {S}}^n:=\partial {\mathbb {B}}^{n+1}$, which is given by $x_0:M \rightarrow \overline{{\mathbb {B}}}^{n+1}$ and M is a compact manifold with smooth boundary $\partial M$. In other words, $\hbox {int}({\varSigma }_0)=x_0(\hbox {int}(M))$, and $\partial {\varSigma }_0=x_0(\partial M)$ intersects $\partial {\mathbb {B}}^{n+1}$ at a constant contact angle $\theta \in (0,\pi )$. Consider a family of embeddings $x:M\times [0,T) \rightarrow \overline{{\mathbb {B}}}^{n+1}$ with $x(\partial M,\cdot )\subset \partial \overline{{\mathbb {B}}}^{n+1}$ such that

$$\begin{aligned} \begin{array}{rcll} (\partial _t x )^\perp &{}=&{}f\nu \quad &{} \hbox { in }M\times [0,T),\\ \langle \nu ,{\overline{N}}\circ x \rangle &{}=&{} -\cos \theta \quad &{} \hbox { on }\partial M\times [0,T),\\ x(\cdot ,0) &{} =&{} x_0(\cdot ) \quad &{} \text { on } {M}, \end{array} \end{aligned}$$

(1.1)

where

$$ f:=n\langle x,a\rangle +n\cos \theta \langle \nu ,a\rangle -H\langle X_a,\nu \rangle , \qquad \hbox { for } a\in {{\mathbb {S}}}^n , $$

$\nu$ and H are the unit normal vector field and the mean curvature of hypersurface $x(\cdot ,t)$ resp., ${\overline{N}}$ is the unit outward normal vector field of ${\mathbb {S}}^n$ , the contact angle $\theta \in (0, \pi )$ is a constant and the vector field $X_a$ will be defined and discussed in the next paragraph. Here, for a vector field $\xi$ along a hypersurface x, we define its normal part by $\xi ^\perp := \langle \xi , \nu \rangle \nu .$ The choice of f is motivated by new Minkowski formulas proved in [35]. If $\theta =\frac{\pi }{2}$, it corresponds to the free boundary problem of parabolic setting, which was studied by Wang and Xia [36].

Before we state our main results, we clarify the notation $X_a$ used above. In this paper $X_a$ is a vector field defined by

$$\begin{aligned} X_a:=\langle x,a\rangle x-\frac{1}{2}\left( |x|^2+1\right) a, \end{aligned}$$

(1.2)

where a is a fixed unit vector in ${\mathbb {R}}^{n+1}$. One can easily to check that $X_a$ is a conformal Killing vector field in ${\mathbb {B}}^{n+1}$. In fact, $X_a$ is exactly the pull back of the position vector field under a conformal transformation from the unit ball to the half Euclidean space. See Sect. 3.2 for the precise discussion. We say that a properly embedded hypersurface ${\varSigma }$ in ${\mathbb {R}}^{n+1}$ is star-shaped with respect to a if ${\varSigma }$ intersects each integral curve of $X_a$ only once. For simplicity in this paper we define a hypersurface of star-shaped by a stronger condition that

$$ \langle X_a,\nu \rangle >0 $$

holds everywhere in M. Our main theorem is the following

Theorem 1.1

If the initial hypersurface is a star-shaped hypersurface with capillary boundary in the unit ball and the contact angle $\theta$ satisfies $| \cos \theta | < \frac{3n+1}{5n-1}$, then flow (1.1) exists globally with uniform $C^{\infty }$-estimates. Moreover, $x(\cdot ,t)$ subsequently converges to a spherical cap in the $C^{\infty }$ topology as $t\rightarrow \infty$, whose enclosed domain has the same volume as the domain enclosed by ${\varSigma }_0$.

If $\theta =\frac{\pi }{2}$, i.e., the free boundary case, this theorem was proved recently by Wang and Xia in [36], where they also proved the global convergence. The free boundary case usually corresponds to a homogeneous or linear Neumann boundary value conditions, see [20, 24, 29, 33, 34, 36] for example. However, the capillary boundary case in general relates to a nonlinear type Neumann boundary value condition, see [11, 13, 15] for example, which is more complicated and technically more difficult to handle from the analytic viewpoint. This difficulty usually prevents us to obtain estimates for a full range of $\theta \in (0, \pi )$. For instance, Guan obtained the gradient estimate (depending on the time T) of solution in [15] for a nonparametric curvature flow with capillary boundary for angle satisfying $|\cos \theta |<\frac{\sqrt{3}}{2}$. Recently, the authors [11] obtained the uniformly gradient estimate (independent of time T) for the nonparametric mean curvature flow with capillary boundary for $\theta$ in a small neighborhood of $\frac{\pi }{2}$. In this paper we obtain for our flow (1.1) a better range $|\cos \theta |<\frac{3n+1}{5n-1}$. The reason why we can have a bigger range of the contact angle is due to an observation that Eq. (3.4) has a good term when we carry out the gradient estimate. See the proof of Proposition 4.3. Also due to this difficulty, we can only prove the subsequence convergence of this flow and are not able to show that the limits are the same spherical cap at the moment. We will consider this problem in the near future. Nevertheless, the limits have the same radius and hence we can provide a flow proof for the isoperimetric problem for hypersurfaces with capillary boundary in the unit ball.

Corollary 1.2

Among star-shaped capillary boundary hypersurfaces with a volume constraint the spherical caps given in Remark 4.1 are the only minimizers of the energy functional E defined in (2.8) below, provided that the contact angle $\theta$ satisfies $|\cos \theta |<\frac{3n+1}{5n-1}$,.

The Corollary follows from Theorem 1.1 and the crucial properties that the flow preserves the enclosed volume and decreases the energy functional E, which are proved in Sect. 2.3 by the new Minkowski formulas established in [35].

This article is organized as follows. In Sect. 2, we give some preliminaries about hypersurfaces with capillary boundary and our mean curvature type flow. In Sect. 3, we convert the flow to a scalar equation on semi-sphere with the help of a conformal transformation. In the last Section, we establish a priori estimates and prove the main theorem.

2 Preliminaries

In this Section we provide basic facts of capillary hypersurfaces and prove the crucial facts of our flow in Proposition 2.4 by using the new Minkowski formulas obtained in [35]. For convenience of the reader we provide complete proofs. For more information about capillary hypersurfaces we refer to the wonderful exposition book [9].

2.1 Integral identities

In this paper we consider hypersurfaces ${\varSigma }\subset \overline{{\mathbb {B}}}^{n+1}$ with capillary boundary $\partial {\varSigma }$ on $\partial \overline{{\mathbb {B}}}^{n+1}$ which will be precisely defined below. Since we will use a flow to study such hypersurfaces, it will convenience to use the parametrization: Let $x:M\rightarrow \overline{{\mathbb {B}}}^{n+1}$ be an isometric immersion of an orientable n-dimensional compact manifold M with smooth boundary $\partial M$ such that ${\varSigma }:=x(M)$ and $\partial {\varSigma }:=x(\partial M)$. However, we will identity M with ${\varSigma }$ and $\partial M$ with $\partial {\varSigma }$, if there is no confusion.

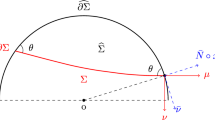
Let ${{\overline{N}}}$ be the unit outward normal ${\overline{N}}$ of the unit sphere $\partial {\mathbb {B}}^{n+1}$. Let ${\varSigma }\subset \overline{{\mathbb {B}}}^{n+1}$ be a smooth oriented hypersurface with boundary $\partial {\varSigma }$ satisfying $\hbox {int}({\varSigma })\subset {\mathbb {B}}^{n+1}$ and $\partial {\varSigma }\subset \partial {\mathbb {B}}^{n+1}$. ${\varSigma }$ divides the unit ball into two parts. We denote one part by ${\varOmega }$ and define $\nu$ the unit outward normal vector field of ${\varSigma }$ w.r.t. ${\varOmega }$. Let $\mu$ be the unit outward conormal vector field along $\partial {\varSigma }$ and ${\overline{\nu }}$ be the unit normal to $\partial {\varSigma }$ in $\partial {\mathbb {B}}^{n+1}$ such that $\{\nu ,\mu \}$ and $\{{\overline{\nu }},{\overline{N}}\}$ have the same orientation in the normal bundle of $\partial {\varSigma }\subset \overline{{\mathbb {B}}}^{n+1}$. See Fig. 1.

We call the angle between $-\nu$ and ${{\overline{N}}}$ contact angle and denote it by $\theta$. It follows

$$\begin{aligned} \begin{aligned} {\overline{N}}&= \sin \theta \mu -\cos \theta \nu , \\ {\overline{\nu }}&= \cos \theta \mu +\sin \theta \nu . \end{aligned} \end{aligned}$$

or equivalently

$$\begin{aligned} \begin{aligned} \mu&= \sin \theta {\overline{N}}+\cos \theta {\overline{\nu }} \\ \nu&= -\cos \theta {\overline{N}}+\sin \theta {\overline{\nu }}. \end{aligned} \end{aligned}$$

Fig. 1

${\varSigma }=x(M)$ and $\partial {\varSigma }=x(\partial M)$

Definition 2.1

Given a smooth oriented hypersurface ${\varSigma }\subset \overline{{\mathbb {B}}}^{n+1}$ with $\hbox {int}({\varSigma })\subset {\mathbb {B}}^{n+1}$ and $\partial {\varSigma }\subset \partial {\mathbb {B}}^{n+1}$, we call that $\partial {\varSigma }$ is a capillary boundary, if the contact angle $\theta \in (0,\pi )$ is constant along $\partial {\varSigma }$. Namely,

$$ \langle \mu ,{\overline{N}}\rangle =\sin \theta $$

is constant on $\partial {\varSigma }$. In particular, if $\theta =\frac{\pi }{2}$, i.e., ${\varSigma }$ meets $\partial {\mathbb {B}}^{n+1}$ orthogonally, we call that $\partial {\varSigma }$ is a free boundary.

We denote D and $\nabla$ derivatives on $({\mathbb {B}}^{n+1},\delta _{{\mathbb {B}}^{n+1}})$ and (M, g) resp., where $\delta _{{\mathbb {B}}^{n+1}}$ is the standard Euclidean metric and g is the induced metric on M.

Recall that $X_a$ is the conformal vector field defined by (1.2). Decompose $X_a$ into ${ X_a:=X_a^T+\langle X_a,\nu \rangle \nu }$, where $X_a^T$ is the tangential projection of $X_a$ on ${\varSigma }$. It is clear to see that $X_a:=\langle x,a\rangle x-a$ on $\partial {\varSigma }$ and ${\overline{N}}=x$ on $\partial {\mathbb {B}}^{n+1}$, which follows that

$$\begin{aligned} \begin{aligned} \langle X_a^T,\mu \rangle&=\langle X_a,\mu \rangle = \langle X_a, \sin \theta N+\cos \theta {\overline{\nu }}\rangle \\&= \cos \theta \langle X_a,{\overline{\nu }}\rangle = \cos \theta \langle \langle x,a\rangle x-a,{\overline{\nu }}\rangle = -\cos \theta \langle a,{\overline{\nu }}\rangle . \end{aligned} \end{aligned}$$

(2.1)

Let h be the second fundamental form of the hypersurface ${\varSigma }$ given by $h(X,Y):=\langle D_X\nu ,Y\rangle$ for any $X,Y\in T{\varSigma }$ with ${\varSigma }:=x(M)$ and H is the mean curvature of ${\varSigma }$. Note that

$$\begin{aligned} h(e,\mu )=0 \end{aligned}$$

(2.2)

for any $e\in T(\partial {\varSigma })$ and

$$\begin{aligned} D_{\mu }\nu =h(\mu ,\mu )\mu \end{aligned}$$

(2.3)

(see Lemma 3.1 in [26] or Proposition 2.1 in [35] for a proof). These two simple facts are important in the study of capillary hypersurfaces. From these two face we have

$$\begin{aligned} \begin{aligned} h(X_a^T,\mu )&=\langle D_{\mu }\nu ,X_a^T\rangle =h(\mu ,\mu ) \langle \mu ,X_a^T\rangle =h(\mu ,\mu ) \langle \mu ,\langle x,a\rangle x-a\rangle \\&=h(\mu ,\mu ) \langle x,a\rangle \sin \theta -h(\mu ,\mu )\langle \mu ,a\rangle \\&=-h(\mu ,\mu )\langle a,\cos \theta {\overline{\nu }}\rangle , \end{aligned} \end{aligned}$$

(2.4)

where we have used the fact $\mu =\sin \theta {\overline{N}}+\cos \theta {\overline{\nu }}$ in the last equality.

The following proposition was proved for hypersurfaces with free boundary recently in [35]. For completeness, we provide a proof here for hypersurfaces with capillary boundary.

Proposition 2.2

Let $x:M\rightarrow \overline{{\mathbb {B}}}^{n+1}$ be an embedded smooth hypersurface in ${\mathbb {B}}^{n+1}$ with capillary boundary of contact angle $\theta \in (0,\pi )$. Then

$$\begin{aligned} \int _{M} H\langle x,a\rangle dA= & {} \frac{2}{n-1} \int _{M} \sigma _2(\kappa ) \langle X_a,\nu \rangle dA \\&+\frac{1}{n-1}\int _{\partial M} \left( H \langle X_a^T,\mu \rangle -h(X_a^T,\mu )\right) d\sigma , \end{aligned}$$

where dA and $d\sigma$ are the area element of M and $\partial M$ respectively with respect to the induced metric g, $\kappa :=(\kappa _1,\ldots ,\kappa _n)$ are the principal curvatures of the Weingarten tensor $(g^{-1}h)$ and $\sigma _2(\kappa )$ is the 2nd elementary symmetric function acting on the principal curvatures.

Proof

Let $\{e_{i}\}_{i=1}^n$ be the orthonormal frame on M and $e_{n+1}={\overline{N}}$. By using equation (3.5) in [35], we have

$$\begin{aligned} \frac{1}{2} \left( \nabla _{i} (X_a^T)_{j}+\nabla _{j} (X_a^T)_{i}\right) =\langle x,a \rangle g_{ij}-h_{ij}\langle X_a,\nu \rangle . \end{aligned}$$

This follows easily from the conformality of the vector field $X_a$. It follows that

$$\begin{aligned} \mathrm{div}\, X_a^T= n\langle x, a \rangle -H\langle X_a,\nu \rangle . \end{aligned}$$

(2.5)

Denote the Newton tensor by $T_1(\kappa ):=\frac{\partial \sigma _2}{\partial (g^{-1}h)}$ . In local coordinates, we have $T_1^{ij}:=\frac{\partial \sigma _2}{\partial h_{j}^{i}}$. Multiplying the both side of the above identity by $T_1^{ij}:=\frac{\partial \sigma _2}{\partial h_{j}^{i}}$ and integrating, we have

$$\begin{aligned} \int _{M} T^{ij}_1(\kappa ) \nabla _{i} (X_a^T)_{j}dA= & {} \displaystyle \int _{M} (Hg_{i j}-h_{ji} ) \cdot (\langle x,a \rangle g_{i j}-h_{i j}\langle X_a,\nu \rangle )dA \\= & {} \displaystyle \int _{M} ( (n-1)H\langle x,a\rangle -(H^2-|h|^2)\cdot \langle X_a,\nu \rangle )dA \\= & {} \displaystyle \int _{M} \left( (n-1) H\langle x,a\rangle -2\sigma _2(h) \langle X_a,\nu \rangle \right) dA . \end{aligned}$$

Since $X_a^T$ is the tangential projection of $X_a$ on M, integrating by parts we have

$$\begin{aligned} \int _{M} T^{ij}_1(\kappa ) \nabla _{i} (X_a^T)_{j}dA= & {} \int _{\partial M} T_1^{ij} (X_a^T)_{j} \mu _{i}d\sigma =\int _{\partial M} T_1(X_a^T,\mu )d\sigma \\= & {} \int _{\partial M} \left( [H \langle X_a^T,\mu \rangle -h(X_a^T,\mu )\right) d\sigma . \end{aligned}$$

Hence the proof is complete. $\square$

The following property is also crucial for us.

Proposition 2.3

Under the same conditions as in Proposition 2.2, it holds that

$$\begin{aligned} (n-1)\int _{M} H\langle \nu ,a\rangle dA=\int _{\partial M}\left( H-h(\mu ,\mu ) \right) \langle {\overline{\nu }},a\rangle d\sigma . \end{aligned}$$

Proof

Set $P_a:=\langle \nu ,a\rangle x-\langle x,\nu \rangle a$. By a direct computation, we have

$$\begin{aligned} \begin{aligned} \nabla _{e_{j}} \langle P_a,e_{i}\rangle&= \nabla _{e_{j}} \left( \langle \nu ,a\rangle \langle x,e_{i}\rangle -\langle x,\nu \rangle \langle a,e_{i}\rangle \right) \\&=\langle h_{jk}e_{k},a\rangle \langle x,e_{i}\rangle +\langle \nu ,a\rangle \delta _{ij}+\langle \nu ,a\rangle \langle x,-h_{ij}\nu \rangle \\&\quad -\langle x,h_{jk}e_{k}\rangle \langle a,e_{i}\rangle +\langle x,\nu \rangle \langle a,h_{ij}\nu \rangle \\&=\langle \nu ,a\rangle \delta _{ij}+ h_{jk}a^{k}x^{i}-h_{jk}x^{k}a^{i} \end{aligned} \end{aligned}$$

(2.6)

and

$$\begin{aligned} \mathrm{div}\, P^T_a=n \langle \nu , a\rangle . \end{aligned}$$

(2.7)

Multiplying (2.6) by $T_1^{ij}:=\frac{\partial \sigma _2}{\partial h_{j}^{i}}$, we obtain

$$\begin{aligned} \begin{aligned} T_1^{ij}(h)\cdot {\nabla }_{e_{j}} \langle P_a,e_{i}\rangle&= \left[ H\delta _{ij}-h_{ji}\right] \cdot \left[ \langle \nu ,a\rangle \delta _{ij}+ h_{j k}a^{k}x^{i}-h_{jk}x^{k}a^{i}\right] \\&=(n-1)H\langle \nu ,a\rangle . \end{aligned} \end{aligned}$$

Integrating by parts we conclude that

$$\begin{aligned} \begin{aligned}&(n-1)\int _{M} H\langle \nu ,a\rangle dA \\&\quad =\int _{M}T_1^{ij}(h)\cdot {\nabla }_{e_{j}} \langle P_a,e_{i}\rangle dA \\&\quad = \int _{\partial M} T_1^{ij}(h)\langle P_a,e_{i}\rangle \langle \mu ,e_{j}\rangle d\sigma \\&\quad = \int _{\partial M} \left[ H\delta _{ij}-h_{ji}\right] \langle P_a,e_{i}\rangle \langle \mu ,e_{j}\rangle d\sigma \\&\quad =\int _{\partial M} \left( H\langle \nu ,a\rangle \langle x,\mu \rangle -H\langle x,\nu \rangle \langle a,\mu \rangle - h(\mu ,x^T)\langle \nu ,a\rangle +h(\mu ,a^T)\langle x,\nu \rangle \right) d\sigma \\&\quad =\int _{\partial M}\left[ H-h(\mu ,\mu )\right] \left[ \langle \nu ,a\rangle \langle x,\mu \rangle - \langle x,\nu \rangle \langle a,\mu \rangle \right] d\sigma \\&\quad =\int _{\partial M}\left[ H-h(\mu ,\mu )\right] \langle {\overline{\nu }},a\rangle d\sigma , \end{aligned} \end{aligned}$$

where we have used Eq. (2.2) in the fifth equality. Therefore we complete the proof. $\square$

2.2 The first variation formulas

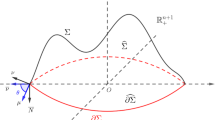
Let $x:(M,\partial M)\rightarrow (\overline{{\mathbb {B}}}^{n+1}, \partial {\mathbb {B}}^{n+1})$ be an isometric embedded of an orientable n-dimensional compact manifold M with smooth boundary $\partial M$ such that ${\varSigma }:=x(M)$ and $\partial {\varSigma }:=x(\partial M)$. We define the volume functional of x as the usual volume of the $n+1$-dimensional domain ${\varOmega }$ enclosed by ${\varSigma }$ and $\partial {\mathbb {B}}^{n+1}$ as in Fig. 1. The so-called wetting area $W({\varSigma })$ is just the area of the region $T:=\partial {\varOmega }\cap \partial {\mathbb {B}}^{n+1}$, which is also bounded by $\partial {\varSigma }$ on $\partial {\mathbb {B}}^{n+1}$. The energy functional is defined as

$$\begin{aligned} E(x)=E({\varSigma }):= \hbox {Area}({\varSigma })-\cos \theta \, \hbox {Area}(T). \end{aligned}$$

(2.8)

Next we present the first variational formula for the energy functional E. An admissible variation of x is a differential map $x: M\times (-\varepsilon ,\varepsilon )\rightarrow \overline{{\mathbb {B}}}^{n+1}$ satisfying that $x_t(\cdot ):=x(\cdot ,t):M\rightarrow \overline{{\mathbb {B}}}^{n+1}$ is an immersion with $x(\hbox {int}(M),t)\subset {\mathbb {B}}^{n+1}$ and $x(\partial M, t)\subset \partial {\mathbb {B}}^{n+1}$, and $x(\cdot ,0)=x_0(\cdot )$. Denote the corresponding hypersurfaces by ${\varSigma }_t=x(M,t)$, its enclosed domain ${\varOmega }_t$ and the “wet” part by $T_t$. It is well-known that the first variations of volume functional and area functional are given by (see for example, [1, 28, 31] or [35] etc.)

$$\begin{aligned} \frac{d}{dt} \hbox {Vol}({\varOmega }_t)= \int _M \langle Y, \nu \rangle dA \end{aligned}$$

and

$$\begin{aligned} \frac{d}{dt} \hbox {Area}({\varSigma }_t)=\int _{M}H\langle Y,\nu \rangle dA+\int _{\partial M} \langle Y,\mu \rangle d\sigma , \end{aligned}$$

where $dV_{ {\mathbb {B}}^{n+1}}$ is the volume element of ${\mathbb {B}}^{n+1}$ and $Y:=\frac{\partial }{\partial t} x_t(\cdot )\big |_{t=0}.$ Moreover the variation of the area of $T_t$ is given by

$$\begin{aligned} \frac{d}{dt} \hbox {Area} (T_t)= \int _{\partial M} \langle Y,{\overline{\nu }}\rangle d\sigma , \end{aligned}$$

For a proof, see [31] (See Sect. 4 Appendix there) for instance. Now, the variation of the energy functional E is given by

$$\begin{aligned} \frac{d}{dt}E({\varSigma }_t)=\int _{M}H\langle Y,\nu \rangle dA+\int _{\partial M} \langle Y,\mu -\cos \theta \,{\overline{\nu }}\rangle d\sigma . \end{aligned}$$

(2.9)

2.3 Key properties of flow (1.1)

From the Minkowski type formula in [35] [see Proposition 3.2 and Eq. (3.4) there], we have the following two important facts of (1.1).

Proposition 2.4

Flow (1.1) preserves the volume functional $\mathrm {Vol}({\varOmega }_t)$ and decreases $E(M_t)$.

Proof

It is easy to see that this flow preserves the enclosed volume ${\varOmega }_t$ of x(M, t) in ${\mathbb {B}}^{n+1}$, since

$$\begin{aligned} \begin{aligned} \frac{d}{dt} \hbox {Vol}({\varOmega }_t)&=\frac{d}{dt}\int _{[0,t]\times M} x^*dV_{{\mathbb {B}}^{n+1}} = \int _M f dA \\&=\int _{M}\left[ n\langle x,a\rangle +n\cos \theta \langle \nu ,a\rangle -H\langle X_a,\nu \rangle \right] dA=0, \end{aligned} \end{aligned}$$

(2.10)

where the last equality is the new Minkowski identity proved in [35]. With the above preparation and for the convenience of the reader, we point out that this formula follows from

$$\begin{aligned} f= \mathrm{div}\, (X_a^T+\cos \theta P^T_a)\quad \text { in }M, \quad \langle X_a^T+\cos \theta P^T_a, \mu \rangle =0, \quad \text { on } \partial M. \end{aligned}$$

which, in turn, follows from Eqs. (2.5), (2.7) and (2.1).

From (2.9) and Proposition 2.2, we have that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt} E(M_t) \\&\quad :=\frac{d}{dt} \left[ \hbox {Area}(M_t)-\cos \theta W(M_t)\right] \\&\quad = \int _{M} H\left( n\langle x,a\rangle +n\cos \theta \langle \nu ,a\rangle -H\langle X_a,\nu \rangle \right) dA \\&\quad =\left[ n \int _{M} \cos \theta H\langle \nu ,a\rangle dA +\frac{n}{n-1}\int _{\partial M} \left( H \langle X_a^T,\mu \rangle -h(X_a^T,\mu )\right) d\sigma \right] \\&\qquad + \int _{M} {\left( \frac{2n}{n-1} \sigma _2(\kappa )-|H|^2\right) } \langle X_a,\nu \rangle dA \\&\quad :={\text {S}}_1+{\text {S}}_2. \end{aligned} \end{aligned}$$

(2.11)

For the term ${\text {S}}_2$, we claim that ${\text {S}}_2\le 0$. In fact, this follows from facts that $\langle X_a,\nu \rangle > 0$ in M and the following well-known fact

$$\begin{aligned} \begin{aligned} \frac{2n}{n-1}\sigma _2(\kappa )-H^2&=\frac{1}{n-1}\left[ 2\sigma _2(\kappa )-(n-1)\sum _{i=1}^{n} \kappa ^2_{i}\right] \\&=-\frac{1}{n-1}\sum _{1\le i<j\le n} (\kappa _{i}-\kappa _{j})^2 \le 0. \end{aligned} \end{aligned}$$

(2.12)

For the term ${\hbox {S}}_1$, from Eqs. (2.1) and (2.4), we have

$$\begin{aligned} \begin{aligned} h(X_a^T,\mu )=-\cos \theta h(\mu ,\mu )\langle a,{\overline{\nu }}\rangle ,\quad \langle X_a^T,\mu \rangle =\langle X_a,\mu \rangle = -\cos \theta \langle a, {\overline{\nu }}\rangle . \end{aligned} \end{aligned}$$

Combining with Proposition 2.3 and the fact that $\theta \equiv const$, we have

$$\begin{aligned} \frac{{\text {S}}_1}{n}= & {} \int _{M} \cos \theta H\langle \nu ,a\rangle dA+\frac{1}{n-1}\int _{\partial M} \left( H \langle X_a^T,\mu \rangle -h(X_a^T,\mu )\right) d\sigma \\= & {} \int _{M} \cos \theta H\langle \nu ,a\rangle dA-\frac{\cos \theta }{n-1}\int _{\partial M} \left[ H-h(\mu ,\mu )\right] \langle a,{\overline{\nu }}\rangle d\sigma =0. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt} E(M_t)&:=\frac{d}{dt}\left[ \hbox {Area}(M_t)-\cos \theta W(M_t)\right] ={\text {S}}_1+{\text {S}}_2\le 0. \end{aligned} \end{aligned}$$

Hence we complete the proof. $\square$

3 A scalar equation

In this section we will reduce flow (1.1) to a scalar flow, provided the initial hypersurface is star-shaped.

3.1 Basic facts

In this subsection, we first recall some basic facts and identities for the relevant geometric quantities of a smooth star-shaped hypersurface $X:M\rightarrow {\varSigma }\subset {\mathbb {R}}^{n+1}_+$ with respect to the origin. If ${\varSigma }$ is star-shaped with respect to the origin, then the position vector X of ${\varSigma }$ can be written as in

$$\begin{aligned} X:=e^{u(x)}x=\rho (x)x \quad x\in {\varOmega }\subset {\mathbb {S}}^n_+, \end{aligned}$$

where $u\in C^2({\varOmega })\cap C^0({\overline{{\varOmega }}})$ and $\rho :=e^u$.

Let $\{e_i\}_{i=1}^n$ be the local frame field on ${\mathbb {S}}^n_+$ with the round metric $\sigma$, and denote $\nabla$ and D the gradient on ${\mathbb {S}}^n_+$ and ${\mathbb {R}}^{n+1}_+$ respectively. Then in terms of $\rho$ the metric $g_{ij}$ is given by

$$\begin{aligned} g_{ij}=\langle D_{e_i}X,D_{e_j}X\rangle =e^{2u}\left( \sigma _{ij}+u_iu_j\right) =\rho ^2\sigma _{ij}+\rho _i\rho _j, \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the standard inner product in ${\mathbb {R}}^{n+1}_+$, $\sigma _{ij}:=\langle e_i,e_j\rangle$ and $\rho _i:=\nabla _{e_i}\rho$, $\rho _{ij}:=\nabla _{e_i}\nabla _{e_j}\rho$. The inverse of metric g is

$$\begin{aligned} g^{ij}=e^{-2u}\left( \sigma ^{ij}-\frac{u^iu^j}{1+|\nabla u|^2}\right) =\rho ^{-2}\left( \sigma ^{ij}-\frac{\rho ^i\rho ^j}{\rho ^2+|\nabla \rho |^2}\right) , \end{aligned}$$

where $\sigma ^{ij}$ denotes the inverse of $\sigma _{ij}$ and $u^i:=\sigma ^{ik}u_k$. The unit outer normal vector field to ${\varSigma }$ in ${\mathbb {R}}^{n+1}_+$ is given by

$$\begin{aligned} \nu (X(x))=\frac{x-\nabla u(x)}{\sqrt{1+|\nabla u|^2}}=\frac{x\rho -\nabla \rho (x)}{\sqrt{\rho ^2+|\nabla \rho |^2}}. \end{aligned}$$

Note that $\langle \nu ,X\rangle =\frac{\rho ^2}{\sqrt{\rho ^2+|\nabla \rho |^2}}=\frac{e^u}{\sqrt{1+|\nabla u|^2}} >0$ which means that $\nu$ satisfies the choice of orientation on a radial graph. The second fundamental form of X is

$$\begin{aligned} h_{ij}=-\langle D_{e_i}D_{e_j}X,\nu \rangle =e^u\frac{\sigma _{ij}+u_iu_j-u_{ij}}{\sqrt{1+|\nabla u|^2}}=-\frac{\rho \rho _{ij}-\rho ^2\sigma _{ij}-2\rho _i\rho _j}{\sqrt{\rho ^2+|\nabla \rho |^2}}, \end{aligned}$$

and the mean curvature is given by

$$\begin{aligned} \begin{aligned} H&:=\sum _{i,j=1}^{n}g^{ij}h_{ij}= \frac{e^{-u}}{\sqrt{1+|\nabla u|^2}} \left( n-{\varDelta }u+\sum _{i,j=1}^{n}\frac{u_{ij}u^iu^j}{1+|\nabla u|^2}\right) \\&=-e^{-u}\hbox {div}_{_{{\mathbb {S}}^n_+}} \left( \frac{\nabla u}{\sqrt{1+|\nabla u|^2}}\right) +\frac{ne^{-u}}{\sqrt{1+|\nabla u|^2}} \\&=-\frac{1}{\rho }\hbox {div}_{_{{\mathbb {S}}^n_+}}\left( \frac{\nabla \rho }{\sqrt{\rho ^2+|\nabla \rho |^2}}\right) + \frac{n}{\sqrt{\rho ^2+|\nabla \rho |^2}} \\&=\frac{n}{\rho v}-\frac{1}{\rho v}\sum _{i,j=1}^{n}\left( \sigma ^{ij}-\frac{\rho ^i\rho ^j}{v^2}\right) \rho _{ij}, \end{aligned} \end{aligned}$$

where $v:=\sqrt{1+|\nabla u|^2}$ and $\hbox {div}_{_{{\mathbb {S}}^n_+}}$ is the divergence operator with respect to the canonical metric $\sigma$ on ${\mathbb {S}}^n_+$.

Using the same method in [12] or [8], we assume that flow Eq. (1.1) is satisfied by a family of the radial graphs over ${\mathbb {S}}^n_+$, that is, $x(\xi ,t):=X(\xi ,t)\rho (X(\xi ,t),t)$ with $X\in {\mathbb {S}}^n_+$. Then we have

$$\begin{aligned} \begin{aligned} f&= \left\langle \frac{\partial x}{\partial t},\nu \right\rangle \\&= \left\langle \frac{\partial X}{\partial t}\rho +X\cdot \left( \nabla \rho \cdot \partial _tX\right) +X\partial _t \rho ,\frac{X\rho -\nabla \rho }{\sqrt{|\nabla \rho |^2+\rho ^2}} \right\rangle \\&=\frac{\partial \rho }{\partial t}\cdot \frac{\rho }{\sqrt{|\nabla \rho |^2+\rho ^2}}=\frac{1}{\sqrt{1+|\nabla u|^2}}\frac{\partial u}{\partial t}. \end{aligned} \end{aligned}$$

(3.1)

3.2 A conformal transformation

We use the following coordinate transformation $\varphi$ as in [36] to transform the unit ball into the half space

$$\begin{aligned} \begin{aligned} \varphi : \quad&{\mathbb {B}}^{n+1}\longrightarrow {\mathbb {R}}^{n+1}_+ \\&(x,x_{n+1}) \longmapsto \frac{2x+(1-|x|^2-x_{n+1}^2)e_{n+1}}{|x|^2+(x_{n+1}-1)^2}:=(y,y_{n+1}), \end{aligned} \end{aligned}$$

where $x:=(x_1,\ldots ,x_n)\in {\mathbb {R}}^n$. Equivalently we have

$$\begin{aligned} \begin{array}{rcll} x_i &{}=&{}\displaystyle \frac{2y_i}{|y|^2+(y_{n+1}+1)^2}, &{}\quad 1\le i\le n,\\ x_{n+1}&{}=&{} \displaystyle \frac{|y|^2+y_{n+1}^2-1}{|y|^2+(1+y_{n+1})^2}. \end{array} \end{aligned}$$

Moreover, $\varphi$ maps ${\mathbb {S}}^n=\partial {\mathbb {B}}^{n+1}$ to $\partial {\mathbb {R}}^{n+1}_+:=\{(y,y_{n+1})\in {\mathbb {R}}^{n+1}:y_{n+1}=0\}$. By a direct computation, one gets

$$\begin{aligned} \varphi ^*(\delta _{{\mathbb {R}}^{n+1}_+})=\frac{4}{\left( |x|^2+(x_{n+1}-1)^2\right) ^2} \delta _{{\mathbb {B}}^{n+1}}, \end{aligned}$$

which means that $\varphi$ is a conformal transformation from $\left( {\mathbb {B}}^{n+1},\delta _{{\mathbb {B}}^{n+1}}\right)$ to $\left( {\mathbb {R}}^{n+1}_+,\delta _{{\mathbb {R}}^{n+1}_+}\right)$. (Another view to see this fact is that it comes from the Möbius transformation $M(z):=\frac{1-iz}{z-i},$ and rotational symmetry with $z:=|x|+x_{n+1} i$.)

We define $X_{n+1}$ to the conformal vector field $X_a$ with $a=-E_{n+1}$, that is, $X_{n+1}:=-\langle {\tilde{x}},E_{n+1}\rangle {\tilde{x}}+\frac{|{\tilde{x}}|^2+1}{2}E_{n+1}$, where $E_{n+1}$ is the standard $(n+1)$-th component vector field in ${\mathbb {B}}^{n+1}$ and ${\tilde{x}}:=(x,x_{n+1})\in {\mathbb {B}}^{n+1}$. One can directly compute to find that

$$ {\varphi _*(X_{n+1})=(y,y_{n+1}):={\tilde{y}}}\quad {\text {in}}\quad {\mathbb {R}}^{n+1}_+. $$

For a hypersurface ${\varSigma }\subset \overline{{\mathbb {B}}}^{n+1}$ with capillary boundary $\partial {\varSigma }\subset {\mathbb {S}}^n$, we have

$$\begin{aligned} \frac{4}{\left[ |x|^2+(x_{n+1}-1)^2\right] ^2} \langle X_{n+1},\nu \rangle =\langle \varphi _*(X_{n+1}),\varphi _*(\nu )\rangle =|\varphi _*(\nu )| \langle {\tilde{y}},{\tilde{\nu }}\rangle , \end{aligned}$$

where $|\varphi _*(\nu )|= \frac{|y|^2+(y_{n+1}+1)^2}{2}$ and ${\tilde{\nu }}:=\frac{\varphi _*(\nu ) }{|\varphi _*(\nu )|}$. Hence the hypersurface $\varphi ({\varSigma })$ is star-shaped in ${\mathbb {R}}^{n+1}_+$ with respect to the origin, i.e., $\langle {{\tilde{y}}}, {{\tilde{\nu }}}\rangle >0$ if and only if $\langle X_{n+1},\nu \rangle > 0$ holds on ${\varSigma }$. Therefore, under the transformation flow (1.1) is equivalent to

$$\begin{aligned} \begin{array}{rcll} \partial _t {\tilde{y}}&{}=&{}\varphi _*(\partial _t {\tilde{x}})=\left( {\tilde{f}}\cdot |\varphi _*(\nu )|\right) {\tilde{\nu }} &{} \hbox { in }\varphi ({\varSigma })\times [0,T), \\ \langle {\tilde{\nu }},{\tilde{N}} \rangle &{}=&{}\cos \theta \ &{} \hbox { on }\varphi (\partial {\varSigma })\times [0,T),\\ {\tilde{y}}(0) &{} =&{}\varphi ({\tilde{x}}(0))=\varphi ({\tilde{x}}_0):={\tilde{y}}_0 \quad &{} \text { on} \quad \varphi ({\overline{{\varSigma }}})\times \{0\}, \end{array} \end{aligned}$$

(3.2)

where ${\tilde{f}}:=f\circ \varphi ^{-1}$, ${\tilde{N}}:=\frac{\partial }{\partial y_{n+1}}$ is the inner normal vector field of $\varphi (\partial {\varSigma })\subset {\mathbb {R}}^n\times \{0\}$ in ${\mathbb {R}}^{n+1}_+$.

Now in ${\mathbb {R}}^{n+1}_+$, we use the polar coordinate $(\rho ,\beta ,\xi )\in [0,+\infty )\times [0,\frac{\pi }{2}]\times {\mathbb {S}}^{n-1}$ as in [36], where $\xi$ is the spherical coordinate in ${\mathbb {S}}^{n-1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho ^2=|y|^2+y_{n+1}^2,\\ y_{n+1}=\rho \cos \beta , |y|=\rho \sin \beta . \end{array}\right. } \end{aligned}$$

Then it implies that the standard Euclidean metric in ${\mathbb {R}}^{n+1}_+$ has the expression

$$\begin{aligned} \begin{aligned} \delta _{{\mathbb {R}}^{n+1}_+}&=|d{\tilde{y}}|^2 =d\rho ^2+\rho ^2g_{_{{\mathbb {S}}^n_+}} \\&= d\rho ^2+\rho ^2(d\beta ^2+\sin ^2\beta g_{_{{\mathbb {S}}^{n-1}}}), \end{aligned} \end{aligned}$$

(3.3)

where $g_{_{{\mathbb {S}}^{n-1}}}$ is the standard spherical metric on ${\mathbb {S}}^{n-1}$. Since $\left( {\mathbb {B}}^{n+1},\delta _{\mathbb {{B}}^{n+1}}\right)$ and $\left( {\mathbb {R}}^{n+1}_+,(\varphi ^{-1})^* (\delta _{{\mathbb {R}}^{n+1}_+})\right)$ are isometric, a proper embedding ${\varSigma }={\tilde{x}}(M)$ in $\left( {\mathbb {B}}^{n+1},\delta _{\mathbb {{B}}^{n+1}}\right)$ can be identified as ${\widetilde{{\varSigma }}}$ in $\left( {\mathbb {R}}^{n+1}_+,(\varphi ^{-1})^*(\delta _{{\mathbb {R}}^{n+1}_+})\right)$.

For a star-shaped hypersurface ${\widetilde{{\varSigma }}}:={\tilde{y}}(M)$ in $\left( {\mathbb {R}}^{n+1}_+,(\varphi ^{-1})^*(\delta _{{\mathbb {R}}^{n+1}_+})\right)$, where ${\tilde{y}}:=\varphi \circ {\tilde{x}}$, we can write it as

$$\begin{aligned} {\tilde{y}}=\rho (z)z=\rho (\beta ,\xi )z,\quad z:=(\beta ,\xi )\in \overline{{\mathbb {S}}}^n_+. \end{aligned}$$

In polar coordinates, a direct computation implies that

$$\begin{aligned} \frac{\partial }{\partial y_{n+1}}=\frac{\partial \rho }{\partial y_{n+1}} \partial _{\rho }+\frac{\partial \beta }{\partial y_{n+1}} \partial _{\beta }=\cos \beta \partial _{\rho }-\frac{\sin \beta }{\rho }\partial _{\beta }. \end{aligned}$$

It gives us

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{n}y_i\partial _{y_i}=\rho \partial _{\rho }-\rho \cos \beta \left( \cos \beta \partial _{\rho }-\frac{\sin \beta }{\rho }\partial _{\beta }\right) =\rho \sin ^2\beta \partial _{\rho }+\frac{\sin 2\beta }{2}\partial _{\beta }. \end{aligned} \end{aligned}$$

From now on, we always set $a:=-E_{n+1}$. We have

$$\begin{aligned} \begin{aligned} -\varphi _*(a)&=\sum _{i=1}^{n}\frac{\partial y_{i}}{\partial x_{n+1}}\frac{\partial }{\partial y_i}+ \frac{\partial y_{n+1}}{\partial x_{n+1}}\frac{\partial }{\partial y_{n+1}} \\&=(1+y_{n+1})\sum _{i=1}^n y_i \frac{\partial }{\partial y_i}+\frac{(1+y_{n+1})^2-|y|^2}{2}\frac{\partial }{\partial y_{n+1}} \\&=y_{n+1}\sum _{i=1}^{n}y_i\partial _{y_i}+\frac{1+y_{n+1}^2-|y|^2}{2} \partial _{y_{n+1}}+\sum _{\alpha =1}^{n+1}y_{\alpha }\partial _{y_{\alpha }} \\&=\rho \cos \beta \left[ \rho \sin ^2\beta \partial _{\rho }+\frac{\sin 2\beta }{2}\partial _{\beta }\right] \\&\quad +\frac{1+\rho ^2\cos 2\beta }{2}\left( \cos \beta \partial _{\rho }-\frac{\sin \beta }{\rho }\partial _{\beta }\right) +\rho \partial _{\rho } \\&=\frac{\rho ^2\cos \beta +2\rho +\cos \beta }{2}\partial _{\rho }+\frac{(\rho ^2-1) \sin \beta }{2\rho }\partial _{\beta }. \end{aligned} \end{aligned}$$

Set $w:=\log \frac{2}{|y|^2+(y_{n+1}+1)^2}=\log \frac{2}{\rho ^2+2\rho \cos \beta +1}$ and $u:=\log \rho$. From the discussion in Sect. 3.1, we know that ${\tilde{\nu }}=\frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v}$ is the unit outward normal vector field of ${\widetilde{{\varSigma }}}$ in $({\mathbb {R}}^{n+1}_+, \delta _{{\mathbb {R}}^{n+1}_+})$. Then the capillary boundary condition gives us that

$$\begin{aligned} \begin{aligned} -e^{-2w}\cos \theta&=e^{-2w}\delta _{{\mathbb {B}}^{n+1}}(\nu ,{\overline{N}}\circ {\tilde{x}}) \\&= \varphi ^*\delta _{{\mathbb {R}}^{n+1}_+}(\nu ,{\overline{N}}\circ {\tilde{x}})\\&= \delta _{{\mathbb {R}}^{n+1}_+}(\varphi _*(\nu ),\varphi _*({\tilde{x}})) \\&= \left\langle e^{-w}{\tilde{\nu }},\frac{\rho ^2+1}{2\rho }\partial _{\beta } \right\rangle =e^{-2w}\left\langle \frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v},\frac{1}{\rho }\partial _{\beta }\right\rangle \\&=-e^{-2w}\frac{\nabla _{\partial _{\beta }}u}{v}, \end{aligned} \end{aligned}$$

It follows that

$$\begin{aligned} \nabla _{\partial _{\beta }}u=\cos \theta v\quad \text {on}\quad \partial {\mathbb {S}}^n_+. \end{aligned}$$

By a straightforward computation as above, under the conformal transformation $\varphi$ we have

$$\begin{aligned} \begin{aligned} \langle \nu ,a\rangle&=e^{2w}\delta _{{\mathbb {R}}^{n+1}_+}(\varphi _*(\nu ),\varphi _*(a))\\&=e^w\left\langle \frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v},\frac{\rho ^2\cos \beta +2\rho +\cos \beta }{2}\partial _{\rho }+ \frac{(\rho ^2-1)\sin \beta }{2\rho }\partial _{\beta }\right\rangle \\&=\frac{e^w}{2v} \left( \rho ^2\cos \beta +2\rho +\cos \beta \right) -\frac{e^w(\rho ^2-1)\sin \beta }{2v} \nabla _{\partial _\beta }u \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \langle {\tilde{x}},a\rangle =\langle \varphi ^{-1}({\tilde{y}}),a\rangle =-x_{n+1}=-\frac{|y|^2+y_{n+1}^2-1}{|y|^2+(y_{n+1}+1)^2}=-\frac{\rho ^2-1}{2}e^w. \end{aligned}$$

Similarly, we have

$$\begin{aligned} \begin{aligned} \langle X_a,\nu \rangle&=\frac{4}{\left[ |y|^2+(y_{n+1}+1)^2\right] ^2} \langle \varphi _*(X_a),\varphi _*(\nu )\rangle \\&=\frac{2}{|y|^2+(y_{n+1}+1)^2} \langle {\tilde{y}},{\tilde{\nu }}\rangle \\&=e^w\left\langle \rho \partial _{\rho },\frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v}\right\rangle \\&=e^w \frac{\rho }{v}. \end{aligned} \end{aligned}$$

Note that $e^{-w}:=\frac{\rho ^2+2\rho \cos \beta +1}{2}$. It then yields that

$$\begin{aligned} \begin{aligned} D_{{\tilde{\nu }}}e^{-w}&=\left\langle D e^{-w},\frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v}\right\rangle \\&=\left\langle (\rho +\cos \beta )\partial _{\rho }+\rho ^{-1}\partial _{\beta } e^{-w}\cdot \rho ^{-1}\partial _{\beta }, \frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v}\right\rangle \\&=\left\langle (\rho +\cos \beta )\partial _{\rho }-\sin \beta \rho ^{-1}\partial _{\beta }, \frac{\partial _{\rho }-\rho ^{-1}\nabla u}{v}\right\rangle \\&=\frac{\rho +\cos \beta +\sin \beta \nabla _{\partial _\beta } u}{v}. \end{aligned} \end{aligned}$$

Applying the transformation law for the mean curvature under a conformal metric, we know that the mean curvature ${\tilde{H}}$ of ${\tilde{{\varSigma }}}$ in $\left( {\mathbb {R}}^{n+1}_+,(\varphi ^{-1})^*(\delta _{{\mathbb {R}}^{n+1}_+})\right)$ is given by (see [36], equation (13) there)

$$\begin{aligned} \begin{aligned} {\tilde{H}}&=e^{-w}\left( H_{{\tilde{\nu }}}+nD _{{\tilde{\nu }}} w\right) \\&=e^{-w}\left[ \frac{n}{\rho v}-\frac{1}{\rho v}\sum _{i,j=1}^{n}\left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) u_{ij}\right] -nD_{{\tilde{\nu }}}e^{-w} \\&=e^{-w}\left[ \frac{n}{\rho v}-\frac{1}{\rho v}\sum _{i,j=1}^{n}\left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) u_{ij}\right] -n \frac{\rho +\cos \beta +\sin \beta \nabla _{\partial _\beta } u}{v} \\&=-\left[ \frac{1}{\rho ve^w} \sum _{i,j=1}^{n}\left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) u_{ij} +\frac{n\sin \beta \nabla _{\partial _\beta }u}{v}+\frac{n(\rho ^2-1)}{2\rho v}\right] , \end{aligned} \end{aligned}$$

where $H_{{\tilde{\nu }}}$ is the mean curvature with respect to ${\tilde{\nu }}$ of ${\widetilde{{\varSigma }}}$ in $({\mathbb {R}}^{n+1}_+, \delta _{{\mathbb {R}}^{n+1}_+})$. From the discussion in Sect. 3.1, in particular, Eq. (3.1), we know that the first equation in (3.2) is reduced to the following scalar equation

$$\begin{aligned} \frac{\partial _t \rho }{v}= \frac{{\tilde{f}}}{e^w}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} \begin{aligned} {\tilde{f}}&:=n\langle x,a\rangle +n\cos \theta \langle \nu ,a\rangle -{\tilde{H}}\langle X_a,\nu \rangle \\&=-\frac{n}{2}(\rho ^2-1)e^w +\frac{n\cos \theta }{2}\frac{e^w}{v}\left( \rho ^2\cos \beta +2\rho +\cos \beta \right) \\&\quad -\frac{n\cos \theta }{2}\frac{e^w}{v} {(\rho ^2-1)\sin \beta } \nabla _{\partial _\beta } u \\&\quad +\left[ \frac{1}{\rho ve^w} \left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) u_{ij}+\frac{n\sin \beta \nabla _{\partial _\beta } u}{v} +\frac{n(\rho ^2-1)}{2\rho v}\right] \\&\quad \cdot \frac{\rho e^w}{v}. \end{aligned} \end{aligned}$$

It is easy to see that Eq. (3.4) is also equivalent to

$$\begin{aligned} \begin{aligned} \partial _t u&=\frac{v}{\rho e^w}{\tilde{f}}=\frac{1}{\rho v e^w}\left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) u_{ij} \\&\quad +\left[ \frac{n\sin \beta u_{\beta }}{v}-\frac{n(\rho ^2-1)}{2\rho }\frac{|\nabla u|^2}{v} +\frac{n\cos \theta }{2\rho }\left( \rho ^2\cos \beta +2\rho +\cos \beta \right) \right. \\&\qquad \left. -\frac{\rho ^2-1}{2\rho } n\cos \theta \sin \beta u_{\beta }\right] \\&=\left[ \hbox {div}_{_{{\mathbb {S}}^n_+}}\left( \frac{\nabla u}{\rho v e^w}\right) -\frac{n+1}{v}\sigma \left( \nabla u,\nabla (\frac{1}{\rho e^w }) \right) \right. \\&\qquad \left. -\frac{n\cos \theta }{2}\cdot \frac{\rho ^2-1}{\rho }\sin \beta \sigma (\nabla u,\partial _{\beta })\right] +\frac{n\cos \theta }{2}\cdot \frac{\rho ^2\cos \beta +2\rho +\cos \beta }{\rho } \\&:=F(\nabla ^2u,\nabla u, \rho ,\beta ). \end{aligned} \end{aligned}$$

In summary, from the above discussion, flow (1.1) is equivalent to (up to a tangential diffeormphism) the following scalar parabolic equation on ${\mathbb {S}}^n_+$ .

$$\begin{aligned} \begin{array}{rcll} \displaystyle \frac{\partial u}{\partial t} &{}=&{} \displaystyle F(\nabla ^2 u,\nabla u, \rho ,\beta ) &{} \quad \text {in} \quad {\mathbb {S}}^n_+\times [0,T),\\ \nabla _{\partial _{\beta }}u&{}=&{} \displaystyle \cos \theta \sqrt{1+|\nabla u|^2} &{}\quad \text {on} \quad \partial {\mathbb {S}}^n_+\times [0,T),\\ u(\cdot ,0)&{}=&{}u_0(\cdot ) &{} \quad \text {on}\quad {\mathbb {S}}^n_+, \end{array} \end{aligned}$$

(3.5)

where $u_0=\log \rho _0$, $\rho _0$ is related to the initial hypersurface $x_0(M)$ under the transformation $\varphi$ and F is defined in the previous equation.

4 A priori estimates

The short-time existence of our flow is established by the standard PDE theory, since due to our assumption of star-shaped,

$$\begin{aligned} \langle X_a,\nu \rangle >0, \end{aligned}$$

for initial hypersurface, the flow is equivalent to the scalar flow (3.5). In this section, we will show the uniform height and gradient estimates for Eq. (3.5). Then the longtime existence of the flow follow immediately from the standard parabolic PDE theory.

In this section, we use the Einstein summation convention, i.e., if not stated otherwise, the repeated arabic indices i, j, k should be summed from 1 to n. We also use the notations $u_{\beta }:=\sigma ( \nabla u,\partial _{\beta })=\nabla _{\partial _\beta }u$ and $|\nabla u|^2:=\sigma (\nabla u,\nabla u)$ in this section. Recall that $\rho =e^u$ and $2e^{-w}={1+\rho ^2+2\rho \cos \beta }$. For the convenience, we introduce the following notations

$$\begin{aligned} F^{ij}&:=\frac{\partial F(r,p,\rho ,\beta )}{\partial r_{ij}}\bigg |_{r=\nabla ^2 u,p=\nabla u} =\frac{1}{\rho ve^w} \left( \sigma ^{ij}-\frac{u^iu^j}{v^2}\right) , \\ F_{p_i}&:=\frac{\partial F(r,p,\rho ,\beta )}{\partial p_i}\bigg |_{r=\nabla ^2 u,p=\nabla u} \\&=-\frac{u_i}{\rho e^w v^3}a^{kl}u_{kl}-\frac{2}{\rho v^3 e^w}a^{il}u_{kl}u_k +\frac{n\sin \beta \sigma ( \partial _{\beta },e_i)}{v}-n\sin \beta u_{\beta }\frac{u_i}{v^3} \\&\quad -\frac{n(\rho ^2-1)}{2\rho } \left( \frac{2}{v}-\frac{|\nabla u|^2}{v^3}\right) u_i-\frac{\rho ^2-1}{2\rho } n\cos \theta \cos \beta \sigma ( \partial _{\beta },e_i), \\ F_{\rho }&:=\frac{\partial F(r,p,\rho ,\beta )}{\partial \rho }\bigg |_{r=\nabla ^2 u,p=\nabla u}\\&=\frac{1}{2v}a^{ij}u_{ij}\left( 1-\frac{1}{\rho ^2}\right) -\frac{n}{2} \left( 1+\frac{1}{\rho ^2}\right) \frac{|\nabla u|^2}{v}-\frac{n}{2}\left( 1+\frac{1}{\rho ^2}\right) \cos \theta \sin \beta u_{\beta }\\&\quad +\frac{n\cos \theta }{2}\left( 1-\frac{1}{\rho ^2}\right) \cos \beta , \\ F_{\beta }&:=\frac{\partial F(r,p,\rho ,\beta )}{\partial \beta }\bigg |_{r=\nabla ^2 u,p=\nabla u}\\&=-\frac{1}{v}a^{ij}u_{ij}\sin \beta +\frac{n\cos \beta }{v}u_{\beta }-\cos \theta \frac{\rho ^2-1}{2\rho }n\cos \beta u_{\beta }-\frac{n\cos \theta }{2\rho } \left( {\rho ^2}+1\right) \sin \beta \end{aligned}$$

and

$$\begin{aligned} a^{ij}=\sigma ^{ij}-\frac{u^iu^j}{v^2},\quad {\mathcal {F}}:=\sum _{i=1}^n F^{ii}. \end{aligned}$$

Remark 4.1

(Spherical caps) For any given constant $\theta \in (0, \pi )$, define

$$\begin{aligned} {\mathcal {C}}_{r,\theta }:=\{z\in {\mathbb {B}}^{n+1} |z+\sqrt{r^2+2r\cos \theta +1}E_{n+1}| \le r\},\quad r\in (0,\infty ). \end{aligned}$$

It is easy to check that $\partial {\mathcal {C}}_{r,\theta }$ is a static solution to the flow (1.1), that is,

$$\begin{aligned} n\langle x,E_{n+1}\rangle + n\cos \theta \langle \nu ,E_{n+1}\rangle +H\langle X_{n+1},\nu \rangle =0 \end{aligned}$$

and meets the support ${{\mathbb {S}}}^n=\partial {\mathbb {B}}^{n+1}$ at the contact angle $\theta$. Such a spherical cap is certainly star-shaped and determines a corresponding radial function $\psi$, which is a stationary solution of flow (3.5).

Now we are ready to show that the radial function u has the following $C^0$ estimate.

Proposition 4.2

Assume that the initial star-shaped hypersurface $x_0(M)$ satisfies

$$\begin{aligned} x_0(M)\subset {\mathcal {C}}_{R_2,\theta }\setminus {\mathcal {C}}_{R_1,\theta }, \end{aligned}$$

for some $R_2>R_1>0$, where ${\mathcal {C}}_{R,\theta }$ is defined in Remark 4.1. Then this property is preserved along flow (1.1). In particular, if u(x, t) solves the initial boundary value problem (3.5) on interval $[0,+\infty )$, then for any $T>0$,

$$\begin{aligned} \Vert u\Vert _{C^0({\mathbb {S}}^n_+\times [0,T])}\le C, \end{aligned}$$

where C is a constant depends only on the initial value and their covariant derivatives with respect to the round metric $\sigma$ on ${\mathbb {S}}^n_+$.

Proof

For any $T>0$, we want to get the $C^0$ estimate of u in ${\mathbb {S}}^n_+\times [0,T]$. Assume that $\psi$ is the radial function of the corresponding upper spherical cap with respect to $\partial {\mathcal {C}}_{R_2,\theta }\cap {\mathbb {B}}^{n+1}$ after the conformal transformation $\varphi$. Since $\psi$ is a static solution to flow (3.5), we know that

$$\begin{aligned} \begin{aligned} \partial _t(u-\psi )&=F(\nabla ^2 u,\nabla u,e^u,\beta )-F(\nabla ^2 \psi ,\nabla \psi ,e^{\psi },\beta ) \\&= A^{ij}\nabla _{ij}(u-\psi )+ b^j\cdot (u-\psi )_j+c\cdot (u-\psi ), \end{aligned} \end{aligned}$$

where $A^{ij}:=\int _0^1 F^{ij}\left( \nabla ^2(su+(1-s)\psi ),\nabla (su+(1-s)\psi ),su+(1-s)\psi ,\beta \right) ds$, $b^j:=\int _0^1 F_{p_j}\left( \nabla ^2(su+(1-s)\psi ),\nabla (su+(1-s)\psi ),su+(1-s)\psi ,\beta \right) ds$, and $c:=\int _0^1 F_\rho \left( \nabla ^2(su+(1-s)\psi ),\nabla (su+(1-s)\psi ),su+(1-s)\psi ,\beta \right) e^{su+(1-s)\psi }ds$. Denote $\lambda :=-\sup \limits _{{\mathbb {S}}^n_+\times [0,T]} |c|$. Applying the maximum principle, we know that $e^{\lambda t}(u-\psi )$ attains its nonnegative maximum value at the parabolic boundary, say $(x_0,t_0)$. That is,

$$\begin{aligned} e^{\lambda t}( u(x,t)-\psi (x))\le \sup _{\partial {\mathbb {S}}^n_+\times [0,T)\cup {\mathbb {S}}^n_+\times \{0\}}\{0,e^{\lambda t} (u(x,t)-\psi (x))\}. \end{aligned}$$

with either $x_0\in \partial {\mathbb {S}}^n_+$ or $t_0=0$. If $x_0\in \partial {\mathbb {S}}^n_+$, from the Hopf lemma, we have

$$\begin{aligned} \nabla '(u-\psi )(x_0,t_0)=0, \nabla _n u(x_0,t_0)<\nabla _n \psi (x_0,t_0), \end{aligned}$$

that is, $|\nabla ' u|=|\nabla ' \psi |:=s$ and $\nabla _nu<\nabla _n\psi$ at $(x_0,t_0)$. Here we denote $\nabla '$ and $\nabla _n$ as the tangential and normal part of $\nabla$ on $\partial {\mathbb {S}}^n_+$, $e_n=-\partial _{\beta }$ is the inner normal vector field on $\partial {\mathbb {S}}^n_+$. From the boundary condition in (3.5) we have

$$\begin{aligned} \frac{\nabla _nu}{\sqrt{1+s^2+|\nabla _{n}u|^2}}=-\cos \theta = \frac{\nabla _n \psi }{\sqrt{1+s^2+|\nabla _{n}\psi |^2}}, \end{aligned}$$

a contradiction to the fact that function $\frac{\tau }{\sqrt{1+s^2+\tau ^2}}$ is strictly increasing with respect to $\tau \in {\mathbb {R}}$ and $\nabla _nu<\nabla _n\psi$ at $(x_0,t_0)$. Hence we have $t_0=0$, which follows that

$$\begin{aligned} e^{\lambda t}(u(x,t)-\psi (x))\le u_0(x_0)-\psi (x_0)\le 0, \quad \text {in}\quad (x,t)\in {\mathbb {S}}^n_+\times [0,T], \end{aligned}$$

that is

$$\begin{aligned} u(x,t)\le \psi (x), \quad \text {in}\quad (x,t)\in {\mathbb {S}}^n_+\times [0,T]. \end{aligned}$$

Hence we obtain the desired upper bound of u. Similarly, we can get the desired lower bound of u. After the conformal transformation we finish the proof of the Proposition. $\square$

In order to obtain the gradient estimate, we need to employ the distance function $d(x):=dist_{\sigma }(x,\partial {\mathbb {S}}^n_+)$. It is well-known that d is well-defined and smooth for x near $\partial {\mathbb {S}}^n_+$ and $\nabla d=-\partial _{\beta }$ on $\partial {\mathbb {S}}^n_+$, where $\partial _{\beta }$ is the unit outer normal vector field on $\partial {\mathbb {S}}^n_+$. In the following, we extend d to be a smooth function on $\overline{{\mathbb {S}}}^n_+$ and satisfying that

$$\begin{aligned} d\ge 0,\quad |\nabla d|\le 1\quad \text {in}\quad \overline{{\mathbb {S}}}^n_+. \end{aligned}$$

We will use O(s) to denote terms that are bounded by Cs for a constant $C>0$, which depends only on the $C^0$ norm of u. Our choice of test functions are motivated from [11, 14] and [22]. Now we show the uniform gradient estimate. This is the key step of this paper.

Proposition 4.3

If u(x, t) solves the initial boundary value problem (3.5) on the interval $[0, T^*)$ $(T^* \in (0, \infty ])$ with $|\cos \theta |<\frac{3n+1}{5n-1}$. Then for any $(x,t)\in {\mathbb {S}}^n_+\times [0,T]$ $(T<T^*)$, we have

$$\begin{aligned} |\nabla u|(x,t)\le C, \end{aligned}$$

where C is a constant depends only on the initial values and the covariant derivatives with respect to round metric $\sigma$ on ${\mathbb {S}}^n_+$.

Proof

Define a function

$$\begin{aligned} {\varPhi }:=(1+Kd)v+\cos \theta \sigma (\nabla u,\nabla d), \end{aligned}$$

where $K>0$ is the positive constant to be determined later. Assume that ${\varPhi }$ attains its maximum value at $(x_0,t_0)\in \overline{ {\mathbb {S}}}^n_+\times [0,T]$. We divide it into the following three cases to complete the proof.

Case 1: $(x_0,t_0)\in \partial {\mathbb {S}}^n_+\times [0,T]$. At $x_0$, we choose local coordinates such that $\frac{\partial }{\partial x_n}$ be the inner normal direction of $\partial {\mathbb {S}}^n_+$, which is exactly equal to $-\partial _{\beta }$ and corresponds to $\nabla d$. And let $\{x_{i}\}_{i=1}^{n-1}$ be the geodesic coordinate of $x_0\in \partial {\mathbb {S}}^n_+$. Along the geodesic $x_n=t$ ($0<t\le \varepsilon$), one takes the parallel transport of tangential direction $\frac{\partial }{\partial x_{i}}$ $(1\le i\le n-1)$ to establish the geodesic coordinate in the neighborhood around point $x_0$ in $\overline{{\mathbb {S}}^n_+}$.

First, we notice that ${\varPhi }=v+\cos \theta u_n$ on the boundary $\partial {\mathbb {S}}^n_+$ from the boundary condition in (3.5). We denote $\nabla ' u$ and $u_n$ the tangential and the normal part of $\nabla u$ on the boundary by our choice of coordinates above. The boundary condition $u_n=-\cos \theta v$ implies that

$$\begin{aligned} \begin{aligned} u_n^2=\cos ^2\theta v^2=\cos ^2 \theta (1+|\nabla ' u|^2+u_n^2), \end{aligned} \end{aligned}$$

in other words,

$$\begin{aligned} \begin{aligned} u_n^2=\cot ^2 \theta (1+|\nabla ' u|^2), \end{aligned} \end{aligned}$$

(4.1)

Moreover we have

$$\begin{aligned} \begin{aligned} {\varPhi }&=v\sin ^2\theta =\sqrt{1+|\nabla 'u|^2+u_n^2} \sin ^2\theta =|\csc \theta |\sqrt{1+|\nabla 'u|^2}\sin ^2\theta \\&= \sqrt{1+|\nabla 'u|^2}|\sin \theta |. \end{aligned} \end{aligned}$$

From the Gauss–Weingarten equation we have

$$\begin{aligned} \begin{aligned} \nabla _nv&=\frac{ \nabla _ku\nabla _{nk}u}{v} =\frac{\sum \limits _{i=1}^{n-1} \nabla _{i}u\nabla _{ni}u }{v}-\cos \theta \nabla _{nn}u \\&=\frac{1}{v} \sum \limits _{i=1}^{n-1} \left( u_{i}u_{ni} +\sum _{j=1}^{n-1}u_{i}b_{ij }u_{j}\right) -\cos \theta \nabla _{nn}u \\&=\sum \limits _{i=1}^{n-1}\frac{ u_{i}u_{ni}}{v} -\cos \theta \nabla _{nn}u, \end{aligned} \end{aligned}$$

where $b_{ij}:=\sigma ( \nabla _{e_{i}} e_n,e_{i})=0$ is the second fundamental form of $\partial {\mathbb {S}}^n_+$ in ${\mathbb {S}}^n_+$ for $1\le i,j\le n-1$. Then at $x_0\in \partial {\mathbb {S}}^n_+$, from the Hopf lemma, it implies that

$$\begin{aligned} \begin{aligned} 0&\ge \nabla _n {\varPhi }(x_0) =\nabla _nv+Kv\nabla _nd+\nabla _n( u_kd_k)\cos \theta \\&= \nabla _nv+Kv+ \nabla _{kn}ud_k\cos \theta + u_k\nabla _{kn}d\cos \theta \\&=\frac{1}{v} \sum \limits _{i=1}^{n-1} u_{i}u_{ni}+Kv + u_k\nabla _{kn}d\cos \theta . \end{aligned} \end{aligned}$$

(4.2)

Since $\{ \partial _{x_i}\}_{i=1}^{n-1}$ are the tangential vector fields on $\partial {\mathbb {S}}^n_+$, for $1\le i\le n-1$, we have that

$$\begin{aligned} \begin{aligned} 0=\nabla '_{i}{\varPhi }(x_0)&=v_{i}+u_{ni}\cos \theta . \end{aligned} \end{aligned}$$

This implies that

$$\begin{aligned} \begin{aligned} v_{i}=-u_{ni}\cos \theta . \end{aligned} \end{aligned}$$

(4.3)

By differentiating the boundary condition of (3.5) and combining with (4.3) we have that

$$\begin{aligned} \begin{aligned} u_{ni}&=-\nabla '_{i} (\cos \theta v)=\cos ^2\theta u_{ni}. \end{aligned} \end{aligned}$$

Since $|\cos \theta |<1$, we get

$$\begin{aligned} u_{ni}=0, \qquad \forall 1\le i\le n-1. \end{aligned}$$

(4.4)

Substituting Eq. (4.4) into Eq. (4.2), we conclude that

$$\begin{aligned} \begin{aligned} 0&\ge \frac{1}{v} \sum \limits _{i=1}^{n-1} u_{i}u_{ni}+ K{v} + u_k\nabla _{kn}d\cos \theta =K{v} +u_k\nabla _{kn}d\cos \theta \\&\ge {\varPhi }\left( K\frac{1}{\sin ^2\theta }-C_1\right) , \end{aligned} \end{aligned}$$

for some universial positive constant $C_1$. By choosing K large enough, say $K:={2C_1}$, we get a contradiction. So Case 1 is impossible.

Case 2: $(x_0,t_0)\in \overline{ {\mathbb {S}}^n_+}\times \{0\}$. In this case we have

$$\begin{aligned} \begin{aligned} {\varPhi }(x,t)&\le {\varPhi }(x_0,0)=(1+Kd)\sqrt{1+|\nabla u_0|^2}+\sigma ( \nabla u_0,\nabla d)\cos \theta \\&\le C. \end{aligned} \end{aligned}$$

It yields that

$$\begin{aligned} \sup _{{\mathbb {S}}^n_+\times [0,T]} v\le C, \end{aligned}$$

(4.5)

where C is a positive constant depending only on n and $u_0$.

Case 3: $(x_0,t_0)\in {\mathbb {S}}^n_+\times (0,T]$. In this case, we have

$$\begin{aligned} 0=\nabla _i {\varPhi }(x_0,t_0)=(1+Kd)v_i+Kd_iv+\cos \theta (u_ld_l)_i, \end{aligned}$$

(4.6)

for all $1\le i\le n$, or equivalently,

$$\begin{aligned} \left( (1+Kd)\frac{\nabla _lu}{v}+\nabla _ld\cos \theta \right) \nabla _{il}u=- \nabla _lu\nabla _{il}d\cos \theta -Kd_iv. \end{aligned}$$

(4.7)

At $(x_0,t_0)$, by rotating the geodesic coordinate $\{(x_1,x_2,\ldots ,x_n)\}$ we may assume

$$\begin{aligned} |\nabla u|=u_1>0,\quad \text {and}\quad \{\nabla _{\alpha \beta }u\}_{2\le \alpha ,\beta \le n}\quad \text {is diagonal}. \end{aligned}$$

We may also assume that $u_1(x_0,t_0)$ large enough in the below computation, such that $u_1, v=\sqrt{1+u_1^2}$, and ${\varPhi }=(1+Kd)v+u_1d_1\cos \theta$ are equivalent to each other at $(x_0,t_0)$. Otherwise, we have completed the proof. All the computation below are done at the point $(x_0,t_0)$.

First it is easy to see

$$\begin{aligned} \left[ (1+Kd)\frac{u_1}{v}+\cos \theta d_1\right] u_{1\alpha }=-\cos \theta u_{\alpha \alpha }d_{\alpha }-\cos \theta u_1d_{1\alpha }-Kd_{\alpha }v, \end{aligned}$$

(4.8)

and

$$\begin{aligned} \left[ (1+Kd)\frac{u_1}{v}+\cos \theta d_1\right] u_{11}=-\cos \theta u_{\alpha 1}d_{\alpha }-\cos \theta u_1d_{11}-Kd_{1}v. \end{aligned}$$

(4.9)

Denote $S:=(1+Kd)\frac{u_1}{v}+\cos \theta d_1$. It is easy to check that $2+K\ge S\ge C(\delta ,\theta )>0$ if we assume that $u_1\ge \delta >0$, otherwise we have obtained the estimate. Equation (4.8) yields that

$$\begin{aligned} u_{1\alpha }=-\frac{\cos \theta d_{\alpha }}{S}u_{\alpha \alpha }-\frac{1}{S}\left( \cos \theta u_1d_{1\alpha }+Kd_{\alpha }v\right) . \end{aligned}$$

(4.10)

Substituting Eq. (4.10) into Eq. (4.9), we conclude that

$$\begin{aligned} \begin{aligned} u_{11}&=-\frac{1}{S}\cos \theta u_{\alpha 1}d_{\alpha }+\frac{1}{S}\left( -\cos \theta u_1d_{11}-Kd_{1}v\right) \\&=\frac{\cos ^2\theta }{S^2}\sum _{\alpha =2}^{n}d_{\alpha }^2u_{\alpha \alpha } \\&\quad +\left[ \sum _{\alpha =2}^{n}\frac{\cos \theta d_{\alpha }}{S^2}\left( \cos \theta u_1d_{1\alpha }+Kd_{\alpha }v \right) - \frac{1}{S}\left( \cos \theta u_1d_{11}+Kd_{1}v\right) \right] \\&=\frac{\cos ^2\theta }{S^2}\sum _{\alpha =2}^{n}d_{\alpha }^2u_{\alpha \alpha }+O(v). \end{aligned} \end{aligned}$$

(4.11)

On the other hand, we have

$$\begin{aligned} \begin{aligned} 0&\le (\partial _t- F^{ij}\nabla _{ij}- F_{p_i}\nabla _i){\varPhi }\\&=\frac{(1+Kd)}{v} {u_l(u_{lt}- F^{ij}u_{lij}- F_{p_i}u_{li})}+d_k\cos \theta \left( u_{kt}- F^{ij}u_{kij} - F_{p_i}u_{ki}\right) \\&\quad + (1+Kd)\left( \frac{F^{ij}u_lu_{li}u_ku_{kj}}{v^3}- \frac{F^{ij}u_{li}u_{lj}}{v}\right) \\&\quad -\left( 2 F^{ij}u_{ki}d_{kj}\cos \theta +2K F^{ij}d_iv_j\right) \\&\quad -\left( F^{ij}u_k d_{kij}\cos \theta +K F^{ij}d_{ij}v\right) - F_{p_i}\left( Kd_iv+\cos \theta u_kd_{ki}\right) \\&:= {\text {J}}_1+{\text {J}}_2+{\text {J}}_3+{\text {J}}_4+{\text {J}}_5+{\text {J}}_6. \end{aligned} \end{aligned}$$

(4.12)

Next we carefully handle these six terms one by one. Differentiating the main equation in (3.5), we get

$$\begin{aligned} u_{tk}= F^{ij}u_{ijk}+ F_{p_i}u_{ik}+F_{\rho }\rho u_k+F_{\beta }\sigma (\partial _{\beta },e_k). \end{aligned}$$

(4.13)

Combining with the communicative formula on ${\mathbb {S}}^n_+$

$$\begin{aligned} u_{ijk}=u_{kij}+u_j\sigma _{ik}-u_k\sigma _{ij}, \end{aligned}$$

(4.14)

we have

$$\begin{aligned} \begin{aligned} {\text {J}}_1&:=\frac{(1+Kd)}{v} {u_l(u_{lt}-F^{ij}u_{lij}-F_{p_i}u_{li})} \\&=\left\{ \frac{(1+Kd)|\nabla u|^2}{2v^2} \rho \left( 1-\frac{1}{\rho ^2}\right) \frac{u_{11}}{v^2}-\frac{(1+Kd)u_{\beta }}{v^2}\sin \beta \frac{u_{11}}{v^2}\right\} \\&\quad + \left\{ \frac{(1+Kd)}{2v^2} |\nabla u|^2 \left( \rho -\frac{1}{\rho }\right) \sum _{\alpha =2}^{n}u_{\alpha \alpha }\right\} \\&\quad - \left\{ \frac{(1+Kd)|\nabla u|^2}{v} \rho \cdot \frac{n}{2}\left( 1+\frac{1}{\rho ^2}\right) \left( \frac{|\nabla u|^2}{v} +\cos \theta \sin \beta u_{\beta }\right) \right\} \\&\quad +\left\{ -\frac{(1+Kd)u_{\beta }}{v^2} \sin \beta \sum _{\alpha =2}^{n}u_{\alpha \alpha }+ \frac{(1+Kd)u_{\beta }}{v} \right. \\&\qquad \left[ \frac{n\cos \beta }{v}u_{\beta } -\cos \theta \frac{\rho ^2-1}{2\rho } n\cos \beta u_{\beta } -\frac{n\cos \theta }{2\rho }(\rho ^2+1)\sin \beta \right] \\&\qquad \left. +\frac{(1-n)(1+Kd)|\nabla u|^2}{\rho e^w v^2} \right\} \\&:={\text {J}}_{11}+{\text {J}}_{12}+{\text {J}}_{13}+{\text {J}}_{14}. \end{aligned} \end{aligned}$$

Now we tackle the above terms one by one. First, by using Eq. (4.11), we obtain that

$$\begin{aligned} \begin{aligned} {\text {J}}_{11}&=\left[ \frac{(1+Kd)|\nabla u|^2}{2v^2} \rho \left( 1-\frac{1}{\rho ^2}\right) \frac{1}{v^2}-\frac{(1+Kd)u_{\beta }}{v^2}\sin \beta \frac{1}{v^2} \right] \\&\quad \cdot \left[ \frac{\cos ^2\theta }{S^2}\sum _{\alpha =2}^{n}d_{\alpha }^2u_{\alpha \alpha }+O(u_1)\right] \\&=O\left( \frac{1}{v^2}\right) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O\left( \frac{1}{v}\right) . \end{aligned} \end{aligned}$$

It is also not difficult to show that ${\text {J}}_{14}=O(\frac{1}{v}) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O(v).$ $J_{12}$ will be considered later, together with $J_{22}$ and $J_{32}$, and $J_{13}$ with $J_{23}$. See below. For the term ${\text {J}}_3$, we have

$$\begin{aligned} \begin{aligned} {\text {J}}_3&:=(1+K_1d)\left( \frac{F^{ij}u_lu_{li}u_ku_{kj}}{v^3}- \frac{F^{ij}u_{li}u_{lj}}{v}\right) \\&=\frac{(1+Kd)}{\rho e^w v}\left( -\frac{1}{v^5}u_{11}^2-\frac{2}{v^3}\sum _{\alpha =2}^{n}u_{1\alpha }^2\right) -(1-\varepsilon )\frac{(1+Kd)}{\rho e^w v^2}\sum _{\alpha =2}^{n}u_{\alpha \alpha }^2\\&\quad -\varepsilon \frac{(1+Kd)}{\rho e^w v^2}\sum _{\alpha =2}^{n}u_{\alpha \alpha }^2 \\&:={\text {J}}_{31}+{\text {J}}_{32}+{\text {J}}_{33}. \end{aligned} \end{aligned}$$

From Eq. (4.13), we deduce that

$$\begin{aligned} {\text {J}}_2&:=d_k\cos \theta \left( u_{kt}-F^{ij}u_{kij} -F_{p_i}u_{ki}\right) \\&=\cos \theta \left( F_{\rho }\rho d_ku_k+F_{\beta } d_{\beta }\right) -\cos \theta \sigma ( \nabla u,\nabla d) {\mathcal {F}}+\cos \theta F^{ij}u_id_j \\&=\left[ \cos \theta \sigma ( \nabla u,\nabla d) \left( \rho -\frac{1}{\rho }\right) \frac{u_{11}}{2v^3}-\cos \theta \sin \beta d_{\beta } \frac{u_{11}}{v^3}\right] \\&\quad +\frac{\cos \theta }{2v} \sigma ( \nabla u,\nabla d) \left( \rho -\frac{1}{\rho }\right) \sum _{\alpha =2}^{n}u_{\alpha \alpha } \\&\quad -\frac{n}{2}\left( \rho +\frac{1}{\rho }\right) \cos \theta \sigma ( \nabla u,\nabla d) \left( \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }\right) \\&\quad +\left\{ -\frac{\cos \theta \sin \beta }{v}d_{\beta }\sum _{\alpha =2}^{n}u_{\alpha \alpha } -\frac{(n-1)u_1^2+n}{\rho v^3 e^w} \cos \theta \sigma ( \nabla u,\nabla d) \right. \\&\quad \qquad +\cos \theta \frac{\sigma ( \nabla u,\nabla d)}{\rho v^3 e^w}+\cos \theta d_{\beta } \\&\quad \qquad \left[ \frac{n\cos \beta }{v}u_{\beta } -\cos \theta \frac{\rho ^2-1}{2\rho }n\cos \beta u_{\beta }-\frac{n\cos \theta }{2\rho } \left( {\rho ^2}+1\right) \sin \beta \right] \\&\quad \qquad \left. +\frac{n}{2} \cos ^2\theta \left( 1-\frac{1}{\rho ^2}\right) \cos \beta \rho \sigma ( \nabla u,\nabla d)\right\} \\&:={\text {J}}_{21}+{\text {J}}_{22}+{\text {J}}_{23}+{\text {J}}_{24}. \end{aligned}$$

For these terms, we first notice that ${\text {J}}_{24}=O(\frac{1}{v}) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O(v).$ Equation (4.11) implies ${\text {J}}_{21}=O(\frac{1}{v^2}) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O(\frac{1}{v}).$ Furthermore, we get by using the arithmetic-geometric inequality

$$\begin{aligned} \begin{aligned} {\text {J}}_{12}+{\text {J}}_{22}+{\text {J}}_{32}&:=\frac{(1+Kd)}{2v^2} |\nabla u|^2 \left( \rho -\frac{1}{\rho }\right) \sum _{\alpha =2}^{n}u_{\alpha \alpha } \\&\quad +\cos \theta \frac{\sigma ( \nabla u,\nabla d)}{2v} \left( \rho -\frac{1}{\rho }\right) \sum _{\alpha =2}^{n}u_{\alpha \alpha } \\&\quad -(1-\varepsilon )\frac{1+Kd}{\rho e^w v^2}\sum _{\alpha =2}^{n} u_{\alpha \alpha }^2 \\&=S\left( \rho -\frac{1}{\rho }\right) \frac{u_1}{2v}\sum _{\alpha =2}^{n} u_{\alpha \alpha }-(1-\varepsilon )\frac{1+Kd}{\rho e^w v^2}\sum _{\alpha =2}^{n}u_{\alpha \alpha }^2 \\&\le \frac{S}{1+Kd}\cdot \frac{(n-1)S \left( \rho -\frac{1}{\rho }\right) ^2 u_1^2}{16(1-\varepsilon )} \rho e^w \\&\le \frac{(n-1)(1+|\cos \theta |)S }{16(1-\varepsilon )} \left( \rho -\frac{1}{\rho }\right) ^2\rho e^wu_1^2. \end{aligned} \end{aligned}$$

Before continuing, we fix a constant $b_0\in (|\cos \theta |, \frac{3n+1}{5n-1})$, for $|\cos \theta |<\frac{3n+1}{5n-1}$. If

$$\begin{aligned} \begin{aligned} \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }< (1-b_0)u_1, \end{aligned} \end{aligned}$$

(4.15)

then

$$\begin{aligned} 0<b_0-|\cos \theta |<b_0-\sin \beta |\cos \theta | |u_\beta | u_1^{-1}<1-\frac{u_1}{v}, \end{aligned}$$

which implies that $u_1$ is uniformly bounded. Therefore, we may assume that

$$\begin{aligned} \begin{aligned} \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }\ge (1-b_0)u_1. \end{aligned} \end{aligned}$$

(4.16)

Now we conclude that this yields

$$\begin{aligned} \begin{aligned} {\text {J}}_{13}+{\text {J}}_{23}&:=-\frac{n}{2}\frac{1+Kd}{v}|\nabla u|^2 \left( \rho +\frac{1}{\rho }\right) \left( \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }\right) \\&\quad - \frac{n}{2}\cos \theta \sigma ( \nabla u,\nabla d) \\&\quad \left( \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }\right) \left( \rho +\frac{1}{\rho }\right) \\&=-\frac{n}{2}u_1 \left( \frac{|\nabla u|^2}{v}+\cos \theta \sin \beta u_{\beta }\right) \left( \rho +\frac{1}{\rho }\right) S \\&\le -\frac{n}{2}(1-b_0) S u_1^2 \left( \rho +\frac{1}{\rho }\right) {.} \end{aligned} \end{aligned}$$

Since $|\cos \theta |\le b_0<\frac{3n+1}{5n-1}$, by choosing $\varepsilon =\frac{\varepsilon _0}{2}\in (0,1)$ with $\varepsilon _0:=\frac{3n+1-b_0(5n-1)}{4n(1-b_0)}>0$, we have that $(n-1)(1+b_0)-4(1-\varepsilon )(1-b_0)n<0$. Then we deduce

$$\begin{aligned} \begin{aligned}&{\text {J}}_{13}+{\text {J}}_{23}+{\text {J}}_{12}+{\text {J}}_{22}+{\text {J}}_{32} \\&\quad \le -\frac{n}{2}(1-b_0) S u_1^2 \left( \rho +\frac{1}{\rho }\right) +u_1^2\frac{(n-1)(1+b_0)S }{16(1-\varepsilon )} \left( \rho -\frac{1}{\rho }\right) ^2\rho e^w \\&\quad \le u_1^2S\left[ \frac{(n-1)(1+b_0)}{16(1-\varepsilon )} \left( \rho -\frac{1}{\rho }\right) ^2\frac{2\rho }{\rho ^2+1}-(1-b_0) \frac{n}{2}\left( \rho +\frac{1}{\rho }\right) \right] \\&\quad =\frac{u_1^2S}{8\rho (\rho ^2+1)(1-\varepsilon )} \left\{ \left[ (n-1)(1+b_0)-4(1-\varepsilon )(1-b_0)n\right] (\rho ^4+1) \right. \\&\qquad \left. -\left[ 2(n-1)(1-b_0)+8(1-\varepsilon )(1-b_0)n\right] \rho ^2 \right\} \\&\quad \le -\alpha _0 u_1^2, \end{aligned} \end{aligned}$$

where $\alpha _0$ is a positive constant, which only depends on $n,b_0$ and $\Vert u\Vert {_{C^0}}$. Using Eqs. (4.10) and (4.11) again, we have

$$\begin{aligned} \begin{aligned} {\text {J}}_4+{\text {J}}_6&= \displaystyle -2F^{ij}u_{ki}d_{kj}\cos \theta -2KF^{ij}d_iv_j-F_{p_i}\left( Kd_iv+\cos \theta \sum _{k=1}^{n}u_kd_{ki}\right) \\&= O\left( \frac{1}{v}\right) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O(1). \end{aligned} \end{aligned}$$

For term $J_5$, it is easy to see ${\text {J}}_5:=-F^{ij}u_k d_{kij}\cos \theta -KF^{ij}d_{ij}v =O(1).$

By adding all above terms into Eq. (4.12), we have

$$\begin{aligned} \begin{aligned} 0&\le \frac{(1+Kd)}{\rho e^w v}\left( -\frac{1}{v^5}u_{11}^2-\frac{2}{v^3}\sum _{\alpha =2}^{n}u_{1\alpha }^2\right) -\varepsilon _0 \frac{(1+Kd)}{2\rho e^w v^2}\sum _{\alpha =2}^{n}u_{\alpha \alpha }^2-\alpha _0 u_1^2\\&\quad +O\left( \frac{1}{v}\right) \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|+O(v) \\&\le -\varepsilon _0 \frac{(1+Kd)}{2\rho e^w v^2}\sum _{\alpha =2}^{n}u_{\alpha \alpha }^2+\frac{C_2}{v} \sum _{\alpha =2}^{n}|u_{\alpha \alpha }|-\alpha _0 u_1^2+C_1v \\&\le -\alpha _0 u_1^2+C_1v+\frac{C_2^2 \rho e^w}{2\varepsilon _0 (1+Kd)}. \end{aligned} \end{aligned}$$

Hence we conclude that

$$\begin{aligned} u_1\le C. \end{aligned}$$

We have completed the proof. $\square$

Remark 4.4

We remark that the condition $|\cos \theta |\le b_0<\frac{3n+1}{5n-1}$ was only used in the estimate of term ${\text {J}}_{13}+{\text {J}}_{23}+{\text {J}}_{12}+{\text {J}}_{22}+{\text {J}}_{32}$. And the main dominating term is ${\hbox {J}}_{{13}}$, which ensures us to obtain the gradient estimate under this contact angle range.

The higher order a priori estimates of u follow from the uniform $C^0$ and $C^1$ estimates. Denote $j(p):= {\sigma (p,\partial _\beta \rangle } -\cos \theta \sqrt{1+|p|^2}$ for $p\in {\mathbb {R}}^n$. It is easy to see that

$$\begin{aligned} \sigma (j_{p}\big |_{p=\nabla u},\partial _\beta )= 1-\cos ^2\theta>1-b_0^2>0, \end{aligned}$$

which means that we have a uniformly oblique boundary condition. To be more precise, from the classical parabolic theory for quasi-linear parabolic equations (see [23] for instance), it follows that

Proposition 4.5

If $u(\cdot ,t)$ solves the initial boundary value problem (3.5) on interval $[0, T^*)$ for $T^*\in (0, \infty ]$ with $|\cos \theta |<\frac{3n+1}{5n-1}$, then for any $0<T<T^*$, we have

$$\begin{aligned} \Vert u(\cdot ,t)\Vert _{C^k}\le C,\quad 0\le t\le T, \end{aligned}$$

where C is a positive constant only depends on k, and the initial values and the covariant derivatives with respect to the round metric on ${\mathbb {S}}^n_+$. It follows, in particular, $T^*=\infty$.

Proof of Theorem 1.1

We only need to show that each subsequential limit is a spherical cap.

As is shown in the proof of Proposition 2.4, integrating the Eq. (2.11) over $t\in [0,+\infty )$ and combining with Proposition 4.5, we have that

$$\begin{aligned} \int _0^{\infty }\int _{{\mathbb {S}}^n_+} \sum _{i<j} |\kappa _i-\kappa _j|^2 d\mu (y) dt\le C, \end{aligned}$$

where $\kappa _i(y,t)$ is the principal curvature of radial graph at $(y,t)\in {\mathbb {S}}^n_+\times [0,\infty )$. Due to the uniform estimates from Proposition 4.5, one can show that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }|\kappa _i-\kappa _j|^2=0, \quad \forall 1\le i,j\le n. \end{aligned}$$

Therefore any convergent subsequence of $x(\cdot ,t)$ must converge to a spherical cap as $t\rightarrow +\infty$. Moreover the capillary boundary condition implies that this spherical caps intersects with the sphere at a contact angle $\theta$. Hence it should belong to the family given in Remark 4.1. Hence we have completed the proof of our main theorem. $\square$