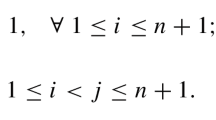Abstract
In this paper, we obtain several new intrinsic and extrinsic differentiable sphere theorems via Ricci flow. For intrinsic case, we show that a closed simply connected \(n(\ge 4)\)-dimensional Riemannian manifold M is diffeomorphic to \(\mathbb {S}^n\) if one of the following conditions holds pointwisely:
Here \(K_{max}\), \(Ric^{[k]}\) and \(R_0\) stand for the maximal sectional curvature, the k-th weak Ricci curvature and the normalized scalar curvature. For extrinsic case, i.e., when M is a closed simply connected \(n(\ge 4)\)-dimensional submanifold immersed in \(\bar{M}\). We prove that M is diffeomorphic to \(\mathbb {S}^n\) if it satisfies some curvature pinching conditions. The only involved extrinsic quantities in our pinching conditions are the maximal sectional curvature \(\bar{K}_{max}\) and the squared norm of mean curvature vector \(\left|H\right|^2\). More precisely, we show that M is diffeomorphic to \(\mathbb {S}^n\) if one of the following conditions holds:
-
(1)
\(R_0\ge \left( 1-\frac{2}{n(n-1)}\right) \bar{K}_{max} +\frac{n(n-2)}{(n-1)^2}\left|H\right|^2\), and strict inequality is achieved at some point;
-
(2)
\(\dfrac{Ric^{[2]}}{2}\ge (n-2)\bar{K}_{max}+\frac{n^2}{8}\left|H\right|^2,\) and strict inequality is achieved at some point;
-
(3)
\(\dfrac{Ric^{[2]}}{2} \ge \frac{n(n-3)}{n-2}\left( \bar{K}_{max}+\left|H\right|^2\right) ,\) and strict inequality is achieved at some point.
It is worth pointing out that, in the proof of extrinsic case, we apply suitable complex orthonormal frame and simplify the calculations considerably. We also emphasize that both of the pinching constants in (2) and (3) are optimal for \(n=4\).
Similar content being viewed by others
References
Andrews, B., Baker, C.: Mean curvature flow of pinched submanifolds to spheres. J. Differ. Geom. 85(3), 357–395 (2010)
Berger, M.: Les variétés Riemanniennes \((1/4)\)-pincées. Ann. Scuola Norm. Sup. Pisa (3) 14, 161–170 (1960)
Böhm, C., Wilking, B.: Manifolds with positive curvature operators are space forms. Ann. Math. (2) 167(3), 1079–1097 (2008)
Brendle, S.: A general convergence result for the Ricci flow in higher dimensions. Duke Math. J. 145(3), 585–601 (2008)
Brendle, S.: Einstein manifolds with nonnegative isotropic curvature are locally symmetric. Duke Math. J. 151(1), 1–21 (2010)
Brendle, S.: Ricci Flow and the Sphere Theorem, Graduate Studies in Mathematics, vol. 111. American Mathematical Society, Providence (2010)
Brendle, S., Schoen, R.: Classification of manifolds with weakly \(1/4\)-pinched curvatures. Acta Math. 200(1), 1–13 (2008)
Brendle, S., Schoen, R.: Manifolds with \(1/4\)-pinched curvature are space forms. J. Amer. Math. Soc. 22(1), 287–307 (2009)
Cheeger, J., Gromoll, D.: On the structure of complete manifolds of nonnegative curvature. Ann. Math. (2) 96, 413–443 (1972)
Costa, E., Ribeiro Jr., E.: Four-dimensional compact manifolds with nonnegative biorthogonal curvature. Mich. Math. J. 63(4), 747–761 (2014)
Ejiri, N.: Compact minimal submanifolds of a sphere with positive Ricci curvature. J. Math. Soc. Jpn. 31(2), 251–256 (1979)
Gromoll, D., Meyer, W.: On complete open manifolds of positive curvature. Ann. Math. (2) 90, 75–90 (1969)
Gu, J., Xu, H.: The sphere theorems for manifolds with positive scalar curvature. J. Differ. Geom. 92(3), 507–545 (2012)
Gu, J., Xu, H., Zhao, E.: A sharp differentiable pinching theorem for manifolds with positive scalar curvature, preprint (2017)
Hamilton, R.: Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17(2), 255–306 (1982)
Hamilton, R.: Four-manifolds with positive curvature operator. J. Differ. Geom. 24(2), 153–179 (1986)
Huisken, G.: Flow by mean curvature of convex surfaces into spheres. J. Differ. Geom. 20(1), 237–266 (1984)
Huisken, G.: Contracting convex hypersurfaces in Riemannian manifolds by their mean curvature. Invent. Math. 84(3), 463–480 (1986)
Karcher, H.: A short proof of Berger’s curvature tensor estimates. Proc. Amer. Math. Soc. 26, 642–644 (1970)
Klingenberg, W.: über Riemannsche Mannigfaltigkeiten mit positiver Krümmung. Comment. Math. Helv. 35, 47–54 (1961)
Lawson Jr., H., Simons, J.: On stable currents and their application to global problems in real and complex geometry. Ann. Math. (2) 98, 427–450 (1973)
Liu, K., Xu, H., Ye, F., Zhao, E.: Mean curvature flow of higher codimension in hyperbolic spaces. Comm. Anal. Geom. 21(3), 651–669 (2013)
Micallef, M., Moore, J.: Minimal two-spheres and the topology of manifolds with positive curvature on totally isotropic two-planes. Ann. Math. (2) 127(1), 199–227 (1988)
Micallef, M., Wang, M.: Metrics with nonnegative isotropic curvature. Duke Math. J. 72(3), 649–672 (1993)
Myers, S.: Riemannian manifolds with positive mean curvature. Duke Math. J. 8, 401–404 (1941)
Perelman, G.: Proof of the soul conjecture of Cheeger and Gromoll. J. Differ. Geom. 40(1), 209–212 (1994)
Rauch, H.: A contribution to differential geometry in the large. Ann. Math. (2) 54, 38–55 (1951)
Seshadri, H.: Manifolds with nonnegative isotropic curvature. Comm. Anal. Geom. 17(4), 621–635 (2009)
Xin, Y.: An application of integral currents to the vanishing theorems. Sci. Sin. Ser. A 27(3), 233–241 (1984)
Xu, H., Gu, J.: An optimal differentiable sphere theorem for complete manifolds. Math. Res. Lett. 17(6), 1111–1124 (2010)
Xu, H., Gu, J.: Geometric, topological and differentiable rigidity of submanifolds in space forms. Geom. Funct. Anal. 23(5), 1684–1703 (2013)
Xu, H., Gu, J.: Rigidity of Einstein manifolds with positive scalar curvature. Math. Ann. 358(1–2), 169–193 (2014)
Xu, H., Tian, L.: A differentiable sphere theorem inspired by rigidity of minimal submanifolds. Pac. J. Math. 254(2), 499–510 (2011)
Yau, S.: Selected expository works of Shing-Tung Yau with commentary. Vol. I. In: Li, Lizhen Ji Peter, Liu, Kefeng, Schoen, Richard (eds.) Advanced Lectures in Mathematics (ALM), vol. 28. International Press and Higher Education Press, Somerville and Beijing (2014)
Acknowledgements
We would like to thank Dr. Jun Sun for useful discussions and suggestions. We also want to thank the referee for his/her careful reading and useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. Jost.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is partially supported by National Natural Science Foundation of China (Grant Nos. 11601442, 11801420, 11571259, 11501470) and Fundamental Research Funds for the Central Universities (Grant Nos. 2682016CX114, 2042018kf0044).