Two dimensional solitary waves in shear flows

Abstract

In this paper we study existence and asymptotic behavior of solitary-wave solutions for the generalized Shrira equation, a two-dimensional model appearing in shear flows. The method used to show the existence of such special solutions is based on the mountain pass theorem. One of the main difficulties consists in showing the compact embedding of the energy space in the Lebesgue spaces; this is dealt with interpolation theory. Regularity and decay properties of the solitary waves are also established.

Appendix

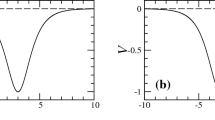
An important question concerning traveling-wave solutions one can ask is about their positivity. In this short appendix we verify that under suitable vanishing conditions at infinity, positive solitary waves do not exist. The numerical result also confirms this fact (see Figure 1).

Fig. 1

The solitary wave of (1.6) and its projection curves for $f(u)=u^2$

Proposition 4.1

(Nonexistence of positive solitary waves) Suppose that f does not change the sign. Then there is no positive solitary-wave solution $\varphi$ of (1.5) satisfying

$$\begin{aligned}&\varphi \rightarrow 0, \quad \hbox {as}\; |(x,y)|\rightarrow +\,\infty , \end{aligned}$$

(4.1)

$$\begin{aligned}&\mathscr {H}\varphi _x\rightarrow 0,\quad \hbox {as}\; |x|\rightarrow +\,\infty , \end{aligned}$$

(4.2)

$$\begin{aligned}&\mathscr {H}\varphi \rightarrow 0, \quad \hbox {as}\; |y|\rightarrow +\,\infty . \end{aligned}$$

(4.3)

Proof

It is straightforward to see that if $\varphi$ is a nontrivial solution of (1.5) satisfying (4.1)–(4.3), then

$$\begin{aligned} \int _{\mathbb {R}}\mathscr {H}\varphi (x,y)\;{d}x=0. \end{aligned}$$

(4.4)

On the other hand, $\mathscr {H}\varphi =\mathscr {H}k*f(\varphi )$, where

$$\begin{aligned} \widehat{\mathscr {H}k}(\xi ,\eta )=-\mathrm{i}\frac{\xi }{|\xi |+\xi ^2+\eta ^2}. \end{aligned}$$

By an argument similar to Lemma 3.8, there holds

$$\begin{aligned} \mathscr {H}k(x,y)=\sqrt{\pi }\int _0^{+\,\infty }t^{5/2}\mathrm{e}^{-t} \left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{3}{2}} \sin \left( \frac{3}{2}\arctan \left( \frac{t|x|}{t^2+y^2}\right) \right) \;{d}t. \end{aligned}$$

The function $\mathscr {H}k$ does not change the sign, since

$$\begin{aligned} \sin \left( \frac{3}{2}\arctan (x)\right) =\frac{\sqrt{2}}{2}\frac{(1+(1+x^2)^{1/2})^{1/2}}{(1+x^2)^{3/4}}\left( 2+(1+x^2)^{1/2}\right) >0. \end{aligned}$$

The proof then follows because if $\varphi$ is positive, $\mathscr {H}\varphi =\mathscr {H}k*f(\varphi )$ has a definite sign, contradicting (4.4). $\square$