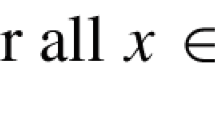Abstract
We consider the following singularly perturbed nonlinear elliptic problem
where f is of critical growth. Using the variational techniques, we construct a solution \(u_\varepsilon \) which concentrates around the saddle points of V as \(\varepsilon \rightarrow 0\).
Similar content being viewed by others
References
Ambrosetti, A., Badiale, M., Cingolani, S.: Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140, 285–300 (1997)
Ambrosetti, A., Malchiodi, A., Ni, W.-M.: Singularly perturbed elliptic equations with symmetry: existence of solutions concentrating on spheres I. Commun. Math. Phys. 235, 427–466 (2003)
Ackermann, N., Weth, T.: Multibump solutions to nonlinear periodic Schrödinger equations in a degenerate setting. Commun. Contemp. Math. 7, 269–298 (2005)
Berestycki, H., Lions, P.L.: Nonlinear scalar field equations I. Existence of a ground state. Arch. Ration. Mech. Anal. 82, 313–346 (1983)
Benci, V., Cerami, G.: Existence of positive solutions of the e quation \(-\Delta u+a(x)u=u^{\frac{N+2}{N-2}}\) in \(\mathbb{R}^N\). J. Funct. Anal. 88, 90–117 (1990)
Byeon, J., Jeanjean, L.: Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Ration. Mech. Anal. 185, 185–200 (2007)
Byeon, J., Tanaka, K.: Semi-classical standing waves for nonlinear Schrödinger equations at structurally stable critical points of the potential. J. Eur. Math. Soc. 15, 1859–1899 (2013)
Byeon, J., Tanaka, K.: Semiclassical standing waves with clustering peaks for nonlinear Schrödinger equations. Memories of the American Mathematical Society, vol. 229, no. 1076. American Mathematical Society, Providence (2014)
Byeon, J., Zhang, J., Zou, W.: Singularly perturbed nonlinear Dirichlet problems involving critical growth. Calc. Var. Partial Differ. Equ. 47, 65–85 (2013)
Chabrowski, J.: Weak Convergence Methods for Semilinear Elliptic Equations. World Scientific, Singapore (1999)
Cortá, C., Elgueta, M., Felmer, P.: Uniqueness of positive solutions of \(\Delta u+f(u)=0\) in \(\beta R^N, N\ge 3\). Arch. Ration. Mech. Anal. 142, 127–141 (1998)
d’Avenia, P., Pomponio, A., Ruiz, D.: Semiclassical states for the nonlinear Schrödinger equation on saddle points of the potential via variational methods. J. Funct. Anal. 262, 4600–4633 (2012)
Dancer, E.N.: Peak solutions without non-degeneracy conditions. J. Differ. Equ. 246, 3077–3088 (2009)
Evequoz, G., Weth, T.: Entire solutions to nonlinear scalar field equations with indefinite linear part. Adv. Nonlinear Stud. 12, 281–314 (2012)
Floer, A., Weinstein, A.: Nonspreading wave packets for the cubic Schrödinger equations with a bounded potential. J. Funct. Anal. 69, 397–408 (1986)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. The locally compact case: Part II. Ann. Inst. H. Poincaré Anal. 1, 223–283 (1984)
Li, Y.Y.: On a singularly perturbed elliptic equation. Adv. Differ. Equ. 2, 955–980 (1997)
Oh, Y.G.: Existence of semiclassical bound states of nonlinear Schrödinger equations with potentials of the class \((V)_a\). Commun. Partial Differ. Equ. 13, 1499–1519 (1988)
del Pino, M., Kowalczyk, M., Wei, J.: Concentration on curves for nonlinear Schrödinger equations. Commun. Pure Appl. Math. 60, 113–146 (2007)
del Pino, M., Felmer, P.: Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4, 121–137 (1996)
del Pino, M., Felmer, P.: Multi-peak bound states of nonlinear Schrödinger equations. Ann. Inst. H. Poincaréaire 15, 127–149 (1998)
del Pino, M., Felmer, P.: Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149, 245–265 (1997)
del Pino, M., Felmer, P.: Semi-classical states for nonlinear Schrödinger equations: a variational reduction method. Math. Ann. 324, 1–322 (2002)
Pohozaev, S.I.: On the eigenfunctions of the equation \(\Delta u+\lambda f(u)=0\). Dokl. Akad. Nauk SSSR 165, 36–39 (1965). (in Russian)
Rabinowitz, P.H.: On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43, 270–291 (1992)
Ramos, M., Wang, Z.-Q., Willem, M.: Positive Solutions for Elliptic Equations with Critical Growth in Unbounded Domains, Calculus of Variations and Differential Equations. Chapman & Hall/CRC Press, Boca Raton (2000)
Wang, X.: On concentration of positive bound states of nonlinear Schrödinger equations. Commun. Math. Phys. 153, 229–244 (2003)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Zhang, J., Chen, Z., Zou, W.: Standing waves for nonlinear Schrödinger equations involving critical growth. J. Lond. Math. Soc. 90, 827–844 (2014)
Zhang, J., Zou, W.: A Berestycki–Lions theorem revisited. Commun. Contemp. Math. 14, 1250033 (2012)
Acknowledgments
The authors are deeply grateful to Professor Zhi-Qiang Wang for his kind support and fruitful discussion. They also would like to express their sincere gratitude to the anonymous referee for his/her careful reading and valuable suggestions. J. Zhang also thanks Dr. Zhijie Chen for his valuable comment on the proof of Lemma 4.7.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Rabinowitz.
Supported by the China Postdoctoral Science Foundation (2013M530868), NSFC (11025106, 11371212, 11271386) and the Both-Side Tsinghua Fund.
Appendix: A splitting Lemma
Appendix: A splitting Lemma
This section is devoted to the proof of Lemma 4.7. The proof is similar to that in [14]. A similar result also can be found in [3]. However, in [3, 14], only the subcritical case was considered and the decay property of u at infinity was required, i.e., \(u(x)\rightarrow 0\) as \(|x|\rightarrow \infty \). In this appendix, the nonlinear term f may involve the critical growth and the decay property of u at infinity is removed.
Proof of Lemma 4.7
It suffices to prove that
where \(f_1\) is given in Sect. 2.
In the following, we denote by C the positive constants, which are independent of \(\varepsilon ,k\) and possibly different. For any fixed \(\varepsilon >0\), by \((f_1)\), we can choose \(s_0=s_0(\varepsilon )\in (0,1)\) such that \(|f_1(t)|\le \varepsilon |t|\) for \(|t|\le 2s_0\). By \((f_2)\), choosing \(s_1=s_1(\varepsilon )>2\) such that \(|f_1(t)|\le \varepsilon |t|^{2^{*}-1}\) for \(|t|\ge s_1-1\). From the continuity of f, there exists \(\delta =\delta (\varepsilon )\in (0,s_0)\) such that \(|f_1(t_1)-f_1(t_2)|\le s_0\varepsilon \) for \(|t_1-t_2|\le \delta , |t_1|,|t_2|\le s_1+1\). Moreover, by \((f_2)\), there exists \(c(\varepsilon )>0\) such that \(|f_1(t)|\le c(\varepsilon )|t|+\varepsilon |t|^{2^{*}-1}\) for \(t\in \mathbb R\). Then there exists \(R=R(\varepsilon )>0\) such that \( \int _{\mathbb R^N{\setminus } B(0,R)}|f_1(u)\phi |\le C\varepsilon \Vert \phi \Vert \). Setting \(A_k:=\{x\in \mathbb R^N{\setminus } B(0,R): |u_k(x)|\le s_0\}\), then
Let \(B_k:=\{x\in \mathbb R^N{\setminus } B(0,R): |u_k(x)|\ge s_1\}\), then
Setting \(C_k:=\{x\in \mathbb R^N{\setminus } B(0,R): s_0\le |u_k(x)|\le s_1\}\), by \(u_k\in H^1(\mathbb R^N)\), we know that \(|C_k|<\infty \). Then
Thus,
Noting that for all k,
and
By \(u\in H^1(\mathbb R^N)\), we get that \(|(\mathbb R^N{\setminus }B(0,R))\cap \{u\ge \delta \}|\rightarrow 0\) as \(R\rightarrow \infty \). Then we can choose \(R=R(\varepsilon )\) large enough, such that
So,
Thus,
Finally, since \(u_k\rightarrow u\) weakly in \(H^1(\mathbb R^N)\), up to a subsequence, \(u_k\rightarrow u\) strongly in \(L^2(B(0,R))\) and there exists \(\omega \in L^2(B(0,R))\) such that \(|u_k(x)|,|u(x)|\le |\omega (x)|\) a.e. \(x\in B(0,R)\). Then it is easy to check that
for k large. Let \(D_k:=\{x\in B(0,R): |u_k(x)-u(x)|\ge 1\}\), then
By \(u_k\rightarrow u\) a.e. \(x\in B(0,R)\), we get that \(|D_k|\rightarrow 0\) as \(k\rightarrow \infty \). Hence,
Since \(u\in H^1(\mathbb R^N)\), we know \(|\{u\ge L\}|\rightarrow 0\) as \(L\rightarrow \infty \), then there exists \(L=L(\varepsilon )>0\) such that for all k,
On the other hand, by the dominated convergence theorem,
as \(k\rightarrow \infty \). So,
for k large enough. Thus,
Then
Therefore,
for k large enough. \(\square \)
Rights and permissions
About this article
Cite this article
Zhang, J., Zou, W. Solutions concentrating around the saddle points of the potential for critical Schrödinger equations. Calc. Var. 54, 4119–4142 (2015). https://doi.org/10.1007/s00526-015-0933-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-015-0933-z