1 Introduction

Surrogate models play an important role in product development, optimization problems, real-time processing, or sub-modeling. In many cases, surrogate models are required to replace simulations due to their high computational costs. Surrogate models can have different purposes, such as:

  • Model integral values of a system for variable parameters. Examples are lift and drag coefficients of an airfoil under variable angles of attack or fuel consumption of a vehicle for variable load weights.

  • Represent spatial or spatio-temporal physical fields of a system for variable parameters of the parameterized geometry. One example is the flow field around an airfoil (geometry) under variable angles of attack (parameter). The above mentioned integral values can than be retrieved from the flow field, if needed. A second example is the stress field of a loaded beam for variable beam lengths.

Such models are useful for analyses and optimization processes of technical systems. A traditional surrogate model can be built via a fit to sample points that can either be simulated or measured. Prevalent models include linear regression, Bayesian models, random forests, support vector machines (SVM), swarm intelligence, and neural networks (NN), among others [1,2,3].

According to Pinkus’ approximation theorem, a single hidden layer NN with enough neurons can approximate any function and its derivatives [4]. This feature makes NN suitable for surrogate modeling as it avoids limitations in regression accuracy to complex functions that are related to other surrogate methods, such as linear regression. Consequently, several investigations showed a superiority of NNs when compared to other regression models [5,6,7]. A vast variety of different architectures and algorithms of NNs have been developed and applied, comprising feedforward NNs, recurrent NNs, convolutional NNs (CNNs), reinforcement learning (RL), long short-term memory (LSTM), or generative adversarial networks (GANs), among others [8,9,10]. A drawback of NNs is the need for large, high-quality datasets in the training process [11].

Recently, physics-informed neural networks (PINNs) have become a focus of research activities. A PINN is a NN that is trained to respect given laws of physics, typically partial differential equations (PDEs) as well as boundary conditions (BCs). In the training process, PINNs create sample data by solving the PDEs subject to the given BCs. Hence, a lack of simulation or measurement data can be compensated by training the satisfaction of the PDEs. PINNs are not restrained to specific networks and any suitable architecture might be applied. However, a governing equation as well as a series of training points containing discrete values of the equations variables is required. Hence, the physics-informed approach can be understood as an unsupervised method to provide additional training information by penalizing any violation of the governing equations at specific points with a corresponding loss without requiring a priori knowledge of the correct solution.

In the process of surrogate modeling, multiple simulations or measurements have to be carried out for different system settings. Hence, PINNs could be deployed to significantly decrease the costs of experiments or simulations.

In the present study, we investigated the capability of PINNs to yield surrogate models of parameterized geometries. For our study, we focused on the field of fluid dynamics. In computational fluid dynamics (CFD), complex computations such as a direct numerical simulations (DNS) or a large eddy simulations (LES), are often not appropriate due to their high computational costs and complex model set-ups. Consequently, RANS simulations are favorable and frequently applied. Multidimensional surrogate models based on PINNs could be trained to predict the Reynolds-averaged solutions and reduce the amount of required RANS computations, whereby interpolations and extrapolations could be predicted by the NN.

In this work, we contribute to the question of how multidimensional surrogate models of Reynolds-averaged flows could be generated using a PINN and how accurately the RANS flow field is then predicted. As an example, we present a PINN-based surrogate model of the DU99W350 airfoil at a high Reynolds number of \(1\times 10^{5}\) using the Python library DeepXDE [12]. To investigate the applicability of PINNs for complex fluid dynamics, the model was designed to predict the developing flow separation on the suction surface. In the training process, the RANS equations were solved. We evaluate the accuracy of the model when compared to CFD simulations and further discuss the limitations and potential improvements of the presented PINN method. The main contributions are:

  1. 1.

    We deployed a feedforward PINN that was designed to take the two-dimensional coordinates as well as the angle of attack as input parameters and predicted the mean pressure and velocity fields around the airfoil.

  2. 2.

    We present and compare an effective method to generate the training points for the geometry that was parameterized by the angle of attack. The training points were obtained from CFD grids.

  3. 3.

    We tested the standard k-\(\omega \) model by Wilcox [13] and a pseudo-Reynolds stress turbulence modeling approach [14, 15], showing that the pseudo-Reynolds stress approach outperformed the traditional turbulence model in terms of accuracy.

  4. 4.

    We show that the scaling of the problem had a significant effect on the training success.

  5. 5.

    The investigation demonstrated that the presented PINN method was capable of accurately learn the flow separation with respect to the angle of attack.

The scope of this work was to investigate the capability of a simple feed-forward network architecture to serve as a surrogate model of a Reynolds-averaged flow around a parameterized geometry at an elevated Reynolds number.

2 Related work

The concept of PINNs has been first described by Lagaris et al. [16] who showed the applicability of PINNs to solve several ordinary differential equations (ODEs), coupled ODEs, and PDEs. Raissi et al. [17,18,19] solved the Burgers equation, the Schrödinger equation, and the Allen–Cahn equation with a PINN for time dependent one-dimensional problems. The results exhibited excellent agreement between the PINN and the exact solution. The publications presented above demonstrated the suitability of FNN PINNs to solve PDEs.

In addition to FNNs, various other physics-informed methods such as CNNs, SVMs, RL, or LSTM have demonstrated efficacy in accurately representing the behavior of complex physical systems [20,21,22,23,24].

PINNs were also applied to the field of fluid dynamics to solve the Navier–Stokes (NS) equations. Here, investigations covered the application of feedforward NNs (FNNs) to two- and three dimensional problems [25], near wall flows [26], thermal flows [27, 28], cavitation flows [29], reconstruction of incomplete data [30, 31], boundary condition enforcement and adaptive activation functions [32], and different formulations of the Navier–Stokes equations [33], among others.

In most publications, PINNs were used to predict flow fields for Reynolds numbers below 300 [25, 28, 32,33,34]. However, many technical problems are subject to high Reynolds numbers and corresponding turbulent flows. Turbulent flows result in highly complex flow fields in both space and time. Hence, solving the Navier-Stokes equations with a PINN for highly turbulent flows can be a challenging task. For many applications, only stationary information is required. Therefore, PINNs to predict flows by solving the Reynolds-averaged Navier–Stokes (RANS) equations must incorporate a turbulence model. A first approach has been done by Hennigh et al. [35] who applied the mixing length turbulence model. Eivazi et al. [14] trained a PINN to satisfy the RANS equations without a transport equation based model. Xu et al. [36] used a similar approach and trained a PINN to predict the turbulent viscosity without any imposed equation and used it to explore the missing flow data inside of a finite area. Pioch et al. [15] applied the mixing length model, the k-\(\omega \) model, an equation-free pseudo-Reynolds stress model, and an equation-free \(\nu _{t}\) model to a backward facing step flow.

In the research presented above, PINNs were trained to predict two- or three-dimensional flow solutions for a single geometry. Wandel et al. [37] presented a convolutional PINN that takes the vector potential as an input. The model was trained with different 3D shapes and they reported plausible flow fields for geometries which were not contained in the training dataset. Hennigh et al. [35] presented the NVIDIA SimNet framework. They applied the framework on the NVSwitch with a parameterized geometry and used a modified Fourier feature PINN to find the optimal parameter configuration. Arthurs and King [38] presented an active learning algorithm and trained a PINN to predict the flow and pressure field in a tube for two shape parameters and reported low errors. These investigations demonstrated the general suitability of PINNs as surrogate models for flows around variable geometries.

However, the literature on multidimensional surrogate models of variable geometries remains sparse. Hence, more work is needed to further assess the capabilities and limitations of PINNs as surrogate models for variable geometries. Furthermore, the literature reveals a lack of studies covering complete flow fields at elevated Reynolds numbers such as flows around airfoils. The present investigation is a combined contribution to both of these open questions.

3 Set up and reference flow field

As an applied example, we used the DU99W350 airfoil positioned inside a channel. This airfoil is employed for blades of wind turbines, such as the NREL 5 MW turbine [39]. We chose this example because the presented surrogate modeling technique could be employed in real-time steering algorithms, as well as in aerodynamic optimization problems. Besides, this example was suitable to investigate the quality of predicted realistic flow fields. The channel had a height and a width of 1 m, and the chord length c of the airfoil was 0.2 m. For variations of the angle of attack (AoA), the airfoil was rotated about the leading edge. Figure 1 schematically illustrates the geometry as well as the simulated mean flow field around the airfoil for an angle of attack of 15.0\(^\circ \). As seen in the figure, the flow featured a stagnation point at the leading edge of the airfoil, a boundary layer around the airfoil, multiple regions of high velocity gradients, and a separated flow on the suction surface.

Fig. 1
figure 1

Features of the simulated reference flow field around the DU99W350 airfoil. 1: Stagnation point; 2: high velocity region on the suction surface; 3: boundary layer on the airfoil surface; 4: separated shear layer; 5: wake and recirculative vortices; 6: constant free flow; 7: high velocity region on the pressure surface

Full size image

4 Methodology

4.1 PINN method

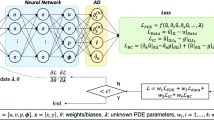
To yield the multidimensional surrogate model, a feedforward NN was trained to predict the Reynolds-averaged velocity and pressure field. The input layer of the NN consisted of three neurons that represent the three input coordinates x, y, and angle of attack \(\alpha \). When the neural network is trained without incorporating any turbulence model, the output layer comprises three neurons and displays the Reynolds-averaged predictions of velocity-components u, v, and pressure p. The PINN then reads:

$$\begin{aligned} NN_{\theta }\begin{pmatrix}x\\ y\\ \alpha \end{pmatrix}=\begin{pmatrix}u\\ v\\ p\end{pmatrix} \end{aligned}$$
(1)

where \(\theta \) are the trainable parameters (weights and biases) of the NN. Figure 2 shows the corresponding architecture. As sketched, the output of the NN was fed into three different losses that build a so-called composed loss function.

Fig. 2
figure 2

Architecture of the deployed neural network

Full size image

In the composed loss function, losses for boundary conditions, simulated training values, and a system of partial differential equations (PDEs) were added. The composed loss function \(\mathcal {L}\) reads:

$$\begin{aligned} \mathcal {L}(\theta ) = \mathcal {L}_{b}(\theta ) + \mathcal {L}_{d}(\theta ) + \mathcal {L}_{e}(\theta ) \end{aligned}$$
(2)

with the adjustable network weights and biases \(\theta \), the loss on the boundary conditions \(\mathcal {L}_{b}\), the loss for the training data \(\mathcal {L}_{d}\), and the loss for the partial differential equations \(\mathcal {L}_{e}\). The individual loss terms were calculated using the mean squared error:

$$\begin{aligned} \mathcal {L}_{b}= & {} \frac{1}{N_{b}} \sum _{n=1}^{N_{b}} |\textbf{U}_{b}^{n}-\tilde{\textbf{U}}_{b}^{n}|^{2} \end{aligned}$$
(3)
$$\begin{aligned} \mathcal {L}_{d}= & {} \frac{1}{N_{d}} \sum _{n=1}^{N_{d}} |\textbf{U}_{d}^{n}-\tilde{\textbf{U}}_{d}^{n}|^{2} \end{aligned}$$
(4)
$$\begin{aligned} \mathcal {L}_{e}= & {} \frac{1}{N_{e}} \sum _{k=1}^{3} \sum _{n=1}^{N_{e}} |\varepsilon _{k}^{n}|^{2} \end{aligned}$$
(5)

where \(N_{b}\), \(N_{d}\), and \(N_{e}\) represent the number of points for which the boundary conditions, labeled training data, and PDEs are trained. \(\textbf{U}_{b}^{n} = [u_{b}^{n}, v_{b}^{n}]\) and \(\textbf{U}_{d}^{n} = [u_{d}^{n}, v_{d}^{n}, p_{d}^{n}]\) are the given data for point n on the boundaries and for the labeled data coordinates, respectively. \(\tilde{\textbf{U}}_{b}^{n}\) and \(\tilde{\textbf{U}}_{d}^{n}\) represent the output of the PINN at the corresponding points and \(\varepsilon _{k}^{n}\) is the residual of the kth equation at point n.

4.2 Governing equations

In our work, the continuity equation and the two-dimensional Reynolds-averaged Navier–Stokes equations for an incompressible fluid were used as PDEs. The corresponding residuals read:

$$\begin{aligned} \mathcal {\varepsilon }_{k=1}= \frac{\partial \overline{u_{i}}}{\partial x_{i}} \end{aligned}$$
(6)
$$\begin{aligned} \mathcal {\varepsilon }_{k=2,3}= \overline{u_{j}}\frac{\partial \overline{u_{i}}}{\partial x_{j}} + \overline{u'_{j}\frac{\partial u'_{i}}{\partial x_{j}}} + \frac{1}{\rho }\frac{\partial \overline{p}}{\partial x_{i}} - \nu \frac{\partial ^2 \overline{u_{i}}}{\partial x_{j}\partial x_{j}} \end{aligned}$$
(7)

with Reynolds-averaged velocities and pressure \(\overline{u_{i}}\), \(\overline{u_{j}}\), and \(\overline{p}\), constant density \(\rho \), and constant kinematic viscosity \(\nu \). The RANS equations contain the Reynolds stress terms:

$$\begin{aligned} \frac{\partial \tau _{ij}'}{\partial x_{j}} = \overline{u'_{j}\frac{\partial u'_{i}}{\partial x_{j}}} \end{aligned}$$
(8)

Here, \(\tau _{ij}'\) represents the Reynolds stresses. For traditional turbulence modeling as applied in computational fluid dynamics (CFD), the Reynolds stresses are estimated using the Boussinesq hypothesis:

$$\begin{aligned} \tau _{ij}' = -\overline{u_{i}'u_{j}'}= \nu _{t}\left(\frac{\partial \overline{u_{i}}}{\partial x_{j}}+\frac{\partial \overline{u_{j}}}{\partial x_{i}}\right)-\frac{2}{3}k\delta _{ij} \end{aligned}$$
(9)

where k is the turbulent kinetic energy, \(\delta _{ij}\) is the Kronecker delta, and \(\nu _t\) is the turbulent viscosity. This approach is based on the gradient diffusion hypothesis which states that the turbulent transport is aligned with the negative gradient of the mean flow. The isotropic turbulent viscosity \(\nu _t\) then serves as a diffusion coefficient, supposing an analogy between viscous stresses and turbulent stresses.

In this work, we considered two different turbulence-modeling approaches. The first model was the standard k-\(\omega \) model of Wilcox [13]. This model is frequently applied for CFD calculations. For the k-\(\omega \) model, the turbulent viscosity is calculated using:

$$\begin{aligned} \nu _{t}=\frac{k}{\omega } \end{aligned}$$
(10)

with the specific dissipation rate \(\omega \). The 2D stationary equations for k and \(\omega \) read:

$$\begin{aligned} \overline{u_{j}}\frac{\partial k}{\partial x_{j}} = \tau _{ij}'\frac{\partial \overline{u_{i}}}{\partial x_{j}} -\beta ^{*}k\omega + \frac{\partial }{\partial x_{j}}\Bigl ((\nu +\sigma ^{*}\nu _{t})\frac{\partial k}{\partial x_{j}}\Bigr ) \end{aligned}$$
(11)
$$\begin{aligned} \overline{u_{j}}\frac{\partial \omega }{\partial x_{j}} = \alpha \frac{k}{\omega }\tau _{ij}'\frac{\partial \overline{u_{i}}}{\partial x_{j}} -\beta \omega ^2 + \frac{\partial }{\partial x_{j}}\Bigl ((\nu +\sigma \nu _{t})\frac{\partial \omega }{\partial x_{j}}\Bigr ) \end{aligned}$$
(12)

with \(\beta ^{*}=9/100,\,\sigma ^{*}=\sigma =0.5,\,\alpha =5/9,\,\beta = 3/40\), as recommended by Wilcox [13]. For the composed loss function, the transport equations for k and \(\omega \) are to be included in the system of PDEs. The corresponding PINN reads:

$$\begin{aligned} NN_{\theta }\begin{pmatrix}x\\ y\\ \alpha \end{pmatrix}= \begin{pmatrix}u\\ v\\ p\\ k\\ \omega \end{pmatrix} \end{aligned}$$
(13)

The second model we considered was the pseudo-Reynolds stress model by Eivazi et al. [14] and Pioch et al. [15]. For this model, the Reynolds stress terms are calculated without specific modeling, using only two pseudo-turbulent velocity fluctuations, \(u_{p}'\) and \(v_{p}'\):

$$\begin{aligned} \frac{\partial \tau _{ij}'}{\partial x_{j}} = u_{j_p}'\frac{\partial u_{i_p}'}{\partial x_{j}} \end{aligned}$$
(14)

With this approach, the training process of the NN was penalized to learn an averaged flow field as well as pseudo-Reynolds variables, which together satisfied the RANS equations. The corresponding PINN reads:

$$\begin{aligned} NN_{\theta }\begin{pmatrix}x\\ y\\ \alpha \end{pmatrix}=\begin{pmatrix}u\\ v\\ p\\ u_{p}'\\ v_{p}'\end{pmatrix} \end{aligned}$$
(15)

4.3 Set up

To calculate the losses associated with the boundary conditions, a slip wall condition was defined for the upper and lower channel walls. For the airfoil surface, we used a no slip wall condition. At the left boundary of the channel, we specified a velocity inlet boundary condition. No pressure outlet condition was defined.

Setup and training of the multidimensional PINN was done with a custom Python code using the TensorFlow-based library DeepXDE [12]. The model was trained with the described RANS equations and boundary conditions as well as with simulated data. We used a PointSetBC to train the labeled reference data and anchor points to train the PDEs.

To define the training points inside the multidimensional training domain, the coordinates of two different CFD grids were used. The grids were generated for different AoAs on a hybrid mesh consisting of unstructured triangular finite elements and layers of quadrilateral elements to account for the boundary layer. The mesh featured 15 inflation layers with a growth rate of 1.1, a maximal base size of 0.01 m with a maximal growth rate of 1.08, as well as a grid refinement on the airfoil surface with a maximum cell size of 0.002 m. To train the PINN, a batch of random data points was drawn from the complete labeled dataset ahead of the training process. The coordinates for the training of the PDEs were derived from a coarser grid without further selection. Some illustrations concerning the training coordinates are given in the Appendix. The advantage of this method was that the training points were concentrated in important regions, such as the boundary layer. The training of the PDEs as well as the boundary conditions was conducted for AoAs of 10.0\(^{\circ }\), 12.5\(^{\circ }\), 15.0\(^{\circ }\), and 17.5\(^{\circ }\). Labeled training data were considered for AoAs of 10.0\(^\circ \) and 15.0\(^\circ \) only.

Figure 3 illustrates the applied boundary conditions as well as the considered training data. As seen, the training domain was constructed as a multidimensional hypercube, and the training of the PINN was conducted at discrete AoAs which represent slices of the hypercube. This procedure facilitated the generation of training coordinates for specific AoAs using a CFD meshing algorithm. The PINN could then be trained on these coordinates using the PointSet boundary conditions for the labeled data and the anchor points for the PDEs. This method was applied to evade the challenging automatic generation of appropriately positioned training coordinates for n-dimensional problems. In this case, it would be necessary to define the n-dimensional geometry as well as a suitable training point coordinate generator. In contrast, the method applied here allowed a point generation using available CFD meshers to discretize the two-dimensional geometries for different AoAs, which were obtained using conventional computer aided design (CAD) software. This method could also be applied to problems of higher dimensionality. If we assume that a three-dimensional geometry was to be trained for one parameter in the fourth dimension, such as AoA, then the training points could as well be generated for the geometry at discrete AoAs using a CFD meshing algorithm.

Fig. 3
figure 3

Illustration of the multidimensional hypercube training domain and the corresponding boundary conditions and training data

Full size image

For the training of the neural network, the loss terms were weighted using:

$$\begin{aligned} \mathcal {L} = \lambda _{b} \mathcal {L}_{b} + \lambda _{d} \mathcal {L}_{d} + \lambda _{e} \mathcal {L}_{e} \end{aligned}$$
(16)

with \(\lambda _{b}\), \(\lambda _{d}\), and \(\lambda _{e}\) as constant weight factors for boundary conditions, labeled training data, and PDEs, respectively. A data weight factor of \(\lambda _{d}=100\) was chosen while \(\lambda _{b}\) and \(\lambda _{e}\) were set to unity to emphasize learning of the reference data. The higher data loss weight was selected to assist the network in finding the correct flow field during training and achieve more accurate predictions. Figure 4 illustrates the effect of \(\lambda _{d}\) on the final prediction accuracy. As seen, the global error was at a maximum for \(\lambda _{d}=1\) and decreased with increasing \(\lambda _{d}\). A data loss of \(\lambda _{d}=100\) yielded a minimal overall error and, hence, was selected for our study.

Fig. 4
figure 4

Effect of data loss weight factor on the overall normalized mean squared error

Full size image

In the training procedure, the weights and biases \(\theta \)Afterwards of the NN were adjusted using the optimizers Adam and L-BFGS to minimize the weighted composed loss function. The model was trained for 30,000 epochs using the Adam optimizer. , the model was further trained with the L-BFGS optimizer under the predefined default settings. In the Appendix, supplementary material concerning the corresponding training algorithm as well as the achieved losses for PDEs, BCs, and labeled data is given. Table 1 lists the relevant training parameters.

Table 1 PINN training parameters
Full size table

We trained a NN consisting of five hidden layers with 128 neurons each. The training was repeated ten times to account for the random initialization of the weights and biases. For further evaluation, the model with the lowest normalized mean squared error (NMSE) was selected.

The initial selection of this architecture was based on a study of Harmening et al. [40] who explored physics-informed deep learning of a similar flow. To further evaluate the network architecture for the present study, a sensitivity analysis was conducted for the flow around the airfoil. For the selection of the architecture, prediction accuracy and training time were considered. As the scope of a surrogate model is to replace simulations, the computational time also is a relevant factor. Figure 5 displays the results of the architecture study. As seen, the error generally decreased with increasing numbers of hidden layers. The lowest errors were obtained by the models featuring five and six hidden layers with 128 neurons each. The model with five hidden layers achieved an overall NMSE of 0.031 while the model featuring six layers achieved an error of 0.026. However, the computational time as well as the required memory distinctly increased with the number of hidden layers. Hence, the architecture of five hidden layers with 128 neurons each was selected for the present study as it featured accurate predictions, as reported in Sect. 6, accompanied by a significantly lower training time. Note that the models featuring 160 neurons per hidden layer achieved the greatest NMSEs values. This was because the L-BFGS solver could not reach a minimum for this configuration and automatically stopped after a limited number of iterations. Consequently, the total computational time was lower for these models.

Fig. 5
figure 5

Results of the sensitivity analysis concerning the network architecture. Left: normalized mean squared error, right: computational time

Full size image

4.4 Dataset

To obtain the labeled training data, two-dimensional simulations using the k-\(\omega \) model were carried out with Comsol Multiphysics 5.6. In the Appendix, detailed information on the numerical set up and the verification of the CFD model are presented. The dataset contained the velocity values as well as the pressure values. The obtained pressure values were downscaled by a factor of \(1\times 10^3\) prior to the training of the PINN.

Three different methods of data extraction were compared in a sensitivity analysis to identify the optimal sampling strategy. For the first method, the data points were randomly drawn from a uniform grid. For the second method, the data points were randomly positioned along several vertical and horizontal lines. For the third method, the data points were randomly drawn from the CFD grid that featured a refinement close to the airfoil surface. Figure 6 illustrates the different training point positioning strategies applied in the sensitivity analysis.

Fig. 6
figure 6

Exemplary illustration of the randomly drawn training point coordinates of the labeled data at an AoA of 15.0\(^{\circ }\). Left: points randomly drawn from a uniform grid; middle: points uniformly placed along several vertical and horizontal lines; right: points randomly drawn from the coordinates of a CFD grid

Full size image

5 Sensitivity analyzes

We performed several preliminary sensitivity analyzes which are presented in this section. For these investigations, we limited the training to an AoA of 15.0\(^{\circ }\). The number of training points \(n_{d}\), \(n_{b}+n_{d}\), and \(n_{e}\) were 800, 1600, and 1558, respectively. The purpose was to identify important training settings and to evaluate the accuracy of the corresponding predictions. We evaluated effects of the Reynolds number and the corresponding scaling method, and the amount and distribution of training data, and we compared the results based on the k-\(\omega \) model and the pseudo-Reynolds stress model.

For the investigations concerning the Reynolds numbers, we tested the accuracy of the training for \(\mathrm {Re_{c} \in \{1\times 10^{2}, 1\times 10^{3}, 1\times 10^{4}, 1\times 10^{5}, 1\times 10^{6}\}}\). These Reynolds numbers were obtained following two different procedures. For the first approach, a fluid with a density \(\rho \) of 1000 \(\mathrm {kg/m^{3}}\) and a dynamic viscosity \(\mu \) of 0.001 \(\mathrm {kgm^{-1}s^{-1}}\) was defined. The inlet velocity u was then varied between and 0.0005 m/s and 5.0 m/s. For the second approach, the inlet velocity was set to 1.0 m/s and the viscosity was varied between 0.2 and 0.0002 \(\mathrm {kgm^{-1}s^{-1}}\). Figure 7 presents the results of the analysis using logarithmic box plots. Here, a box represents the interquartile range, extending from the first quartile to the third quartile of the evaluated relative error. The red line identifies the median value, and the whiskers range up to one and a half times the interquartile value. The training runs with different inlet velocities exhibited severe deviations from the reference solutions at lower Reynolds numbers. The training using a variable viscosity showed excellent agreement between the RANS predictions and the reference data over the entire range of Reynolds numbers. However, the absolute error grew non-linearly with the associated Reynolds number. This finding agreed with the results of Sun et al. [32] who, however, covered lower Reynolds numbers. These results demonstrate the necessity for an appropriate scaling of the investigated problem. For a successful training, input and output dimensions of the neural net needed to match. This was also found by Laubscher and Rousseau [28] who trained the non-dimensional Navier–Stokes equations.

Fig. 7
figure 7

Results of the sensitivity analysis concerning the training accuracy for different Reynolds numbers. The relative deviations are presented on a logarithmic scale

Full size image

For the investigation concerning the amount of labeled training data, we used different numbers \(n_{d}\) of training points: \(n_{d}~\mathrm { \in \{100, 200, 400, 800, 1600\}}\). The total number of points \(n_{b}+n_{d}\) on the boundaries and drawn from the labeled dataset was consequently set to \(n_{b}+n_{d}~\mathrm { \in \{200, 400, 800, 1600, 3200\}}\). Figure 8 exhibits the corresponding results. As illustrated, the accuracy positively correlated with the amount of training data. This finding emphasizes the requirement of introducing enough labeled training data to successfully train the PINN and is in agreement with the observations of Pioch et al. [15]. As \(n_{d} > 800\), the reduction of the error stagnated. In the subsequent analysis, \(n_{d}\) was, consequently, set to 800 for every trained AoA that was supplied with labeled training data.

Fig. 8
figure 8

Results of the sensitivity analysis concerning the amount of labeled training data

Full size image

In a third step, a comparison between three different labeled training data sampling strategies was performed. For this analysis, the accuracy obtained using 800 randomly selected coordinates from a CFD grid as well as from a uniform grid with a spacing of 0.005 m was compared to a distribution of training data along several vertical and horizontal lines. The vertical lines were positioned at \(x~\mathrm { \in \{0.21, 0.28, 0.35, 0.42\}}\) and the horizontal lines were positioned at \(y~\mathrm { \in \{0.485, 0.515, 0.545, 0.575\}}\). The number of points \(n_{d}\) on the lines was 767. The extraction of data from a CFD grid is a simple method to set a higher density of training points in regions such as the boundary layer. The equidistant randomized method represents a simple method frequently applied for PINNs. The distribution of training points along several lines is an additional method suitable for sparse datasets obtained from measurements or simulations. Some illustrations concerning the training coordinates are given in the Appendix. Figure 9 shows the results of this analysis. From these results it is evident that the randomly selected training data drawn from a CFD grid outperformed the other approaches.

Fig. 9
figure 9

Results of the sensitivity analysis concerning the distribution method of labeled training data

Full size image

To assess the effect of different turbulence models, we compared the standard k-\(\omega \) model and the pseudo-Reynolds stress model, as described above. Figure 10 illustrates the obtained predictions. The pseudo-Reynolds stress model exhibited a favorable agreement with the reference CFD data, while the predictions obtained with the k-\(\omega \) model were subject to significant deviations. This result demonstrates the importance of an appropriate turbulence modeling approach. A potential explanation for the different outcomes of the two models is documented in Sects. 6.6 and 6.7.

Fig. 10
figure 10

Results of the sensitivity analysis concerning different turbulence models. The absolute deviations are presented on a logarithmic scale

Full size image

As the described investigations revealed the superiority of a scaling using a variable viscosity, a random distribution of data points drawn from a CFD grid, the pseudo-Reynolds stress model, as well as the requirement to set at least 800 points of labeled training data per AoA into the domain, the training of the multidimensional surrogate model for variable angles of attack was set up accordingly.

We further tested the application of a Fourier-feature NN as well as different weighting factors \(\lambda _{b}\), \(\lambda _{d}\), and \(\lambda _{r}\). However, these investigations did not show significant effects on improving the performance and, hence, are not covered here.

6 Results and discussion

In this section, the results of the multidimensional training for the PINN predicting the two-dimensional flow field for variable AoAs are presented. We first show the results at an AoA of 15.0\(^{\circ }\). At this angle, labeled training data were provided during the training. Subsequently, the capability of the PINN to interpolate and to extrapolate is evaluated for AoAs of 12.5\(^{\circ }\) and 17.5\(^{\circ }\). In the following, we discuss the accuracy of the results as well as challenges and potential future improvements.

6.1 Prediction at an AoA of 15.0\(^{\circ }\)

Figure 11 presents the results of the PINN in comparison with the reference data for an AoA of 15.0\(^{\circ }\). The prediction accounted for all relevant flow features and accurately depicted the flow separation as well as the high speed regions. Mean deviations of axial velocities between PINN and CFD results were \(\mathrm {3.8\times 10^{-3}}\) m/s which represents 0.38% of the reference inlet velocity. The highest errors were observed to occur at the leading edge of the airfoil, in the stagnation point region, and in the separated shear layer. For the AoA of 15.0\(^{\circ }\), 800 labeled training points were provided during training. The accurate prediction of the flow fields proves that the PINN method successfully learned the reference data and was capable to interpolate between the data points using the physics-informed approach.

Fig. 11
figure 11

Results and absolute error of the axial velocity around the DU99W350 airfoil at an angle of attack of 15.0\(^{\circ }\) using a PINN in comparison with the reference data. Note that for this angle of attack, reference data were provided for the training of the PINN

Full size image

6.2 Interpolation at an AoA of 12.5\(^{\circ }\)

Figure 12 exhibits a comparison of the PINN predictions with the CFD results for an AoA of 12.5\(^{\circ }\). At this angle, since no labeled data were provided during the training, the predictions represent an interpolation. The PINN correctly captured the low separation, which was less pronounced than at an AoA of 15.0\(^{\circ }\). Furthermore, all relevant flow features were predicted. The mean deviation between PINN and CFD based axial velocities was \(\mathrm {3.7\times 10^{-3}}\) m/s which represents 0.37% of the reference inlet velocity.

Fig. 12
figure 12

Results and absolute error of velocity and pressure around the DU99W350 airfoil at an angle of attack of 12.5\(^{\circ }\) using a PINN in comparison with the reference data. Note that for this angle of attack, no reference data were provided for the training of the PINN

Full size image

Figure 13 presents an evaluation of the accuracy along several vertical lines positioned on the suction surface of the airfoil. The predicted separating flow in the boundary layer agreed favorably with the reference data. The absolute deviation between PINN and CFD was mostly below 0.02 m/s, which represents 2% of the reference inlet velocity.

Fig. 13
figure 13

Results and residual of the axial velocity on the suction surface of the DU99W350 airfoil at an angle of attack of 12.5\(^{\circ }\) using a PINN in comparison with the reference data. Left: axial velocity; right: residual between PINN and CFD results. Note that for this angle of attack, no reference data were provided for the training of the PINN

Full size image

For the AoA of 12.5\(^{\circ }\), zero labeled training points were provided during training. However, the progressively separated flow field could still be favorably learned by the FNN. Hence, a successful interpolation between the AoAs of 10.0\(^{\circ }\) and 15.0\(^{\circ }\) for that labeled data were provided was obtained. The velocity and pressure values were learned due to the physics-informed learning at the training points \(n_{e}\).

6.3 Extrapolation at an AoA of 17.5\(^{\circ }\)

Figure 14 compares the results at an AoA of 17.5\(^{\circ }\). This represents an extrapolation of the PINN as the provided labeled training data were restricted to lower AoAs. The predictions featured the recirculating flux associated with the separation, the high speed regions, the stagnation regions, as well as the boundary layer. The PINN successfully predicted the progressed flow separation occurring at this AoA. The mean deviation of the axial velocity from the CFD results was \(\mathrm {7.1\times 10^{-3}}\) m/s which represents 0.71% of the reference inlet velocity.

Fig. 14
figure 14

Results and absolute error of velocity and pressure around the DU99W350 airfoil at an angle of attack of 17.5\(^{\circ }\) using a PINN in comparison with the reference data. Note that for this angle of attack, no reference data were provided for the training of the PINN

Full size image

Figure 15 displays a comparison of these results along several vertical lines positioned on the suction surface. As for the other AoAs, the separating boundary layer was captured accurately by the PINN and even the reversal of flow direction close to the surface at \(\mathrm {x=0.3~m}\) was depicted. However, the deviations from the CFD results were greater than for the interpolated flow field at an AoA of 12.5\(^{\circ }\).

Fig. 15
figure 15

Results and residual of the axial velocity on the suction surface of the DU99W350 airfoil at an angle of attack of 17.5\(^{\circ }\) using a PINN in comparison with the reference data. Left: axial velocity; right: residual between PINN and CFD results. Note that for this angle of attack, no reference data were provided for the training of the PINN

Full size image

For the AoA of 17.5\(^{\circ }\), zero labeled training points were provided during training and the prediction represents an extrapolation from the labeled dataset, which only contained AoAs of 10.0 and 15.0\(^{\circ }\). Yet, the flow field and the progressed flow separation was accurately predicted by the PINN. However, the achieved accuracy was slightly lower than that obtained for the interpolation case at 12.5\(^{\circ }\). This was due to the increased difficulty of extrapolations from a dataset. Using the phyiscs-informed deep learning approach, the extrapolation could still successfully be predicted.

6.4 Evaluation of lift and drag

The PINN-based multidimensional surrogate method presented here was used to obtain the integral aerodynamic forces for the parameterized airfoil geometry. Figure 16 exhibits the lift and drag results based on pressure and viscous stresses as predicted by the PINN in comparison with the CFD results. Lift L and drag D were calculated as follows:

$$\begin{aligned} L= & {} \int _{C}{\rm{d}} F_y \approx \sum p\hat{n}_{y} {\rm{d}}C + \sum \tau _{ij} \hat{n} {\rm{d}}C \quad \text {for} \quad i=2 \end{aligned}$$
(17)
$$\begin{aligned} D= & {} \int _{C}{\rm{d}} F_x \approx \sum p\hat{n}_{x} {\rm{d}}C + \sum \tau _{ij} \hat{n} {\rm{d}}C \quad \text {for} \quad i=1 \end{aligned}$$
(18)

where \({\rm{d}}F_{x}\) and \({\rm{d}}F_{y}\) are the resulting forces in x and y direction acting on the discrete surface element dC, \(\hat{n}_{x}\) and \(\hat{n}_{y}\) denote the x and y components of the surface normal vector \(\hat{n}\) of dC, and \(\tau _{ij}\) is the viscous stress tensor of an incompressible fluid:

$$\begin{aligned} \tau _{ij} = \mu \Bigl ( \frac{\partial \overline{u_{i}}}{\partial x_{j}} + \frac{\partial \overline{u_{j}}}{\partial x_{i}} \Bigr ) \end{aligned}$$
(19)

The derivations of the velocity field with respect to the coordinates were obtained using the automatic differentiation (AD) applied on the trained PINN. As seen in Fig. 16, the PINN results were subject to a bias error resulting in an underestimation of the lift and drag forces. Overall, the PINN predictions compared favorably to the CFD results for interpolations as well as the extrapolations from the training data set. The PINN reproduced the increasing lift and drag forces as well as the decreasing lift-to-drag ratio correctly. A supplementary illustration concerning the pressure distribution on the airfoil surfaces is given in the Appendix.

Fig. 16
figure 16

Lift and drag results for the DU99W350 airfoil as predicted by the PINN in comparison with the CFD results

Full size image

6.5 Accuracy of the method

The results show that it was possible to create a multidimensional surrogate model of a turbulent flow using the PINN-based method proposed here. For all AoAs investigated, the NN predicted the existence of the stagnation point, an attached or separated flow, boundary layers, the high-speed region on the suction surface of the airfoil, and the high- and low-pressure regions around the airfoil. Consequently, the velocity and pressure fields matched the simulated reference fields. Hence, all dominant flow phenomena were reproduced by the neural network for variable AoAs. This finding is in accordance with the results by Wandel et al. [37]. As distinguished from the approach used here, they trained a convolutional PINN that takes the vector potential as an input. This indicates that different kinds of PINNs can be used successfully for multidimensional surrogate models.

Although the important flow phenomena were reproduced, the predictions exhibited deviations from the reference solution. This especially accounted for high gradient regions such as the low-speed region at the stagnation point and the boundary layer on the suction side near the leading edge. As seen in Figs. 11 and 12, the velocity field of the stagnation point was erratic and exhibited intermittent regions of high and low velocities. These results were associated with the Reynolds number and were much less pronounced at the lower Reynolds numbers investigated in our sensitivity analysis. Moreover, the boundary layer comprised only a small fraction of the training domain and, hence, was difficult to train.

The accuracy varied for different AoAs. For cases with available simulated labeled training data as well as the interpolation, the solution accuracy was superior. Nonetheless, the results showed that accurate extrapolations of the flow field are possible. Even the onset and progression of flow separation could be predicted by the PINN.

6.6 Challenges and limitations

Several publications reported excellent agreement between PINN predictions and reference solutions [19, 25, 32]. However, in other cases a PINN might only be capable to capture the correct solution to some extent.

One limitation is related to the achievable errors of the prediction. The root of these errors lies in the numerical traits of the posed optimization problem characterized by parameters such as PDE, BC, activation function, network architecture, optimizer, learning rate, training points, and loss function. For a corresponding numerically sensitive non-convex loss landscape, the optimizer might not reach the global minimum, and a correspondingly large optimization error occurs. Besides, the choice of attributes such as the network architecture or the activation function corresponds to approximation and generalization errors. Jin et al. [33] investigated effects of the training point sampling, the optimizer, and the network size on these errors for several fluid dynamic cases and obtained low errors. While there are error estimates guaranteeing the smallness of the error, this only pertains if the global minimum is found by the optimizer and if the \(C^{1}\) norm of the underlying solution is small [41]. Consequently, PINN predictions have been shown to be subject to larger errors for flow fields with sharp gradients [42]. This issue is also evident from the results of this work, particularly in the case of the k-\(\omega \) model. Here, the complexity of the nonlinear transport equations as well as the sharp gradients caused by the elevated Reynolds number of \(1\times 10^{5}\) co-occurred and no physically plausible predictions were attainable. In Sect. 6.8, we describe methods aimed at potentially reducing these challenges.

In this study, we used labeled simulated data for the training. In many publications, PINNs were used to predict the flow field without any labeled training data [25, 28, 32,33,34]. However, the Reynolds numbers of the investigated flows were below 300 and, hence, laminar. Sun et al. [32] observed that the error of the prediction of a pipe flow increased with Reynolds number. For the Reynolds number investigated in this work, especially the boundary layer and the stagnation point region were challenging to be predicted in a satisfying manner and labeled training data were necessary to obtain an acceptable error. Indeed, the success of the training was heavily influenced by both the quantity and distribution of the training data. For the presented example, it was necessary to support the PINN with training data in the small high gradient boundary layer. This finding is supported by the results of Pioch et al. [15], who observed that the training of a Reynolds-averaged turbulent flow field failed when no labeled training data were provided. Therefore, the availability of labeled training data either from simulations or experiments could be another limitation of the PINN method used here when applied to other turbulent high Reynolds number flows.

6.7 Turbulence modeling

The pseudo-Reynolds turbulence modeling approach used here differs from the two-equation turbulence models typically used in CFD. For two-equation turbulence models, such as the k-\(\epsilon \) or the k-\(\omega \) models, two transport equations need to be solved to obtain solutions for turbulent kinetic energy and dissipation rate [43]. In contrast, for the pseudo-Reynolds stress model, no transport equation is prescribed. Nevertheless, in the work presented here, the predicted velocity and pressure fields compared favorably to the simulations. To some extent, this was attributed to the employment of simulated training data with which reliable values were prescribed at several positions in the flow domain. Harmening et al. [40] also applied the pseudo-Reynolds method to a high-Reynolds flow around a square using labeled training data, and they found favorable agreement with CFD results as well. Furthermore, Eivazi et al. [14] applied a similar approach and reported very good agreements with simulations without using labeled training data inside the domain.

For training using the k-\(\omega \) model, solving the transport equations for k and \(\omega \) added to the complexity of the system of PDEs that needed to be modeled by the PINN. In fact, the k-\(\omega \) model suffered from stability problems which were attributed to Eq. (10). Bounding the predictions of k and \(\omega \) stabilized the training, but the results were still unfavorable, as shown in Fig. 10. In a study of the flow around a backward-facing step, Pioch et al. [15] obtained favorable results using the k-\(\omega \) model. However, the Reynolds number used by Pioch et al. was \(\mathrm {5.1\times 10^{3}}\) while the Reynolds number of this work was \(\mathrm {1\times 10^{5}}\). More work needs to be done concerning two-equation models and their limitations as well as successful training conditions.

6.8 Potential improvements of the method

The attained levels of accuracy as well as the discussed inherent limitations of the PINN method suggest a consideration of potential improvements.

As discussed above, other kinds of NN might outperform the feedforward kind that was used here. Many investigations used convolutional or U-Net PINNs [20, 21, 34, 37, 44]. On the one hand, those networks have the advantage that important features of the geometry can be identified by the autoencoder part of the CNN. On the other hand, CNNs process two- or three-dimensional maps as input and output and, hence, require significantly more weights and biases. This increases the computational costs for training. However, a direct comparison between the performance of FNNs and CNNs using physics-informed learning is an open question. Other suitable kinds of NN might be a (modified) Fourier feature NN or DeepONet [35, 45, 46].

The selected architecture featured favorable results and agreed well with the reference data. However, for other cases, different architectures might be suitable. The optimal architecture of a PINN could be obtained using an automatic architecture search methods such as neural architecture search (NAS) or swarm intelligence algorithms [47, 48].

In our work, the boundary conditions were trained by penalizing any violation with a higher loss. Hence, the BCs were not satisfied exactly. This can lead to small fluxes through the wall resulting in losses of mass and momentum through the wall, as shown in [15]. A possible solution might be to apply hard boundary enforcement [32]. With such an approach, the exact value is enforced at the boundary using a specifically designed distance function. However, obtaining the distance function might be difficult for complex geometries [32].

As reported by Krishnapriyan et al. [49], high parameter values in the PDEs, such as large convection coefficients, might impose limitations in the learning capability of PINNs. One proposed solution is curriculum regularization [49]. With this approach, the PINN is trained in several steps of increased numerical difficulty. Krishnapriyan et al. [49] reported that errors decreased by one to two orders of magnitude using this method. This method is interesting as the convection terms also dominate the PDEs for high Reynolds number flows. Another promising incremental method is ensemble learning, which utilizes multiple networks trained in a sequence to yield a superior outcome [50].

To increase the accuracy in small regions, one could apply the residual adaptive refinement (RAR) method proposed by Lu et al. [12]. Using this method, additional training points for the PDEs are added to the training set in regions of large residuals. Wu et al. [51] investigated several sampling methods and found that residual-based adaptive distribution (RAD) and residual-based adaptive refinement with distribution (RAR-D) provide superior accuracy with fewer residual points when compared to non-adaptive distribution methods.

The labeled training points are another factor affecting the accuracy. The amount of training data correlated positively with the achieved accuracy, as shown by our sensitivity analysis. The distribution of the points was another major factor. This is visible in Figs. 12 and 14 which illustrate the effect of the training data positioning on the prediction of the stagnation point region. Note that the depicted quality of the predicted stagnation point could be improved by introducing more training points in that region. Cai et al. [52] trained a PINN to predict a shock wave problem. They obtained good results using 7,000 points for the PDEs, 3,000 points of labeled training data for the density gradient, and 800 points of labeled training data for the velocity. The procedure applied by Cai et al. gives a conception of a training point distribution that could yield an ideal highly accurate prediction of the stagnation point.

Weight factors of the composed loss terms can be set a priori, as done here, or adjusted during training. Xiang et al. [53] trained a PINN to solve the incompressible Navier Stokes equations using a self-adaptive loss function method that adjusts the losses based on a Gaussian probabilistic model. They achieved increased accuracy. A similar approach was applied by Li et al. [54]. Wang et al. [55] proposed a method that adaptively adjusts the loss weights using the eigenvalues of the neural tangent kernel of the PINN.

Another method to increase the accuracy of the PINN in the boundary layer and at the stagnation point region might be a distributed PINN. Dwivedi et al. [56] applied a distributed PINN to predict the stationary flow in a lid-driven cavity at a low Reynolds number. They distributed the flow domain in several cells. The flow in every cell then was predicted with separate PINNs that were interconnected using interface conditions. The method has also been deployed by Shukla et al. [57].

6.9 Future work

As discussed above, the proposed PINN-based surrogate modeling approach could possibly be improved in accuracy by several methods. Future work should comprise testing and comparing the methods mentioned above, especially concerning high Reynolds numbers. For such investigations, the focus should be on improving the prediction of important flow phenomena, such as the boundary layer flow and flows in the vicinity of the stagnation point. Furthermore, developing strategies to reduce the required amount of labeled training data are vital. Additionally, the model needs to be enhanced to account for three-dimensional flows.

7 Summary and conclusions

In this work, we trained a fully-connected feedforward PINN to predict the Reynolds-averaged flow field around the DU99W350 airfoil at arbitrary AoAs between 10.0\(^{\circ }\) and 17.5\(^{\circ }\). The PINN was trained with simulated data randomly drawn from a CFD grid for angles of attack of 10.0\(^{\circ }\) and 15.0\(^{\circ }\). Additionally, satisfaction of the boundary conditions as well as the RANS equations were trained on the coordinates of a second CFD grid.

A sensitivity analysis was conducted to investigate the effects of the Reynolds number, the amount and distribution of labeled training data, as well as the turbulence model. The error grew non-linearly with increasing Reynolds number, and the PINN yielded accurate solutions over a range of Reynolds numbers only when the problem was scaled by varying the viscosity. It was shown that a minimum of labeled training data for supervised learning was required to obtain satisfactory solutions at the Reynolds number of \(1\times 10^{5}\). Furthermore, the sampling of training data from the coordinates of a CFD grid exhibited superior results when compared with other non-adaptive sampling strategies. The k-\(\omega \) model yielded unfavorable predictions while the equation-free pseudo-Reynolds stress model compared favorably to the reference data.

The predictions of the PINN trained for variable AoAs exhibited good agreement with the RANS reference data for interpolations between the training data as well as extrapolations outside of the labeled training dataset. The predictions exhibited good agreement even within the separating boundary layer on the suction surface of the airfoil. However, the results also revealed challenges in predicting high gradient regions accurately. This was evident for the stagnation point at the leading edge of the airfoil.

Using the method presented in this work, we successfully generated a surrogate model of RANS flow fields around a variable geometry. The results of our work demonstrate the capability of feedforward PINNs to predict the Reynolds-averaged flow field around variable geometries at high Reynolds numbers.