1 Introduction

The reactivity of soils is a characteristic that affects the mechanical properties of most clayey grounds [1]. Reactive soils undergo substantial volume changes in response to the variations in soil moisture content through swelling and shrinking. The shrink–swell ground movement leads to distresses concerning infrastructures built on and in the vicinity of reactive soils [2, 3]. The damages to lightweight structures such as pavements, underground pipes, and residential structures due to these shrink–swell ground movements are well known [4, 5]. The severe damage brought by reactive soils has been recorded in Australia, China, Egypt, India, Israel, South Africa, the UK, and the USA, totalling a significant annual financial loss [6, 7]. In the UK, the impact of reactive soils summed up to £3 billion from 1991 to 2001 due to the effect of droughts, making it the most damaging geohazard in the region [8]. In the USA, the cumulative rehabilitation costs were more than twice the financial loss incurred from natural disasters due to floods, hurricanes, tornadoes, and earthquakes, amounting to around US$ 15 billion per year [8]. Li et al. [9] found that the damage caused by reactive soils in Australia was mostly to lightweight structures even though no combined estimates are reported in the literature. Approximately 20% of the Australian land can be categorised as moderately to very highly reactive soils, with six out of eight major cities being affected, causing geohazards to structures and infrastructures [6].

The shrink–swell soil index (Iss) is a soil parameter commonly used to determine the potential characteristic surface movement (ys) of sites having reactive soils in Australia [10]. This index is determined through laboratory testing using undisturbed soil samples collected from the field. The Iss index has been used in Australia for more than 15 years and the Australian Standards, AS 1289 7.1.1. provides standardised testing procedures. Estimates of ys have generally been successful in determining the dimensions of residential slabs and footings.

Determining the value of Iss requires the collection of undisturbed soil samples for the swell test and the simplified core shrinkage test. Undisturbed soil sampling costs relatively higher and is more difficult to implement than disturbed sampling. Determining Iss takes a longer time to obtain results, which can take more than four days involving around two hours of hands-on experimental work depending on the skill level of the individual performing the tests [1]. This can be a significant waiting period for most practitioners and researchers, and the results are sensitive to instrumental conditions, skills and experience of the tester, and changing ambient conditions.

Several studies had attempted to correlate Iss with other soil properties such as the Atterberg limits (i.e. liquid limit (LL), plasticity limit (PL), plasticity index (PI), and linear shrinkage (LS)) to estimate Iss indirectly. However, most studies have found sub-par correlation coefficients (R2 < 0.80) between Iss and the Atterberg limits, which ranged from 0.20 to 0.53 [9]. For instance, Young and Parmar [11] performed more than 300 laboratory tests to correlate Iss with more common soil indices such as gravimetric soil moisture content (ω), LL, PL, PI, and LS that resulted in low correlation factors. Earl [12] suggested that the Atterberg limits alone may not be reliable to estimating values of Iss based on his investigations using clay samples from the Shepparton geologic formation. Reynolds [13] performed similar correlation analyses for a dataset of clay samples collected from Central, Southeast, and Northwest Queensland for a pavement design application and also reported weak relationships. Similar weak correlations were found in the investigations conducted by Zou [14] and Li et al. [9], where soil samples were collected from 47 study sites from 37 suburbs in Melbourne. However, these investigations employed simple univariate regressions that limit the capturing of nonlinear relationships between extracted features or variables. Contrarily, Jayasekera and Mohajerani [15] found a relatively stronger correlation with R2 values that ranged from 0.85 to 0.91. However, their investigation had a low variance dataset, with Iss values that varied from 3.8 to 5.5, which limited the predictive capacity of their model [15].

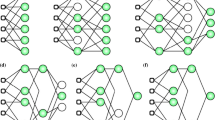
Recent advances in data engineering and data science have expanded the application of artificial intelligence (AI) techniques to many disciplines [16]. AI refers to the ability of a machine or robot to display intelligence comparable to humans by learning through experiences in performing a specific task with improving measured performance [17]. Machine learning (ML) is a subset of AI referring to algorithms capable of learning and improving performance without explicit programming or hard coding (Fig. 1a). ML tasks include recognising objects, understanding speech, responding to a conversation, solving problems, optimising solutions, greeting people, and driving a vehicle [18,19,20]. Rumelhart et al. [21] initially proposed shallow learning that initiated ML applications (Fig. 1b). These shallow neural networks restrict algorithmic support and are unable to train multiple hidden layers due to limitations in the computing power and available data [22].

Fig. 1
figure 1

Defining a the difference between artificial intelligence (AI), machine learning (ML), and deep learning (DL), b a sample shallow artificial neural network (ANN), and c a sample DL network

Full size image

Recent applications of AI in geotechnical engineering include geotextile [23, 24], tunnelling [25], geothermal energy [26], unsaturated flow [27], geo-structural health monitoring [28, 29], liquefaction [30], nanotechnology [31], carbon sequestration [32], and soil properties and behaviour prediction [33,34,35]. The ML techniques applied in these past investigations include artificial neural network (ANN), support vector machine (SVM), genetic algorithms (GA), fuzzy logic, image analysis, and adaptive neuro-fuzzy inference systems (ANFIS). One of the emerging ML techniques in geotechnical engineering is deep learning (DL), an implementation of ANN with multiple hidden layers as presented in Fig. 1c. It allows computation of more complex features of the input layer [36, 37]. Each hidden layer computes a nonlinear transformation of the preceding layer [38]. This deep network can have a substantially greater representation of the extracted features that can learn significantly more complex functions than a shallow network [22]. However, understanding the implementation of DL can be a challenge due to its complex network. It is beneficial for users to understand the implementation of algorithms to enable the accurate and confident application of complex models such as DL [22, 36, 38].

The application of AI to investigate the properties and nonlinear behaviour of reactive soil is currently not well explored, although there has been an increased application of AI in geotechnical engineering in general [39]. As linear correlations between Iss, and Atterberg limits had potential, most model accuracy and data ranges of the previous studies found sub-par results. DL has the potential to give better accuracy in the prediction of Iss using the Atterberg limits given the ability of neural networks to handle complex nonlinear scenarios. The application of Atterberg limits can be used by promoting adaptive nonlinear models and providing insightful findings [16]. Therefore, the objective of this study is to employ DL to predict more accurate values of Iss using different combinations of soil properties including LL, PL, PI, LS, and %fines. This can contribute to an efficient process of calculating the maximum potential characteristic surface movement, ys. This study also carries out a sensitivity analysis to identify the relative influence of each input variable, LL, PL, PI, LS, and %fines, on the targeted output, Iss in %/pf. The sensitivity analyses elaborate on how the specific DL prediction mechanism functions with respect to the input features, increasing the applications.

2 Methodology

The concept of ANN is analogous to the neural network of a human brain in the way it processes information and establishes logical relationships [40]. A collection of connected nodes called artificial neurons comprise a network comparative to those of a human brain. The artificial neurons are connected by links called edges to transmit signals from a single neuron to other neurons. These signals are represented by real numbers. Each node and edge have weights that serve as a correlation factor that adjusts signals as learning occurs. The main function of this network is to obtain the lowest value of a loss or cost function, L(y,ŷ), that will give the optimum weights. The DL process is influenced by two main considerations: the architecture of the neural network and the learning process of the implemented algorithm.

2.1 Deep learning architecture

In this current study, a DL network was used to obtain the acceptable weights for Iss prediction and comprised of an input layer, ten hidden dense layers, and an output layer. The input and the output values are the expected number of input and output neurons, which indicate the size of the matrices for the calculation. The input layer contained the input vector extracted from a dataset and the number of artificial neurons in the input layer was determined by the input features extracted. In this study, two scenarios were considered. The first scenario, or Scenario 1, used the input features LL, PL, PI, and LS, whereas the second scenario, or Scenario 2, also used %fines.

Earl [12] and Reynolds [13] suggested that LL, PL, PI, and LS were not sufficient to be employed for estimating the values of Iss. Thus, Earl [12] added clay and silt fraction, and Reynolds [13] included California Bearing Ratio (CBR), per-cent swell, and other polynomial features as inputs. The resulting values of R2 were higher compared to those with Atterberg limits alone and ranged from 0.51 to 0.78 [13] and from 0.54 to 0.82 [12]. However, the data samples they used were limited (n < 30). In addition, the dataset had low variance (0.1 < Iss < 4.0), and the models were not tested or validated for their prediction capacity. These improved outcomes led to the development of Scenario 2 of this study, which included %fines as an additional input to predict Iss. The addition of the CBR by Reynolds [13] as an input did not result in greater R2 compared to the addition of; thus, in the current study, the CBR was not considered.

In this current study, the number and size of hidden dense layers were determined by trial and error. The hidden dense layers connect each neuron, receiving input from its preceding layer. The dimension of the first five hidden dense layers was restrained to eight since greater dimensions resulted in the model calculation divergence (i.e. erratic and high values of calculated loss). The dimension of the last five hidden dense layers was increased to 128 to generate more nonlinearity in the relationship between neurons. The increase in the number of hidden layers and the value of the dimension, depending on a specific scenario, often leads to improved accuracy [41]. The consequence is the time inefficiency in performing the DL algorithm, specifically for the training period to obtain the optimum weights. The output layer concludes the DL learning process using one neuron.

2.2 Deep learning process

The learning process of a DL neural network comprises five main stages, (1) pre-processing, (2) random initialisation, (3) forward propagation, (4) backward propagation, and (5) evaluation. The DL process implemented in this study is summarised in Fig. 2.

Fig. 2
figure 2

Deep learning (DL) neural network process for two scenarios

Full size image

Pre-processing a dataset is an essential step that can increase the accuracy of a DL network training and validation. The common pre-processing techniques applied to previous DL networks include the removal of data entries with outliers and missing values, creation of polynomial features, implementing feature scaling, and employing normalisation to a dataset [42].

The dataset used in this study was extracted from the five studies conducted by [12,13,14, 43, 44], as presented in Appendix 1. A total of 169 and 116 data entries were collected for Scenarios 1 and 2, respectively, with a summary description presented in Fig. 3 and Table 1. Outliers were determined using the interquartile range (IQR), calculated as

$${\text{Outlier}}_{lb} = Q1 - 1.5{\text{IQR}}$$
(1)
$${\text{Outlier}}_{ub} = Q3 + 1.5{\text{IQR}},$$
(2)
Fig. 3
figure 3

Boxplot of the dataset for Scenario 1 showing a the target Iss and b the features LL, PL, PI, and LS, and Scenario 2 showing: c the target Iss and d the features LL, PL, PI, LS, and fines, where Iss = shrink–swell index, LL—Liquidity limit, PL = Plasticity limit, PI = Plasticity index, LS = Linear shrinkage, and n is the number of data entries or samples

Full size image
Table 1 Descriptive statistics of the target (Iss) and features for Scenario 1 and Scenario 2
Full size table
Table 2 Upper and lower bounds to generate the input features for Scenarios 1 and 2 using the scheme by Saltelli [51]
Full size table

where IQR is described as

$$\mathrm{IQR}=Q3-Q1,$$
(3)

where Q1 is the first quartile, Q3 is the third quartile, and subscripts lb and ub indicate the lower bound and the upper bound outliers.

The circles in Fig. 3 represent the outliers less than or more than the calculated values of Outlierlb and Outlierub. A comparison between DL with and without the outliers showed comparable results indicating a negligible effect of the outliers. Therefore, in this study, the complete dataset without removing the outliers was used. Data entries with missing values of Iss, LL, PL, PI, LS, and %fines were omitted for Scenario 2. Polynomial features are commonly created to incorporate a nonlinear relationship between the target and the input features. Polynomial features are added to improve the accuracy of linear models with limited features or when one feature is dependent on another. The use of polynomial features was initially implemented in the dataset but did not result in a noteworthy effect on the accuracy of the algorithm. Therefore, these features were not implemented in the DL of this study. The entire dataset was randomly split into two; one for training and the other for testing, with a ratio of 70–30%, as listed in Table 1. The 70–30% ratio was considered the most suitable division for training and validating neural network models with small dimensional datasets [45].

Two feature scalings, standard scaling and min–max scaling, were tested to check if the DL process would improve. The feature scaling using the standard scaling was observed to be more applicable to the study and was employed using the following equation:

$$\mathrm{Standard} \mathrm{scaling}= \frac{x-\overline{x}}{s },$$
(4)

where x is the data entry, x̄ is the mean value of a feature, and s is the standard deviation of a feature.

The values of x̄ and s for the input parameters LL, PL, PI, and LS are presented in Table 1, for both training and testing data. Applying normalisation was considered and implemented in preliminary model runs. However, normalising resulted in a lesser accuracy of the results, compared to standard scaling.

The random initialisation method of He et al. [46] was used to initialise the DL process. Following this method, the weights were randomly initialised with values close to zero and then multiplied by \(\sqrt{\frac{2}{{\mathrm{size}}^{L-1}}}\), where sizeL−1 was the number of neuron in layer L − 1. Multiplying this term helps consider the nonlinearity of the activation functions. This initialisation proposed by He et al. [46] was specifically used together with the Rectified Linear Units (ReLU) activation, solving learning inefficiency and vanishing gradient issues. The loss function employed in the DL process is the mean squared error (MSE), which is a commonly used function for regression. The calculated loss is the mean overseen data of the squared differences between a true value in the dataset and a predicted value calculated by the DL algorithm described as

$$L\left( {y,\hat{y}} \right) = \frac{1}{N}\mathop \sum \limits_{i = 0}^{N} \left( {y_{i} - \widehat{{y_{i} }}} \right)^{2}$$
(5)

where yi is the actual value, ŷi is the predicted value, and N is the total number of data entries.

ReLU by Nair and Hinton [47] was implemented as the activation function for the forward and backward propagation, which reads

$$f\left(x\right)=\mathrm{max}\left(0,x\right)=\left\{\begin{array}{c}{x}_{i}, if {x}_{i}\ge 0\\ 0, if {x}_{i}<0\end{array}\right. ,$$
(6)

where xi is the input value of feature i.

A simplified representation of the usage of the activation function is presented in Fig. 4. Ridge Regression or L2 Regularisation was also used since the preliminary DL runs experienced overfitting. L2 regularisation adds a squared magnitude of coefficient as penalty term to the loss function defined as

Fig. 4
figure 4

Typical biologically inspired artificial neuron showing activation and transformation

Full size image
$$L\left(y,\widehat{y} \right)=\frac{1}{N}\sum_{i=0}^{N}{\left({y}_{i}-\widehat{{y}_{i}} \right)}^{2} +\lambda \sum_{i=0}^{N}{{w}_{i}}^{2}$$
(7)

where λ is a hyperparameter for regularisation, and wi is a weight of a feature.

The value of λ is taken to be greater than zero. Taking the value of λ too high may lead to larger weights and underfitting. After fine-tuning the hyperparameter λ, the value was specified as 1.00 for Scenario 1 and 2.35 for Scenario 2.

The Adaptive Moment (Adam) estimation by Kingma and Ba [48] was used in the DL neural network. The Adam stochastic optimisation is widely used due to its benefits of straightforward implementation, computational efficiency, and lower required memory. The Adam method combines the momentum gradient descent method and the Root Mean Squared Propagation (RMSprop), which is modelled as

$$V\mathrm{d}w={\beta }_{1}V\mathrm{d}w+\left(1-{\beta }_{1}\right)\mathrm{d}w,$$
(8)
$$V\mathrm{d}b={\beta }_{1}V\mathrm{d}b+\left(1-{\beta }_{1}\right)\mathrm{d}b,$$
(9)
$$S\mathrm{d}w={\beta }_{2}S\mathrm{d}w+\left(1-{\beta }_{2}\right){\mathrm{d}w}^{2}, \mathrm{and}$$
(10)
$$S\mathrm{d}b={\beta }_{2}S\mathrm{d}b+\left(1-{\beta }_{2}\right){\mathrm{d}b}^{2},$$
(11)

where Vdw, Vdb, Sdw, and Sdb are the derivative of the weights and bias, which is being computed in iteration or epoch, t. The initial values of Vdwi, Vdbi, Sdwi, and Sdbi are assigned to zero and then calculated for each weight. The calculated values of Vdw, Vdb, Sdw, and Sdb are then corrected using the power of the current epoch, t, described below

$${V\mathrm{d}w}^{\mathrm{corrected}}=\frac{V\mathrm{d}w}{1-{{\beta }_{1}}^{t}},$$
(12)
$${V\mathrm{d}b}^{\mathrm{corrected}}=\frac{V\mathrm{d}b}{1-{{\beta }_{1}}^{t}},$$
(13)
$${S\mathrm{d}w}^{\mathrm{corrected}}=\frac{S\mathrm{d}w}{1-{{\beta }_{2}}^{t}}, \mathrm{and}$$
(14)
$${S\mathrm{d}b}^{\mathrm{corrected}}=\frac{S\mathrm{d}b}{1-{{\beta }_{2}}^{t}}.$$
(15)

Each weight and bias will be updated using the equations below

$$w=w-\alpha \frac{{{V}_{\mathrm{d}w}}^{\mathrm{corrected}}}{\sqrt{{{S}_{\mathrm{d}w}}^{\mathrm{corrected}}+\epsilon }} \mathrm{and}$$
(16)
$$b=b-\alpha \frac{{{V}_{\mathrm{d}b}}^{\mathrm{corrected}}}{\sqrt{{{S}_{\mathrm{d}b}}^{\mathrm{corrected}}+\epsilon }} .$$
(17)

The learning rates (α) for Scenarios 1 and 2 were taken as 7.5 × 10–5 and 5.0 × 10–5 after fine-tuning using trial and error. The decay rates for both scenarios were β1 = 0.9, β2 = 0.999, and ϵ = 5.0 × 10–6. The forward and backward propagation was implemented in a loop until the specified epoch was achieved, as shown in the DL process in Fig. 2. Note that every iteration of the optimisation loop comprises forward propagation, cost calculation, backward propagation, and weights updating. The epoch of the final DL run was 500 since this value had resulted in an optimum and stable loss curve with an acceptable learning period, completing the deep learning processes in less than three minutes for each scenario.

2.3 Sensitivity analysis

Sensitivity analyses help identify the independent influence of input variables on a targeted output. There are two types of sensitivity analyses; local and global approaches. A local sensitivity analysis assesses the local impact of feature variations concentrated on the sensitivity in the proximate vicinity of a set of feature values [49]. On the other hand, a global sensitivity analysis quantifies the overall importance of the features and their interactions with the predicted results by implementing a comprehensive coverage of input values [50]. This study used a global sensitivity analysis approach by implementing the method by Saltelli [51] and Sobol [52, 53].

The bounds to generate the input features were specified as LL = 15–130, PL = 5–60, PI = 0–100, LS = 0–40, and %fines = 1–100 listed in Table 1, and then the scheme by Saltelli [51] was implemented. This was based on the range of values presented in Fig. 3b. Three indices were calculated. The first one was the first-order Sobol index (S1), calculated as [52, 53]

$${S}_{1}=\frac{\mathrm{var}({x}_{i})}{\mathrm{var}(\widehat{y})}=\frac{\mathrm{var}(E\left(\widehat{y}|{x}_{i}\right))}{\mathrm{var}(\widehat{y})},$$
(18)

where var(xi) is the variance of a feature, var(\(\widehat{y}\)) is the variance of the target output, Iss, E denotes expectation, xi is a feature, and \(\widehat{y}\) is the target output, Iss.

The term E(\(\widehat{y}\)|xi) in Eq. 18 indicates the expected value of the output \(\widehat{y}\) when feature xi is fixed. The first-order Sobol index, S1, reflects the expected reduction in the variance of the model when feature xi is not changing. Thus, S1 measures the direct effect of each feature on the variance of the model. It is worth noting that the sum of all the calculated values of S1 should be equal to or less than one. It is common to perform the calculation of S1, and the total Sobol sensitivity ST, which includes the sensitivity of first-order effects and the sensitivity due to interactions between a feature Xi and all other features [54] given by

$${S}_{T}=1-\frac{\mathrm{var}\left(E\left(\widehat{y}|{x}_{-i}\right)\right)}{\mathrm{var}\left(\widehat{y}\right)},$$
(19)

where x-i denoted the features except xi, and the sum of all the calculated values of ST is equal or greater than one.

If the values of ST are substantially larger than the values of S1, then there are likely higher-order interactions occurring. Hence, it is worth calculating the second-order or higher-order sensitivity indices (e.g. S2).

The second-order and higher-order sensitivity indices can similarly be expressed as

$${S}_{2}=\frac{\mathrm{var}({x}_{i},{x}_{j})}{\mathrm{var}(\widehat{y})},$$
(20)

where var(xi, xj) is the variance of features xi and xj. This calculates the amount of variance of \(\widehat{y}\) explained by the interaction of features xi and xj.

3 Results and discussion

The results of the DL training, testing, and sensitivity analysis are discussed in the following sections.

3.1 Prediction of I ss using deep learning

The DL process outlined in Fig. 3 was implemented to the randomly allocated dataset for training (118 and 81 data entries for Scenarios 1 and 2, respectively) and testing (51 and 35 data entries for Scenarios 1 and 2, respectively) listed in Table 1. The calculated loss values of the training and testing set using Eq. (7) against epochs are presented in Fig. 5. The loss values of both Scenarios 1 and 2 showed acceptable learning curves. This curve is a diagnostic tool for algorithms that learn from training datasets incrementally. The learning curves for both Scenarios 1 and 2 display a good fit that is negligibly experiencing underfitting or overfitting. This is characterised by training and testing loss values that decrease to the point of stability with a minimal gap between the two, as shown in Fig. 5. It is common to have a difference between the final loss values of the training and testing curves. Training curves having loss values less than testing curves are referred to as a “generalisation gap”. It can be observed that Scenario 1 (Fig. 5a) had a relatively wider gap between the training and testing loss values than Scenario 2 (Fig. 5b). This shows that Scenario 2, with features LL, PL, PI, LS, and fines, can give relatively better Iss predictions with less overfitting due to generalisation.

Fig. 5
figure 5

Results and comparison of the calculated loss functions (L(y, ŷ)) of training and testing sets for a Scenario 1 with features LL, PL, PI, and LS and b Scenario 2 with features LL, PL, PI, LS, and fines

Full size image

The final performance training and testing of the model was assessed in terms of root mean squared error (RMSE) calculated as

$$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i=1}^{N}({y}_{i}-{\widehat{{y}_{i}})}^{2}}{N}}.$$
(21)

The RMSE indicates the average deviation of predictions from the measured values, with values closer to zero indicating better performance. The calculated RMSE for Scenario 1 was 1.26, whilst Scenario 2 had a lower RMSE of 0.90. This strengthens the authors’ inference that adding %fines as an input feature, even though this reduces the size of the dataset, can more reliably predict Iss.

Further evaluation of the models of Scenarios 1 and 2 was carried out using an identity line or 1:1 line, as shown in Fig. 6. The 1:1 line has a slope of 1, forming a 45° angle. This line is used as a reference in a 2-dimensional scatter plot comparing two datasets that are expected to be alike under ideal conditions. When all the actual and predicted data points have equal values from the two datasets, the corresponding scatters fall along the 1:1 line [55]. Using the 1:1 line, there are two measurements we want to obtain that reflect the reliability of the predictions of the models. The first measurement is the coefficient of determination, R2, calculated as

Fig. 6
figure 6

Comparison between the predicted and actual values of Iss of a the training set of Scenario 1, b the testing set of Scenario 1, c the training set of Scenario 2, and d the testing set of Scenario 2. The grey line represents the 1:1 line and the black line represents the regression line (color figure online)

Full size image
$${R}^{2}=1-\frac{\mathrm{RSS}}{\mathrm{TSS}}$$
(22)

where RSS is the sum of squares of residuals and TSS is the total sum of squares.

The second measure is the linear regression coefficient or slope that describes the relationship between the predicted and actual values. The values of R2 and slope range between zero and one, with unity indicating a perfect fit.

The training set of Scenario 1 estimated R2 to be 0.81 and the slope to be 0.75 (Fig. 6a), whilst the testing set of Scenario 1 resulted in a value of R2 of 0.76 and a slope of 0.59 (Fig. 6b). These obtained correlations showed improvements compared to most previous studies. For instance, Li et al. [9] reported that the correlation between Iss and the Atterberg limits ranged from R2 = 0.20 to R2 = 0.53. Most of the performed studies up to date have concluded that Iss and Atterberg limits are poorly correlated [11,12,13,14], except in the case of Jayasekera and Mohajerani [15] that found a relatively stronger correlation with R2 values, which ranged from 0.85 to 0.91. However, the study of Jayasekera and Mohajerani [15] focused on a dataset with a low variance that limits the predictive ability of their model, with Iss values that varied from 3.8 to 5.5.

The training set of Scenario 2 estimated R2 to be 0.84 and the slope to be 0.95 (Fig. 6c), whilst the testing set of Scenario 2 resulted in a value of R2 of 0.82 and a slope of 0.85 (Fig. 6d). The values of R2 in the training and testing sets using the DL architecture and process implemented in Scenario 2 were comparable with Earl [12], noting that Scenario 2 had a wider variance (0.1 < Iss < 9.0). It can be observed from Fig. 6c that the slope is 0.95, which can be considered a strong correlation. However, due to the generalisation gap discussed earlier, the testing set commonly has lower accuracy than the training set. This holds in Fig. 7d, where the slope decreased to 0.85, which still shows a stronger correlation.

Fig. 7
figure 7

Sobol indices for Scenario 1 showing a the total Sobol indices, b the first-order indices, c the second-order indices, and for Scenario 2 showing d the total Sobol indices, e the first-order indices, and f the second-order indices

Full size image

3.2 Sensitivity analysis

The bounds to generate the input features are specified in Table 1. The scheme by Saltelli [51] was implemented to generate the input features for predicting the values of Iss. Sensitivity analysis was then performed (1) to assess the influence of the features on the targeted output, and (2) to identify the relationship between input features and their influence on the target output. Descriptive statistics of the generated input variables using the scheme by Saltelli [51] and the predicted results using DL for Scenarios 1 and 2 are listed in Table 3. The generated input features of Scenario 1 were similar to the figures in Scenario 2. Interestingly, the predicted values of Iss of Scenario 1 were observed to have higher values than Scenario 2, leading to higher calculated x̄, s, minimum value, Q1, median, Q3, and maximum value. It is important to note that in Table 3, the maximum value of the predicted Iss in Scenario 1 was 16.8, which is almost twice greater than the maximum value in the training set (9%/pF) presented in Fig. 3 and Table 1. On the other hand, the maximum value of the predicted Iss in Scenario 2 was comparable to the training data (≈ 9%/pF). Thus, the range of predicted values of Scenario 2 is more practical and within the acceptable range.

Table 3 Descriptive statistics of the generated input variables using the scheme by Saltelli [51] and the predicted results using DL for Scenario 1 (with features LL, PL, PI, and LS) and Scenario 2 (with features LL, PL, PI, LS, and fines)
Full size table

The results of the global sensitivity analysis using Sobol [52, 53] for Scenario 1 and Scenario 2 are presented in Fig. 7. In Scenario 1, it can be observed in the first-order Sobol indices, S1, presented in Fig. 7b, that LS exhibited first-order sensitivities. This signifies that LS has the highest contribution of a single parameter to the output variance of Iss. On the other hand, LL appears to have no first-order effects suggesting that it has a low contribution to the variation of the predicted values of Iss. The values of the total-order Sobol index, ST, were checked afterwards and are shown in Fig. 7a. If the values of ST are markedly higher than those of S1, then there are likely higher-order interactions occurring. Higher-order interactions indicate that the fractional contribution of parameter interactions to the output variance exists. The values of ST revealed (Fig. 7a) higher values than S1. Hence, the second-order indices, S2, were calculated. PI and LS had the strongest feature interaction followed by PL and LS in Scenario 1, as shown in Fig. 7c. The remaining interactions can be considered insignificant.

In Scenario 2, it can be observed in S1 presented in Fig. 7e that fines exhibited first-order sensitivities. This signifies that %fines has the highest contribution of a single parameter to the variance of Iss. The other features, LL, PL, PI, and LS, appear to still have substantial first-order effects on the variation of the predicted values of Iss. The values of S1 in Scenario 2 (Fig. 7d) were more than four times lower than Scenario 1 (Fig. 7b). This reveals that the individual contribution of features in Scenario 2 is more distributed to other variables than Scenario 1. The values of ST were then computed (Fig. 7d) and were found to be substantially larger than that of S1, hence, likely higher-order interactions are occurring. The interaction between LS and %fines had the largest values of S2, followed by PL-%fines, PI-LS, and PI-%fines, as shown in Fig. 7f.

4 Model comparison

The predictive accuracy of Scenario 1 was comparable to the models of Earl [12], Reynolds [13], and Li et al. [9]. The accuracy of the developed DL model was compared to the proposed models in previous studies. The comparison involved same seeded scenarios to predict the values of Iss using the models listed in Table 4.

Table 4 Model comparison to predict values of Iss
Full size table

The developed DL neural network of Scenario 2 performed the best among the models, with the most desirable values of slope, R2, and RMSE. This indicates that Scenario 2 predicted the most accurate values among the considered models in Table 4.

The models of Earl [12] and Reynolds [13] with LL as input had fairly acceptable values of slope, R2, and RMSE. The performance of the models and the values of R2 conformed to the published work of Earl [12], Reynolds [13], and Li et al. [9] when applied to the compiled dataset used in this study (shown in Appendix). However, the models by Jayasekera and Mohajerani [15] underperformed when applied to the test dataset of this study. This may be due to the limited data and low variance of Iss values used in their dataset and when applied to the compiled dataset in this study, the predictive range became inappropriate.

5 Conclusion

The soil parameter Iss is widely used in Australia to determine the potential ground surface movement. However, determining Iss takes a longer time to obtain results taking more than four days and involving hours of hands-on experimental work. This study developed an efficient method to estimate accurate values of Iss through DL neural networks. This study proposed two scenarios; Scenario 1 involved the features LL, PL, PI, and LS whilst Scenario 2 added the input feature of %fines. The proposed models were further investigated using sensitivity analysis to identify the relative influence of the input features on the targeted output, Iss. This predictive DL model may significantly reduce the waiting period for the laboratory test results that are highly sensitive to instrumental conditions, skills and experience of the tester, and changing ambient conditions.

Results of implementing DL neural networks showed more reliable predictions in Scenario 2 (training: R2 = 0.84 and slope = 0.95; testing R2 = 0.82 and slope = 0.85) than Scenario 1 (training: R2 = 0.81 and slope = 0.75; testing R2 = 0.76 and slope = 0.59). These results suggested that adding a more relevant feature can be more beneficial than more data samples. Furthermore, the sensitivity analysis resulted in a more practical range of predicted values in Scenario 2, with %fines having the highest contribution to the variance of Iss. The values of R2 in the training and testing sets using the DL architecture and process implemented in Scenario 2 were considerably higher and had a wider variance than those of the previously conducted studies. This makes Scenario 2, the proposed model, around 10–65% more accurate than the models considered in this study for predicting Iss. The developed DL neural network of Scenario 2 can then be used to estimate more accurate values of Iss if an expedited result is required for design calculations.