Skip to main content
SpringerLink
Log in

Neural networks with block diagonal inner product layers: a look at neural network architecture through the lens of random matrices

  • Brain inspired Computing &Machine Learning Applied Research-BISMLARE
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

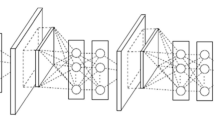
Two difficulties continue to burden deep learning researchers and users: (1) neural networks are cumbersome tools, and (2) the activity of the fully connected (FC) layers remains mysterious. We make contributions to these two issues by considering a modified version of the FC layer we call a block diagonal inner product (BDIP) layer. These modified layers have weight matrices that are block diagonal, turning a single FC layer into a set of densely connected neuron groups; they can be achieved by either initializing a purely block diagonal weight matrix or by iteratively pruning off-diagonal block entries. This idea is a natural extension of group, or depthwise separable, convolutional layers. This method condenses network storage and speeds up the run time without significant adverse effect on the testing accuracy, addressing the first problem. Looking at the distribution of the weights through training when varying the number of blocks in a layer gives insight into the second problem. We observe that, even after thousands of training iterations, inner product layers have singular value distributions that resemble that of truly random matrices with iid entries and that each block in a BDIP layer behaves like a smaller copy. For network architectures differing only by the number of blocks in one inner product layer, the ratio of the variance of the weights remains approximately constant for thousands of iterations, that is, the relationship in structure is preserved in the parameter distribution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. In our work, we chose to implement all blocks with the same size, but blocks do not need to have the same size in general.

  2. When using BDIP layers, one should alter the output format of the previous layer and the expected input format of the following layer accordingly, in particular to row major ordering.

  3. Here we denote the baseline architecture using our notation \((1, \ldots ,1)\)-BD\(_m\).

  4. With more complex datasets, BDIP layers, especially without any pruning or block shuffling to assist information flow, are more appropriate in deeper layers.

  5. The ip2 layer weights also appear to have the same behavior, but the matrix size is much smaller so the estimate of the variance is lower order and the asymptotic assumptions of Marchenko–Pastur are far from met.

References

  1. Ailon N, Chazelle B (2009) The fast Johnson Lindenstrauss transform and approximate nearest neighbors. IAM J Comput 39(1):302–322

    MathSciNet  MATH  Google Scholar 

  2. Boahen K (2014) Neurogrid: a mixed-analog-digital multichip system for large-scale neural simulations. IEEE 102(5):699–716

    Google Scholar 

  3. Cheng Y, Yu FX, Feris R, Kumar S, Choudhary A, Chang S (2015) An exploration of parameter redundancy in deep networks with circulant projections. In: ICCV

  4. Chollet F (2017) Xception: deep learning with depthwise separable convolutions. arXiv:1610.02357

  5. Glorot X, Bengio Y (2010) Understanding the difficulty of training deep feedforward neural networks. In: International conference on artificial intelligence and statistics, vol 9, pp 249–256

  6. Han S, Mao H, Dally WJ (2015) Deep compression: compressing deep neural networks with pruning, trained quantization and huffman coding. In: ICLR

  7. Han S, Pool J, Tran J, Dally WJ (2015) Learning both weights and connections for efficient neural networks. In: NIPS, pp 1135–1143

  8. He T, Fan Y, Qian Y, Tan T, Yu K (2014) Reshaping deep neural network for fast decoding by node-pruning. In: IEEE ICASSP, pp 245–249

  9. Herculano-Houzel S (2012) The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost. In: NAS

  10. Hinton G, Vinyals O, Dean J (2014) Distilling the knowledge in a neural network. In: NIPS

  11. Ioannou Y, Robertson D, Cipolla R, Criminisi A (2017) Deep roots: improving CNN efficiency with hierarchical filter groups. In: CVPR

  12. Jhurani C, Mullowney P (2015) A gemm interface and implementation on nvidia gpus for multiple small matrices. J Parallel Distrib Comput 75:133–140

    Google Scholar 

  13. Krizhevsky A (2009) Learning multiple layers of features from tiny images. Technical report, Computer Science, University of Toronto

  14. Krizhevsky A (2012) cuda-convnet. Technical report, Computer Science, University of Toronto

  15. Krizhevsky A (2012) cuda-convnet: high-performance C++/cuda implementation of convolutional neural networks

  16. Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. In: NIPS, pp 1106–1114

  17. L2 Q, Sarlo T, Smola A (2013) Fastfood—approximating kernel expansions in loglinear time. In: ICML

  18. Lebedev V, Lempitsky V (2016) Fast convnets using group-wise brain damage. In: CVPR

  19. LeCun Y, Bottou L, Bengio Y, Haffner P (1998) Gradient-based learning applied to document recognition. IEEE 86(11):2278–2324

    Google Scholar 

  20. LeCun Y, Cortes C, Burges CJ The mnist database of handwritten digits. Technical report

  21. Marchenko VA, Pastur L (1967) Distribution of eigenvalues for some sets of random matrices. Math USSR Sb 1(4):457–483

    MATH  Google Scholar 

  22. Masliah I, Abdelfattah A, Haidar A, Tomov S, Baboulin M, Falcou J, Dongarra J (2016) High-performance matrix-matrix multiplications of very small matrices. In: Euro-Par 2016: parallel processing, vol 9833, pp 659–671

    Google Scholar 

  23. Merolla PA, Arthur JV, Alvarez-Icaza R, Cassidy AS, Sawada J, Akopyan F, Jackson BL, Imam N, Guo C, Nakamura Y, Brezzo B, Vo I, Esser SK, Appuswamy R, Taba B, Amir A, Flickner MD, Risk WP, Manohar R, Modha DS (2014) A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 345(6197):668–673

    Google Scholar 

  24. Moczulski M, Denil M, Appleyard J, de Freitas N (2016) ACDC: a structured efficient linear layer. arXiv:1511.05946

  25. Netzer Y, Wang T, Coates A, Bissacco A, Wu B, Ng A (2011) Reading digits in natural images with unsupervised feature learning. In: NIPS

  26. Nickolls J, Buck I, Garland M, Skadron K (2008) Scalable parallel programming with cuda. ACM Queue 6(2):40–53

    Google Scholar 

  27. Tishby N (2017) Information theory of deep learning

  28. Rajan K (2010) What do random matrices tell us about the brain? Grace Hopper Celebration of Women in Computing

  29. Rajan K, Abbott LF (2006) Eigenvalue spectra of random matrices for neural networks. Phys Rev Lett 97(18):188104

    Google Scholar 

  30. Reed R (1993) Pruning algorithms—a survey. IEEE Trans Neural Netw 4(5):740–747

    Google Scholar 

  31. Sainath TN, Kingsbury B, Sindhwani V, Arisoy E, Ramabhadran B (2013) Low-rank matrix factorization for deep neural network training with high-dimensional output targets. IEEE ICASSP

  32. Saxe AM, Koh PW, Chen Z, Bhand M, Suresh B, Ng AY (2011) On random weights and unsupervised feature learning. In: ICML

  33. Simonyan K, Zisserman A (2014) Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556

  34. Sindhwani V, Sainath T, Kumar S (2015) Structured transforms for small-footprint deep learning. In: NIPS, pp 3088–3096

  35. Sompolinsky H, Crisanti A, Sommers H (1988) Chaos in random neural networks. Phys Rev Lett 61(3):259–262

    MathSciNet  Google Scholar 

  36. Srinivas S, Babu RV (2015) Data-free parameter pruning for deep neural networks. arXiv:1507.06149

  37. Sun KHXZSRJ (2015) Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. arXiv:1502.01852

  38. Wen W, Wu C, Wang Y, Chen Y, Li H (2016) Learning structured sparsity in deep neural networks. In: NIPS, pp 2074–2082

  39. Yuan M, Lin Y (2006) Model selection and estimation in regression with grouped variables. J R Stat Soc B 68(1):49–67

    MathSciNet  MATH  Google Scholar 

  40. Zeiler MD, Fergus R (2013) Visualizing and understanding convolutional networks. arXiv:1311.2901

  41. Zhang X, Zhou X, Lin M, Sun J (2017) Shufflenet: an extremely efficient convolutional neural network for mobile devices. arXiv:1707.01083

Download references

Acknowledgements

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1256260. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant No. OCI-1053575. Specifically, it used the Bridges system, which is supported by NSF Award No. ACI-1445606, at the Pittsburgh Supercomputing Center (PSC).

Author information

Authors and Affiliations

  1. University of Michigan, Ann Arbor, USA

    Amy Nesky & Quentin F. Stout

Authors
  1. Amy Nesky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Quentin F. Stout
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Amy Nesky.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nesky, A., Stout, Q.F. Neural networks with block diagonal inner product layers: a look at neural network architecture through the lens of random matrices. Neural Comput & Applic 32, 6755–6767 (2020). https://doi.org/10.1007/s00521-019-04531-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04531-z

Keywords

Search

Navigation