Skip to main content
SpringerLink
Log in

A compact Crank–Nicholson scheme for the numerical solution of fuzzy time fractional diffusion equations

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

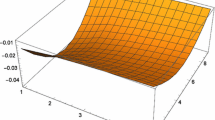
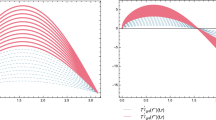
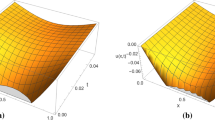
Abstract

Fuzzy fractional partial differential equations are a generalization of classical fuzzy partial differential equation which can, in certain circumstances, provide a better explanation for certain phenomena. In this paper, a compact Crank–Nicholson scheme is developed, analyzed and applied to solve the fuzzy time diffusion equation with fractional order \(0 < \alpha \le 1\). It is based on double parametric form of fuzzy numbers and the time fractional derivative is defined using the Caputo definition. The truncation error and stability of the proposed scheme is discussed. The compact Crank–Nicholson scheme is shown to be a feasible scheme via a numerical example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Bakalis E, Zerbetto F (2016) Time fractional diffusion equations and analytical solvable models. In: Journal of Physics: Conference Series (vol. 738, No. 1, p. 012106). IOP Publishing

  2. Al-Smadi M, Arqub OA (2019) Computational algorithm for solving Fredholm time-fractional partial integrodifferential equations of Dirichlet functions type with error estimates. Appl Math Comput 342:280–294

    MathSciNet  MATH  Google Scholar 

  3. Çetinkaya A, Kıymaz O (2013) The solution of the time-fractional diffusion equation by the generalized differential transform method. Math Comput Model 57(9–10):2349–2354

    Article  MATH  Google Scholar 

  4. Al-Smadi M (2018) Simplified iterative reproducing kernel method for handling time-fractional BVPs with error estimation. Ain Shams Eng J 9(4):2517–2525

    Article  Google Scholar 

  5. Arqub OA, Al-Smadi M (2018) Atangana–Baleanu fractional approach to the solutions of Bagley–Torvik and Painlevé equations in Hilbert space. Chaos, Solitons Fractals 117:161–167

    Article  MathSciNet  Google Scholar 

  6. Al-Smadi M, Freihat A, Khalil H, Momani S, Ali Khan R (2017) Numerical multistep approach for solving fractional partial differential equations. Int J Comput Methods 14(03):1750029

    Article  MathSciNet  MATH  Google Scholar 

  7. Das S (2009) Analytical solution of a fractional diffusion equation by variational iteration method. Comput Math Appl 57(3):483–487

    Article  MathSciNet  MATH  Google Scholar 

  8. Ghazanfari B, Ebrahimi P (2015) Differential transformation method for solving fuzzy fractional heat equations. Int J Math Model Comput 5(1):81–89

    Google Scholar 

  9. Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications (vol 198). Elsevier, Amsterdam

    Google Scholar 

  10. Lin Y, Xu C (2007) Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys 225(2):1533–1552

    Article  MathSciNet  MATH  Google Scholar 

  11. Ma Y (2014) Two implicit finite difference methods for time fractional diffusion equation with source term. J Appl Math Bioinform 4(2):125–145

    MathSciNet  MATH  Google Scholar 

  12. Cui M (2009) Compact finite difference method for the fractional diffusion equation. J Comput Phys 228(20):7792–7804

    Article  MathSciNet  MATH  Google Scholar 

  13. Gao GH, Sun ZZ (2011) A compact finite difference scheme for the fractional sub-diffusion equations. J Comput Phys 230(3):586–595

    Article  MathSciNet  MATH  Google Scholar 

  14. Karatay I, Bayramoglu SR (2014) High-order compact difference scheme for the numerical solution of time fractional heat equations. Sci World J. https://doi.org/10.1155/2014/642989

    Article  MATH  Google Scholar 

  15. Al-Shibani FS, Ismail AIM, Abdullah FA (2013) Compact finite difference methods for the solution of one dimensional anomalous sub-diffusion equation. G E N 18(2):104–119

    MathSciNet  Google Scholar 

  16. Ghazanfari B, Ebrahimi P (2015) Differential transformation method for solving fuzzy fractional heat equations. Int J Math Model Comput 5(1):81–89

    Google Scholar 

  17. Salah A, Khan M, Gondal MA (2013) A novel solution procedure for fuzzy fractional heat equations by homotopy analysis transform method. Neural Comput Appl 23(2):269–271

    Article  Google Scholar 

  18. Chakraverty S, Tapaswini S (2014) Non-probabilistic solutions of imprecisely defined fractional-order diffusion equations. Chin Phys B 23(12):120–202

    Article  MATH  Google Scholar 

  19. Zureigat H, Ismail AI, Sathasivam S (2018) Numerical solutions of fuzzy fractional diffusion equations by an implicit finite difference scheme. Neural Comput Appl. https://doi.org/10.1007/s00521-017-3299-7

    Article  Google Scholar 

  20. Karatay İ, Bayramoğlu ŞR, Şahin A (2011) Implicit difference approximation for the time fractional heat equation with the nonlocal condition. Appl Numer Math 61(12):1281–1288

    Article  MathSciNet  MATH  Google Scholar 

  21. Yuste SB (2006) Weighted average finite difference methods for fractional diffusion equations. J Comput Phys 216(1):264–274

    Article  MathSciNet  MATH  Google Scholar 

  22. Ding HF, Zhang YX (2011) Notes on Implicit finite difference approximation for time fractional diffusion equations [Comput. Math. Appl. 56 (2008) 1138–1145]. Comput Math Appl 61(9):2924–2928

    Article  MathSciNet  MATH  Google Scholar 

  23. Liu F, Zhuang P, Anh V, Turner I, Burrage K (2007) Stability and convergence of the difference methods for the space–time fractional advection–diffusion equation. Appl Math Comput 191(1):12–20

    MathSciNet  MATH  Google Scholar 

  24. Arqub OA, Mohammed AS, Momani S, Hayat T (2016) Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput 20(8):3283–3302

    Article  MATH  Google Scholar 

  25. Arqub OA, Al-Smadi M, Momani S, Hayat T (2017) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput 21(23):7191–7206

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Pinang, Malaysia

    Hamzeh Zureigat, Ahmad Izani Ismail & Saratha Sathasivam

Authors
  1. Hamzeh Zureigat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmad Izani Ismail
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saratha Sathasivam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamzeh Zureigat.

Ethics declarations

Conflict of interest

All authors declare they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zureigat, H., Ismail, A.I. & Sathasivam, S. A compact Crank–Nicholson scheme for the numerical solution of fuzzy time fractional diffusion equations. Neural Comput & Applic 32, 6405–6412 (2020). https://doi.org/10.1007/s00521-019-04148-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04148-2

Keywords

Search

Navigation