Skip to main content
SpringerLink
Log in

An inertial-type method for solving image restoration problems

  • Optimization
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

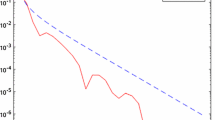
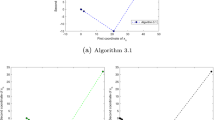
We first establish weak convergence results regarding an inertial Krasnosel’skiĭ-Mann iterative method for approximating common fixed points of countable families of nonexpansive mappings in real Hilbert spaces with no extra assumptions on the considered countable families of nonexpansive mappings. The method of proof and the imposed conditions on the iterative parameters are different from those already available in the literature. We then present some applications to the Douglas–Rachford splitting method and image restoration problems, and compare the performance of our method with that of other popular inertial Krasnosel’skiĭ-Mann methods which can be found in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Alvarez F, Attouch H (2001) An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set Valued Anal 9:3–11

    MathSciNet  MATH  Google Scholar 

  • Aoyama K, Kimura Y, Takahashi W, Toyoda M (2007) Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Anal 67:2350–2360

    MathSciNet  MATH  Google Scholar 

  • Attouch H, Cabot A (2020) Convergence of a relaxed inertial proximal algorithm for maximally monotone operators. Math Program 184:243–287

    MathSciNet  MATH  Google Scholar 

  • Attouch H, Goudon X, Redont P (2000) The heavy ball with friction. I. The continuous dynamical system. Commun Contemp Math 2(1):1–34

    MathSciNet  MATH  Google Scholar 

  • Attouch H, Czarnecki MO (2002) Asymptotic control and stabilization of nonlinear oscillators with non-isolated equilibria. J Differ Equ 179(1):278–310

    MathSciNet  MATH  Google Scholar 

  • Attouch H, Peypouquet J, Redont P (2014) A dynamical approach to an inertial forward-backward algorithm for convex minimization. SIAM J Optim 24:232–256

    MathSciNet  MATH  Google Scholar 

  • Attouch H, Peypouquet J (2016) The rate of convergence of Nesterov’s accelerated forward-backward method is actually faster than \(\frac{1}{k^2}\). SIAM J Optim 26:1824–1834

    MathSciNet  MATH  Google Scholar 

  • Bauschke HH (1996) The approximation of fixed points of compositions of nonexpansive mappings in Hilbert space. J Math Anal Appl 202:150–159

    MathSciNet  MATH  Google Scholar 

  • Bauschke HH, Combettes PL (2011) Convex analysis and monotone operator theory in Hilbert spaces. CMS books in mathematics. Springer, New York

    MATH  Google Scholar 

  • Bauschke HH, Burachik RS, Combettes PL, Elser V, Luke DR, Wolkowicz H (eds) (2011) Fixed-point algorithms for inverse problems in science and engineering, springer optimization and its applications. Springer, New York

    Google Scholar 

  • Bauschke HH, Matoušková E, Reich S (2004) Projection and proximal point methods: convergence results and counterexamples. Nonlinear Anal 56:715–738

    MathSciNet  MATH  Google Scholar 

  • Beck A, Teboulle M (2009) A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci 2(1):183–202

    MathSciNet  MATH  Google Scholar 

  • Berinde V (2007) Iterative approximation of fixed points. Lecture notes in mathematics, vol 1912. Springer, Berlin

    MATH  Google Scholar 

  • Bot RI, Meier D (2021) A strongly convergent Krasnosel’skiĭ-Mann-type algorithm for finding a common fixed point of a countably infinite family of nonexpansive operators in Hilbert spaces. J Comput Appl Math 395:113589

    MATH  Google Scholar 

  • Bot RI, Csetnek ER, Hendrich C (2015) Inertial Douglas-Rachford splitting for monotone inclusion problems. Appl Math Comput 256:472–487

    MathSciNet  MATH  Google Scholar 

  • Bot RI, Csetnek ER (2016) An inertial alternating direction method of multipliers. Minimax Theory Appl 1:29–49

    MathSciNet  MATH  Google Scholar 

  • Bot RI, Csetnek ER (2016) An inertial forward-backward-forward primal-dual splitting algorithm for solving monotone inclusion problems. Numer Algorithms 71:519–540

    MathSciNet  MATH  Google Scholar 

  • Browder FE (1968) Semicontractive and semiaccretive nonlinear mappings in Banach spaces. Bull Am Math Soc 74:660–665

    MathSciNet  MATH  Google Scholar 

  • Bruck RE Jr (1973) Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Trans Am Math Soc 179:251–262

    MathSciNet  MATH  Google Scholar 

  • Cegielski A (2012) Iterative methods for fixed point problems in Hilbert spaces. Lecture notes in mathematics, vol 2057. Springer, Berlin

    MATH  Google Scholar 

  • Chambolle A, Dossal C (2015) On the convergence of the iterates of the fast iterative shrinkage/thresholding algorithm. J Optim Theory Appl 166:968–982

    MathSciNet  MATH  Google Scholar 

  • Chang SS, Cho YJ, Zhou H (eds) (2002) Iterative methods for nonlinear operator equations in Banach spaces. Nova Science, Huntington

    MATH  Google Scholar 

  • Chen C, Chan RH, Ma S, Yang J (2015) Inertial proximal ADMM for linearly constrained separable convex optimization. SIAM J Imaging Sci 8:2239–2267

    MathSciNet  MATH  Google Scholar 

  • Chidume CE (2009) Geometric properties of Banach spaces and nonlinear iterations. Lecture notes in mathematics, vol 1965. Springer, London

    MATH  Google Scholar 

  • Cho YJ, Kang SM, Qin X (2008) Approximation of common fixed points of an infinite family of nonexpansive mappings in Banach spaces. Comput Math Appl 56:2058–2064

    MathSciNet  MATH  Google Scholar 

  • Dong QL, Huang JZ, Li XH, Cho YJ, Rassias TM (2019) MiKM: multi-step inertial Krasnosel’skiĭ-Mann algorithm and its applications. J Global Optim 73:801–824

    MathSciNet  MATH  Google Scholar 

  • Dong QL, Kazmi KR, Ali R, Li X-H (2019) Inertial Krasnosel’skiǐ-Mann type hybrid algorithms for solving hierarchical fixed point problems. J Fixed Point Theory Appl 21:57

    MATH  Google Scholar 

  • Dong QL, Yuan HB, Cho YJ, Rassias TM (2018) Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim Lett 12:87–102

    MathSciNet  MATH  Google Scholar 

  • Dong Y, Fischer A (2010) A family of operator splitting methods revisited. Nonlinear Anal 72:4307–4315

    MathSciNet  MATH  Google Scholar 

  • Dong Y (2020) New inertial factors of the Krasnosel’skiĭ-Mann iteration. Set Valued Var Anal. https://doi.org/10.1007/s11228-020-00541-5

    Article  MATH  Google Scholar 

  • Douglas J, Rachford HH (1956) On the numerical solution of heat conduction problems in two or three space variables. Trans Am Math Soc 82:421–439

    MathSciNet  MATH  Google Scholar 

  • Genel A, Lindenstrauss J (1975) An example concerning fixed points. Isr J Math 22:81–86

    MathSciNet  MATH  Google Scholar 

  • Goebel K, Reich S (1984) Uniform convexity, hyperbolic geometry, and nonexpansive mappings. Marcel Dekker, New York

    MATH  Google Scholar 

  • Kimura Y, Takahashi W, Toyoda M (2005) Convergence to common fixed points of a finite family of nonexpansive mappings. Arch Math 84:350–363

    MathSciNet  MATH  Google Scholar 

  • Klin-eam C, Suantai S (2010) Strong convergence of composite iterative schemes for a countable family of nonexpansive mappings in Banach spaces. Nonlinear Anal 73:431–439

    MathSciNet  MATH  Google Scholar 

  • O’Hara JG, Pillay P, Xu H-K (2003) Iterative approaches to finding nearest common fixed points of nonexpansive mappings in Hilbert spaces. Nonlinear Anal 54:1417–1426

    MathSciNet  MATH  Google Scholar 

  • Krasnoselskii MA (1955) Two remarks on the method of successive approximations. Uspekhi Mat Nauk 10:123–127

    MathSciNet  Google Scholar 

  • Lions PL, Mercier B (1979) Splitting algorithms for the sum of two nonlinear operators. SIAM J Numer Anal 16:964–979

    MathSciNet  MATH  Google Scholar 

  • Lorenz DA, Pock T (2015) An inertial forward-backward algorithm for monotone inclusions. J Math Imaging Vis 51:311–325

    MathSciNet  MATH  Google Scholar 

  • Maingé PE (2008) Convergence theorems for inertial KM-type algorithms. J Comput Appl Math 219:223–236

    MathSciNet  MATH  Google Scholar 

  • Mann WR (1953) Mean value methods in iteration. Bull Am Math Soc 4:506–510

    MathSciNet  MATH  Google Scholar 

  • Matsushita S-Y (2017) On the convergence rate of the Krasnoselskii-Mann iteration. Bull Aust Math Soc 96:162–170

    MathSciNet  MATH  Google Scholar 

  • Nesterov Y (1983) A method of solving a convex programming problem with convergence rate O(\(1/k^2\)). Sov Math Dokl 27:372–376

    MATH  Google Scholar 

  • Nilsrakoo W, Saejung S (2009) Weak convergence theorems for a countable family of Lipschitzian mappings. J Comput Appl Math 230:451–462

    MathSciNet  MATH  Google Scholar 

  • Nilsrakoo W, Saejung S (2009) Strong convergence theorems for a countable family of quasi-Lipschitzian mappings and its applications. J Math Anal Appl 356:154–167

    MathSciNet  MATH  Google Scholar 

  • Ochs P, Brox T, Pock T (2015) iPiasco: inertial proximal algorithm for strongly convex optimization. J Math Imaging Vis 53:171–181

    MathSciNet  MATH  Google Scholar 

  • Opial Z (1967) Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull Am Math Soc 73:591–597

    MathSciNet  MATH  Google Scholar 

  • Polyak BT (1964) Some methods of speeding up the convergence of iterarive methods. Zh Vychisl Mat Mat Fiz 4:1–17

    Google Scholar 

  • Reich S (1979) Weak convergence theorems for nonexpansive mappings in Banach spaces. J Math Anal Appl 67:274–276

    MathSciNet  MATH  Google Scholar 

  • Sahu DR, Colao V, Marino G (2013) Strong convergence theorems for approximating common fixed points of families of nonexpansive mappings and applications. J Glob Optim 56:1631–1651

    MathSciNet  MATH  Google Scholar 

  • Shimizu T, Takahashi W (1997) Strong convergence to common fixed points of families of nonexpansive mappings. J Math Anal Appl 211:71–83

    MathSciNet  MATH  Google Scholar 

  • Shioji N, Takahashi W (1997) Strong convergence of approximated sequences for nonexpansive mappings in Banach spaces. Proc Am Math Soc 125:3641–3645

    MathSciNet  MATH  Google Scholar 

  • Vong S, Liu D (2018) An inertial Mann algorithm for nonexpansive mappings. J Fixed Point Theory Appl 20:102

    MathSciNet  MATH  Google Scholar 

  • Yao Y, Liou Y-C (2008) Weak and strong convergence of Krasnoselski-Mann iteration for hierarchical fixed point problems. Inverse Prob 24:015015

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the editor and anonymous referees whose insightful comments and suggestions have helped them to substantially improve an earlier version of this paper.

Funding

Simeon Reich was partially supported by the Israel Science Foundation (Grant 820/17), by the Fund for the Promotion of Research at the Technion (Grant 2001893) and by the Technion General Research Fund (Grant 2016723).

Author information

Authors and Affiliations

  1. School of Mathematics, University of the Witwatersrand, Private Bag 3, Johannesburg, 2050, South Africa

    Chinedu Izuchukwu

  2. School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

    Yekini Shehu

  3. Department of Mathematics, The Technion – Israel Institute of Technology, 3200003, Haifa, Israel

    Simeon Reich

Authors
  1. Chinedu Izuchukwu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yekini Shehu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Simeon Reich
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed equally to the final version of the manuscript.

Corresponding author

Correspondence to Yekini Shehu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

All the authors approved the final version of this manuscript.

Informed consent

All the authors understand the purpose of the research and their individual roles.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Izuchukwu, C., Shehu, Y. & Reich, S. An inertial-type method for solving image restoration problems. Soft Comput 27, 16571–16587 (2023). https://doi.org/10.1007/s00500-023-08921-3

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-08921-3

Keywords

Search

Navigation