Attribute reduction of SE-ISI concept lattices for incomplete contexts

Abstract

Three-way concept analysis in incomplete contexts lays the theory dealing with the data in incomplete contexts, especially three kinds of partially known formal concepts including SE-ISI formal concept, ISE-SI formal concept and ISE-ISI formal concept. Generally speaking, not every attribute is essential in an incomplete context since the purpose of research is different. Thus, we propose four kinds of attribute reduction of SE-ISI concept lattices based on different criteria. Then, we discuss the relationships among the four kinds of attribute reduction, including the relationships among the consistent sets and relationships among the reducts. Finally, based on discernibility matrices and discernibility functions, the approaches to obtaining these attribute reduction are presented.

1 Introduction

Formal concept analysis (FCA), an efficient tool for decision making and knowledge discovery, was proposed by Wille (1982) and Ganter and Wille (1999). Formal context, formal concept and concept lattice are three basic notions of FCA. Formal context is the data foundation of FCA. Based on a formal context, formal concept, a pair of extent and intent, is obtained by a pair of derivation operators. All the formal concepts can form a complete lattice called a concept lattice, which is the basic structure of FCA. As an effective mathematical tool for conceptual data analysis and knowledge processing, both the theoretical researches and practical applications of FCA have been promoted. For the promotion of theoretical researches, many scholars have studied attribute reduction (Zhang et al. 2005; Wang and Ma 2006; Wei et al. 2008; Wang and Zhang 2008; Wu et al. 2009; Liu et al. 2009; Qi 2009; Li and Wu 2011; Medina 2012; Shao et al. 2013; Liang et al. 2013; Li et al. 2013a; Kumar et al. 2015; Ganter and Obiedkov 2016; Shao and Li 2016; Dias and Vieira 2017; Chen et al. 2018; Li and Zhang 2019), rules acquisition (Wille 1989; Missaoui et al. 1994; Li et al. 2013b; Shao et al. 2014), concept lattice construction (Nourine and Raynaud 1999; Djouadi and Prade 2010; Qian et al. 2017) and so on. For the development of practical applications, FCA has been used in disease control, chemistry, information retrieval, smart city, etc. (Tilley 2004; Kumar and Srinivs 2010; Quintero and Restrepo 2017; Xie et al. 2018).

In fact, being one of the key issues in knowledge discovery, attribute reduction has been extensively studied in different fields, since it can decrease the dimension and make data analysis easier. Attribute reduction is also an interesting topic in FCA, and many significant results about it have been obtained. For example, Ganter and Obiedkov (2016) proposed attribute reduction which refers to omitting attributes/objects that are equivalent to combinations of other attributes/objects. Zhang et al. (2005) discussed the attribute reduction that can keep the original concept lattice. Within such framework, Zhang et al. (2005) constructed judgment theorems of consistent sets, and developed approaches to attribute reduction based on discernibility matrix, which was further simplified by Qi (2009) from the viewpoint of parent–child concepts. Moreover, based on irreducible elements that play key roles in lattice construction, Wang and Ma (2006) and Li et al. (2013a) proposed the attribute reduction preserving the extents of meet-irreducible and join-irreducible elements in the original concept lattices, respectively. From the viewpoint of granular computing, Wu et al. (2009) proposed granular reduction. In general, the attribute reduction in References (Zhang et al. 2005; Wang and Ma 2006; Wu et al. 2009; Li et al. 2013a) is taken as four basic kinds of attribute reduction in FCA. Additionally, Liu et al. (2009) studied the attribute reduction of object oriented concept lattices and property oriented concept lattices. Furthermore, Wang and Zhang (2008) discussed the relationship between the attribute reduction of object and property oriented concept lattices. Besides, Li and Wu (2011) and Shao et al. (2013) studied attribute reduction from the perspectives of covering rough set theory and linear dependence of vectors, respectively.

In the framework of FCA, the relationship between objects and attributes is discussed from the perspectives of “commonly possess” and “be commonly possessed.” A formal concept has good semantic, since it can show some kind of “balance” between extent and intent. That is, all objects in the extent commonly possess all attributes in the intent, and all attributes in the intent are shared by all objects in the extent. Actually, the formal context also offers us the information whether an object (attribute) does not possess (is not shared by) an attribute (object), but this meaning is not reflected in formal concepts. Then, Qi et al. (2014, (2016) generalized FCA to three-way concept analysis (3WCA) through considering the “negative” property shown in formal contexts and introducing the idea of three-way decisions (Yao 2012, 2016; Fujita et al. 2016). Two key notions in 3WCA are object/attribute-induced three-way concepts and object/attribute-induced three-way concept lattices. Based on two kinds of three-way concept lattices, Ren and Wei (2016) defined four kinds of basic attribute reduction, and studied their relationships.

Both FCA and 3WCA are based on formal contexts, in which the relations between every object and every attribute are definite. However, we often encounter some situations with missing information in the real world; therefore, Burmeister and Holzer (2000) proposed incomplete contexts to reflect such situations. As for incomplete contexts, Djouadi et al. (2009) and Li et al. (2013c) defined ill-known formal concepts and approximate concepts, respectively. And then Yao (2017) gave a general framework for incomplete contexts, and defined three kinds of partially known formal concepts, including SE-ISI formal concept (i.e., approximate concept), ISE-SI formal concept and ISE-ISI formal concept (i.e., ill-known formal concept). To distinguish from three-way concepts and partially known formal concepts, formal concepts in FCA can be called classical formal concepts or SE-SI formal concepts. Furthermore, Ren et al. (2018) presented an analysis of the relationships among the three kinds of partially known formal concepts and SE-SI formal concepts.

With regard to attribute reduction of incomplete contexts, Li and Wang (2016) defined three-way approximate concept lattice reduction. Table 1 is a summary of some current works about attribute reduction.

Table 1 A summary of some current works about attribute reduction

In the above three kinds of partially known formal concepts, we think that SE-ISI formal concept has better semantic interpretation than the other two. Because the extent of an SE-ISI formal concept is a crisp set that is in more accordance with human cognition, and the intent of it is an interval set that can effectively process the uncertain information. Thus, for the extensive usages of SE-ISI formal concepts, we should make the discovery and representation of implicit knowledge in SE-ISI concept lattices easier and simpler. Therefore, based on different criteria, we propose four kinds of attribute reduction of SE-ISI concept lattices.

SE-ISI concept lattices constructed by SE-ISI formal concepts and their hierarchy relations can be viewed as the knowledge generated from the contexts. Thus, if an attribute reduct can preserve the basic structure of the lattice, then we consider that all the knowledge of the context is preserved. We know that the meet(join)-irreducible elements in a lattice play important roles; therefore, we propose two types of reduction, which can preserve all the extents of the two kinds of irreducible elements. Further, all the elements in SE-ISI concept lattices can be obtained by the join of SE-ISI object concepts induced by an object; therefore, SE-ISI object concepts can be viewed as information granules. Hence, we propose the reduction which can keep all the extents of such special concepts.

The main contributions of this paper include: (1) four kinds of attribute reduction of SE-ISI concept lattices are defined; (2) the relationships among four kinds of attribute reduction of SE-ISI concept lattices are analyzed; (3) the approaches to obtaining four kinds of attribute reduction of SE-ISI concept lattices are presented.

The rest of the paper is organized as follows. In Sect. 2, the basic knowledge of formal concept analysis and three-way concept analysis in incomplete contexts is reviewed. In Sect. 3, four different kinds of attribute reduction of SE-ISI concept lattices are defined, and their relationships including the relationships among the corresponding consistent sets and reducts are also discussed. Then, the approaches to computing the attribute reduction are presented in Sect. 4. Next, an empirical case is shown in Sect. 5. Finally, conclusions and future studies are given in Sect. 6.

2 Preliminaries

In order to make this paper self-contained, we first review some basic notions about formal concept analysis.

2.1 Basic notions about formal concept analysis

Definition 1

(Ganter and Wille 1999) A formal context ${\mathbb {K}}=(U,A,I)$ consists of two sets U and A and a relation I between U and A. The elements of U are called the objects and the elements of A are called the attributes of the context. In order to express that an object x is in a relation I with an attribute a, we write xIa or $(x,a)\in I$.

Given a formal context ${\mathbb {K}}=(U,A,I)$, a pair of derivation operators can be defined on $X\subseteq U,\ B\subseteq A$ by

$$\begin{aligned} \begin{aligned} X^{*}=\{a\in A\mid xIa\ \mathrm{for\ all}\ x\in X\},\\ B^{*}=\{x\in U\mid xIb\ \mathrm{for\ all}\ b\in B\}. \end{aligned} \end{aligned}$$

Based on the pair of derivation operators, a formal concept is defined as follows:

Definition 2

(Ganter and Wille 1999) Let ${\mathbb {K}}=(U,A,I)$ be a formal context. For any $X\subseteq U$, $B\subseteq A$, if $X^{*}=B, B^{*}=X$, then we call the pair (X, B) a formal concept, and call X the extent and B the intent of (X, B), respectively.

We use $L({\mathbb {K}})$ or L(U, A, I) to denote the set of all the formal concepts of ${\mathbb {K}}=(U,A,I)$. If any two formal concepts $(X_{i},B_{i})$, $(X_{j},B_{j})$ in $L({\mathbb {K}})$ are ordered by

$$\begin{aligned}&(X_{i},B_{i})\le (X_{j},B_{j})\Leftrightarrow X_{i}\\&\quad \subseteq X_{j}\Leftrightarrow B_{j}\subseteq B_{i}, \end{aligned}$$

and the infimum and supremum of them are defined by

$$\begin{aligned} \begin{aligned} (X_{i},B_{i})\wedge (X_{j},B_{j})=(X_{i}\cap X_{j},(B_{i}\cup B_{j})^{**}),\\ (X_{i},B_{i})\vee (X_{j},B_{j}) =((X_{i}\cup X_{j})^{**},B_{i}\cap B_{j}), \end{aligned} \end{aligned}$$

then the set $L({\mathbb {K}})$ is a complete lattice, which is called the concept lattice of ${\mathbb {K}}$.

Definition 3

(Zhang et al. 2005) Let ${\mathbb {K}}=(U,A,I)$ be a formal context and $L_{U}(U,A,I)=\{X|$$(X,B)\in L(U,A,I)\}$. If there exists an attribute set $D\subseteq A$ such that $L_{U}(U,D,I_{D})$$=L_{U}(U,A,I)$, where $I_{D}=I\cap U\times D$, then D is called a consistent set of ${\mathbb {K}}$. Further, if for any $d\in D$, $L_{U}(U,D-\{d\},I_{D-\{d\}})\not =L_{U}(U,A,I)$ holds, then the set D is called a reduct of ${\mathbb {K}}$.

Definition 4

(Davey and Priestley 1990) Let L be a lattice. An element $x\in L$ is called join-irreducible, if

• 1. $x\ne 0$ (in case L has a zero),

• 2. $x=a\vee b$ implies $x=a$ or $x=b$ for all $a,b\in L$. And the meet-irreducible element can be defined dually.

Example 1

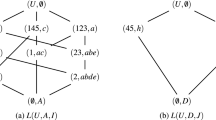
Table 2 shows a formal context ${\mathbb {K}}=(U,A,I)$, in which $U=\{1,2,3,4\}$ and $A=\{a,b,c,d,e\}$, where $(x,a_{i})=+$ means $xIa_{i}$ and $(x,a_{i})=-$ means $xI^{c}a_{i}$ for any $x\in U$ and $a_{i}\in A$. Figure 1 is the corresponding concept lattice of ${\mathbb {K}}$.

Table 2 A formal context ${\mathbb {K}}=(U,A,I)$

For convenience, we use the element sequence of a set to represent the set itself in a formal concept except the universal set and empty set. For instance, we denote $(\{1,2,4\},\{a,b\})$ as (124, ab) in Fig. 1. It is easily obtained that (124, ab) and (1, abde) are meet-irreducible and join-irreducible in $L({\mathbb {K}})$, respectively. For this formal context, $D=\{a,c,d\}$ is a reduct, whose corresponding concept lattice $L(U,D,I_{D})$ is shown in Fig. 2.

Fig. 1

$L({\mathbb {K}})$

Fig. 2

$L(U,D,I_{D})$

2.2 Basic notions about three-way concept analysis in incomplete contexts

Firstly, we introduce the notion of interval set in set theory.

An interval set on the finite set U is defined as: $[{\underline{A}}, {\overline{A}}]$=$\{A\subseteq U\mid {\underline{A}}\subseteq A \subseteq {\overline{A}}\}$=$\{A\in 2^{U} \mid {\underline{A}}\subseteq A \subseteq {\overline{A}}\}$, where ${\underline{A}}$ and ${\overline{A}}$ are called the lower bound and the upper bound of the interval set, respectively.

Let U be a finite set and $I(2^{U})=\{[{\underline{A}},\overline{A}]\mid {\underline{A}},{\overline{A}} \subseteq U, {\underline{A}}\subseteq {\overline{A}}\}$ be the set of all the interval sets over it. A partially order $\le$ between $[\underline{A_{1}}, \overline{A_{1}}]$, $[\underline{A_{2}}, \overline{A_{2}}]$ is defined by

$$\begin{aligned}{}[\underline{A_{1}}, \overline{A_{1}}]\le [\underline{A_{2}}, \overline{A_{2}}] \Leftrightarrow \underline{A_{1}}\subseteq \underline{A_{2}}\ \mathrm{and}\ \overline{A_{1}}\subseteq \overline{A_{2}}. \end{aligned}$$

In particularly, $[\underline{A_{1}}, \overline{A_{1}}]$ is said to be equal to $[\underline{A_{2}}, \overline{A_{2}}]$, denoted by $[\underline{A_{1}}, \overline{A_{1}}]=[\underline{A_{2}}, \overline{A_{2}}]$, if $\underline{A_{1}}=\underline{A_{2}}$ and $\overline{A_{1}}=\overline{A_{2}}$. And $[\underline{A_{1}}, \overline{A_{1}}]<[\underline{A_{2}}, \overline{A_{2}}]\Leftrightarrow [\underline{A_{1}}, \overline{A_{1}}]\le [\underline{A_{2}}, \overline{A_{2}}]$ and $[\underline{A_{1}}, \overline{A_{1}}]\not =[\underline{A_{2}}, \overline{A_{2}}]$. The intersection $(\sqcap )$, union $(\sqcup )$ and difference $(-)$ in $I(2^{A})$ are defined, respectively, as follows:

$$\begin{aligned} \begin{aligned}&[\underline{A_{1}}, \overline{A_{1}}]\sqcap [\underline{A_{2}}, \overline{A_{2}}]=[\underline{A_{1}}\cap \underline{A_{2}},\overline{A_{1}}\cap \overline{A_{2}}],\\&[\underline{A_{1}}, \overline{A_{1}}]\sqcup [\underline{A_{2}}, \overline{A_{2}}]=[\underline{A_{1}}\cup \underline{A_{2}},\overline{A_{1}}\cup \overline{A_{2}}],\\&[\underline{A_{1}}, \overline{A_{1}}]-[\underline{A_{2}}, \overline{A_{2}}]=[\underline{A_{1}}-\underline{A_{2}},\overline{A_{1}}-\overline{A_{2}}]. \end{aligned} \end{aligned}$$

In the rest of this section, the notions about three-way concept analysis in incomplete contexts are presented, and illustrated by an example.

Definition 5

(Burmeister and Holzer 2000) An incomplete context is a quadruple ${{\mathbb {I}}}{{\mathbb {K}}}=(U, A, \{+, ?, -\}, I)$, where U and A are the sets of objects and attributes under consideration, respectively, “$+$,” “?” and “−” are the three possible entries of the corresponding table, and I is a ternary relation $I\subseteq U\times A\times \{+, ?, -\}$, which can also be considered as the graph of a mapping—also designated by I—$I : U \times A\rightarrow \{+, ?, -\}$ from the set $U \times A$ of all pairs of objects and attributes into the set $\{+, ?, -\}$ of possible values. The interpretation of the relation I is as follows:

$(o, a, +) \in I$: it is known that the object o has the attribute a,

$(o, a, -) \in I$: it is known that the object o does not have the attribute a,

$(o, a, ?) \in I$: it is unknown whether or not the object o has the attribute a.

In general, we write $\{+, ?, -\}$ as V, then $(U,A,\{+, ?, -\},I)$ is denoted as (U, A, V, I).

Based on an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U, A,V, I)$ , the derivation operators ${\underline{R}}$ and ${\overline{R}}$ are defined on $O\in 2^{U}$ and $B\in 2^{A}$ by

$$\begin{aligned} \begin{aligned} {\underline{R}}(O)&= \{a\in A\vert \forall o\in O,\ (o, a, +)\in I \},\\ {\overline{R}}(O)&= \{a\in A\vert \forall o\in O,\ (o, a, +)\in I\vee (o, a, ?)\in I \},\\ {\underline{R}}(B)&= \{o\in U\vert \forall b\in B,\ (o, b, +)\in I \},\\ {\overline{R}}(B)&= \{o\in U\vert \forall b\in B,\ (o, b, +)\in I\vee (o, b, ?)\in I \}. \end{aligned} \end{aligned}$$

Then, extended derivation operators are defined in the next definition based on the derivation operators ${\underline{R}}$ and ${\overline{R}}$.

Definition 6

(Yao 2017) Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U, A, V, I)$ be an incomplete context, two extended derivation operators, $\unlhd : 2^U\rightarrow I(2^A)$, and $\unrhd : I(2^A)\rightarrow 2^U$ are defined on $O\in 2^{U}$ and $[{\underline{B}}, {\overline{B}}]\in I(2^{A})$ by

$$\begin{aligned} \begin{aligned}&O^{\unlhd }\ =\ [{\underline{R}}(O),{\overline{R}}(O)],\\&[{\underline{B}}, {\overline{B}}]^{\unrhd } \ =\ \underline{R}({\underline{B}})\cap {\overline{R}}({\overline{B}}). \end{aligned} \end{aligned}$$

Given an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$, then for any $O,\ O_{i},\ O_{j}\in 2^{U}$, $[{\underline{B}}, \overline{B}],[\underline{B_{i}}, \overline{B_{i}}],\ [\underline{B_{j}}, \overline{B_{j}}]\in I(2^{A})$, the following statements hold Ren et al. (2018).

$$\begin{aligned} \begin{aligned}&(1)\, O_{i}\subseteq O_{j} \Rightarrow O_{j}^{\unlhd }\le O_{i}^{\unlhd },\ [\underline{B_{i}}, \overline{B_{i}}]\\&\quad \le [\underline{B_{j}}, \overline{B_{j}}] \Rightarrow [\underline{B_{j}}, \overline{B_{j}}]^{\unrhd }\subseteq [\underline{B_{i}}, \overline{B_{i}}]^{\unrhd },\\&(2)\, O \subseteq O^{\unlhd \unrhd },\ [{\underline{B}}, {\overline{B}}]\le [{\underline{B}}, {\overline{B}}]^{\unrhd \unlhd },\\&(3)\, O^{\unlhd } = O^{\unlhd \unrhd \unlhd },\ [{\underline{B}}, {\overline{B}}]^{\unrhd } = [{\underline{B}}, {\overline{B}}]^{\unrhd \unlhd \unrhd },\\&(4)\, (O_{i}\cup O_{j})^{\unlhd } = O_{i}^{\unlhd }\sqcap O_{j}^{\unlhd },\ ([\underline{B_{i}}, \overline{B_{i}}]\sqcap [\underline{B_{j}}, \overline{B_{j}}])^{\unrhd }\\&\quad = [\underline{B_{i}}, \overline{B_{i}}]^{\unrhd }\cup [\underline{B_{j}}, \overline{B_{j}}]^{\unrhd }.\\ \end{aligned} \end{aligned}$$

Based on the pair of extended derivation operators, an SE-ISI formal concept is defined as follows:

Definition 7

(Yao 2017) In an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$, a pair of a set of objects and an interval set of attributes, $(O,[\underline{B},{\overline{B}}])$, is called a partially known formal concept with a set extent and an interval-set intent, or simply a partially known SE-ISI formal concept, if the following conditions hold:

$$\begin{aligned} O^{\unlhd }=[{\underline{B}},{\overline{B}}],\ [{\underline{B}},\overline{B}]^{\unrhd }=O. \end{aligned}$$

We call a partially known SE-ISI formal concept an SE-ISI formal concept in this paper. And in particular, for any $o\in U$, we know that $(o^{\unlhd \unrhd },o^{\unlhd })$ is an SE-ISI formal concept, which is called an SE-ISI object concept. Here, we write $o^{\unlhd }$ instead of $\{o\}^{\unlhd }$.

$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ or $L_{{\text {SE-ISI}}}(U,A,V,I)$ is used to denote the set of all the SE-ISI formal concepts of ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$. If every two SE-ISI formal concepts $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$ in $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ are ordered by

$$\begin{aligned}&(O_{i}, [\underline{B_{i}}, \overline{B_{i}}]) \le (O_{j}, [\underline{B_{j}}, \overline{B_{j}}]) \Leftrightarrow O_{i}\subseteq O_{j}\Leftrightarrow [\underline{B_{j}}, \overline{B_{j}}]\\&\quad \le [\underline{B_{i}}, \overline{B_{i}}] \end{aligned}$$

and the infimum and supremum of them are defined by

$$\begin{aligned} \begin{aligned}&(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\wedge (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\\&\quad =(O_{i} \cap O_{j},([\underline{B_{i}}, \overline{B_{i}}]\sqcup [\underline{B_{j}}, \overline{B_{j}}])^{\unrhd \unlhd }),\\&(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\vee (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\\&\quad =((O_{i} \cup O_{j})^{\unlhd \unrhd },\ [\underline{B_{i}}, \overline{B_{i}}]\sqcap [\underline{B_{j}}, \overline{B_{j}}]), \end{aligned} \end{aligned}$$

then the set $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ is a complete lattice, called the lattice of partially known formal concepts with a set extent and an interval-set intent, or simply partially known SE-ISI concept lattice. And we call it SE-ISI concept lattice for short.

Furthermore, we define the parent–child relation in an SE-ISI concept lattice as follows: if $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])<(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$ and there is no SE-ISI formal concept $(O_{k}, [\underline{B_{k}}, \overline{B_{k}}])$ such that $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])<(O_{k}, [\underline{B_{k}}, \overline{B_{k}}])<(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, then $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ is called a child concept of $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$ is called a parent concept of $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$, which is denoted by $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, where $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])<(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\Leftrightarrow (O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\le (O_{j}, [\underline{B_{j}},$$\overline{B_{j}}])$ and $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\not =(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$.

Example 2

Table 3 shows an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ in Anderson et al. (2004), in which the object set $U=\{1,2,3,4\}$ is a set of four patients who suffer from severe acute respiratory syndrome (SARS), and the attribute set A=$\{a,b,c,d,e,f,g\}$ is a set of seven symptoms (Fever, Cough, Headache, Difficulty Breathing, Diarrhea, Arrhythmia and Insomnia). Figure 3 is the corresponding SE-ISI concept lattice of ${{\mathbb {I}}}{{\mathbb {K}}}$.

Table 3 An incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$

Fig. 3

$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$

In fact, Yao (2017) has defined three kinds of partially known formal concepts. That is, SE-ISI formal concept, ISE-SI formal concept and ISE-ISI formal concept, and the differences of partially known formal concepts from SE-SI formal concept are that extents or/and intents of partially known formal concepts are interval sets. The details are briefly described in the following part and summarized in Table 4.

Given an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}=(U, A, V, I)$, another two pairs of extended derivation operators $\unlhd$ and $\unrhd$, $\lhd$ and $\rhd$ can be defined by

$$\begin{aligned} \begin{aligned} B^{\unlhd }&=[{\underline{R}}(B),{\overline{R}}(B)],\ [{\underline{O}}, {\overline{O}}]^{\unrhd } ={\underline{R}}({\underline{O}})\cap {\overline{R}}({\overline{O}}),\\ [{\underline{O}}, {\underline{O}}]^{\lhd }&=[{\underline{R}}(\underline{O}),{\overline{R}}({\underline{O}})], [{\underline{B}}, \underline{B}]^{\rhd }=[{\underline{R}}({\underline{B}}),{\overline{R}}({\underline{B}})], \end{aligned} \end{aligned}$$

where $B\in 2^{A}$, $[{\underline{O}}, \overline{O}]\in I(2^{U})$ and $[{\underline{B}}, {\overline{B}}]\in I(2^{A})$, then

• 1. A pair $([{\underline{O}},{\overline{O}}], B)$ is called a partially known formal concept with an interval-set extent and a set intent, or simply a partially known ISE-SI formal concept, if the following conditions hold: $[{\underline{O}},\overline{O}]^{\unrhd }=B,\ B^{\unlhd }=[{\underline{O}},{\overline{O}}]$.

• 2. A pair$([{\underline{O}},{\overline{O}}], [{\underline{B}},{\overline{B}}])$ is called a partially known formal concept with an interval-set extent and an interval-set intent, or simply a partially known ISE-ISI formal concept, if the following conditions hold: $[{\underline{O}},{\overline{O}}]^{\lhd }=[{\underline{B}},{\overline{B}}],\ [{\underline{B}},{\overline{B}}]^{\rhd }=[{\underline{O}},{\overline{O}}]$.

Example 3

(Continued with Example 2) It can be verified that ([14, 124], ab) is an ISE-SI formal concept and ([24, 24], [c, abcf]) is an ISE-ISI formal concept of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3.

Table 4 Four types of formal concepts

As we have introduced, SE-ISI formal concept has the better semantics and applications than the other two kinds of partially known formal concepts. Therefore, we just focus on SE-ISI formal concepts to study the attribute reduction of incomplete contexts in this paper.

3 Four types of attribute reduction of SE-ISI concept lattices

In this section, four kinds of attribute reduction of incomplete contexts are first proposed from different perspectives, that is, the structure of SE-ISI concept lattices, the construction of SE-ISI concept lattices and granular computing. Then, the relationships among the four kinds of attribute reduction are analyzed.

3.1 The definitions of attribute reduction of SE-ISI concept lattices

First, we denote the set of all the extents of concepts, the meet-irreducible concepts, the join-irreducible concepts of the SE-ISI concept lattice $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ by $Ext_\mathrm{L}({{\mathbb {I}}}{{\mathbb {K}}})$, $Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$, $Ext_{\mathrm{{J}}}({{\mathbb {I}}}{{\mathbb {K}}})$, respectively.

Definition 8

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, and $D\subseteq A$.

• 1. If $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{L}}(U,D,V,I_{D})$, then D is called an SE-ISI lattice (SE-ISIL for short) consistent set of ${{\mathbb {I}}}{{\mathbb {K}}}$, where $I_{D}=I\cap U\times D$.

• 2. If $Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{M}}(U,D,V,I_{D})$, then D is called an SE-ISI meet-irreducible elements-preserving (SE-ISIM for short) consistent set of ${{\mathbb {I}}}{{\mathbb {K}}}$, where $I_{D}=I\cap U\times D$.

• 3. If $Ext_{\mathrm{{J}}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{{J}}}(U,D,V,I_{D})$, then D is called an SE-ISI join-irreducible elements-preserving (SE-ISIJ for short) consistent set of ${{\mathbb {I}}}{{\mathbb {K}}}$, where $I_{D}=I\cap U\times D$.

• 4. If $o^{\unlhd \unrhd }=o^{\unlhd _{D}\unrhd _{D}}$ for any $o\in U$, then D is called an SE-ISI granular (SE-ISIG for short) consistent set of ${{\mathbb {I}}}{{\mathbb {K}}}$, where $\unlhd _{D}$ and $\unrhd _{D}$ are the derivation operators of $(U,D,V,I_{D})$.

Furthermore, if D is an SE-ISIL(resp. SE-ISIM, SE-ISIJ, SE-ISIG) consistent set, and no proper subset of D is, then D is called an SE-ISIL(resp. SE-ISIM, SE-ISIJ, SE-ISIG) reduct.

The reasons why four kinds of attribute reduction are proposed are as follows: First, we can see that all the information of an incomplete context can be reflected by the corresponding SE-ISI concept lattice straightforwardly, then SE-ISIL reduction is defined based on the structure of the lattices.

Then, based on lattice theory, the set of all the meet(join)-irreducible elements of a finite lattice is infimum(supremum)-dense in the lattice, that is, every element in the lattice can be represented by the meet(join) of meet(join)-irreducible elements, then these elements are the basic ones in lattice construction. Therefore, SE-ISIM reduction and SE-ISIJ reduction are defined from the viewpoint of lattice construction.

Finally, for the peculiarity of SE-ISI object concepts, all the SE-ISI formal concepts can be represented by the join of them, then SE-ISI object concepts can be regarded as information granules. Then, we propose the notion of SE-ISIG reduction from the viewpoint of granular computing.

In some application occasions, the equivalent description of SE-ISIL reduction may be more useful; we present it in the next lemma. First, the isomorphic relation between two SE-ISI concept lattices are defined as follows:

Definition 9

Let $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$, $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$ be the set of all the extents of SE-ISIL formal concepts in $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$, $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$, respectively. If for any $O_{j}\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$, there exists $O_{i}\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$ such that $O_{i}=O_{j}$, then we say that $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$ is finer than $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$, and denote by $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})\le L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$. Further, if $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})\le L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$ and $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})\le L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$, we call that $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})$ is isomorphic to $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$, and denote by $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{i})\cong L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{j})$.

Lemma 1

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, and $D\subseteq A$. Then, D is an SE-ISIL consistent set if and only if $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})\cong L_{{\text {SE-ISI}}}(U,D,V,I_{D})$.

Proof

It can be obtained from the definitions straightforwardly. $\square$

To make our discussion more convenient, the sets of four kinds of consistent sets of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ are, respectively, denoted by $\textit{CS}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})$, $\textit{CS}_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$, $\textit{CS}_\mathrm{J}({{\mathbb {I}}}{{\mathbb {K}}})$ and $\textit{CS}_{\mathrm{G}}({{\mathbb {I}}}{{\mathbb {K}}})$ by the order of being proposed. The sets of four kinds of reducts are, respectively, denoted by $\textit{Red}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})$, $\textit{Red}_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$, $\textit{Red}_\mathrm{J}({{\mathbb {I}}}{{\mathbb {K}}})$ and $\textit{Red}_{\mathrm{G}}({{\mathbb {I}}}{{\mathbb {K}}})$. If there is no ambiguity, $({{\mathbb {I}}}{{\mathbb {K}}})$ can be omitted.

Example 4

(Continued with Example 2) For the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3, the attribute subset $A_{1}=\{a,d,f,g\}$ is an SE-ISIL reduct, and its corresponding concept lattice $L_{{\text {SE-ISI}}}(U,A_{1},V,I_{A_{1}})$ is shown in Fig. 4 which is obviously isomorphic to $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ in Fig. 3. $A_{2}=\{b,c,d,g\}$ is an SE-ISIM reduct preserving all the extents of meet-irreducible elements (i.e., $C_{2}$, $C_{3}$, $C_{4}$, $C_{6}$ and $C_{7}$) in $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, and its concept lattice $L_{{\text {SE-ISI}}}(U,$$A_{2},V,I_{A_{2}})$ is shown in Fig. 5. $A_{3}=\{d,f,g\}$ is both an SE-ISIJ and SE-ISIG reduct, since it can preserve all the extents of join-irreducible elements (i.e., $C_{4}$, $C_{8}$, $C_{9}$ and $C_{10}$) and SE-ISI object concepts (i.e., $C_{4}$, $C_{8}$, $C_{9}$ and $C_{10}$) in $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, and the concept lattice of it is shown in Fig. 6.

Fig. 4

$L_{{\text {SE-ISI}}}(U,A_{1},V,I_{A_{1}})$

Fig. 5

$L_{{\text {SE-ISI}}}(U,A_{2},V,I_{A_{2}})$

Fig. 6

$L_{{\text {SE-ISI}}}(U,A_{3},V,I_{A_{3}})$

3.2 The relationships among four types of attribute reduction of SE-ISI concept lattices

Because the aforementioned four kinds of attribute reduction of SE-ISI concept lattices are proposed from different perspectives, the relationships among them deserve being discussed.

3.2.1 The relationship between SE-ISIL reduction and SE-ISIM reduction

In this section, we investigate the relationship between SE-ISIL reduction and SE-ISIM reduction, including the relationship between the corresponding consistent sets and the reducts.

Lemma 2

Davey and Priestley (1990) Let L be a finite lattice, then every element in L is the join(meet) of join(meet)-irreducible elements.

Theorem 1

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, then $\textit{CS}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})= \textit{CS}_\mathrm{M}({{\mathbb {I}}}{{\mathbb {K}}})$ and $\textit{Red}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})= \textit{Red}_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$ hold.

Proof

We prove $\textit{CS}_{\mathrm{L}}=\textit{CS}_{\mathrm{M}}$ firstly. To prove $\textit{CS}_{\mathrm{L}}= \textit{CS}_{\mathrm{M}}$ holds, we only need to prove that $\textit{CS}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{M}}$ and $\textit{CS}_{\mathrm{M}}\subseteq \textit{CS}_{\mathrm{L}}$.

First, we prove that $\textit{CS}_{\mathrm{L}}\subseteq \textit{CS}_\mathrm{M}$. Suppose $D\in \textit{CS}_{\mathrm{L}}$, then $Ext_{\textit{L}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\textit{L}}(U,D,V,I_{D})$ holds. For all $O_{i}\in Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$, we can know that if $O_{i}\not =O_{j}$ and $O_{i}\not =O_{k}$, then $O_{i}\not =O_{j}\cap O_{k}$ for any $O_{j},\ O_{k}\in Ext_{\textit{L}}({{\mathbb {I}}}{{\mathbb {K}}})$. Since $Ext_\mathrm{L}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\textit{L}}(U,D,V,I_{D})$, then $O_{i}$, $O_{j}$, $O_{k}\in Ext_{\mathrm{L}}(U,D,V,I_{D})$, thus, $O_{i}\in Ext_{\mathrm{M}}(U,D,V,I_{D})$. That is, $Ext_\mathrm{M}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq Ext_{\mathrm{M}}(U,D,V,I_{D})$. And for $D\subseteq A$, it is easy to know that $Ext_\mathrm{M}(U,D,V,I_{D})\subseteq Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})$. Thus, we have $Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{M}}(U,D,V,I_{D})$. Then, $D\in \textit{CS}_{\mathrm{M}}$ can be obtained, that is, $\textit{CS}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{M}}$.

Then, we prove $\textit{CS}_{\mathrm{M}}\subseteq \textit{CS}_{\mathrm{L}}$. For any $D\in \textit{CS}_{\mathrm{M}}$, if we want to prove $D\in \textit{CS}_{\mathrm{L}}$, then $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_\mathrm{L}(U,D,V,I_{D})$ needs to be proved. Since $Ext_\mathrm{L}(U,D,V,I_{D})\subseteq Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})$, then we only need to prove $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq Ext_\mathrm{L}(U,D,V,I_{D})$. For every $O\in Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})$, there exists $\{O_{i}|O_{i}\in Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}}),$$i\in T\}$ such that $O=\cap _{i\in T}O_{i}$. And for $D\in \textit{CS}_{\mathrm{M}}$, we can get that $Ext_{\mathrm{M}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{M}}(U,D,V,I_{D})$. Thus, we obtain that $O\in Ext_{\mathrm{L}}(U,D,V,I_{D})$, then $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq Ext_{\mathrm{L}}(U,D,V,I_{D})$ holds. Therefore, we have $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_\mathrm{L}(U,D,V,I_{D})$. Then, $D\in \textit{CS}_{\mathrm{L}}$ can be obtained, that is, $\textit{CS}_{\mathrm{M}}\subseteq \textit{CS}_{\mathrm{L}}$. $\square$

From the above discussion, $\textit{CS}_{\mathrm{L}}=\textit{CS}_{\mathrm{M}}$ is proved, which is the first part of the theorem. And the another part $\textit{Red}_{\mathrm{L}}=\textit{Red}_{\mathrm{M}}$ can be naturally proved from the relations between consistent sets and reducts.

Theorem 1 shows that SE-ISIL reducts (consistent sets) equals to SE-ISIM reducts (consistent sets), which can be verified by the next example.

Example 5

(Continued with Example 2) For the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ shown in Table 3, we can verify that $\textit{CS}_\mathrm{L}=\textit{CS}_{\mathrm{M}}$=$\{\{a,c,d,g\},$$\{a,d,f,g\},\ \{b,c,d,g\},$$\{b,d,f,g\}\}$, $\textit{Red}_\mathrm{L}=\textit{Red}_{\mathrm{M}}$=$\{\{a,c,d,g\},$$\{a,d,f,g\},\ \{b,c,d,g\},$$\{b,d,f,g\}\}$

3.2.2 The relationship between SE-ISIL reduction and SE-ISIG reduction

In this section, the relationship between SE-ISIL reduction and SE-ISIG reduction is discussed.

Lemma 3

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, $O\subseteq U$. If $D\subseteq A$, then $O^{\unlhd \unrhd }\subseteq O^{\unlhd _{D} \unrhd _{D}}$ holds. Further, if D is an SE-ISIL consistent set, then $O^{\unlhd \unrhd }= O^{\unlhd _{D} \unrhd _{D}}$ holds.

Proof

For any $O\subseteq U$ and $D\subseteq A$, we have $O^{\unlhd _{D}}\le O^{\unlhd }$, then $O^{\unlhd \unrhd }\subseteq O^{\unlhd _{D} \unrhd _{D}}$ holds from the properties of derivation operators. Further, if D is an SE-ISIL consistent set, then $Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})=Ext_{\mathrm{L}}(U,D,V,I_{D})$ holds. Since $O^{\unlhd \unrhd }\in Ext_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $O^{\unlhd _{D} \unrhd _{D}}\in Ext_{\mathrm{L}}(U,D,V,I_{D})$, then we have $O^{\unlhd \unrhd }=O^{\unlhd _{D} \unrhd _{D}}$. $\square$

From Lemma 3, we can indicate that if D is an SE-ISIL consistent set, then $o^{\unlhd \unrhd }=o^{\unlhd _{D} \unrhd _{D}}$ holds for every $o\in U$. That is, D is an SE-ISIG consistent set, so we obtain the next theorem.

Theorem 2

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, then $\textit{CS}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq \textit{CS}_\mathrm{G}({{\mathbb {I}}}{{\mathbb {K}}})$ and $\textit{Red}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq \textit{CS}_{\mathrm{G}}({{\mathbb {I}}}{{\mathbb {K}}})$ hold.

Proof

First, we can obtain that $\textit{CS}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{G}}$ based on Lemma 3, and we also know that $\textit{Red}_{\mathrm{L}}$$\subseteq \textit{CS}_{\mathrm{L}}$. Thus, $\textit{Red}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{G}}$ can be proved straightforwardly. $\square$

From Theorem 2, we know that if D is an SE-ISIL consistent set (reduct), it must be an SE-ISIG consistent set, but it may not be an SE-ISIG reduct. And vice versa, if D is an SE-ISIG consistent set (reduct), it may not be an SE-ISIL consistent set (reduct). The above statement can be illustrated by Example 6.

Example 6

(Continued with Example 4) For the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ shown in Table 3, $A_{1}=\{a,d,f,g\}$ is both an SE-ISIL reduct and SE-ISIG consistent set of ${{\mathbb {I}}}{{\mathbb {K}}}$, but it is not an SE-ISIG reduct. Because there exists a proper subset $A_{3}=\{d,f,g\}\subset A_{1}$ being an SE-ISIG reduct. And vice versa, the set $A_{3}$ is an SE-ISIG reduct rather than an SE-ISIL consistent set (reduct).

3.2.3 The relationship between SE-ISIL reduction and SE-ISIJ reduction

In this section, we present the relationship between SE-ISIL reduction and SE-ISIJ reduction.

Theorem 3

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, then $\textit{CS}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq \textit{CS}_\mathrm{J}({{\mathbb {I}}}{{\mathbb {K}}})$ and $\textit{Red}_{\mathrm{L}}({{\mathbb {I}}}{{\mathbb {K}}})\subseteq \textit{CS}_{\mathrm{J}}({{\mathbb {I}}}{{\mathbb {K}}})$ hold.

Proof

Based on the definitions of SE-ISIL and SE-ISIJ reduction, we can obtain that $\textit{CS}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{J}}$, and we also have that $\textit{Red}_{\mathrm{L}}\subseteq \textit{CS}_\mathrm{L}$. Then, $\textit{Red}_{\mathrm{L}}\subseteq \textit{CS}_{\mathrm{J}}$ holds. $\square$

From Theorem 3, we know that if D is an SE-ISIL consistent set (reduct), it must be an SE-ISIJ consistent set, but may not be an SE-ISIJ reduct. And vice versa, if D is an SE-ISIJ consistent set (reduct), it may not be an SE-ISIL consistent set (reduct). As shown in Example 6, $A_{3}$ is also an SE-ISIJ reduct, so the example can verify the statement too.

3.2.4 The relationship between SE-ISIJ reduction and SE-ISIG reduction

It is worth noting that there is actually no direct relationship between SE-ISIJ reduction and SE-ISIG reduction, which is explained in details in the next three examples. First, we state that an SE-ISIJ reduct may not be an SE-ISIG reduct.

Example 7

Table 5 is an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{1}=(U_{1},A_{4},V,I_{A_{4}})$, where the object set $U_{1}=\{1,2,3,4,5\}$, the attribute set $A_{4}=\{a,b,c,d,e\}$. $A_{5}=\{c,d,e\}$ is an attribute subset, Figs. 7 and 8 are the SE-ISI concept lattices of ${{\mathbb {I}}}{{\mathbb {K}}}_{1}$ and $(U_{1},A_{5},V,I_{A_{5}})$, respectively. It can be verified that $A_{5}=\{c,d,e\}$ is an SE-ISIJ reduct rather than an SE-ISIG consistent set (reduct), because $5^{\unlhd _{A_{4}}\unrhd _{A_{4}}}=\{1,3,5\}$ in ${{\mathbb {I}}}{{\mathbb {K}}}_{1}$ and $5^{\unlhd _{A_{5}}\unrhd _{A_{5}}}=U_{1}$ in $(U_{1},A_{5},V,I_{A_{5}})$.

Table 5 An incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{1}=(U_{1},A_{4},V,I_{A_{4}})$

Fig. 7

$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{1})$

Fig. 8

$L_{{\text {SE-ISI}}}(U_{1},A_{5},V,I_{A_{5}})$

Then, we show that an SE-ISIG reduct may not be an SE-ISIJ reduct.

Example 8

Table 6 is an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{2}=(U_{2},A_{6},V,I_{A_{6}})$ whose object set $U_{2}=\{1,2,3,4\}$ and attribute set $A_{6}=\{a,b,c,d,e\}$. $A_{7}=\{a,b,d,e\}$ is an attribute subset, and SE-ISI concept lattices of ${{\mathbb {I}}}{{\mathbb {K}}}_{2}$ and $(U_{2},A_{7},V,I_{A_{7}})$ are shown in Figs. 9 and 10, respectively.

From the figures, we can know that $A_{7}=\{a,b,d,e\}$ is an SE-ISIG reduct rather than an SE-ISIJ consistent set or reduct, because the element $C_{2}$ in $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{2})$ is join-irreducible and $C_{2}=C_{3} \cup C_{4}$ is join-reducible in $L_{{\text {SE-ISI}}}(U_{2},A_{7},V,I_{A_{7}})$, thus $Ext_{{\mathrm{J}}}({{\mathbb {I}}}{{\mathbb {K}}}_{2})\not =Ext_\mathrm{J}(U_{2},A_{7},V,$$I_{A_{7}})$. Actually, $Ext_\mathrm{J}({{\mathbb {I}}}{{\mathbb {K}}}_{2})=\{1,2,4,123\}$ and $Ext_\mathrm{J}(U_{2},A_{7},V,I_{A_{7}})=\{1,2,4\}$

Table 6 An incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{2}=(U_{2},A_{6},V,I_{A_{6}})$

Fig. 9

$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{2})$

Fig. 10

$L_{{\text {SE-ISI}}}(U_{2},A_{7},V,I_{A_{7}})$

At last, we state that there exists an attribute subset being both an SE-ISIJ reduct and SE-ISIG reduct.

Example 9

It can be verified that $A_{3}=\{d,f,g\}$ is both an SE-ISIJ reduct and SE-ISIG reduct of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ in Example 2.

From Examples 7 to 9, we can conclude that there is no precise relationship between SE-ISIJ reduction and SE-ISIG reduction.

Based on the above analysis, we can sum up the relationships among these four kinds of attribute reduction of SE-ISI concept lattices in Fig. 11. Moreover, further explanations about the relationships among SE-ISI consistent sets and SE-ISI reducts are presented in Figs. 12 and 13, respectively.

Fig. 11

The relationships among the four kinds of attribute reduction of SE-ISI concept lattices

Fig. 12

The explanation of the relationships among the four kinds of SE-ISI consistent sets

Fig. 13

The explanation of the relationships among the four kinds of SE-ISI reducts

4 Approaches to attribute reduction of SE-ISI concept lattices

In Sect. 3, we introduced four different attribute reduction of SE-ISI concept lattices, and gave some examples to illustrate the definitions and the relationships about them. In this section, the approaches to computing the attribute reduction by discernibility matrices and discernibility functions are proposed.

The method of discernibility matrix put forward by Zhang et al. (2005) aims to complete contexts, we generalize it to incomplete contexts as follows:

Definition 10

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$. Then, the set

$\textit{Dis}_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]), (O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))$

$$\begin{aligned} =\left\{ \begin{array}{l@{\quad }l} (\underline{B_{i}}-\underline{B_{j}})\cup (\overline{B_{i}}-\overline{B_{j}}), &{} \text {if }(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\\ \ \ \ \ \ \ \ \ \ \ {\varnothing }, &{} \text {otherwise}\\ \end{array} \right. \end{aligned}$$

is called the SE-ISIL discernibility attribute set of $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$.

$\varLambda _{\mathrm{L}}=(\textit{Dis}_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]), (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])))$ is called the SE-ISIL discernibility matrix of ${{\mathbb {I}}}{{\mathbb {K}}}$, where $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$, $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\in L_{{\text {SE-ISI}}} ({{\mathbb {I}}}{{\mathbb {K}}})$. Furthermore, if $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ is a join(meet)-irreducible element, then the matrix is called the SE-ISIJ(SE-ISIM) discernibility matrix of ${{\mathbb {I}}}{{\mathbb {K}}}$, denoted by $\varLambda _{\mathrm{J}}$($\varLambda _{\mathrm{M}}$). If $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ is an SE-ISI object concept, then $(Dis_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]), (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])))$ is called the SE-ISIG discernibility matrix of ${{\mathbb {I}}}{{\mathbb {K}}}$, written as $\varLambda _{\mathrm{G}}$.

Example 10

(Continued with Example 2) The SE-ISIL discernibility matrix of ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3 is shown in Table 7, in which the concepts of the 1st column(row) are child(parent) concepts. If an SE-ISIL discernibility attribute set is $\varnothing$, then we denote it as a space.

Table 7 The SE-ISIL discernibility matrix of ${{\mathbb {I}}}{{\mathbb {K}}}$

Based on SE-ISIL discernibility matrix, how to judge an attribute subset is an SE-ISIL consistent set or not will be illustrated in the next theorem. First, we give several lemmas which are useful in the proof of the theorem.

Lemma 4

Li et al. (2013c) Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, $D\subseteq A$, $O\in 2^{U}$ and $[{\underline{B}}, {\overline{B}}]\in I(2^{D})$, then $O^{\unlhd _{D}}=O^{\unlhd }\sqcap [D,D]$, $[{\underline{B}}, \overline{B}]^{\unrhd _{D}}=[{\underline{B}}, {\overline{B}}]^{\unrhd }$ hold, where $\unlhd _{D}$, $\unrhd _{D}$ is the derivation operators of $(U,D,V,I_{D})$.

Given an incomplete context, Lemma 4 actually presents an easier way to obtain the extents and intents of SE-ISI concepts of its subcontexts. For instance, for the subcontext $(U,A_{3},V,I_{3})$ in Example 4, $\{2,4\}^{\unlhd _{A_{3}}}$=$\{2,4\}^{\unlhd _{A}}\sqcap [A_{3},A_{3}]$=$[c,abcf]\sqcap [A_{3},A_{3}]$=$[\varnothing ,f]$ and $[1,13]^{\unrhd _{A_{3}}}$=$[1,13]^{\unrhd _{A}}$= [d, dg].

Lemma 5

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, $D\subseteq A$, $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$, $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, $(O_{k}, [\underline{B_{k}}, \overline{B_{k}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$$\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\le (O_{k}, [\underline{B_{k}}, \overline{B_{k}}])$. If $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$, then $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]$ holds.

Proof

Since $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, we know that $[\underline{B_{j}}, \overline{B_{j}}]<[\underline{B_{i}}, \overline{B_{i}}]$, then $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\le [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ holds. On one hand, we have $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]<[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ from $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$. On the other hand, for $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\le (O_{k}, [\underline{B_{k}}, \overline{B_{k}}])$, then $[\underline{B_{k}}, \overline{B_{k}}]\le [\underline{B_{j}}, \overline{B_{j}}]$ holds, thus we have $[\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]\le [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$. From the above analysis, we can obtain that $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]$. $\square$

Lemma 6

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context, $D\subseteq A$, $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\in PC((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]))$, where $PC((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]))$ is the set of all the parent concepts of $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$ . If D is an SE-ISIL consistent set, then $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]<[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ holds.

Proof

For $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{i}, [\underline{B_{j}}, \overline{B_{j}}])$, we have $[\underline{B_{j}}, \overline{B_{j}}]<[\underline{B_{i}}, \overline{B_{i}}]$, then $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\le [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ holds. In order to prove this lemma, we only need to prove $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$. Suppose $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$, then $O_{j}^{\unlhd _{D}}=[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]=O_{i}^{\unlhd _{D}}$ holds, this means that $O_{j}^{\unlhd _{D}\unrhd _{D}}=O_{i}^{\unlhd _{D}\unrhd _{D}}$. For D is an SE-ISIL consistent set, we know that $O_{j}=O_{j}^{\unlhd \unrhd }=O_{j}^{\unlhd _{D}\unrhd _{D}}=O_{i}^{\unlhd _{D}\unrhd _{D}}=O_{i}^{\unlhd \unrhd }=O_{i}$, which is contradict to $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{i}, [\underline{B_{j}}, \overline{B_{j}}])$. Then, $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ can be obtained. $\square$

Lemma 6 actually describes the properties of SE-ISIL consistent sets. The statements in Example 4 can be used to verify this lemma. The set $A_{1}$ =$\{a,d,f,g\}$ is an SE-ISIL consistent set of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3, then it can be verified that Lemma 6 holds in every pair of child-parent SE-ISI concepts in Fig. 3.

The judging theorem of SE-ISIL consistent set is proposed based on the above lemmas as follows:

Theorem 4

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context. For any $D\subseteq A$ and $D\not =\varnothing$, the following statements are equivalent.

• (1) D is an SE-ISIL consistent set.

• (2) For $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$, $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$$\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, if $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, then $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\ne [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$ holds.

• (3) For $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, if $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\in PC((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]))$, then $D\cap Dis_\mathrm{L}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]),(O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))\not =\varnothing$ holds.

Proof

Firstly we prove that $(1)\Leftrightarrow (2)$.

$(1)\Rightarrow (2)$. Suppose $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])$, $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$$\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$. Since D is an SE-ISIL consistent set, then $L_{{\text {SE-ISI}}}(U,D,V,I_{D})\cong$$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ holds, thus there exist $\underline{E_{i}},\ \overline{E_{j}},\ \underline{F_{j}}$ and $\overline{F_{j}}\subseteq D$ such that $(O_{i}, [\underline{E_{i}}, \overline{E_{i}}])$, $(O_{j}, [\underline{F_{j}}, \overline{F_{j}}])\in L_{{\text {SE-ISI}}}(U,D,V,I_{D})$. For $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, we have $O_{i}\not = O_{j}$; therefore, we can know that $[\underline{E_{j}}, \overline{E_{j}}]\not =[\underline{F_{j}}, \overline{F_{j}}]$. Based on Lemma 4, $[\underline{E_{j}}, \overline{E_{j}}]=O_{i}^{\unlhd _{D}}=O_{i}^{\unlhd _{A}}\sqcap [D,\ D]=[\underline{B_{i}}, \overline{B_{i}}]\sqcap [D,D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ and $[\underline{F_{j}}, \overline{F_{j}}]=[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$ hold naturally. Hence, $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\ne [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$ can be obtained.

$(2)\Rightarrow (1)$. Suppose statement (2) holds, to prove D is an SE-ISIL consistent set, we need to prove $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})\cong L_{{\text {SE-ISI}}}(U,D,V,I_{D})$, that is, $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$$\le L_{{\text {SE-ISI}}}(U,D,V,I_{D})$ and $L_{{\text {SE-ISI}}}(U,D,V,I_{D})\le L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$. Since for any $D\subseteq A$, we have $L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})\le L_{{\text {SE-ISI}}}(U,D,V,I_{D})$, then we only need to prove that $L_{{\text {SE-ISI}}}$$(U,D,V,I_{D})\le L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$. That is, for any $(O_{i},[\underline{B_{i}}, \overline{B_{i}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}),$$(O_{i},[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D])\in L_{{\text {SE-ISI}}}(U,D,V,I_{D})$. Therefore, $O_{i}^{\unlhd _{D}}=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ and $O_{i}=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd _{D}}$ need to be proved. Because $O_{i}^{\unlhd _{D}}=O_{i}^{\unlhd _{A}}\sqcap [D,D]=[\underline{B_{i}}, \overline{B_{i}}]\sqcap [D,D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$, we only need to prove $O_{i}=$$[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd _{D}}$.

Suppose $O_{i}\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd _{D}}$. Since $([\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd },[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd })\in L_{{\text {SE-ISI}}} ({{\mathbb {I}}}{{\mathbb {K}}})$, we obtain $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\not =[\underline{B_{i}}, \overline{B_{i}}]$. Further, $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\le [\underline{B_{i}}, \overline{B_{i}}]\Rightarrow O_{i}=[\underline{B_{i}}, \overline{B_{i}}]^{\unrhd }\subseteq [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd }\Rightarrow [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\le O_{i}^{\unlhd }=[\underline{B_{i}}, \overline{B_{i}}]$, then $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }<[\underline{B_{i}}, \overline{B_{i}}]$ holds. So there must exists $(O_{j},[\underline{B_{j}},\overline{B_{j}}])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ such that $(O_{i},[\underline{B_{i}},\overline{B_{i}}])\prec (O_{j},[\underline{B_{j}},\overline{B_{j}}])$ and $(O_{j},[\underline{B_{j}},\overline{B_{j}}])\le ([\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd },[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd })$. From $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]$, we can obtain that $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\cap [D,D]$ based on Lemma 5. However, we have $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\le [\underline{B_{i}}, \overline{B_{i}}]\Rightarrow [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\sqcap [D,D]<[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ and $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\le [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\Rightarrow [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\sqcap [D,D]\le [\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\sqcap [D,D]$. Then, $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\sqcap [D,D]$ holds, which contradicts to $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]\not =[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }\sqcap [D,\ D]$. Therefore $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]^{\unrhd \unlhd }=O_{i}$.

Then, we prove that $(1)\Leftrightarrow (3)$.

$(1)\Rightarrow (3)$. Suppose $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])=(O_{i},O_{i}^{\unlhd })\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}])\in PC((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]))$. If $D\subseteq A$ is an SE-ISIL consistent set, then $O_{i}^{\unlhd _{D}\unrhd _{D}}=O_{i}$ holds. We discuss it in two situations.

• (a) If $(O_{j}, [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D])\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, then $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]=[\underline{B_{j}}, \overline{B_{j}}]$. Since $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])\prec (O_{j}, [\underline{B_{j}}, \overline{B_{j}}])$, we have $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]<[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$ based on Lemma 6. Therefore, $[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]-[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]=[(\underline{B_{i}}-\underline{B_{j}})\cap D,(\overline{B_{i}}-\overline{B_{j}})\cap D]\not =[\varnothing ,\varnothing ]$. Obviously, we can see that $D\cap \textit{Dis}_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]),(O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))\not =\varnothing$.

• (b) If $(O_{j}, [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D])\notin L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, then $O_{i}\subset O_{j}\subset [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]^{\unlhd _{D}}$. Since $([\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]^{\unrhd _{D}},[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]^{\unrhd _{D} \unlhd })\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, we can get that $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]\le [\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]^{\unrhd _{D} \unlhd }<O_{i}^{\unlhd }$. Moreover, it is sure that $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]<O_{i}^{\unlhd _{D}}$. Because if $O_{i}^{\unlhd _{D}}=[\underline{R}(O_{i})\cap D,{\overline{R}}(O_{i})\cap D]=[\underline{B_{i}}\cap D, \overline{B_{i}}\cap D]$, then $O_{i}=O_{i}^{\unlhd _{D} \unrhd _{D}}= [{\underline{R}}(O_{i})\cap D,{\overline{R}}(O_{i})\cap D]^{ \unrhd _{D}}>[[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]^{\unrhd _{D}}$ holds, which is a contradiction. Thus, $[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]<O_{i}^{\unlhd _{D}}=[{\underline{R}}(O_{i})\cap D,\overline{R}(O_{i})\cap D]$, that is, $[{\underline{R}}(O_{i})\cap D,\overline{R}(O_{i})\cap D]-[\underline{B_{j}}\cap D, \overline{B_{j}}\cap D]=[(\underline{B_{i}}-\underline{B_{j}})\cap D,(\overline{B_{i}}-\overline{B_{j}})\cap D]\not =[\varnothing ,\varnothing ]$. Therefore, $D\cap \textit{Dis}_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]),(O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))\not =\varnothing$.

$(3)\Rightarrow (1)$ Let $(O_{i}, [\underline{B_{i}}, \overline{B_{i}}])=(O_{i},O_{i}^{\unlhd })\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ and $D\cap \textit{Dis}_{\mathrm{L}}((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]),$$(O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))\not =\varnothing$. For any $(O_{j}, [\underline{B_{j}}, \overline{B_{j}}]))\!\in \! PC((O_{i}, [\underline{B_{i}}, \overline{B_{i}}]))$ and $O_{i}\!\not =\!O_{i}^{\unlhd _{D} \unrhd _{D}}$, we have that $O_{i}\!\subset \! O_{i}^{\unlhd _{D} \unrhd _{D}}\!=\! O_{i}^{\unlhd _{D} \unrhd }$. Since $(O_{i}^{\unlhd _{D} \unrhd },O_{i}^{\unlhd _{D} \unrhd \unlhd })\in L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$, then we obtain that $(O_{i},O_{i}^{\unlhd _{D}})< (O_{i}^{\unlhd _{D} \unrhd },O_{i}^{\unlhd _{D} \unrhd \unlhd })$. Moreover it is sure $(O_{i},O_{i}^{\unlhd })\!\prec \! (O_{i}^{\unlhd _{D} \unrhd },O_{i}^{\unlhd _{D} \unrhd \unlhd })$. If there exists $(O_{k},[\underline{B_{k}}, \overline{B_{k}}])\!\in \! L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}})$ such that $(O_{i},O_{i}^{\unlhd })\prec (O_{k},[\underline{B_{k}}, \overline{B_{k}}])<(O_{i}^{\unlhd _{D} \unrhd },X^{\unlhd _{D} \unrhd \unlhd })$, then $O_{i}^{\unlhd _{D} \unrhd \unlhd }<[\underline{B_{k}}, \overline{B_{k}}]< O_{i}^{\unlhd }$, which implies $[{\underline{R}} (O_{i}^{\unlhd _{D}\unrhd })\cap D,\overline{R}(O_{i}^{\unlhd _{D} \unrhd })\cap D]<[\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]< [{\underline{R}}(O_{i})\cap D,\overline{R}(O_{i})\cap D]$. From assumption, we have $[\underline{B_{k}}, \overline{B_{k}}]< O_{i}^{\unlhd }<[{\underline{R}}(O_{i}),\overline{R}(O_{i})]$. Then, we obtain $[\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]<[{\underline{R}}(O_{i})\cap D, \overline{R}(O_{i})\cap D]$ and $O_{i}^{\unlhd }< [\underline{B_{k}}\cap D, \overline{B_{k}}\cap D]< [{\underline{R}}(X)\cap D, \overline{R}(O_{i})\cap D]$, which is impossible. Then, $(O_{i}, O_{i}^{\unlhd })\prec (O_{i}^{\unlhd _{D} \unrhd }, O_{i}^{\unlhd _{D} \unrhd \unlhd })$ holds. Based on the assumption, we have $D\cap \textit{Dis}_{\mathrm{L}}((O_{i}, O_{i}^{\unlhd }), (O_{i}^{\unlhd _{D} \unrhd }, O_{i}^{\unlhd _{D} \unrhd \unlhd }))\not =\varnothing$. That is, $O_{i}^{\unlhd _{D}\unrhd \unlhd }\sqcap [D, D]< [\underline{R}(O_{i})\cap D, {\overline{R}}(O_{i})\cap D]$. Therefore, $O_{i}^{\unlhd _{D}}=O_{i}^{\unlhd }\sqcap [D, D]\le O_{i}^{\unlhd _{D} \unrhd \unlhd }\sqcap [D, D]< O_{i}^{\unlhd }$, which is a contradiction. Hence, $O_{i}^{\unlhd \unrhd }=O_{i}$, that is, D is an SE-ISIL consistent set. $\square$

Example 11

(Continued with Examples 4 and 9) Considering the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3 , the sets $A_{1}$=$\{a, d, f, g\}$ and $A_{3}$=$\{d, f, g\}$, we can validate that the statements (2) and (3) of Theorem 4 hold on $A_{1}$, then $A_{1}$ is an SE-ISIL consistent set according to the theorem. In contrast, $(12,[\varnothing , abg]))\prec (123, [\varnothing ,dg])$, but $[\varnothing \cap A_{3}, abg\cap A_{3}]$=$[\varnothing , g]$=$[\varnothing \cap A_{3}, dg\cap A_{3}]$, and there also exist an element $ab\in \varLambda _{\mathrm{L}}$ such that $ab\cap A_{3}$=$\varnothing$. Therefore, $A_{3}$ is not an SE-ISIL consistent set. On the other hand, the statements that $A_{1}$=$\{a, d, f, g\}$ is an SE-ISIL consistent set and $A_{3}$=$\{d, f, g\}$ is not an SE-ISIL consistent set of the incomplete context are illustrated in Example 4 based on Figs. 3, 4 and 6.

On the basis of Theorem 4 that is the theoretic base of the reduction approaches, we define SE-ISI discernibility functions as follows to calculate all the SE-ISI reducts.

Definition 11

Let ${{\mathbb {I}}}{{\mathbb {K}}}=(U,A,V,I)$ be an incomplete context. The SE-ISIL(SE-ISIM, SE-ISIJ, SE-ISIG) discernibility function is defined as follows:

$$\begin{aligned} \begin{aligned}&f(\varLambda _{\mathrm{L}})=f(\varLambda _{\mathrm{M}})=\wedge _{H\in \varLambda _{\mathrm{L}}}(\vee _{h\in H}h),\\&f(\varLambda _{\mathrm{J}})=\wedge _{H\in \varLambda _{\mathrm{J}}}(\vee _{h\in H}h),\\&f(\varLambda _{\mathrm{G}})=\wedge _{H\in \varLambda _{\mathrm{G}}}(\vee _{h\in H}h). \end{aligned} \end{aligned}$$

Based on the absorption law and distribute law of logical theory, every SE-ISI discernibility function f can be represented by a minimal disjunctive normal form, whose items are all SE-ISI reducts of ${{\mathbb {I}}}{{\mathbb {K}}}$.

Example 12

(Continued with Example 9) Based on the SE-ISIL discernibility matrix shown in Table 7, we obtain the SE-ISIL reducts of ${{\mathbb {I}}}{{\mathbb {K}}}$ in Table 3 as follows:

$f(\varLambda _{\mathrm{L}})=f(\varLambda _{\mathrm{M}})=\wedge _{H\in \varLambda _\mathrm{L}}(\vee _{h\in H}h)=g\wedge (a\vee b)\wedge d\wedge (c\vee f)\wedge (a\vee b\vee d\vee e\vee g) \wedge (a\vee b\vee e\vee g)\wedge (d\vee e\vee g)\wedge (a\vee b\vee f)\wedge (a\vee b\vee d\vee e\vee f\vee g)=(a\wedge c\wedge d\wedge g)\vee (a\wedge d\wedge f\wedge g)\vee (b\wedge c\wedge d\wedge g)\vee (b\wedge d\wedge f\wedge g)$.

It means, there are four SE-ISIL (SE-ISIM) reducts, which are $\{a, c, d, g\}$, $\{a, d, f, g\}$, $\{b, c, d, g\}$ and $\{b, d, f, g\}$.

Specially, if we choose $C_{\mathrm{{i}}}$ to be a join-irreducible SE-ISI formal concept or an SE-ISI object concept, then we can obtain SE-ISIJ discernibility matrix and SE-ISIG discernibility matrix, respectively. Thus, we can get the SE-ISIJ reducts and SE-ISIG reducts as follows:

$f(\varLambda _{\mathrm{J}})=\bigwedge _{H\in \varLambda _{\mathrm{J}}}(\vee _{h\in H}h)=d\wedge (c\vee f)\wedge (a\vee b\vee d\vee e\vee g) \wedge (a\vee b\vee e\vee g)\wedge (d\vee e\vee g)\wedge (a\vee b\vee f)\wedge g=(a\wedge c\wedge d\wedge g)\vee (b\wedge c\wedge d\wedge g)\vee (d\wedge f\wedge g)$.

$f(\varLambda _{\mathrm{G}})=\bigwedge _{H\in \varLambda _{\mathrm{G}}}(\vee _{h\in H}h)=d\wedge (c\vee f)\wedge (a\vee b\vee d\vee e\vee g) \wedge (a\vee b\vee e\vee g)\wedge (d\vee e\vee g)\wedge (a\vee b\vee f)\wedge g=(a\wedge c\wedge d\wedge g)\vee (b\wedge c\wedge d\wedge g)\vee (d\wedge f\wedge g)$.

Therefore, the SE-ISIJ reducts are $\{a, c, d, g\}$, $\{b, c, d, g\}$ and $\{d, f, g\}$, the SE-ISIG reducts are $\{a, c, d, g\}$, $\{b, c, d, g\}$ and $\{d, f, g\}$.

Table 8 Some data from the postoperative-patient-data

Table 9 An incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$ transformed from Table 8

Table 10 The SE-ISI concepts corresponding to ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$ in Table 9

5 An empirical study

In this section, a real-life database is analyzed to illustrate the semantics and demonstrate the applications of the proposed attribute reduction methods. The presented database is about the patients after surgery and their physical indexes, the details of which are as follows.

Example 13

Table 8 depicts some data from a UCI dataset called postoperative-patient-data (UCI Machine Learning Repository 1993), in which $\{1,2,3,4,5,6\}$ is a set of patients after surgery, {L-SURF, L-O$_2$, L-BP, COMFORT} is a set of four attributes about the physical indexes. L-SURF is the patient’s surface temperature in degree Celsius measured as high (> 36.5), mid ($\le$ 36.5 and $\ge$ 35) and low (< 35); L-O2 is the oxygen saturation in $\%$ measured as excellent ($\ge$ 98), good (< 98 and $\ge$ 90), fair (< 90 and $\ge$ 80) and poor (< 80); L-BP is the last measurement of blood pressure measured by high (> 130/90), mid ($\le$ 130/90 and $\ge$ 90/70) and low (< 90/70); COMFORT is the patient’s perceived comfort at discharge measured as an integer between 0 and 20. For the convenience of analysis, we transform the values of the fourth attribute into three levels, that is III($\ge$ 14), II(< 14 and > 7) and I($\le$ 7). The value of patient 5 on the attribute COMFORT is missing.

Then, nominal scale Ganter and Wille (1999) is used to transform Table 8 into an incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$=$(U_{3}, A_{8}, V, I_{A_{8}})$ as shown in Table 9, in which $U_{3}$=$\{1, 2, 3, 4, 5, 6\}$ is a set of six patients after surgery and $A_{8}$=$\{a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}, c_{3}, d_{1}, d_{2}, d_{3}\}$ is a set of ten nominal attributes, that is $a_{1}$ is (L-SURF, high), $a_{2}$ is (L-SURF, low), $b_{1}$ is (L-O$_2$, excellent), $b_{2}$ is (L-O$_2$, good), $c_{1}$ is (L-BP, high), $c_{2}$ is (L-BP, mid), $c_{3}$ is (L-BP, low), $d_{1}$ is (COMFORT, III), $d_{2}$ is (COMFORT, II) and $d_{3}$ is (COMFORT, I). The SE-ISI concepts of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$ are listed in Table 10 and the corresponding SE-ISI concept lattice is shown in Fig. 14.

Fig. 14

$L_{{\text {SE-ISI}}}({{\mathbb {I}}}{{\mathbb {K}}}_{3})$

In order to obtain all SE-ISI concepts and the corresponding SE-ISI concept lattice of an incomplete context, one needs to consider all the attributes in the incomplete context. As we can see from Table 10, there are only ten attributes in this case, but the representations of all SE-ISI concepts are a little bit complicated. In fact, the data that we meet in real life are usually more complicated , then the attribute reduction of incomplete contexts is necessary to be considered.

Table 11 The SE-ISI concepts of $(U_{3},M_{1},V,I_{M_{1}})$

Fig. 15

$L_{{\text {SE-ISI}}}(U_{3},M_{1},V,I_{M_{1}})$

Since the ordered hierarchical structure of all the SE-ISI concepts is reflected by the SE-ISI concept lattice, and SE-ISI concept lattice is the core structure in three-way concept analysis in incomplete contexts, then SE-ISIL attribute reduction needs to be considered. Based on the proposed SE-ISIL discernibility matrix and SE-ISIL discernibility function in Sect. 4, we can obtain that the SE-ISIL (SE-ISIM) reduct of the incomplete context ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$ is $M_{1}=$$\{a_{1},a_{2},b_{1},b_{2},c_{2},d_{2},d_{3}\}$. The SE-ISI concepts of $(U_{3},M_{1},V,I_{M_{1}})$ are listed in Table 11, and their corresponding SE-ISI concept lattice is presented in Fig. 15.

From Figs. 14 and 15, we can see the SE-ISI concept lattice of $(U_{3},M_{1},V,I_{M_{1}})$ is isomorphic to the SE-ISI concept lattice of ${{\mathbb {I}}}{{\mathbb {K}}}_{3}$. Then, the classifications of patients and the hierarchy structure of SE-ISI concepts keep unchanged, but only smaller amount of attributes needs to be considered. For instance, only based on the two nominal attributes $b_{1}$ and $d_{2}$, the patients 2, 3 and 5 can still be classified into one class. Then, the knowledge in SE-ISI concept is represented in a more concise way after SE-ISIL reduction without knowledge loss.

Table 12 The SE-ISI concepts of $(U_{3},M_{2},V,I_{M_{2}})$

Then, based on the proposed SE-ISIJ discernibility matrix and SE-ISIJ discernibility function, the SE-ISIJ reducts are $\{a_{1},a_{2},b_{1},b_{2},d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{2},c_{1},$$d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{1},b_{2},c_{2},d_{1},d_{2}\}$, $\{a_{1},a_{2},b_{1},c_{2},d_{1},d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{1},c_{2},c_{3},d_{2},d_{3}\}$, $\{a_{1},a_{2},c_{1},c_{2},c_{3},d_{2},d_{3}\}$. The SE-ISI concepts of $(U_{3},M_{2},V,I_{M_{2}})$ are listed in Table 12, and their corresponding SE-ISI concept lattice of $(U,M_{2},V,I_{M_{2}})$ is presented in Fig. 16. Here, $M_{2}$ is the SE-ISIJ reduct $\{a_{1},a_{2},b_{2},c_{1},d_{2},d_{3}\}$.

From Fig. 16, we can see that the SE-ISIJ reduct cannot preserve the structure of the SE-ISI concept lattice which means that some knowledge may be lost after SE-ISIJ reduction. For example, the patients 1, 2, 3 and 5 cannot belong to one class in Fig. 16 because the attribute $b_{1}$ has been removed after SE-ISIJ reduction. But the extents of all the join-irreducible elements (i.e., $C_{16}$-$C_{21}$) of SE-ISI concept lattice in Fig. 14 don’t change in Fig. 16. Since the join-irreducible elements are the basic elements in the lattice construction, SE-ISIJ reduction is important in SE-ISI concept lattice construction.

Fig. 16

$L_{{\text {SE-ISI}}}(U_{3},M_{2},V,I_{M_{2}})$

Finally, based on the proposed SE-ISIG discernibility matrix and SE-ISIG discernibility function, the SE-ISIG reducts are $\{a_{1},a_{2},b_{1},b_{2},d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{2},c_{1},$$d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{1},b_{2},c_{2},d_{1},d_{2}\}$, $\{a_{1},a_{2},b_{1},c_{2},d_{1},d_{2},d_{3}\}$, $\{a_{1},a_{2},b_{1},c_{2},c_{3},d_{2},d_{3}\}$, $\{a_{1},a_{2},c_{1},c_{2},c_{3},d_{2},d_{3}\}$. The SE-ISI concepts of $(U_{3},M_{3},V,I_{M_{3}})$ are listed in Table 13, and their corresponding SE-ISI concept lattice of $(U,M_{3},V,I_{M_{3}})$ is presented in Fig. 17. Here, $M_{3}$ is the SE-ISIG reduct $\{a_{1},a_{2},b_{1},b_{2},d_{2},d_{3}\}$.

Table 13 The SE-ISI concepts of $(U_{3},M_{3},V,I_{M_{3}})$

Fig. 17

$L_{{\text {SE-ISI}}}(U_{3},M_{3},V,I_{M_{3}})$

Similar to SE-ISIJ reduction, we can see that the SE-ISIG reduct cannot preserve the structure of the SE-ISI concept lattice from Fig. 17, which means some knowledge may be lost after SE-ISIG reduction. But the extents of SE-ISI object concepts (i.e., $C_{16}$-$C_{21}$) of SE-ISI concept lattice in Fig. 14 are unchanged in Fig. 17. Since the SE-ISI object concepts are important in granular computing, SE-ISIG reduction has more applications in granular computing.

From the above discussion, we can see that the core semantic of the attribute reduction of an incomplete context is to find some minimal attribute subsets that can preserve some characteristics of the SE-ISI concept lattice of the incomplete context. And in this paper, four kinds of attribute reduction of incomplete contexts, that is SE-ISIL, SE-ISIM, SE-ISIJ and SE-ISIG are proposed, which can preserve all the extents of SE-ISI concepts, meet-irreducible SE-ISI concepts, join-irreducible SE-ISI concepts and SE-ISI object concepts, respectively. These different attribute reduction consider different perspectives or different information of the incomplete contexts and they can be applied in different occasions. If we want to preserve all the knowledge of the incomplete context, SE-ISIL reduction needs to be considered; if we want to preserve the basic elements of lattice construction, we need to use SE-ISIM or SE-ISIJ reduction; if we want to preserve the information granules, SE-ISIG reduction needs to be applied.

6 Conclusions and future studies

In this paper, attribute reduction of SE-ISI concept lattices has been systematically studied. First, we have defined four kinds of attribute reduction of SE-ISI concept lattices. Then, the relationships among these newly proposed attribute reduction have been investigated. Finally, the approaches to computing these attribute reducts have been presented.

The basic ideas of these attribute reduction are inspired by reduction theory based on a formal context in formal concept analysis and three-way concept analysis. However, all the attribute reduction in this paper are based on SE-ISI concept lattices of incomplete contexts, which are different from the existing reduction theory based on a completed formal context.

In order to apply the theories discussed in this paper to the real world, we will propose the corresponding algorithms of these different attribute reduction in the future, which may help us to deal with the big data problems in our daily lives conveniently, and can make our study more suitable in practices.