Abstract
Non-predictive or inaccurate weather forecasting can severely impact the community of users such as farmers. Numerical weather prediction models run in major weather forecasting centers with several supercomputers to solve simultaneous complex nonlinear mathematical equations. Such models provide the medium-range weather forecasts, i.e., every 6 h up to 18 h with grid length of 10–20 km. However, farmers often depend on more detailed short-to medium-range forecasts with higher-resolution regional forecasting models. Therefore, this research aims to address this by developing and evaluating a lightweight and novel weather forecasting system, which consists of one or more local weather stations and state-of-the-art machine learning techniques for weather forecasting using time-series data from these weather stations. To this end, the system explores the state-of-the-art temporal convolutional network (TCN) and long short-term memory (LSTM) networks. Our experimental results show that the proposed model using TCN produces better forecasting compared to the LSTM and other classic machine learning approaches. The proposed model can be used as an efficient localized weather forecasting tool for the community of users, and it could be run on a stand-alone personal computer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Non-predictive or inaccurate weather forecasting can severely impact the community of users. For example, farmers depend on the weather forecast so that various farming activities can be undertaken such as ploughing, cultivation, harvesting, and others. An inaccurate forecast directly impacts the farmer’s ability to engage these activities, influencing their capability of managing the resources related to such operations (Ho et al. 2012). In addition, there are significant risks to life and property loss due to unexpected weather conditions all over the world (Fente and Singh 2018). Furthermore, the regional weather forecast may not be accurate based on the geographical appearance of the location, such as but not limited to the top of a mountain, land covered by several mountains, and the slope of the land (Mass and Kuo 1998). Therefore, accurate localized weather prediction system would be valuable to the community of users, as global/regional forecasting could be inaccurate for local use.
Weather forecasting is a complex process which has three main stages, namely understanding the current weather conditions, calculating how this change in the future, and refine details by meteorological expertise (Met Office 2019). Numerical weather prediction (NWP) focuses on gathering current weather data and processing them with computer models to predict the state of the atmosphere based on a specific time frame and location (Lynch 2006; NCEI 2019). These NWP models run in major weather forecasting centers with large grids of supercomputers specifically addressing global/regional forecast (Met Office 2019).
There are several challenges in NWP models, such as massive computational power required by these models, limited model accuracy due to the chaotic nature of the atmosphere, and reliability issues impacted by the time difference between the current time and forecasting time. In addition, the complexity of such models poses significant difficulties in their implementation. (Baboo and Shereef 2010; Hayati and Mohebi 2007; Powers et al. 2017).
There are freely available datasets, which can be utilized with the NWP models, such as Global Forecast System (GFS) data (Earth Science 2018). In particular, the GFS 0.25 degrees dataset, which is the freely available highest-resolution data, is often used by atmospheric researchers and forecasters. This dataset allows forecasting the weather at a horizontal resolution about 27 km (Commerce 2015; Noaa 2017). This implies that the NWP model can forecast data resolution up to 27 km. The lesser-resolution prediction data are calculated by the model based on results obtained for the maximum resolution. As a consequence, these models are viable for long-range forecast and not for a selected fine-grained geographical location, such as a farm, school, places of interest, and so on (Powers et al. 2017; Routray et al. 2016; Skamarock et al. 2008).
To reduce the computational power of NWP systems, data-driven computer modeling systems can be utilized (Hayati and Mohebi 2007). In particular, artificial neural networks (ANN) have the capability of capturing nonlinear or complex underlying characteristics of a physical process with a high degree of accuracy (Fente and Singh 2018). Recently, temporal convolutional neural network (TCN), recurrent neural networks (RNN), and deep learning have attracted considerable attention due to their superior performance (Jozefowicz et al. 2015; Kim and Reiter 2017). Weather information is captured by time-series data, and thus, the machine learning regression modeling techniques can be utilized to develop and evaluate artificial intelligence (AI) models for accurate weather predictions (Choi et al. 2011).
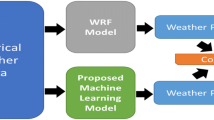
The aim of this research is to develop and evaluate a lightweight and novel short-to medium-range weather forecasting system for the community of users utilizing modern AI technologies. The prediction is entirely based on input local weather station data. Figure 1 depicts the general overview of the research discussed in this article. More specifically, the first part of this research focuses on the evaluation of different machine learning approaches and compares performances and then proposes a localized weather forecasting model. While recurrent neural network is designed for sequence data processing, understanding, and prediction, it has an inherent issue of the vanishing gradient problem and thus low efficiency. Even though the long short-term memory (LSTM) can overcome this vanishing gradient problem, it can easily use up the memory available. In this article, we propose to use the temporal convolutional neural network (TCN) instead, which has not been explored in the past for weather forecasting of as many as 10 parameters on a local scale within hours. The main idea of this proposed model is to produce a fine-grained, location-specific, and accurate weather forecast for the selected geographical location. In the second part, we analyze and evaluate the proposed model for short-term and long-term weather forecasting. The rest of this article is organized as follows: Sect. 2 discusses the related work, Sect. 3 discusses the research aim and objectives, and Sect. 4 presents the basics of local weather stations; Sect. 5 discusses proposed machine learning approaches; Sects. 6 and 7 present the methodology and results, and finally, Sect. 8 concludes the article.
Overview of the research: developed local weather station, which transfers time-series weather data to the server using a GSM module. The server runs the proposed machine learning models (MISO and MIMO), based on state-of-the-art deep learning. The proposed models provide accurate and reliable fine-grained forecasting to farmers
2 Related work
Weather forecast using machine learning has made considerable progress in the last two decades. A multi-layered perception (MLP) neural network and Elman recurrent neural network (ERNN) were introduced to model temperature and wind speed forecasting in 2002 (Choi et al. 2011). After comparing MLP, ERNN, and radial basis functions network (RBFN), the researcher concluded that the ERNN could efficiently capture the dynamic behavior of the weather parameters. In 2005, fuzzy neural network (FNN) was proposed in (Li and Liu 2005) for forecasting of temperature, dew point, wind speed, and visibility. This method consists of a number of fuzzy rules, and their initial weights were estimated with a deeper network for weather prediction. Temperature forecasting with the last 10 years historical data has been done in 2007 (Hayati and Mohebi 2007).
In 2008, a feature-based neural network model for maximum temperature, minimum temperature, and relative humidity forecasting was introduced (Mathur et al. 2008). The author concluded that the neural network signal processing approach for weather forecasting is capable of yielding good results and can be considered as an alternative to traditional meteorological approaches. A backpropagations neural network (BPN) methodology was implemented in 2012 for temperature forecasting while identifying the structural nonlinear relationship between various input weather parameters. The regression tree approach was utilized for wind speed prediction in 2015 (Troncoso et al. 2015). In this work, eight kinds of novel regression tree structures have been used to predict the short-term wind speed and compare the results with some other regression modeling outcome and observed comparatively accurate results.
In 2014, a hybrid model for temperature forecasting using ensemble of neural network (ENN) was introduced in Ahmadi et al. (2014), and the author suggested including image data would improve the prediction results. The LSTM deep learning approach was introduced to precipitation forecasting in 2015 (Shi et al. 2015). The authors formulated a precipitation prediction as a spatiotemporal sequence forecasting problem and proposed a new extension of LSTM called convolutional LSTM. As a result, the new model was able to predict the future rainfall intensity in a local region over a relatively short period of time. In the same year, a deep neural network with stacked denoising auto-encoders was introduced to predict temperature in the Nevada, USA (Hossain et al. 2015). The results show that the new model has higher accuracy, 97.94%, of temperature prediction compared to that, 94.92%, traditional neural network. In 2016, research was undertaken to analyze machine learning methods for radiation forecasting (Voyant et al. 2017). The researcher compared the different machine learning and AI approaches to solar radiation prediction and came to the conclusion that SVM, regression trees, and forests will produce promising results. The deep learning approaches are not considered within these experiments.
In 2018, temperature prediction models were investigated by comparing different machine learning methods such as linear regression, regression trees, and BPN (Sharaff and Roy 2018). The results show that the BPN with proper configuration produces a significantly better prediction. In the same year, the local weather station data were used for a very short-term (less than 60 min) forecast for temperature and rain (Yonekura et al. 2018). Different machine learning methods were utilized by the authors, and different approaches for each parameter were proposed. Subsequently, a neural network approach for the prediction of the sea surface temperature and soil moisture was introduced in Patil and Deo (2018) and Rodríguez-Fernández et al. (2018). This was subsequently developed into a deep learning neural network approach with LSTM layers for weather forecasting (Fente and Singh 2018).
It is, therefore, clear that it will be vital and highly beneficial if a complete weather forecasting model for a community of users could be fully implemented. The existing models are developed for regional parameter forecasting except Yonekura et al. (2018). Although Yonekura et al. (2018) introduces the deep learning method with long short-term memory (LSTM) layers for localized weather forecasting, it does not reflect why this technique is recommended. Besides, this is not a complete forecasting system as this model holds the ability to forecast temperature and rain only.
The existing machine learning-based weather forecasting models are only able to predict up to a maximum of three weather parameters. Moreover, the weather forecasting is not a linear process as each weather parameter could depend upon one or more other parameters (Elsner and Tsonis 1992; Glahn and Lowry 1972; Taylor and Buizza 2002). For instance, the temperature could be depended on pressure, humidity, wind, dew point, etc. The regional numerical weather prediction models, such as Weather Research and Forecasting (WRF), use many input weather parameters (NCAR/UCAR 2019). These interrelated parameters work together to produce an accurate weather forecast. The existing machine learning weather forecasting models have considered only one or up to four parameters for the weather forecasting, mainly on regional scale often over a long term of days.
In this article, we propose a novel weather forecasting model using the modern TCN approach for the localized weather prediction for the community of users with 10 weather parameters. This prediction can be used for weather-related decision making for the community of users. Moreover, we also provide flexibility to our model that can be applied to predicting as many as 10 parameters at local scale within hours.
3 Research aims and objectives
The aim of this research is to develop novel and location specific weather forecasting model with 10 surface parameters using a machine learning (ML) method, utilizing local weather station data, while achieving the following objectives.
-
1.
Build, calibrate, and place local weather stations and logged weather data to the server.
-
2.
Identify optimal configurations and controls to produce accurate and localized weather forecasting for 1 h (i.e., short term) using deep learning with LSTM layers and deep learning with TCN layers.
-
3.
Compare performances of traditional ML (standard regression and support vector regression) with cutting edge deep learning techniques (LSTM and TCN) to identify an efficient short-term localized weather forecasting model with a minimum error.
-
4.
Re-tune the optimal short-term model to use for efficient long-term localized weather prediction and evaluate it to determine up to what extent this can use for long-term weather prediction (i.e., how many hours).
We addressed the above objectives in detail in various sections in this article. Objective 1, local weather stations, is discussed in Sect. 4. Objective 2, identify optimal configurations and control, is discussed in Sect. 5. Objective 3 and Objective 4, compare performances of different techniques, are discussed in Sect. 6.
4 Local weather stations
Local weather stations are placed in farms to measure actual weather parameters. These stand-alone systems directly communicate with the server to send fine-grained temporal resolution (e.g., every 15 min) of weather data. There are key features of these weather stations such as full computer-controlled kit, weather underground support, use of standard grove connectors, a real-time clock, and fully open source code, which can be edited according to the purpose (SwitchDoc Labs 2016).
The main components of the local weather stations include:
-
Weatherboard to attach different weather sensors and data logging to the Raspberry Pi device. The layout of the weatherboard circuit is presented in Fig. 2.
Fig. 2 Layout of a weatherboard circuit [image reference (SwitchDoc Labs 2016)]
-
Raspberry Pi device for computation, data preparation, and logging activities. Figure 3 shows that the Raspberry Pi device is connected to the weatherboard.
-
Different sensors, such as and not limited to wind vane, anemometer, barometer, thermometer, photodetector, lightning detector, hygrometer, pyranometer, and rain gauge to measure environmental values. Figure 4 presents the basic components in a weather station.
Fig. 4 Basic component of a local weather station [image reference (SwitchDoc Labs 2016)]
-
Solar panel to power up and operate the entire weather station. Figure 5 shows how to connect the solar panel to the weatherboard.
-
Global System for Mobile (GSM) module to communicate with the server. The weatherboard comes with a WI-FI module for wireless high-speed connection to the Internet to send data to the server. The GSM module is useful in locations where WI-FI signals are not available.
Several weather sensors can be attached to the weatherboard to measure over 20 different environmental values such as but not limited to wind speed, wind direction, rain, outside temperature, outside humidity, lighting detection, barometric pressure, atmospheric pressure, altitude, in-box temperature, in-box humidity, wind gust, rain rate, soil temperature, soil moisture, ultraviolet density, dust count, and light color (sensing air pollution) (SwitchDoc Labs 2016). Figure 6 depicts the main components of a weather station.
Main components of a local weather station. The solar panel charges the internal battery. This battery power uses the Raspberry Pi to control all the components of the weather station. The purple color internal sensors are applied to measure in-box parameters such as in-box temperature and in-box humidity. The green color sensors attached externally to the box to measure outside box environmental values
As depicted in Fig. 1, the captured time-series weather parameters using different sensors are sent to the data server using the GSM module which is attached to the Raspberry Pi. The GSM module uses ordinary mobile phone signals to transmit data. This process is continued at every 15 min intervals to record different environmental values within the data server. We use this data server to access data and to develop and evaluate different weather forecasting models. As a consequence, the most effective and accurate model is selected as the proposed model.
There are six weather stations, which are used to collect time-series weather data. Table 1 presents the actual latitude and longitude of these weather stations (i.e., where they are placed). The reason for using many weather stations is to train different models for different locations as the forecasting can vary depending upon the geographical appearance of the location/farm. Besides, these weather stations are placed to cover various parts of the UK.
5 Sequence modeling and prediction
Before defining a network structure, we highlight the modeling task involving time-series weather data sequence \( x_{0} , \ldots , x_{T} \) and wish to predict some corresponding outputs \( y_{0} , \ldots , y_{T} \) at each time. The data at a given time \( t, x_{t} = \left[ {p_{1} , \ldots , p_{10} } \right] \) consist of 10 different weather parameters, which are presented in Table 2. The goal is to predict the value \( y_{t} \) at time \( t \) and is constrained to only previously observed inputs: \( x_{0} , \ldots ,x_{t} \). Thus, a sequence modeling network is any function \( {\mathcal{F} }:{ \mathcal{X}}^{{{\text{T}} + 1}} \to {\mathcal{Y}}^{T + 1} \) that produces the mapping \( \hat{y}_{0} , \ldots , \hat{y}_{T} = { \mathcal{F}}\left( {x_{0} , \ldots , x_{T} } \right) \), if it satisfies the causal constraints, i.e., \( y_{t} \) only depends on \( x_{0} , \ldots ,x_{t} \) and not on any future inputs \( x_{t + 1} , \ldots ,x_{T} \). The focus of learning in the sequence modeling is to find a network \( {\mathcal{F} } \) that minimizes the loss between the actual outputs and the predictions, \( \ell \left( {y_{0} , \ldots ,y_{T} ,{ \mathcal{F}}\left( {x_{0} , \ldots ,x_{T} } \right)} \right) \) in which the sequences and predictions are drawn according to some distribution.
A single weather station can produce a large amount of sequential data. Therefore, an extremely expressive model such as deep neural network (DNN) is more appropriate in such a scenario and can learn highly complex vector-to-vector mapping. The recurrent neural network (RNN) is a DNN that is designed for sequence modeling (Elman 1990; Graves 2012). As a result, RNN is also extremely expressive. RNNs are made of high-dimensional hidden states \( \varvec{H} \), which are updated with nonlinear activation function \( {\mathcal{F}} \). At a given time \( t \), the hidden state \( \varvec{H}_{t} \) is updated by \( \varvec{H}_{t} = { \mathcal{F}}\left( {\varvec{H}_{t - 1} , x_{t} } \right) \). The structure of \( \varvec{H} \) works as the memory of the network; the state of the hidden layer at a time is conditioned on its previous state. RNNs are a structure through time and maintains a vector of activations at each timestep, which makes the RNN extremely deep. As a result, their depth makes their training time-consuming due to the exploding and the vanishing gradient problems (Jozefowicz et al. 2015). This has been addressed by the development of long short-term memory (LSTM) architecture (Hochreiter and Schmidhuber 1997), which is resistant to the gradient vanishing problem. Therefore, we use LSTM and temporal convolution network (TCN) architecture to minimize the loss \( \ell (y_{0} , \ldots ,y_{T} ,{ \mathcal{F}}\left( {x_{0} , \ldots ,x_{T} )} \right) \) for effective modeling and prediction of time-series weather data.
5.1 DNN with long short-term memory (LSTM) layers
DNN with long short-term memory (LSTM) layers, a specialized form of the RNN, allows stacked neural networks and includes several layers as part of overall composition known as nodes. These nodes use the combination of data and input through a set of coefficients allowing to carry out computational tasks (Jozefowicz et al. 2015). The proposed DNN with stacked LSTM layers is presented in Fig. 7a. The number of layers and the number of memory cells in each layer are decided experimentally for the best performance. These models have the ability to long-term dependencies by incorporating memory units. These memory units allow the network to learn, forget previously hidden states, and update hidden states (Behera et al. 2018). Figure 7b depicts the general arrangement of an LSTM memory cell.
The LSTM memory architecture used in our experiments is depicted in Fig. 7b. The proposed model has inputs about weather parameters \( x_{t} = \left[ {p_{t}^{1} , \ldots , p_{t}^{10} } \right] \) at a given time stamp \( t \). In a given time \( t \), the model updates the memory cells for hidden states \( \varvec{H}_{t - 1} \), which consists of short-term hidden states \( h_{t - 1} \) and long-term hidden states \( c_{t - 1} \), recall from the previous time stamp \( \left( {t - 1} \right) \) by
where \( w_{x} , b_{x} , \odot , i_{t} , j_{t} , f_{t} , o_{t} \) are weight matrices, biases, element-wise vector product, input gate contributing to memory, input moderation gate contributing to memory, forget gate, and output gate as a multiplier between memory gates, respectively. The \( c_{t} \) and \( h_{t} \) are the two types of hidden layers to allow the LSTM to make complex decisions over a short period of time (Behera et al. 2018; Jozefowicz et al. 2015). The \( i_{t} \) and \( f_{t} \) gates are switching each other to selectively consider the current inputs or forget its previous memory. Similarly, the output gate \( o_{t} \) learns how much memory cell \( c_{t} \) needs to be transferred to the hidden state \( h_{t} \). These additional memory cells allow the LSTM to learn complex and long-term temporal dynamics compared to RNNs.
A typical criticism of the LSTM architecture is that it has a large number of components whose purpose is not immediately apparent (Jozefowicz et al. 2015). Moreover, LSTMs can easily use up a lot of memory in storing partial results for their multiple cell gates in the case of the long input sequence. This is the case for our time-series weather data. Therefore, we explore the state-of-the-art TCN architecture for modeling and predicting fine-grained weather data.
5.2 DNN with temporal convolutional neural (TCN) layers
The TCN approach was initially developed to examine long-range patterns using a hierarchy of temporal convolutional filters (Lea et al. 2017). The key characteristics of TCNs are: (1) it involves convolutions, which are causal and (2) like in RNN, the network can take a sequence of any length and map it to an output sequence of the same length. The proposed architecture is informed by recent generic convolutional architectures for sequential data (Bai et al. 2018; Lea et al. 2017). The architecture is simple (e.g., no skip connections across layers, conditioning, context stacking, or gated activations), uses autoregressive prediction and a very long memory. Moreover, it allows for both very deep networks and very long effective history and is achieved through dilated convolutions that enable an exponentially large receptive field (Yu and Koltun 2015). For example, for a 1-D sequence of a given weather parameter \( p^{1} \), i.e., \( p = \left( {p_{0}^{1} , \ldots , p_{t}^{1} } \right) \) and a filter \( f :\left\{ {0, \ldots , k - 1} \right\} \), the dilation convolution operation \( F \) on element \( s = p_{{\hat{t}}}^{1} \) (where \( \hat{t} = 0, \ldots ,t \)) of the sequence is defined as:
where \( d \) is the dilation factor, \( k \) refers to the filter size, and \( s - d.i \) accounts for the direction of the past. Stacked units of one-dimensional convolution with activation functions are used to build the TCN (Kim and Reiter 2017). Figure 8 depicts the architectural elements in a TCN with configurations dilation factors \( d = 1, 2,\; {\text{and}}\; 4. \) The dilation introduces a fixed step between every adjacent filter taps. Larger dilations and larger filter sizes \( k \) enable effectively expanding the receptive filed (Bai et al. 2018; Lea et al. 2017). In these convolutions, the increment of \( d \) exponentially commonly increases the depth of the network. This guarantees that there is some filter that hits each input within the effective history (Bai et al. 2018).
We use Keras as a tool to implement both deep learning LSTM and TCN (Gulli and Pal 2017; Keras 2019a; Krizhevsky et al. 2012).
6 Methodology
This study is based on an experimental approach and is focused on the analysis of quantitative temporal data. There are 10 weather parameters utilized within this research.
6.1 Weather parameters
Meteorological data can be classified into two main types, namely surface weather data and the upper air data. The surface weather data contain physical parameters that are measured directly by instrumentation at the earth’s surface (i.e., somewhere between ground level and 10 meters) (US EPA 2016). Therefore, the surface weather data can be considered tangible data and include air pressure, wind speed, wind direction, rain, rain rate, soil moisture, soil temperature, dew point, snow, heat index, temperature, etc. (Faroux et al. 2007; Thornton et al. 2014; US EPA 2016). In contrast, upper air data contain physical parameters that are measured in different vertical layers of the atmosphere (US EPA 2016). For example, GFS data considered 36 different pressure layers when collecting upper air data (Hamill et al. 2011; NCAR/UCAR 2019).
Surface weather data can be observed simply using local weather stations. These are the fundamental data used for weather forecasting and issue relevant warning messages (Gounaris et al. 2010; Mittal et al. 2015). The upper air data can be measured using radars and satellites (Haimberger et al. 2008). Lahoz et al. (2010) argued that low-resolution weather prediction could be made using only surface weather parameters. Klein and Glahn (1974) and Gneiting and Raftery (2005) developed a successful local weather prediction model using surface weather data. Therefore, the surface weather parameters can be used for local weather forecasting.
As described in Sect. 4, the local weather station data are collected for various surface weather parameters. Table 2 shows the weather parameters which are utilized within the research. In Table 2, some weather parameters are ignored among the approximately 20 weather station data parameters in the surface weather parameters. The reason is that the preliminary experiments show that they have minimal impact on the weather forecasting results. These include in-box temperature, in-box humidity, wind gust, and altimeter. Moreover, the underground weather is not measured in these experiments.
6.2 Data collection and preparing
The weather data are collected for every 15-minute interval for the period of 20/01/2018 to 22/08/2018 to train the proposed model. Similarly, data have been collected for the period of 23/08/2018 to 11/09/2018 to test, and data from 12/09/2018 to 30/09/2018 to validate the proposed model. The test dataset is used to test different models with different configurations and controls to identify the optimal model for the localized weather prediction. This optimal model is used with the evaluation dataset to get the weather prediction and analyze the results. Each dataset has been linearly interpolated to include missing values, and each weather parameter is normalized using \( \hbox{min} \) and \( \hbox{max} \) operation to keep the value in between − 1 and 1, i.e., \( \hat{p}_{i} = 2\{ (p_{i} - \hbox{min} (p_{i} ))/(\hbox{max} (p_{i} ) - \hbox{min} (p_{i} ))\} - 1 \), where \( i = 1, \ldots , 10 \) (weather parameters in Table 2).
A temporal sliding window is used to prepare the data. Seven days sequential data are used as a sample input and next 2 h data as a label (i.e., model output or prediction). The gap between two consecutive sliding windows is an hour. The final training dataset consists of 5726 samples, and each sample consists of 6800 columns of data (680 timesteps with a dimension of 10 at each timestep).
6.3 Neural network-based proposed forecasting models
In this section, we analyze the performance of the proposed short-term forecasting model and fine-tune this model for long-term forecasting for weather station data. In our study, short-term refers to 1 h and long-term refers to 2, 3, 6, 9, 12, 18, and 24 h. Two deep models are proposed to solve the regression problem involving weather forecasting, namely multi-input multi-output (MIMO) and multi-input single-output (MISO). As LSTM and TCN deep neural approaches are proposed for the weather forecasting models, the proposed models are MIMO-LSTM, MISO-LSTM, MIMO-TCN, and MISO-TCN.
Figure 9 depicts the main difference between the MIMO and MISO. In MIMO, all 10 variables are fed to the network, and the network provides the same number of outputs as the weather prediction. In contrast, in the MISO, all 10 variables are fed to the network, and the network provides single parameter output as the prediction. With respect to Figs. 3 and 4, the MIMO is used with 10 inputs to produce 10 output parameters, and the MISO uses 10 input parameters to produce one output parameter.
6.3.1 Proposed short-term forecasting model
For the LSTM approach, we use different configurations and controls. As Fig. 7a depicts, each layer consists of a number of nodes, and we experiment with a different number of layers with a different number of nodes for each layer. We also experiment with different optimizers to minimize the cost function. Subsequently, we use both fixed learning rate and adaptive learning rate methods to train the LSTM models. Similarly, we use different configurations and controls with the TCN approach, such as a different number of TCN layers with different filter sizes, different dilation factors, and different optimizers.
Each approach is an experiment with both MIMO and MISO. The results are subsequently evaluated to determine the short-term forecasting model.
6.3.2 Proposed long-term forecasting model
The short-term optimal model is fine-tuned for long-term weather forecasts, such as 2, 3, 6, 9, 12, 18, and 24 h. This is two different ways to determine the optimal performance model. Firstly, the optimal model which is found in the short-term forecasting is re-tuned for the data in 2, 3, 6, 9, 12, 18, and 24 timeslots. This is taken as the TCN-WL (i.e., TCN model without loading the optimal model weight). These models are evaluated using the weather station testing dataset. Moreover, the optimal model is investigated with loading optimal weights in addition to the optimal configurations and controls. This is taken as the TCN-LW (i.e., TCN model with loaded optimal weights). These TCN-LW models are also evaluated using the weather station testing dataset. Finally, a comparison is made between TCN-WL and TCN-LW to identify an optimal model for long-term forecasting.
Based on the performance, the optimal model is selected as the proposed model for long-term forecasting. Subsequently, the selected optimal model is used for weather prediction for the weather station validation dataset for each timeslot and results are compared with the ground truth.
6.4 Evaluation metric
There are several evaluation metrics which can be used to calculate the loss in a neural network such as but not limited to mean squared error (MSE), mean absolute error (MAE), root mean squared error (RMSE), quadratic cost, cross-entry cost, exponential cost, Hellinger distance, and Kullback–Leibler divergence (Joho et al. 2001; Jozefowicz et al. 2015; Mandic and Chambers 2000). Most of these evaluation metrics are suited for classification machine learning algorithms (i.e., predicting a label or a discrete output variable). The common metrics for regression machine learning algorithm (i.e., predicting a quantity or a continuous output variable) are MSE, MAE, and RMSE (Duan et al. 2016; Zhao et al. 2017).
The mean squared error (MSE) metric is used in this work as the evaluation metric, which is calculated as (Jozefowicz et al. 2015; Keras 2019b):
where \( N \) is the number of samples, \( y_{i} \) is the actual expected output, and \( \hat{y}_{i} \) is the model’s prediction.
6.5 Baseline approaches
We also compare the performance of the proposed LSTM and TCN architecture with the classical machine learning approaches such as standard linear regression (Bishop 2006) and support vector regression (SVR) (Chang and Lin 2011). Such approaches do not consider the temporal information which is only considered as another dimension in multivariate weather data. For SVR, we use both linear and RBF (radial basis function) kernels in our experiments. The parameter \( C \) in the linear kernel is selected among the range [0.01–10,000] with multiples of 10. The parameter \( C \) in RBF is selected as above, but \( \gamma \) is selected among the range [0.0001, 0.001, 0.01, 0.1, 0.2, 0.5, 0.6, 0.9]. We use the grid search algorithm technique to optimize both \( C \) and \( \gamma \) parameters. The best baseline performance is compared with the proposed LSTM and TCN networks.
7 Results and discussion
As described in Sect. 6.3, there are two main sections of this research, namely identifying optimal configurations of proposed model for both short-term and long-term forecasting.
7.1 Proposed model for short-term forecasting
As described in Sect. 6.3, all the machine learning models are evaluated in two different methods, namely MIMO and MISO. Each machine learning model is trained with different configurations and controls. Figure 10 shows the comparison of each model in MIMO. The SVR approach is not supported for MIMO (Bhattacharyya 2018; Kavitha et al. 2016). Therefore, we only compare here standard regression, deep learning with LSTM layers, and deep learning with TCN.
In MIMO, the optimal model with LSTM has three layers, and each layer consists of 128, 512, and 256 nodes. The ‘Adam’ optimizer is utilized within this model with a fixed learning rate of 0.01 and batch size of 128. The MIMO-TCN model is configured with one TCN layer, 256 filters, kernel size of 2, learning rate of 0.02, dilations of 32, and ‘tanh’ activation. Similarly, we use different configurations and controls for MIMO. In MISO-LSTM, the optimal configuration is found with four LSTM layers, and each layer consists of 128, 512, 512, and 256 nodes. The ‘Adam’ is the mostly used optimizer (Brownlee 2017) to optimize MSE (Eq. 3) with a fixed learning rate of 0.01 and batch size of 128. In MISO-TCN, the optimal configuration is found with one TCN layer, 256 filters, kernel size of 2, learning rate of 0.02, dilations of 32, and ‘tanh’ activation.
Figure 10 bar charts illustrate that the TCN provides better results in six parameters out of 10. Therefore, TCN model has been selected as the proposed model in MIMO. Similarly, we evaluate Fig. 11 the MISO to determine the best option with the least mean squared error for each parameter. Figure 11 shows the comparison of each MISO model. As Fig. 11 bar charts indicate, the TCN provides better prediction results for the MISO compared to other models. The deep learning model with LSTM layers also provides significant prediction results, but out of 10 six parameters provides better results in TCN. Thus, the TCN combined model with 10 parameters has been selected as the MISO proposed model. All these 10 models have 10 different TCN configurations with a different number of TCN layers, activation function, and a number of filters.
In Figs. 10 and 11, both LSTM and TCN deep learning models produce comparatively smaller errors compared to the standard regression and SVR. This implies that there is a nonlinear interrelationship among parameters (Graves 2012; Jozefowicz et al. 2015; Kavitha et al. 2016) and the selected parameter does not follow a linear path within selected sequential timeslots (Bishop 2006; McCREA et al. 2005). Moreover, the standard regression and the SVR do not encode sequential information, while LSTM and TCN encode both multivariate and sequential information by taking them into another dimension in the input data (Bai et al. 2018; Basak et al. 2007; Jozefowicz et al. 2015).
As seen in Figs. 10 and 11, there are some parameters that have quite larger errors. For instance, the humidity error is higher compared to seven other parameters. The reason is that the actual humidity figures are within a higher range of 70–100. According to Eq. 3, part of the MSE calculation is the square value of the difference between actual and predicted ones. The predicted values should be a higher range figure. Therefore, the MSE can get higher values if the actual figures are higher and predicted values not much closer to the actual. The similar condition is applied to the wind direction, dew point, and heat index parameters. Especially in wind direction, the variance is quite high and this could lead to a higher error rate. For instance, the wind direction is measured in degrees (0°–360°) and assume the actual value is 3° and predicted value is 359°. The prediction is much more accurate (i.e., both values represent wind direction to north), but the error value is quite high.
According to Figs. 10 and 11, the LSTM provides better or much similar results compared to the TCN for the parameters wind speed, wind direction, rain rate, and dew point. This could be a higher variance of actual data in these parameters (Schmidhuber 2015). These data items enormously diverted from mean compared to the other variables such as pressure, temperature, barometer, rain, and heat index. In addition, there is a difference between error values in rain and rain rate in Figs. 10 and 11. The rain rate is classified according to the rate of precipitation per hour (Sachidananda and Zrnić 1987). Therefore, the rain rate value is calculated for the last hour and rain is measured based on frequency of data logged to manually calculate the cumulative rain. This indicates that there could be a substantial difference between rain and rain rate values endorsing different error values.
Table 3 and Fig. 12 show a comparison between MIMO and MISO error values. According to Table 3 and Fig. 12, the MISO model has lesser error values compared to MIMO except for the parameter rain. This is probably because it took into account the interactions and correlations between different weather parameters. Therefore, the MISO model has been selected as the tool to forecast the weather for a selected geographical area using local weather station parameters.
The proposed MISO model is used to predict data using the evaluation dataset. The predicted parameter values are compared with the actual ones. Figure 13 compares a random 100 samples of predicted data and the ground truth from the evaluation dataset. For each graph in Fig. 13, the predicted values are represented with red color, and actual values are represented in blue color. This figure demonstrates that the red color line chart (predicted values) closely follows the blue line chart (ground truth) in many parameters. The predicted values are diverted exceedingly in rain rate and rain parameters. According to Fig. 13g, h, the highest figures for rain and rain rates are 0.24 mm and 0.25 mm/h, respectively. These values are relatively quite small and can be negligible. Overall, the proposed TCN model is producing effective results which can be utilized to the short-term weather forecasting for a selected geographical area.
7.2 Proposed model for long-term forecasting
As described in Sect. 6.3.2, the MISO-TCN generated higher accuracy short-term (1 h) prediction for local weather station data. This section aims to fine-tune the proposed MISO-TCN model for longer periods of 2, 3, 6, 9, 12, 18, and 24 h. As described in Sect. 6.3.2, the performance of long-term models of TCN-WL (without loading short-term optimal model weights) and TCN-LW (loaded with short-term optimal model weights) is compared. The weather station training dataset is used to train/fine-tune these models, and the weather station testing dataset is used to evaluate those models. The optimal model is chosen based on the performance for each timeslot. Comparison of overall MSE for TCN-WL and TCN-LW for each timeslot is shown in Table 4 and Fig. 14.
As per information from Fig. 14 and Table 4, the TCN-LW yields better performance with minimum MSE for each timeslot compared to the TCN-WL. The reason is that the TCN-LW has used an already trained model for a specific domain issue (i.e., weather forecasting), and then re-tunes the model weights match to the new dataset. This process is highly efficient and directed to an accurate result (Hochreiter and Schmidhuber 1997). Therefore, TCN-LW models are selected as the long-term weather forecasting models for the weather station data. Table 5 and Fig. 15 present the summary of evaluation results for the optimal models for each parameter at each timeslot. These are calculated on the data in the normalized form.
As shown in Fig. 15, the MSE values are increasing (i.e., accuracy of the model decreasing) when the prediction time increases. Similar to the short-term forecasting, the wind direction parameter shows higher error values compared to all the other parameters. The reason for this is that the variance of the wind direction data is quite high (Schmidhuber 2015). The barometer and pressure predictions provide minor error values until 9–12 h and then increase rapidly. This is because of the areas of high atmospheric pressure moving to the low-pressure areas and vice versa. Usually, these areas refer to many hundreds of miles (Anderberg 2015). Therefore, it is quite hard to predict these parameters for quite a long time as the data are taken from a single location (i.e., location of the local weather station). Moreover, the temperature, humidity, dew point, and heat index parameters often change, while the atmospheric pressure is changing (Anderberg 2015; Ji et al. 2018; National Geographic Society 2011).
Figure 16 shows how these MSE values change with the time for each parameter. As per Fig. 16g, h, the rain and rain rate MSE values are changed marginally throughout each timeslot, and these are quite small values. This means the prediction accuracy is quite high for these parameters. This also proved that the prediction results for the rain are quite accurate for the deep neural networks (Yonekura et al. 2018).
As indicated in Fig. 15, the proposed deep learning MISO-TCN model can be used for weather forecasting. There are some parameters able to produce slightly improved accuracy of forecasting results up to 24 h (i.e., Rain and Rainnc), while others can produce slightly accurate forecasting up to 9–12 h.
The MISO-TCN optimal model is used with the weather station validation dataset to get a prediction and compared with the ground truth and results shown in Fig. 17. The predicted result is de-normalized and compared with the real ground truth. A random 50 data samples are selected to present as it is not practical to present the whole dataset. For each graph, the ground truth and the proposed MISO-TCN deep model’s predictions are represented by each line with blue and red colors, respectively.
Figure 17i, ii shows that the predicted results of the barometer and pressure values change rapidly after 9–12 h. But, the proposed MISO-TCN model can produce a more accurate prediction for these two parameters for up to 12 h. Even though the parameters rain and rain rates look diverted exceedingly in Fig. 17vii, viii, the actual figures are quite small and can be considered negligible (i.e., highest rain—0.25 mm and highest rain rate—0.024 mm/h). For all other parameters, the predicted values closely follow the ground truth up to 9–12 h and then divert from the actual. Overall, the proposed MISO-TCN can be used for weather forecasting, and it has the ability to produce some accurate results up to 9–12 h.
8 Conclusion and future work
In this paper, we have introduced a novel lightweight weather model which can be utilized to weather forecasting for up to 9 h for a selected fine-grained geographical location. The existing weather forecasting models that are limited to regional forecasting, limited to a maximum of two weather parameters. Our new model can, however, predict as many as 10 parameters, easily be deployed and be run on a stand-alone computer. Consequently, this new model could make a huge impact on a community of users who rely on the weather for their day-to-day activities. For example, the weather condition can be predicted and monitored within a few hours’ time interval, by running the TCN code, without relying on the regional weather forecasting. The only requirement is to access the local weather station data, which could be achieved by setting up an economical weather station in specific locations or farms. Furthermore, a wider set of users who rely on favorable weather conditions could get the advantage of the model, such as places of interest, schools, outdoor sports centers, and construction sites.
The proposed model is able to overcome challenges with the regional and global forecasting models including lesser computational power consumption, easy to understand and install, and portability. While the NWP models are viable for long-range forecast and not for a fine-grained geographical area, we could make a reliable and accurate prediction using the proposed model as this uses the data related to that specific location.
In this research, we use only 93 days of data to train the proposed model. Increasing the size of the training data sample could result in better prediction in ANN (Jozefowicz et al. 2015). The created model can be fine-tuned with more data to get better performance. Furthermore, we use a Raspberry Pi weather station within this research which is able to attach many sensors to measure the atmosphere. There could be a possibility to improve the prediction if we introduce some more weather parameters which support the Raspberry Pi weatherboard such as soil temperature, soil moisture, snow, solar radiation balance, and pressure at different levels.
References
Ahmadi A, Zargaran Z, Mohebi A, Taghavi F (2014) Hybrid model for weather forecasting using ensemble of neural networks and mutual information. Presented at the 2014 IEEE geoscience and remote sensing symposium, pp 3774–3777. https://doi.org/10.1109/IGARSS.2014.6947305
Anderberg J (2015) How to use a barometer. Art manliness. https://www.artofmanliness.com/articles/fair-or-foul-how-to-use-a-barometer. Accessed 23 July 2019
Baboo SS, Shereef IK (2010) An efficient weather forecasting system using artificial neural network. Int J Environ Sci Dev. https://doi.org/10.7763/IJESD.2010.V1.63
Bai S, Kolter JZ, Koltun V (2018) An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv:180301271Cs
Basak D, Pal S, Patranabis D (2007) Support vector regression. Neural Inf Process Lett Rev 11:203–224
Behera A, Keidel A, Debnath B (2018) Context-driven multi-stream LSTM (M-LSTM) for recognizing fine-grained activity of drivers. Pattern Recognit 16:298–314
Bhattacharyya I (2018) Support vector regression or SVR. Coinmonks. https://medium.com/coinmonks/support-vector-regression-or-svr-8eb3acf6d0ff. Accessed 22 Feb 2019
Bishop CM (2006) Pattern recognition and machine learning. Springer, New York
Brownlee J (2017) Gentle introduction to the Adam optimization algorithm for deep learning. Mach Learn Mastery. https://machinelearningmastery.com/adam-optimization-algorithm-for-deep-learning/. Accessed 28 Jan 2019
Chang C-C, Lin C-J (2011) LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol 2:27:1–27:27. https://doi.org/10.1145/1961189.1961199
Choi T, Hui C, Yu Y (2011) Intelligent time series fast forecasting for fashion sales: a research agenda. Presented at the 2011 international conference on machine learning and cybernetics, pp 1010–1014. https://doi.org/10.1109/ICMLC.2011.6016870
Duan Y, Lv Y, Wang F-Y (2016) Travel time prediction with LSTM neural network. Presented at the 2016 IEEE 19th international conference on intelligent transportation systems (ITSC), IEEE, pp 1053–1058
Earth Science [WWW Document] (2018). http://geometocea.res.in/home/online-links/online-data-links. Accessed 21 Feb 2019
Elman JL (1990) Finding structure in time. Cogn Sci 14:179–211. https://doi.org/10.1207/s15516709cog1402_1
Elsner JB, Tsonis AA (1992) Nonlinear prediction, chaos, and noise. Bull Am Meteorol Soc 73:49–60. https://doi.org/10.1175/1520-0477(1992)073%3c0049:NPCAN%3e2.0.CO;2
Faroux S, Masson V, Roujean J (2007) ECOCLIMAP-II: a climatologic global data base of ecosystems and land surface parameters at 1 km based on the analysis of time series of VEGETATION data. Presented at the 2007 IEEE international geoscience and remote sensing symposium, pp 1008–1011. https://doi.org/10.1109/IGARSS.2007.4422971
Fente DN, Singh DK (2018) Weather forecasting using artificial neural network. Presented at the 2018 second international conference on inventive communication and computational technologies (ICICCT), pp 1757–1761. https://doi.org/10.1109/ICICCT.2018.8473167
Glahn HR, Lowry DA (1972) The use of model output statistics (MOS) in objective weather forecasting. J Appl Meteorol 11:1203–1211. https://doi.org/10.1175/1520-0450(1972)011%3c1203:TUOMOS%3e2.0.CO;2
Gneiting T, Raftery AE (2005) Weather forecasting with ensemble methods. Science 310:248–249. https://doi.org/10.1126/science.1115255
Gounaris G, Vlissidis A, Michail K (2010) Weather stations distributed model for data process and on-line internet presentation 8
Graves A (2012) Supervised sequence labelling. In: Graves A (ed) Supervised sequence labelling with recurrent neural networks, studies in computational intelligence. Springer, Berlin, pp 5–13. https://doi.org/10.1007/978-3-642-24797-2_2
Gulli A, Pal S (2017) Deep learning with Keras. Packt Publishing Ltd, Birmingham
Haimberger L, Tavolato C, Sperka S (2008) Toward elimination of the warm bias in historic radiosonde temperature records—some new results from a comprehensive intercomparison of upper-air data. J Clim 21:4587–4606. https://doi.org/10.1175/2008JCLI1929.1
Hamill TM, Whitaker JS, Kleist DT, Fiorino M, Benjamin SG (2011) Predictions of 2010’s tropical cyclones using the GFS and ensemble-based data assimilation methods. Mon Weather Rev 139:3243–3247. https://doi.org/10.1175/MWR-D-11-00079.1
Hayati M, Mohebi Z (2007) Application of artificial neural networks for temperature forecasting. Int J Electr Comput Eng 1:5
Ho CK, Stephenson DB, Collins M, Ferro CAT, Brown SJ (2012) Calibration strategies: a source of additional uncertainty in climate change projections. Bull Am Meteorol Soc 93:21–26. https://doi.org/10.1175/2011BAMS3110.1
Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9:1735–1780. https://doi.org/10.1162/neco.1997.9.8.1735
Hossain M, Rekabdar B, Louis SJ, Dascalu S (2015) Forecasting the weather of Nevada: a deep learning approach. Presented at the 2015 international joint conference on neural networks (IJCNN), pp 1–6. https://doi.org/10.1109/IJCNN.2015.7280812
Ji D, Dong W, Hong T, Dai T, Zheng Z, Yang S, Zhu X (2018) Assessing parameter importance of the weather research and forecasting model based on global sensitivity analysis methods. J Geophys Res Atmos 123:4443–4460. https://doi.org/10.1002/2017JD027348
Joho M, Lambert RH, Mathis H (2001) Elementary cost functions for blind separation of non-stationary source signals. Presented at the 2001 IEEE international conference on acoustics, speech, and signal processing. Proceedings (Cat. No. 01CH37221), IEEE, pp 2793–2796
Jozefowicz R, Zaremba W, Sutskever I (2015) An empirical exploration of recurrent network architectures. In: International conference on machine learning, pp 2342–2350
Kavitha S, Varuna S, Ramya R (2016) A comparative analysis on linear regression and support vector regression. Presented at the 2016 online international conference on green engineering and technologies (IC-GET), pp 1–5. https://doi.org/10.1109/GET.2016.7916627
Keras (2019a) Home—Keras documentation [WWW document]. https://keras.io/. Accessed 28 Jan 2019
Keras (2019b) Metrics—Keras documentation [WWW Document]. https://keras.io/metrics/. Accessed 28 Jan 2019
Kim TS, Reiter A (2017) Interpretable 3D human action analysis with temporal convolutional networks. arXiv:170404516Cs
Klein WH, Glahn HR (1974) forecasting local weather by means of model output statistics. Bull Am Meteorol Soc 55:1217–1227. https://doi.org/10.1175/1520-0477(1974)055%3c1217:FLWBMO%3e2.0.CO;2
Krizhevsky A, Sutskever I, Hinton GE (2012) ImageNet classification with deep convolutional neural networks. In: Pereira F, Burges CJC, Bottou L, Weinberger KQ (eds) Advances in neural information processing systems, vol 25. Curran Associates Inc, Red Hook, pp 1097–1105
Lahoz W, Khattatov B, Ménard R (2010) Data assimilation and information. In: Lahoz W, Khattatov B, Menard R (eds) Data assimilation: making sense of observations. Springer, Berlin, pp 3–12. https://doi.org/10.1007/978-3-540-74703-1_1
Lea C, Flynn MD, Vidal R, Reiter A, Hager GD (2017) Temporal convolutional networks for action segmentation and detection. In: Presented at the 2017 IEEE conference on computer vision and pattern recognition (CVPR), IEEE, Honolulu, HI, pp 1003–1012. https://doi.org/10.1109/CVPR.2017.113
Li K, Liu YS (2005) A rough set based fuzzy neural network algorithm for weather prediction. Presented at the 2005 international conference on machine learning and cybernetics, vol 3, pp 1888–1892. https://doi.org/10.1109/ICMLC.2005.1527253
Lynch P (2006) The emergence of numerical weather prediction: Richardson’s dream. Cambridge University Press, Cambridge
Mandic DP, Chambers JA (2000) On the choice of parameters of the cost function in nested modular RNN’s. IEEE Trans Neural Netw 11:315–322
Mass CF, Kuo Y-H (1998) Regional real-time numerical weather prediction: current status and future potential. Bull Am Meteorol Soc 79:253–264. https://doi.org/10.1175/1520-0477(1998)079%3c0253:RRTNWP%3e2.0.CO;2
Mathur S, Kumar A, Ch M (2008) A feature based neural network model for weather forecasting. Int J Comput Intell
McCREA M, Barr WB, Guskiewicz K, Randolph C, Marshall SW, Cantu R, Onate JA, Kelly JP (2005) Standard regression-based methods for measuring recovery after sport-related concussion. J Int Neuropsychol Soc 11:58–69. https://doi.org/10.1017/S1355617705050083
Met Office (2019) How weather forecasts are created [WWW document]. Met Off. https://www.metoffice.gov.uk/weather/learn-about/how-forecasts-are-made/_index_. Accessed 21 Feb 2019
Mittal Y, Mittal A, Bhateja D, Parmaar K, Mittal VK (2015) Correlation among environmental parameters using an online Smart Weather Station System. Presented at the 2015 annual IEEE India conference (INDICON), pp 1–6. https://doi.org/10.1109/INDICON.2015.7443621
National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce (2015) NCEP GFS 0.25 Degree Global Forecast Grids Historical Archive. https://doi.org/10.5065/D65D8PWK
National Geographic Society (2011) Atmospheric pressure [WWW document]. National Geographic Society. http://www.nationalgeographic.org/encyclopedia/atmospheric-pressure/. Accessed 23 July 2019
NCAR/UCAR (2019). WRF model users site [WWW document]. http://www2.mmm.ucar.edu/wrf/users/. Accessed 21 Jan 2019
NCEI (2019) Numerical Weather Prediction | National Centers for Environmental Information (NCEI) formerly known as National Climatic Data Center (NCDC) [WWW Document]. National Centers for Environmental Information. https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/numerical-weather-prediction. Accessed 21 Feb 2019
Noaa (2017) Reading GRIB files [WWW document]. http://www.cpc.ncep.noaa.gov/products/wesley/reading_grib.html. Accessed 23 Jan 2019
Patil K, Deo MC (2018) Basin-scale prediction of sea surface temperature with artificial neural networks. Presented at the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), pp 1–5. https://doi.org/10.1109/OCEANSKOBE.2018.8558780
Powers JG, Klemp JB, Skamarock WC, Davis CA, Dudhia J, Gill DO, Coen JL, Gochis DJ, Ahmadov R, Peckham SE, Grell GA, Michalakes J, Trahan S, Benjamin SG, Alexander CR, Dimego GJ, Wang W, Schwartz CS, Romine GS, Liu Z, Snyder C, Chen F, Barlage MJ, Yu W, Duda MG (2017) The weather research and forecasting model: overview, system efforts, and future directions. Bull Am Meteorol Soc 98:1717–1737. https://doi.org/10.1175/BAMS-D-15-00308.1
Rodríguez-Fernández NJ, de Rosnay P, Albergel C, Aires F, Prigent C, Richaume P, Kerr YH, Drusch M (2018) SMOS neural network soil moisture data assimilation. Presented at the IGARSS 2018—2018 IEEE international geoscience and remote sensing symposium, pp 5548–5551. https://doi.org/10.1109/IGARSS.2018.8519377
Routray A, Mohanty UC, Osuri KK, Kar SC, Niyogi D (2016) Impact of satellite radiance data on simulations of bay of bengal tropical cyclones using the WRF-3DVAR modeling system. IEEE Trans Geosci Remote Sens 54:2285–2303. https://doi.org/10.1109/TGRS.2015.2498971
Sachidananda M, Zrnić DS (1987) Rain rate estimates from differential polarization measurements. J Atmos Ocean Technol 4:588–598. https://doi.org/10.1175/1520-0426(1987)004%3c0588:RREFDP%3e2.0.CO;2
Schmidhuber J (2015) Deep learning in neural networks: an overview. Neural Netw 61:85–117. https://doi.org/10.1016/j.neunet.2014.09.003
Sharaff A, Roy SR (2018) Comparative analysis of temperature prediction using regression methods and back propagation neural network. Presented at the 2018 2nd international conference on trends in electronics and informatics (ICOEI), pp 739–742. https://doi.org/10.1109/ICOEI.2018.8553803
Shi X, Chen Z, Wang H, Yeung D-Y, Wong W, Woo W (2015) Convolutional LSTM network: a machine learning approach for precipitation nowcasting. In: Cortes C, Lawrence ND, Lee DD, Sugiyama M, Garnett R (eds) Advances in neural information processing systems, vol 28. Curran Associates Inc, Red Hook, pp 802–810
Skamarock C, Klemp B, Dudhia J, Gill O, Barker D, Duda G, Huang X, Wang W, Powers G (2008) A description of the advanced research WRF version 3. https://doi.org/10.5065/D68S4MVH
SwitchDoc Labs (2016) Tutorial: part 1—building a solar powered raspberry Pi weather station—GroveWeatherPi. Switch. Labs. https://www.switchdoc.com/2016/12/tutorial-part-1-building-a-solar-powered-raspberry-pi-weather-station-groveweatherpi/. Accessed 14 May 2019
Taylor JW, Buizza R (2002) Neural network load forecasting with weather ensemble predictions. IEEE Trans Power Syst 17:626–632. https://doi.org/10.1109/TPWRS.2002.800906
Thornton PE, Thornton MM, Mayer BW, Wilhelmi N, Wei Y, Devarakonda R, Cook RB (2014) Daymet: daily surface weather data on a 1-km grid for North America, Version 2. Oak Ridge National Lab. (ORNL), Oak Ridge
Troncoso A, Salcedo-Sanz S, Casanova-Mateo C, Riquelme JC, Prieto L (2015) Local models-based regression trees for very short-term wind speed prediction. Renew Energy 81:589–598. https://doi.org/10.1016/j.renene.2015.03.071
US EPA O (2016) Surface and upper air databases | TTN—support center for regulatory atmospheric modeling | US EPA [WWW document]. https://www3.epa.gov/scram001/metobsdata_databases.htm. Accessed 13 Aug 2019
Voyant C, Notton G, Kalogirou S, Nivet M-L, Paoli C, Motte F, Fouilloy A (2017) Machine learning methods for solar radiation forecasting: a review. Renew Energy 105:569–582. https://doi.org/10.1016/j.renene.2016.12.095
Yonekura K, Hattori H, Suzuki T (2018) Short-term local weather forecast using dense weather station by deep neural network. Presented at the 2018 IEEE international conference on big data (big data), pp 1683–1690. https://doi.org/10.1109/BigData.2018.8622195
Yu F, Koltun V (2015) Multi-scale context aggregation by dilated convolutions. arXiv:151107122Cs
Zhao Z, Chen W, Wu X, Chen PC, Liu J (2017) LSTM network: a deep learning approach for short-term traffic forecast. IET Intell Transp Syst 11:68–75
Acknowledgements
This research work is partly supported by Clive Blaker and Rich Kavanagh (Precision Decisions Ltd). We are grateful to Prof Mark Anderson (Former Professor at Edge Hill University) for his valuable inputs and support at the initial stage of this study. We are grateful to Dr. Alan Gadian (National Centre for Atmospheric Sciences, University of Leeds) for his valuable support to identify weather parameters.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by V. Loia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hewage, P., Behera, A., Trovati, M. et al. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput 24, 16453–16482 (2020). https://doi.org/10.1007/s00500-020-04954-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-04954-0