Multiple criteria decision making based on weighted Archimedean power partitioned Bonferroni aggregation operators of generalised orthopair membership grades

Abstract

In this paper, a multiple criteria decision making (MCDM) method based on weighted Archimedean power partitioned Bonferroni aggregation operators of generalised orthopair membership grades (GOMGs) is proposed. Bonferroni mean operator, geometric Bonferroni mean operator, power average operator, partitioned average operator, and Archimedean T-norm and T-conorm operations are introduced into generalised orthopair fuzzy sets to develop the Bonferroni aggregation operators. Their formal definitions are provided, and generalised and specific expressions are constructed. On the basis of the specific operators, a method for solving the MCDM problems based on GOMGs is designed. The working process, characteristics, and feasibility of the method are, respectively, demonstrated via a numerical example, a qualitative comparison at the aspect of characteristics, and a quantitative comparison using the example as benchmark. The demonstration results show that the proposed method is feasible that has desirable generality and flexibility in the aggregation of criterion values and concurrently has the capabilities to deal with the heterogeneous interrelationships of criteria, reduce the negative influence of biased criterion values, and capture the risk attitudes of decision makers.

1 Introduction

Multiple criteria decision making (MCDM), or multiple criteria decision analysis, is a process of finding optimal alternatives in complex scenarios via evaluating the values of multiple criteria of all alternatives synthetically (Greco et al. 2016). In this process, the first important task is to express criterion values accurately and effectively. For such expression, there are various kinds of available tools (Abualigah and Hanandeh 2015; Abualigah and Khader 2017; Abualigah et al. 2018a, b, c; Abualigah 2019), where fuzzy sets are one of the most representative kinds (Yager 1981). So far, over twenty different types of fuzzy sets have been presented within academia (Bustince et al. 2016). Among them, Zadeh’s fuzzy set (FS) (Zadeh 1965) is a well-known type of fuzzy set that uses a degree of membership μ (0 ≤ µ ≤ 1) to quantify the degree of satisfaction. In some real applications, FS is enough for the representation of fuzzy information. However, it cannot be used to describe complex fuzzy information, such as the degree of dissatisfaction and the degree of hesitancy. To make up for this deficiency, Atanassov (1986) presented the theory of intuitionistic fuzzy set (IFS). Compared with a FS, an IFS has a degree of membership μ and a degree of non-membership ν (0 ≤ µ ≤ 1; 0 ≤ ν ≤ 1; 0 ≤ µ + ν ≤ 1), which can, respectively, express the degree of satisfaction and the degree of dissatisfaction, and thus, the degree of hesitancy can be obtained by 1 − µ − ν. Due to such characteristic, IFSs have been widely used to describe the values of criteria in MCDM during the past three decades. A number of research topics about IFSs in MCDM, such as operational rules of intuitionistic membership grades (IMGs) (De et al. 2000; Wang and Liu 2012; Jamkhaneh and Garg 2018), aggregation operators of IMGs (Xu and Yager 2011; Xia et al. 2012, 2013; Liu and Chen 2017; He et al. 2017; Liu et al. 2018a), intuitionistic preference relations (Xu 2007; Liao and Xu 2014a; Zhang and Pedrycz 2017), intuitionistic fuzzy calculus (Lei and Xu 2015, 2016; Ai and Xu 2018), and MCDM methods based on IFSs (Wei 2010; Liu and Zhang 2011; Liao and Xu 2014b; Garg 2017), have received extensive attention in this period.

Although IFSs have showed great potential in MCDM, their application range is limited by their capability to express fuzzy information. More specifically, the two components μ and ν in an IFS must satisfy the condition that 0 ≤ µ + ν ≤ 1. In this case, the criterion values whose µ and ν do not satisfy this condition cannot be described by IFSs. For example, IFS is not capable of expressing a criterion value whose µ = 0.8 and ν = 0.4 because 0.8 + 0.4 > 1. To address this issue, Yager (2014) proposed the theory of Pythagorean fuzzy set (PFS), which relaxes the condition to 0 ≤ µ² + ν² ≤ 1. For this reason, PFSs can express more fuzzy information than IFSs. For instance, the criterion value whose µ = 0.8 and ν = 0.4 can be described by a PFS because 0.8² + 0.4² < 1. Due to the stronger expressiveness, PFSs have also had a wide range of applications in MCDM. For example, Yager and Abbasov (2013) investigated the relationships between Pythagorean membership grades (PMGs) and complex numbers; Zhang and Xu (2014) presented an extension of TOPSIS to MCDM with PFSs; Peng and Yang (2015) proposed division and subtraction operations on PFSs and developed a Pythagorean fuzzy superiority and inferiority ranking method to address the MCDM problems with uncertainty; Garg (2016) proposed a new generalised weighted Einstein operator to aggregate PMGs and studied its application in MCDM; Dick et al. (2016) developed interpretations of complex-valued PMGs; Chen (2018) developed novel VIKOR-based methods for MCDM involving Pythagorean fuzzy information; Wei and Lu (2018) presented a set of Pythagorean fuzzy weighted power aggregation operators to resolve MCDM problems; Liang et al. (2018) proposed a model of three-way decisions and developed the corresponding decision-making process based on PFSs; Khan et al. (2019) presented a set of Pythagorean hesitant fuzzy Choquet integral aggregation operators for MCDM.

To further improve the expressiveness of PFSs, Yager (2017) presented the theory of generalised orthopair fuzzy set (GOFS). In a GOFS, the condition of µ and ν is further relaxed to 0 ≤ µ^q + ν^q ≤ 1 (q = 1, 2, 3, …). Obviously, GOFS is the generalisation of FS, IFS, and PFS because: when q = 1 and 0 < µ^q + ν^q = 1, GOFS will become FS; when q = 1 and 0 ≤ µ^q + ν^q ≤ 1, GOFS will become IFS; when q = 2 and 0 ≤ µ^q + ν^q ≤ 1, GOFS will become PFS. It is also not difficult to find that the greater of the value of the rung q, the stronger the expressiveness of a GOFS. This provides a mechanism to obtain certain fuzzy information expression range via assigning an appropriate value to q. As an example, suppose there is a criterion value whose µ = 0.9 and ν = 0.5. This value cannot be described by PFS since 0.9² + 0.5² > 1. However, when q is assigned at least 3, the value can be expressed by GOFS. From this example, it is no doubt that GOFSs have the strongest expressiveness compared with FSs, IFSs, and PFSs. Due to this, GOFSs have also received extensive attention during the past 2 years. Various research topics regarding GOFSs, which mainly include approximate reasoning in GOFSs (Yager and Alajlan 2017), aspects of GOFSs (Yager et al. 2018), distance measures of GOFSs (Du 2018), correlation and correlation coefficient of GOFSs (Du 2019), MCDM methods based on GOFSs (Liu et al. 2018b; Wang and Li 2018), and aggregation operators of generalised orthopair membership grades (GOMGs) (Liu and Wang 2018a, b; Liu and Liu 2018; Yang and Pang 2019; Liu et al. 2018c, d; Wei et al. 2018, 2019; Bai et al. 2018; Wang et al. 2019; Peng et al. 2018; Xing et al. 2019), are gaining importance within academia.

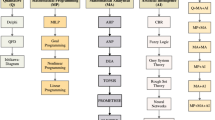
For solving the MCDM problems, there are generally two categories of methods. One category consists of conventional methods (e.g. TOPSIS, VIKOR, PROMETHEE, ELECTRE). The other category includes the methods based on aggregation operators (Grabisch et al. 2009, 2011). Aggregation operators can solve the MCDM problems more effectively because they can provide comprehensive values and rankings of alternatives, while conventional methods can only generate rankings (Liu and Wang 2018b). So far, over twenty different aggregation operators of GOMGs have been presented, which include the weighted averaging (WA) operator and the weighted geometric (WG) operator (Liu and Wang 2018a), the weighted Bonferroni mean (WBM) operator and the weighted geometric Bonferroni mean (WGBM) operator (Liu and Liu 2018), the weighted Archimedean Bonferroni mean (WABM) operators (Liu and Wang 2018b), the weighted partitioned Bonferroni mean (WPBM) operator and the weighted partitioned geometric Bonferroni mean (WPGBM) operator (Yang and Pang 2019), the weighted extended Bonferroni mean (WEBM) operator (Liu et al. 2018b), the weighted Heronian mean (WHM) operator and the weighted geometric Heronian mean (WGHM) operator (Wei et al. 2018), the WHM* operator and the weighted partitioned Heronian mean (WPHM) operator (Liu et al. 2018c), the weighted Maclaurin symmetric mean (WMSM) operator and the weighted geometric Maclaurin symmetric mean (WGMSM) operator (Wei et al. 2019), the weighted power Maclaurin symmetric mean (WPMSM) operator (Liu et al. 2018d), the weighted power partitioned Maclaurin symmetric mean (WPPMSM) operator (Bai et al. 2018), the weighted Muirhead mean (WMM) operator and the weighted geometric Muirhead mean (WGMM) operator (Wang et al. 2019), the weighted exponential (WE) operator (Peng et al. 2018), and the weighted point (WP) operators (Xing et al. 2019). The main characteristics of these operators are listed in Table 1. As can be summarised from the table, among the MCDM methods based on the operators, there is not yet a method that has the following characteristics at the same time: (1) provide desirable generality and flexibility in the aggregation of GOMGs; (2) deal with the case where the criteria are divided into several partitions and there are interrelationships between different criteria in each partition, whereas the criteria in different partitions are independent of each other; (3) reduce the negative effect of the unduly high or unduly low criterion values on the aggregation results; (4) capture the risk attitudes of decision makers.

Table 1 The main characteristics of the existing aggregation operators of GOMGs

In practical MCDM problems, aggregation of values of criteria is a complicated process, in which decision makers’ preferences could vary. A desirable aggregation operator should be general and flexible enough to adapt to such variation. Also, there are generally interrelationships among the criteria considered in the problems. It is also of necessity for an aggregation operator to model such interrelationships to obtain more reasonable aggregation results. Further, criterion values are usually evaluated by domain experts, which are always not absolutely objective. This means that a few domain experts could provide unduly high or unduly low criterion values. To achieve reasonable aggregation results, it is of importance to reduce the effect of such values in the aggregation process. Finally, MCDM problems have certain subjectivity and the preferences of decision makers are their important input. Among various preferences, decision makers’ risk attitudes (e.g. pessimistic, neutral, and optimistic) are an important type. A desirable aggregation operator should have the capability to capture such risk attitudes. Based on these considerations, the motivations of the present paper are explained as follows:

• (1) To develop an aggregation operator of GOMGs that can capture the interrelationships of criteria and the risk attitudes of decision makers, the Bonferroni mean (BM) operator (Bonferroni 1950), geometric BM (GBM) operator (Xia et al. 2013), and partitioned average operator (Dutta and Guha 2015) are introduced to construct partitioned Bonferroni aggregation operators of GOMGs. The BM and GBM operators can capture the interrelationships between the aggregated arguments and were found to, respectively, provide pessimistic and optimistic expectations in MCDM. The partitioned average operator can handle the situation where the aggregated arguments are divided into several partitions and the arguments in different partitions have different interrelations.

• (2) To enable the aggregation operator to reduce the influence of extreme criterion values on the aggregation results, the power average operator (Yager 2001) is combined into the partitioned Bonferroni aggregation operators of GOMGs. The power average operator can assign weights to the aggregated arguments. This makes it possible to reduce the effect of unreasonable arguments values on the aggregation results.

• (3) To improve the generality and flexibility of the combined aggregation operators of GOMGs, the operational rules based on the Archimedean T-norm and T-conorm (ATT) (Klement et al. 2000; Deschrijver and Kerre 2002) are used to perform the operations in them. The ATT are important tools that can generate versatile operational rules for membership grades, and the aggregation operators based on them are flexible in the aggregation of fuzzy information.

To sum up, this paper aims to present a set of weighted Archimedean power partitioned BM (WAPPBM) operators and weighted Archimedean power partitioned GBM (WAPPGBM) operators of GOMGs and a MCDM method based on them. This aim is achieved via the combination of the BM, GBM, power average, and partitioned average operators with weights and the operational rules based on ATT in the context of MCDM based on GOMGs. The major contribution of the paper is as follows: A MCDM method based on weighted Archimedean power partitioned Bonferroni aggregation operators of GOMGs is proposed. Compared to the existing MCDM methods based on aggregation operators of GOMGs, the proposed MCDM method simultaneously has the four characteristics above.

The remainder of the paper is organised as follows. A brief introduction of some related basic concepts is given in Sect. 2. Sections 3 and 4, respectively, explain the details of the presented aggregation operators and the proposed MCDM method. A numerical example and qualitative and quantitative comparisons are reported to illustrate and demonstrate the method in Sect. 5. Section 6 ends the paper with a conclusion.

2 Preliminaries

To better understand this paper, some prerequisites in GOFS theory, operational rules of GOMGs based on ATT, BM operator, GBM operator, power average operator, and partitioned average operator are briefly introduced in this section.

2.1 GOFS theory

Yager’s GOFS (Yager 2017) is the generalisation of Zadeh’s FS (Zadeh 1965), Atanassov’s IFS (Atanassov 1986), and Yager’s PFS (Yager 2014). Its formal definition is as follows:

Definition 1

A qROFS S in a finite universe of discourse X is S = {〈x, µ_S(x), ν_S(x)〉  | x∈X}, where µ_S: X → [0, 1] is the degree of membership of the element x∈X to the set S, and ν_S: X → [0, 1] is the degree of non-membership of x ∈ X to S, with the condition that 0 ≤ (µ_S(x))^q + (ν_S(x))^q ≤ 1 (q = 1, 2, 3, …). The degree of hesitancy of x ∈ X to S is π_S(x) = (1 − (µ_S(x))^q − (ν_S(x))^q)^1/q.

For convenience, a pair 〈µ_S(x), ν_S(x)〉 is called as a GOMG, which is usually denoted as G = 〈µ, ν〉. To compare two GOMGs, their scores and accuracies are needed to calculate. The followings are the definitions of the score and the accuracy of a GOMG.

Definition 2

Let G = 〈µ, ν〉 be a GOMG. Then, the score of G is

$$ S\left( G \right) \, = \mu^{q} - \nu^{q} $$

(1)

Obviously, −1 ≤ S(G) ≤ 1.

Definition 3

Let G = 〈µ, ν〉 be a GOMG. Then, the accuracy of G is

$$ A\left( G \right) \, = \mu^{q} + \nu^{q} $$

(2)

Obviously, 0 ≤ A(G) ≤ 1.

Based on S(G) and A(G), two GOMGs can be compared according to the following definition:

Definition 4

Let G₁ = 〈µ₁, ν₁〉 and G₂ = 〈µ₂, ν₂〉 be two arbitrary GOMGs, S(G₁) and S(G₂) be, respectively, the scores of G₁ and G₂, and A(G₁) and A(G₂) be, respectively, the accuracies of G₁ and G₂. Then: (1) If S(G₁) > S(G₂), then G₁ > G₂; (2) If S(G₁) = S(G₂) and A(G₁) > A(G₂), then G₁ > G₂; (3) If S(G₁) = S(G₂) and A(G₁) = A(G₂), then G₁ = G₂.

To compute the distance between two GOMGs, a distance measure of GOMGs is required. The following definition provides the Minkowski-type distance measure of GOMGs (Du 2018):

Definition 5

Let G₁ = 〈µ₁, ν₁〉 and G₂ = 〈µ₂, ν₂〉 be any two GOMGs. Then, the Minkowski-type distance between G₁ and G₂ is

$$ D\left( {G_{1} ,G_{2} } \right) = \left( {0.5\left| {\mu_{1} - \mu_{2} } \right|^{\sigma } + \, 0.5\left| {\nu_{1} - \nu_{2} } \right|^{\sigma } } \right)^{1/\sigma } $$

(3)

where σ = 1, 2, … If σ = 1, the Minkowski-type distance between G₁ and G₂ will reduce to the Hamming distance between G₁ and G₂: D(G₁, G₂) = 0.5(|µ₁ − µ₂| + |ν₁ − ν₂|); If σ = 2, the Minkowski-type distance between G₁ and G₂ will reduce to the Euclidean distance between G₁ and G₂: (0.5|µ₁ − µ₂|² + 0.5|ν₁ − ν₂|²)^1/2; If σ = ∞, the Minkowski-type distance between G₁ and G₂ will reduce to the Chebyshev distance between G₁ and G₂: D(G₁, G₂) = max(|µ₁ − µ₂|, |ν₁ − ν₂|).

2.2 Operational rules

In mathematics, a T-norm is a binary operation on the unit interval [0, 1] that satisfies commutativity, associativity, monotonicity, and boundary condition (Klement et al. 2000, 2005; Pap 1997, 2008). The dual notion of a T-norm is its conorm. Formally, a T-norm and its conorm can be defined as follows:

Definition 7

A T-norm is a function T: [0, 1]² → [0, 1] such that for all x, y, z ∈ [0, 1]: (1) T(x, y) = T(y, x); (2) T(x, T(y, z)) = T(T(x, y), z); (3) If y ≤ z, then T(x, y) ≤ T(x, z); (4) T(x, 1) = x.

Definition 8

If T is a T-norm, then its conorm T^C: [0, 1]² → [0, 1] is T^C(x, y) = 1 − T(1 − x, 1 − y).

A T-norm T is called Archimedean if every sequence x_n (where n = 1, 2, …; x₁ < 1; and x_n+1 = T(x_n, x_n)) converges to 0. The conorm of an Archimedean T-norm is called as an Archimedean T-conorm.

For an Archimedean T-norm T and its conorm T^C: (1) If a function f(t) (t ∈ R) is monotonically decreasing and satisfies the conditions that f(t): (0, 1] → R⁺; f⁻¹(t): R⁺ → (0, 1]; lim_t→∞f⁻¹(t) = 0; and f⁻¹(0) = 1, then f(t) can be used to generate T: T(x, y) = f⁻¹(f(x) + f(y)) and is called as an additive generator of T; (2) If a function g(t) (t ∈ R) is monotonically increasing and satisfies the conditions that g(t): (0, 1] → R⁺; g⁻¹(t): R⁺ → (0, 1]; lim_t→∞g⁻¹(t) = 1; and g⁻¹(0) = 0, then g(t) can be used to generate T^C: T^C(x, y) = g⁻¹(g(x) + g(y)) and is called as an additive generator of T^C. According to the definition of the conorm of a T-norm, f(t) is actually equal to g(1 − t), that is, f(t) = g(1 − t).

During the past few decades, the studies of ATTs and their additive generators have received a lot of attention. Various families of ATTs have been presented in this period. Four well-known families of ATTs and their additive generators are as follows:

• (1) If f(t) = − Int, then g(t) = − In(1 − t), f⁻¹(t) = e^−t, and g⁻¹(t) = 1 − e^−t. Based on this, the algebraic T-norm and T-conorm are obtained as

  $$ T_{\text{A}} (x,y) = xy\quad {\text{and}}\quad T_{\text{A}}^{\text{C}} (x,y) = x + y - xy $$

• (2) If f(t) = In[(2 − t)/t], then g(t) = In[(1 + t)/(1 − t)], f⁻¹(t) = 2/(e^t+ 1), and g⁻¹(t) = (e^t− 1)/(e^t+ 1). Based on this, the Einstein T-norm and T-conorm are obtained as

  $$ T_{\text{E}} (x,y) = \frac{xy}{1 + (1 - x)(1 - y)}\quad {\text{and}}\quad T_{\text{E}}^{\text{C}} (x,y) = \frac{x + y}{1 + xy} $$

• (3) If f(t) = In{[λ + (1 − λ)t]/t} (λ > 0), then g(t) = In{[λ + (1 − λ)(1 − t)]/(1 − t)}, f⁻¹(t) = λ/(e^t+ λ−1), and g⁻¹(t) = (e^t− 1)/(e^t+ λ−1). Based on this, the Hamacher T-norm and T-conorm are obtained as

  $$ T_{\text{H}} (x,y) = \frac{xy}{\lambda + (1 - \lambda )(x + y - xy)}\quad {\text{and}}\quad T_{\text{H}}^{\text{C}} (x,y) = \frac{x + y - xy - (1 - \lambda )xy}{1 - (1 - \lambda )xy} $$

• (4) If f(t) = − In[(ε − 1)/(ε^t− 1)] (ε > 1), then g(t) = − In[(ε − 1)/(ε^1−t−1)], f⁻¹(t) = log_ε[(ε − 1+e^−t)/e^−t], and g⁻¹(t) = 1 − log_ε[(ε − 1 + e^−t)/e^−t]. Based on this, the Frank T-norm and T-conorm are obtained as

  $$ T_{\text{F}} (x,y) = \log_{\varepsilon } \left( {1 + \frac{{(\varepsilon^{x} - 1)(\varepsilon^{y} - 1)}}{\varepsilon - 1}} \right)\quad {\text{and}}\quad T_{\text{F}}^{\text{C}} (x,y) = 1 - \log_{\varepsilon } \left[ {1 + \frac{{(\varepsilon^{1 - x} - 1)(\varepsilon^{1 - y} - 1)}}{\varepsilon - 1}} \right] $$

Based on ATT, a set of general and versatile operational rules of GOMGs can be established according to the following definition (Liu and Wang 2018b):

Definition 9

Suppose G = 〈μ, ν〉, G₁ = 〈μ₁, ν₁>, and G₂ = 〈μ₂, ν₂〉 are three arbitrary GOMGs, and δ and τ are two arbitrary real numbers and δ, τ > 0. Then, the sum and product operations between GOMGs based on the Archimedean T-norm T(x, y) = f⁻¹(f(x) + f(y)) and the Archimedean T-conorm T^C(x, y) = g⁻¹(g(x) + g(y)) and the multiplication and power operations of GOMGs based on T(x, y) and T^C(x, y) can be, respectively, defined as follows:

$$ G_{1} \oplus G_{2} = \,\left\langle {T^{\text{C}} \left( {\mu_{1} ,\mu_{2} } \right),T\left( {\nu_{1} ,\nu_{2} } \right)} \right\rangle \, = \,\left\langle {g^{ - 1} \left( {g\left( {\mu_{1} } \right) + g\left( {\mu_{2} } \right)} \right),\,f^{ - 1} \left( {f\left( {\nu_{1} } \right) + f\left( {\nu_{2} } \right)} \right)} \right\rangle $$

(4)

$$ G_{1} \oplus G_{2} = \,\left\langle {T\left( {\mu_{1} ,\mu_{2} } \right),\,T^{\text{C}} \left( {\nu_{1} ,\nu_{2} } \right)} \right\rangle \, = \,\left\langle {f^{ - 1} \left( {f\left( {\mu_{1} } \right) + f\left( {\mu_{2} } \right)} \right),\,g^{ - 1} \left( {g\left( {\nu_{1} } \right) + g\left( {\nu_{2} } \right)} \right)} \right\rangle $$

(5)

$$ \delta G = \,\left\langle {g^{ - 1} \left( {\delta g\left( \mu \right)} \right),\,f^{ - 1} \left( {\delta f\left( \nu \right)} \right)} \right\rangle $$

(6)

$$ G^{\tau } = \,\left\langle {f^{ - 1} \left( {\tau f\left( \mu \right)} \right),\,g^{ - 1} \left( {\tau g\left( \nu \right)} \right)} \right\rangle $$

(7)

2.3 BM operator

The BM operator was presented by Bonferroni (1950). It is capable of describing the interrelationships between different non-negative real numbers. The formal definition of BM operator is as follows:

Definition 10

Let Ξ_k (k = 1, 2, …, n) be a collection of non-negative real numbers and a and b be two real numbers and a, b ≥ 0 but not at the same time a = b = 0. Then, the aggregation function

$$ {\text{BM}}^{(a,b)} (\varXi_{1} ,\varXi_{2} , \ldots ,\varXi_{n} ) = \left( {\frac{1}{n(n - 1)}\sum\limits_{\begin{subarray}{l} i,j = 1 \\ j \ne i \end{subarray} }^{n} {\left( {\varXi_{i}^{a} \varXi_{j}^{b} } \right)} } \right)^{{\frac{1}{a + b}}} $$

(8)

is called the BM operator. In this operator, the interrelationships between Ξ_i and Ξ_j are captured by a and b. The interrelationships will only be considered when both a and b are not 0.

2.4 GBM operator

The GBM operator was introduced by Xia et al. (2013). It was found to obtain more optimistic expectations in MCDM than the BM operator. The GBM operator is actually the dual form of the BM operator. Its formal definition is as follows:

Definition 11

Let Ξ_k (k = 1, 2, …, n) be a collection of non-negative real numbers and a and b be two real numbers and a, b ≥ 0 but not at the same time a = b = 0. Then, the aggregation function

$$ {\text{GBM}}^{(a,b)} (\varXi_{1} ,\varXi_{2} , \ldots ,\varXi_{n} ) = \frac{1}{a + b}\prod\limits_{\begin{subarray}{l} i,j = 1 \\ j \ne i \end{subarray} }^{n} {\left( {a\varXi_{i} + b\varXi_{j} } \right)}^{{\frac{1}{n(n - 1)}}} $$

(9)

is called the GBM operator. In this operator, the interrelationships between Ξ_i and Ξ_j are also captured by a and b. The interrelationships will only be considered when both a and b are not 0.

2.5 Power average operator

The power average operator, introduced by Yager (2001), can assign weights to the aggregated arguments via calculating the degrees of support between these arguments. This makes it possible to reduce the negative effect of the unduly high or unduly low argument values on the aggregation results. The formal definition of the operator is as follows:

Definition 12

Let (Ξ₁, Ξ₂, …, Ξ_n) be a collection of crisp numbers, S(Ξ_i, Ξ_j) = 1 − D(Ξ_i, Ξ_j) (i, j = 1, 2, …, n and j ≠ i; D(Ξ_i, Ξ_j) is the distance between Ξ_i and Ξ_j) be the degree of support for Ξ_i from Ξ_j which has the following properties: (1) 0 ≤ S(Ξ_i, Ξ_j) ≤ 1; (2) S(Ξ_i, Ξ_j) = S(Ξ_j, Ξ_i); (3) S(Ξ_i, Ξ_j) ≥ S(Ξ_r, Ξ_s) if |Ξ_i− Ξ_j| ≤ |Ξ_r− Ξ_s|, and

$$ T(\varXi_{i} ) = \sum\limits_{j = 1,j \ne i}^{n} {S(\varXi_{i} , \, \varXi_{j} )} $$

Then, the aggregation function

$$ {\text{PA}}(\varXi_{1} ,\varXi_{2} , \ldots ,\varXi_{n} ) = \frac{{\sum\nolimits_{i = 1}^{v} {\left( {\left( {1 + T(\varXi_{i} )} \right)\varXi_{i} } \right)} }}{{\sum\nolimits_{v}^{n} {\left( {1 + T(\varXi_{i} )} \right)} }} $$

(10)

is called the power average operator.

2.6 Partitioned average operator

The partitioned average operator can aggregate the arguments in different partitions using the same aggregation operator and aggregate the aggregation results of different partitions using the arithmetic average operator (Dutta and Guha 2015). Its formal definition is as follows:

Definition 13

Let (Ξ₁, Ξ₂, …, Ξ_n) be a collection of crisp numbers, S = {Ξ₁, Ξ₂, …, Ξ_n} be a set of Ξ₁, Ξ₂, …, Ξ_n, S_k = {Ξ₁, Ξ₂, …, Ξ_|Sk|} (k = 1, 2, …, N) be N partitions of S (i.e. S₁ ∪ S₂ ∪ … ∪ S_N = S and S₁ ∩ S₂ ∩ … ∩ S_N = Ø), and AO be a specific aggregation operator. Then, the aggregation function

$$ {\text{Pt}}A(\varXi_{1} ,\varXi_{2} , \ldots ,\varXi_{n} ) = \frac{1}{N}\sum\limits_{k = 1}^{N} {\left( {\mathop {\text{AO}}\limits_{{i_{k} = 1}}^{{\left| {S_{k} } \right|}} \left( {\varXi_{{i_{k} }} } \right)} \right)} $$

(11)

is called the partitioned average operator.

3 Bonferroni aggregation operators

In this section, a WAPPBM operator and a WAPPGBM operator of GOMGs are presented. The formal definitions of the two operators are provided, and their generalised and specific expressions are constructed.

3.1 WAPPBM operator

A WAPPBM operator of GOMGs is an aggregation operator of GOMGs combining the BM operator, the power average operator, and the partitioned average operator with weights, in which the sum, product, multiplication, and power operations are performed using the operational rules of GOMGs based on ATT. Its formal definition is as follows:

Definition 14

Let G₁, G₂, …, G_n (G_i = 〈μ_i, ν_i〉, i = 1, 2, …, n) be n GOMGs (q = 1, 2, 3, …), (G₁, G₂, …, G_n) be a collection of G₁, G₂, …, G_n, S = {G₁, G₂, …, G_n} be an ordered set of G₁, G₂, …, G_n, S_k = {G₁, G₂, …, G_|Sk|} (k = 1, 2, …, N) be N partitions of S (i.e. S₁ ∪ S₂ ∪ … ∪ S_N = S and S₁ ∩ S₂ ∩ … ∩ S_N = Ø), a and b be two real numbers such that a, b ≥ 0 but not at the same time a = b = 0, G_i$\oplus$G_j and G_i$\otimes$G_j (i, j = 1, 2, …, n) be, respectively, the sum and product operations of G_i and G_j based on ATT, cG_r and G^d_s (r, s = 1, 2, …, n; c, d > 0) be, respectively, the multiplication operation of G_r and the power operation of G_s based on ATT, S(G_r, G_s) = 1 − D(G_r, G_s) (r, s = 1, 2, …, n and s ≠ r; D(G_r, G_s) is the distance between G_r and G_s) be the degree of support for G_r from G_s which satisfy 0 ≤ S(G_r, G_s) ≤ 1, S(G_r, G_s) = S(G_s, G_r), and S(G_r, G_s) ≥ S(G_u, G_v) if |G_r− G_s| ≤ |G_u− G_v|, w₁, w₂, …, w_n be, respectively, the weights of G₁, G₂, …, G_n such that 0 ≤ w₁, w₂, …, w_n ≤ 1 and w₁ + w₂ + …+w_n = 1, and

$$ T(G_{r} ) = \sum\limits_{s = 1,s \ne r}^{n} {S(G_{r} ,G_{s} )} $$

Then, the aggregation function

$$ {\text{WAPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \frac{1}{N}\left( {\mathop \oplus \limits_{k = 1}^{N} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} } \right) $$

(12)

where

$$ \varpi_{{i_{k} }} = {{\left( {w_{{i_{k} }} \left( {1 + T(G_{{i_{k} }} )} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{i_{k} }} \left( {1 + T(G_{{i_{k} }} )} \right)} \right)} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }},\quad \varpi_{{j_{k} }} = {{\left( {w_{{j_{k} }} \left( {1 + T(G_{{j_{k} }} )} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{j_{k} }} \left( {1 + T(G_{{j_{k} }} )} \right)} \right)} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}, $$

is called the WAPPBM operator. In this operator, the values of a and b are used to capture the interrelationships between the aggregated GOMGs in each of the N partitions S: (1) If a = 0 and b > 0 or a > 0 and b = 0, then the GOMGs in each partition S_k are independent of each other; (2) If a > 0 and b > 0, then the interrelationships between the GOMGs in S_k are considered.

According to Eqs. (4)–(7) and (12), the following theorem is obtained:

Theorem 1

Let G₁, G₂, …, G_n (G_i = 〈μ_i, ν_i〉, i = 1, 2, …, n) be n GOMGs (q = 1, 2, 3, …) and (G₁, G₂, …, G_n) be a collection of G₁, G₂, …, G_n. Then,

$$ {\text{WAPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left\langle {\mu , \, \nu } \right\rangle $$

(13)

and it is still a GOMG, where

$$ \begin{aligned} & \mu = g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right), \\ & \nu = f^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

and D(G_ik, G_r), D(G_jk, G_r), and D(G_h, G_s) are, respectively, the Minkowski-type distances between G_ikand G_r, G_jkand G_r, and G_hand G_s, which can be calculated using Eq. (3).

For the details regarding the proof of this theorem, please refer to “Appendix A”.

Equation (13) is a generalised expression of the WAPPBM operator. If specific additive generators are applied to f, then specific expressions can be constructed according to this equation:

• (1) If f(t) = − Int^q, then g(t) = − In(1 − t^q), f⁻¹(t) = (e^−t)^1/q, and g⁻¹(t) = (1 − e^−t)^1/q. A weighted Archimedean algebraic power partitioned BM (WAAPPBM) operator of GOMGs is constructed as follows:

  $$ \begin{aligned} & {\text{WAAPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) \\ & \quad = \left\langle {\left( {1 - \left( {\prod\limits_{k = 1}^{N} {\left( {1 - \left( {1 - \left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {1 - \left( {1 - \left( {1 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} } \right)^{a} \left( {1 - \left( {1 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} } \right)^{b} } \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } \right)^{{\frac{1}{a + b}}} } \right)} } \right)^{{\frac{1}{N}}} } \right)^{1/q} } \right., \\ & \quad \quad \left. {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {1 - \left( {1 - \left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {1 - \left( {1 - \nu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} } \right)^{a} \left( {1 - \nu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} } \right)^{b} } \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } \right)^{{\frac{1}{a + b}}} } \right)} } \right)^{{\frac{1}{N}}} } \right)^{1/q} } \right\rangle \\ \end{aligned} $$

  (14)

• (2) If f(t) = In[(2 − t^q)/t^q], then g(t) = In[(1 + t^q)/(1 − t^q)], f⁻¹(t) = [2/(e^t+ 1)]^1/q, and g⁻¹(t) = [(e^t− 1)/(e^t+ 1)]^1/q. A weighted Archimedean Einstein power partitioned BM (WAEPPBM) operator of GOMGs is constructed as follows:

  $$ {\text{WAEPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left\langle {\left( {\frac{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + 3}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} - 1}}{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + 3}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + 1}}} \right)^{1 /q} , \, \left( {\frac{2}{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + 3}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + 1}}} \right)^{1 /q} } \right\rangle $$

  (15)

  where

  $$ \begin{aligned} & \mu^{\prime \prime } = {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} + 3} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} + 3} \right)^{{\frac{1}{a + b}}} } {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} - 1} \right)}}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} - 1} \right)}}^{{\frac{1}{a + b}}} , \\ & \nu^{\prime \prime } = {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} + 3} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} + 3} \right)^{{\frac{1}{a + b}}} } {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} - 1} \right)^{{\frac{1}{a + b}}} }}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} - 1} \right)^{{\frac{1}{a + b}}} }}, \\ & \mu^{\prime } = \left( {\frac{{\left( {1 + \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + 3\left( {1 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}{{\left( {1 + \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - \left( {1 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {1 + \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + 3\left( {1 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}{{\left( {1 + \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - \left( {1 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}} \right)^{b} , \\ & \nu^{\prime } = \left( {\frac{{\left( {2 - v_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + 3v_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}{{\left( {2 - v_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - v_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {2 - v_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + 3v_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}{{\left( {2 - v_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - v_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}} \right)^{b} \\ \end{aligned} $$

• (3) If f(t) = In{[λ + (1 − λ)t^q]/t^q} (λ > 0), then g(t) = In{[λ + (1 − λ)(1 − t^q)]/(1 − t^q)}, f⁻¹(t) = [λ/(e^t+ λ−1)]^1/q, and g⁻¹(t) = [(e^t− 1)/(e^t+ λ−1)]^1/q. A weighted Archimedean Hamacher power partitioned BM (WAHPPBM) operator of GOMGs is constructed as follows:

  $$ {\text{WAHPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left\langle {\left( {\frac{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} - 1}}{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1}}} \right)^{1/q} , \, \left( {\frac{\lambda }{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1}}} \right)^{1/q} } \right\rangle $$

  (16)

  where

  $$ \begin{aligned} & \mu^{{\prime \prime }} = {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} - 1} \right)}}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} - 1} \right)}}^{{\frac{1}{a + b}}} , \\ & \nu^{{\prime \prime }} = {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} - 1} \right)^{{\frac{1}{a + b}}} }}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} - 1} \right)^{{\frac{1}{a + b}}} }}, \\ & \mu^{{\prime }} = \left( {\frac{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{k} }}^{q} )} \right)^{{n\varpi_{{i_{k} }} }} + (\lambda^{2} - 1)\left( {1 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{i_{k} }}^{q} )} \right)^{{n\varpi_{{i_{k} }} }} - \left( {1 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{j_{k} }}^{q} )} \right)^{{n\varpi_{{j_{k} }} }} + (\lambda^{2} - 1)\left( {1 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )(1 - \mu_{{j_{k} }}^{q} )} \right)^{{n\varpi_{{j_{k} }} }} - \left( {1 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}} \right)^{b} , \\ & \nu^{{\prime }} = \left( {\frac{{\left( {\lambda + (1 - \lambda )v_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + (\lambda^{2} - 1)v_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )v_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - v_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {\lambda + (1 - \lambda )v_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + (\lambda^{2} - 1)v_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )v_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - v_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}} \right)^{b} \\ \end{aligned} $$

• (4) If f(t) = − In[(ε − 1)/(ε^y− 1)] (y = t^q; ε > 1), then g(t) = − In[(ε − 1)/(ε^1−y−1)], f⁻¹(t) = {log_ε[(ε − 1+e^−t)/e^−t]}^1/q, and g⁻¹(t) = {1 − log_ε[(ε − 1+e^−t)/e^−t]}^1/q. A weighted Archimedean Frank power partitioned BM (WAFPPBM) operator of GOMGs is constructed as follows:

  $$ \begin{aligned} & {\text{WAFPPBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) \\ & \quad = \left\langle {\left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \mu^{\prime\prime\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \mu^{\prime\prime\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right)} \right)^{1/q} } \right., \\ & \quad \quad \left. {\left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\nu^{\prime\prime\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\nu^{\prime\prime\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right)} \right)^{1/q} } \right\rangle \\ \end{aligned} $$

  (17)

  where

  $$ \begin{aligned} & \mu^{{{\prime \prime \prime }}} = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\mu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\mu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right),\quad \nu^{{{\prime \prime \prime }}} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \nu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \nu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right), \\ & \mu^{{\prime \prime }} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \mu^{\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \mu^{\prime}}} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} }}} \right),\quad \nu^{{\prime \prime }} = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\nu^{{\prime }} }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\nu^{{\prime }} }} - 1}}} \right)} } \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} }}} \right), \\ & \mu^{{\prime }} = \log_{\varepsilon } \left( {1 + {{\left( {\left( {\varepsilon^{{\mu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{\mu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\varepsilon^{{\mu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{\mu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right),\quad \nu^{{\prime }} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\left( {\varepsilon^{{1 - \nu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{1 - \nu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\varepsilon^{{1 - \nu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{1 - \nu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right), \\ & \mu_{{i_{k} }}^{{\prime }} = \left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \mu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \mu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right)} \right)^{1 /q} ,\quad \nu_{{i_{k} }}^{{\prime }} = \left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\nu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\nu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right)} \right)^{1 /q} , \\ & \mu_{{j_{k} }}^{{\prime }} = \left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \mu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \mu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right)} \right)^{1 /q} ,\quad \nu_{{j_{k} }}^{{\prime }} = \left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\nu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\nu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right)} \right)^{1 /q} \\ \end{aligned} $$

3.2 WAPPGBM operator

A WAPPGBM operator of GOMGs is the dual form of the WAPPBM operator of GOMGs. Its formal definition is as follows:

Definition 15

On the basis of Definition 14, the aggregation function

$$ {\text{WAPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left( {\mathop \otimes \limits_{k = 1}^{N} \left( {\frac{1}{a + b}\left( {\mathop \otimes \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {aG_{{i_{k} }}^{{n\varpi_{{i_{k} }} }} } \right) \oplus \left( {bG_{{j_{k} }}^{{n\varpi_{{j_{k} }} }} } \right)} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } \right)} \right)} \right)^{{\frac{1}{N}}} $$

(18)

is called the WAPPGBM operator. In this operator, the functions of a and b are the same as their functions in the WAPPBM operator.

According to Eqs. (4)–(7) and (18), the following theorem is obtained:

Theorem 2

Let G₁, G₂, …, G_n (G_i = 〈μ_i, ν_i〉, i = 1, 2, …, n) be n GOMGs (q = 1, 2, 3, …) and (G₁, G₂, …, G_n) be a collection of G₁, G₂, …, G_n. Then,

$$ {\text{WAPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left\langle {\mu ,\nu } \right\rangle $$

(19)

and it is still a GOMG, where

$$ \begin{aligned} & \mu = f^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right), \\ & \nu = g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

For the details regarding the proof of this theorem, please refer to “Appendix B”.

Equation (19) is a generalised expression of the WAPPGBM operator. If specific additive generators are applied to f, then specific expressions can be constructed according to this equation:

• (1) If f(t) = − Int^q, then g(t) = − In(1 − t^q), f⁻¹(t) = (e^−t)^1/q, and g⁻¹(t) = (1 − e^−t)^1/q. A weighted Archimedean algebraic power partitioned GBM (WAAPPGBM) operator of GOMGs is constructed as follows:

  $$ \begin{aligned} & {\text{WAAPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) \\ & \quad = \left\langle {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {1 - \left( {1 - \mu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} } \right)^{a} \left( {1 - \mu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} } \right)^{b} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } } \right)^{{\frac{1}{a + b}}} } \right)} } \right)^{{\frac{1}{N}}} } \right)^{1/q} ,} \right. \\ & \quad \quad \left. {\left( {1 - \left( {\prod\limits_{k = 1}^{N} {\left( {1 - \left( {1 - \prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {1 - \left( {1 - \left( {1 - \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} } \right)^{a} \left( {1 - \left( {1 - \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} } \right)^{b} } \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } } \right)^{{\frac{1}{a + b}}} } \right)} } \right)^{{\frac{1}{N}}} } \right)^{1/q} } \right\rangle \\ \end{aligned} $$

  (20)

• (2) If f(t) = In[(2 − t^q)/t^q], then g(t) = In[(1 + t^q)/(1 − t^q)], f⁻¹(t) = [2/(e^t+ 1)]^1/q, and g⁻¹(t) = [(e^t− 1)/(e^t+ 1)]^1/q. A weighted Archimedean Einstein power partitioned GBM (WAEPPGBM) operator of GOMGs is constructed as follows:

  $$ {\text{WAEPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) = \left\langle {\left( {\frac{2}{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + 3}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + 1}}} \right)^{1/q} , \, \left( {\frac{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + 3}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} - 1}}{{\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + 3}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + 1}}} \right)^{1/q} } \right\rangle $$

  (21)

  where

  $$ \begin{aligned} & \mu^{{\prime \prime }} = {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + 3} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + 3} \right)^{{\frac{1}{a + b}}} } {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)^{{\frac{1}{a + b}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + 3}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)^{{\frac{1}{a + b}}} }}, \\ & \nu^{{\prime \prime }} = {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + 3} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + 3} \right)^{{\frac{1}{a + b}}} } {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)}}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + 3}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)}}^{{\frac{1}{a + b}}} , \\ & \mu^{{\prime }} = \left( {\frac{{\left( {2 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + 3\mu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}{{\left( {2 - \mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - \mu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {2 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + 3\mu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}{{\left( {2 - \mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - \mu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}} \right)^{b} , \\ & \nu^{{\prime }} = \left( {\frac{{\left( {1 + \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + 3\left( {1 - \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}{{\left( {1 + \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - \left( {1 - \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {1 + \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + 3\left( {1 - \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}{{\left( {1 + \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - \left( {1 - \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}} \right)^{b} \\ \end{aligned} $$

• (3) If f(t) = In{[λ + (1 − λ)t^q]/t^q} (λ > 0), then g(t) = In{[λ + (1 − λ)(1 − t^q)]/(1 − t^q)}, f⁻¹(t) = [λ/(e^t+ λ−1)]^1/q, and g⁻¹(t) = [(e^t− 1)/(e^t+ λ−1)]^1/q. A weighted Archimedean Hamacher power partitioned GBM (WAHPPGBM) operator of GOMGs is constructed as follows:

  $$ \begin{aligned} & {\text{WAHPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) \\ & \quad = \left\langle {\left( {{\lambda \mathord{\left/ {\vphantom {\lambda {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1} \right)}}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\mu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1} \right)}}} \right)^{1/q} } \right., \\ & \quad \quad \left. {\left( {{{\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} - 1} \right)} {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1} \right)}}} \right. \kern-0pt} {\left( {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{{\nu^{{\prime \prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime \prime }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} + \lambda - 1} \right)}}} \right)^{1/q} } \right\rangle \\ \end{aligned} $$

  (22)

  where

  $$ \begin{aligned} & \mu^{{\prime \prime }} = {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)^{{\frac{1}{a + b}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\mu^{{\prime }} + (\lambda^{2} - 1)}}{{\mu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)^{{\frac{1}{a + b}}} }}, \\ & \nu^{{\prime \prime }} = {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } + \lambda^{2} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)}}} \right. \kern-0pt} {\left( {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {\left( {\frac{{\nu^{{\prime }} + (\lambda^{2} - 1)}}{{\nu^{{\prime }} - 1}}} \right)^{{\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}}} } - 1} \right)}}^{{\frac{1}{a + b}}} , \\ & \mu^{{\prime }} = \left( {\frac{{\left( {\lambda + (1 - \lambda )\mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} + (\lambda^{2} - 1)\mu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )\mu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} - \mu_{{i_{k} }}^{{qn\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {\lambda + (1 - \lambda )\mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} + (\lambda^{2} - 1)\mu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )\mu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} - \mu_{{j_{k} }}^{{qn\varpi_{{j_{k} }} }} }}} \right)^{b} , \\ & \nu^{{\prime }} = \left( {\frac{{\left( {\lambda + (1 - \lambda )(1 - \nu_{{i_{k} }}^{q} )} \right)^{{n\varpi_{{i_{k} }} }} + (\lambda^{2} - 1)\left( {1 - \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )(1 - \nu_{{i_{k} }}^{q} )} \right)^{{n\varpi_{{i_{k} }} }} - \left( {1 - \nu_{{i_{k} }}^{q} } \right)^{{n\varpi_{{i_{k} }} }} }}} \right)^{a} \left( {\frac{{\left( {\lambda + (1 - \lambda )(1 - \nu_{{j_{k} }}^{q} )} \right)^{{n\varpi_{{j_{k} }} }} + (\lambda^{2} - 1)\left( {1 - \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}{{\left( {\lambda + (1 - \lambda )(1 - \nu_{{j_{k} }}^{q} )} \right)^{{n\varpi_{{j_{k} }} }} - \left( {1 - \nu_{{j_{k} }}^{q} } \right)^{{n\varpi_{{j_{k} }} }} }}} \right)^{b} \\ \end{aligned} $$

• (4) If f(t) = − In[(ε − 1)/(ε^y− 1)] (y = t^q; ε > 1), then g(t) = − In[(ε − 1)/(ε^1−y−1)], f⁻¹(t) = {log_ε[(ε − 1+e^−t)/e^−t]}^1/q, and g⁻¹(t) = {1 − log_ε[(ε − 1+e^−t)/e^−t]}^1/q. A weighted Archimedean Frank power partitioned GBM (WAFPPGBM) operator of GOMGs is constructed as follows:

  $$ \begin{aligned} & {\text{WAFPPGBM}}^{(a,b)} (G_{1} ,G_{2} , \ldots ,G_{n} ) \\ & \quad = \left\langle {\left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\mu^{\prime \prime \prime } }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\mu^{\prime \prime \prime } }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right)} \right)^{1/q} } \right., \\ & \left. {\quad \quad \left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \nu^{\prime \prime \prime } }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right. \kern-0pt} {\left( {\prod\limits_{k = 1}^{N} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \nu^{\prime \prime \prime } }} - 1}}} \right)} } \right)^{{\frac{1}{N}}} }}} \right)} \right)^{1/q} } \right\rangle \\ \end{aligned} $$

  (23)

  where

  $$ \begin{aligned} & \mu^{{{\prime \prime \prime }}} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \mu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \mu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right),\quad \nu^{{{\prime \prime \prime }}} = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\nu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\nu^{{\prime \prime }} }} - 1} \right)^{{\frac{1}{a + b}}} } {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{\frac{1}{a + b} - 1}} }}} \right), \\ & \mu^{{\prime \prime }} = \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\mu^{{\prime }} }} - 1}}} \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} } }}} \right. \kern-0pt} {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{\mu^{{\prime }} }} - 1}}} \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} } }}} \right),\quad \nu^{{\prime \prime }} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - 1} \right)} {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \nu^{{\prime }} }} - 1}}} \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} } }}} \right. \kern-0pt} {\prod\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {\left( {\frac{\varepsilon - 1}{{\varepsilon^{{1 - \nu^{{\prime }} }} - 1}}} \right)^{{\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}}} } }}} \right), \\ & \mu^{\prime} = 1 - \log_{\varepsilon } \left( {1 + {{\left( {\left( {\varepsilon^{{1 - \mu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{1 - \mu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\varepsilon^{{1 - \mu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{1 - \mu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right),\quad \nu^{{\prime }} = \log_{\varepsilon } \left( {1 + {{\left( {\left( {\varepsilon^{{\nu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{\nu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\varepsilon^{{\nu_{{i_{k} }}^{{\prime }} }} - 1} \right)^{a} \left( {\varepsilon^{{\nu_{{j_{k} }}^{{\prime }} }} - 1} \right)^{b} } \right)} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{a + b - 1} }}} \right), \\ & \mu_{{i_{k} }}^{{\prime }} = \left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\mu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\mu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right)} \right)^{1 /q} ,\quad \nu_{{i_{k} }}^{{\prime }} = \left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \nu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \nu_{{i_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{i_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{i_{k} }} - 1}} }}} \right)} \right)^{1 /q} , \\ & \mu_{{j_{k} }}^{{\prime }} = \left( {\log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{\mu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{\mu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right)} \right)^{1 /q} ,\quad \nu_{{j_{k} }}^{{\prime }} = \left( {1 - \log_{\varepsilon } \left( {1 + {{\left( {\varepsilon^{{1 - \nu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } \mathord{\left/ {\vphantom {{\left( {\varepsilon^{{1 - \nu_{{j_{k} }}^{q} }} - 1} \right)^{{n\varpi_{{j_{k} }} }} } {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right. \kern-0pt} {\left( {\varepsilon - 1} \right)^{{n\varpi_{{j_{k} }} - 1}} }}} \right)} \right)^{1 /q} \\ \end{aligned} $$

4 MCDM method

Relatively, the GBM operator can generate more optimistic results for MCDM, while the BM operator can provide more pessimistic expectations (Xia et al. 2013). To consider the risk attitudes of decision makers in MCDM, the two operators can be combined to resolve a MCDM problem. In this section, a risk attitude factor is introduced to linearly combine the scores and accuracies of the aggregation results of the presented WAPPBM and WAPPGBM operators, and a MCDM method based on such combination is proposed to solve the MCDM problems based on GOMGs.

Generally, a MCDM problem based on GOMGs can be formalised using a set of alternatives A = {A₁, A₂, …, A_m}, a set of criteria C = {C₁, C₂, …, C_n} such that C is divided into N partitions C_k = {C₁, C₂, …, C_|Ck|} (k = 1, 2, …, N) and there are interrelationships between the criteria in each partition, whereas there are no interrelationships between the criteria in different partitions, a vector of weights of criteria w = [w₁, w₂, …, w_n] such that 0 ≤ w₁, w₂, …, w_n ≤ 1, w₁ + w₂ + … + w_n = 1, and each element, respectively, stands for the relative importance of C₁, C₂, …, C_n, and a generalised orthopair fuzzy decision matrix M = [G_i,j]_m×n (i = 1, 2,…, m; j = 1, 2,…, n) such that G_i,j = 〈μ_i,j, ν_i,j〉 is a GOMG that stands for the value of C_j with respect to A_i. On the basis of these components, the MCDM problem can be described as: determining the best alternative according to a ranking of all alternatives in A based on C, M, and w. Based on the presented WAPPBM and WAPPGBM operators, the problem is solved according to the following steps:

• (1) Normalise the generalised orthopair fuzzy decision matrix M. In general, a MCDM problem may have two types of criteria, i.e. benefit and cost criteria. They, respectively, have positive and negative effects on decision-making results. To remove the effects of different types of criteria, the decision matrix M is normalised as

  $$ \varvec{M}^{{\mathbf{N}}} = \left[ {G_{i,j} } \right]_{m \times n} = \left\{ \begin{array}{ll} \left[ {\left\langle {\mu_{i,j} ,\nu_{i,j} } \right\rangle } \right]_{m \times n} ,\quad {\text{if}}\;C_{j} \;{\text{is}}\;{\text{a}}\;{\text{benefit}}\;{\text{criterion}} \hfill \\ \left[ {\left\langle {\nu_{i,j} ,\mu_{i,j} } \right\rangle } \right]_{m \times n} ,\quad {\text{if}}\;C_{j} \;{\text{is}}\;{\text{a}}\;{\text{cost}}\;{\text{criterion}} \hfill \\ \end{array} \right. $$

  (24)

• (2) Compute the power weights of G_i,j. The power weights of G_i,j are calculated via

  $$ \varpi_{i,j} = {{\left( {w_{j} \left( {1 + \sum\limits_{r = 1,r \ne j}^{n} {\left( {1 - D(G_{i,j} , \, G_{i,r} )} \right)} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{j} \left( {1 + \sum\limits_{r = 1,r \ne j}^{n} {\left( {1 - D(G_{i,j} , \, G_{i,r} )} \right)} } \right)} \right)} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \left( {1 + \sum\limits_{s = 1,s \ne t}^{n} {\left( {1 - D(G_{i,t} , \, G_{i,s} )} \right)} } \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {w_{t} \left( {1 + \sum\limits_{s = 1,s \ne t}^{n} {\left( {1 - D(G_{i,t} , \, G_{i,s} )} \right)} } \right)} \right)} }} $$

  (25)

  where D(G_i,j, G_i,r) and D(G_i,t, G_i,s) are, respectively, the Minkowski-type distances between G_i,j and G_i,r and G_i,t and G_i,s, which can be calculated using Eq. (3).

• (3) Compute the collective values of G_i,j. Let S_i = {G_i,1, G_i,2, …, G_i,n} be an ordered set of G_i,1, G_i,2, …, G_i,n and S_i,k = {G_i,1, G_i,2, …, G_i,|Sk|} be N partitions of S corresponding to C_k. Then, the collective values of Ξ_i,j are computed via

  $$ \varXi_{i} = \left\langle {\mu_{i} ,\nu_{i} } \right\rangle = {\text{WAPPBM}}^{(a,b)} (G_{i,1} ,G_{i,2} , \ldots ,G_{i,n} ) $$

  (26)
  $$ \varXi_{i} = \left\langle {\mu_{i} ,\nu_{i} } \right\rangle = {\text{WAPPGBM}}^{(a,b)} (G_{i,1} ,G_{i,2} , \ldots ,G_{i,n} ) $$

  (27)

  where WAPPBM is a specific WAPPBM operator, such as the WAAPPBM operator in Eq. (14), the WAEPPBM operator in Eq. (15), the WAHPPBM operator in Eq. (16), and the WAFPPBM operator in Eq. (17), and WAPPGBM is the dual operator of the specific operator in WAPPBM, such as the WAAPPGBM operator in Eq. (20), the WAEPPGBM operator in Eq. (21), the WAHPPGBM operator in Eq. (22), and the WAFPPGBM operator in Eq. (23).

• (4) Compute the combined scores and accuracies of G_i. According to Eqs. (1) and (2), the scores and accuracies of G_i of WAPPBM and WAPPGBM are, respectively, calculated. Let S_BM(G_i) and A_BM(G_i), respectively, be the score and accuracy of G_i computed by WAPPBM, S_GBM(G_i) and A_GBM(G_i), respectively, be the score and accuracy of G_i computed by WAPPGBM, and 0 ≤ α ≤ 1 be a risk attitude factor that denotes the degree of risk attitude of a decision maker (there are five different degrees of risk attitude in the method: pessimistic, moderately pessimistic, neutral, moderately optimistic, and optimistic, which are represented by α = 1, α = 0.75, α = 0.5, α = 0.25, and α = 0, respectively). Then, the combined scores and accuracies of G_i are calculated via:

  $$ S\left( {G_{i} } \right) \, = \alpha S_{\text{BM}} \left( {G_{i} } \right) \, + \, \left( {1 - \alpha } \right)S_{\text{GBM}} \left( {G_{i} } \right) $$

  (28)
  $$ A\left( {G_{i} } \right) \, = \alpha A_{\text{BM}} \left( {G_{i} } \right) \, + \, \left( {1 - \alpha } \right)A_{\text{GBM}} \left( {G_{i} } \right) $$

  (29)

• (5) Generate a ranking of A_i. On the basis of the combined scores and accuracies of G_i, a ranking of A_i is generated according to the comparison rules in Definition 4.

• (6) Determine the best alternative. The alternative that ranks first is determined as the best alternative.

According to the abovementioned steps, the general procedure of the proposed MCDM method is depicted in Fig. 1.

Fig. 1

General procedure of the proposed MCDM method

5 Example and comparisons

In this section, a numerical example is firstly leveraged to demonstrate the proposed MCDM method. Then, qualitative and quantitative comparisons to the existing methods are made to illustrate its characteristics and verify its feasibility.

5.1 Example

A numerical example regarding the determination of the best investment area from five possible areas (cited from Yang and Pang 2019) is used to illustrate the proposed MCDM method. In this example, the five possible areas are gold (A₁), tourism (A₂), real estate (A₃), energy industry (A₄), and artificial intelligence (A₅). There are five criteria for decision-making, which are the market potential (C₁), the amount of interests received (C₂), the growth potential (C₃), the risk of capital loss (C₄), and the inflation (C₅). The relative importance of these criteria is measured by w = [0.10, 0.15, 0.25, 0.30, 0.20]. The five criteria are divided into two partitions C₁ = {C₁, C₂, C₃} and C₂ = {C₄, C₅}, and there are interrelationships between the three criteria in C₁, so do the two criteria in C₂, and there is no interrelationship between C₁ and C₂. The evaluation results of the five criteria of the five possible areas are listed in the following matrix:

$$ \varvec{M} = \left[ \begin{aligned} \begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 3 { > }} & {{ < 0} . 6 , { 0} . 8 { > }} & {\begin{array}{*{20}c} {{ < 0} . 9 , { 0} . 2 { > }} & {{ < 0} . 6 , { 0} . 3 { > }} & {{ < 0} . 7 , { 0} . 5 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 2 { > }} & {{ < 0} . 7 , { 0} . 5 { > }} & {\begin{array}{*{20}c} {{ < 0} . 5 , { 0} . 6 { > }} & {{ < 0} . 3 , { 0} . 7 { > }} & {{ < 0} . 5 , { 0} . 4 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 5 , { 0} . 7 { > }} & {{ < 0} . 6 , { 0} . 2 { > }} & {\begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 3 { > }} & {{ < 0} . 3 , { 0} . 5 { > }} & {{ < 0} . 2 , { 0} . 7 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 3 { > }} & {{ < 0} . 8 , { 0} . 1 { > }} & {\begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 4 { > }} & {{ < 0} . 4 , { 0} . 3 { > }} & {{ < 0} . 4 , { 0} . 7 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 4 , { 0} . 8 { > }} & {{ < 0} . 6 , { 0} . 4 { > }} & {\begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 2 { > }} & {{ < 0} . 3 , { 0} . 7 { > }} & {{ < 0} . 2 , { 0} . 6 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \end{aligned} \right] $$

On the basis of the known conditions above, the determination of the best investment area can be carried out using the proposed MCDM method. This process consists of the following six steps:

• (1) Normalise the generalised orthopair fuzzy decision matrix M. Among the five criteria, the market potential (C₁), the amount of interests received (C₂), and the growth potential (C₃) are benefit criteria, and the risk of capital loss (C₄) and the inflation (C₅) are cost criteria. Based on this, the matrix M is normalised according to Eq. (24) and a normalised matrix is obtained as:

  $$ \varvec{M}^{{\mathbf{N}}} = \left[ {G_{i,j} } \right]_{5 \times 5} = \left[ \begin{aligned} \begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 3 { > }} & {{ < 0} . 6 , { 0} . 8 { > }} & {\begin{array}{*{20}c} {{ < 0} . 9 , { 0} . 2 { > }} & {{ < 0} . 3 , { 0} . 6 { > }} & {{ < 0} . 5 , { 0} . 7 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 2 { > }} & {{ < 0} . 7 , { 0} . 5 { > }} & {\begin{array}{*{20}c} {{ < 0} . 5 , { 0} . 6 { > }} & {{ < 0} . 7 , { 0} . 3 { > }} & {{ < 0} . 4 , { 0} . 5 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 5 , { 0} . 7 { > }} & {{ < 0} . 6 , { 0} . 2 { > }} & {\begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 3 { > }} & {{ < 0} . 5 , { 0} . 3 { > }} & {{ < 0} . 7 , { 0} . 2 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 3 { > }} & {{ < 0} . 8 , { 0} . 1 { > }} & {\begin{array}{*{20}c} {{ < 0} . 7 , { 0} . 4 { > }} & {{ < 0} . 3 , { 0} . 4 { > }} & {{ < 0} . 7 , { 0} . 4 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{ < 0} . 4 , { 0} . 8 { > }} & {{ < 0} . 6 , { 0} . 4 { > }} & {\begin{array}{*{20}c} {{ < 0} . 6 , { 0} . 2 { > }} & {{ < 0} . 7 , { 0} . 3 { > }} & {{ < 0} . 6 , { 0} . 2 { > }} \\ \end{array} } \\ \end{array} \hfill \\ \end{aligned} \right] $$

• (2) Compute the power weights of G_i,j. According to Eq. (25) (when calculating the Minkowski-type distances, σ = 3), the power weights of G_i,j are calculated and the calculated results are listed in the following matrix:

  $$ \left[ {\varpi_{i,j} } \right]_{5 \times 5} = \left[ \begin{aligned} \begin{array}{*{20}c} { 0. 1 0 1 8} & { 0. 1 5 2 9} & {\begin{array}{*{20}c} { 0. 2 2 3 6} & { 0. 3 0 6 4} & { 0. 2 1 5 3} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 0 9 7 3} & { 0. 1 5 1 3} & {\begin{array}{*{20}c} { 0. 2 4 8 8} & { 0. 3 0 5 6} & { 0. 1 9 7 0} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 0 8 4 1} & { 0. 1 5 3 7} & {\begin{array}{*{20}c} { 0. 2 5 6 7} & { 0. 3 0 2 9} & { 0. 2 0 2 6} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 1 0 6 7} & { 0. 1 4 3 0} & {\begin{array}{*{20}c} { 0. 2 6 5 8} & { 0. 2 7 1 8} & { 0. 2 1 2 7} \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { 0. 0 7 8 8} & { 0. 1 5 3 1} & {\begin{array}{*{20}c} { 0. 2 5 5 6} & { 0. 3 0 8 0} & { 0. 2 0 4 5} \\ \end{array} } \\ \end{array} \hfill \\ \end{aligned} \right] $$

• (3) Compute the collective values of G_i,j. According to the partitions C₁ = {C₁, C₂, C₃} and C₂ = {C₄, C₅}, the matrix M^N is divided into S_i,1 = {G_i,1, G_i,2, G_i,3} and S_i,2 = {G_i,4, G_i,5}. Taking them and the power weight matrix [ϖ_i,j]_5×5 as input, the collective values of G_i,j can be calculated using Eqs. (26) and (27). Without loss of generality, the WAHPPBM operator in Eq. (16) and the WAHPPGBM operator in Eq. (22) (when adapting the two operators, q = 2, λ = 3, and (a, b) = (1, 2)) are, respectively, used in Eqs. (26) and (27) to complete the calculation. The calculated results are, respectively, listed as follows:

  $$ \begin{aligned} & G_{1} = \;\left\langle {0.4509, \, 0.8967} \right\rangle ,\quad G_{2} = \;\left\langle {0.4114, \, 0.8889} \right\rangle ,\quad G_{3} = \;\left\langle {0.4357, \, 0.8243} \right\rangle , \quad G_{4} = \;\left\langle {0.4441, \, 0.8479} \right\rangle ,\\ & \quad G_{5} = \;\left\langle {0.4362, \, 0.8267} \right\rangle \\ & G_{1} = \;\left\langle {0.8131, \, 0.3872} \right\rangle ,\quad G_{2} = \;\left\langle {0.8042, \, 0.3134} \right\rangle ,\quad G_{3} = \;\left\langle {0.8207, \, 0.2163} \right\rangle , \quad G_{4} = \;\left\langle {0.8166, \, 0.2454} \right\rangle ,\\ & \quad G_{5} = \;\left\langle {0.8206, \, 0.2283} \right\rangle \\ \end{aligned} $$

• (4) Compute the combined scores and accuracies of G_i. Using Eqs. (28) and (29) (when adapting the two equations, α = 0.5), the combined scores and accuracies of G_i are calculated and the calculated results are listed as follows:

  $$ \begin{aligned} & S\left( {G_{1} } \right) = - 0.0448,\quad S\left( {G_{2} } \right) = - 0.0362,\quad S\left( {G_{3} } \right) = 0.0686,\quad S\left( {G_{4} } \right) = 0.0424,\quad S\left( {G_{5} } \right) = 0.0640 \\ & A\left( {G_{1} } \right) = 0.9092,\quad A\left( {G_{2} } \right) = 0.8521,\quad A\left( {G_{3} } \right) = 0.7948,\quad A\left( {G_{4} } \right) = 0.8216,\quad A\left( {G_{5} } \right) = 0.7997 \\ \end{aligned} $$

• (5) Generate a ranking of A_i. According to the computed S(G_i) and A(G_i) and the comparison rules in Definition 4, a ranking of A_i is generated as: A₃ ≻ A₅ ≻ A₄ ≻ A₂ ≻ A₁.

• (6) Determine the best alternative. According to the generated ranking, the best alternative is determined as A₃. That is, the best investment area is real estate.

5.2 Comparisons

More than twenty different MCDM methods based on the aggregation operators of GOMGs have been presented so far. Representative examples are the methods based on WA and WG (Liu and Wang 2018a), WBM and WGBM (Liu and Liu 2018), WABM (Liu and Wang 2018b), WPBM and WPGBM (Yang and Pang 2019), WEBM (Liu et al. 2018b), WHM and WGHM (Wei et al. 2018), WHM* and WPHM (Liu et al. 2018c), WMSM and WGMSM (Wei et al. 2019), WPMSM (Liu et al. 2018d), WPPMSM (Bai et al. 2018), WMM and WGMM (Wang et al. 2019), WE (Peng et al. 2018), and WP (Xing et al. 2019). In this subsection, qualitative and quantitative comparisons between these methods and the proposed MCDM method are made to illustrate its characteristics and verify its feasibility.

5.2.1 Qualitative comparison

Generally, a qualitative comparison among different MCDM methods can be made via comparing their characteristics. For the above MCDM methods and the proposed MCDM method, the generality and flexibility in the aggregation of GOMGs, the capability to deal with the heterogeneous interrelationships of criteria,¹ the capability to reduce the negative effect of the biased criterion values, and the capability to capture the risk attitudes of decision makers are selected as the comparison characteristics. The results of the comparison are listed in Table 2, which can be explained from the following aspects:

Table 2 The results of the qualitative comparison

• (1) Generality and flexibility. The method based on WP provides twenty aggregation operators which are suitable for different application scenarios for MCDM. The generality and flexibility of this method can be regarded as moderate. The generality and flexibility of both the method based on WABM and the proposed method are desirable, because the aggregations in them can be carried out using the operations of any family of ATTs, which are important tools that can generate general and flexible operational rules for membership grades. The remaining methods perform the aggregations by the operation of Algebraic T-norm and T-conorm. They have relatively limited generality and flexibility.

• (2) Capability to deal with heterogeneous interrelationships. The partitioned average operator combined into the methods based on WPBM and WPGBM, WEBM, WPHM, and WPPMSM and the proposed method can aggregate the GOMGs in different partitions using the same aggregation operator and aggregate the aggregation results of different partitions using the arithmetic average operator. Because of this, these methods have the capability to deal with heterogeneous interrelationships.

• (3) Capability to reduce negative effect. The power weights used in the methods based on WPMSM and WPPMSM and the proposed method are obtained via calculating the support degrees between the aggregated GOMGs. This enables these methods possible to reduce the negative effect of the unduly high or unduly low values of GOMGs on the aggregation results.

• (4) Capability to capture risk attitudes. The method based on WABM captures the risk attitudes of decision makers via the argument λ when the weighted Archimedean Hamacher BM operator is used. It was found in the method that the greater the value of λ is, the more optimistic attitude the decision makers have. The proposed method can not only leverage this argument to describe risk attitudes, but also introduce a risk attitude factor α. Through assigning different values (e.g. 1, 0.75, 0.5, 0.25, 0) to α, different degrees of risk attitudes (e.g. pessimistic, moderately pessimistic, neutral, moderately optimistic, and optimistic) can be captured. Thus, the proposed method can capture the risk attitudes of decision makers more comprehensively than the method based on WABM.

5.2.2 Quantitative comparison

Generally, a quantitative comparison among different MCDM methods can be made using the same numerical example. Here, the numerical example in subsection 5.1 is used to carry out a quantitative comparison between the MCDM methods based on WA, WG, WBM, WGBM, WABM, WPBM, WPGBM, WHM, WGHM, WHM*, WPHM, WMSM, WGMSM, WPMSM, WPPMSM, WMM, and WGMM² and the proposed MCDM method. The details and results of the comparison are shown in Table 3 and Fig. 2.

Table 3 The details of the quantitative comparison

Fig. 2

The results of the quantitative comparison. Note The scale of the grid represents the score

From Table 3 and Fig. 2, it can be seen that the rankings generated by the methods based on WG, WBM, WGBM, WPBM, WGHM, WGMSM, and WPPMSM have no significant difference with that of the proposed method. In addition, the best investment area determined by these methods is exactly the same as that of the proposed method. These demonstrate the feasibility of the proposed method. It can be known from Table 2 that the method based on WPPMSM and the proposed method are the most similar in nature. The rankings of these two methods are, respectively, A₃ ≻ A₄ ≻ A₅ ≻ A₂ ≻ A₁ and A₃ ≻ A₅ ≻ A₄ ≻ A₂ ≻ A₁, which just have difference at the second and third places. This also verifies that the proposed method is feasible. As can also be seen from Table 3, the best investment areas of the methods based on WA, WPGBM, WMSM, WPMSM, WMM, and WGMM are all energy industry (A₄), while those of the methods based on WABM, WHM, WHM*, and WPHM are all artificial intelligence (A₅). Such results are completely different from the result of the proposed method. The reason can be analysed from two aspects. On the one hand, the specific aggregation operators on which most of these methods (except the methods based on WPBM and WABM) are based are different from that of the proposed method. On the other hand, these methods and the proposed methods have their respective characteristics. Even though the quantitative comparison has tried to ensure the same input, the inputs of some methods are not exactly the same as that of the proposed method, since these methods have their special arguments and the proposed method does not have such arguments.

Finally, it is of necessity to point out that the purpose of the comparison is not to find out the best method, but to verify the feasibility of the proposed method. In general, it is difficult to conclude that one MCDM method is better than the others, since different methods have their specific features, which determine their specific application environments. What decision makers need to do is choose a suitable method based on the specific application environment.

6 Conclusion

In this paper, a WAPPBM operator and a WAPPGBM operator of GOMGs have been presented to solve the MCDM problems based on GOMGs. The formal definitions and generalised expressions of the two operators have been provided and the specific expressions of them have been constructed using the operational rules of GOMGs based on the Algebraic, Einstein, Hamacher, and Frank families of ATTs and their additive generators. On the basis of the specific operators, a method for solving the GOMGs-based MCDM problems has been proposed. The paper has also introduced a numerical example to explain the working process of the proposed method and reported qualitative and quantitative comparisons to illustrate its characteristics and demonstrate its feasibility. The main contribution of the paper is the development of a MCDM method based on weighted Archimedean power partitioned Bonferroni aggregation operators of GOMGs. Compared to the existing MCDM methods based on aggregation operators of GOMGs, the developed method is general and flexible in the aggregation of criterion values and simultaneously has the capabilities to deal with the heterogeneous interrelationships of criteria, reduce the negative influence of the distortion of criterion values, and capture the risk attitudes of decision makers. One major limitation of the method is that it cannot work properly under incomplete criterion information. Future work will focus especially on addressing this limitation. In addition, the application of the method in resolving the practical MCDM problems in manufacturing domain will also be studied.

Appendices

Appendix A: Proof of Theorem 1

Proof

• (1) To prove WAPPBM^(a,b) (G₁, G₂, …, G_n) = 〈μ, ν〉, we need to prove

  $$ \frac{1}{N}\left( {\mathop \oplus \limits_{k = 1}^{N} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {\frac{{nw_{{i_{k} }} \left( {1 + T(G_{{i_{k} }} )} \right)}}{{\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}G_{{i_{k} }} } \right)^{a} \otimes \left( {\frac{{nw_{{j_{k} }} \left( {1 + T(G_{{j_{k} }} )} \right)}}{{\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} } \right) = \left\langle {\mu , \, \nu } \right\rangle $$

The proof process is as follows:

Let

$$ \varpi_{{i_{k} }} = {{\left( {w_{{i_{k} }} \left( {1 + T(G_{{i_{k} }} )} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{i_{k} }} \left( {1 + T(G_{{i_{k} }} )} \right)} \right)} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}\quad {\text{and}}\quad \varpi_{{j_{k} }} = {{\left( {w_{{j_{k} }} \left( {1 + T(G_{{j_{k} }} )} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{j_{k} }} \left( {1 + T(G_{{j_{k} }} )} \right)} \right)} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }}} \right. \kern-0pt} {\sum\limits_{h = 1}^{n} {\left( {w_{h} \left( {1 + T(G_{h} )} \right)} \right)} }} $$

Then, the equation above can be simplified as

$$ \frac{1}{N}\left( {\mathop \oplus \limits_{k = 1}^{N} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} } \right) = \left\langle {\mu , \, \nu } \right\rangle $$

According to the operational rule in Eq. (6), we have

$$ \begin{aligned} & (n\varpi_{{i_{k} }} )G_{{i_{k} }} = \left\langle {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right), \, f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right\rangle \\ & (n\varpi_{{j_{k} }} )G_{{j_{k} }} = \left\langle {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right), \, f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (7), we can obtain

$$ \begin{aligned} & \left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} = \left\langle {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right)} \right), \, g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right)} \right)} \right\rangle \\ & \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} = \left\langle {f^{ - 1} \left( {bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right), \, g^{ - 1} \left( {bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (5), we have

$$ \begin{aligned} & \left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} = \left\langle {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right., \\ & \quad \left. {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (4), we can obtain

$$ \begin{aligned} & \mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right) = \left\langle {g^{ - 1} \left( {\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right., \\ & \left. {\quad \, f^{ - 1} \left( {\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (6), we have

$$ \begin{aligned} & \frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right) \\ & \quad = \left\langle {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right., \\ & \quad \quad \left. {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (7), we can obtain

$$ \begin{aligned} & \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} \\ & \quad = \left\langle {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right., \\ & \left. {\quad \quad g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right\rangle \\ \end{aligned} $$

According to the operational rule in Eq. (4), we have

$$ \begin{aligned} & \mathop \oplus \limits_{k = 1}^{N} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} \\ & \quad = \left\langle {g^{ - 1} \left( {\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} } \right)} \right., \\ & \left. {\quad \quad \, f^{ - 1} \left( {\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} } \right)} \right\rangle \\ \end{aligned} $$

Finally, the following equation is obtained according to the operational rule in Eq. (6)

$$ \begin{aligned} & \frac{1}{N}\left( {\mathop \oplus \limits_{k = 1}^{N} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\mathop \oplus \limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} \left( {\left( {(n\varpi_{{i_{k} }} )G_{{i_{k} }} } \right)^{a} \otimes \left( {(n\varpi_{{j_{k} }} )G_{{j_{k} }} } \right)^{b} } \right)} \right)^{{\frac{1}{a + b}}} } \right) \\ & \quad \left\langle {g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right)} \right., \\ & \left. {\quad \quad f^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right)} \right\rangle \\ \end{aligned} $$

• (2) To prove WAPPBM^(a,b) (G₁, G₂, …, G_n) is still a GOMG, we need to prove 0 ≤ μ ≤ 1, 0 ≤ ν ≤ 1, and 0 ≤ μ^q + ν^q ≤ 1. We firstly prove 0 ≤ μ ≤ 1 and 0 ≤ ν ≤ 1. The proof process is as follows:

According to the definition of a GOMG (Definition 1), we have 0 ≤ μ_ik, μ_jk ≤ 1 and 0 ≤ ν_ik, ν_jk ≤ 1. Because g(t) is monotonically increasing and f(t) is monotonically decreasing, we further have

$$ \begin{aligned} & (n\varpi_{{i_{k} }} )g(0) \le (n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} ) \le (n\varpi_{{i_{k} }} )g(1);\quad (n\varpi_{{j_{k} }} )g(0) \le (n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} ) \le (n\varpi_{{j_{k} }} )g(1) \\ & (n\varpi_{{i_{k} }} )f(0) \ge (n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} ) \ge (n\varpi_{{i_{k} }} )f(1);\quad (n\varpi_{{j_{k} }} )f(0) \ge (n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} ) \ge (n\varpi_{{j_{k} }} )f(1) \\ \end{aligned} $$

Since g⁻¹(t) is monotonically increasing and f⁻¹(t) is monotonically decreasing, we can obtain

$$ \begin{aligned} & g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right) \le g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right) \le g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right);\quad g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right) \le g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right) \le g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right) \\ & f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right) \le f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right) \le f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right);\quad \, f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right) \le f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right) \le f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right) \\ \end{aligned} $$

Because f(t) is monotonically decreasing and g(t) is monotonically increasing, we have

$$ \begin{aligned} & af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) \ge af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \ge af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) \\ & bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right) \ge bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \ge bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right) \\ & ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) \le ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \le ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) \\ & bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right) \le bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \le bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right) \\ \end{aligned} $$

and thus

$$ \begin{aligned} & af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right) \ge af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \\ & \quad \ge af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right) \\ & ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right) \le ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \\ & \quad \le ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right) \\ \end{aligned} $$

Since f⁻¹(t) is monotonically decreasing and g⁻¹(t) is monotonically increasing, we can obtain

$$ \begin{aligned} & f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right) \hfill \\ \end{aligned} \right) \le f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right) \le f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right) \hfill \\ \end{aligned} \right) \\ & g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right) \hfill \\ \end{aligned} \right) \le g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right) \le g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right) \hfill \\ \end{aligned} \right) \\ \end{aligned} $$

Because g(t) is monotonically increasing and f(t) is monotonically decreasing, we have

$$ \begin{aligned} & g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right)} \right)} \right) \le \frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} \\ & \quad \le g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right)} \right)} \right) \\ & f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right)} \right)} \right) \ge \frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ bg\left( { + \,f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} \\ & \quad \ge f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right)} \right)} \right) \\ \end{aligned} $$

Since g⁻¹(t) is monotonically increasing and f⁻¹(t) is monotonically decreasing, we can obtain

$$ \begin{aligned} & f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right)} \right) \le g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right) \\ & \quad \le f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right)} \right) \\ & g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right)} \right) \le f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right) \\ & \quad \le g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right)} \right) \\ \end{aligned} $$

Because f(t) is monotonically decreasing and g(t) is monotonically increasing, we have

$$ \begin{aligned} & \frac{1}{a + b}\left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + \hfill \\ bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right) \hfill \\ \end{aligned} \right) \ge \frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right) \\ & \quad \ge \frac{1}{a + b}\left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right) \hfill \\ \end{aligned} \right) \\ & \frac{1}{a + b}\left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + \hfill \\ bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right) \hfill \\ \end{aligned} \right) \le \frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right) \\ & \quad \le \frac{1}{a + b}\left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right) \hfill \\ \end{aligned} \right) \\ \end{aligned} $$

Since f⁻¹(t) is monotonically decreasing and g⁻¹(t) is monotonically increasing, we can obtain

$$ \begin{aligned} & f^{ - 1} \left( {\frac{1}{a + b}\left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right)} \right)} \right) \\ & \quad \le f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ & \quad \le f^{ - 1} \left( {\frac{1}{a + b}\left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right)} \right)} \right) \\ & g^{ - 1} \left( {\frac{1}{a + b}\left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right)} \right)} \right) \\ & \quad \le g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ & \quad \le g^{ - 1} \left( {\frac{1}{a + b}\left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right)} \right)} \right) \\ \end{aligned} $$

Because g(t) is monotonically increasing and f(t) is monotonically decreasing, we have

$$ \begin{aligned} & g\left( {f^{ - 1} \left( {\frac{1}{a + b}\left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(0)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(0)} \right)} \right)} \right)} \right)} \right) \\ & \quad \le \frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ & \quad \le g\left( {f^{ - 1} \left( {\frac{1}{a + b}\left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(1)} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(1)} \right)} \right)} \right)} \right)} \right) \\ & f\left( {g^{ - 1} \left( {\frac{1}{a + b}\left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(0)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(0)} \right)} \right)} \right)} \right)} \right) \\ & \quad \ge \frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ & \quad \ge f\left( {g^{ - 1} \left( {\frac{1}{a + b}\left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(1)} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(1)} \right)} \right)} \right)} \right)} \right) \\ \end{aligned} $$

Since

$$ \begin{aligned} \sum\limits_{k = 1}^{N} {\sum\limits_{{i_{k} = 1}}^{{\left| {\varvec{S}_{k} } \right|}} {(n\varpi_{{i_{k} }} )} = n} \left( {\sum\limits_{{i_{1} = 1}}^{{\left| {\varvec{S}_{1} } \right|}} {\varpi_{{i_{1} }} } + \sum\limits_{{i_{2} = 1}}^{{\left| {\varvec{S}_{2} } \right|}} {\varpi_{{i_{2} }} } + \cdots + \sum\limits_{{i_{N} = 1}}^{{\left| {\varvec{S}_{N} } \right|}} {\varpi_{{i_{N} }} } } \right) = n\frac{1}{n} = 1 \hfill \\ \sum\limits_{k = 1}^{N} {\sum\limits_{{j_{k} = 1}}^{{\left| {\varvec{S}_{k} } \right|}} {(n\varpi_{{j_{k} }} )} = n} \left( {\sum\limits_{{j_{1} = 1}}^{{\left| {\varvec{S}_{1} } \right|}} {\varpi_{{j_{1} }} } + \sum\limits_{{j_{2} = 1}}^{{\left| {\varvec{S}_{2} } \right|}} {\varpi_{{j_{2} }} } + \cdots + \sum\limits_{{j_{N} = 1}}^{{\left| {\varvec{S}_{N} } \right|}} {\varpi_{{j_{N} }} } } \right) = n\frac{1}{n} = 1 \hfill \\ \end{aligned} $$

we can obtain

$$ \begin{aligned} & g\left( 0 \right) \le \frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} \le g\left( 1 \right) \\ & f\left( 0 \right) \ge \frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} \ge f\left( 1 \right) \\ \end{aligned} $$

Finally, because g⁻¹(t) is monotonically increasing and f⁻¹(t) is monotonically decreasing, we can obtain

$$ \begin{aligned} & 0 \le g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \le 1 \\ & 0 \le f^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \le 1 \\ \end{aligned} $$

They are 0 ≤ μ ≤ 1 and 0 ≤ ν ≤ 1, respectively.

We then prove 0 ≤ μ^q + ν^q ≤ 1. The proof process is as follows:

Since 0 ≤ μ ≤ 1 and 0 ≤ ν ≤ 1, we have 0 ≤ μ^q ≤ 1 and 0 ≤ ν^q ≤ 1, and thus, 0 ≤ μ^q + ν^q ≤ 2.

According to the definition of a GOMG (Definition 1), we have μ^q_ik  + ν^q_ik  ≤ 1 and μ^q_jk  + ν^q_jk  ≤ 1, and thus, μ^q_ik  ≤ 1 − ν^q_ik and μ^q_jk  ≤ 1 − ν^q_jk . Since g(t) is monotonically increasing, we further have

$$ (n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} ) \le (n\varpi_{{i_{k} }} )g(1 - \nu_{{i_{k} }}^{q} );\quad (n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} ) \le (n\varpi_{{j_{k} }} )g(1 - \nu_{{j_{k} }}^{q} ) $$

Because g(1 − t) = f(t), we have

$$ (n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} ) \le (n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} );\quad (n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} ) \le (n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} ) $$

Since g⁻¹(t) is monotonically increasing, we can obtain

$$ g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right) \le g^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right);\quad g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right) \le g^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right) $$

Because g⁻¹(t) = 1 − f⁻¹(t), we have

$$ g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right) \le 1 - f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right);\quad g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right) \le 1 - f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right) $$

Since f(t) is monotonically decreasing, we further have

$$ af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) \ge af\left( {1 - f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right);\quad bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right) \ge bf\left( {1 - f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right) $$

Because f(1 − t) = g(t), we can obtain

$$ af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) \ge ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right);\quad bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right) \ge bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right) $$

and

$$ af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right) \ge ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right) $$

Since f⁻¹(t) is monotonically decreasing, we have

$$ f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right) \le f^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right) $$

Because f⁻¹(t) = 1 − g⁻¹(t), we further have

$$ f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right) \le 1 - g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right) $$

Since g(t) is monotonically increasing, we can obtain

$$ \begin{aligned} & \frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} \\ & \quad \le \frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {1 - g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} \\ \end{aligned} $$

Because g(1 − t) = f(t), we can obtain

$$ \begin{aligned} & \frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} \\ & \quad \le \frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} \\ \end{aligned} $$

Since g⁻¹(t) is monotonically increasing, we have

$$ \begin{aligned} & g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right) \\ & \quad \le g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

Because g⁻¹(t) = 1 − f⁻¹(t), we further have

$$ \begin{aligned} & g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right) \\ & \quad \le 1 - f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

Since f(t) is monotonically decreasing, we can obtain

$$ \begin{aligned} & \frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right) \\ & \quad \ge \frac{1}{a + b}f\left( {1 - f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right) \\ \end{aligned} $$

Because f(1 − t) = g(t), we can obtain

$$ \begin{aligned} & \frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right) \\ & \quad \ge \frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right) \\ \end{aligned} $$

Since f⁻¹(t) is monotonically decreasing, we have

$$ \begin{aligned} & f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ & \quad \le f^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ \end{aligned} $$

Because f⁻¹(t) = 1 − g⁻¹(t), we can obtain

$$ \begin{aligned} & f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ & \quad \le 1 - g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right) \\ \end{aligned} $$

Since g(t) is monotonically increasing, we have

$$ \begin{aligned} & \frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ & \quad \le \frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {1 - g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ \end{aligned} $$

Because g(1 − t) = f(t), we can obtain

$$ \begin{aligned} & \frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {g\left( {f^{ - 1} \left( {af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ & \quad \le \frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {S_{k} } \right|\left( {\left| {S_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {S_{k} } \right|}} {f\left( {g^{ - 1} \left( {ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right)} \right)} \right)} } \right)} \right)} \right)} \right)} \\ \end{aligned} $$

Since g⁻¹(t) is monotonically increasing, we have

$$ \begin{aligned} & g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ & \quad \le g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

Finally, because g⁻¹(t) = 1 − f⁻¹(t), we can obtain

$$ \begin{aligned} & g^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {g\left( {f^{ - 1} \left( {\frac{1}{a + b}f\left( {g^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {g\left( {f^{ - 1} \left( \begin{aligned} af\left( {g^{ - 1} \left( {(n\varpi_{{i_{k} }} )g(\mu_{{i_{k} }}^{q} )} \right)} \right) \hfill \\ + bf\left( {g^{ - 1} \left( {(n\varpi_{{j_{k} }} )g(\mu_{{j_{k} }}^{q} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ & \quad \le 1 - f^{ - 1} \left( {\frac{1}{N}\sum\limits_{k = 1}^{N} {f\left( {g^{ - 1} \left( {\frac{1}{a + b}g\left( {f^{ - 1} \left( {\frac{1}{{\left| {\varvec{S}_{k} } \right|\left( {\left| {\varvec{S}_{k} } \right| - 1} \right)}}\sum\limits_{\begin{subarray}{l} i_{k} ,j_{k} = 1 \\ j_{k} \ne i_{k} \end{subarray} }^{{\left| {\varvec{S}_{k} } \right|}} {f\left( {g^{ - 1} \left( \begin{aligned} ag\left( {f^{ - 1} \left( {(n\varpi_{{i_{k} }} )f(\nu_{{i_{k} }}^{q} )} \right)} \right) \hfill \\ + bg\left( {f^{ - 1} \left( {(n\varpi_{{j_{k} }} )f(\nu_{{j_{k} }}^{q} )} \right)} \right) \hfill \\ \end{aligned} \right)} \right)} } \right)} \right)} \right)} \right)} } \right) \\ \end{aligned} $$

When q = 1, according to the above inequality, we have μ ≤ 1 − ν. Therefore, we can obtain μ + ν ≤ 1. Now we need to prove the inequality also holds when q = 2, 3, … Let m = 2, 3, … We need to prove μ^m + ν^m ≤ 1. According to μ + ν ≤ 1 and the binomial theorem, we can obtain

$$ \left( {\mu + \nu } \right)^{m} = \sum\limits_{k = 0}^{m} {\left( {C_{m}^{k} \mu^{m - k} \nu^{k} } \right)} = \mu^{m} + \nu^{m} + \sum\limits_{k = 1}^{m - 1} {\left( {C_{m}^{k} \mu^{m - k} \nu^{k} } \right)} \le 1 $$

Because μ ≥ 0 and ν ≥ 0, we have

$$ \sum\limits_{k = 1}^{m - 1} {\left( {C_{m}^{k} \mu^{m - k} \nu^{k} } \right)} \ge 0 $$

Therefore, we can obtain μ^m + ν^m ≤ 1. Now it can be concluded that μ^q + ν^q ≤ 1 for q = 1, 2, 3, …

Since we have proved 0 ≤ μ^q + ν^q ≤ 2 and μ^q + ν^q ≤ 1, we can obtain 0 ≤ μ^q + ν^q ≤ 1.□

Appendix B: Proof of Theorem 2

Proof

This theorem can be proved by swapping the positions of μ and ν in the proof of Theorem 1 since WAPPGBM^(a,b) (G₁, G₂, …, G_n) is the dual form of WAPPBM^(a,b) (G₁, G₂, …, G_n).□

The implementation code of the proposed method and all methods in the quantitative comparison is being released at https://github.com/YuchuChingQin/AOsOfGOMGs, which is expected to foster further research in the development of new MCDM methods based on GOMGs.