Quantifying the sampling error on burn counts in Monte-Carlo wildfire simulations using Poisson and Gamma distributions

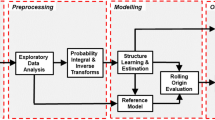
Abstract

This article provides a precise, quantitative description of the sampling error on burn counts in Monte-Carlo wildfire simulations - that is, the prediction variability introduced by the fact that the set of simulated fires is random and finite. We show that the marginal burn counts are (very nearly) Poisson-distributed in typical settings and infer through Bayesian updating that Gamma distributions are suitable summaries of the remaining uncertainty. In particular, the coefficient of variation of the burn count is equal to the inverse square root of its expected value, and this expected value is proportional to the number of simulated fires multiplied by the asymptotic burn probability. From these results, we derive practical guidelines for choosing the number of simulated fires and estimating the sampling error. Notably, the required number of simulated years is expressed as a power law. Such findings promise to relieve fire modelers of resource-consuming iterative experiments for sizing simulations and assessing their convergence: statistical theory provides better answers, faster.

Appendices

Appendix A: Probability theory prerequisites

1.1 A.1   Random variables

We write $X \sim \text {Poisson}(\lambda = z)$ to denote that X is a random variable following a Poisson distribution of parameter $\lambda$ equal to $z$.

We write $\mathbb {E}[X]$ for the expected value of random variable $X$, $\text {Var}[X]$ for its variance, and $\text {StdDev}[X]$ for its standard deviation.

Expected value is linear. That is, if $(\lambda _i)_i$ are non-random numbers, then:

$$\begin{aligned} \mathbb {E}\left[ \sum _i \lambda _i X_i\right] = \sum _i \lambda _i \mathbb {E}\left[ X_i\right] \end{aligned}$$

The above formula holds even if the $(X_i)_i$ are not independent.

If $\mu = \mathbb {E}[X]$, then $\text {Var}[X] = \mathbb {E}[(X - \mu )^2]$, and $\text {StdDev}[X] = \sqrt{\text {Var}[X]}$.

It follows that if $\lambda$ is a non-negative, non-random scalar, then $\text {Var}[\lambda X] = \lambda ^2 \text {Var}[X]$ and $\text {StdDev}[\lambda X] = \lambda \text {StdDev}[X]$.

Variance is additive on independent variables. That is, if $(X_i)_i$ are independent random variables, then:

$$\begin{aligned} \text {Var}\left[ \sum _i X_i\right] = \sum _i \text {Var}\left[ X_i\right] \end{aligned}$$

If $\pi _C$ and $\hat{n}_C$ are random variables, $\pi _C | \hat{n}_C$ ($\pi _C$ given $\hat{n}_C$) denotes a random variable which represents the uncertainty about $\pi _C$ that remains after observing a particular value of $\hat{n}_C$.

1.2 A.2   Probability distributions

1.2.1 A.2.1   Dirac distributions

The most trivial type of probability distribution is the one followed by non-random (constant) variables: $X$ follows a Dirac distribution of value $x_0$, denoted $X \sim \text {Dirac}(v=x_0)$, if $\mathbb {P}[X = x_0] = 1$.

The less trivial families of distributions described below have Dirac distributions as limit cases, for choices of parameters which set their variance to zero.

1.2.2 A.2.2   Bernoulli and Binomial distributions

$X \sim \text {Bernoulli}(p=\pi )$ if $X = 1$ with probability $\pi$, and $X = 0$ otherwise. Then $\mathbb {E}[X] = \pi$ and $\text {Var}[X] = \pi (1 - \pi )$.

$X \sim \text {Binomial}(p=\pi , n=N)$ if $X$ is the sum of $N$ independent Bernoulli variables of parameter $\pi$. As such, $\mathbb {E}[X] = N\pi$ and $\text {Var}[X] = N\pi (1 - \pi )$.

1.2.3 A.2.3   Poisson and gamma distributions

$X$ follows a Poisson distribution with mean $\nu$ (denoted $X \sim \text {Poisson}(\lambda = \nu )$) if $X$ takes its values in the natural integers, and its Probability Mass Function $n \mapsto \mathbb {P}[X = n]$ is proportional to $n \mapsto \frac{\nu ^n}{n!}$.

The $\lambda$ parameter is both the mean of $X$ and its variance : $\mathbb {E}[X] = \text {Var}[X] = \nu$.

• 1. Poisson approximation to Binomial A Poisson distribution is the limit of a Binomial distribution as the $p$ parameter is driven to zero while the $n$ parameter is driven to infinity:

  $$\begin{aligned} \text {Binomial}\left( p=\frac{\nu }{N}, n=N \right) \underset{N \rightarrow \infty }{\approx }\ \text {Poisson}(\lambda = \nu ) \end{aligned}$$

• 2. Sums of Poisson variables A sum of Poisson-distributed independent variables is also Poisson-distributed. That is, if $X_i \sim \text {Poisson}(\lambda = \nu _i)$ and the $(X_i)_{i=1}^m$ are independent, then:

  $$\begin{aligned} \sum _{i=1}^m X_i \sim \text {Poisson}(\lambda = \sum _{i=1}^m \nu _i) \end{aligned}$$

• 3. Binomial-Given-Poisson Yields Poisson If $X, N$ are two random variables such that $N \sim \text {Poisson}(\lambda = \lambda _0)$ and $X | N \sim \text {Binomial}(p = p_0, n = N)$, then $X \sim \text {Poisson}(\lambda = p_0 \lambda _0)$.

• 4. Gamma Distribution $X$ follows a Gamma distribution of shape parameter $k > 0$ and scale parameter $\theta > 0$ (denoted $X \sim \text {Gamma}(k, \theta )$) if it takes its values among nonnegative real numbers, and its Probability Density Function $x \mapsto \frac{d \mathbb {P}[X = x]}{dx}$ is proportional to $x \mapsto x^{k-1} e^{- \frac{x}{\theta }}$. Then $\mathbb {E}[X] = k \theta$ and $\text {Var}[X] = k \theta ^2$. A special case is $k = 1$, in which case $X$ follows an Exponential distribution of mean $\theta$. This is the distribution of highest differential entropy for a given mean, which arguably makes it attractive as a prior distribution in a Bayesian context; informally, this is because it is the “least prejudiced” distribution in some sense. The family of Gamma distributions is stable by rescaling: that is, if $\lambda > 0$ is a non-random scalar and $X \sim \text {Gamma}(k=k_0, \theta =\theta _0)$, then $\lambda X \sim \text {Gamma}(k=k_0, \theta =\lambda \theta _0)$.

• 5. Gamma-Poisson-Gamma Bayesian Updating If $\nu \sim \text {Gamma}(k=k_0, \theta =\theta _0)$ and $\hat{n} | \nu \sim \text {Poisson}(\lambda = \nu )$, then by Bayes’ Theorem:

  $$\begin{aligned} \nu | \hat{n} \sim \text {Gamma}(k=(\hat{n} + k_0), \theta =(1 + \theta _0^{-1})^{-1}) \end{aligned}$$

  When we have a random variable $\hat{n} \sim \text {Poisson}(\lambda = \nu )$ and are trying to estimate $\nu$ from $\hat{n}$ by Bayesian Inference, the above property makes it mathematically convenient to model the prior distribution for $\nu$ as a Gamma distribution, because the posterior will also be Gamma-distributed, and thus expressible in closed form using only 2 parameters.

1.2.4 A.2.4   Gaussian asymptotics

Binomial / Poisson / Gamma distributions are asymptotically equivalent to a Normal distribution of the same mean and variance as their $n$ / $\lambda$ / $k$ parameters grow large and other parameters remain fixed. In the context of this article, this happens when the number of simulated years is driven to infinity.

Appendix B: Notes on the posterior distribution on $\nu _C$

This appendix revisits the posterior distribution described in Section 2.9 with some detailed observations:

• 1. This posterior distribution fully specifies our Monte-Carlo uncertainty about $\nu _C$ using only two numbers (e.g $k$ and $\theta$, or the mean $k \theta$ and standard-deviation $\sqrt{k} \theta$), making it a better statistical summary than an interval. It may be worth reporting these two numbers instead of just $\hat{n}_C$, so that users can factor this Monte-Carlo uncertainty into their own use of the results.

  • 1. If $k_0 = 1$, users can even work out $\hat{n}_C$ and $\theta _0$ from those reported numbers, and then re-do the inference with their own prior distribution.

• 2. This posterior distribution has mean $\frac{\hat{n}_C + k_0}{1 + \theta _0^{-1}}$, mode $\frac{\hat{n}_C + k_0 - 1}{1 + \theta _0^{-1}}$, and variance $\frac{\hat{n}_C + k_0}{(1 + \theta _0^{-1})^2}$. If we chose our number of ignitions high enough, we’ll tend to have $\hat{n}_C \gg k_0$ and $\theta _0 \gg 1$, and the mean, mode and variance will be asymptotically equivalent to $\hat{n}_C$.

• 3. For the recommended $k_0 = 1, \theta _0 = \nu ^0_C$, the posterior distribution now becomes $\text {Gamma}(k=(\hat{n}_C + 1), \theta =(1 + (\nu ^0_C)^{-1})^{-1})$, with mean $\frac{\hat{n}_C + 1}{1 + (\nu ^0_C)^{-1}}$, mode $\frac{\hat{n}_C}{1 + (\nu ^0_C)^{-1}}$, and variance $\frac{\hat{n}_C + 1}{(1 + (\nu ^0_C)^{-1})^2}$.

  • 1. When $\nu ^0_C \gg 1$, the posterior mode tends to agree with the Maximum Likelihood Estimate we’ve been using so far, as $\frac{\hat{n}_C}{1 + (\nu ^0_C)^{-1}} \approx \hat{n}_C$.

  • 2. The Bayesian posterior distribution has most added value when both $\hat{n}_C$ and $\nu ^0_C$ are small, then reporting a broad uncertainty which would not be perceptible with $\hat{n}_C$ alone.

  • 3. For non-burnable cells, it makes sense to choose $\nu ^0_C=0$. Then the posterior distribution will be a Dirac at 0, as it should be.

  • 4. Typically, whenever $\pi ^0_C \ne 0$, we will have $\frac{N_I}{F_\mathcal {A}} \gg \frac{1}{\pi ^0_C}$, and therefore $\left( 1 - \frac{1}{1 + \frac{N_I}{F_\mathcal {A}} \pi ^0_C} \right) \approx 1$, which simplifies Eq. 22 while revealing that the posterior distribution is insensitive to the precise value chosen for $\pi ^0_C$ unless it is extremely small. In other words, when simulating tens of thousands of years, it makes no practical difference whether $\pi ^0_C$ is chosen to be $0.1 \text { yr}^{-1}$, $1 \text { yr}^{-1}$ or $0.01 \text { yr}^{-1}$. Consequently, we recommend that fire modelers waste no time on this sort of fine tuning.

Appendix C: The Poisson approximation in non-Binomial experimental designs

This section illustrates how the Poisson approximation can still be accurate even when the burn count does not follow a Binomial distribution (due to fires not being sampled i.i.d.).

1.1 C.1   When ignitions are drawn from separate batches

For example, instead of drawing a fixed number of i.i.d ignitions, we can imagine that the space-time domain of the simulation is partitioned into $M$ geographic tiles or years, and that a fixed number of ignitions is drawn from each partition component.

Then, the total burn count $\hat{n}_C$ is the sum of M independent burn counts:

$$\begin{aligned} \hat{n}_C = \sum _{j=1}^M \hat{n}_C^{(j)} \end{aligned}$$

This sum is the sensible way to aggregate burn counts when the same number of years is simulated in each partition component.

Now, if we assume that each of the $\hat{n}_C^{(j)}$ is Poisson-distributed:

$$\begin{aligned} \hat{n}_C^{(j)} \sim \text {Poisson}(\lambda = \nu _C^{(j)}) \end{aligned}$$

... then $\hat{n}_C$ is a sum of independent Poisson variables, thus it itself is Poisson-distributed:

$$\begin{aligned} \hat{n}_C \sim \text {Poisson}(\lambda = \sum _j \nu _C^{(j)}) \end{aligned}$$

1.2 C.2   When ignitions are drawn as a Poisson point process

Instead of drawing a predetermined number of ignitions $N_I$, it can be simpler to draw ignitions as a Poisson Point Process (that is, the number of ignitions contributed by each space-time pixel is drawn independently of the others pixels), which implies that the total number of simulated ignitions becomes a random variable $\hat{N}_I \sim \text {Poisson}(\lambda = N_I)$.

In this case, the “Binomial-given-Poisson yields Poisson” property presented in Appendix A.2.3 tells us that $\hat{n}_C$ is exactly (not just approximately) Poisson-distributed.

Such a sampling process can be convenient because the total $F_\mathcal {A}$ need no longer be computed, which in particular can make it more practical to parallelize simulations.

1.3 C.3   Drawing independent years

Some wildfire behavior models like FSim¹ and BURN-P3⁶ offer yet another variant of randomness structure: instead of drawing independent ignitions, they start by drawing independent years, then within each year they draw a random number of ignitions (much like a Poisson Point Process⁷) depending on the conditions in that year.

Again, it can be seen that the Poisson approximation to $\hat{n}_C$ is still accurate. It is very unlikely for a given cell $C$ to burn more than once in a given year; therefore, the burn count $\hat{n}_{C,y}$ in the $y$ -th year is well approximated by a Bernoulli variable, $\hat{n}_C = \left( \sum _y \hat{n}_{C,y}\right)$ is a sum of a large number of i.i.d. Bernoulli variables with small $p$ parameter, and is therefore a Binomial distribution which is well approximated by a Poisson distribution.