Locally adaptive change-point detection (LACPD) with applications to environmental changes

Abstract

We propose an adaptive-sliding-window approach (LACPD) for the problem of change-point detection in a set of time-ordered observations. The proposed method is combined with sub-sampling techniques to compensate for the lack of enough data near the time series’ tails. Through a simulation study, we analyse its behaviour in the presence of an early/middle/late change-point in the mean, and compare its performance with some of the frequently used and recently developed change-point detection methods in terms of power, type I error probability, area under the ROC curves (AUC), absolute bias, variance, and root-mean-square error (RMSE). We conclude that LACPD outperforms other methods by maintaining a low type I error probability. Unlike some other methods, the performance of LACPD does not depend on the time index of change-points, and it generally has lower bias than other alternative methods. Moreover, in terms of variance and RMSE, it outperforms other methods when change-points are close to the time series’ tails, whereas it shows a similar (sometimes slightly poorer) performance as other methods when change-points are close to the middle of time series. Finally, we apply our proposal to two sets of real data: the well-known example of annual flow of the Nile river in Awsan, Egypt, from 1871 to 1970, and a novel remote sensing data application consisting of a 34-year time-series of satellite images of the Normalised Difference Vegetation Index in Wadi As-Sirham valley, Saudi Arabia, from 1986 to 2019. We conclude that LACPD shows a good performance in detecting the presence of a change as well as the time and magnitude of change in real conditions.

1 Introduction

Detecting distributional changes in time-ordered observations is an important initial step before turning to identifying the effect of change-points in model fitting and studying the change mechanism. Generally speaking, changes in characteristics such as the mean and/or variance might either happen smoothly (e.g. slow growing deviation from the past average) or in an abrupt/sudden manner (e.g. up/down-ward shift in the average of data). In order to put this in a statistical context, let $X_i,~1 \le i \le n < \infty ,$ be a sequence of random variables, which in a general setting can be considered independent or not, from a known distribution $F(\cdot )$. Then the existence of a change-point at time index $1 \le t \le n$ means that $X_i,~ 1 \le i \le t,$ have a common distribution $F_1(\cdot )$ whereas $X_i,~ t+1 \le i \le n,$ have a common distribution $F_2(\cdot )$ in which $F_1(\cdot ) \ne F_2(\cdot )$ based on at least one specific characteristic.

The study of change-points dates back to the 1950s when Page (1954, 1955) proposed some procedures to test the existence of a change in mean, and also to identify homogeneous subsets in a set of random samples. Since then various non-parametric and parametric methods have been developed; hence the corresponding literature is quite extensive, and such problems have been further raised in different contexts such as agronomy (Brault et al. 2018), hydrology (Serinaldi et al. 2018), environmental applications (Moura e Silva et al. 2020), and finance (Bandt 2020). The methods are generally grouped in two main categories: online techniques which study the data as they become available and detect changes as soon as they happen in real time, and offline methods that assume all samples are already received. A non-parametric test which has been frequently used in different contexts is the Pettitt’s test (Pettitt 1979; Xie et al. 2014; Serinaldi and Kilsby 2016) which indicates the growth/decrease in the mean of time series. Other earlier change-point detection methods may include Buishand Range and Buishand U approaches which assume data come from a normal distribution (Buishand 1982, 1984). Generally, the problem of detecting change-points has been addressed from different points of view. Zeileis et al. (2003) developed an approach to detect structural changes by fitting linear models to the observations between any two consecutive change-points. Verbesselt et al. (2010) suggested to decompose time series into trend, seasonal, and reminder components, and then iteratively search for changes in each component based on the ordinary least squares (OLS) residuals-based MOving SUM (MOSUM) test. Matteson and James (2014) proposed non-parametric hierarchical clustering algorithms based on distances between observations. Fryzlewicz (2014) proposed the wild binary segmentation (WBS) approach which combines the original binary segmentation (BS) idea with sub-sampling techniques. A Bayesian approach for the detection of change-points for the marked Poisson processes is also proposed by Shaochuan (2019). Liu et al. (2020) focused on high dimensional data and proposed an adaptive framework for change-point detection based on a generalised version of the classical cumulative sum statistic. Ma et al. (2020) considered dependent data and developed a three-step approach based on the likelihood ratio scan statistics over sliding windows, spectral discrimination, and p-value adjustment. Since results from different algorithms do not always match, Bullock et al. (2020) proposed a sequential ensemble algorithm to combine different techniques, detecting change-points and then removing false positives. In addition, some methods can be further considered in multivariate settings (Matteson and James 2014; Liu et al. 2020). General overviews of various (non)parametric change-point detection methods can be found in e.g. Eckley et al. (2011), Chen and Gupta (2011), Brodsky and Darkhovsky (2013), Aminikhanghahi and Cook (2017), Truong et al. (2020).

Amongst all, the sliding-window-based approach, which is based on measuring the discrepancy between two adjacent windows sliding over the entire time series, has been a simple and fast search method to detect change-points (Truong et al. 2020). In other words, for each time index the discrepancy between the downstream and upstream windows with fixed width is measured. Hence, a discrepancy curve could be obtained in which its peaks may alert about the existence of change-points. However, the performance of such sliding-window-based approaches depends on the width of sliding windows. Wide windows mostly take the global behaviour of observations into account, whereas narrow windows only consider the local information. Yau and Zhao (2016) proposed a rule-of-thumb for width selection which depends on the number of observations and at least demands the width 25. However, such choice may not always be practical especially when time series are short or changes occur near the time series’ tails (Ma et al. 2020). It has often been hard, for most methods, to detect a change near the tails of a time series due to the lack of enough samples before/after such change (Hoga 2018; Militino et al. 2020).

Looking for remedies for the above-mentioned concerns, in this paper we propose a locally-adaptive sliding-window-based approach (LACPD) which combines the results of various windows with different widths. Such combination of windows brings the benefit of taking advantage of both wide and narrow windows. In order to avoid the practical limitations in the time series’ tails we suggest to employ sub-sampling techniques. Furthermore, we make use of two-sample tests to measure the discrepancies between adjacent windows which in turn leads to a p-value (discrepancy) curve as well. Since such procedure consists of multiple comparisons, we adjust the p-values to control the so-called Family-Wise Error-Rate and/or False Discovery Rate (Benjamini and Yekutieli 2001). We study the performance of LACPD under different settings, and based on type I error probability, power, ROC curves, absolute bias, variance, and Root-Mean-Square Error (RMSE). We also compare its performance with various alternative methods. The proposed methodology is further applied to two real datasets concerning environmental abrupt changes.

The rest of the paper is organised as follows. In Sect. 2, we present our locally adaptive change-point detection (LACPD) procedure. Section 3 is devoted to evaluate the performance of our procedure under different settings, and compare its practicality with other alternative methods. In Sect. 4, we apply LACPD to two real datasets: annual flow of the Nile river in Awsan, Egypt, from 1871 to 1970, and a novel remote sensing data application consisting of a 34-year time-series of satellite images of the Normalised Difference Vegetation Index (NDVI) in Wadi As-Sirham Valley, Saudi Arabia, from 1986 to 2019. Finally, the paper ends with a discussion in Sect. 5.

2 Methodology

The distributional behaviour of time-ordered observations may generally experience short/long-term changes, e.g. abrupt changes in the mean and/or variance. Throughout the paper, let ${{\mathbf {x}}}=\{x_1,x_2,\ldots ,x_n \}$ be a finite set of time-ordered observations. In this section, we propose an adaptive procedure based on an iteration of sliding windows and sub-sampling for the purpose of detecting a single abrupt change.

Change-point detection based on sliding windows has been a quick technique to get an insight into the existence of change-points in time-ordered observations (Truong et al. 2020). The idea is to measure the discrepancy between two adjacent sliding windows, with fixed width, that slide along the time series. Once these two such windows contain parts of the time series with different behaviours/parameters, the discrepancy measure alerts. In other terms, for each time index $t, 1<t<n$, the discrepancy between the immediate left and right side, within a fixed period, is measured. Doing so, a discrepancy curve would be obtained in which its peaks point to probable change-points. In practice such discrepancy is measured by employing a two-sample statistical test such as t-test, Mann-Whitney. For additional details see Truong et al. (2020) and references therein. Generally, for each time index $t,~ 1<t<n$, the null hypothesis ${\mathcal {H}}_0: F^t_L=F^t_R$ is tested against the alternative hypothesis ${\mathcal {H}}_1: F^t_L \ne F^t_R$ in which $F^t_L$ and $F^t_R$ refer to the distribution functions of data within the left and right windows of t respectively. This technique is quite simple and quick, however its performance depends on the width of sliding windows, and moreover the fixed width of the sliding windows may face/bring limitation in the time series’ tails. Note that considering a fixed-width window shows two restrictions: 1) we need to only search for change-point for indexes t that are far enough from the tails, or 2) for some indexes t near the tails, one of the windows may include less observations than the other one when considering different width for left/right windows. Below, we propose to employ sub-sampling techniques to overcome the lack of data in the tails, and further combine the output from several sliding windows of different sizes to benefit from both narrow and wide windows.

Definition 1

Let ${{\mathbf {x}}}=\{ x_1,x_2,\ldots ,x_t,\ldots ,x_n\}$ be a finite set of independent time-ordered observations, and assume there only exists a single change-point $t,~1<t<n$. A new set of observations, having $x_t$ in the centre, can be constructed by sub-sampling (with replacement) from data before t, i.e. $\{ x_1,x_2,\ldots ,x_{t-1}\}$, and after t, i.e., $\{ x_{t+1},x_{t+2},\ldots ,x_n\}$. Denote the two random samples obtained from the left and right-side of $x_t$ by ${{\mathbf {x}}}^{L}_t=\{x_1^{L},x_2^{L},\ldots ,x_{n-t+1}^{L} \}$ and ${{\mathbf {x}}}^{R}_t=\{x_1^{R},x_2^{R},\ldots ,x_{t}^{R} \}$, respectively. Then, $x_t$ is placed in the middle of

$$\begin{aligned} {{\mathbf {y}}}^t = \{ {{\mathbf {x}}}^{L}_t, {{\mathbf {x}}}, {{\mathbf {x}}}^{R}_t \} = \{ x_1^{L},x_2^{L},\ldots ,x_{n-t+1}^{L},x_1,\ldots ,x_t,\ldots ,x_n,x_1^{R},x_2^{R},\ldots ,x_{t}^{R}\} = \{ y_1^t,y_2^t, \ldots , y_{2n+1}^t \}.~ \end{aligned}$$

(1)

We shall call ${{\mathbf {y}}}^t$ a $x_t$-centred version of ${{\mathbf {x}}}$.

Note that the length of ${{\mathbf {y}}}^t$ in (1) is $2n+1$, wherein ${{\mathbf {x}}}^{L}_t$ and ${{\mathbf {x}}}^{R}_t$ are taken such that $x_t$ is the $(n+1)$-th observation of ${{\mathbf {y}}}^t$, i.e. $y_{n+1}^t=x_t$. For each time index t, one may construct the $x_t$-centred version of ${{\mathbf {x}}}$, and employ a two-sample statistical test to measure the discrepancy between the immediate left and right of $y_{n+1}^t (x_t)$ based on a previously selected width for sliding windows. Although this might seem rational, however, due to the effect of sub-sampling, there might be an intense similarity in the tails of ${{\mathbf {y}}}^t$ when t is an early or late time index. In other terms, it is more likely to find a change-point when one of the legs of the sliding window misrepresents the variability due to sub-sampling in the tails. Therefore, if we were to look for a single early/late change-point, that would be probably found in the first or last time-periods of ${{\mathbf {x}}}$. Moreover, it might be the case that, in a long time series, there appear several small/big changes dominating each other. Thus, it is important to further consider local information when looking for change-points. Taking local information into account basically means considering a small/narrow window around each $x_t$ within ${{\mathbf {y}}}^t$. In order to avoid such concerns and reduce the randomness effect of sub-sampling, we next present a procedure showing how the sub-sampling technique introduced in Definition 1 can get along with a two-sample statistical test, e.g. Mann-Whitney, for proposing an adaptive change-point detection procedure based on sliding windows. We highlight that we here only consider two-sided hypothesis tests.

Procedure 1

(LACPD) Let ${{\mathbf {x}}}=\{ x_1,x_2,\ldots ,x_n\}$ be a finite set of independent time-ordered observations which contains a single change-point in a characteristic such as mean or variance. For any $t,~ 1<t<n$, some $m \ge 1$, and k given widths $\{h_1,h_2,\ldots ,h_k \}$ for sliding windows, the test statistic and an approximate p-value of the locally adaptive change-point detection (LACPD) procedure are given by

$$\begin{aligned} Z_{t}^{m,k} = \frac{1}{k} \sum _{j=1}^{k} \frac{1}{m} \sum _{i=1}^{m} | Z_{t}^{i,j} |, \qquad p_{t}^{m,k} = \frac{1}{k} \sum _{j=1}^{k} \frac{1}{m} \sum _{i=1}^{m} p_{t}^{i,j}, \end{aligned}$$

(2)

where $Z_{t}^{i,j}$ and $p_{t}^{i,j}$ are the test statistic and its corresponding p-value of a given two-sample statistical test, upon the i-th $x_t$-centred sample based on j-th width for sliding window ($h_j$), applied to the immediate left and right of $x_t$. The most probable change-point is the t which owns the smallest significant p-value. This coincides with the t that owns the minimum/maximum (depending on the considered statistical test) of $Z_{t}^{m,k}$.

Note that the exact p-value of LACPD clearly depends on the distribution of implemented test. For instance, if one considers the Mann-Whitney test, $Z_t^{m,k}$ reduces to

$$\begin{aligned} Z_{t}^{m,k} = \frac{1}{k} \sum _{j=1}^{k} \frac{1}{m} \sum _{i=1}^{m} Z_{t}^{i,j}, \end{aligned}$$

with the average

$$\begin{aligned} {\mathbb {E}}\left[ Z_{t}^{m,k}\right] = \frac{1}{k} \sum _{j=1}^{k} \frac{1}{m} \sum _{i=1}^{m} {\mathbb {E}}\left[ Z_{t}^{i,j} \right] = \frac{1}{k} \sum _{j=1}^{k} h_j^2/2, \end{aligned}$$

and the variance

$$\begin{aligned} \mathrm {Var} \left[ Z_{t}^{m,k} \right]&= \frac{1}{k^2} \mathrm {Var} \left[ \sum _{j=1}^{k} \frac{1}{m} \sum _{i=1}^{m} Z_{t}^{i,j} \right] \\&= \frac{1}{k^2 m^2} \left[ \sum _{j=1}^{k} \mathrm {Var} \left[ \sum _{i=1}^{m} Z_{t}^{i,j} \right] + \sum _{j \ne l} \mathrm {Cov} \left[ \sum _{i=1}^{m} Z_{t}^{i,j} , \sum _{i=1}^{m} Z_{t}^{i,l} \right] \right] , \end{aligned}$$

where

$$\begin{aligned} \mathrm {Var} \left[ \sum _{i=1}^{m} Z_{t}^{i,j} \right]&= \sum _{i=1}^{m} \mathrm {Var} \left[ Z_{t}^{i,j} \right] + \sum _{i \ne l} \mathrm {Cov} \left[ Z_{t}^{i,j} , Z_{t}^{l,j} \right] \\& \le \left( m + {{m}\atopwithdelims (){2}} \right) \frac{h_j^2 (2h_j + 1)}{12}, \end{aligned}$$

and

$$\begin{aligned} \mathrm {Cov} \left[ \sum _{i=1}^{m} Z_{t}^{i,j} , \sum _{i=1}^{m} Z_{t}^{i,l} \right] \le \mathrm {Var} \left[ \sum _{i=1}^{m} Z_{t}^{i,j} \right] . \end{aligned}$$

In the above paragraph, we have used the mean and variance of the test statistics of the Mann-Whitney test ( Mann and Whitney (1947) and Wackerly et al. (2014, Sec. 15.6)). If we could have obtained the exact variance of $Z_t^{m,k}$, under certain conditions for the central limit theorem for (weakly) dependent variables (Hoeffding et al. 1948; Chen et al. 2020), another approximate p-value, for the given large enough widths $h_j,j=1,\ldots ,k,$ may be obtained as

$$\begin{aligned} 2\min \left\{ p({\mathcal {Z}} < \frac{Z_{t}^{m,k} - \frac{1}{k} \sum _{j=1}^{k} h_j^2/2}{ \sqrt{\mathrm {Var} \left[ Z_{t}^{m,k} \right] } }) , p({\mathcal {Z}} > \frac{Z_{t}^{m,k} - \frac{1}{k} \sum _{j=1}^{k} h_j^2/2}{ \sqrt{\mathrm {Var} \left[ Z_{t}^{m,k} \right] } }) \right\} , \qquad {\mathcal {Z}} \sim N(0,1) . \end{aligned}$$

However, due to the aforementioned limitations, we propose to approximate the p-value of LACPD by (2) which for each target point averages its corresponding obtained p-values from different windows, and in fact shows a good performance in practice (see Sects. 3 and 4). Moreover, one may also think of a weighted average approximation to obtain p-values. We recommend to use non-parametric tests within the machinery of LACPD due to the fact that the distribution of the test statistics of LACPD may not coincide with that of the used test.

Finally, the outcomes of the LACPD procedure are the curves of $Z_{t}^{m,k}$ and $p_{t}^{m,k}$, $1<t<n$, that monitor the small/big changes in the characteristic in question, e.g. mean. Note that, assigning p-values to each time index t provides us with the possibility of detecting significant change-points without the need to apply peak search methods to the discrepancy curve $Z_{t}^{m,k}$. This further allows to obtain interval estimation for change-points at an arbitrary significance level. We add that the magnitude of change can also be captured in the same way as $Z_{t}^{m,k}$ and $p_{t}^{m,k}$. For instance, if the characteristic in question is the mean, for each sliding windows that we apply the two-sided statistical test, we also measure the absolute difference between the mean of the immediate right and left of time index t, and then we average over different iterations and windows. Therefore, LACPD delivers three discrepancy curves $Z_{t}^{m,k}$, $p_{t}^{m,k}$, and magnitude versus time.

2.1 p-value adjustment

Since the LACPD procedure consists of a family of tests (one test per time index $1<t<n$ for each iteration and each width of window), an increase in the type I error probability might erroneously arise. Thus, the obtained p-values $p_t^{i,j}$ in (2) need to be adjusted to keep under control the so-called Family-Wise Error-Rate and/or False Discovery Rate. The Family-Wise Error-Rate (FWE) concerns about the probability to erroneously reject at least one true hypothesis, whereas the False Discovery Rate (FDR) is the expected proportion of erroneous rejections among all rejections. The literature proposes several adjustments’ techniques for such an issue (Holm 1979; Hommel 1988; Hochberg 1988; Wright 1992; Shaffer 1995; Benjamini and Hochberg 1995; Sarkar and Chang 1997; Sarkar 1998; Benjamini and Yekutieli 2001). When all tested hypotheses are true, then controlling FDR turns to controlling FWE (Benjamini and Hochberg 1995; Benjamini and Yekutieli 2001). Throughout the paper, we make use of an adjustment technique proposed by Benjamini and Yekutieli (2001) which is known as BY, since it takes into account the dependency between test statistics when making multiple comparisons which is the case of the LACPD procedure. Note that the intersection of the sliding windows around nearby time indexes is non-empty. We now give a brief run-through of the p-value adjustment technique BY. Let ${\mathcal {H}}_0^{i}$, $i=1,\ldots ,n$, correspond to n null hypotheses, and denote their p-values by $p_i$, $i=1,\ldots ,n$. Further, denote the sorted p-values by $p_{(i)}$, and let $p_{(r)}$ be the largest value for which

$$\begin{aligned} p_{(r)} \le \frac{rq}{n \sum \limits _{i=1}^n 1/i}, \end{aligned}$$

where q is a desirable significance level. If there exists such r, then we reject the hypotheses corresponding to $p_{(1)},\ldots ,p_{(r)}$. Otherwise, no hypothesis would be rejected. In other terms, BY-adjusted p-values may be defined as

$$\begin{aligned} p_{(i)}^{\textsc {BY}}= \min \left( \left( \min _{j \ge i} \frac{np_{(j)} \sum \limits _{l=1}^n 1/l}{j} \right) , 1 \right) , \qquad i=1,\ldots ,n. \end{aligned}$$

Finally, the adjusted p-values $p_{(i)}^{\textsc {BY}}$ are used to make a decision concerning the null hypothesis. The use of such adjusted p-values enhances the performance of LACPD in terms of type I error probability, even though this may come with a slight reduction in power. See Benjamini and Yekutieli (2001) and Benjamini et al. (2009) for more details.

2.2 Parameter selection

The question that remains relates to the choices of width for sliding windows, and the number of iterations m per each sliding window. Among the two, the number of iterations m might be of less importance since we have seen that results are robust when considering a large enough value of m. The width of sliding windows, however, may have significant effect on the performance of LACPD. The rule-of-thumb $\max \{50, 2 \log (n)^2 \}$ (or $\max \{ 25, \log (n)^2 \}$ for time series with sample size less than 800) is suggested by Yau and Zhao (2016) as the width (radius in their language) of the sliding window. However, as pointed out by Ma et al. (2020), such fixed width may not always be practical, especially when a change-point occurs in an early or late time, or the length of time series is short. Ma et al. (2020) implemented a sensitivity analysis to find an optimal width in their simulation studies, however, they relied on such rule-of-thumb in their real data analysis. We note that wide windows may result in high power of the test since they include more observations compared to narrow ones, whereas narrow windows may lead to a low type I error probability. Hence, we propose to combine the outcomes of wide and narrow windows to benefit from both. Our proposal is to use a large enough m, start by wide windows and then in a step-wise manner incorporate narrower windows until a stop condition is satisfied. Therewith, we propose the following steps:

• 1. Fix the iteration parameter m, an adjustment method for p-values, a significance level, and a sequence of width for sliding windows as $k_i=\{ n/2, \ldots , n/(2+i)\}$, $i=1,2,\ldots , n-2$, where n is the number of observations.

• 2. Calculate the test statistic and its p-value in (2) for time indexes $t, 1<t<n$ based on $k_i$, $i=1,2,\ldots , n-2$.

• 3. Once the detected change-point based on three different consecutive sets of widths coincide or the $\min _t p_{t}^{m,k}$ is larger than the significance level, stop considering more sequences of width, and use the results of the one before the last considered sequence of width as final results. For instance, if the detected change-points based on $k_1, k_2,$ and $k_3$ coincide or $\min _t p_{t}^{m,k_3}$ is larger than the considered significance level, then the selected sequence of width is $k_2$, otherwise return to step 2 and incorporate $k_i, 3<i\le n-2$, until the stop rule is satisfied.

Note that, rather than considering the coincidence of detected change-points based on three different consecutive sets of widths, one may decide to stop when the difference between such consecutive sets of widths is less than a fixed value.

3 Numerical evaluation

This section is devoted to study the performance of LACPD when data have experienced a single up-ward shift in mean. We consider the Mann-Whitney statistical test in the LACPD procedure with $m=100$, significant level 0.05, and BY p-value adjustment technique. We have seen that $m=100$ is adequate, since conclusions are robust after repeating the analysis $m=100$ times. Thereafter, we simulate 500 time series, each one of length 200, from the standard normal distribution. These time series do not contain any change, thus we first apply the LACPD procedure (and other alternative methods) to each of them in order to measure the type I error probability. Next, for each of these simulated time series, we produce (single) artificial abrupt changes (up-ward shift) of magnitude 1 (0.5, 0.75) unit from time indexes 40, 80, 100, 120 and 160 onward. The corresponding results for magnitudes 0.5 and 0.75 are presented in the “Appendix”. To evaluate the performance of LACPD, we consider different criteria such as (1) Type I error probability , (2) Power , (3) ROC curves, (4) Absolute Bias (AB), (5) Variance (${{\,\mathrm{Var}\,}}$), and (6) Root-Mean-Square Error (RMSE):

$$\begin{aligned} \mathrm {AB} =&\left| {\widehat{{\mathbb {E}}}} \left[ ~{\widehat{t}}~\right] - t \right| = \left| \frac{1}{n^*} \sum _{i=1}^{n^*} {\widehat{t}}_i - t \right| , \\ \mathrm {Var} =&{\widehat{{{\,\mathrm{Var}\,}}}} ({\widehat{t}}) = {\widehat{{\mathbb {E}}}} \left[ {\widehat{t}} - {\widehat{{\mathbb {E}}}} \left[ ~{\widehat{t}}~\right] \right] ^2 = \frac{1}{n^*} \sum _{i=1}^{n^*} \left[ {\widehat{t}}_i - \frac{1}{n^*} \sum _{j=1}^{n^*} {\widehat{t}}_j \right] ^2, \\ \mathrm {RMSE} =&\sqrt{\frac{1}{n^*} \sum _{i=1}^{n^*} ({\widehat{t}}_i - t)^2}, \end{aligned}$$

where t stands for the true change-point, and $n^* \le n=500$ denotes the number of significantly detected change-points. We also compare the performance of LACPD with the Pettitt‘s test (Pettitt 1979; Xie et al. 2014), Buishand Range and Buishand U tests (Buishand 1982, 1984), Strucchange (Zeileis et al. 2003), bfast (Verbesselt et al. 2010), e.divisive (Matteson and James 2014), wild binary segmentation (wbs) (Fryzlewicz 2014), and the adaptive method (AdaptiveCpt) of Liu et al. (2020). These methods are accessible through their corresponding R packages (R Core Team 2020). We highlight that such methods have proven quite useful in the literature and are generally used within different fields. In addition, we emphasise that in the calculation of each of these methods, we have followed their corresponding recommendations which lead to their best performance. For instance the minimum number of observation between change-points are considered 30 for Strucchange, bfast, and e.divisive which is their default, and also suits our length of data and time of change-points. In the calculation of wbs method, we have used the standard Bayesian Information Criterion bis.penalty which actually leads to similar results as other choices. In the calculation of AdaptiveCpt, we follow the recommendations of Zhou et al. (2018) and Liu et al. (2020) to consider $p=1000$ which corresponds to $L_{\infty }$ norm in which case the choices of other parameters are of least importance.

Table 1 represents the mean type I error probability together with the mean power, at significance level 0.05, when a single change-point is placed at different times indexes. LACPD generally seems more conservative than other methods (except bfast) which might be partly caused by its averaging machinery, adjusting p-values, our strict stop condition, and/or our implemented test, i.e. Mann-Whitney. The performance of bfast is also quite poor in terms of power.

Table 1 The mean power and mean type I error probability (FP) at significance level 0.05

Apart from Strucchange and bfast which look for change-points based on regression relationships, and wbs that reveals change-points based on segmentation and penalties, other methods provide p-values. Hence, we next compare the performance of other methods based on ROC curves that indicates the relationship between the rate of false and true positives. For this purpose we compute the true (TPR) and false (FPR) positive rates at different significance levels, considering in fact a sequence of values starting from 0. Figure 1 shows the ROC curves for cases where FPR is less than 0.05 since all considered methods show a similar performance for FPR larger than 0.05. We only represent the ROC curve of Buishand U due to its similar performance as Buishand Range. From Fig. 1 we can see that in the cases where FPR is less than 0.01, LACPD generally outperforms other alternative methods by having a quite higher TPR, and in other cases methods perform similarly. In other words, in cases that other methods have a quite low rate of false positives they suffer from a quite low rate of true positives, whereas LACPD does not face such an issue. For change-points 80, 100, and 120 the curve of Buishand U is covered by that of e.divisive, being quite similar. Moreover, the closer the area under such curves to 0.05, the better the performance. Table 2 shows the area under the displayed curves in Fig. 1, and we see that LACPD is superior to other methods regardless of the time of change-point. Therefore, taking the presented results in Tables 1 and 2 into account together with Fig. 1, we can say that LACPD outperforms other alternative methods based on a combination of true and false positive rates.

Fig. 1

ROC curves for different change-point methods according to times of change 40, 80, 100, 120, and 160. TPR stands for true positive rate and FPR for false positive rate, in which the latter is limited to 0.05 since after that differences are negligible

Table 2 Area under the displayed curves (AUC) in Fig. 1

We next turn to compare the performance of considered methods based on other criteria. Table 3 shows the absolute bias, variance, and RMSE for LACPD and the other methods. It can be seen that LACPD clearly outperform other methods based on absolute bias, having quite lower bias than others especially when change-points are placed near the tails of the time series, i.e. time indexes 40 and 160. The only methods which seem to be competitive with LACPD, in terms of bias, are Strucchange and wbs. Strucchange performs slightly better than LACPD for change-points 80 and 120, while performing poorer for change-points 40, 100, and 160. The absolute bias of wbs is also slightly less than LACPD for change-points 80 and 120, while in other cases LACPD is superior. We can further see that the performance of Pettitt, Buishand U, Buishand Range, bfast, and AdaptiveCpt is clearly affected by the time of change-points. These methods have a better performance when change-points are close to the middle of time series. In other words, when change-points are closer to the tails, these methods have a quite larger bias than when change-points are near the middle of data. These methods also face the same issue with variance and RMSE (which is generally dominated by variance). When change-points are placed at time indexes 40 and 160, LACPD has a quite lower variance than other methods. For change-points at time indexes 80, 100, and 120, the methods Pettitt, Buishand Range, Buishand U, and AdaptiveCpt generally have lower variance than others. In terms of RMSE, for change-points 40 and 160, the performance of LACPD is similar to Strucchange, e.divisive, and wbs, outperforming other methods. For change-points 80 and 120, all methods show a similar performance having RMSE around 5-6, apart from bfast which has quite higher value depending on the time index of change. For change-point 100, Pettitt, Buishand Range, Buishand U, and AdaptiveCpt have a lower RMSE than others. We conclude that, among the considered methods, the performance of LACPD, Strucchange, e.divisive, and wbs is not affected by the time of change-point, whereas this is not the case of other methods. In addition, LACPD generally outperforms other methods especially in terms of absolute bias, and with respect to variance and RMSE, it is either better (mainly for change-points 40 and 160) than others or similar to them. Moreover, combining the results of Tables 1 and 3, we can see that the slightly higher power of the other methods compared to LACPD might have actually been caused by either false positives or detecting a true change-point at an earlier/later time. Tables 4 and 5 (presented in the “Appendix”) generally confirm similar conclusions when the magnitude of change is of 0.75 and 0.50 respectively, while a reduction in the performance of all methods is obvious including a drastic reduction in the power of LACPD.

Table 3 Absolute Bias ($\mathrm {AB}$), variance ($\mathrm {Var}$), and Root-Mean-Square Error (RMSE) at significance level 0.05

Figure 2 shows the average of all discrepancy curves of Z, p-values, and magnitude of change versus time for all 500 time series. We can observe that all the curves of Z and p-values correctly point to the inserted change-points by having their minima at such times. Furthermore, interval estimates are displayed for each change-point based on obtained p-values and significance level 0.05. These estimates are [37–45], [74–87], [95–106], [115–126], and [157–164] for change-points 40, 80, 100, 120, and 160 respectively. The discrepancy curves of magnitude also correctly show that the magnitude of change in all scenarios is 1 unit. Furthermore, among all considered methods, only LACPD and bfast reports the magnitude of change according to which LACPD is quite superior to bfast in terms of both bias and variance of the estimated magnitude of change. In particular, the average of absolute bias and variance of the magnitude’s estimate for LACPD are 0.06 and 0.02, whereas such benchmarks take values of 0.18 and 0.45 on average for bfast, respectively.

Fig. 2

The averaged Z, p-value, and magnitude of change obtained by LACPD for all 500 simulated time series from the standard normal distribution. The red and gold vertical lines show the actual change-point and the interval estimation respectively, and the horizontal brown line shows the significance level of 0.05

4 Real data analyses

This section is devoted to two applications of the LACPD procedure: (1) Annual flow of the Nile river in Awsan, Egypt, (2) remotely sensed vegetation index from the Wadi As-Sirham valley, Saudi Arabia. Throughout this section we consider the iteration parameter $m=100$, the BY (Benjamini and Yekutieli 2001) p-value adjustment, significance level 0.05, and the Mann-Whitney statistical test.

4.1 Annual flow of the Nile river in Awsan, Egypt

Figure 3 represents the annual flow (in $10^8$ m$^3$) of the Nile river, in Aswan, Egypt, from 1871 to 1970 (Durbin and Koopman 2012). This dataset is publicly available in R, and has been previously analysed in various papers (see e.g. Zeileis et al. 2003). We are interested in checking whether the average flow of the Nile river has experienced any change over time. The LACPD procedure detects a change-point (downward shift) with magnitude 260 (in $10^8$ m$^3$) in the year 1898 which is, in fact, the year that the Awsan dam was built. Figure 4 shows the Z, p-value, and magnitude curves obtained from LACPD wherein the minimum p-value (maximum Z/magnitude) belongs to the year 1898. Moreover, the p-value curve stays under the significance level 0.05 from 1893 to 1911.

Fig. 3

Annual flow (in $10^8$ m$^3$) of the Nile river in Awsan, Egypt, from 1871 to 1970. The red vertical line shows the detected change-point by LACPD

Fig. 4

The p-value, Z, and magnitude of change obtained by the LACPD procedure for annual flow of the Nile river in Awsan, Egypt. The red and gold vertical lines show the detected change-point and the interval estimation respectively, and the horizontal brown line shows the significance level of 0.05

4.2 Normalised difference vegetation index in Wadi As-Sirham Valley, Saudi Arabia

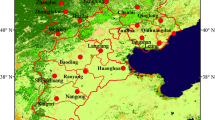
Figure 5 shows the the Wadi As-Sirham Valley, a desert area in the north-west of the Al-Jouf region, in Saudi Arabia. The agricultural activity over the last 3 decades has dramatically changed the landscape of the valley. According to Youssef et al. (2019), irrigated croplands have expanded over an area of 2698km$^{2}$ of desert, potentially causing a severe depletion of groundwater from nearby aquifers.

Fig. 5

Region of the real data analysis. Maximum value yearly composite for 2019 of the Normalised Difference Vegetation Index (NDVI) at the Wadi As-Sirham Valley (Saudi Arabia). Red squares delineate the crop fields used for further inspection: Field 1, 2, and 3 are located at the north, south-east, and west of the region. The smaller graph on the top-right corner shows the location of the valley within Saudi Arabia, and the Landsat tiles intersecting with the region (path-rows: 171-39, 171-40, 172-39)

The analysis is conducted using satellites images captured by Landsat 4-8 missions during 1986-2019. The scenes have a spatial resolution of 30m and a temporal frequency of 16 days. The NDVI is a remote sensing index that depicts the vegetation greenness on the surface of the ground, so that its values oscillate between -1 and 1, where values closer to 1 indicate greener vegetation. The Landsat time series was additionally processed following common practices (Zhu 2017), such as removing clouds and shadows from the scenes based on the quality bands from each mission and applying the maximum value compositing technique (MVC) (Holben 1986) on a yearly basis. The result is a time series of 34 images with the maximum value of NDVI reached every year between 1986 and 2019. The satellite data handling, from acquisition to processing, was carried out in R using the RGISTools package, version 1.0.2 (Pérez-Goya et al. 2020).

We then take a closer look at three crop fields (red squares in Fig. 5) which began with their agricultural activity in 1992, 2006, and 2014, and hereafter are referred as fields 1, 2, and 3, respectively. We add that the agricultural activity, after initiated, is permanent, and the crop fields are surrounded by non-cultivated areas, which presumably enables a comparison between pixels with and without change in the same image. We crop the agricultural fields and reduce the image resolution to 60m to spatially smooth the data. The resulting NDVI images of the crop fields contain 750 pixels on average.

Fig. 6

Spatial representation of the results from the LACPD procedure using $m=100$ and the p-value adjustment technique BY, in the valley of Wadi As-Sirham (Saudi Arabia). From top to bottom, the rows display the p-values, time, and magnitude of change respectively. Time is measured in years, and the magnitude refers to the average discrepancy between the observations before and after the detected change. The columns, from left to right, refer to the crop fields 1, 2, and 3 established in 1992, 2006, and 2014. These map were generated using the R package tmap (Tennekes 2018)

The LACPD procedure is applied to each pixel independently in order to evaluate its practicality and automatic window-selection process when facing data with different changes or without change. Note that in each field there might be changes of different magnitudes at different time indexes, and consequently each pixel may demand a different choice of sliding window. Figure 6 shows the spatial distribution of the change-point detection results for the three agricultural fields. The rows represent the p-values (top), time of change (centre), and magnitude of change (bottom) correspond to each pixel in the NDVI Landsat scenes, and the columns stand for the fields 1, 2, and 3. In general, the p-value graphs show that the transformation from bare into cultivated land is detected as significant (p-value$< 0.05$) by LACPD in all situations. The significant pixels, coloured in blue, clearly delimit the extension of the circular crop fields. Conversely, surrounding pixels in red tones remain non-significant (p-value$> 0.05$). Hence, LACPD suitably detects the land use change.

The graphs of p-values (top row of Fig. 6) further show that there are some significant pixels outside the circular fields. A closer look into these areas reveals that the majority of these pixels correspond to farms placed nearby the crop fields (see Figs. 8 and 9). The middle row in Fig. 6 displays the detected time of change using a blue-to-yellow continuous colour palette to denote years between 1986 and 2019. The first and second crop fields began their activity in 1992 and 2006 respectively in contrast with the farm pixels whose changes are generally detected around 2005 and 2008. This pattern indicates that the farms were likely built during or after initiating the agricultural activity. The last row in Fig. 6 shows the shift in NDVI before and after the detected change, with greener pixels for larger changes. The presence of farms is coherent with a lower change in magnitude (close to 0.1, shown in brown colour) compared to the crop fields (around $\sim 0.6$, in green colour).

Also, there are significant pixels south-west and north-west the second and third fields (Fig. 6, middle and right columns). These pixels belong to sparsely vegetated areas (see Figs. 9 and 10). These sparsely vegetated areas appear in (dark) green and yellow for the second and third field respectively, so apparently these areas started their activities at a later or similar time period than the circular crop fields, considering that the crop fields began in 2006 and 2014 (middle row of Fig. 6). Their low plant density may explain the slight change detected in NDVI ($0-0.1$) (bottom row of Fig. 6), which is represented as white-brown pixels. Some other significant pixels, especially those nearby field 1, are difficult to explain. Field 1 is separated from other crop fields by narrow strips of bare land. Due to the small gap between the fields, these strips might be affected by water runoff or the aerial water transport from the irrigation system, maybe favouring the growth of natural vegetation.

Figure 7 displays the evolution of the test statistic Z (top), p-value (centre), and changing magnitude (bottom) versus time for the three fields, and based on the pixels within the crop fields. These pixels were segregated from the rest using a twofold filter based on the significance level (p-value $< 0.05$) and magnitude of change (Delta NDVI > 0.6). The p-value curves decrease as they approach to the year when agricultural activities started, that are 1992, 2006 and 2014 for the first, second, and third field respectively. The p-values stay below the significance level during the periods $1991-1995$, $2003-2011$, and $2011-2016$, and reach to their minimum values in 1992, 2006, and 2014. Lastly, the curves of the magnitude show the average NDVI difference between the posterior and prior legs of a moving sliding window. Magnitudes increase as they approach to the actual time of change (NDVI=$0.6-0.7$) and decrease thereafter.

Fig. 7

Temporal representation of the results from the LACPD procedure using $m=100$ and the p-value adjustment technique BY, in the valley of Wadi As-Sirham (Saudi Arabia). The left, centre, and right columns correspond to the first, second, and third crop field respectively. The rows, from top to bottom, show the average curves for the test statistic Z, p-value, and magnitude of change for all the significant pixels (p-value $< 0.05$) within the crop fields (Delta NDVI $> 0.6$). The red and gold vertical lines show the established year of fields and the interval estimation respectively, and the horizontal brown line shows the significance level of 0.05

As an additional step, within each field, we select some arbitrary pixels corresponding to the highest delta NDVI, infrastructures and/or secondary cultivated, and a zone with no change. All considered methods in Sect. 3 are applied to the time series of such pixels (see Fig. 11 and Table 6 in the “Appendix”) according to which they correctly detect the change-points within pixels with the highest delta NDVI. However, for the pixels corresponding to non-cultivated and/or secondary cultivated, LACPD seems to provide more reliable results.

4.2.1 Detailed imagery

In this section, we inspect the high-resolution ($<1$m) RGB satellite images of the agricultural fields from the Wadi As-Sirham Valley, Saudi Arabia. These images are intended to check and support the changes detected by LACPD out of the circular croplands. These figures represent the border of the area under analysis in light-blue, and adjacent farms or sparsely vegetated areas in red. In every figure, the first image (left panel) provides an overview of the study area, followed by pictures of infrastructures and secondary cultivated areas. The images below are part of the publicly available ESRI World Imagery Collection (ESRI 2020).

Figure 8 shows the crop field number 1. The image on the right-hand side displays the farm located north-east the study area, which is detected as significant by LACPD. Additionally, the image reveals two distinctive areas within the crop field; an inner circle and an outer ring, which may represent two crops with different planting densities. These differences are visible in the results shown in Fig. 6 when representing the time and magnitude of change in field 1 (first column).

Fig. 8

Detailed high-resolution ($<1$m) colour images of the crop field established in 1991. On the left, the image provides a general overview of the region under analysis. The blue square delimits the area under analysis. The red square highlights a farm located north-east the crop field, which is seen in detail on the right-hand side image. Satellite imagery belongs to the Esri World Imagery Collection (ESRI 2020) and was displayed with the leaflet package (Cheng et al. 2019)

Similarly, the middle image in Fig. 9 shows a closer view of some building (probably a farm) that was built north-east the agricultural land (field 2) and detected as significant by the LACPD. This field also has an inner circle which was also detected by LACPD. The image on the right-hand side highlights what seems to be another cultivated area south-west the cropland. This area shows sparse and regularly spaced vegetation next to a building.

Fig. 9

Detailed high-resolution ($<1$m) colour images of the crop field established in 2006. The left hand-side image provides a general overview of the region under analysis. The blue square delimits the area under analysis. The red squares located north-east and south-west the crop field highlight the location of a farm and a sparsely cultivated area, respectively. Images on the centre and right-hand side shown scenes zooming into the farm and adjacent cultivated areas. Satellite imagery belongs to the Esri World Imagery Collection (ESRI 2020) and was displayed with the leaflet package (Cheng et al. 2019)

Finally, Fig. 10 displays the RGB images for the field number 3. The area enclosed by the red rectangle located north-west the study area shows a similar vegetation pattern as the cultivated area adjacent to field 2. Some pixels in this part of the images were detected as significant. Moreover, the magnitude of change in the inner circle is detected as quite lower than the rest of crop field.

Fig. 10

Detailed high-resolution ($<1m$) colour images of the crop field established in 2014. On the left, the scene provides a general overview of the region under analysis. The blue and red squares delimit the analysed zone and a sparsely cultivated area located north-west the crop field. On the right, the low-density agricultural area is seen in detail. Satellite imagery belongs to the Esri World Imagery Collection (ESRI 2020) and was displayed with the leaflet package (Cheng et al. 2019)

5 Discussion and conclusions

The detection of change-points in time-ordered observations has been an important task in many fields such as environmental applications due to the effect of change-points on model fitting and prediction. In this paper, we have proposed a locally adaptive search method based on sliding windows to benefit from both local and global distributional properties of observations since it might not be the best to look at all data at once, especially when dealing with long time series. However, the strength of sliding-window-based approaches is generally affected by the width of windows; wide windows mainly take global information into account and as a result some changes may dominate each other, whereas narrow windows only consider local information. Note that very narrow windows contain quite similar data since neighbours usually behave similarly. Another general limitation with sliding-window-based approaches is that depending on the width of windows they may not be practical to look for changes near the time series’ tails. Our proposed approach, LACPD, is based on sub-sampling in the tails of time series and an iteration of sliding windows of different widths to tackle the aforementioned concerns. Since LACPD is based on averaging over the results obtained from several sliding windows, it could easily benefit from both wide and narrow windows. Moreover, the use of sub-sampling in the time series’ tails compensates for the lack of enough data before/after a change-point near the tails. By doing so we obtain discrepancy curves in terms of test statistics, adjusted approximate p-values, and magnitudes, which are then used to reveal change-points through both point and interval estimation. Since the approximate p-values are obtained through averaging, it is recommended to use non-parametric tests within the machinery of LACPD due to the fact that the the distribution of the test statistics of LACPD may not coincide with that of the used test.

We have evaluated the performance of LACPD through a simulation study, in which we have compared its performance with various classical and recently developed methods for detecting change-points. The simulation study has confirmed the beneficial effects of combining the outcome of several sliding windows and sub-sampling through several criteria. In particular, we have seen that LACPD generally has quite lower bias and type I error probability than other alternative methods. In terms of power, LACPD is slightly poor which might be partly caused by adjusting p-values and/or our strict stop condition which is in favour of low type I error probability, bias, and variance, rather than high power. It dramatically gets even poorer with respect to changes of small magnitudes that might be due to the power of the implemented test (i.e. Mann–Whitney) as well. Nevertheless, the sub-sampling and averaging machinery of LACPD generally lead to outperforming other methods in terms of bias, variance, and RMSE when changes occur near the tails, whereas it shows a similar performance (sometimes slightly poorer) as other methods when changes happen near the middle of time series. In addition, it has shown a good performance in measuring the magnitude of change, based on the same adaptive sliding-window and iteration used for change-point detection, which is an information that could be quite relevant in real applications. Besides, the performance of LACPD does not depend on the time of change and/or the length of time series as, in our simulation study and real data analyses, it is already applied to time series of different length with change-points at different time indexes.

Since LACPD has shown that a combination of sliding windows of different size turns to a technique with a reliable/acceptable performance with low bias and variance, it would be interesting to see if such an idea can enhance the performance of other (fixed) sliding-window-based methods (Yau and Zhao 2016; Ma et al. 2020), or can be adapted for change-point prediction. Moreover, implementing a more powerful test than Mann–Whitney or tweaking the stop condition may improve its performance in terms of power to reach a better trade-off between type I error probability and power. Another relevant idea could involve theoretical developments regarding p-values. Although in this paper we focused on the detection of an abrupt change in the average/mean of time series, it would be also interesting and relevant to study the performance of LACPD when looking for changes in variance, by using alternative two-samples statistical tests such as the Bartlett’s test (Bartlett 1937), the Levene’s test (Fox 2015) or the F-test. Another idea would be adapting the LACPD procedure for multiple/multivariate settings. Concerning other possible applications, it could be also used to detect outbreaks and/or change-points in time series of intensity images of spatio-temporal point processes (cf. Chaudhuri et al. (2021)), and/or trajectory data (cf. Moradi (2018)).

Finally we would like to highlight that the LACPD procedure is accommodated in the R package LACPD which together with our R codes to reproduce our results (simulation study and real data analyses) will be available at https://github.com/spatialstatisticsupna/LACPD.

Appendix: Simulation study

1.1 Magnitude 0.75 unit

See Table 4.

Table 4 Mean power, Absolute Bias ($\mathrm {AB}$), variance ($\mathrm {Var}$), and Root-Mean-Square Error (RMSE) at significance level 0.05

1.2 Magnitude 0.5 unit

See Table 5.

Table 5 Mean power, Absolute Bias ($\mathrm {AB}$), variance ($\mathrm {Var}$), and Root-Mean-Square Error (RMSE) at significance level 0.05

1.3 Normalised difference vegetation index in Wadi As-Sirham Valley, Saudi Arabia

For each field, Fig. 11 shows the NDVI times series for arbitrary pixels corresponding to the highest delta NDVI (solid curves), infrastructures and/or secondary cultivated (dotted curves), and a zone with no change (dashed curves). Table 6 presents the detected change-points within the displayed time series in Fig. 11. All methods correctly detect the change-points with the highest delta NDVI. For the change-points corresponding to the infrastructures and/or secondary cultivated, generally there is no agreement between methods. Bfast did not detect any change in such pixels. Concerning the pixels with no change, only LACPD and bfast successfully did not detect any change. The performance of other alternative methods varies from one field to another, showing a better performance for fields 2 and 3. Overall, apparently LACPD shows a more reliable performance than other methods within pixels corresponding to infrastructures and/or secondary cultivated and non-cultivated zones.

Fig. 11

NDVI time series at arbitrary selected pixels corresponding to the highest delta NDVI (solid curves), infrastructures and/or secondary cultivated (dotted curves), and zone with no change (dashed curves). From left to right: Field 1, Filed 2, Filed 3

Table 6 Change-point detection for the NDVI time series in Fig. 11