1 Introduction

Large populations and economic activities concentrate along coastal China. The rapid socioeconomic development in coastal China, with many megacities such as Tianjin, Shanghai, and Guangzhou, plays a leading role in China’s economic development. While coastal provinces in China account for only 13% of the land area, they are home to 40% of the national population and contribute to more than 60% of the gross domestic product (Fang et al. 2017). The low elevation coastal zone (LECZ: contiguous coastal area less than 10 m elevation) in China is about 194,000 km2, and nearly 164 million people (in the year 2011) live in the LECZ (Liu et al. 2015). China experiences frequent coastal flooding and has the world’s largest flood-induced mortality (Hu et al. 2018). Between 1989 and 2019, extreme sea level (ESL) events caused by typhoon-induced storm surge led to more than $71 billion direct economic losses, and about 4,392 fatalities (Fang et al. 2017). Several studies have identified coastal China as the region with the largest exposure to ESLs and as one of the most vulnerable areas under climate change (McGranahan et al. 2007; Hinkel et al. 2014; Muis et al. 2016; Fang et al. 2019). Under the Belt and Road Initiative, it is foreseeable that coastal exposure, such as ports, bridges and critical infrastructure, will continue to experience significant growth. Thus, an improved understanding of ESLs in China, and especially the associated uncertainties and their impacts, is important and essential for coastal disaster risk reduction and adaptation planning.

Many studies have assessed spatial and temporal changes of ESLs and relevant driving factors, showing that ESLs are increasing at most places across the globe (Woodworth and Blackman 2004; Marcos et al. 2009; Menéndez and Woodworth 2010), including coastal China (Feng and Tsimplis 2014; Feng et al. 2015, 2019). These changes are predominantly driven by mean sea level rise, but are also affected by other factors such as changes in storm surge activity (related to changes in storminess), or modifications in tidal wave patterns (e.g. due to changes in the bathymetry) (Wahl and Chambers 2015). The current analysis framework for ESLs contains two categories: statistical models (e.g. Obeysekera and Park 2012) and hydrodynamic models (Muis et al. 2016; Vousdoukas et al. 2016a, b). Wahl et al. (2017) evaluated the uncertainties in future global SLR projections and present-day ESL estimates. When compared to SLR, the uncertainties of ESL estimates may be higher, but are typically ignored, which may lead to over- or underestimation and limited understanding of coastal flooding risk, even under present-day climate conditions. Addressing this issue of robust calculation of ESLs, and related uncertainties, is of great importance for the design and planning of offshore adaptation/defense facilities (Dixon and Tawn 1994).

Uncertainties in contemporary ESL estimations are poorly understood in coastal China. Some relevant studies using various definitions of extreme events and distributions for parametrization are displayed in Table 1. Most research on ESLs in coastal China is limited to a specific station or regional area due to a lack of publicly available observational datasets. Meanwhile, large uncertainties exist because of various assumptions that underlie the extreme value analysis (EVA). Firstly, ESLs are affected by SLR, introducing non-stationarity, which needs to be accounted for, either by using non-stationary EVA methods or detrending, to satisfy the assumption of independence and stationarity (Arns et al. 2013). However, this assumption is sometimes ignored or not fully included in statistical analysis (e.g. Li and Li 2013). Secondly, the definition of extremes is another critical issue. In general, the annual maximum values were taken as extremes in previous studies, in parts because local authorities only provide annual maxima considering confidentiality of the full (high frequency) sea level records (e.g. Wu et al. 2017). However, different sampling methods may result in heterogeneous estimates of ESL return periods even when the same distribution functions are used. Moreover, various probability distributions are available for parameterization (Haigh et al. 2010), and those can produce different results. In China, the Gumbel distribution or the Pearson-III type distribution were recommended for the design of sea dike projects (MWR 2014). Those probability functions have a rigorous requirement in the sample size and the results are also dependent on the parameter estimation method. Probability distribution functions used in relevant studies in Table 1 were also constrained to specific EVA models without considering sampling effects and selection of distributions. Different probability functions produce different results which potentially leads to a lack of comparability or greater uncertainty. To our knowledge, no comprehensive assessment of ESL uncertainty, and how it affects flood inundation estimates, has been conducted for coastal China.

Table 1 Case studies of extreme sea levels (ESLs) in China
Full size table

In this study, we evaluate the uncertainties in ESLs for China by considering the sampling of extremes and the selection of different probability distributions. Hourly observations from 13 tide gauges are analyzed to quantify uncertainties of ESLs. Considering the sparse spatial coverage of the tide gauges, a hydrodynamic modeling dataset, i.e. the Global Tide and Surge Reanalysis (GTSR), is also analyzed. Subsequently, the impacts of ESLs on the exposure assessment to coastal flooding for China are evaluated by a GIS-approach. Finally, we assess the impact of SLR on extremes using the concept of AFs (Buchanan et al. 2017). The overall aim of this study is to enhance the understanding of ESL uncertainties and associated impacts (e.g. for inundation analysis) in coastal China, as a basis for developing guidance for coastal engineers and relevant stakeholders.

2 Data and methods

2.1 Data

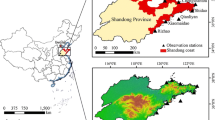
In this study, two kinds of sea level datasets, observations and hydrodynamic model output are analyzed. The observed tide gauge data are collected from the GESLA-2 database (GESLSA-2 2017; Woodworth et al. 2017). Hourly sea level data with at least 20-year length from 13 tide gauges along coastal China are used. Locations and data series lengths are illustrated in Fig. 1. The publicly available time series at nine stations stop in 1997. For each tide gauge, we assess the quality of the raw observational data and remove suspicious outliers, datum shifts, and time shifts. The observations at Hong Kong are obtained from combining the records at North Point (1962–1986) and Quarrybay (since 1986) after datum adjustment (Ding et al. 2001).

Fig. 1
figure 1

a Locations of 13 tide gauges and b the lengths of hourly records

Full size image

GTSR is the first global dataset comprising ESLs derived from a hydrodynamic model (Muis et al. 2016). ESLs were constructed by combining tidal levels and surge levels for the period of 1979–2014. Tidal levels were simulated with the Finite Element Solution model and storm surge with the Global Tide and Surge Model, forced by 6 hourly meteorological fields from the ERA-Interim climate reanalysis (Muis et al. 2016). Numerical simulations were carried out at a 10-min temporal resolution. These simulations were resampled to daily maximum values.

2.2 Methods

2.2.1 Extreme value analysis (EVA)

The procedure of EVA is shown in Fig. 2 with five main analysis steps (following Arns et al. 2013; Wahl et al. 2017).

Fig. 2
figure 2

Analysis procedure of for extreme value analyses (modified after Arns et al. 2013)

Full size image

The five main steps of the EVA procedure include:

  1. 1.

    Detrending: annual average sea level is subtracted year-by-year to remove interannual mean sea level variability and rise. This approach has been widely used in previous studies (e.g., Muis et al. 2016; Wahl et al. 2017).

  2. 2.

    Sampling: two distinct approaches are used to sample extreme events, i.e. the Block Maximum (BM) method, which fits a Generalized Extreme Value (GEV) distribution; and the Peaks Over Threshold (POT) method, which fits a Generalized Pareto distribution (GPD). The BM method selects the r largest values for each time interval (r-largest). In this study, we select a range from r = 1 value/yr to r = 10 values/yr. The POT method uses threshold exceedances. To be able to compare the two approaches, we select percentile thresholds leading to sample sizes that match the ones used in the r-largest analysis (i.e. 99.88% leads to r = 1 value/yr on average, 99.44% leads to r = 10 values/yr on average). We also select other thresholds between the 98th and 99.25th percentiles in 0.25 percentile increments (98%, 98.25%, 98.5%, 98.75%, 99% and 99.25%). In addition to the GEV and GPD, we also use the widely applied Gumbel distribution, fitted to annual maxima values (GUM-AMAX), as reference.

  3. 3.

    Declustering: to ensure independence of all identified extreme events, a decluster time of 3 days (72 h) between events is adopted (Arns et al. 2013; Wahl et al. 2017; Feng and Tsimplis 2014). This is the approximate time most storm surge events influence sea levels at the coast.

  4. 4.

    Parameter estimation: a range of parameter estimation methods exist, such as L-Moments, least squares method, Method of Moments, or Maximum Likelihood Estimation (MLE). As the effects of choosing a certain parameter estimation method are small compared to other key uncertainties (Wahl et al. 2017), this study uses MLE to estimate parameters.

  5. 5.

    Distributions: we fit GEV and GPD distributions for the BM and POT sampling methods, respectively. In the GEV (Eq. 1), when ξ = 0, it is the Type I distribution, i.e. the Gumbel distribution; when ξ < 0, it is the Type III distribution, i.e. the Weibull distribution; when ξ > 0, it becomes the Type II distribution, i.e. the Fréchet distribution. The GEV is also used to fit the time series from r = 1 to r = 10 values per year (GEV-r1, GEV-r2, …, GEV-r10).

    $${\text{GEV}} = {\text{exp}}\left\{ { - \left( {1 + \xi \frac{\chi - \mu }{\sigma }} \right)^{ - 1/\xi } } \right\},{ }\;\;\left( {1 + \xi \frac{\chi - \mu }{\sigma }} \right) > 0\;\;\mu ,{ }\xi \in R,{ }\sigma > 0$$
    (1)

Where \(\mu\) is the location parameter, \(\xi\) is the shape parameter, and \(\sigma\) is the scale parameter. As mentioned above, the Gumbel distribution is also used to fit the annual maximum sea levels (GUM-AMAX). The GPD distribution (Eq. 2), where \(u{ }\) is the threshold value, is used for the POT samples.

$${\text{GPD}} = 1 - \left[ {1 + \frac{\xi y}{{\mathop \sigma \limits }}} \right]^{ - 1/\xi } ,\;\;\tilde{\sigma } = \sigma + \xi \left( {u - \mu } \right)$$
(2)

Thus, various EVA methods are used to estimate return periods of ESLs by considering the uncertainties from different sampling strategies and probability functions. The Root Mean Square Error (RMSE), Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Nash-Sutcliff efficiency (NSE) are used to evaluate the goodness-of-fit in a quantitative sense (Sadegh et al. 2017). Lower RMSE/AIC/BIC indicate higher model quality. NSE closer to 1 indicates a better fit.

2.2.2 Bias correction

Bias exists between observations and the hydrodynamic model output from GTSR (Muis et al. 2016). We apply quantile-mapping to quantify the bias at each tide gauge station (e.g., Arns et al. 2015; Cid et al. 2018). Empirical Cumulative Distribution Functions (CDFs) for the modelled and observed values are obtained, and the differences are added to the CDFs of the modelled values. The bias correction is then interpolated from the 13 tide gauge locations to the remainder of the GTSR output points. The interpolation is performed by using the inverse distance weighted (IDW) method (e.g. Arns et al. 2015). After accounting (and correcting) for the model bias, we apply the same EVA methods as outlined above to the GTSR data. To validate the performance of the model dataset vs the tide gauge data set, we only use the overlapping time series of the modeled GTSR and observed tide gauge records. The RMSE and Pearson correlation coefficient are calculated based on daily maximum sea levels, before and after bias correction.

2.2.3 Inundation analysis

Inundated areas due to coastal flooding are calculated using a bath-tub method with a GIS-based approach (e.g. Kebede and Nicholls 2012; Muis et al. 2017). The Digital Elevation Model (DEM) used here is SRTM (Shuttle Radar Topography Mission) with a spatial resolution of 90 m × 90 m (Rabus et al. 2003). Before inundation modeling, ESLs and elevation should be referenced to the same vertical datum. ESLs calculated here are referenced to mean sea level, whereas global elevation datasets are generally referenced to the EGM96 geoid. The datum offset is corrected using the same approach as in Muis et al. (2017), by using mean dynamic ocean topography to correct for the difference between mean sea level and the geoid. Ignoring such datum correction can significantly affect impact studies (Cheng and Chen 2017), leading to over- or underestimation. We quantify inundated areas as those lower than the estimated ESLs and hydrologically connected to the sea. Flood protection measures are not included in this study.

2.2.4 Impacts of relative SLR on ESLs

SLR modulates extreme value distributions and can lead to large changes in the frequencies with which certain critical thresholds are exceeded (Buchanan et al. 2017; Vitousek et al. 2017). To illuminate the impact of SLR on the occurrence probability of ESLs for Coastal China, we consider uniform SLR associated with two Representative Concentration Pathway (RCP) scenarios for 2050 and 2100. For 2050 SLR is 18 cm for RCP2.6 and 23 cm for RCP8.5; for 2100 SLR is 38 cm for RCP2.6 and 85 cm for RCP8.5 (Church et al. 2013; Hinkel et al. 2014; Fang et al. 2019). We also account for land subsidence, but due to missing data only for Hong Kong, as an example, where observed subsidence was about 19.0–459.0 mm/yr in coastal reclaimed lands (Wang et al. 2016); here we assume subsidence will continue at this location at a rate of 10 mm/yr until 2050.

We follow the method by Buchanan et al. (2017) to calculate AFs caused by SLR for the 13 tide gauges. The AF is \(N\left( {z - \delta } \right)/N\left( z \right)\), where \(N\left( {z - \delta } \right)\) refers to the new expected number of exceedances of a specified level with SLR. AFs are estimated (exemplarily) with the GPD-99.75% method.

$${\text{AF}}\left( {\text{z}} \right) = \frac{{N\left( {z - \delta } \right)}}{N\left( z \right)} = \left\{ {\begin{array}{*{20}l} {\left( {1 - \frac{\delta }{{\left( {\frac{\sigma }{\xi }} \right) + z - \mu }}} \right)^{{\frac{ - 1}{\xi }}} } \hfill & {{\text{for}}\;\; \xi \ne 0} \hfill \\ {\exp \left( {\frac{\delta }{\sigma }} \right)} \hfill & {{\text{for}}\;\; \xi = 0} \hfill \\ \end{array} } \right.$$
(3)

3 Results and discussion

3.1 Uncertainties in EVA results from different sources

3.1.1 Sampling

To evaluate uncertainties stemming from the sampling method, we apply the BM and POT methods. The size of extreme samples depends on the sampling method and the record length. We select thresholds in the POT analysis to obtain similar sample sizes as with the BM method. Taking the Kanmen station as an example (Fig. 3a), the extreme events selected by POT are very different to the ones selected with the annual maxima method (the most commonly applied BM approach). The latter often includes lower events as it is forced to extract the maximum value each year (or more if r-largest is used). By selecting annual maxima, not necessarily all relevant extremes are used, as multiple extreme events may have happened in a given year (as shown in Fig. 3a). In this regard the POT method has the advantage of including all events above a given threshold. However, it is critical to select an appropriate threshold. Threshold selection is a tradeoff between variance and bias. If the threshold is too low, the sample will include non-extreme events, which may lead to poor fitting of the extreme value distribution. If the threshold is too high, the samples will be too small for robust estimation of the distribution parameters. Different methods have been proposed for selecting thresholds automatically, e.g. Northrop et al. (2017) and Caballero-Megido et al. (2018).

Fig. 3
figure 3

a Sampling of the extreme values using the block maxima (BM) and peaks of thresholds (POT) methods for the Kanmen station; b the resulting return sea levels for the Generalized Extreme Value (GEV) and Generalized Pareto Distribution (GPD)

Full size image

Different sampling methods may result in different ESL estimates, especially for long return periods. As POT captures extremes better than BM for Kanmen, the estimated return levels derived with the GPD distribution are also higher than those derived with the GEV distribution (Fig. 3b). For Lusi (Fig. 4a), the estimated ESLs with r = 2 values/yr and r = 3 values/yr and from fitting the GEV distribution are higher than those from using annual maxima (r = 1 value/yr). These results imply that the BM method (and annual maxima in particular) misses some important extremes, leading to an underestimation of ESLs.

Fig. 4
figure 4

Results for the Generalized Extreme Value (GEV) distribution with r = 1–10 values/yr and the Generalized Pareto Distribution (GPD) with thresholds leading to the same sample sizes as in the r-largest approach; results are shown for four tide gauges

Full size image

3.1.2 Distribution functions

To identify which sampling method and probability distribution leads to the highest and the lowest ESLs, Fig. 5 demonstrates the maximum and the minimum ESLs including the underlying EVA method. The maximum ESLs with a 100-year return period at 6 tide gauges are obtained with the GUM-AMAX and the GEV-r1 methods (Fig. 5c). Substantial differences occur at some stations. For example, the 100-year ESLs at Kanmen are 4.69 m and 5.18 m derived with the GUM-AMAX and the GEV-r1 methods, respectively, a difference of ~ 0.5 m (Supplementary Figure S1). The differences across EVA methods become larger for longer return period events (Fig. 5a, b and Supplementary Figure S1). The estimated minimum ESLs are obtained mainly by the GPD distribution with the threshold of 98% (Fig. 5d). For the POT method, a lower threshold results in a larger sample, which in turn tends to lead to lower ESLs associated with the different return periods.

Fig. 5
figure 5

Maximum and minimum estimated extreme sea levels (ESLs) at individual tide gauges among 29 sampling methods and distributions: a ESLs of 50-year return period; b ESLs of 100-year return period; c method leading to maximum 100-year return period ESLs; d methods leading to minimum 100-year return period ESLs

Full size image

To examine the goodness-of-fit, four metrics are calculated between the empirical and theoretical distributions (Supplementary Table S1). These measures are highly sensitive to sample size; therefore, it is inappropriate to use them if the sample size varies greatly. For example, RMSE converges when sample sizes increase (lower thresholds). Amidst all EVA methods, for most tide gauges the best fit is derived with GPD-98% or GPD-98.25% as these have the largest sample sizes. The goodness-of-fit can be directly compared for GEV-r1, GUM-r1 and GPD-r1 as they have similar sample sizes (Supplementary Table S1). When subtracting the goodness-of-fit metrics derived with all methods from those derived with GUM-r1, most tide gauges have positive residual RMSE/NSE/AIC/BIC values, indicating that Gumbel performs poorly compared to GEV and GPD. For RMSE/AIC/BIC, 10 out 13 tide gauges show better results for GPD than for GEV; in terms of NSE, GEV and GPD perform similarly.

3.2 Spatial patterns of ESLs and associated uncertainties

To validate the modeled GTSR dataset with observed tide gauge data, Supplementary Figure S2 shows scatter density plots of modeled and observed daily maximum sea levels for 13 China tide gauges. The majority of the daily maxima lie close to the perfect-fit line, indicating good model performance. However, at all 13 tide gauges, the slope of the least-squares line is lower than the perfect-fit line, indicating that the modeled sea levels are lower than observed sea levels. The RMSE, based on the modeled and observed daily maximum sea levels, is between 0.12 and 0.47 m with an average of 0.28 m (Std. is 0.12 m) (Supplementary Table S2). The Pearson correlation coefficients for modeled and observed daily maximum sea levels are between 0.55 and 0.85, the average correlation coefficient is 0.71 (Std. is 0.1). The correlation coefficients at the Kanmen, Zhapo and Xiamen stations are higher than 0.8 (p < 0.05). Compared to the average RMSE of 0.17 m based on 472 tide gauges globally (Muis et al. 2016), the average RMSE of 0.28 m over eastern China is larger. Similarly, the average correlation coefficient for modeled and observed daily maximum sea levels of China is 0.71, which is lower than the average correlation coefficient of 0.77 in tropical regions (Muis et al. 2016). The underestimation of ESLs and poorer performance are primarily due to those regions being prone to tropical cyclones. It is also inevitable due to the relatively coarse resolution of bathymetry and meteorological forcing (Muis et al. 2016). As outlined above, we apply a bias correction to improve the model results. After the bias correction, the average RMSE is 0.27 m (Std. is 0.1 m), indicating an improvement of the hindcast dataset (Supplementary Table S2). We also validate ESLs for various return periods between modeled and observed ESLs (Supplementary Figure S3).

After bias correction, we apply the same EVA methods as were applied to the observed dataset to the modeled and corrected GTSR dataset. As shown in Fig. 6a, ESLs in coastal China present high spatial heterogeneity and large uncertainty. High ESLs are mainly found in the eastern coastal China, such as Fujian, Zhejiang, Shanghai, Jiangsu and the southern coastal areas of Guangxi and Guangdong. The high ESLs along the southeastern coasts are mainly caused by typhoon-induced storm surge (Shi et al. 2015). Figure 6b shows the difference of the maximum and minimum values of 100-year return period ESLs for the different EVA methods. Large differences of up to 1.0 m exist along the coasts of the Yangtze River Delta, especially in the river mouth of the Yangtze River and the Qiantang River. In many places, the differences caused by using different EVA methods are larger than the projected SLR by the middle of the century (18 cm and 23 cm for RCP2.6 and 8.5) and in some cases even larger than the projected SLR for the end of the century (38 cm and 85 cm for RCP2.6 and 8.5).

Fig. 6
figure 6

a Difference of the maximum minus the minimum value of 100-year return period ESLs; b maximum extreme sea levels of 100-year return period ESLs along coastal China; c spatial distribution of potentially inundated areas from 100-year return period ESLs (based on maximum values) at the county level

Full size image

3.3 Effects of uncertainties in ESLs on inundation assessment

As discussed before, large uncertainties exist in estimated ESLs by applying various EVA methods, which also leads to uncertainties in the estimation of inundation. To assess the sensitivity of inundation under various EVA methods, inundation is calculated by using the EVA method leading to maximum and minimum ESLs. The results show the potential inundated areas under maximum 100-year return period ESLs along coastal China is about 58,549 km2 (~ 0.62% of the national land area), while inundated areas under minimum 100-year return period ESLs reduce to about 54,568 km2 (~ 0.58% of the national land area). This is a difference of 7.3% compared to the minimum, equivalent to about 0.04% of the national land areas. The inundated areas are mainly located in the Yangtze River Delta, north plain in Jiangsu Province, the Pearl River Delta and coastal areas along the Bohai Sea (Fig. 6c). The Yangtze River Delta (including Shanghai, northern Zhejiang and southern Jiangsu) and the northern plain of Jiangsu are the largest continuous inundated areas, because of the wide flat areas along the Yangtze River Delta coasts. Other potential inundated areas (but smaller depth) are mainly distributed along the coastal areas of Zhejiang and Fujian, Shandong peninsula, and Liaodong peninsula.

3.4 Effects of SLR on ESL estimates

The amplification of critical ESL frequencies is highly sensitive to local relative SLR and characteristics of the ESL frequency curves (Hunter 2012). SLR not only amplifies ESL probabilities but also changes the relation of critical thresholds (e.g. tied to flood levels) and the associated frequency (Buchanan et al. 2017). As shown in Fig. 7, under the RCP8.5 scenario, the 100-year return period ESL at the Haikou station is shortened to about 22-years to a 50-year return period by the end of this century. A similar pattern is also observed for Hong Kong, where the 100-year return period ESL is shortened to 23-years by 2050, and to 1-year by 2100 due to SLR. Human-induced subsidence will exacerbate this situation. If subsidence is considered, the 100-year return period ESL will shorten to nearly 1-year by 2050 already (Supplementary Table. S3). Apart from Hong Kong, subsidence has been widely observed in other coastal cities, such as Shanghai and Tianjin (Hu et al. 2004), but good estimates of the actual rates are missing and hence not included here. The reduction in return periods (or increase in frequency of exceedances) will decrease the efficiency of coastal protection, assuming that no adaptation takes place.

Fig. 7
figure 7

ESLs for the Hong Kong and Haikou tide gauge stations under SLR scenarios and subsidence scenario (for Hong Kong) (dashed grey line for display purpose, sampling method is annual maximum and distribution is GEV)

Full size image

Figure 8 shows AFs of 50-year and 200-year ESLs and the ratio between them for the two SLR scenarios. Under RCP8.5, a median sixfold increase (range: 2–98) in the annual number of 50-year ESL events is expected by 2050. These values increase significantly with a median 1614-fold increase (range: 16–292,680) by 2100.

Fig. 8
figure 8

AFs for 50-year (a, e) and 200-year (b, f) ESLs estimated by GPD-99.75% for 2050 (a, b) and 2100 (e, f) assuming SLR associated with RCP8.5; AF ratio between the 200-year to 50-year ESLs for 2050 (c) and 2100 (g)

Full size image

3.5 Sources of uncertainty

In this study, we focus on inter-model uncertainties in EVA methods for ESL estimation stemming from sampling of extreme events and probability distributions. The results show substantial uncertainties exist in the ESL estimation and results from assessing inundation can vary when different ESL input is used. However, there are still other sources of uncertainty involved which could be further analyzed in future works.

First, the parameters involved in EVA analysis have their own range of uncertainty, usually expressed as confidence levels; these intra-model uncertainties may be even larger than the inter-model uncertainties considered here. Regional frequency analysis (Weiss and Bernardara 2013) and Monte Carlo or Bayesian modelling (Coles and Tawn 2005) approaches make better use of the available information and can lead to a reduction of the uncertainties in the ESL estimation.

Second, in this study we assume ESLs to be stationary. For coastal China, mean sea level rise was 3.4 mm/yr between 1980 and 2019 (SOA 2020). SLR is removed through the detrending procedure based on the annual mean. This has been shown to be inappropriate in areas where the changes in ESLs are not caused by changes in mean sea level alone, but also due to other factors such as changes in the tides (Mudersbach et al. 2013) or due to changes in storm tracks (Lai et al., 2020). It has been observed that the frequency of tropical cyclones has increased over southeastern China (Yeh et al. 2010). The northwestward-moving track, which indicates likely landfall on the southeastern coasts of China, has become the most dominant track mode after the late 1990s (He et al. 2015). Trends of ESLs range from 2.0 to 14.1 mm/yr between 1954 and 2012 (Feng and Tsimplis 2014) with large differences across tide gauges. This suggests that in some places, in addition to changes in mean sea level, storm surge climate has also changed. Hence, although here we use the annual mean to detrend the timeseries, future research could explore the effect of different detrending methods, for example based on mean high water (Arns 2013), on the estimation of ESLs.

In addition to differences in the ESL estimation by using different EVA methods, uncertainties in inundation assessment could also result from the applied GIS method and quality of the elevation and water level datasets. The bath-tub approach employed here may overestimate the flooded areas. Dynamic models usually exhibit a higher accuracy but at much higher computational cost, which is not feasible at the large spatial scale considered in this study (Vousdoukas et al. 2016a, b). Thus, the bath-tub approach is still widely used for large-scale coastal flood mapping (Muis et al. 2016; Kulp and Strauss 2019). There is likely also an overestimation of potentially inundated areas due to ignoring existing flood protection. On the other hand, some coastal mega-cities are suffering serious land subsidence due to over-exploitation of underground fluids (e.g. Tianjin and Shanghai), causing underestimation of flood extent. Furthermore, the GTSR dataset underestimates ESLs in areas prone to tropical cyclones. Only limited number of tide gauge sites and limited length of observational time-series are available. Thus, there is an urgent need for longer open-accessible observational datasets to better understand ESLs along coastal China. Other threats, such as waves, precipitation (Wahl et al. 2015) and riverine floods (Ikeuchi et al. 2017) may compound in coastal cities, especially for those located in delta areas (e.g. Shanghai), which will lead to more serious flood impacts.

4 Conclusions

In conclusion, based on observations from 13 tide gauges we showed that the use of various EVA methods considering different sampling methods and probability distributions leads to large uncertainties in the ESL estimation. Uncertainties and spatial variations of ESLs were further explored using the GTSR dataset derived from hydrodynamic modeling. High ESLs are found mainly along the eastern coastal China due to typhoon-induced storm surge. Large differences of ESLs derived from different EVA methods exist along the coasts of the Yangtze River Delta, especially in the river mouth. Areas exposed to coastal flooding in China are also assessed by a GIS-approach (ignoring coastal protection measures). Results show that potentially inundated areas when using minimum or maximum 100-year return period ESLs are 54,568 km2 and 58,549 km2, respectively. This is a difference of 7.3% compared to the minimum, equivalent to about 0.04% of the national land area, and shows that the uncertainties of ESL propagate to the inundation assessment. The largest potentially inundated areas are located in the Yangtze River Delta (including Shanghai, northern of Zhejiang and southern of Jiangsu) and the north plain of Jiangsu. Those coastlines with wide flat areas (e.g. Jiangsu Province) are more prone to flooding associated with ESL events.

SLR leads to an amplification of the probabilities (or frequencies) with which given critical water level thresholds are exceeded; AF values are highly sensitive to the SLR scenario considered and the shape of the probability distribution. SLR and subsidence will significantly shorten the return periods of given ESLs, which will decrease the efficiency of coastal protection, assuming that no adaptation takes place. Hotspots identified here need more attention considering future SLR, compound flood events, and human-induced factors.

This study highlights the necessity to carefully assess present-day ESLs with appropriate EVA methods. If more observations would be available, a more detailed and robust analysis could be carried out. Given the existing data constraints our analysis provides important insights into the existing uncertainties and a baseline for future assessments to set the protection standards and give a better understanding of ESLs for coastal engineers and relevant stakeholders.