Iterative algorithms for non-conditional and conditional simulation of Gaussian random vectors

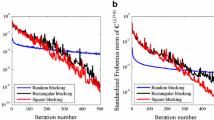
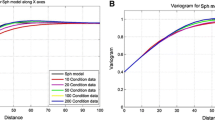
Abstract

The conditional simulation of Gaussian random vectors is widely used in geostatistical applications to quantify uncertainty in regionalized phenomena that have been observed at finitely many sampling locations. Two iterative algorithms are presented to deal with such a simulation. The first one is a variation of the propagative version of the Gibbs sampler aimed at simulating the random vector without any conditioning data. The novelty of the presented algorithm stems from the introduction of a relaxation parameter that, if adequately chosen, allows quickening the rates of convergence and mixing of the sampler. The second algorithm is meant to convert the non-conditional simulation into a conditional one, based on the successive over-relaxation method. Again, a relaxation parameter allows quickening the convergence in distribution to the desired conditional random vector. Both algorithms are applicable in a very general setting and avoid the pivoting, inversion, square rooting or decomposition of the variance-covariance matrix of the vector to be simulated, thus reduce the computation costs and memory requirements with respect to other discrete geostatistical simulation approaches.

Appendix 1

Let X⁽⁰⁾ = 0 and, for any positive integer k, X^(k) be the random vector defined as per Eqs. (1) and (3). The sequence {X^(k): k = 0, 1, 2, …} so obtained constitutes a Markov chain. It is easy to check that this chain is homogeneous (for k ≥ 1, the distribution of X^(k) knowing X^(k−1) does not depend on k), irreducible (because 1–ρ² ≠ 0, any nonempty open set of ${\mathbb{R}}^n$ can be reached by the chain after finitely many iterations) and aperiodic.

Accordingly, to prove that the chain converges in probability to X, it remains to show that the distribution of X is invariant under the transition kernel of the chain (Lantuéjoul 2002). Suppose that X^(k−1) is a Gaussian random vector with zero mean and variance-covariance matrix B. In such a case, the simple kriging error $- {\mathbf{C}}_{JJ}^{ - 1} \,{\mathbf{C}}_{JI} \,{\mathbf{X}}_{I}^{(k - 1)} - {\mathbf{X}}_{J}^{(k - 1)}$ and S_J U^(k) are two independent Gaussian random vectors with zero mean and variance-covariance matrix ${\varvec{\Upsigma }}_{J}$ and are independent of ${\mathbf{X}}_{I}^{(k - 1)}$. R^(k), as defined by Eq. (3), is therefore a Gaussian random vector independent of ${\mathbf{X}}_{I}^{(k - 1)}$, with zero mean and variance-covariance matrix ${\varvec{\Upsigma }}_{J}$, irrespective of the choice of ρ. The proof by Arroyo et al. (2012) can be adapted to establish that, under these conditions, X^(k) is a Gaussian random vector with zero mean and variance-covariance matrix B, Q.E.D.