Introduction

Climate change is causing rapid changes in health and function of forest ecosystems (e.g., Ciais et al. 2005; Allen et al. 2010; Gharun et al. 2020). Especially extreme droughts cause forest decline due to increased tree mortality (e.g., Allen et al. 2010, 2015; Lorenz and Becher 2012; Hartmann et al. 2018; Schuldt et al. 2020). As a consequence, ecosystem services provided by forests, like carbon storage, water and climate regulation, and the amount of produced timber are decreasing (Kannenberg et al. 2019). Understanding the underlying mechanisms that alter single-tree vitality under drought conditions is crucial to protect forests and maintain those ecosystem services (e.g., Bréda and Badeau 2008; McDowell et al. 2008; Adams et al. 2009; McDowell and Sevanto 2010). Consequently, hydraulic functioning, which describes the ability of tree organs to transport water, has recently been studied as a reaction of trees to drought. Losses in hydraulic conductance, possibly leading to hydraulic failure, can result in leaf shrinking, defoliation, and partial branch dieback (e.g., Walthert et al. 2021; Arend et al. 2022). A typical additional cause by continued drought stress is the production of short instead of long shoots in tree crowns (Roloff 1988). The combination of crown dieback and shorter shoots can in turn lead to carbon starvation of a tree (Plaut et al. 2012). Ultimately, it can lead to tree death (Brodribb and Cochard 2009; Choat et al. 2012; Nardini et al. 2013). Thus, it is a common strategy to visually examine the external shape of a tree to draw conclusions about alterations in its vitality. A well-known visual approach is to estimate the percentage of a tree’s crown defoliation (Dobbertin et al. 2009; BMEL 2020, 2023). Although widely used in forestry practice in Europe (Bussotti and Pollastrini 2017), this visual approach is highly subjective and of questionable reproducibility (Dobbertin and Brang 2001). To our knowledge, an objective, non-destructive, and efficient approach to estimate single-tree vitality in situ is still lacking.

Today, three-dimensional (3D) laser scanning is a widely accepted, efficient, and powerful tool for measuring tree shape (e.g., Seidel et al. 2011a; Bayer et al. 2013; Metz et al. 2013; Saarinen et al. 2017, 2020), its structural complexity (Seidel et al. 2015), or detailed branching structures (Hackenberg et al. 2015). 3D scanning therefore also might bear the potential to be used in the context of an assessment of tree vitality, as far as this is expressed in the morphology of the tree. This morphology of a scanned tree is available in the form of a 3D point cloud, in which each point represents a location where a laser beam has hit an element of the tree (Seidel et al. 2011b). Laser scanning as a tool to derive tree vitality has already been introduced by Jacobs et al. (2021), who used crown transparency and roughness to assess drought-affected tree vitality. They found that drought stress led to smaller crowns and increased crown transparency. In addition, a first attempt was recently made to derive tree vitality from the structural complexity of single trees and a relationship with the percentage of crown defoliation was discovered (Heidenreich and Seidel 2022). However, this approach relies on structural data acquired both in the leaf-on and leaf-off seasons and on comparing the two conditions, which is laborious and not possible for evergreen species. Despite these drawbacks, it has been illustrated that laser-scanning data bears potential to be used in the vitality characterization of trees. However, we assume that the full potential has not yet been exploited. In particular, the use of Quantitative Structure Models (QSMs) could be beneficial. Those models are created from tree point clouds and represent the branching pattern of a tree based on cylindrical objects of varying sizes and orientations, fitted to the location of the points (Hackenberg et al. 2014). Yet, it was shown that this reconstruction of branching structures is subject to inaccuracies, as the quality of the QSM is dependent on the point cloud quality, which in turn can deteriorate with increasing tree distance from the scanner, especially for thin branches (Morhart et al. 2024). However, to our knowledge QSMs are the only way to objectively represent the branching pattern of trees in an efficient way and could reveal the influence of environmental factors on the branching pattern of trees.

In this context, we set out to test a new approach and its potential contribution to objectively assess the vitality of trees based on 3D-laser scans. Trees under drought stress suffer from crown dieback (Anderegg et al. 2012a; Schuldt et al. 2020; Walthert et al. 2021). Crown dieback occurs specifically in the top crown (Roloff 1988; Arend et al. 2021) and includes the shedding of particularly fine branches (e.g., Roloff 1988; Rust and Roloff 2002, 2004; Bréda et al. 2006). Additional reduced twig growth (e.g., Power 1994) due to the formation of short instead of long shoots in the tree top (Roloff 1988) is present. Hence, we think it seems promising to delve deeper into the quantification of fine branch lengths.

In our study, we focused on Fagus sylvatica L., the European beech, as it is the most common and most important broadleaved tree species in Central Europe (e.g., Pretzsch et al. 2020). Although beech is able to cope with a wide range of site conditions, it is moderately drought sensitive (e.g., Gessler et al. 2007; Meier and Leuschner 2008; Leuschner 2020) and was significantly affected during the recent period of intense droughts in Europe (Pflug et al. 2018; Walthert et al. 2021). Hence, we believe that shedding and reduced growth of fine branches can be detected in beech trees of decreased vitality. We decided to compare beech trees from stands with different levels of drought damage, thereby equating the degree of drought damage with a vitality class. Less vital trees are expected to have shorter fine branches and fewer fine branches in the upper crown due to shedding and reduced growth, mainly occurring in the top crown. As a result, the overall vertical profile of fine branch lengths should be less top-heavy. Shedding and reduced growth of fine branches should also lead to an increased proportion of main branches, as they persist until a critical state of tree health is reached (Roloff 1988). Hence, the ratio of fine branches to lower orders branches might also be an interesting indicator for the vitality of trees.

We tested the following hypotheses:

  1. (1)

    The total length of fine branches per meter of crown length is lower for less vital beech trees, especially in the upper crown.

  2. (2)

    The total relative length of fine branches of less vital beech trees is larger in the lower crown and lower in the upper crown compared to vital beech trees.

  3. (3)

    The 50% quantile of the absolute length of fine branches is located at lower heights for less vital beech trees.

  4. (4)

    The ratio of fine branches to larger, low-order branches is lower for less vital beech trees, especially within the upper crown.

Material and methods

Study site and study objectives

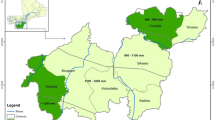
The study sites were located in Germany and are distributed over the three federal states of Hesse, Lower Saxony, and Thuringia. In each state, eight study sites of 0.25 ha with varying degrees of drought damage were selected, resulting in a total of 24 study sites. A qualified person visually estimated the vitality of the study sites based on the average crown defoliation percentage of the individual trees, which is a common procedure in Germany (e.g., BMEL 2020). Based on this assessment, each study sites’ vitality was assigned in one of four categories: healthy, slightly damaged, moderately damaged, and severely damaged. Each category was replicated twice in each federal state. On each study site, five trees were randomly selected (and one additional reserve tree) to provide a dataset containing 121 European beech trees. To capture more variability (age and mean height of the dominant trees) within the groups and to increase the sample size per class, we combined beech trees from the categories healthy and slightly damaged in vitality class one. Beech trees from the categories moderately damaged and severely damaged were classified in vitality class two. A rough characterization of the plots including their center coordinates is presented (see Table 1).

Table 1 Characterization of the study sites; modified from Höwler et al. (2024)
Full size table

Data acquisition and preparation

All study sites were scanned in winter 2022/2023 during November and January, using a mobile laser scanner (ZEB Horizon, GeoSLAM Ltd., Nottingham, United Kingdom). Each scan started at a corner point of the respective plot, followed by a walk around the other corners. The plot was then walked in parallel lanes with a maximum distance of approximately 10 m between them. In the end, the stand was crossed diagonally to come back to the starting point. The presented scanning trajectory shows an exemplary walking path (Fig. 1).

Fig. 1
figure 1

Exemplary MLS trajectory of a plot

Full size image

The resulting 3D point clouds were then automatically processed and exported (LAZ files) using GeoSLAM Hub 6.2.1 (GeoSLAM Ltd., Nottingham, United Kingdom). The point clouds were subsampled with a minimum spacing setting of 1 cm, noise filtered with a sphere radius of 10 cm and a maximum relative error setting of 1.00 using the basic methods provided by Cloud Compare (version 2.11.3, www.danielgm.net). In the following, they got cut to a size of 65 m × 65 m. This included a 7.5 buffer on each side of the 0.25 ha (50 × 50 m) plot to ensure that the crowns of the beech trees at the edges were fully covered. Subsequently, LiDAR360 (Greenvalley Inter., CA, USA; version 6.0) was used for single-tree segmentation. For all methods in LiDAR360, the standard settings were used. First, the method ‘Remove Outliers’ was applied to remove remaining noise in the plot’s point cloud. Then, ‘Classify Ground Points’ to detect ground points and ‘Normalize by Ground Points’ using that ground point information were performed with the aim to remove non-tree points and topographic effects. To finally classify the individual trees in the point cloud, the method ‘Point Cloud Segmentation’ was applied, followed by ‘Extract by Tree ID’ to export the resulting point clouds. In Cloud Compare, they were visually checked for segmentation inaccuracies as visual assessment is still the benchmark (Todd et al. 2004). Tree parts that were falsely assigned were manually corrected. Subsequently, the individual tree point clouds were once more noise filtered with a sphere radius of 2 cm and the maximum relative error set to 1.00. In addition, remaining isolated points were removed. A subsequent conversion into QSMs using the software CompuTree (Vers. 5.0, CompuTree Group; http://computree.onf.fr) with the SimpleTree Plugin (Hackenberg et al. 2015) using the methods ‘SphereFollowing’ (Table 2) and ‘QSM Allometric Correction’ (Table 3) was performed. Different settings were tested and those with the best visual results were chosen and used for all trees.

Table 2 Configuration settings for the method ‘SphereFollowing’ in CompuTree
Full size table
Table 3 Configuration settings for the method ‘QSM Allometric Correction’ in CompuTree
Full size table

Two exemplary beech trees, one healthy and one severely damaged, are presented as point clouds and QSMs (see Fig. 2) to illustrate the quality of the QSMs and visual differences between vitalities.

Fig. 2
figure 2

Exemplary illustration of a healthy (class one) tree’s point cloud (left), its QSM (middle-left) and a severely damaged (class two) tree’s point cloud (middle-right) and its QSM (right)

Full size image

Branch length processing

We used the QSMs to evaluate the vertical branching pattern of the 121 beech trees. For this purpose, we restricted each QSM to the actual tree crown. This was done by determining the z-coordinate of the bottom of the lowermost cylinder with a branch order greater than zero, which is the lowermost branch segment of the QSM. All other cylinders that were fully located below that coordinate were not considered as they were regarded as stem. For each of the resulting individual crown QSMs, we calculated the branch lengths of all branches, divided by their order, within vertical layers of 1 cm thickness (= height steps). We have chosen to look at the lengths rather than the volume of the branches, as the length is less sensitive to noise in the point cloud, based on our visual assessment of the QSMs and earlier studies (e.g., Demol et al. 2022) and it is directly related to the longitudinal growth of shoots. For calculating the branch lengths per height step, we used the approach published in Heidenreich and Seidel (2022). In this study, we used height steps of one centimeter and subsequently converted them into relative values to ensure a very precise assignment of each’s branch cylinder segment to its vertical position in the tree crown. The calculation of a cylinder’s branch length is done as follows: The lowest height step in centimeter (= lower boundary), in which the cylinder lies, got calculated by rounding off the cylinder’s lower z-coordinate to centimeter, while the highest height step (= upper boundary) got determined by rounding up the higher z-coordinate. Then, the vertical distance of the cylinder’s end coordinates to the respective boundaries got calculated and subtracted from one to obtain the length in z-direction in the boundary classes. In addition, the cylinder’s start and end coordinates were used to form a directional vector to determine the angle to an infinite horizontal plane. Using the angle and the lengths in z-direction—as adjacent legs of right-angled triangles—between the lower boundary and the lower coordinate as well as between the upper boundary and the upper coordinate, the lengths of the cylinder parts—calculated as the hypothenuses of the triangles—got calculated. All cylinder segment lengths between the ones located next to the boundaries were determined using the same angle but the vertical length of 1 cm, as those cylinder parts always covered the whole height step length. An illustration of the exemplary procedure of the method based on a cylinder can also be found in Heidenreich and Seidel (2022). For each tree, this procedure got repeated for each cylinder. The sum of all tree’s cylinder segment lengths which fall into a centimeter step got computed, divided according to orders.

At this point, the step numbers differed between the individual beech crown QSMs since they did not have the same initial crown length. Therefore, in the next step, the vertical height steps of 1 cm were converted into relative heights in relation to total crown length in order to equalize the number of height increments. The length of each cylinder segment was assigned to a 1-percent height step based on its relative position in the crown. As a result, we obtained the sum of branch lengths in each relative step of one percent for each branch order of each beech tree. First- and second-order branches were considered as base order branches while all orders higher than two as fine branches. The second order was defined as a base order to ensure we only use fine branches in our analysis. We aimed to compare vertical characteristics of fine branch length distribution between the vitality classes.

Branch lengths pattern analysis

Our specific objective was to use the obtained data of each tree to determine characteristics of fine branch distribution in each height step and to perform a class-wise comparison to test our hypotheses. To do so, in a first step, we divided the total fine branch lengths (sum lengthfine) by the crown length for each tree and tested if there was a significant difference between the two vitality classes. The smoothed mean progression of the fine branch length (lengthfine) with 95% confidence intervals was in addition plotted for each crown layer to analyze the distribution and potential differences between the two vitality classes.

Second, we plotted the smoothed progression of the relative fine branch length (rel. lengthfine) for each crown layer, calculated by the layer’s lengthfine divided by sum lengthfine of the tree, to investigate the extent to which the distribution patterns varied between vitality classes. Here, the aim was to identify different crown areas showing specific drought stress related characteristics. Since we expected a lower proportion of fine branches in the top crown for less vital beech trees and consequently a larger proportion of fine branches in the lower crown compared to more vital ones, we tested for significant differences in the mean of the summed rel. lengthfine in these crown parts between the two vitality classes.

In a third step, the 50% quantile of lengthfine was determined for each tree and tested for significant differences in the mean between both vitality classes. The underlying premise was that beech trees with a lower proportion of fine branches in the upper part of the crown (due to fine branch shedding and reduced longitudinal growth in the top crown) should have the 50% quantile of lengthfine located at lower heights than vital beech trees.

Finally, we plotted the class-wise length ratio between fine and base order branch lengths (length ratiofine/base) in ten-percent height steps to see if length ratiofine/base was showing dependencies on crown height position and different patterns for the two vitality classes. The 10-percent height steps were used to prevent an occasionally occurring division by zero (empty crown layer). Nevertheless, this case occurred sporadically, reducing the data set of vital beech trees to 57 and that of the less vital beech trees to 55.

All used branching pattern-related metrics are also presented in Table 4 for a comprehensive overview.

Table 4 Description and spatial level of computation for the used fine branch length characteristics
Full size table

Statistics

All statistical analyses were carried out using R software (R Core Team 2021). We tested the calculated class-wise means for normal distribution and variance homogeneity. In the case of a violation of the normal distribution, we performed the two-tailed Mann-Whitney-U-Test (Mann and Whitney 1947) to check for significant differences between both vitality classes. In case of a violation of variance homogeneity, two-tailed Welch’s t-test (Welch 1938) was used to test for significant differences. In order to plot the height step progression lengthfine, rel. lengthfine, and length ratiofine/base, we used a loess-fit (Cleveland and Grosse 1991) to smooth the data points since there was no linear relationship between the relative crown height and the respective values.

Results

Tree characteristics

The main characteristics of the trees of the two vitality classes are shown (Table 5). The classes mean differences (class one minus class two) showed that the beech trees, including their crowns, were similarly sized: The difference in tree height was 2.43 m, in DBH 2.35 cm, in crown length − 1.78 m, and in crown radius 0.27 m.

Table 5 Mean height (m), mean DBH (cm), mean crown length (m), and the mean crown radius (m) with standard deviation (SD) for both vitality classes; 61 beech trees in the first vitality class (healthy to only slightly damaged), 60 beech trees in the second vitality class (moderately to severely damaged)
Full size table

Absolute fine branch Llengths

The subsequent boxplots (Fig. 3) show the tree-wise distribution of sum lengthfine divided by the crown length. The mean was 48.42 m ± 29.71 m for the first class and 35.25 m ± 21.44 m for the second class. We found significant differences between the groups (p-value < 0.01) with a higher mean for the first class, which was 13.17 m longer than the second class.

Fig. 3
figure 3

Distribution of sum lengthfine per meter crown length for the first vitality class (grey; 61 beech trees; healthy to slightly damaged) and the second vitality class (dark grey; 60 beech trees; moderately to severely damaged); significance levels are denoted as follows: *p < 0.05, **p < 0.01, ***p < 0.001

Full size image

Vertical distribution of fine branch lengths

The loess-fit of the mean progression of lengthfine over relative crown height is presented (Fig. 4). After an initial steady increase in lengthfine with each percent increase in relative height, lengthfine increased stronger for class one and exceeded the increase observed in class two, as the trend remained rather constant for the latter. Both curves reached their maximum at around three-quarters (73%) of the crown’s total heights. Here, the observed difference between class one (18.12 m) and class two (11.84 m) was largest, with a value of 6.29 m. After the maxima, lengthfine of both classes as well as the difference between them decreased with progressing relative crown height.

Fig. 4
figure 4

lengthfine for each 1-percent height step of the tree crowns’ vertical extension with confidence intervals (95% confidence interval); grey line for the first vitality class (61 beech trees; healthy to slightly damaged), dark grey line for the second vitality class (60 beech trees; moderately to severely damaged)

Full size image

The loess-fit of the progression of rel. lengthfine over the relative crown height is plotted for both vitality classes (Fig. 5). Starting from zero percent, rel. lengthfine of both vitality classes increased constantly up to a relative crown height of 74%, where both curve maxima were located with a rel. lengthfine of 1.98% for the first vitality class and of 1.68% for the second vitality class. Above the maximum, rel. lengthfine decreased with progressing relative height for both vitality classes. Below the curve intersection at a relative crown height of 57%, each value of rel. lengthfine was larger for vitality class two. Above the curve intersection, each value of rel. lengthfine of vitality class one was larger.

Fig. 5
figure 5

rel. lengthfine for each crown 1-percent height step with confidence intervals (95% confidence interval); grey line for the first vitality class (61 beech trees; healthy to slightly damaged), dark grey line for the second vitality class (60 beech trees; moderately to severely damaged), dotted line for the curve intersection

Full size image

The following boxplots (Fig. 6) show the class-wise distribution of the sum of rel. lengthfine in the areas below and above the curve intersection. Below 58% relative crown height, we found a significantly higher mean of the total rel. lengthfine of 31.02 ± 17.78% for the first vitality class (p < 0.01) and compared to 41.84% ± 24.26% for the second vitality class. Above 57% relative crown height, we found a significantly higher mean of the total rel. lengthfine of 68.98 ± 17.78% for the first vitality class (p < 0.01) and compared to a mean of 58.16 ± 24.26% for the second vitality class.

Fig. 6
figure 6

Distribution of the sum of rel. lengthfine between the first vitality class (grey; 61 beech trees; healthy to slightly damaged) and the second vitality class (dark grey; 60 beech trees; moderately to severely damaged)—for the areas below the 58% (a) and above 57% (b) of the relative crown height; significance levels are denoted as follows: *p < 0.05, **p < 0.01, ***p < 0.001

Full size image

The relative height at which the 50% quantile of lengthfine was located separately for the two vitality classes is visualized using boxplots (Fig. 7). On average, the 50% quantile was located significantly higher (p < 0.05) for vitality class one at 67.54% ± 10.27% of the crown’s relative height while it was located at 62.08% ± 13.52% for vitality class two.

Fig. 7
figure 7

Distribution of the relative crown height where the 50% quantile of lengthfine lies for the first vitality class (grey; 61 beech trees; healthy to slightly damaged) and the second vitality class (dark grey; 60 beech trees; moderately to severely damaged); significance levels are denoted as follows: *p < 0.05, **p < 0.01, ***p < 0.001

Full size image

Ratio of fine branch to base order branch length

The loess-fit progression of length ratiofine/base over the relative crown height in 10 percent steps is shown in a class-wise view (Fig. 8). The value of length ratiofine/base for the vitality class one constantly increased with progressing relative crown height and had its maximum at the crown top (100%) with 1.52 units. For vitality class two it hit the maximum with 1.16 units at a relative crown height of 70% and decreased with progressing relative crown height.

Fig. 8
figure 8

length ratiofine/base for each ten-percent height step of the beech tree crowns with confidence intervals (95% confidence interval); grey line for the first vitality class (57 beech trees; healthy to slightly damaged), dark grey line for the second vitality class (55 beech trees; moderately to severely damaged); significance levels are denoted as follows: *p < 0.05, **p < 0.01, ***p < 0.001

Full size image

Discussion

Consequences of drought stress in trees can be substantial crown dieback including branch shedding (Arend et al. 2022; Neycken et al. 2022) and a reduced growth of newly formed shoots (Roloff 1988; Power 1994) leading to higher probability of tree death (Leuschner 2020; Schuldt et al. 2020). Following this, we investigated the relationship between the vitality conditions of European beech trees based on drought-damage assessment and fine branch length characteristics using laser scanning derived crown QSMs. Accordingly, we aim to discuss the potential contribution of fine branch length patterns derived from those QSMs to the vitality assessment of individual trees and forest stands.

Fine branching patterns under drought conditions

At class level, we found less vital beech trees to have significantly lower values of sum lengthfine related to their crown length (Fig. 3). This difference was mainly based on the values of lengthfine in the upper part of the crown (Fig. 4). The lower fine branch lengths of less vital beech trees could be partly explained by drought-induced hydraulic dysfunction in the crowns leading to crown dieback (Brodribb and Cochard 2009; Choat et al. 2012; Adams et al. 2017; Walthert et al. 2021) including branch shedding (Roloff 1988; Arend et al. 2022). Complementary to this, Jacobs et al. (2021) found an increased crown transparency for beech trees under drought outside the vegetation period with branch shedding as the only possible cause. Haase and Hellwig (2022) selected shoot death as a drought-damage characteristic influencing tree health and crown dieback was estimated based on the occurrence of dead branches in the crown (Walthert et al. 2021) including shed ones (Frei et al. 2022). Our data indicates the shedding of fine branches, which is in line with the fundamental work of Roloff (1988) on drought damage in beech trees. Further, it is supported by other studies with similar results for other tree species, for example, Eucalyptus piperita Sm. (Li et al. 2018) and Quercus robur L. (Rust and Roloff 2004). A physiological explanation is the reduction of hydraulic conductivity (Rust and Roloff 2002). An additional explanation for the reduced total length of fine branches in less vital beech trees is lower shoot growth (Power 1994; Roloff 1988). Vital trees are expected to have long and densely arranged shoots (Rust and Roloff 2002). Consequently, we assume that the significantly lower total length of the fine branch network is related to the decreased vitality of the beech trees in the second vitality class.

Nevertheless, trees develop differently shaped and sized crowns under different growing conditions (phenotypic plasticity). Hence, relating absolute fine branch length characteristics to the vitality of significantly differently shaped trees does not seem to be good for comparing trees of different shapes. Therefore, we decided to consider the distributions of fine branch lengths along the vertical crown profile to test the validity of this size-independent approach for possible future research. We found a significantly higher proportion of lengthfine in the lower crown for less vital beech trees in contrast to vital ones and the other way around in the upper crown, visible in the values of rel. lengthfine in these crown areas (Figs. 5,  6). This was also visible in the 50% quantile being located at a significantly lower relative height for less vital trees (Fig. 7). The increased rel. lengthfine in the lower crown of less vital beech trees can be explained by the shedding of fine branches mainly in the top crown (Roloff 1988; Arend et al. 2022). This is consistent with the physiologic explanation given by Kutsch et al. (2009) who found that adult beech trees have smaller sun leaves at the top crown. Those are the first to die during the process of crown dieback, as they may serve to protect sun leaves located lower in the crown. It is likely that the related fine branches should be the first to die off and to be shed while the lower branches remain. Afterward, the next layer of sun leaves is exposed to light, which in turn may also die and expose the next leaf layer, possibly repeating the process over and over again. In addition, the formation of short instead of long shoots in the tree top and the development of long shoots in the lower crown due to a thinned crown tip (Roloff 1988) influences the relative distribution of fine branches. Less longitudinal shoot growth in the top crown but increased growth in the lower crown combined with fine branch shedding at the top crown are characteristic for less vital beech trees and can explain the observed lower values of rel. lengthfine in the upper crown.

Because main branches remain in the crown of a tree until severe damage leads to dieback of full crown areas (Roloff 1988), we additionally assumed that fine branch shedding and reduced fine branch growth altered the ratio between the length of fine and base order branches. The class-wise comparison showed a lower length ratiofine/base for less vital beech trees, especially in the top crown (Fig. 8). The progression started to decrease above a relative crown height of 70% only for less vital beech trees. This observation is consistent with the literature since it has been stated that especially fine branches are shed in the process of crown dieback for different broadleaved tree species (Rust and Roloff 2002, 2004; Bréda et al. 2006), particularly in the top crown (Roloff 1988; Arend et al. 2021). The formation of short instead of long shoots at the treetop as a result of drought-induced beech decline (Roloff 1988) and the resulting short internodes of the shoots (Roloff 1993) also go well with the finding of a reduced length ratiofine/base in the upper crown for less vital trees.

Limitations of the examination of fine branching patterns

Our results showed that there was a relationship between the vitality characteristics of beech trees and the total length of their fine branches. These results can be very well explained on a physiological level, but it is important to highlight the uncertainties of our approach and the implications for reliability and application. Therefore, in the following, the relevance and limitations of our results are discussed in terms of their reliability for assessing the vitality of individual trees or a forest stand.

The modeled branching structure of QSMs can deviate from the actual tree branching architecture. This deviation is primarily caused by a reduced detection of tree points with increasing scanning distance which occurs especially for thin branches below a diameter of 3 cm (Morhart et al. 2024), as well as by the occlusion of tree parts during the scanning procedure (Wang et al. 2019), both leading to an incomplete point cloud or a point cloud that is partially too sparse for modeling. In addition, we used a mobile laser scanner, which on the one hand can be used to record point clouds very quickly and easily, but on the other hand usually has a poorer resolution than a stationary terrestrial scanner (Liang et al. 2014). However, compared to a terrestrial laser scanner, a mobile laser scanner has the advantage that it is easier to capture the tree closely from any direction which reduces the occlusion of tree parts. Still, we observed a reduced point cloud density as the result of the scanning distance and occlusion effects in particular in the upper crowns. Consequently, the underestimation of fine branch lengths is expected to be maximized here, surely introducing a deviation of our QSMs from the actual tree architecture, which was also noticeable when looking at the QSMs and the point clouds (Fig. 2). This may have led to the differences between the vitality classes not appearing as large as they really were, as the differences in the fine branching patterns between the vitality classes are expected to be largest in the upper crown, where drought-induced dieback and reduced growth of fine branches mainly take place (Roloff 1988; Arend et al. 2021). Despite these uncertainties associated with our approach, the fact that we found considerable fine branching pattern differences between the vitalities especially in the upper crown (Figs. 4 and 8) highlights its underlying potential. Because we used the same scanner and trajectory for each scan and the studied beech trees were similarly dimensioned, we assume that the error, which causes an underrepresentation of the branch lengths, is systematic making it still possible to detect clear differences between vitalities (cf. Neudam et al. 2022).

Although the mean values and curve shapes of the fine branch patterns differed significantly between vitality classes, the differences were not very large and the variance between individual trees was quite high. Some vital beech trees had a lower sum lengthfine relative to their crown length compared to some of the less vital beech trees (Fig. 3). Also, beech trees in the less vital class had a greater proportion of their fine branch lengths in the upper crown than some of the beech trees in the vital class, visible in the distribution of the 50% quantile of lengthfine (Fig. 7). Besides possible branch-reconstruction issues due to the point cloud quality, this could be due to the fact that not all trees are necessarily representative of their vitality class because the assessment was done on plot level. Together with the relatively small sample size, it gets clear that we cannot solely draw conclusions on the vitality at the individual tree level from the analyzed fine branch length characteristics. However, the approach is suitable for comparing the vitality condition of beech stands if the dimension of the beech trees are similar and the scanning conditions regarding the scanner and the trajectory are the same. Due to its limitations, we would therefore like to clarify that our results rather emphasize the potential of analyzing fine branching patterns to study drought damage for further research. For more reliability, it would be more appropriate to combine fine branch lengths characteristics taken from QSMs with other tree vitality measures like the crown transparency of Jacobs et al. (2021). As increased crown transparency is also indicative of branch loss, one should be able to rely more on the results if there are signs of increased crown transparency that fit to observed fine branch losses detected by our approach. The assessment of foliage characteristics should also be included in the vitality determinations, as this is the only way to obtain a holistic picture of drought damage (Haase and Hellwig 2022). Therefore, combining fine branch pattern characteristics with the crown defoliation percentage could also be beneficial, as one would look at the shrinkage and dieback of foliage at the one hand and on the other hand at dieback and reduced growth of fine branches. In doing so, multiple signs of drought stress would be covered (e.g., Coder and Daniel 1999).

In addition, our study was limited to similarly-sized beech trees. This had the advantage that we were able to exclude a size effect of the trees on the fine branching pattern to a certain extent, but made it unable to draw conclusions on differences between vitalities of widely differently-sized beech trees. We argue that the use of relative distributions of fine branch length along the vertical axis, the ratio between fine and base order branch length, and especially the 50% quantile of lengthfine might be suitable indicators when comparing differently-sized trees, as they are characteristics that are independent of crown size and also account for the drought-induced effects of fine branch shedding and reduced longitudinal growth in the top crown. To test this, further research in stands with differently-dimensioned trees is necessary.

In future research regarding drought related fine branch pattern assessment, it is also important to consider that crown dieback due to drought is not necessarily an immediate reaction (Arend et al. 2022). The assessment of a tree’s crown vitality, for example in national forest monitoring data, has often shown a delayed reaction to drought (Bréda et al. 2006; Seidling 2007). Tree ring studies have shown drought legacies, which may be related to crown development at later times (Anderegg et al. 2015). Observations in Germany have shown that early defoliation in the second half of September 2018 resulted in delayed crown dieback in 2019 (Walthert et al. 2021). Also, reduced twig growth as an effect of drought is delayed as it is more likely controlled by drought during bud formation rather than in the year of shoot growth (Coder and Daniel 1999). Roloff (1988) even stated that temporary droughts do not significantly affect crown structure and that a severe loss of vitality under drought is more likely to occur when drought has persisted for at least 5 years. Accordingly, we argue that the detection of drought stress by analyzing fine branch length characteristics in tree QSMs is limited when scans are conducted immediately after drought or in cases of mild droughts. Anyway, drought-damage characteristics had shown up some years ago in our study plots and severe impacts on crown structure were found, so, apart from possible modeling inaccuracies, the branch pattern differences between vitalities are most likely drought related.

Conclusion

The results of this study indicate evidence that trees growing in moderately or severely drought damaged stands had reduced fine branch lengths, shifted fine branch length proportions, and altered ratios between the length of fine and base order branches when compared to healthy trees, particularly in the middle and upper crown. We explain these findings by typical drought symptoms of beech: fine branch shedding and reduced shoot growth due to the formation of short rather than long shoots. Because the beech trees and their crowns were similarly-sized, it is likely that the differences were due to the drought damage in the stands and therefore related to their vitality. Still, there are reasons why conclusions should be drawn with caution: Fine branch lengths can generally be influenced by other factors than drought (such as tree size) and the length of time a tree responds to drought events varies from case to case. In addition, some beech trees within a vitality class exhibited fine branching characteristics more closely associated with the other vitality class, thus conclusions about single-tree vitality are not yet possible. The effect of a reduced point cloud quality, especially in the top crown, leading to inaccuracies in the modeling of the branching structure of QSMs also plays a role here. Nevertheless, we highlight the potential of laser scanning to derive fine branch length patterns of trees from QSMs and its possible application for the vitality assessment at least on plot level. The approach is objective and revealed significant differences between vitalities. However, further investigations are essential to be able to make reliable statements on the basis of QSMs for a practical application and to assess the suitability for heterogeneously structured stands and other tree species. Long-term studies could in addition provide evidence on the relationship between the severity of damage in the fine branch pattern and the long-term development of tree vitality. The use of a stationary terrestrial laser scanner could be tested and the combination with other vitality estimation methods should further improve the validity of our approach.