Determining parameters related to the likelihood of failure of red oak (Quercus rubra L.) from winching tests

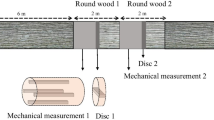
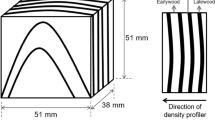
Abstract

Key message

This study provides data necessary to develop mechanistic models of the failure of open-grown trees. The literature contains few such data. Some results contrast previous studies on conifers.

Abstract

In cities and towns, tree failure can cause damage and injury. Few studies have considered large, open-grown trees when measuring parameters related to tree failure. To measure elastic modulus and maximum bending moment and stress, we winched red oaks (Quercus rubra L.), including some with co-dominant stems and others with extant decay. To simulate decay in a subsample of trees, we cut voids in the trunk before pulling trees to failure. Maximum bending moment was greatest for uprooted trees, but maximum bending and shear stresses were greatest for trees that failed in the crown in the vicinity of branches. The likelihood of failure at a void or area of extant decay increased as the loss in area moment of inertia increased. The moduli of elasticity and rupture of specimens taken from trees were greater than values measured on the trees themselves. Failure at the union of co-dominant stems only occurred when we pulled them apart, loading them perpendicular to the plane bifurcating the union. Some of the results are inconsistent with previous work on conifers; more data on open-grown trees are necessary to develop mechanistic models to predict tree failure.

Appendix A

In standing trees, the effect of axial growth stress is additive to axial and wind-induced bending stresses. Axial stress due to self-weight is uniformly compressive throughout the cross section. Bending stresses are tensile and compressive, and their magnitude is greatest at the circumference of the cross section. Growth stresses are compressive near the pith and maximally tensile at the circumference of the cross section. During the winching tests, tensile growth stress at the circumference of the cross section counteracts the combined compressive axial and bending stress due to self-weight and the test itself. We used two methods to estimate the combined effect of axial compressive stress due to self-weight and tensile growth stress and compared it to the total compressive stress (axial and bending) induced by winching.

In the first method, we gleaned values of axial tensile growth stress from the literature. On stems of oaks growing without a lean, the magnitude of axial tensile growth stress was about 6 MPa (Wilhelmy and Kubler 1973; Yao 1979), similar to the value reported for the compression side of a leaning red oak (Okuyama et al. 1994). Since none of the measured red oaks expressed a lean, we assumed the value of 6 MPa. Next, we estimated axial compressive stress due to self-weight from (1) the volume of the stem above the height at which we sawed the void, (2) the density of the wood measured from green specimens sampled from the tree, and (3) the cross-sectional area of the stem excluding the sawn void. For each tree, we subtracted axial compressive stress due to self-weight from tensile growth stress of 6 MPa.

In the second method, we calculated the difference between baseline axial displacements (i.e., before applying the load, but after branches were pruned) before and after we cut voids into the trees. For each tree, we converted the difference to a strain and multiplied by the elastic modulus of green specimens sampled from the tree and tested in 3-point bending (ASTM 2014). This estimated the combined effect of axial compressive stress due to self-weight and axial tensile growth stress after notching. For either method and all trees, the maximum ratio of (1) the combined effect of axial compressive stress due to self-weight and tensile growth stress to (2) the total compressive stress (axial and bending) induced while winching the tree to failure was 0.002.