A variationally consistent reproducing kernel enhanced material point method and its applications to incompressible materials

Abstract

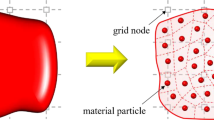
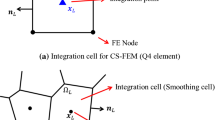
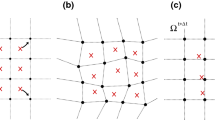
The material point method (MPM) suffers from poor accuracy and suboptimal convergence rates compared to other numerical methods due to the under-integration of the weak form; the locations of material points with respect to the background grid are suboptimal in performing numerical quadrature. Although this approach enables the MPM to model large deformation efficiently, it also results in the loss of Galerkin exactness in the variational equation and possible stress oscillation due to the cell-crossing instability. This paper introduces a novel MPM formulation that employs the reproducing kernel approximation to overcome the cell-crossing instability due to the higher-order continuity employed. The reproducing kernel method also ensures completeness in the approximation. In addition, this paper implements a variationally consistent material point integration scheme into the MPM framework to address the issue of Galerkin exactness, which is shown to recover theoretical convergence and increase the robustness of the formulation. Numerical examples demonstrate that the proposed method recovers optimal accuracy and stability compared to the conventional approaches and removes spurious pressure oscillation. The F-bar stabilization method of overcoming pressure instability is then coupled with the presented formulation to demonstrate its ability to accurately model incompressible materials.

Appendix

The results of the curve fitting problem of Eq. (24) show that the GIMP formulation is able to satisfy the linear reproducing condition when the uniform particle distribution is employed, but not for the non-uniform particle distribution. This can be explained by deriving the constraint necessary for GIMP to satisfy the linear reproducing condition, as follows. We first start by plugging the GIMP shape function into the completeness condition of Eq. (23):

$${{\varvec{x}}}^{\alpha }=\sum_{I\in {G}_{{\varvec{x}}}}{\widetilde{\Psi }}_{I}\left({\varvec{x}}\right){{\varvec{x}}}_{I}^{\alpha }, \left|\alpha \right|\le n$$

(49)

where ${\widetilde{\Psi }}_{I}\left({\varvec{x}}\right)$ represents the GIMP shape function. Within the context of the MPM, and implementing the particle domain averaging approach of Eq. (25), the completeness condition is then defined as:

$${{\varvec{x}}}_{p}^{\alpha }=\sum_{I}\left[\frac{1}{{V}_{p}}\sum_{q\in {S}_{p}}{\Psi }_{I}\left({{\varvec{x}}}_{q}\right){w}_{q}\right]{{\varvec{x}}}_{I}^{\alpha }$$

(50)

which, using commutativity and associativity of the summation, is redefined as follows:

$$ {\varvec{x}}_{p}^{\alpha } = \frac{1}{{V_{p} }}\mathop \sum \limits_{{q \in S_{p} }}^{{}} \left[ {\mathop \sum \limits_{{I \in G_{{\varvec{x}}_{q}} }}^{{}} \Psi_{I} \left( {{\varvec{x}}_{q} } \right){\varvec{x}}_{I}^{\alpha } } \right]w_{q} $$

(51)

GIMP employs finite element shape functions, which satisfy linear completeness. Therefore, if we set $\alpha =1$ for linear completeness, Eq. (51) is simplified as:

$$ {\varvec{x}}_{p} = \frac{1}{{V_{p} }}\sum\limits_{{q \in S_{p} }} {{\varvec{x}}_{q} w_{q} } $$

(52)

The above constraint to achieve linear completeness can be interpreted as a statement that the weighted average of all smoothing points ${{\varvec{x}}}_{q}$ should be equal to the particle location ${{\varvec{x}}}_{p}$. Therefore, as long as the smoothing points ${{\varvec{x}}}_{q}$ and weights ${w}_{q}$ are chosen carefully such that Eq. (52) is satisfied, the GIMP shape functions can satisfy the linear reproducing condition.

For the curve fitting problem of Sect. 2.2, it can be shown that only the particle domain averaging scheme used for the uniform discretization satisfies the constraint in Eq. (52), whereas the scheme used for the non-uniform discretization does not. Therefore, the same curve fitting problem of Eq. (24) is then repeated, to show that GIMP shape functions can satisfy linear completeness such that additional measures are taken to satisfy the constraint. Here, we recalculate the weights ${w}_{q}$ under the constraint that $\sum_{q\in {S}_{p}}{w}_{q}={V}_{p}$ in order to satisfy Eq. (52). The particle domains used are also conforming. The results for the linear exact solution of Eq. (30) are shown below in Table

Table 5 ${L}_{2}$ error norms for the linear completeness test by the modified GIMP

5, where it is seen that the GIMP shape functions are able to reproduce the exact solution to machine precision for each mesh employed.

The convergence test results for the exponential exact solution of Eq. (31) are shown below in Fig. 

Fig. 21

Convergence test with uniform (left) and non-uniform (right) spatial discretization to measure interpolation error of RK, B-Spline functions, and the modified GIMP for the curve fitting problem. The numbers in the legends denote convergence rates

21, and are again compared with results for the RK approximation as well as cubic B-splines. Results demonstrate that GIMP can recover near optimal convergence rates for both the uniform and non-uniform particle distributions, and its accuracy approaches the RK approximation result.