A micromorphic phase-field model for brittle and quasi-brittle fracture

Abstract

In this manuscript, a robust and variationally consistent technique is proposed for local treatment of the phase-field fracture irreversibility. This technique involves an extension of the phase-field fracture energy functional through a micromorphic approach. Consequently, the phase-field is transformed into a local variable, while a micromorphic variable regularizes the problem. The local nature of the phase-field variable enables an easier implementation of its irreversibility using a pointwise ‘max’ with system level precision. Unlike the popular history variable approach, which also enforces local fracture irreversibility, the micromorphic approach yields a variationally consistent framework. The efficacy of the micromorphic approach in phase-field fracture modelling is demonstrated in this work with numerical experiments on benchmark brittle and quasi-brittle fracture problems in linear elastic media. Furthermore, the extensibility of the micromorphic phase-field fracture model towards multiphysics problems is demonstrated. To that end, a theoretical extension is carried out for modelling hydraulic fracture, and relevant numerical experiments exhibiting crack merging are presented. The source code as well as the data set accompanying this work would be made available on GitHub (https://github.com/ritukeshbharali/falcon).

1 Introduction

The phase-field fracture model emerged from the the variational treatment of the Griffith fracture criterion in [1], and its numerical adaptation in [2, 3]. The model introduces an auxiliary scalar variable, the phase-field, which interpolates between intact and fully broken (fractured) material states. In the recent decade, the model has been adopted as a promising alternative to discrete fracture modelling techniques (for instance, XFEM [4, 5] and cohesive zone models [6,7,8]). This is due to ability of the phase-field fracture model in handling topologically complex fractures (branching, kinking and merging) on a fixed mesh, solely based on energy minimization.

The development of a thermodynamically consistent phase-field fracture framework in [9] spurred its popularity. Following this development, the model has been extended towards ductile fracture [10, 11], anisotropic fracture [12, 13], hydraulic fracture [14, 15], desiccation cracking [16, 17], corrosion [18, 19], fracture in thin films [20], to cite a few applications. While most literature pertaining to the phase-field fracture is confined to brittle fracture, Wu [21] proposed a unified phase-field fracture model, encompassing both brittle and quasi-brittle fracture. The unified phase-field fracture model has been applied in the investigation of size effect of concrete [22], hydrogen assisted cracking [23], electro-mechanical fracture in piezo-electric solids [24], and fracture of thermo-elastic solids [25], to cite a few applications. Furthermore, the phase-field fracture models have also been investigated in a multi-scale modelling context, both in concurrent multi-scale modelling [26,27,28,29] and hierarchical multi-scale modelling [30, 31].

The popularity of the phase-field fracture models, however, comes at the cost of minimising a non-convex energy functional. In this context, monolithic solution techniques like the Newton–Raphson (NR) method demonstrate a poor convergence behaviour. This has led to active research in the development of solution techniques for phase-field fracture models. For instance, Gerasimov and De Lorenzis [32] proposed the use of both positive and negative line-search directions to improve convergence of the NR method, while Kopaničáková and Kraus [33] advocated the use of trust region methods. Other efforts at developing monolithic solution techniques for phase-field fracture models include modified NR methods [34], arc-length method with dissipation-based arc-length constraints [35,36,37,38] and quasi-Newton (secant-based) methods [39, 40]. In yet another approach, a convexification strategy for the system of equations was proposed in [41]. Therein, the phase-field for the momentum balance equation is extrapolated from that obtained in the last two (pseudo) time steps. This strategy not only improves the convergence behaviour of the NR method but also offers an ease of implementation in existing finite element frameworks. As such, the extrapolation technique in [41] is adopted in this manuscript. At this point, the authors would like to emphasize that this manuscript does not focus on the development of monolithic solution techniques. Rather, the focus is on another computational challenge in phase-field fracture models, the treatment of variational inequality.

Minimisation of the phase-field fracture energy functional, in conjunction with the notion of fracture irreversibility results in a variational inequality Euler–Lagrange equation for the phase-field [42]. Since the phase-field is a global field variable with higher regularity, enforcing its irreversibility via the Karush–Kuhn–Tucker (KKT) conditions is not trivial. This has led to several methods being proposed by different researchers, the simplest of them is the penalisation approach [32, 43]. Other techniques include the primal-dual active set method [41], Augmented Lagrangian formulation based on the Moreau–Yoshida indicator function [34, 44], and the history variable approach [45]. Among all techniques, the penalisation approach and the history variable approach remain popular, owing to their ease in implementation into existing finite element frameworks. However, the penalisation approach has the potential to render a stiffness matrix ill-conditioned, particularly when a stricter irreversibility tolerance is desired. This is clear from the expressions for the penalty term derived in Section 3.3.3 in [43]. The history variable approach enforces KKT conditions locally (in pointwise sense) on the fracture driving energy. However, this not only results in the loss of variational consistency but also introduces an error which has so far never been quantified. In order to circumvent the aforementioned issues pertaining to the penalisation approach and the history variable approach, a micromorphic approach towards phase-field fracture model is proposed in this manuscript. Leveraging on the micromorphic theory [46], this approach admits local KKT conditions on the phase-field, albeit in a variationally consistent framework. Moreover, the fracture irreversibility is enforced with system level precision.

The theory of micromorphic media was introduced for gradient elasticity, viscoplasticity and damage in [46]. Since then, it has been extended towards crystal plasticity [47,48,49], small and finite deformation plasticity coupled with damage [50, 51], and ductile phase-field fracture [52], to cite a few. To the best of authors’ knowledge, a micromorphic phase-field framework for brittle and quasi-brittle fracture have not yet been proposed for the more basic problem of linear elasticity. Another important application for which the micromorphic regularization has not been addressed is that of fracture in porous media. This manuscript addresses the above research gaps, specifically, exploiting the micromorphic theory to enable a variationally consistent local fracture irreversibility enforcement technique (local KKT conditions). To this end, the phase-field fracture energy functional is extended in the spirit of [46]. This transforms the phase-field into a local quantity, while introducing a ‘new’ micromorphic variable that regularises the problem. The local nature of the phase-field enables a simpler KKT treatment¹ at material integrations points, for enforcing the fracture irreversibility. Thereafter, the micromorphic phase-field fracture energy functional is extended towards porous media, specifically in the context of hydraulic fracturing. A fluid transport equation is then added to the system of equations for modelling fluid content variation within the computational specimen. The ease of introducing fracture dependent coefficients is discussed adopting a dual permeability model [53, 54], where the fracture intrinsic permeability is computed through the phase-field adaption of the cubic law [55], presented in [56]. A scaling function with the micromorphic variable as its argument is introduced to iterate between bulk and fracture intrinsic permeabilities. The efficacy of the novel micromorphic phase-field fracture model is demonstrated with linear elastic and porous media benchmark problems, exhibiting both brittle and quasi-brittle fracture. These include a single edge notched specimen under tension and shear, the Winkler L-panel experiment [57], the three-point bending experiment carried out in [58], and hydraulic fracturing experiments presented in [59].

This manuscript is structured as follows: Sect. 2 introduces the reader to the phase-field model for fracture, its underlying energy functional and pertinent Euler–Lagrange equations. The main contribution of this manuscript, the micromorphic phase-field fracture model for linear elastic and porous media are presented in Sects. 3 and 4, respectively. The numerical benchmark problems are addressed in Sect. 5, followed by concluding remarks in Sect. 6.

2 Phase-field fracture model

2.1 The energy functional

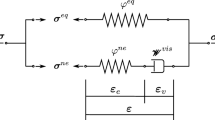
Let ${\Omega }\in \mathbb {R}^2$ be a 2D domain occupied by a fracturing continuum, as shown in Fig. 1. The fracture is represented by a diffused band of finite width ${l}>0$. Within this band, the phase-field, ${\varphi }\in [0,1]$ interpolates between intact and fully broken (fractured) material states. Furthermore, the external surface of the domain ${\Omega }$ is split into a Dirichlet boundary ${{\Gamma }_{D}^{{u}}}$ and a Neumann boundary ${{\Gamma }_{N}^{{u}}}$, such that ${\Gamma }= {{\Gamma }_{D}^{{u}}} \cup {{\Gamma }_{N}^{{u}}}$ and ${{\Gamma }_{D}^{{u}}} \cap {{\Gamma }_{N}^{{u}}} = \emptyset$.

Fig. 1

A fracturing continuum ${\Omega }\in \mathbb {R}^2$ embedded a diffused (smeared) crack. Dirichlet and Neumann boundaries are indicated as ${{\Gamma }_{D}^{{u}}}$ and ${{\Gamma }_{N}^{{u}}}$ respectively. Figure reproduced from [31]

The energy functional for the (phase-field) fracturing continuum in Fig. 1 is given by,

$$\begin{aligned} \displaystyle E({\textbf{u}},{\varphi })= & {} \int _{{\Omega }}^{} g({\varphi }) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega }+ \int _{{\Omega }}^{} \Psi ^-({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega }\nonumber \\{} & {} - \int _{{{\Gamma }_{N}^{{{\textbf{u}}}}}}^{} {\textbf{t}_{p}^{{{u}}}} \, {\textbf{u}}\, \cdot \text {d}{\Gamma }+ \int _{{\Omega }}^{} \dfrac{{G_c}}{c_w {l}} \left( w({\varphi }) + {l}^2 |{\varvec{\nabla }}{\varphi }|^2 \right) \, \text {d}{\Omega },\nonumber \\ \end{aligned}$$

(1)

accounting for prescribed external traction ${\textbf{t}_{p}^{{{\textbf{u}}}}}$. Here, the strain energy density is decomposed into a fracture driving part $\Psi ^+$, and residual part $\Psi ^-$. The strain energy densities are a function of ${{\varvec{\epsilon }}}[{\textbf{u}}]$, the symmetric part of the deformation gradient, with ${\textbf{u}}$ as the displacement. A monotonically decreasing degradation function $g({\varphi })$ is attached to $\Psi ^+$ to account for the loss of bulk energy upon fracture. Furthermore, the last integral in the above equation represents the fracture energy, where ${G_c}$ and ${l}$ are the Griffith fracture energy and the fracture length-scale respectively. The normalisation constant, $c_w$ is associated with the choice of the locally dissipated fracture energy function $w({\varphi })$. The phase-field fracture model allows great flexibility in choosing the degradation function $g({\varphi })$ and the locally dissipated fracture energy function $w({\varphi })$. This has led to several variants being proposed by different researchers. Table 1 presents some of these phase-field fracture model variants.

Table 1 Brittle and quasi-brittle phase-field fracture models

In Table 1, it is observed that the quasi-brittle phase-field fracture model requires additional parameters p, $a_1$, $a_2$ and $a_3$ in the degradation function. These parameters are user-defined quantities, and are chosen such that different traction–separation laws may be obtained. Following [21], the constant $a_1$ is given by,

$$\begin{aligned} a_1 = \dfrac{4 E_0 {G_c}}{\pi {l}f_t^2}, \end{aligned}$$

(2)

where the newly introduced parameters $E_0$ and $f_t$ represent the Young’s Modulus and the material tensile strength respectively. The other parameters (p, $a_2$ and $a_3$) vary depending on chosen traction–separation law, as observed from Table 2.

Furthermore, the flexibility of the phase-field fracture models also extends to the choice of fracture driving and residual strain energy densities. Table 3 presents some of commonly adopted strain energy density decompositions in the phase-field literature. Here, $\lambda$, $\mu$ represent the Lame constants, and K is the bulk modulus of the material. Furthermore, ${{\varvec{\epsilon }}}^{\pm }$ represents the tensile/compressive strains obtained through spectral decomposition, ${{\varvec{\epsilon }}}_{dev}$ is the deviatoric strain, tr is a trace operator, and $\langle \bullet \rangle _{\pm }$ indicates the positive/negative Macaulay brackets.

Given the strain energy decompositions in Table 3, the fracture driving and residual stresses maybe obtained as

$$\begin{aligned} {{\varvec{\sigma }}}^{\pm } :=\dfrac{\partial \Psi ^{\pm }}{\partial {{\varvec{\epsilon }}}}, \end{aligned}$$

(3)

where the function argument ${{\varvec{\epsilon }}}[{\textbf{u}}]$ in $\Psi ^{\pm }$ as well as in ${{\varvec{\sigma }}}^{}\pm$ is dropped henceforth.

2.2 Euler–Lagrange equations

In order to simulate the initiation and propagation of fracture(s) in a continuum, the energy functional (1) is minimised w.r.t. its field variables, vector-valued displacements ${\textbf{u}}$ and scalar-valued phase-field ${\varphi }$. This results in the set of Euler–Lagrange equations. Adopting the stress definition in (3), along with appropriately defined test and trial spaces, they result in the following problem:

2.3 Treatment of variational inequality

The variational inequality phase-field evolution equation (4b), observed in Problem 1 stems from the fracture irreversibility constraint, $\dot{{\varphi }} \ge 0$. Consequently, special solution techniques are required to treat the variational inequality in a computational efficient way. Some of the popular techniques adopted for the phase-field fracture model are presented in this section.

Table 2 Quasi-brittle phase-field fracture model parameters for different traction–separation laws [21]

Table 3 Strain energy density decompositions in phase-field fracture models

2.3.1 Relaxed ‘crack-set’ irreversibility

The relaxed ‘crack-set’ irreversibility technique, proposed in [2, 3] introduces a crack-set,

$$\begin{aligned} S_{n} :=\{ \textbf{x} \in {\Omega }| {\varphi }_{n} \ge {\varphi }_{tol} \}. \end{aligned}$$

(6)

Here, n refers to the previous time-step and $0 \ll {\varphi }_{tol} < 1$. For all $\textbf{x} \in S_{n}$, a Dirichlet constraint ${\varphi }= 1$ is applied. Consequently, fracture irreversibility constraint holds only for ${\varphi }\ge {\varphi }_{tol}$. In all other cases, healing of cracks is allowed.

2.3.2 Penalisation

The penalisation technique proposed in [43] augments the phase-field fracture energy functional (1) with,

$$\begin{aligned} P({\varphi }) :=\dfrac{\gamma }{2} \int _{{\Omega }} \langle {\varphi }_n - {\varphi }\rangle ^2 \, \text {d}{\Omega }, \end{aligned}$$

(7)

where $\gamma$ is an appropriately chosen penalty parameter and n refers to the previous time-step. For $\gamma \longrightarrow \infty$, Problem 1 is recovered. Although, the penalisation technique is easier to implement in existing finite element software, it has a potential to render the problem ill-conditioned when a high value of $\gamma$ is used. Furthermore, Wick [44] reported possible stability issues with the penalization technique in (7), and proposed the augmentation of the Moreau–Yosida approximation of the fracture irreversibility indicator function,

$$\begin{aligned} P({\varphi }) :=\dfrac{1}{2 \gamma } \int _{{\Omega }} \langle \Sigma + \gamma ({\varphi }- {\varphi }_{n}) \rangle ^{2}_{-} \, \text {d}{\Omega }, \end{aligned}$$

(8)

to the phase-field fracture energy functional (1) instead. Here, $\gamma > 0$ is a penalty parameter, $\Sigma \in L^2({\Omega })$ is an additional unknown and $\langle \cdot \rangle _{-}$ indicates a negative Macauley bracket. However, the introduction of the Moreau-Yosida indication function introduces an additional field $\Sigma$, which increases the dimension of the problem.

2.3.3 Semi-smooth Newton–Raphson method

The semi-smooth Newton–Raphson method was proposed in [63], and extended to phase-field fracture models in [41]. The method incorporates the fracture irreversibility constraint $\dot{{\varphi }} \ge 0$ using a Lagrange multiplier. The resulting system of equations is then treated using a primal-dual active set strategy [63]. An active set $\mathcal {A}_k$ in the kth Newton–Raphson iteration is defined as,

$$\begin{aligned} \mathcal {A}_k = \{ i | (\textbf{B}^{-1})_{ii} (\textbf{R}_k)_i + c ( \textbf{U}^{k} + \delta \textbf{U}^k - \textbf{U}^n )_i < 0 \}, \end{aligned}$$

(9)

where i represents a phase-field Degree Of Freedom (DOF) in the discrete system of equations, $\textbf{B}$ is a fictitious lumped mass matrix with unit density, $\textbf{R}$ being the residual, a scalar constant c, and the discrete solution vector and its increment represented by $\textbf{U}$ and $\delta \textbf{U}$ respectively. Furthermore, n refers to the previous time-step. For every Newton–Raphson iteration, the active set DOFs are eliminated from the system of equations. Convergence is achieved when the norm of the residual is below a certain tolerance limit and the active set does not change. Although, this technique circumvents the need for any user-defined parameters, the explicit tracking of the active and inactive sets increases the computational expense [42].

2.3.4 History-variable approach

The history-variable approach was proposed in [45], based on a local phase-field evolution, i.e., (4b) without the gradient term. The fracture driving energy $\Psi ^+$ is then identified as the ‘load term’ driving the phase-field. With this assumption, a local history field is introduced as

$$\begin{aligned} \mathcal {H} = max ( \mathcal {H}_{n}, \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) ) \end{aligned}$$

(10)

where n refers to the previous time-step. Thereafter, in the phase-field evolution Eq. (4b), the history field $\mathcal {H}$ replaces $\Psi ^+$, resulting in an equality-based equation, with relaxed test and trial space. Although, the history variable approach offers an ease in implementation and has been popular in the phase-field literature, the variational consistency of the problem is lost [42].

3 Micromorphic phase-field fracture model

In this section, a micromorphic phase-field fracture model is developed as an alternative variational inequality treatment technique. The model is based on an extension of the phase-field fracture energy functional (1) in the spirit of [46]. Consequently, the phase-field ${\varphi }$ becomes a local quantity, and a new micromorphic field variable ${d}$ is introduced to regularise the problem. This enables a local treatment of phase-field irreversibility constraint with system level precision in a variationally consistent fashion.

3.1 The energy functional

The energy functional for the micromorphic phase-field fracture model is an extension of the (1) in the spirit of [46],

$$\begin{aligned} \tilde{E}({\textbf{u}},{\varphi },{d})&= \int _{{\Omega }}^{} g({\varphi }) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega }+ \int _{{\Omega }}^{} \Psi ^-({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega } \nonumber \\&\quad -\int _{{{\Gamma }_{N}^{{{\textbf{u}}}}}}^{}{\textbf{t}_{p}^{{{u}}}} \, {\textbf{u}}\, \text {d}{\Gamma }+ \int _{{\Omega }}^{} \dfrac{{G_c}}{c_w {l}} \left( w({\varphi }) + {l}^2 |{\varvec{\nabla }}{d}|^2 \right) \, \text {d}{\Omega }\nonumber \\&\quad + \int _{{\Omega }}^{} \frac{\eta }{2} ({\varphi }-{d})^2 \, \text {d}{\Omega }. \end{aligned}$$

(11)

Here, ${d}$ is a ‘new’ micromorphic field variable, and $\alpha$ is an interaction parameter. Theoretically, in the limit, the interaction parameter, $\alpha \rightarrow \infty$, the original energy functional (1) is recovered. Comparing (11) with (1), it is observed that the micromorphic variable replaces the phase-field in the gradient term. Consequently, the regularity requirements on the phase-field w.r.t. the existence of its derivatives is circumvented. In other words, the phase-field becomes a local quantitiy.

3.2 Euler–Lagrange equations

The set of Euler–Lagrange equations for the micromorphic phase-field fracture model is obtained upon minimising the energy functional (11) w.r.t. its solution variables ${\textbf{u}}$, ${\varphi }$ and ${d}$. Adopting the stress definition in (3), along with appropriately defined test and trial spaces, it results in the following problem:

3.3 Treatment of variational inequality

The micromorphic phase-field fracture model yields a local variational inequality phase-field evolution equation (12b), as observed in Problem 2. As such, (12b) is assumed to hold ‘point-wise’ in the computational domain ${\Omega }$. In other words, a local phase-field ${\varphi }$ is obtained as the root(s) of the possibly nonlinear scalar equation,

$$\begin{aligned} g'({\varphi }) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) + \dfrac{{G_c}}{c_w {l}} w'({\varphi }) + \eta ({\varphi }- {d}) = 0, \end{aligned}$$

(14)

for ${}^{n}{\varphi }< {\varphi }< 1$. With locally computed phase-field ${\varphi }$, a two-field micromorphic phase-field problem is stated as:

It is worth mentioning that the local phase-field evolution (14) is linear for Brittle AT1 and AT2 fracture models. This is due to the quadratic nature of the degradation function $g({\varphi }) = (1-{\varphi })^2$ coupled with linear/quadratic locally dissipated fracture energy function $w({\varphi }) = {\varphi }$ and ${\varphi }^2$ for the AT1 and AT2 models respectively. This yield explicit expressions for the local phase-field variable,

$$\begin{aligned} {\varphi }= {\text {min}} \Bigg ( {\text {max}} \bigg ( \dfrac{2 \Psi ^+ + \eta {d}- \frac{3 G_c}{8 l}}{2 \Psi ^+ + \alpha }, {}^{n}{\varphi }\bigg ), 1 \Bigg ), \end{aligned}$$

(17)

for AT1, and

$$\begin{aligned} {\varphi }= {\text {min}} \Bigg ( {\text {max}} \bigg ( \dfrac{2 \Psi ^+ + \eta {d}}{2 \Psi ^+ + \eta + \frac{G_c}{l}}, {}^{n}{\varphi }\bigg ), 1 \Bigg ). \end{aligned}$$

(18)

for AT2 model respectively. In the case of quasi-brittle phase-field fracture model, the rational nature of the degradation function (see Table 1) results in nonlinear scalar equation for the local phase-field variable. The equation is then solved using the Newton–Raphson method.

Remark 1

The irreversibility constraint on the locally computed phase-field ${\varphi }$, ${\varphi }\ge {\varphi }_n$ may be enforced with system level precision.

3.4 Convexification via extrapolation

Similar to the conventional phase-field fracture mode, the energy functional corresponding to the micromorphic phase-field fracture model is also non-convex. This renders monolithic solution techniques, like the Newton–Raphson method ineffective. In order to circumvent this issue, the convexification strategy was proposed in [41] for conventional phase-field fracture model is adapted to the micromorphic phase-field fracture model. To this end, the micromorphic variable is extrapolated from the two previous converged (time) steps as,

$$\begin{aligned} \hat{{d}} = {d}^{n-1} + \dfrac{\Delta t + \Delta t^n}{\Delta t^n} ({d}^{n} - {d}^{n-1}). \end{aligned}$$

(19a)

The extrapolated micromorphic variable, $\hat{{d}}$ is then used to compute an approximated local phase-field $\hat{{\varphi }}$ for the momentum balance equation (12a) using,

$$\begin{aligned} g'(\hat{{\varphi }}) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) + \dfrac{{G_c}}{c_w {l}} w'(\hat{{\varphi }}) + \eta (\hat{{\varphi }} - \hat{{d}}) = 0, \end{aligned}$$

(19b)

where n and $n-1$ represents the two previous converged (time) steps. However, for the micromorphic variable evolution equation (15b), the local phase-field ${\varphi }$ is computed using the current micromorphic variable ${d}$, and not the extrapolated variable $\hat{{d}}$. In order to emphasize this difference, the computation of the local phase-field without extrapolation, (14) is restated,

$$\begin{aligned} g'({\varphi }) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) + \dfrac{{G_c}}{c_w {l}} w'({\varphi }) + \eta ({\varphi }- {d}) = 0. \end{aligned}$$

(20)

On applying the above convexification strategy to Problem 3, its convex variant is obtained as:

Remark 2

The convexification strategy through extrapolation is adopted for the micromorphic phase-field fracture model in this manuscript due to the ease in implementation. It is possible to adopt other strategies as well ...

3.5 Discrete equations

In this manuscript, the Euler–Lagrange equations of the micromorphic phase-field fracture Problem 4 is discretized using the finite element method [64, 65], using triangular (T3) elements. This allows assuming the displacement and the micromorphic fields at the nodes ($\tilde{{\textbf{u}}}_i,\tilde{{d}}_i$) are considered as the primary unknowns, with the corresponding continuous fields (${\textbf{u}}$, ${d}$) approximated as,

$$\begin{aligned} {\textbf{u}}= \sum \limits _{i = 1}^m {N_i^{\varvec{u}}\tilde{\varvec{u}}_i}\;\;\;\text { , } {d}= \sum \limits _{i = 1}^m N_i^{d}\tilde{{d}}_i. \end{aligned}$$

(23)

In the above equation, $N_i^{\varvec{u}}$ and $N_i^{d}$ are the interpolation functions for the displacement and the micromorphic phase-field, associated with the ith node. The spatial derivatives of the interpolation functions $N_i^{\varvec{u}}$ and $N_i^{{d}}$ in a two-dimensional case are given by,

$$\begin{aligned} \textbf{B}_i^{\varvec{u}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ 0 \\ {{N_{i,y}}}\\ \end{array}}&{}\quad {\begin{array}{*{20}{c}} 0 \\ {{N_{i,y}}} \\ {{N_{i,x}}} \\ \end{array}} \end{array}} \right] , \quad \textbf{B}_i^{d} = \left[ {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ {{N_{i,y}}} \end{array}} \right] . \end{aligned}$$

(24)

Here, the subscripts , x and , y indicate spatial derivatives in x and y directions respectively. Using (24), the strain ${{\varvec{\epsilon }}}$, and the gradient of the micromorphic variable ${\varvec{\nabla }}{d}$ are defined as,

$$\begin{aligned} \varvec{\epsilon } = \sum \limits _{i = 1}^m {\textbf{B}_i^{\varvec{u}} \tilde{\varvec{u}}_i},\quad {\varvec{\nabla }}{d}= \sum \limits _{i = 1}^m {\textbf{B}_i^{d} \tilde{{d}}}. \end{aligned}$$

(25)

The discrete phase-field fracture problem is obtained upon inserting (23–25) in the Euler–Lagrange equations from Problem 4. Thereafter, (21a) and (21b) are assumed as the internal forces, and stiffness matrix derived from its derivative. This notation is consistent with [66], and allows the presentation of the phase-field fracture problem in the incremental iterative framework as:

4 Extension towards fracture in porous media

In this section, the micromorphic phase-field fracture model is extended towards modelling fracture in porous media, specifically, hydraulic fracturing. To that end, a biphasic porous rock material is assumed, comprising of a solid matrix and fluid filling up the pore space. Modelling such a material requires the extension of the energy functional (11) with an additional fluid contribution term. Furthermore, a fluid transport equation is added to the system of equations to account for variation in the fluid content. The following subsections explain these modelling choices in detail, and derives the corresponding Euler–Lagrange and discrete finite element equations.

4.1 The energy functional and the fluid transport equation

The micromorphic phase-field fracture model, developed in the previous section, allows a straightforward extension towards modelling fracture in porous media. Upon incorporating the contribution of the fluid phase, the energy functional in (11) assumes the form,

$$\begin{aligned} \tilde{E}({\textbf{u}},{\varphi },{d})&= \int _{{\Omega }}^{} g({\varphi }) \Psi ^+({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega }+ \int _{{\Omega }}^{} \Psi ^-({{\varvec{\epsilon }}}[{\textbf{u}}]) \, \text {d}{\Omega }\nonumber \\&\quad - \underbrace{\int _{{\Omega }}^{} \alpha \, p \, {\varvec{\nabla }}\cdot {\textbf{u}}\, \text {d}{\Omega }}_{\text {fluid phase contribution}} \nonumber \\&\quad -\int _{\mathbf{\Gamma }_N^{\textbf{u}}}{} \textbf{t}_p^u \textbf{u} \textbf{d}{} \mathbf{\Gamma } + \int _{{\Omega }}^{} \dfrac{{G_c}}{c_w {l}} \left( w({\varphi }) + {l}^2 |{\varvec{\nabla }}{d}|^2 \right) \, \text {d}{\Omega }\nonumber \\&\quad + \int _{{\Omega }}^{} \frac{\eta }{2} ({\varphi }-{d})^2 \, \text {d}{\Omega }. \end{aligned}$$

(27)

The coefficient in the fluid phase contribution term, $\alpha$ represents the Biot coefficient. Since, the energy functional corresponds to a fixed pressure, a fluid transport equation is added to account for the variation in fluid phase content. Following [67], the fluid transport equation for saturated porous media is stated as,

$$\begin{aligned} \Bigg [\dfrac{\alpha - n}{K_s} + \dfrac{n}{K_f} \Bigg ] \dfrac{\partial p}{\partial t} + \alpha \dfrac{\partial {{\varvec{\epsilon }}}_{vol}}{\partial t} + {\varvec{\nabla }}\cdot \Bigg [- \dfrac{k_i}{\mu _{f}} ( {\varvec{\nabla }}p - \rho _{f} \textbf{g} ) \Bigg ] = 0. \end{aligned}$$

(28)

Here, $K_s$ and $K_f$ are the solid grain and fluid bulk stiffness, n is the initial porosity, ${{\varvec{\epsilon }}}_{vol}$ is the volumtric strain, $\kappa _i$ is the intrinsic permeability of the material, $\mu _f$ is the fluid dynamic viscosity, $\rho _f$ is the density of the fluid, $\textbf{g}$ is vectorial representation of the acceleration due to gravity.

Furthermore, the effect of fracture on the intrinsic permeability of the porous media is accounted for, using a dual permeability model [54, 54]. To that end, the intrinsic permeability $k_i({d})$ is assumed to be comprising of a bulk contribution $k_{i,b}$ and a fracture contribution $k_{i,f}$,

$$\begin{aligned} k_i({d}) = [1 - h(d)] \, k_{i,b} + h(d) \, k_{i,f}. \end{aligned}$$

(29)

A micromorphic variable dependent scaling function h(d) is introduced as,

$$\begin{aligned} h(d) = \langle 25 ( d - 0.8)^2 \rangle _{+}, \end{aligned}$$

(30)

such that the effect of the fracture intrinsic permeability begins at ${d}= 0.8$ and reaches it maximum value at ${d}= 1$. Note that ${d}$ is used as an argument instead of the local phase-field variable ${\varphi }$ under the assumption $d \approx {\varphi }$. The bulk intrinsic permeability is considered a material property, while the fracture intrinsic permeability is computed based on a Poiseullie type flow between the parallel fractured surfaces, first proposed in [55]. The original work in [55] considered discrete fractures, however, it was adapted for the phase-field fracture model in [56]. Following [56], the fracture intrinsic permeability is defined as,

$$\begin{aligned} k_{i,f} = \dfrac{w_h^2}{12}. \end{aligned}$$

(31)

where $w_h$ is an approximate fracture aperture, given by,

$$\begin{aligned} w_h :=|| h_{el} ( 1 + \textbf{n}_{d} \cdot {{\varvec{\epsilon }}}[{\textbf{u}}] \cdot \textbf{n}_{d} ) ||, \end{aligned}$$

(32)

using the characteristic element size $h_{el}$, and the normalized gradient of the micromorphic variable $\textbf{n}_{d}$.

Remark 3

The micromorphic phase-field fracture model offers flexibility in parametrization of model parameters/coefficients w.r.t. both, the local phase-field ${\varphi }$ and the micromorphic variable d. For a sufficiently high value of the interaction parameter, ${\varphi }\approx d$, and the parametrization choice does not affect the solution. The only difference between the choice ${\varphi }$ or d is that the former results in additional derivatives w.r.t. the strain and the micromorphic variable, while the latter circumvents these derivatives.

4.2 Euler–Lagrange equations

The set of Euler–Lagrange equations pertaining to micromorphic phase-field modelling of hydraulic fracturing is obtained upon minimising the energy functional (27) w.r.t. its solution variables ${\textbf{u}}$, ${\varphi }$ and ${d}$, and incorporating an Euler–Lagrange equation for the fluid transport. Adopting the strategy demonstrated in Sects. 3.2 and 3.3, the local phase-field evolution Eq. (14) is obtained. However, in order to obtain a convex problem, the strategy proposed in [41] and demonstrated in Sect. 3.4 is adopted. This results in a local phase-field evolution equation (19b) for the momentum balance equation. Next, the fluid transport equation (28) is, however, stated in its strong form. A Bubnov–Galerkin procedure is adopted to obtained the corresponding Euler–Lagrange equation. Finally, a three-field problem is stated as:

4.3 Discrete equations

The set of Euler–Lagrange equations pertaining to hydraulic fracturing (see Problem 6) is discretized using the finite element method [64, 65], with triangular (T3) elements. Following the strategy in Sect. 3.5, the displacement, fluid pressure, and the micromorphic fields at the nodes ($\tilde{{\textbf{u}}}_i$,$\tilde{p}_i$, $\tilde{{d}}_i$) are considered as the primary unknowns. The corresponding continuous fields (${\textbf{u}}$, p, ${d}$) are approximated as,

$$\begin{aligned} {\textbf{u}}= \sum \limits _{i = 1}^m {N_i^{\varvec{u}}\tilde{\varvec{u}}_i,}\;\;\; p = \sum \limits _{i = 1}^m {N_i^{p}\tilde{p}_i,}\;\;\; {d}= \sum \limits _{i = 1}^m N_i^{d}\tilde{{d}}_i. \end{aligned}$$

(35)

In the above equation, $N_i^{\varvec{u}}$, $N_i^{p}$ and $N_i^{d}$ are the interpolation functions for the displacement, the fluid pressure and the micromorphic phase-field, associated with the ith node. The spatial derivatives of the interpolation functions $N_i^{\varvec{u}}$, $N_i^{p}$, and $N_i^{{d}}$ in a two-dimensional case are given by,

$$\begin{aligned} \textbf{B}_i^{\varvec{u}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ 0 \\ {{N_{i,y}}}\\ \end{array}}&{}\quad {\begin{array}{*{20}{c}} 0 \\ {{N_{i,y}}} \\ {{N_{i,x}}} \\ \end{array}} \end{array}} \right] ,\; \textbf{B}_i^{p} = \left[ {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ {{N_{i,y}}} \end{array}} \right] ,\; \textbf{B}_i^{d} = \left[ {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ {{N_{i,y}}} \end{array}} \right] . \end{aligned}$$

(36)

Here, the subscripts , x and , y indicate spatial derivatives in x and y directions respectively. Using (24), the strain ${{\varvec{\epsilon }}}$, and the gradient of the fluid pressure ${\varvec{\nabla }}p$ and the micromorphic variable ${\varvec{\nabla }}{d}$ are defined as,

$$\begin{aligned} \varvec{\epsilon } = \sum \limits _{i = 1}^m {\textbf{B}_i^{\varvec{u}} \tilde{\varvec{u}}_i},\;\;\;\; {\varvec{\nabla }}p = \sum \limits _{i = 1}^m {\textbf{B}_i^{p} \tilde{p}},\;\;\;\; {\varvec{\nabla }}{d}= \sum \limits _{i = 1}^m {\textbf{B}_i^{d} \tilde{{d}}}. \end{aligned}$$

(37)

The discrete problem is obtained upon inserting (35–37) in the Euler–Lagrange equations from Problem 6. Thereafter, Equations (33a), (33b) and (33c) are assumed as the internal forces, and the stiffness matrix is derived from their derivatives. This notation is consistent with [66], and allows the presentation of the micromorphic phase-field fracture problem in the incremental iterative framework as:

5 Numerical study

In this section, numerical experiments are carried out on benchmark brittle and quasi-brittle phase-field fracture problems in linear elastic and poroelastic media. For each problem, the geometry, loading conditions as well as the additional model parameters are presented in the respective sub-sections. Unless mentioned otherwise, all geometries are discretised with three-noded triangular element with a single integration point. The phase-field fracture topology in the final step of the analysis, the fluid pressure distribution, and the load–displacement curves are also shown, wherever relevant, therein.

All problems are solved in a fully coupled (monolithic) sense, adopting the Newton–Raphson method. The iterative procedure is terminated when an error measure defined as ratio of the norm of the residual in the current iteration to that of the first iteration is less than $1e{-}4$. The linear problem within each iteration is solved using the Intel Pardiso solver. Moreover, for all numerical experiments, the interaction parameter $\eta$ is parametrized as

$$\begin{aligned} \eta = \beta \dfrac{{G_c}}{{l}}, \end{aligned}$$

(39)

with $\beta$ being a user-defined non-dimensional scalar.

5.1 Single edge notched specimen under tension (SENT)

The single edge notched specimen [45] has been studied extensively under tensile and shear loading in the phase-field fracture literature. The geometry consists of a unit square (in mm) embedded with a horizontal notch, midway along height and equal to half of the edge length as shown in Fig. 2. The notch is modelled explicitly in the finite element mesh. A quasi-static loading is applied at the top boundary in the form of prescribed displacement increment $\Delta {u}= 1e{-}4$ [mm] for the first 55 steps, following which it is changed to $1e{-}6$ [mm]. The bottom boundary remains fixed. The model parameters are presented in Table 4.

Fig. 2

SENT experiment

Fig. 3

Figure a presents the load–displacement curves for the single edge notched specimen under tension. Here, $\beta$ is varied as {10, 100, 200}. Figure b shows the distribution of the phase-field variable at the final step of the analysis

Figure 3a present the load–displacement curves, corresponding to the brittle AT2 model. They are compared with the load–displacement curves from the literature [19, 45, 68]. While $\beta = 100, 200$ yield curves similar to those obtained by [68], $\beta = 10$ results in under-estimation of the peak load. The latter observation is due to the insufficient regularization of the phase-field. This is evident from Fig. 4a, where the phase-field ${\varphi }$ and the micromorphic variable ${d}$ is plotted for a section, $x = 0.75$ [mm] of the specimen. Therein, a localized behaviour is observed for ${\varphi }\ge 0.6$. Upon increasing $\beta$ to 100 and 200, the ${\varphi }$ and ${d}$ curves are similar, i.e., ${\varphi }\approx {d}$, which is an indication of sufficient regularization. When ${\varphi }\approx {d}$, the micromorphic phase-field fracture model is similar to the conventional phase-field fracture model. This explains the similar load–displacement curves for $\beta = 100,200$ and those obtained with conventional phase-field fracture model in the literature [19, 45, 68]. Moreover, the phase-field fracture topology in the final step of the simulation in Fig. 3b is also similar to those in the literature [19, 45, 68].

Table 4 Model parameters

Fig. 4

Figures present the phase-field (${\varphi }$) and the micromorphic variable (${d}$) for different $\beta$ values at $x=0.75$ [mm], along the height of the SENT specimen

5.2 Single edge notched specimen under shear (SENS)

The single edge notched specimen in the previous section is loaded horizontally along the top edge as shown in Fig. 5 for a shear test. Following the recommendations in [68], the geometry is discretised with four-noded quad elements with four integration points. The relevant model parameters are presented in Table 5, where a spectral decomposition based energy split is adopted to capture the tension–compression asymmetric response. A quasi-static loading is applied to the top boundary in the form of prescribed displacement increment $\Delta {u}= 1e{-}4$ [mm] for the first 85 steps, following which it is changed to $1e{-}6$ [mm]. Furthermore, the bottom boundary remains fixed, and roller supports are implemented in left and right edges restricting the vertical displacement.

Figure 6a shows the load displacement curves obtained using $\beta = 10, 100, 200$, and from [45]. The curves from [40, 68] are excluded since the former adopts a variationally inconsistent hybrid formulation, and the latter used a different set of boundary conditions. While $\beta = 100, 200$ yield curves similar to those obtained by [45], $\beta = 10$ results in under-estimation of the peak load. The latter observation is due to the insufficient regularization of the phase-field. The effect of the insufficient regularization has been explained in the previous sub-section. Moreover, the phase-field topology at the final step of the analysis is presented in Fig. 6b), where the fracture path is similar to that presented in [45].

Fig. 5

SENS experiment

Table 5 Model parameters

5.3 Winkler L-panel

The concrete L-shaped panel studied by [57, 69] is considered in this sub-section. Figure 7 shows the geometry as well as the loading conditions. The longer edges of the panel are 500 [mm] and the smaller edges are 250 [mm]. The loading is applied on the edge marked in blue, 30 [mm] in length, and is in the form of displacement increments of $\Delta {u}= 1e{-}3$ [mm]. The model parameters are presented in Table 6. The reader is referred to Sect. 2.1 for a detailed explanation of these parameters.

Figure 8a presents the load–displacement curves using the micromorphic phase-field fracture model, with $\beta = 100,200$. The range of the experimentally obtained load–displacement curves is shown in the shaded region. For both values of $\beta$, the load–displacement curves exhibit a good agreement with the experimental region. Moreover, the phase-field topology in the final step of the simulation in Fig. 8b is similar to that from the literature [57].

5.4 Quasi-brittle: concrete three-point bending

A three-point bending experiment on a notched concrete beam reported in [58] is considered here. The beam has dimensions $450\times 100$ [mm$^2$], and has a notch $5\times 50$ [mm$^2$]. A schematic of the beam along with the loading conditions is presented in Fig. 9. Displacement-based load increments of $\Delta {u}= 1e{-}3$ [mm] is enforced throughout the simulation. The model parameters are presented in Table 7. The reader is referred to Sect. 2.1 for a detailed explanation of these parameters.

Fig. 6

Figure a presents the load–displacement curves for the single edge notched specimen under shear. Here, $\beta$ is varied as {10, 100, 200}. Figure b shows the distribution of the phase-field variable at the final step of the analysis

Figure 10a presents the load–displacement curves using the micromorphic phase-field fracture model, with $\beta = 100,200$. The range of the experimentally obtained load–displacement curves is exhibited by the shaded region. For both values of $\beta$, the load–displacement curves exhibit a good agreement with the experimental region. Moreover, the phase-field topology in the final step of the simulation in Fig. 10b is similar to that from the literature [58].

5.5 Hydraulic fracturing

Two numerical experiments, adopted from [59] are considered for simulating hydraulic fracturing. The geometry consists on a square ($2 \times 2$ [m$^2$]) embedded with a Single Natural Fracture (SNF) in Fig. 11 and Three Natural Fractures (TNF) in Fig. 12. The fracture in the SNF specimen has a length 0.4 [m] and is located midway along the height. In the TNF specimen, two additional fractures are introduced. The vertical fracture has a length 1 [m] and is located at an x-offset 0.6 [m] from the centre of the specimen. The third fracture is a line segment from coordinates ($-$ 0.8, $-$ 0.3) to ($-$ 0.3, $-$ 0.8) assuming the axes origin placed at the centre of the specimen. Furthermore, on the external boundaries of the SNF and TNF models, the displacements and the fluid flux are set to zero. fluid is injected into the existing fractures (shown in red in Figs. 11 and 12) at a rate $q^p$. Note that in [59], the fluid injection is carried out using a point source instead of a line source. The model parameters, required for the simulation, are presented in Table 8.

Fig. 7

Winkler L-panel

Table 6 Parameters for L-shaped panel test [69]

Figure 13 presents the distribution of the phase-field in the SNF specimen at different times ($t = 0.01$, 0.1 and 0.2 [s]) during the fluid driven fracture propagation simulation. A similar fracture topology compared to [59] has been observed. Furthermore, the corresponding fluid pressure distributions are presented in Fig. 14. The localization of the fluid pressure follows from the dual permeability model (see Sect. 4.1), wherein the intrinsic permeability in the fracture is larger than the intrinsic permeability of the bulk material. Furthermore, as reported in [59], negative fluid pressure values are observed at the fracture tips, throughout the simulation.

Next, the TNF specimen is presented in this manuscript to demonstrate the fracture merging capabilities of the micromorphic phase-field fracture model. To this end, Fig. 15 presents the distribution of the phase-field in the SNF specimen at different times ($t = 0.001$, 0.024 and 0.048 [s]) during the fluid driven fracture propagation simulation. Figure 15b illustrates the merging of the evolving phase-field from the horizontal fracture onto the vertical fracture. In the same figure, the phase-field from the horizontal fracture evolves leftwards in a curved fashion subsequently merging with the inclined fracture, as shown in Fig. 15c. Furthermore, owing to the dual permeability model, localized fluid pressure distributions are observed in Fig. 16. Similar observations were made in [59] albeit with a point source of fluid injection, and a different dual permeability relationship.

Fig. 8

Figure a presents the load–displacement curves for the concrete Winkler L-panel test, for $\beta = 100, 200$. The experimental range is represented by the shaded area. Figure b shows the distribution of the phase-field variable at the final step of the analysis

6 Conclusions and outlook

A novel phase-field fracture model is proposed in this manuscript, based on the micromorphic extension of the phase-field fracture energy functional. In this model, the phase-field variable is local, and a ‘new’ micromorphic variable is introduced for regularization. In conjunction with the fracture irreversibility criterion, the phase-field evolution equation is a local variational inequality. This local equation is then solved pointwise (i.e., at integration points) in the computational domain. For brittle AT1 and AT2 fracture models, an explicit closed-form expression exist for the phase-field. However, for quasi-brittle fracture models, a nonlinear scalar equation needs to be solved iteratively. Furthermore, the local nature of the phase-field also provides the ease in implementing bounds, ${\varphi }\in [0,1]$ using the trivial ‘min’ and ‘max’ operations. The micromorphic phase-field fracture model enforces fracture irreversibility and bounds on the phase-field with system-level precision without the need for any user-defined parameter, tracking of active/inactive sets, and without any loss of variational consistency.

Fig. 9

Three point bending test

Table 7 Parameters for three point bending test

Fig. 10

Figure a presents the load–displacement curves for the concrete three-point bending test, with $\beta = 100, 200$. The experimental range is represented by the shaded area. Figure b shows the distribution of the phase-field variable at the final step of the analysis in a section of the beam

The micromorphic phase-field fracture model converges towards the conventional phase-field fracture model for an appropriately chosen interaction parameter $\eta$. An appropriately chosen value of $\alpha$ results in ${\varphi }\approx {d}$, thereby establishing the equivalence of the energy functional of the two models. This convergent behaviour is demonstrated in this manuscript through numerical experiments on a single edge notched specimen loaded in tension with varying $\alpha$. For $\alpha > rsim 100 {G_c}/ l$, ${\varphi }\approx {d}$ for an arbitrarily chosen section of the computational domain. In this case, both, the fracture topology as well as the load–displacement curve is similar to those obtained with conventional phase-field fracture models in the literature. For lower values of $\alpha$, the regularization is insufficient, and a local material behaviour is obtained. Additional numerical experiments were conducted, loading the aforementioned specimen in shear, and Winkler L-shaped panel and the concrete three-point bending tests for demonstrating quasi-brittle fracture phenomenon. For all experiments, the fracture topology as well as the load–displacement curve for $\alpha > rsim 100 {G_c}/ l$ were in agreement with results from the literature. The micromorphic phase-field fracture model, is thus able to demonstrate both brittle and quasi-brittle fracture in linear elastic media.

Furthermore, the feasibility of extending the micromorphic phase-field fracture model towards multiphysics problems is demonstrated through hydraulic fracturing simulations. To this end, the energy functional developed for linear elastic media is extended towards porous media, with an additional fluid phase contribution. A fluid transport equation is added to the system of equations, wherein a dual permeability model is introduced. The dual permeability model is defined using a fracture dependent scaling function that iterates between the bulk and fracture intrinsic permeabilities. For a sufficiently high $\eta$, the phase-field ${\varphi }\approx$ the micromorphic variable ${d}$. This allows the construction of a fracture dependent scaling function using the micromorphic variable instead of the phase-field. This choice circumvents the additional derivatives of the scaling function w.r.t. the strain and the micromorphic variable. Numerical experiments in hydraulic fracture demonstrates the fracture merging capabilities of the micromorphic phase-field fracture model in a multiphysics hydraulic fracturing context.

Fig. 11

Single natural fracture

Fig. 12

Three natural fractures

Table 8 Model parameters

Fig. 13

Figures a–c present the distribution of the phase-field variable at the different times during the analysis of the single natural fracture (SNF) specimen

Finally, the novel micromorphic phase-field fracture model opens a plethora of future research extensions, particularly, in other multi-physics applications, or composite laminates [70]. Other studies may include the implementation of a dissipation-based arc-length method [36, 38] or quasi-Newton methods [39, 40] for addressing the non-convexity of energy functional.

Fig. 14

Figures a–c present the distribution of the fluid pressure at the different times during the analysis of the single natural fracture (SNF) specimen

Fig. 15

Figures a–c present the distribution of the phase-field variable at the different times during the analysis of the three natural fractures (TNF) specimen

Fig. 16

Figures a–c present the distribution of the fluid pressure at the different times during the analysis of the three natural fractures (TNF) specimen