1 Introduction

Numerical analysis of inelastic deformations as well as of damage and fracture processes on different scales must be based on accurate modeling of material behavior. Therefore, different material approaches and corresponding efficient and robust numerical models have been published during the last decades, see for example [7, 8, 15, 25, 38]. Based on several experimental observations it is well known that damage and fracture in ductile metals are a result of nucleation, growth and coalescence of micro-defects which can accumulate to macro-cracks leading to final failure of engineering structures. Thus, a straight-forward way to develop appropriate material models is based on the numerical analysis of the deformation behavior of individual elastic–plastic representative volume elements (RVE) containing micro-defects revealed by scanning electron microscopy [6, 30, 33, 39]. Three-dimensional finite element analyses of microscopic cell models have been proposed to get insight in damage and fracture processes in isotropic materials and to study the evolution, growth and deformation of micro-defects under different loading conditions [3, 10, 17, 18, 26, 27, 34]. It has been shown that the current stress state has a remarkable influence on damage mechanisms on the micro-scale and the corresponding macroscopic failure behavior. Using the results of the numerical calculations on the micro-level it is possible to develop macroscopic phenomenological constitutive theories which can be used to numerically propose safety and life time of engineering structures [10]. The results can also be considered to validate evolution equations for damage variables or to identify micro-mechanically motivated material parameters.

In ductile metal sheets often anisotropies occur during production processes caused by internal changes in the crystallographic structure. Since these manufacturing-induced anisotropies remarkably affect the inelastic deformations they have to be taken into account in constitutive approaches to be able to realistically simulate the deformation and failure behavior of thin metal sheets. In the literature different anisotropic yield conditions have been discussed, for example, considering quadratic [1, 22, 35], non-quadratic [2, 4, 5, 20, 24] or spline functions [36] of stresses with independence of hydrostatic stress to adequately simulate experimentally observed deformation processes. In addition, for hydrostatic-stress-dependent materials the Hoffman yield criterion [23] has been introduced. This anisotropic yield criterion has been used to propose a damage criterion characterizing onset of damage based on numerical simulations of experiments with differently biaxially loaded cruciform specimens [14].

In the present paper an anisotropic material model is presented to numerically study the inelastic deformation and damage behavior of micro-defect-containing representative volume elements. Evolution of macroscopic damage strains is examined based on unit cell calculations under different three-dimensional loading conditions. In the present investigation the well-known 3D-unit-cell-analysis is enhanced for materials with plastic anisotropy and results for formation of damage strains for different load ratios and loading directions are discussed. The numerical results are used to propose a stress-state-dependent damage rule for anisotropic metals and to identify the corresponding material parameters.

2 Anisotropic material model

Analysis of finite inelastic deformation, damage and fracture behavior of metals is based on the phenomenological continuum model [8] which has been enhanced for anisotropic plasticity by [11, 13, 14]. It is based on several experimental observations [9, 16] as well as on results from numerical studies on the micro-level [10, 12, 21]. The theoretical material approach is briefly summarized in the present paper to demonstrate the need of experimental investigations with uniaxially and biaxially loaded specimens as well as of numerical simulations on the micro-scale to develop and to validate yield and damage criteria as well as evolution equations for plastic and damage strain tensors.

The continuum damage model considers damaged and corresponding fictitious undamaged configurations [31, 32, 37, 38]. In the initial undeformed configuration the base vectors \({\overset{o}{\textbf{g}}}_i\) and in the current inelastically deformed and damaged configuration the base vectors \({\textbf{g}}_i\) are introduced. This leads to the definition of the deformation gradient \({\textbf{F}} = {\textbf{g}}_i \otimes {\overset{o}{\textbf{g}}}^i\). In the present continuum model all stress and strain tensors are referred to the current configuration, see [8] for further details. The base vectors \({\overset{o}{\textbf{g}}}_i\) are chosen to be the Cartesian base. For plastic anisotropic materials the base vector \({\overset{o}{\textbf{g}}}_1\) corresponds to the rolling direction (RD) of the metal sheet, \({\overset{o}{\textbf{g}}}_2\) to the transverse direction (TD) and \({\overset{o}{\textbf{g}}}_3\) to the normal direction (ND).

Furthermore, the basic idea of the phenomenological framework is the introduction of the damage strain tensor, \({\textbf{A}}^{{da}}\), characterizing the evolution of macroscopic strains caused by damage mechanisms on the micro-level. In the kinematical approach, the strain rate tensor is separated into elastic, \({\varvec{\dot{\textrm{H}}}}^{el}\), effective plastic, \({\varvec{\dot{\bar{\textrm{H}}}}}^{pl}\), and damage parts, \({\varvec{\dot{\textrm{H}}}}^{da}\) [8].

Elastic–plastic constitutive equations are formulated with respect to the effective undamaged configurations. The effective Kirchhoff stress tensor

$$\begin{aligned} {\bar{\textbf{T}}} = 2 G \; {\textbf{A}}^{el} + \left( K - \frac{2}{3} G \right) \; {\textrm{tr}} {\textbf{A}}^{el} \; {\textbf{1}} \end{aligned}$$
(1)

characterizes the stress state in the undamaged matrix material where \({\textbf{A}}^{el}\) represents the elastic strain tensor and G and K are the constant shear and bulk modulus, respectively. For the investigated aluminum alloy EN AW-2017A these parameters have been determined as G = 28,500 MPa and K = 61,700 MPa based on numerical analysis of uniaxial tension tests with flat unnotched specimens [11]. The anisotropic plastic behavior is described by the Hoffman yield condition [23]

$$\begin{aligned} f^{{pl}} = {\textbf{C}} \cdot {\bar{\textbf{T}}} + \sqrt{ \frac{1}{2} {\bar{\textbf{T}}} \cdot {{\mathcal {D}}} \, {\bar{\textbf{T}}}} - c = 0, \end{aligned}$$
(2)

where the tensor of coefficients

$$\begin{aligned} {\textbf{C}} = C^{i}_{.j} \; {\textbf{g}}_i \otimes {\textbf{g}}^j = C_{(i)} \, {\textbf{g}}_i \otimes {\textbf{g}}^i \end{aligned}$$
(3)

with the components (in Voigt notation)

$$\begin{aligned} \left[ C^{i}_{.j} \right] = \left[ C_1 \;\, C_2 \;\, C_3 \;\, 0 \;\, 0 \;\, 0 \right] ^T \end{aligned}$$
(4)

taking into account the different yield stresses in uniaxial tension and compression tests. In addition, further material parameters in the tensor

$$\begin{aligned} {{\mathcal {D}}} = {D}^{i. \, k}_{. j. \, l} \; \textbf{g}_i \otimes {\textbf{g}}^j \otimes {\textbf{g}}_k \otimes {\textbf{g}}^l \end{aligned}$$
(5)

with

$$\begin{aligned} \left[ {D}^{i. \, k}_{. j. \, l} \right] = \left[ \begin{array}{c} C_4 + C_5 \;\; -C_4 \;\;\;\;\;\; -C_5 \;\;\;\;\;\; 0 \;\;\; 0 \;\;\; 0 \\ \;\; -C_4 \;\;\;\; C_4 + C_6 \;\;\; -C_6 \;\;\;\;\;\;\; 0 \;\;\; 0 \;\;\; 0 \\ \;\;\; -C_5 \;\;\;\;\; -C_6 \;\;\;\;\; C_5 + C_6 \;\;\; 0 \;\;\; 0 \;\;\; 0 \\ \;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\; C_7 \;\; 0 \;\;\; 0 \\ \;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\; 0 \;\; C_8 \;\;\; 0 \\ \;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\; 0 \;\;\; 0 \;\;\; C_9 \\ \end{array} \right] \end{aligned}$$
(6)

model the plastic anisotropy. The anisotropy parameters \(C_i\) in Eqs. (3) and (5) are determined considering stress and plastic strain behavior of unnotched, uniaxially loaded specimens cut in different directions with respect to the rolling direction [14]. These parameters are listed in Table 1.

Table 1 Anisotropy parameters
Full size table

In addition, in Eq. (2)

$$\begin{aligned} c = c_o + R_o \gamma + R_{\infty } \left( 1 - e^{- b \, \gamma } \right) \end{aligned}$$
(7)

is the equivalent yield stress of the undamaged metal which in the present analysis is taken to be the yield stress of the tensile test with the uniaxially loaded specimen cut in rolling direction of the thin metal sheet, \(c = c_x\). In Eq. (7) \(c_o\) denotes the initial yield stress, \(R_o\) and \(R_{\infty }\) are the hardening moduli, b represents the hardening exponent and \(\gamma \) is the equivalent plastic strain measure. For the investigated ductile anisotropic aluminum alloy EN AW-2017A the parameters are listed in Table 2. They have been determined by a uniaxial tension test of a flat dog-bone-shaped specimen, see [11] for further details.

Table 2 Plastic material parameters
Full size table

To characterize the stress state in the anisotropic ductile metal generalized invariants of the effective Kirchhoff stress tensor \({\bar{\textbf{T}}}\) are defined based on the yield condition (2)[14]: the first Hoffman stress invariant can be expressed in the form

$$\begin{aligned} {\bar{I}}^H_1 = \frac{1}{a} {\textbf{C}} \cdot {\bar{\textbf{T}}} \;\;\;{\textrm{with}} \; \; \; a = \frac{1}{3} \; {\textrm{tr}} {\textbf{C}} \end{aligned}$$
(8)

whereas the second and third deviatoric stress invariants are given by

$$\begin{aligned} {\bar{J}}^H_2 = \frac{1}{2} {\bar{\textbf{T}}} \cdot {{\mathcal {D}}} \, {\bar{\textbf{T}}} \end{aligned}$$
(9)

and

$$\begin{aligned} {\bar{J}}^H_3 = {\textrm{det}} \left( {{\mathcal {D}}} \; {\bar{\textbf{T}}} \right) \;. \end{aligned}$$
(10)

With these definitions the Hoffman yield criterion (2) is rewritten in the form

$$\begin{aligned} f^{pl} = a \, {\bar{I}}^H_1 + \sqrt{{\bar{J}}^H_2} - c = 0 \;. \end{aligned}$$
(11)

Furthermore, evolution of isochoric plastic strains is given by the flow rule

$$\begin{aligned} {\dot{\bar{\textbf{H}}}}^{{pl}} = {\dot{\gamma }} {\bar{\textbf{N}}}. \end{aligned}$$
(12)

with the equivalent plastic strain rate \({\dot{\gamma }}\) and the normalized deviatoric effective stress tensor

$$\begin{aligned} {\bar{\textbf{N}}} = \frac{{{\mathcal {D}}} \, {\bar{\textbf{T}}}}{\left\| {{\mathcal {D}}} \, {\bar{\textbf{T}}}\right\| } \;. \end{aligned}$$
(13)

Moreover, the damaged configurations are examined to model the behavior of the anisotropically damaged ductile metals. It has been shown in many experiments [28, 29] that the elastic behavior is also affected by damage and, thus, the elastic material equation is taken to be a function of both the elastic and the damage strain tensor, \({\textbf{A}}^{el}\) and \({\textbf{A}}^{da}\). Then, the Kirchhoff stress tensor is given by

$$\begin{aligned} {\textbf{T}} =&2&\left( G + \eta _2 \; {\textrm{tr}} {\textbf{A}}^{da} \right) \; {\textbf{A}}^{el}\nonumber \\+ & {} \left( K - \frac{2}{3} G + 2 \eta _1 \; {\textrm{tr}} {\textbf{A}}^{da} \right) {\textrm{tr}} {\textbf{A}}^{el} \; {\textbf{1}} \; \nonumber \\+ & {} \eta _3 \; \left( {\textbf{A}}^{da} \cdot {\textbf{A}}^{el} \right) \; {\textbf{1}} \; \nonumber \\+ & {} \eta _3 \; {\textrm{tr}} {\textbf{A}}^{el} {\textbf{A}}^{da} + \eta _4 \; \left( {\textbf{A}}^{el} {\textbf{A}}^{da} + {\textbf{A}}^{da} {\textbf{A}}^{el} \right) \, \end{aligned}$$
(14)

where the additional material parameters \(\eta _1, \, \eta _2, \, \eta _3\) and \(\eta _4\) are introduced describing deterioration of the macroscopic elastic properties caused by damage and fracture mechanisms on the micro-scale. To be able to characterize the stress state in the damaged configurations invariants of the Kirchhoff stress tensor (14) for anisotropic material behavior are also defined based on the Hoffman yield condition (2): the generalized first stress invariant is defined as

$$\begin{aligned} {I}^H_1 = \frac{1}{a} {\textbf{C}} \cdot {\textbf{T}} \;\;\;{\textrm{with}} \; \; \; a = \frac{1}{3} \; {\textrm{tr}} {\textbf{C}} \end{aligned}$$
(15)

and the second and third deviatoric stress invariants are expressed in the form

$$\begin{aligned} {J}^H_2 = \frac{1}{2} {\textbf{T}} \cdot {{\mathcal {D}}} \, {\textbf{T}} \end{aligned}$$
(16)

and

$$\begin{aligned} {J}^H_3 = {\textrm{det}} \left( {{\mathcal {D}}} \; {\textbf{T}} \right) \;. \end{aligned}$$
(17)

Alternatively, based on these equations further stress parameters can be defined to characterize the current stress state of the investigated anisotropic aluminum alloy: the generalized Hoffman stress triaxiality

$$\begin{aligned} {\eta }^H = \frac{{I}^H_1}{3 \sqrt{3 {J}^H_2}} \end{aligned}$$
(18)

and the generalized Hoffman Lode parameter

$$\begin{aligned} {L}^H = \frac{-3 \sqrt{3} \, {J}^H_3}{2 \, ({J}^H_2)^{(3/2)}} \;. \end{aligned}$$
(19)

With these stress parameters the damage condition

$$\begin{aligned} f^{{da}} = \alpha I^H_1 + \beta \sqrt{J^H_2} - \sigma = 0 \end{aligned}$$
(20)

can be formulated describing the onset and evolution of damage in the investigated plastically anisotropic ductile material. In Eq. (20) \(\sigma \) represents the equivalent damage stress measure. The parameters \(\alpha \) and \(\beta \) depend on stress state and loading direction and have been determined by series of experiments performed with different biaxially loaded specimens, see [14] for further details. Analyzing onset of damage for different stress states and loading directions, it has been shown that the parameter \(\alpha \) only depends on the stress triaxiality \(\eta ^H\)

$$\begin{aligned} \alpha (\eta ^H) = \left\{ \begin{array}{l} 0 \; \; \text{ for } \; \; \eta ^H \le 0 \\ \frac{1}{3} \; \; \text{ for } \; \; \eta ^H > 0 \end{array}\right. \;. \end{aligned}$$
(21)

whereas for the parameter \(\beta \) additional dependence on the loading direction has been detected:

$$\begin{aligned} \beta (\eta ^H, \theta ) = \left\{ \begin{array}{l} 1 \; \; \text{ for } \; \; \eta ^H \le 0 \\ k (\theta ) \; \eta ^H + 1 \; \; \text{ for } \; \; \eta ^H > 0 \end{array}\right. \; \end{aligned}$$
(22)

with the loading-direction-dependent factor

$$\begin{aligned} k (\theta ) = -0.167 \, {\textrm{cos}}^2 \theta - 0.062 \, {\textrm{cos}} \theta - 1.467 \; \end{aligned}$$
(23)

where \(\theta \) represents the angle with respect to the rolling direction (RD) of the metal sheet.

In addition, formation of macroscopic irreversible strains caused by damage and failure processes on the micro-scale is described by the damage rule

$$\begin{aligned} {\dot{\textbf{H}}}^{{da}} = {\dot{\mu }} \left( \frac{1}{\sqrt{3}} {\tilde{\alpha }} {\textbf{1}} + {\tilde{\beta }} {\textbf{N}} \right) \end{aligned}$$
(24)

where

$$\begin{aligned} {\textbf{N}} = \frac{{{\mathcal {D}}} {\textbf{T}}}{\left\| {{\mathcal {D}}} {\textbf{T}}\right\| } \end{aligned}$$
(25)

is the normalized deviatoric part of the Kirchhoff stress tensor, \({\dot{\mu }}\) is the rate of the equivalent damage strain measure representing the increase of amount of damage strains, and the parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) characterize the stress and loading direction dependence of the damage strain rate tensor (24). In Eq. (24) the first (volumetric) term corresponds to growth of micro-voids whereas the second (deviatoric) term is related to formation of micro-shear-cracks. It was not possible to detect the respective stress- and loading-direction-dependent functions for the damage rule by the performed experiments and, thus, an alternative way is followed. For isotropic material behavior these dependencies have been revealed by numerical simulations on the micro-level analyzing the deformation behavior of micro-defect-containing representative volume elements [10, 12, 21]. This proceeding is also used for the investigated anisotropic metal to detect the inelastic deformation of unit cells and damage mechanisms on the micro-level. This will render possible to develop stress-state- and loading-direction-dependent functions for the macroscopic damage strain rates.

3 Numerical analysis

Fig. 1
figure 1

Finite element mesh of one eighth of the unit cell

Full size image

The proposed phenomenological continuum damage model is based on macroscopic damage strains describing the current state of damage caused by different damage and failure mechanisms on the micro-scale. The formation of these damage strains is governed by the damage rule (24) which takes into account the parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) modeling the dependence of macroscopic stress state and loading direction with respect to the rolling direction of the damage strain rates. To detect these dependencies numerical simulations with the representative volume element containing an initially spherical void shown in Fig. 1 have been performed. The initial void volume fraction is chosen to be \(3 \%\) and different three-dimensional loading conditions are considered. The respective numerical calculations are performed with the finite element program ANSYS which has been enhanced by a user-defined material subroutine corresponding to the proposed phenomenological anisotropic elastic–plastic material model. In particular, the numerical analysis is based on eight-node solid elements of type SOLID185. During the loading process the initially plane surfaces of the unit cell remain plane. With these symmetry boundary conditions the RVE simulates the behavior of a pre-damaged structural element with regular and equidistant distribution of uniform micro-defects. Numerical studies taking into account variation of void shape and of distribution of voids showed that the analysis with the spherical void with \(3 \%\) porosity leads to the mean value for the parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) [21]. Therefore, only the behavior of the unit cell with initially spherical void in its center with \(3 \%\) initial void volume fraction is numerically analyzed. For the investigated anisotropic material the x-direction is taken to be the rolling direction (RD), the y-direction is the transverse direction (TD) whereas the z-direction is the thickness direction of the metal sheet. It is worthy to note that these numerical studies on the micro-level only give an idea for the formulation of constitutive equations. Afterwards, they have to be validated by various experiments and eventually to be modified if results of numerical simulations do not coincide with experimental data.

The kinematics of the continuum damage model takes into account the decomposition of the strain rate tensor into elastic \({\varvec{\dot{\textrm{H}}}}^{el}\), effective plastic, \({\varvec{\dot{\bar{{\textrm{H}}}}}}^{pl}\), and damage parts, \({\varvec{\dot{\textrm{H}}}}^{da}\). This leads to the additive decomposition of the components of the macroscopic strain rate tensor in the principal directions (i)

$$\begin{aligned} \dot{H}_{(i)}^{unit-cell} = \dot{H}_{(i)}^{el} + \dot{H}_{(i)}^{pl} + \dot{H}_{(i)}^{da} \end{aligned}$$
(26)

into elastic, plastic and damage strain rates. During loading of the unit cell the finite solid elements only undergo elastic and plastic strain rates on the micro-level, \(\varvec{\dot{h}}^{el}\) and \(\varvec{\dot{h}}^{pl}\). This leads to corresponding elastic–plastic macroscopic strain rates

$$\begin{aligned} \varvec{\dot{\textrm{H}}}^{ep} = \varvec{\dot{\textrm{H}}}^{el} + \varvec{\dot{\textrm{H}}}^{pl} = \frac{1}{V} \int _{V_{matrix}} \left( \varvec{\dot{h}}^{el} + \varvec{\dot{h}}^{pl} \right) \, \text{ d } v \end{aligned}$$
(27)

where V is the current volume of the representative volume element and \(V_{matrix}\) means the current volume of the matrix material (solid elements). With Eq. (26) the macroscopic damage strain rate tensor is then given by

$$\begin{aligned} \dot{H}_{(i)}^{da} = \dot{H}_{(i)}^{unit-cell} - \dot{H}_{(i)}^{ep} \;. \end{aligned}$$
(28)

This leads to the principal components of the damage strain tensor

$$\begin{aligned} A_{(i)}^{da} = \int \dot{H}_{(i)}^{da} \, \text{ d } t \;. \end{aligned}$$
(29)

In the numerical investigations the amount of strains and strain rates can be described with the definition of corresponding scalar-valued measures: the equivalent plastic strain rate

$$\begin{aligned} {\dot{\epsilon }}_{pl} = \sqrt{\frac{2}{3} {\varvec{\dot{\textrm{H}}}}^{pl} \cdot {\varvec{\dot{\textrm{H}}}}^{pl}} \; \end{aligned}$$
(30)

and the equivalent plastic strain

$$\begin{aligned} \epsilon _{pl} = \int {\dot{\epsilon }}_{pl} \, \text{ d } t \;. \end{aligned}$$
(31)
Fig. 2
figure 2

Formation of principal damage strain components for a \(F_x/F_y/F_z\) = 1/0/0, b \(F_x/F_y/F_z\) = 1/0/\(-\)1, c \(F_x/F_y/F_z\) = 1/0.63/0.27, d \(F_x/F_y/F_z\) = \(-\)1/\(-\)1/0.5

Full size image

The effect of loading of the void-containing representative volume elements (RVE) for different load ratios \(F_x/F_y/F_z\) on deformation and damage behavior is examined in detail. Different loading conditions are numerically analyzed and results are qualitatively compared with available experimental observations taken from tests with biaxially loaded specimens [11, 13].

In particular, for the load ratio \(F_x/F_y/F_z\) = 1/0/0 the numerically predicted formation of the principal components of the damage strain tensor is shown in Fig. 2(a) where loading in rolling direction (RD), diagonal direction (DD) and transverse direction (TD) is considered, respectively. With increasing deformation the damage strain \(A^{da}_x\) increases up to 0.032 for loading in RD and TD whereas slightly smaller damage strains can be seen under loading in DD. In this loading case, the damage strain \(A^{da}_y\) reaches \(-\)0.005 for loading in RD and TD and here about \(20 \%\) larger negative damage strains occur in DD whereas the damage strain \(A^{da}_z\) decreases up to \(-\)0.010 with only marginal differences for the different loading directions. The load ratio \(F_x/F_y/F_z\) = 1/0/0 corresponds to uniaxial loading leading for loading in RD to the stress triaxiality \(\eta ^H\) = 0.44 and the Lode parameter \(L^H\) = \(-\)0.70 on the macro-scale based on the Hoffman yield criterion. These results for the damage strain components detected by numerical simulations on the micro-level considering the behavior of void-containing RVEs agree with experimental observations taken from biaxially loaded specimens for loading cases with moderate positive stress triaxialities [11, 13]. Increase in pores has been seen after the tests for loading in RD and TD whereas after loading in DD smaller voids are revealed by scanning electron microscopy (SEM) corresponding to smaller damage strain components.

In addition, Fig. 2b shows numerical results from micro-mechanical analysis for the load ratio \(F_x/F_y/F_z\) = 1/0/\(-\)1 corresponding to shear loading conditions. The damage strain \(A^{da}_x\) increases up to 0.016 with increasing deformation of the RVE whereas \(A^{da}_z\) decreases up to \(-\)0.029 and \(A^{da}_y\) nearly remains 0.0. In this case only marginal effect of the loading direction with respect to the principal axes of anisotropy can be seen. For this load ratio the Hoffman stress parameters for loading in RD are \(\eta ^H\) = 0.21 and \(L^H\) = 0.00. After the respective experiments with the X0- and the H-specimen [11, 13] under shear loading conditions shear deformation on the micro-level with only very few initial voids has been revealed by SEM corresponding to the numerically predicted components of the damage strain tensor and also no influence of the loading direction has been seen.

Furthermore, for the load ratio \(F_x/F_y/F_z\) = 1/0.63/0.27 the evolution of the damage strain components is shown in Fig. 2c. Remarkable increase of the damage strains is numerically predicted up to 0.064 for \(A^{da}_x\), 0.037 for \(A^{da}_y\) and 0.011 for \(A^{da}_z\). For \(A^{da}_x\) and \(A^{da}_z\) larger increases occur for loading in TD and DD compared to RD whereas only larger increase in TD can be seen for \(A^{da}_y\). For this load ratio the stress triaxiality \(\eta ^H\) = 0.75 and the Lode parameter \(L^H\) = 0.23 based on the Hoffman criterion are computed for loading in RD indicating high hydrostatic stress state. In the experiment with the X0-specimen under biaxial tension loading similar stress state is reached [11] and SEM pictures show remarkable growth of voids with slightly smaller ones appeared after loading in RD.

On the other hand, the formation of damage strains for the load ratio \(F_x/F_y/F_z\) = \(-\)1/\(-\)1/0.5 is shown in Fig. 2d. The corresponding Hoffman stress parameters for loading in RD are \(\eta ^H\) = \(-\)0.34 and \(L^H\) = \(-\)1.00 indicating a compressive stress state. With increasing loading the damage strain components \(A^{da}_x\) and \(A^{da}_y\) decrease up to \(-\)0.015 whereas \(A^{da}_z\) increases up to 0.017 and this deformation behavior is nearly unaffected by the loading direction. It is worthy to note that for this loading case the volumetric damage strain tr\({\textbf{A}}^{da}\) is negative and, therefore, the initial void is compressed indicating that no further damage occurs. This behavior has also been observed in experiments under compression-dominated stress states [19].

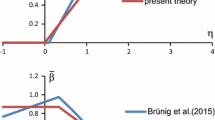
Since details of the damage and failure processes on the micro-level and their influence on the macroscopic damage behavior could not be revealed in the experiments, micro-mechanical numerical analysis of the deformation and damage behavior of the investigated void-containing unit cell under a wide range of loading conditions in the tensile, compressive and shear range as well as their combinations have been performed. The obtained numerical results discussed above can be seen as quasi-experimental ones which can be used to propose and to validate constitutive equations of phenomenological continuum models. Based on these quasi-experiments stress-state-dependent functions for the prediction of the damage strain rate tensor (24) are proposed. As can be seen in Fig. 2 the effect of the loading direction on the formation of damage strain components seems to be very small and, therefore, it will be neglected. Analysis of the results of the micro-mechanical numerical studies leads to the functions

$$\begin{aligned} \tilde{\alpha }(\eta ^{H} ) = \left\{ {\begin{array}{*{20}l} {0.0672{\hspace{0.55542pt}} \eta ^{H} - 0.2421} &{} {{\text {for}}\;\;\eta ^{H} < 0.21} \\ {2.671{\hspace{0.55542pt}} \eta ^{H} - 0.859} &{} {{\text {for}}\;\;0.21 \le \eta ^{H} \le 0.70} \\ {0.8{\hspace{0.55542pt}} \eta ^{H} + 0.285} &{} {{\text {for}}\;\;\eta ^{H} > 0.7} \\ \end{array} } \right. \nonumber \\ \end{aligned}$$
(32)

and

$$\begin{aligned} \tilde{\beta }(\eta ^{H} ,{\hspace{0.55542pt}} L^{H} ) = \left\{ {\begin{array}{*{20}l} {0.9821} &{} {{\text {for}}\;\;\eta ^{H} < 0.45} \\ {1.244 - 0.9866{\hspace{0.55542pt}} \eta ^{H} + 0.4471{\hspace{0.55542pt}} L^{H} } &{} {{\text {for}}\;\;\eta ^{H} > 0.45} \\ \end{array} } \right. \nonumber \\ \end{aligned}$$
(33)

fitting the micro-numerically obtained damage strain curves by the macroscopic damage rule (24). These functions are visualized in Fig. 3.

Fig. 3
figure 3

Damage strain parameters \({\tilde{\alpha }}\) and \({\tilde{\beta }}\) in the space of the stress parameters \(\eta ^H\) and \(L^H\)

Full size image
Fig. 4
figure 4

Numerical simulation of the formation of damage strains for a \(\eta ^H\) = 0.44 and \(L^H\) = \(-\)0.70, b \(\eta ^H\) = 0.21 and \(L^H\) = 0.00, c \(\eta ^H\) = 0.75 and \(L^H\) = 0.23, d \(\eta ^H\) = \(-\)0.34 and \(L^H\) = \(-\)1.00, e \(\eta ^H\) = 0.66 and \(L^H\) = 1.00, f \(\eta ^H\) = 0.33 and \(L^H\) = 1.00

Full size image

Based on the damage rule (24) with the the stress-state-dependent functions (32) and (33) macroscopic numerical simulations have been performed to predict the elastic–plastic-damage behavior of a homogeneous material element made of the investigated aluminum alloy EN AW-2017A. As can be seen from Eq. (24) the parameter \(\tilde{\alpha }\) is related to the volumetric part of the damage strain rate tensor whereas the parameter \({\tilde{\beta }}\) corresponds to its deviatoric part modeling isochoric strains caused by damage. To validate the functions (32) and (33) numerical simulations covering a wide range of stress states are performed. The results based on the numerical analysis of the void-containing unit cell (RVE) and the numerical simulations based on the continuum model (Sim) are shown in Fig. 4.

For the load ratio \(F_x/F_y/F_z\) = 1/0/0 the quasi-experimental and numerical results are shown in Fig. 4a. The evolution of the damage strain component \(A^{da}_x\) is very well numerically predicted and for \(A^{da}_y\) and \(A^{da}_z\) which are identical in the numerical simulation only small differences can be seen. However, these components are small and, therefore, this deviation will not remarkably affect the predicted damage behavior. In Fig. 4b, results for the load ratio \(F_x/F_y/F_z\) = 1/0/\(-\)1 are compared. In this shear loading case the formation of the damage strain \(A^{da}_x\) is nicely simulated. For \(A^{da}_z\) the results show good agreement for the first loading process and after \(30 \%\) plastic deformation smaller negative damage strains are numerically predicted. In the quasi-experiments the damage strain component \(A^{da}_y\) is nearly zero whereas a very small component of \(-\)0.007 is computed. In this case the global trend of damage mechanisms is well simulated. For the loading case \(F_x/F_y/F_z\) = 1/0.63/0.27 with remarkable hydrostatic stress the results are shown in Fig. 4c. For \(A^{da}_x\) and \(A^{da}_y\) nearly perfect agreement of quasi-experimental and numerical results can be seen and only the prediction of the at the beginning of the loading process nearly zero and then slightly increasing damage strain component \(A^{da}_z\) show small deviation but later also good agreement. In Fig. 4d results for the load ratio \(F_x/F_y/F_z\) = \(-\)1/\(-\)1/0.5 can be compared. In this loading case with high hydrostatic pressure perfect agreement for the evolution of all damage strain components \(A^{da}_x\), \(A^{da}_y\) and \(A^{da}_z\) are visible. In addition to the quasi-experimental results shown in Fig. 2 two further interesting load cases are shown in Fig. 4. For example, results for the load ratio \(F_x/F_y/F_z\) = 1/1/0.25 leading to the Hoffman stress parameters \(\eta ^H\) = 0.66 and \(L^H\) = 1.00 are shown in Fig. 4(e). This case is in contrast to the other load ratios characterized by high stress triaxiality and high Lode parameter. It can be seen that the damage strain components \(A^{da}_x\) and \(A^{da}_y\) only show marginal differences of quasi-experimental and numerical results and only the nearly zero component \(A^{da}_z\) have slight deviations. The alternative load ratio \(F_x/F_y/F_z\) = 1/1/\(-\)0.5 (Fig. 4f) is also considered with the moderate stress triaxiality \(\eta ^H\) = 0.33 and the high Lode parameter \(L^H\) = 1.00. In this case, all numerically predicted damage strain components agree very well with the quasi-experimental ones.

In the numerical analysis a wide range of stress states has been considered with stress triaxialities between \(\eta ^H\) = 0.75 and \(-\)0.34 as well as Lode parameters between \(L^H\) = 1.00 and \(-\)1.00. In Fig. 4 in all cases very good agreement of quasi-experimental and numerical results has been achieved demonstrating the accuracy of the proposed damage rule (24) with the stress-state-dependent parameters (32) and (33). Thus, these equations of the continuum model are validated by results of numerical simulations on the micro-scale.

4 Conclusions

In the present paper the effect of the stress state and of the loading direction with respect to the principal axes of anisotropy on deformation behavior as well as on damage and failure processes on the micro- and macro-level has been examined. A continuum damage model including the Hoffman yield criterion for anisotropic plasticity as well as a stress-state- and loading-direction-dependent damage criterion has been discussed. For the investigated aluminum alloy EN AW-2017A the stress state is characterized by the generalized stress triaxiality and the generalized Lode parameter both related to the Hoffman yield criterion. Since it is difficult to reveal information on damage and failure processes on the micro- and the macro-scale as well as their interaction by experiments alone numerical simulations on the micro-level have been performed. In these studies the deformation behavior of micro-void-containing representative volume elements have been multiaxially loaded and variation of load ratios in different directions with respect to the rolling direction has been taken into account. Based on these calculations on the micro-scale formation of components of the damage strain tensors are detected. These results have been qualitatively compared with pictures from scanning electron microscopy published in the literature. The numerically predicted evolution of principal damage strain components can be seen as quasi-experimental results. They clearly demonstrate the influence of the stress state and of the loading direction on damage evolution. Using these quasi-experimental results stress-state-dependent functions for the damage rule describing the formation of macroscopic damage strains have been proposed. These equations have been validated by numerical simulation of the quasi-experiments covering a wide range of stress triaxilities and Lode parameters. In all cases, very good agreement of the results have been achieved. Of course, in the present paper the damage rule has only been validated by results of numerical analysis on the micro-level. But with these studies it was possible to propose constitutive equations which in the next step must be validated by experiments with biaxially loaded specimens also covering a wide range of stress states. This will be the subject of a forthcoming paper. Then, with this theoretical framework it will be possible to perform numerical studies to examine the deformation, damage and failure behavior of structural components built with anisotropic sheet metals.