The parametrized superelement approach for lattice joint modelling and simulation

Abstract

From large scale structures such as bridges and cranes to small-scale structures such as lattices, mechanical structures today increasingly consist of “tuneable parts”: parts with a simple geometry described by a small set of strongly varying parameters. For example, although a bridge is a macroscale structure with a complex geometry, it is made from simple beams, bolts and plates, all of which depend on spatially varying, geometrical parameters such as their length-to-width ratio. Accelerating this trend is the concurrent improvement of, on one hand, Additive Manufacturing techniques that allow for increasingly complex parts to be manufactured and, on the other, structural optimization techniques that exploit this expanded design space. However, this trend also poses a challenge to current simulation techniques, as for example the Finite Element Method requires large amounts of elements to represent such structures. We propose to exploit the large conformity between parts inside the mechanical structure through construction of semi-analytic “Parametrized Superelements”, built by meshing with solid elements, reduction to a fixed interface and approximation of the reduced stiffness matrices. These new elements can be employed next to standard elements, enabling the simulation of more complex geometries. The technique we propose is applied to lattice structures and provides a flexible, differentiable, more accurate but still efficient way to simulate their elastic response. A net gain in total computation time occurs after simulating more than twenty lattices. As such, the proposed method enables large-scale parameter exploration and optimization of lattice structures for improved energy absorption, mass and/or stiffness.

Appendices

Appendix A: Traction vector on a plane surface

Consider a planar surface on which a reaction force $\mathbf {f}$ and a reaction moment $\mathbf {m}$ is applied. If the traction vector is linear over the surface, then it can be written as

$$\begin{aligned} \mathbf {t}_{ \mathbf {n}}(x,y,z) = \mathbf {t}_{f} + \mathbf {t}_{m} \times ( \mathbf {p}- \mathbf {p}_C), \end{aligned}$$

(18)

where $\mathbf {p}_C$ is the surface centroid and $\mathbf {t}_{ \mathbf {f}}$ and $\mathbf {t}_{ \mathbf {m}}$ are unknown but constant vectors that depend on the reaction force and moment via the averaging Eqs. 2 and 3, respectively. Substituting Eq. (18) into Eq. (2), it can readily be seen that $\mathbf {t}_{ \mathbf {f}} = \mathbf {f}/A$, i.e. applying a force to a plane surface leads to a constant traction vector. Substituting Eq. (18) into Eq. (3) leads to:

$$\begin{aligned} \mathbf {m}&= \int _A ( \mathbf {t}_{f} + \mathbf {t}_{ \mathbf {m}} \times ( \mathbf {p}- \mathbf {p}_C)) \times ( \mathbf {p} - \mathbf {p}_C) \,\mathrm {d}A \\&= \int _A \mathbf {t}_{f} \times ( \mathbf {p} - \mathbf {p}_C) \,\mathrm {d}A \\&\quad + \int _A ( \mathbf {t}_{m} \times ( \mathbf {p}- \mathbf {p}_C)) \times ( \mathbf {p} - \mathbf {p}_C) \,\mathrm {d}A \\&= \int _A \left\Vert \mathbf {p} - \mathbf {p}_C\right\Vert ^2_2 \mathbf {t}_{m} \,\mathrm {d}A -\int _A (( \mathbf {p} - \mathbf {p}_C) \cdot \mathbf {t}_{m}) ( \mathbf {p}- \mathbf {p}_C) \,\mathrm {d}A . \end{aligned}$$

The last equality holds due to the vector triple product. Introducing the second moment of area tensor $\{ \mathbf {J}:J_{i,j}=\int _A (x_i-x_{i,C})(x_j-x_{j,C}) \,\mathrm {d}A\}$, this can be rewritten as:

$$\begin{aligned} ( \mathbf {J} - {\text {tr}}( \mathbf {J}) \mathbf {I}_3) \mathbf {t}_{ \mathbf {m}} = \mathbf {m}, \end{aligned}$$

where $\mathbf {I}_3$ is the $3 \times 3$ unit matrix. The matrix $\hat{ \mathbf {J}}$ is defined as

$$\begin{aligned} \hat{ \mathbf {J}} = \mathbf {J} - {\text {tr}}( \mathbf {J}) \mathbf {I}_3 , \end{aligned}$$

simplifying the expression for the rotational component of the traction vector to $\hat{ \mathbf {J}} \mathbf {t}_{ \mathbf {m}} = \mathbf {m}$.

Appendix B: Sampling algorithm details

The sampling algorithm’s details are now elaborated. It consists of two main decision steps and an acceptance-rejection step.

The first decision step chooses the required number of samples for the training and the test set. For the training set, a decision is made based on the required number of samples $N_{training}$ for the subsequent approximation to be unique. That is, there should be at least as many samples as there are parameters (e.g. basis function coefficients) in the approximate model. Of course, the number of approximation parameters is only known after increasing their number until approximation error convergence is achieved. This was done for some joint types starting from a rough estimate of $N_{training} \approx R \cdot n_b \cdot N_D$, where R is the expected rank and $N_D$ the expected number of basis function coefficients for a single dimension, based on [5, Question 4]. Initial attempts showed $R \approx 30$ and $N_D \approx 6$, yielding between 100 and 800 training samples for diamond lattice joints. It must be noted that the amount of training samples increases (usually by at most 10 samples) during approximation, since samples are added in an adaptive way, close to test samples with a large approximation error. To conclude, the number of test samples is chosen such that the test set contains roughly ten percent of the total amount of samples.

The second decision step chooses the number and distribution of “sparse” samples, i.e. samples containing one or more zero features. These sparse samples thus represent joints that lack one or more beams. These samples are important since they lie at the boundary of the sample domain and are thus otherwise very hard to sample. In general, training and test sets are created consisting of roughly thirty percent sparse samples. When a sample is chosen to be sparse, a decision is made on the measure of “sparsity” of this sample or, in other words, how many features should be zero. This decision is made by uniformly dividing the sparse samples over all possible measures of sparsity, going from only a single zero feature to all of them except one (ensuring of course that the joint still has external faces).

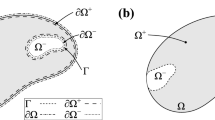
Finally, an acceptance-rejection method creates the samples in three substeps. Consider the required generation of a sample $(r_1, \ldots , r_{n_b})$ with $n_0$ zero features. First, a random selection is performed: a total of $n_0$ features are chosen and kept at zero. Second, the remaining $n_b - n_0$ features are generated in a randomized fashion. Third, the generated samples are either accepted or rejected based on both the symmetry and the overlap constraints mentioned in Sect. 5.1 and visualized in Fig. 12. The workings of the second substep are now further explained.

Test sample features are generated from two types of normal distributions, $\mathcal {N}_1(\mu _1, \sigma _1)$ and $\mathcal {N}_2(\mu _2, \sigma _2)$. $\mathcal {N}_1$ has a large standard deviation $\sigma _1$ (e.g. 0.25) to ensure the bulk of the feature space is properly sampled, whereas $\mathcal {N}_2$ has a smaller deviation $\sigma _2$ (usually 0.1) but a larger mean $\mu _2$ (around 0.8) to better sample the feature space boundaries. For both, features are bounded to be in the interval $[r_{min}, r_{max}]$ by applying $\max (\min (r, r_{max}), r_{min})$ to a sampled value r. Here, $r_{min}$ is usually chosen at 0.1 since meshing problems occur for smaller radii.

Training sample features are generated in a similar way. However, since a tensor decomposition is used during approximation, a discrete grid is employed. Consider an $n_b$-dimensional feature space with N points in every dimension, thus containing a total of $N^{n_b}$ points (see Fig. 19). The k-th dimension of this multidimensional grid is indexed by $i_k$, where $k=1, \ldots , n_b$, such that $f_k(i_k) = f_k^{\min } + i_k \frac{f_k^{max} - f_k^{min}}{N - 1}$, $i_k=0, \ldots , N-1$. Discrete versions of the normal distributions⁷ are employed to sample the grid. This results in a sampled multi-index $(i_1, \ldots , i_{n_b})$ that correspond to joints with a reduced representations $\mathbf {L}(f_1(i_1), \ldots , f_{n_b}(i_{n_b}))$. Since the sampling is quite sparse and a lot of samples are rejected, for a dimension k only a subset of all possible indices $i_k \in [0, \ldots , N-1]$ are used. The indices $i_k$ are therefore omitted in favor of the reduced indices

$$\begin{aligned} j_k \in [1, N_k], \end{aligned}$$

(19)

where $N_k \le N+1$. For example, in Fig. 19 there is no sample with $i_1 = 0$ and thus $N_1 = N - 1 = 2$. The reduced joint representations can also be written as $\mathbf {L}(f_1(j_1), \ldots , f_{n_b}(j_{n_b}))$, which we abbreviate to $\mathbf {L}(j_1, \ldots , j_{n_b})$.

Fig. 19

Multidimensional feature grid for features $f_1$, $f_2$ and $f_3$ with $N=3$ and three randomly selected samples shown in red

A major challenge with the above sampling method is the difficulty of sampling close to the feature space boundary (see Fig. 12). This boundary is essential since in practice only joints lying on this boundary are used. Consider a joint in the bulk region, such as the one shown in Fig. 11. The radius of this joint can be reduced without causing overlap, and therefore, as is also clear from Sect. 3, such a joint will be omitted in favor the closest joint on the feature boundary. However, during sampling the joint radius is fixed at 1 and complicates sampling the boundary. Although the $\mathcal {N}_2$ distribution used for this purpose comes reasonable close to the feature space boundary for test samples, training samples are limited by the hypergrid. An obvious improvement could therefore be to refine the grid spacing to a certain tolerance. From a higher level though, this challenge stems from the fact that the feature space has one superfluous parameter, namely the joint radius currently kept at 1. Future work will focus on this challenge.

Appendix C: Approximation algorithm details

Two techniques are developed for the approximation of the map from the feature space to the reduced stiffness matrix space: a matrix-level and an entry-level technique. Both employ tensor decomposition, more specifically the canonical polyadic decomposition (CPD) [17]. A detailed overview of both methods will be given here.

In general, CPD decomposes a k-dimensional tensor $T \in \mathbb {R}^{n_1 \times \cdots \times n_k}$ into an approximate sum of rank-1 tensors, similar to a singular value decomposition,

$$\begin{aligned} T \approx \sum _{r=1}^R \mathbf {u}_r^1 \otimes \cdots \otimes \mathbf {u}_r^{k}, \end{aligned}$$

where $\mathbf {u}_r^j \in \mathbb {R}^{n_j}$ are called factor vectors and R is the length or rank of the CPD. Recall that the tensor product $\mathbf {A} = \mathbf {u}_r^1 \otimes \cdots \otimes \mathbf {u}_r^k$ is defined elementwise as

$$\begin{aligned} \mathbf {A}(i_1,\ldots ,i_k) = \mathbf {u}_r^1(i_1) \cdot \cdots \cdot \mathbf {u}_r^k(i_k). \end{aligned}$$

In particular, $\mathbf {A} = \mathbf {u}_r^1 \otimes \mathbf {u}_r^2 = \mathbf {u}_r^1 ( \mathbf {u}_r^2)^T$.

Both the matrix- and the entry-level method convert the reduced joint matrix representation $\mathbf {L}$ of the sample points to two or more tensors. More specifically, the matrix-level method constructs a tensor $\mathbf {T}_1$ containing the normalized stiffness matrices of the samples and another tensor $\mathbf {T}_2$ containing the sample L2 norms, whereas the entry-level method constructs a tensor for every entry of $\mathbf {L}$. These tensors are incomplete since not all points on the hypergrid are sampled.

After the tensors are generated, they are assumed to be decomposable into a CPD of small length where some or all of the factor vectors $\mathbf {u}_r^j$ are restricted to be the evaluation univariate functions $u_r^j$ (“factor functions”) of their corresponding feature $f_j$. That is, the entries in the factor vectors are the evaluations of the factor functions on the multidimensional regular, $n_b$-dimensional grid from the sample generation step. This is enforced through structured data fusion [33]. In this paper, both polynomial and rational functions are used.

Next, a decomposition that satisfies these restrictions is found through the solution of a nonlinear least-squares optimization problem that minimizes the error between the decomposition and the reduced joint stiffness matrices of the sampled joint configurations inside the tensors.

Finally, the decomposition and more specifically, the factor function’s coefficients, are extracted and transformed into an approximation $I(f_1, \ldots , f_{n_b})$ of the reduced joint stiffness matrix representation $\mathbf {L}(f_1, \ldots , f_{n_b})$, such that $\mathbf {L}(f_1, \ldots , f_{n_b}) \approx I(f_1, \ldots , f_{n_b})$.

Matrix-level approximation In the matrix-level approach, two tensors are used. The first tensor, $\mathbf {T}_1$, contains the normalized, reduced joint stiffness matrices and is thus used to approximate the normalized joint matrix. The second tensor, $\mathbf {T}_2$, contains the $L_2$ norms of the reduced joint matrices and is used to approximate the norm of the joint matrix. This division into a tensor for the matrix norm and a tensor for the normalized matrix is employed to prevent the optimization algorithm from focusing solely on joint matrices with a high norm.

The first tensor $\mathbf {T}_1$ has $n_b+1$ dimensions, i.e.

$$\begin{aligned} \mathbf {T}_1 \in \mathbb {R}^{N_1 \times \cdots \times N_{n_b} \times N_{n_b+1}}. \end{aligned}$$

Fig. 20

Visualization of the matrix-level CPD approximation for a corner joint in a diamond lattice

Each dimension $N_k$ is indexed by a reduced index $j_k$ from Eq. (19). The first $n_b$ dimensions are the feature dimensions and indexed by the first $n_b$ reduced hypergrid indices. They are from now on referred to as the feature indices. The last, $n_b+1$-th dimension is the ‘matrix’ dimension and its index $j_{n_b+1} \in [1, N_{n_b+1}]$ selects an entry from the linearized $\mathbf {L}_n$ matrix by converting it to a vector $\mathbf {l}_n \in \mathbb {R}^{N_{n_b+1}}$. Since $\mathbf {L}_n \in \mathbb {R}^{n_r \times n_r}$ is lower-triangular, $N_{n_b+1} = {n_r +1 \atopwithdelims ()2}$.

As an example, consider a sample with feature indices $(j_1, \ldots , j_{n_b})$ and its corresponding reduced representation of the joint matrix $\mathbf {L}(j_1, \ldots , j_{n_b})$. The normalization of this matrix is then defined as

$$\begin{aligned} \mathbf {L}_n(j_1, \ldots , j_{n_b}) = \frac{ \mathbf {L}(j_1, \ldots , j_{n_b})}{\left\Vert \mathbf {L}(j_1, \ldots , j_{n_b})\right\Vert _2} \in \mathbb {R}^{n_r \times n_r}. \end{aligned}$$

The entries of $\mathbf {L}_n(j_1, \ldots , j_{n_b})$ are then found by indexing $\mathbf {T}_1$ as $\mathbf {T}_1 [j_1, \ldots , j_{n_b}, :]$. Here, the  :  index is a slice across the matrix dimension and thus contains the entries of the lower-triangular part of $\mathbf {L}_n(j_1, \ldots , j_{n_b})$. Selecting an entry of that matrix is defined as $\mathbf {T}_1 [j_1, \ldots , j_{n_b}, j_{n_b+1}] = \mathbf {l}_n(j_1, \ldots , j_{n_b})[j_{n_b+1}]$.

The second tensor $\mathbf {T}_2$ has $n_b$ feature dimensions and only contains the norms of the reduced joint matrices, i.e. $\mathbf {T}_2 [l_1, \ldots , l_{n_b}]=\left\Vert \mathbf {L}(l_1, \ldots , l_{n_b})\right\Vert _2$.

Both $\mathbf {T}_1$ and $\mathbf {T}_2$ are then approximated with a CPD. The first is decomposed as follows:

$$\begin{aligned} \mathbf {T}_1 \approx \sum _{r=1}^{R_1} \mathbf {u}_r^1 \otimes \cdots \otimes \mathbf {u}_r^{n_b} \otimes \mathbf {u}_r^{n_b+1}. \end{aligned}$$

The feature factor vectors $\mathbf {u}_r^k$, with $k=1, \ldots , n_b$, are restricted to be the evaluations of polynomial or rational functions $u_r^k(f_k)$. Their degree, together with the number of terms $R_1$, is increased until the approximation error reached the discretization error observed during the mesh convergence tests. Based on our experiments, around thirty terms and rational functions with a sixth-degree numerator and a second-degree denominator usually suffice to properly represent the joints inside a diamond lattice. The last factor vectors $\mathbf {u}_r^{n_b+1}$, $r=1, \ldots , R_1$, are not restricted. They are thus optimized freely and afterwards delinearized into $R_1$ lower-triangular basis matrices $\mathbf {L}_r^b \in \mathbb {R}^{n_r \times n_r}$, $r=1, \ldots , R_1$. The following functional approximation for the normalized, reduced joint matrix representation $\mathbf {L}_n(f_1, \ldots , f_{n_b})$ is then obtained:

$$\begin{aligned} \mathbf {L}_n(f_1, \ldots , f_{n_b})&\approx \sum _{r=1}^{R_1} u_r^1(f_1) \cdot \cdots \cdot u_r^{n_b}(f_{n_b}) \cdot \mathbf {L}_r^b \\&=: \mathbf {I}_1(f_1, \ldots , f_{n_b}). \end{aligned}$$

The second tensor is decomposed as

$$\begin{aligned} \mathbf {T}_2 \approx \sum _{r=1}^{R_2} \mathbf {v}_r^1 \otimes \cdots \otimes \mathbf {v}_r^{n_b}, \end{aligned}$$

where, again, the feature factor vectors $\mathbf {v}_r^k$, with $k=1, \ldots , n_b$, are restricted to be the evaluations of polynomial or rational functions $v_r^k(f_k)$. Due to the very smooth behaviour of the joint matrix norm, a low degree and a limited number of terms $R_2$ is required to represent it with sufficient accuracy. In this paper, around ten terms and fifth-degree polynomials are used. The functional approximation $I_2(f_1, \ldots , f_{n_b})$ for the reduced joint matrix norm $\left\Vert \mathbf {L}(j_1, \ldots , j_{n_b})\right\Vert _2$ is then obtained

$$\begin{aligned} \left\Vert \mathbf {L}(j_1, \ldots , j_{n_b})\right\Vert _2&\approx \sum _{r=1}^{R_2} v_r^{1}(f_1) \cdot \cdots \cdot v_r^{n_b}(f_{n_b}) \\&=: I_2(f_1, \ldots , f_{n_b}) \end{aligned}$$

and the approximation of the reduced joint matrix $\mathbf {L}(f_1, \ldots , f_{n_b})$ can be written as

$$\begin{aligned} \mathbf {L}(f_1, \ldots , f_{n_b}) \approx \mathbf {I}_1(f_1, \ldots , f_{n_b}) \cdot I_2(f_1, \ldots , f_{n_b}). \end{aligned}$$

Figure 20 visualizes a basis matrix and two factor vectors with corresponding factor functions of an exemplar matrix-level approximation of a corner joint. The factor vectors are interpolated exactly by the factor functions since this is a constraint enforced during the least-squares optimization.

Entry-level approximation While the matrix-level approximator simultaneously constructs an approximation for all entries inside $\mathbf {L}$, the entry-level method approximates every entry separately, similarly to how the matrix-level method approximates the matrix norm.

Consider again the reduced representation of the joint stiffness matrices $\mathbf {L}(j_1, \ldots , j_{n_b})$. For every lower-diagonal entry (m, n), ${n_r +1 \atopwithdelims ()2}$ in total, a tensor $\mathbf {T}_{m, n} \in \mathbb {R}^{N_1 \times \cdots \times N_{n_b}}$ is constructed such that

$$\begin{aligned} \mathbf {T}_{m, n}(j_1, \ldots , j_{n_b}) = \mathbf {L}(j_1, \ldots , j_{n_b})[m, n]. \end{aligned}$$

The tensor $\mathbf {T}_{m, n}$ is then decomposed as

$$\begin{aligned} \mathbf {T}_{m, n} \approx \sum _{r=1}^{R_{m,n}} \mathbf {w}^1_{r, m, n} \otimes \cdots \otimes \mathbf {w}^{n_b}_{r, m, n}, \end{aligned}$$

where $\mathbf {w}^k_{r, m, n}$ are feature factor vectors indexed by the feature dimension index $k=1, \ldots , n_b$, the CPD term index $r=1, \ldots , R_{m,n}$ and the indices into the lower-triangular part of $\mathbf {L}$, m and n. The feature factor vectors are again restricted to be the evaluations of rational functions $w^k_{r, m, n}(f_k)$. Furthermore, entries are known to become zero when their corresponding beam has zero radius. The corresponding factors are therefore restricted to have that property as well. Based on our experiments, around 15 terms, a sixth-degree numerator and a second-degree denominator suffice to obtain sufficient accuracy. The approximation $I_{m, n}(f_1, \ldots , f_{n_b})$ for the (m, n) entry of the reduced joint matrix representation $\mathbf {L}(l_1, \ldots , l_{n_b})[i, j]$ is then obtained:

$$\begin{aligned} \mathbf {L}(l_1, \ldots , l_{n_b})[m, n]&\approx \sum _{r=1}^{R_{m, n}} w^1_{r, m, n}(f_1) \cdot \cdots \cdot w^{n_b}_{r, m, n}(f_{n_b})\\&=: I_{m, n}(f_1, \ldots , f_{n_b}). \end{aligned}$$