A thermo-viscoplasticity model for metals over wide temperature ranges- application to case hardening steel

Abstract

In this contribution, a model for the thermomechanically coupled behaviour of case hardening steel is introduced with application to 16MnCr5 (1.7131). The model is based on a decomposition of the free energy into a thermo-elastic and a plastic part. Associated viscoplasticity, in terms of a temperature-depenent Perzyna-type power law, in combination with an isotropic von Mises yield function takes respect for strain-rate dependency of the yield stress. The model covers additional temperature-related effects, like temperature-dependent elastic moduli, coefficient of thermal expansion, heat capacity, heat conductivity, yield stress and cold work hardening. The formulation fulfils the second law of thermodynamics in the form of the Clausius–Duhem inequality by exploiting the Coleman–Noll procedure. The introduced model parameters are fitted against experimental data. An implementation into a fully coupled finite element model is provided and representative numerical examples are presented showing aspects of the localisation and regularisation behaviour of the proposed model.

1 Introduction

During the manufacturing of parts from case hardening steel high temperature differences occur. The first step, forging, is usually followed by the first chipping step, together defining the geometry of the parts. These intermediate parts are then exposed to a carbon rich environment at elevated temperature which promotes diffusion of carbon into the material and therefore leads to an increase of the carbon content close to the surface. Thus, these case hardened parts gain surface hardness while still having a ductile interior.

Experimental data provided by [4, 11, 13, 25, 29, 32] shows significant temperature dependency of the elastic moduli and a coupled temperature and rate dependency of the plastic deformation behaviour. As elaborated in, e.g. [39], other thermomechanical properties, such as the thermal expansion, the heat capacity and the heat conductivity, are also highly temperature dependent. To obtain reasonable results in numerical simulations, these effects have to be covered. Commonly, this is done by, e.g. interpolating between yield curves experimentally obtained at constant temperatures and deformation rates, as applied by, e.g. [32], or by using direct approximations of the yield curve, as discussed in, e.g. [15, 18]. However, the temperature evolution either remains unconsidered or is approximated by semi-analytical methods.

Another method is to consider the temperature and rate dependency a priori and to formulate the material model within the framework of rational thermodynamics established by [9]. This framework is used for thermoplasticity in, e.g. [3, 31, 34]; see also references cited in these works. The related numerical treatment is proposed by [34] along with an implementation into a coupled finite element framework. In [5] thermo-viscoplasticity is discussed and non-linear models for the treatment of rate-dependent yield stress are proposed. The works [6,7,8] demonstrate the advantages of considering temperature dependent material properties along with non-linear kinematic hardening. The special focus on the amount of plastic work transformed to heat and calibration to experiments is emphasised in [12, 30].

The localisation and regularisation behaviour of a Perzyna-type viscoplastic model with strain softening is investigated in [21] and the influences of the applied loading rate and the choice of the model parameters are studied.

Thermoplasticity and the related localisation effects are numerically investigated in, e.g. [27, 28, 42] and gradient-enhancement by an additional differential equation introducing an internal length scale is proposed as a solution strategy to overcome mesh dependency issues.

The key focus of this paper is the elaboration of a thermo-viscoplasticy model which is applicable to various ductile thermo-viscoplastic materials, especially metals. The material model includes temperature-dependent material parameters in a thermodynamically consistent manner and covers various effects related to thermo-viscoplasticity, such as non-linear hardening, thermal softening as well as heat generation due to structural cooling and plastic deformation. The choice of the ansatzes for the temperature-dependencies makes the model applicable over wide temperature ranges. The thermo-viscoplasticity model is embedded into a fully coupled finite-element framework. Moreover, aspects of the related localisation and regularisation behaviour are discussed based on numerical examples.

This paper is organised as follows: In Sect. 2 the theory of thermo-viscoplasticity, involving temperature-dependent material properties, is introduced and is specified for 16MnCr5 (1.7131) case hardening steel. The implementation into a fully coupled finite element framework is outlined in Sect. 3 followed by the specification of the approximation functions for the temperature-dependent model parameters for steel grade 16MnCr5 and their identification in Sect. 4. Results of representative numerical examples, demonstrating the performance of the proposed model, are presented and discussed in Sect. 5. Finally, this paper is closed by a summary in Sect. 6.

2 Thermo-viscoplasticity

In this section, the essential balance relations for the closed thermo-mechanical system are presented in a general framework using thermodynamics with internal variables. Thereafter, the model used for the implementation as this work proceeds shall be specified.

2.1 Essential balance relations

The thermomechanical system considered shall fulfil the balance of linear momentum

$$\begin{aligned} \mathrm{div}\varvec{\sigma }+ \rho {\varvec{b}} = {\varvec{0}} \, , \end{aligned}$$

(1)

here given for the quasi-static case, as well as the balance of internal energy

$$\begin{aligned} \rho \dot{u} = \varvec{\sigma }: {\dot{{\varvec{\varepsilon }}}}+ \rho r - \mathrm{div}{\varvec{q}} \end{aligned}$$

(2)

and the Clausius-Duhem inequality

$$\begin{aligned} \rho \dot{s} \ge \rho \frac{r}{T} - \mathrm{div}\left( \frac{{\varvec{q}}}{T}\right) \, , \end{aligned}$$

(3)

describing the first and the second law of thermodynamics, respectively, cf. [31]. Therein, T denotes the absolute temperature, $\varvec{\sigma }$ the stress tensor,

$$\begin{aligned} {\varvec{\varepsilon }}= \nabla ^\text {sym} {\varvec{u}} = \frac{1}{2}\left[ \nabla {\varvec{u}} + \nabla ^{\text {t}} {\varvec{u}} \right] \end{aligned}$$

(4)

the small strain tensor, ${\varvec{u}}$ the displacement vector, and ${\varvec{q}}$ the heat flux vector. Since these local forms of the balance laws are given per unit volume, all quantities per unit mass, i.e. the body force ${\varvec{b}}$, the heat source r, the entropy s, and the internal energy u, are transformed by the mass density $\rho$, whereby conservation of mass is assumed. The operator $\,{\dot{\bullet }}\,$ indicates the time derivative $\frac{\text {d}}{\text {d}t}$ of the quantity $\bullet$. In addition, for any Cauchy-Boltzmann continuum the balance of angular momentum is fulfilled a priori by the symmetry of the stress tensor, i.e. $\varvec{\sigma }= \varvec{\sigma }^{\mathrm{t}}$.

2.2 Dissipation inequality and heat equation

It is common to rewrite the energy balance and entropy inequality into more convenient formats. Therefore, the Helmholtz (free) energy is obtained from the Legendre transformation based on $\psi = u - T s$ and inserted into (2), which results in the balance of Helmholtz energy

$$\begin{aligned} \rho \dot{\psi }= \varvec{\sigma }: {\dot{{\varvec{\varepsilon }}}}+ \rho r - \mathrm{div}{\varvec{q}} - \rho s \dot{T} - \rho T \dot{s} \, . \end{aligned}$$

(5)

Inserting this relation into (3) yields the dissipation inequality

$$\begin{aligned} \mathcal {D} := \varvec{\sigma }: {\dot{{\varvec{\varepsilon }}}}- \rho s \dot{T} - \rho \dot{\psi }- \frac{1}{T} {\varvec{q}} \cdot \nabla T \ge 0 \, , \end{aligned}$$

(6)

which defines the dissipation rate per unit volume, $\mathcal {D}$. For the Helmholtz energy of the thermo-mechanical system, the ansatz

$$\begin{aligned} \psi (T,{\varvec{\varepsilon }},{\varvec{z}}) \end{aligned}$$

(7)

is assumed, depending on observable quantities, i.e. the temperature and the total strain tensor as well as internal variables, see [9], here denoted as (second order tensor) ${\varvec{z}}$. Inserting (7) into (6) specifies the dissipation inequality

$$\begin{aligned}&\mathcal {D} = \left[ \varvec{\sigma }- \rho \frac{\partial \psi }{\partial {\varvec{\varepsilon }}} \right] : {\dot{{\varvec{\varepsilon }}}}- \rho \left[ s + \frac{\partial \psi }{\partial T} \right] \dot{T} \nonumber \\&\quad -\rho \frac{\partial \psi }{\partial {\varvec{z}}} :\dot{{\varvec{z}}} - \frac{1}{T} \, {\varvec{q}} \cdot \nabla T \ge 0 \, . \end{aligned}$$

(8)

Therein, the entropy and the stress tensor are identified as entities, energetically conjugated to the strain tensor and the temperature and, similarly, following the framework of rational thermodynamics, also the dissipative stress, ${\varvec{\zeta }}$, is defined according to

$$\begin{aligned} s&\equiv - \frac{\partial \psi }{\partial T} \, ,&\varvec{\sigma }&\equiv \rho \frac{\partial \psi }{\partial {\varvec{\varepsilon }}}&\text {and}&{\varvec{\zeta }}&:= - \rho \frac{\partial \psi }{\partial {\varvec{z}}} \, . \end{aligned}$$

(9)

With these relations, the terms in brackets in (8) vanish and the reduced dissipation inequality takes the compact form

$$\begin{aligned} \mathcal {D} = {\varvec{\zeta }}:\dot{{\varvec{z}}} - \frac{1}{T} {\varvec{q}} \cdot \nabla T \ge 0 \ . \end{aligned}$$

(10)

Following the Coleman–Noll procedure [10], restricts this condition by separating the two terms into independent conditions, i.e.

$$\begin{aligned} \mathcal {D}_\text {m}&:= {\varvec{\zeta }}:\dot{{\varvec{z}}} \, \ge 0&\text {and}&\mathcal {D}_\vartheta&:= - \frac{1}{T} {\varvec{q}} \cdot \nabla T \ge 0 \ , \end{aligned}$$

(11)

which are referred to as the mechanical and the thermal dissipation inequality. By inserting the constitutive ansatz (7) and the constitutive relations (9) into the energy balance (5), it is transformed into the heat balance

$$\begin{aligned} \rho \, c_{{\varvec{\varepsilon }}} \, \dot{T} = Q_\text {m} + \rho \, r - \mathrm{div}{\varvec{q}} \ , \end{aligned}$$

(12)

where

$$\begin{aligned} c_{{\varvec{\varepsilon }}} := - T \frac{\partial ^2 \psi (T,{\varvec{\varepsilon }},{\varvec{z}})}{\partial T^2} \end{aligned}$$

(13)

denotes the heat capacity at constant strains and where

$$\begin{aligned} Q_\text {m} := T \frac{\partial \varvec{\sigma }}{\partial T} : {\dot{{\varvec{\varepsilon }}}}+ \mathcal {D}_\text {m}- T \frac{\partial {\varvec{\zeta }}}{\partial T} : \dot{{\varvec{z}}} \end{aligned}$$

(14)

represents the mechanical heat production rate.

While a heat conduction model is used to fulfil the thermal part of the dissipation inequality, the mechanical dissipation inequality must be satisfied and, moreover, is assumed to fulfil the postulate of maximum plastic dissipation. Therefore, following the framework of generalised standard materials [14], the existence of a yield function $f(T,{\varvec{\zeta }})$ is assumed limiting the elastic region as the admissible space, i.e.

$$\begin{aligned} {\mathbb {E}}_{{\varvec{\zeta }}} := \left\{ \, {\varvec{\zeta }}\in {\mathbb {R}}^m \, \big | \, f(T,{\varvec{\zeta }}) \le 0 \, \right\} \, . \end{aligned}$$

(15)

The optimisation problem

$$\begin{aligned} \underset{{\varvec{\zeta }}\in {\mathbb {E}}_{{\varvec{\zeta }}}}{\min } \mathcal {D}_\tau (T,{\varvec{\zeta }};\dot{{\varvec{z}}})\ , \quad \mathcal {D}_\tau := - \mathcal {D}_\text {m} + \frac{1}{\tau } \gamma ^+ (T,f) \end{aligned}$$

(16)

is formulated, here using the penalty method with the penalty factor $\tau > 0$, commonly interpreted as relaxation time, and the penalty function

$$\begin{aligned} \gamma ^+ : {\mathbb {R}} \mapsto {\mathbb {R}}_+ \, \big | \, \gamma ^+ \in \mathcal {C}^1 \wedge \gamma ^+(T,f) \ge 0 \Leftrightarrow f \ge 0 \, . \end{aligned}$$

(17)

From the optimality condition

$$\begin{aligned} \frac{\partial \mathcal {D}_\tau }{\partial {\varvec{\zeta }}} = \varvec{0} \end{aligned}$$

(18)

the associated evolution equation follows for the internal variables

$$\begin{aligned} \begin{aligned} \dot{{\varvec{z}}}&= \dot{\lambda }^\text {vp} \, \frac{\partial f}{\partial {\varvec{\zeta }}} \, ,&\text {with}&\dot{\lambda }^\text {vp}&:= \frac{1}{\tau } \frac{\partial \gamma ^+}{\partial f} \, . \end{aligned} \end{aligned}$$

(19)

The definition of the viscoplastic flow rate $\dot{\lambda }^\text {\!\! vp}$ can be rewritten into the residual format

$$\begin{aligned} f^\text {vp} := \frac{\partial \gamma ^+}{\partial f} - \tau \, \dot{\lambda }^\text {\!\! vp} = 0 \end{aligned}$$

(20)

that provides the rate-dependent yield surface and, accordingly, $f^\text {vp}$ can be denoted as the viscoplastic yield function. In addition, this formulation resolves the definition gap for $\tau \rightarrow 0$ and thus also allows the rate-independent case, see [33].

2.3 Model specification

In the case of elasto-plasticity in an infinitesimal strain setting, the total strain tensor decomposes additively into the reversible thermo-elastic strain tensor, ${\varvec{\varepsilon }}_\text {r}$, and the irreversible plastic strain tensor, ${\varvec{\varepsilon }}_\text {p}$, as

$$\begin{aligned} {\varvec{\varepsilon }}= {\varvec{\varepsilon }}_\text {r}+ {\varvec{\varepsilon }}_\text {p}\, . \end{aligned}$$

(21)

Thus, the internal variables contain the plastic strain tensor as well as, e.g. hardening variables. The reversible strains split into the thermal strains, ${\varvec{\varepsilon }}_\vartheta$, and the elastic strains, ${\varvec{\varepsilon }}_\text {e}$, according to

$$\begin{aligned} {\varvec{\varepsilon }}_\text {r}= {\varvec{\varepsilon }}_\vartheta + {\varvec{\varepsilon }}_\text {e}\, . \end{aligned}$$

(22)

For these effective thermal strains, related to the absolute temperature of an initial stress-free state $T_0$, the isotropic relation

$$\begin{aligned} {\varvec{\varepsilon }}_\vartheta = \Bigl [ \alpha _\text {m}(T) \, \bigl [T - T_{0^\circ \text {C}} \bigr ] - \alpha _\text {m}(T_0) \, \bigl [T_0 - T_{0^\circ \text {C}} \bigr ] \Bigr ] {\varvec{I}} \end{aligned}$$

(23)

is assumed with the mean coefficient of linear thermal expansion, $\alpha _\text {m}$, as defined in Remark 1, and ${T_{0^\circ \text {C}} = 273.15 \, \text {K}}$ providing the Celsius temperature scale.

This model will restrict to isotropic cold-work hardening with the related internal variable k, so that ${\varvec{z}} = \{ {\varvec{\varepsilon }}_\text {p}, k \}$. Inserting the linearised kinematics into (11) and (14) leads for the mechanical dissipation inequality and the mechanical heat production rate to

$$\begin{aligned} \mathcal {D}_\text {m}&= \varvec{\sigma }:{\dot{{\varvec{\varepsilon }}}}_\text {p}+ \kappa \dot{k} \ge 0 \, , \end{aligned}$$

(24)

$$\begin{aligned} \text {and} \quad Q_\text {m}&= T \frac{\partial \varvec{\sigma }}{\partial T} : {\dot{{\varvec{\varepsilon }}}}_\text {r}+ \mathcal {D}_\text {m} - T \frac{\partial \kappa }{\partial T} \dot{k} \, , \end{aligned}$$

(25)

respectively, with ${\kappa =-\rho \frac{\partial \psi }{\partial k}}$ denoting the isotropic cold-work hardening related stress. The mechanical heat production rate can be split into an reversible and irreversible (plastic) contribution according to

$$\begin{aligned} Q_\text {r}&:= T \frac{\partial \varvec{\sigma }}{\partial T} : {\dot{{\varvec{\varepsilon }}}}_\text {r} \end{aligned}$$

(26)

$$\begin{aligned} Q_\text {p}&:= \mathcal {D}_\text {m} - T \frac{\partial \kappa }{\partial T} \dot{k} \, , \end{aligned}$$

(27)

where the reversible part considers the Gough-Joule effect and the plastic part provides the heat production due to plastic yielding and hardening effects.

It is assumed that the Helmholtz energy can be decomposed according to

$$\begin{aligned} \psi (T,{\varvec{\varepsilon }},{\varvec{\varepsilon }}_\text {p}, k) := \psi _\vartheta (T) + \psi _\text {e}(T, {\varvec{\varepsilon }}_\text {e}(T,{\varvec{\varepsilon }},{\varvec{\varepsilon }}_\text {p})) + \psi _\text {p}(k)\nonumber \\ \end{aligned}$$

(28)

into a purely thermal part, depending only on the temperature, a thermo-elastic part, depending on the temperature and elastic strain tensor, and into a purely plastic part, depending only on the hardening variable. For the respective contributions the following specifications are introduced, i.e.

$$\begin{aligned}&\psi _\vartheta (T) {=} c_0 \left[ \bigl [T {-} T_{0^\circ \text {C}} \bigr ] {-} T \ln \left( \frac{T}{T_{0^\circ \text {C}}}\right) \right] {-} \sum _{i=0}^{n} \frac{{w_{c}}_{i+1}}{[i{+}1][i{+}2]} [T{-}T_\text {r}]^{i+2} \nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned}&\psi _\text {e}(T, {\varvec{\varepsilon }}_\text {e}) = \frac{1}{2 \, \rho } \Bigl [ K(T) \mathrm{tr}^2 {\varvec{\varepsilon }}_\text {e}+ 2 G(T) \, \Vert {\varvec{\varepsilon }}_\text {e}^{\mathrm{dev}}\Vert ^2\Bigr ] \ , \end{aligned}$$

(30)

$$\begin{aligned}&\psi _\text {p}(k) = \frac{1-r^\text {mix}}{\rho } \Delta Y_{\infty 0} \left[ k + k_0 \exp \left( -\frac{k}{k_0}\right) \right] + \frac{r^\text {mix}}{\rho } \frac{H_0}{2} \, k^2 \, .\nonumber \\ \end{aligned}$$

(31)

Therein, K and G denote the elastic moduli for bulk and shear response, respectively. Parameters $c_0$, and $w_{c_i}$ ($i=1,\ldots , \, n-1$) are model parameters for the temperature-dependency of the heat capacity with respect to a reference temperature $T_\text {r}$. For the thermoelastic contribution to the free energy, a volumetric deviatoric split is assumed, with ${\varvec{\varepsilon }}_\text {e}^{\mathrm{dev}} = {\varvec{\varepsilon }}_\text {e}- \frac{1}{3} \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\, {\varvec{I}}$ denoting the deviatoric elastic strain tensor. The chosen plastic part of the free energy is able to describe exponentially saturating hardening with the isothermal saturation yield stress increment $\Delta Y_{\infty 0}$ and the saturation parameter $k_0$, as well as linear hardening with the isothermal hardening modulus $H_0$. The mix parameter $r^\text {mix} \in [0,1]$ specifies the fraction of linear hardening. The stress tensor and the cold-work hardening stress (9) read

$$\begin{aligned} \varvec{\sigma }= K(T) \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\, {\varvec{I}} + 2 G(T) {\varvec{\varepsilon }}_\text {e}^{\mathrm{dev}} \, , \end{aligned}$$

(32)

and

$$\begin{aligned} \begin{aligned} \kappa :=&- \rho \frac{\partial \psi (T,{\varvec{\varepsilon }},{\varvec{\varepsilon }}_\text {p},k)}{\partial k} \\=&[1-r^\text {mix}] \Delta Y_{\infty 0} \left[ \exp \left( -\frac{k}{k_0}\right) -1 \right] - r^\text {mix} H k \, . \end{aligned} \end{aligned}$$

(33)

The isomorphic heat capacity as present in the energy balance (12) results in

$$\begin{aligned} \begin{aligned} c_{{\varvec{\varepsilon }}} =&- \frac{T}{2\rho } \biggl [ \frac{\text {d}^2 K}{\text {d}T^2} \mathrm{tr}^2 {\varvec{\varepsilon }}_\text {e}- 4 \frac{\text {d}K}{\text {d}T} \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\gamma + 2 K \! \left[ \gamma ^2 - \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\frac{\text {d}\gamma }{\text {d}T} \right] \\&+ 2 \frac{\partial ^2 G}{\partial T^2} \Vert {\varvec{\varepsilon }}_\text {e}^{\mathrm{dev}} \Vert ^2 \biggr ] + c_0 + T \sum _{i=0}^{n} {w_{c}}_{i+1} [T-T_\text {r}]^i \end{aligned} \end{aligned}$$

(34)

Therein, $\gamma = 3 \left[ \alpha _\text {m} + \frac{\text {d}\alpha _\text {m}}{\text {d}T} \left[ T - T_{0\, ^\circ \text {C}} \right] \right]$ denotes the coefficient of volumetric thermal expansion. In experiments usually the heat capacity at constant stresses is determined, i.e.

$$\begin{aligned} c_{\varvec{\sigma }}=-T \frac{\partial ^2 \varphi (T,\varvec{\sigma },{\varvec{z}})}{\partial T^2} \, , \end{aligned}$$

(35)

as discussed in Remark 2, where $\varphi$ denotes the Gibbs (free) energy of the thermo-mechanical system obtained from the Helmholtz (free) energy by the Legendre transformation ${\varphi = \psi + \frac{1}{\rho }\varvec{\sigma }: {\varvec{\varepsilon }}}$. Based on the ansatz specified in (28), (29), (30) and (31) one obtains

$$\begin{aligned} \varphi (T,\varvec{\sigma },{\varvec{z}})= & {} \psi _T(T) - \frac{\rho }{2}\left[ \frac{p^2}{K(T)} + \frac{\Vert \varvec{\sigma }^{\mathrm{dev}} \Vert ^2}{2G(T)} \right] \nonumber \\&\quad + \psi _{\text {p}}(k) + \frac{p}{\rho } \mathrm{tr}\left( {\varvec{\varepsilon }}_\vartheta (T) \right) - \frac{1}{\rho } \varvec{\sigma }^{\mathrm{dev}} : {\varvec{\varepsilon }}_\text {p}\, . \end{aligned}$$

(36)

Therein, $p=-\frac{1}{3} \mathrm{tr}(\varvec{\sigma })$ and $\varvec{\sigma }^{\mathrm{dev}} = \varvec{\sigma }+ p {\varvec{I}}$ denote the hydrostatic pressure and the deviatoric stress tensor, respectively. Combination of (35) and (36) yields

$$\begin{aligned} \begin{aligned} c_{\varvec{\sigma }} =&\frac{T}{2 \rho } \Biggl [\frac{p^2}{K^2} \left[ \frac{2}{K} \left[ \frac{\text {d}K}{\text {d}T}\right] ^2 - \frac{\text {d}^2 K}{\text {d}T^2} \right] \\&+ \frac{\Vert \varvec{\sigma }^{\mathrm{dev}} \Vert ^2}{2 G^2} \left[ \frac{2}{G} \left[ \frac{\text {d}G}{\text {d}T}\right] ^2 - \frac{\text {d}^2 G}{\text {d}T^2} \right] - 2 p \frac{\text {d}\gamma }{\text {d}T} \Biggr ]\\&+ c_0 + T \sum _{i=0}^{n} {w_{c}}_{i+1} [T-T_\text {r}]^i \, . \end{aligned} \end{aligned}$$

(37)

It is remarked that for $\varvec{\sigma }= \varvec{0}$ the isobaric heat capacity reduces to a polynomial in T. Similar approaches of second order have been proposed by, e.g. [36, 41].

Since the plastic deformation of metals is assumed deviatoric, i.e. ${\mathrm{tr}{\varvec{\varepsilon }}_\text {p}\equiv 0}$, and, moreover, considering isotropic plastic response, the use of the von Mises yield function

$$\begin{aligned} f = \Vert \varvec{\sigma }^{\mathrm{dev}} \Vert - \sqrt{\frac{2}{3}} \Bigl [ y_0(T) - \varphi _\kappa (T) \kappa \Bigr ] \end{aligned}$$

(38)

as yield criterion and plastic potential is appropriate. Therein, $y_0$ denotes the initial yield stress and $\varphi _\kappa$ accounts for the thermal softening of the contribution related to cold-work hardening, $\kappa$. For the penalty function, the power-type ansatz

$$\begin{aligned} \gamma ^+ = \frac{m(T)}{m(T)+1} d_0(T) \left\langle \frac{f}{d_0(T)} \right\rangle ^{\frac{m(T)+1}{m(T)}} \end{aligned}$$

(39)

is chosen, with the temperature-dependent parameter m, and $d_0$, the stress-like scaling parameter, cf. [5]. Here, ${d_0=\sqrt{2/3} \, y_0}$ is assumed. The associated evolution equations of the internal variables (19) can be derived from these quantities, to be specific

$$\begin{aligned} {\dot{{\varvec{\varepsilon }}}}_\text {p}= \dot{\lambda }^\text {vp} \, {\varvec{n}} \quad \qquad \,\, \text {and} \quad \dot{k} = \dot{\lambda }^\text {vp} \sqrt{\frac{2}{3}} \varphi _\kappa \,, \end{aligned}$$

(40)

where

$$\begin{aligned} \dot{\lambda }^\text {vp} = \frac{1}{\tau } \left\langle \frac{f}{y_0} \right\rangle ^{\frac{1}{m}} \quad \text {and} \quad {\varvec{n}} = \frac{\varvec{\sigma }^{\mathrm{dev}}}{\Vert \varvec{\sigma }^{\mathrm{dev}}\Vert } \end{aligned}$$

(41)

denote the Perzyna-type viscoplastic flow rate and the deviatoric yield direction, respectively. The formulation of the viscoplastic yield function (20) in terms of stresses,

$$\begin{aligned} f^\text {vp} = \left\langle \frac{3}{2}\, f \right\rangle - y_0 \left[ \tau \dot{\lambda }^\text {vp} \right] ^m =0 \ , \end{aligned}$$

(42)

allows the identification of viscous overstress

$$\begin{aligned} \Delta \sigma := y_0 \left[ \tau \dot{\lambda }^\text {vp} \right] ^m \end{aligned}$$

(43)

which describes a power-law relation between the overstress and the viscoplastic flow rate.

The thermal part of the dissipation inequality is fulfilled by Fourier’s law of heat conduction

$$\begin{aligned} {\varvec{q}}(T,\nabla T) = - {\varvec{K}} \cdot \nabla T \end{aligned}$$

(44)

such that

$$\begin{aligned} \mathcal {D}_\vartheta =\nabla T \cdot {\varvec{K}} \cdot \nabla T \ge 0 \end{aligned}$$

(45)

with the positive semi-definite heat conductivity tensor ${\varvec{K}}$. As this work proceeds, the isotropic relation ${\varvec{K}} = \varLambda (T) \, {\varvec{I}}$ shall be assumed.

Remark 1

In the literature, definitions of two different coefficients of linear thermal expansion can be found: The real coefficient of linear thermal expansion

$$\begin{aligned} \alpha (T,T_{0 \, ^\circ \text {C}}) = \frac{1}{L(T_{0 \, ^\circ \text {C}})} \left. \frac{\text {d}\, L(T)}{\text {d}\, T}\right| _{\varvec{\sigma }} \end{aligned}$$

(46)

and the mean coefficient of linear thermal expansion

$$\begin{aligned} \alpha _\text {m}(T,T_{0 \, ^\circ \text {C}}) = \frac{1}{L(T_{0 \, ^\circ \text {C}})} \frac{L(T)-L(T_{0 \, ^\circ \text {C}})}{T-T_{0 \, ^\circ \text {C}}} \, , \end{aligned}$$

(47)

where L(T) denotes the length of a specimen at temperature T and $T_{0 \, ^\circ \text {C}}$ is the reference temperature, commonly chosen at $T_{0 \, ^\circ \text {C}}=273.15 \, \text {K}$, see, e.g. [19, 37, 41]. From both relations, the thermal strain between an initial temperature $T_0$ and the current temperature T, i.e.

$$\begin{aligned} \begin{aligned} \varepsilon _\vartheta (T,T_0)&= \frac{L(T)}{L(T_0)} = \int _{T_0}^{T} \alpha ({\tilde{T}}) \, \text {d}{\tilde{T}} \\&= \alpha _\text {m}(T)\left[ T-T_{0 \, ^\circ \text {C}} \right] - \alpha _\text {m}(T_0)\left[ T_0-T_{0 \, ^\circ \text {C}} \right] \, , \end{aligned} \end{aligned}$$

(48)

can be obtained. From (48) one may conclude that the relation

$$\begin{aligned} \alpha (T) = \alpha _\text {m}(T,T_{0 \, ^\circ \text {C}}) + \frac{\text {d}\, \alpha _\text {m}(T,T_{0 \, ^\circ \text {C}})}{\text {d}\, T} \left[ T_0-T_{0^\circ \text {C}}\right] \end{aligned}$$

(49)

between the real and mean coefficient of linear thermal expansion holds. Due to its simple definition, $\alpha _\text {m}(T,T_{0 \, ^\circ \text {C}})$ is mostly measured in experiments, cf. [19, sec. 3.2.1.2], and thus, for different materials, values for $\alpha _\text {m}(T_i,T_{0 \, ^\circ \text {C}})$ at different temperatures $T_i$ and interpolating functions for $\alpha _\text {m}(T,T_{0 \, ^\circ \text {C}})$ or $\varepsilon _\vartheta (T,T_{0 \, ^\circ \text {C}})= \alpha _\text {m}(T,T_{0 \, ^\circ \text {C}}) \left[ T-T_{0 \, ^\circ \text {C}} \right]$ are commonly provided in the literature, as in, e.g. [20, 35, 37].

Remark 2

The isobaric heat capacity is defined by

$$\begin{aligned} c_{\varvec{\sigma }}(T) := \frac{1}{m} \left. \frac{\text {d}Q}{\text {d}T}\right| _{\varvec{\sigma }} \, , \end{aligned}$$

(50)

where Q specifies the heat in a body of mass m. For the experimental determination of $c_{\varvec{\sigma }}(T)$, the heat in a specimen of mass m is increased by the portion $\Delta Q$ and the resulting temperature change from $T_1$ to $T_2$ is measured, see, e.g. [19, sec. 3.3.4.1]. For solids, the experiment is commonly performed at constant stress, mostly at $\varvec{\sigma }= - p_\text {at} {\varvec{I}}$, where $p_\text {at}=1013.25 \, \text {hPa}$. This setup motivates the definition of the mean isobaric heat capacity

$$\begin{aligned} c_{\varvec{\sigma }\, \text {m}}(T_2,T_1) = \frac{1}{m} \left. \frac{\Delta Q}{T_2 - T_1}\right| _{\varvec{\sigma }} = \frac{1}{T_2 - T_1} \int _{T_1}^{T_2} c_{\varvec{\sigma }}(\Theta ) \, \text {d}\Theta ,\nonumber \\ \end{aligned}$$

(51)

see, e.g. [19, 36]. If the temperature difference $T_2 - T_1$ becomes sufficiently small, the mean heat capacity approaches the real heat capacity, i.e. $c_{\varvec{\sigma }\text {m}}(T_2,T_1) \longrightarrow c_{\varvec{\sigma }}(T_1)$ as $T_2 \longrightarrow T_1$, see, e.g. [19, sec. 3.3.4]. Thus, values of the mean isobaric heat capacity $c_{\varvec{\sigma }\, \text {m}}(T_i,T_{0 \, ^\circ \text {C}})$ at different temperatures $T_i$ with respect to a reference temperature, commonly $T_{0 \, ^\circ \text {C}}=273.15 \, \text {K}$, are often found in the literature and interpolating functions for $c_{\varvec{\sigma }\, \text {m}}(T,T_{0 \, ^\circ \text {C}})$ are provided as in, e.g. [20, 35, 36]. In analogy to the relation between the coefficients of thermal expansion, the relation

$$\begin{aligned} c_{\varvec{\sigma }}(T) = c_{\varvec{\sigma }\, \text {m}}(T,T_{0 \, ^\circ \text {C}}) + \frac{\text {d}\, c_{\varvec{\sigma }\, \text {m}}(T,T_{0 \, ^\circ \text {C}})}{\text {d}\, T} \left[ T_0-T_{0^\circ \text {C}}\right] \nonumber \\ \end{aligned}$$

(52)

holds between the real and mean isobaric heat capacity.

Remark 3

The particular model proposed in the present paper introduces temperature-dependencies of cold-work hardening within the evolution equations of the related internal variables rather than within the related driving stress-type quantities. This ansatz implies that $\kappa$ shows no direct dependencies on the temperature T so that ${Q_\text {p} = \mathcal {D}_\text {m} \ge 0}$ (27) can be satisfied straightforwardly. The similar ansatz for the plastic contribution to the free energy

$$\begin{aligned} \textstyle {\widehat{\psi }}_\text {p}(T,k)= & {} \frac{1-r^\text {mix}}{\rho } \Delta y_{\infty }(T)\nonumber \\&\left[ k + k_0 \exp \left( -\frac{k}{k_0}\right) \right] + \frac{r^\text {mix}}{2 \, \rho } h(T) \, k^2 \end{aligned}$$

(53)

and the yield function

$$\begin{aligned}&\textstyle {\widehat{f}}(T,\varvec{\sigma },{\hat{\kappa }}) = \Vert \varvec{\sigma }^{\mathrm{dev}} \Vert - \sqrt{\frac{2}{3}} \left[ y_0(T) - {\widehat{\kappa }} \right] \nonumber \\&\text {with} \quad \ {\widehat{\kappa }} := - \rho \frac{\partial \widehat{\psi }(T,k)}{\partial k} \, , \end{aligned}$$

(54)

including the temperature dependency of the cold-work hardening directly in the free energy by the temperature dependent hardening moduli $\Delta y_\infty$ and h, implies that ${\widehat{\kappa }}(T, k)$. Although, the contributions of the cold work-hardening $\varphi _\kappa (T) \kappa (k)$ in (38) and ${\widehat{\kappa }}(T, k)$ in (54) are identical for both models, i.e. ${{\widehat{\kappa }} = \varphi _\kappa \kappa }$ holds and thus, the resulting dissipation rates are equivalent, the rates of plastic heat production (27) are not. Therefore, such model introduces the additional constraint $Q_\text {p} \ge 0 \ \forall \ k\ge 0$ to the ansatz for the temperature dependencies and the choice of the related model parameters.

Fig. 1

Thermo-mechanically coupled boundary value problem. Separation into a mechanical and a thermal sub-problem

Table 1 Algorithmic box of the presented material model. The subscript $\text {K}$ denotes the use of Kelvin notation for symmetric tensors

Table 2 Model parameters for steel grade 16MnCr5

3 Numerical treatment

In this section, the numerical treatment of the balance equations in a finite element framework and of the presented material model in a predictor-corrector scheme are outlined.

3.1 Finite element framework

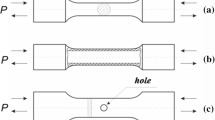
The balance equations (1) and (12) of the thermo-mechanical initial boundary value problem describe its mechanical and its thermal sub-problem. A related graphical illustration is depicted in Fig. 1. The mechanical sub-problem, Fig. 1a, is built up by the surface of the body $\partial {\mathscr {B}}$ being subjected to displacement (Dirichlet) boundary conditions ${\varvec{u}} = {\varvec{{\bar{u}}}}$ on $\partial {\mathscr {B}}^{\varvec{u}}$ and traction (Neumann) boundary conditions $\varvec{\sigma }\cdot {\varvec{n}} = {\varvec{{\bar{t}}}}$ on $\partial {\mathscr {B}}^{\varvec{t}}$ with $\partial {\mathscr {B}}=\partial {\mathscr {B}}^{\varvec{u}} \cup \partial {\mathscr {B}}^{\varvec{t}} \wedge \partial {\mathscr {B}}^{\varvec{u}} \cap \partial {\mathscr {B}}^{\varvec{t}}=\emptyset$ and outward surface normal unit vector ${\varvec{n}}$. In the interior domain ${\mathscr {B}}$ volume forces $\rho \, {\varvec{b}}$ are active.

The thermal sub-problem, Fig. 1b, consists of heating of the body by volumetric heat sources, $\rho \, r$, and mechanical heat production $Q^\text {m}$ in the interior domain, as well as by surface heat fluxes (Neumann), $- {\varvec{q}} \cdot {\varvec{n}}=\bar{q}_{{\varvec{n}}}$ on $\partial {\mathscr {B}}^q$, and by prescribed temperatures (Dirichlet) $T = {\bar{T}}$ on $\partial {\mathscr {B}}^\vartheta$ with $\partial {\mathscr {B}} = \partial {\mathscr {B}}^{\vartheta } \cup \partial {\mathscr {B}}^q \wedge \partial {\mathscr {B}}^{\vartheta } \cap \partial {\mathscr {B}}^q = \emptyset$.

Following the standard procedure, as outlined in, e.g. [1], and discretising the body by ${{\,\mathrm{{n}_\text {el}}\,}}$ non-intersecting finite elements ${\mathscr {B}}^e$, with $n_\text {el}^\text {sur}$ surface elements $\partial {\mathscr {B}}^e$, the weak forms

$$\begin{aligned}&\sum _{e=1}^{{{\,\mathrm{{n}_\text {el}}\,}}} \int _{{\mathscr {B}}^{e}} \Bigl [ \nabla \delta {\varvec{u}} : \varvec{\sigma }- \delta {\varvec{u}} \cdot \rho \, {\varvec{b}} \Bigr ] \,{\mathrm {d}}v - \sum _{e=1}^{n_\text {el}^\text {sur}} \int _{\partial {\mathscr {B}}^e} \delta {\varvec{u}} \cdot {\varvec{t}} \, \mathrm{d}a = 0\nonumber \\ \end{aligned}$$

(55)

$$\begin{aligned}&\sum _{e=1}^{{{\,\mathrm{{n}_\text {el}}\,}}} \int _{{\mathscr {B}}^{e}} \Bigl [ \delta T \bigl [ \rho \, c_{{\varvec{\varepsilon }}} \dot{T} - \rho \, r - Q^\text {m} \bigr ] - \nabla \delta T \cdot {\varvec{q}} \Bigr ] \,{\mathrm {d}}v \nonumber \\&\quad - \sum _{e=1}^{n_\text {el}^\text {sur}} \int _{\partial {\mathscr {B}}^e} \delta T q_{{\varvec{n}}} \,{\mathrm {d}}a = 0 \end{aligned}$$

(56)

of the balance equations (1) and (12), are obtained for all admissible virtual fields, $\delta {\varvec{u}}$ and $\delta T$. Within the finite elements ${\mathscr {B}}^e$, the approximations $\delta {\varvec{u}}({\varvec{x}}) \approx \sum _{A=1}^{{{\,\mathrm{{n}_\text {en}}\,}}} \delta {\varvec{u}}^{eA} N^A({\varvec{x}})$ and $\delta T({\varvec{x}}) \approx \sum _{C=1}^{{{\,\mathrm{{n}_\text {en}}\,}}} \delta T^{eC} N^C({\varvec{x}})$ are applied, where ${{\,\mathrm{{n}_\text {en}}\,}}$ denotes the number of element nodes of element e and where $\delta {\varvec{u}}^{eA}$ and $\delta T^{eC}$ are the values of the respective global field at node A, respectively C, of the particular element e. The element shape functions are denoted as $N^A({\varvec{x}})$ and an isoparametric approach is adopted. The residual format of the balance equations in global form reduces to

(57)

Therein, the operator as introduced in [16] denotes the assembly of the element vectors

$$\begin{aligned} \mathbf{f} _{\bullet }^{e} = \begin{bmatrix} \mathbf{f} _{{\varvec{u}} \bullet }^{e \, 1} ,&\mathbf{f} _{\vartheta \bullet }^{e \, 1},&\mathbf{f} _{{\varvec{u}} \bullet }^{e \, 2} ,&\mathbf{f} _{\vartheta \bullet }^{e \, 2},&\ldots ,&\mathbf{f} _{{\varvec{u}} \bullet }^{e \, {{\,\mathrm{{n}_\text {en}}\,}}} ,&\mathbf{f} _{\vartheta \bullet }^{e \, {{\,\mathrm{{n}_\text {en}}\,}}} \end{bmatrix}^{\text {t}} \end{aligned}$$

(58)

Fig. 2

Approximation of the temperature dependent elastic moduli E(T), K(T), G(T), and experimental data from [13, 38]

Fig. 3

Approximation of the mean coefficient of thermal expansion $\alpha _\text {m}$, experimental data from [35] and resulting real coefficient of thermal expansion $\alpha$

Fig. 4

Approximation of the mean isobaric heat capacity $c_{\varvec{\sigma }\, \text {m}}$, experimental data from [35], resulting real isobaric heat capacity $c_{\varvec{\sigma }}$, and isomorphic heat capacity $c_{{\varvec{\varepsilon }}}$. For $c_{\varvec{\sigma }}$ and $c_{\varvec{\sigma }\, \text {m}}$ a purely volumetric stress state with the atmospheric standard pressure $p = p_\text {at}=1013.25\,\text {hPa}$ is assumed and, moreover, ${\varvec{\varepsilon }}={\varvec{0}}$ is assumed for $c_{{\varvec{\varepsilon }}}$

Fig. 5

Approximation of the heat conductivity $\varLambda (T)$ and experimental data from [35]

Fig. 6

Approximation of the initial yield stress, $y_0(T)$, saturation yield stress, $y_\infty =y_0(T)+\varphi _\kappa (T)\Delta Y_{\infty 0}$, and experimental data from [25]

Fig. 7

Normalised viscous over-stress $\Delta \sigma /y_0(T,{\dot{\varepsilon }}_{\text {p}}) = \left[ \tau (T) {\dot{\varepsilon }}_{\text {p}} \right] ^{m(T)}$ at selected effective plastic strain rates ${\dot{\varepsilon }}_{\text {p}} = \sqrt{2/3}\Vert {\dot{{\varvec{\varepsilon }}}}_\text {p}\Vert$

Fig. 8

Stress–strain curves for uniaxial stress state at selected effective strain rates and temperatures. The solid lines show the results of the material model. The experimental data are taken from [32] and depicted as $\dot{\varepsilon }= 0.1 \, /{\text {s}}: \circ$, $\dot{\varepsilon }= 1 \, /{\text {s}}:$ $\triangle$, and $\dot{\varepsilon }= 10 \, /{\text {s}}:$ $\square$

into the global residuum vector $\mathbf{r}$. The nodal contributions to the vectors $\mathbf{f} _{\bullet }^{e}$ are identified according to

(59)

The constitutive equations for $c_{\varepsilon }, \, \varvec{\sigma }, \, {\varvec{q}}, \, {\varvec{b}}, \, r, \, Q^{\text {m}}, {\varvec{t}}$ and $q_{{\varvec{n}}}$ may, in general, depend on the state variable fields, i.e. displacement ${\varvec{u}}$ and temperature T, as well as on internal variables ${\varvec{z}}$, and on related gradients and rates.

According to the Bubnov-Galerkin formulation, the displacement ${\varvec{u}}({\varvec{x}}) \approx \sum _{A=1}^{{{\,\mathrm{{n}_\text {en}}\,}}} {\varvec{u}}^{eA} N^A({\varvec{x}})$ and temperature field ${T({\varvec{x}}) \approx \sum _{C=1}^{{{\,\mathrm{{n}_\text {en}}\,}}} T^{eC} N^C({\varvec{x}}) + T_0}$ as well as their rates are approximated by using the same ansatzes as for their virtual equivalents. Therein, $T_0$ indicates the temperature of the initial stress-free state, here assumed to be constant over the entire body. Global vectors for the global degrees of freedom (DOFs) of the ${{\,\mathrm{{n}_\text {np}}\,}}$ nodes of the system can be defined as

$$\begin{aligned} \mathbf{d} := \begin{bmatrix} {\varvec{u}}^{1}, \Delta T^{1}, {\varvec{u}}^{2}, \Delta T^{2}, \cdots , {\varvec{u}}^{{{\,\mathrm{{n}_\text {np}}\,}}}, \Delta T^{{{\,\mathrm{{n}_\text {np}}\,}}} \end{bmatrix}^\text {t} \, . \end{aligned}$$

(60)

which similarly applies to the rates, $\dot{\mathbf{d }}$. These are approximated within a time integration scheme referred to discretised time intervals with the increments $\Delta t = t_{n+1} - t_n$ as function of the current and previous values of the degrees of freedom and initial conditions such that $\dot{\mathbf{d }}(\mathbf{d} ,\mathbf{d} _n,\dot{\mathbf{d }}_n)$. Therein and in the progression of this work, the index $n+1$ is omitted for better readability. In the material subroutine, discussed in Sect. 3.2, the internal variables ${\varvec{z}}$ and their rates $\dot{{\varvec{z}}}$ are computed implicitly from the constitutive assumptions, which depend only on the current values of the state variables $\mathbf{d}$ as well as on the internal variables of the previous time step ${\varvec{z}}_n$. Thus, the residuum can be expressed as

$$\begin{aligned} \mathbf{r} = \mathbf{r} (\mathbf{d} , \mathbf{d} _n,\dot{\mathbf{d }}_n, \mathbf{z} _n) \, . \end{aligned}$$

(61)

Since in the numerical examples in Sect. 5 only surface loads independent of the nodal state variables and their rates are discussed, the further derivations will be restricted to ’dead’ loads. To solve this discrete spatio-temporal non-linear residual system of equations by means of the Newton-Raphson scheme, the global tangent matrix $\mathbf{J}$ is required. It is defined by

(62)

Therein, the tangent matrix of element e is defined by

$$\begin{aligned} \mathbf{J} ^{e} := \frac{\partial \mathbf{r} ^{e}(\mathbf{d} ^e, \mathbf{d} _n^e,\dot{\mathbf{d }}_n^e, \mathbf{z} _n)}{\partial \mathbf{d} ^e} \end{aligned}$$

(63)

as the derivative of the element residuum vector

$$\begin{aligned} \mathbf{r} ^{e} := \mathbf{f} _{{{\,\mathrm{\text {dyn}}\,}}}^{e} + \mathbf{f} _{{{\,\mathrm{\text {int}}\,}}}^{e} - \mathbf{f} _{{{\,\mathrm{\text {vol}}\,}}}^{e} \end{aligned}$$

(64)

with respect to the vector of DOFs associated to element e, i.e.

$$\begin{aligned} \mathbf{d} ^e := \left[ {\varvec{u}}^{e \, 1}, \ \Delta T^{e \, 1}, \ {\varvec{u}}^{e \, 2}, \ \Delta T^{e\, 2}, \cdots , \ {\varvec{u}}^{e \, {{\,\mathrm{{n}_\text {en}}\,}}}, \ \Delta T^{e \, {{\,\mathrm{{n}_\text {en}}\,}}} \right] ^\text {t} \ .\nonumber \\ \end{aligned}$$

(65)

Fig. 9

Perturbed simple shear boundary value problem with discretisation for ${{\,\mathrm{{n}_\text {el}}\,}}=8$

Fig. 10

Comparison of force-displacement curves for shear simulation at initial temperature $T_0=20 \, ^\circ$C with and without heat conduction for different number of elements $n_\text {el}$ and averaged shear rates $\dot{{\bar{\gamma }}}_{xy}$

Fig. 11

Comparison of the normalised shear angle distribution $\gamma _{xy}(x) / {\bar{\gamma }}_{xy}$ at initial temperature $T_0=20 \, ^\circ$C and averaged shear rates $\dot{\bar{\gamma }}_{xy}$. Only values of the bottom row of integration points are depicted

Fig. 12

Comparison of the temperature distribution $\Delta T(x)$ at initial temperature $T_0=20 \, ^\circ$C and averaged shear rates $\dot{\bar{\gamma }}_{xy}$

Fig. 13

Dependency of the shear zone width b on the average shear rate $\dot{{\bar{\gamma }}}_{xy}$ at different initial temperatures $T_0$ a) with heat conduction ($\varLambda _0/\varLambda _0^\text {16MnCr5} = 1$), b) no heat conduction ($\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$). The width of the shear zone b is identified as $x \in [-b,\ b] \mid \gamma _{xy}(x) \ge {\bar{\gamma }}_{xy}$

For the implementation of the proposed material model, it is convenient to use the AceGen-Toolbox [22, 23] for Wolfram Mathematica [43]. It generates exact derivatives and allows the automatic generation of optimised source code, here for a FEAP [40] user element. To keep the time for automatic code generation short and the size of the generated code small, the use of pseudo-potentials on quadrature point level for the generation of the element contributions to the residuum vector and tangent matrix is recommended, see [23, ch. 4.3]. For the presented thermo-mechanically coupled problem, the pseudo potential of volume element e is established by

$$\begin{aligned} {\tilde{\varPi }}^{e}:= & {} {\tilde{\varPi }}^{e}_{\text {m}} + {\tilde{\varPi }}^{e}_{{\vartheta }} \end{aligned}$$

(66a)

$$\begin{aligned} {\tilde{\varPi }}^{e}_{\text {m}}:= & {} \int _{{\mathscr {B}}^e} \Bigl [ \nabla {\varvec{u}} : \varvec{\sigma }- {\varvec{u}} \cdot \bigl [ \rho \, {\varvec{b}} \bigr ] \Bigr ] \,\mathrm {d}v \end{aligned}$$

(66b)

$$\begin{aligned} {\tilde{\varPi }}^{e}_{{\vartheta }}:= & {} \int _{{\mathscr {B}}^e} \Bigl [ T \bigl [ \rho \, c_{{\varvec{\varepsilon }}} \, \dot{T} - \rho \, r - Q^{\text {m}} \bigr ] - \nabla T \cdot {\varvec{q}} \Bigr ]\, \mathrm {d}v \end{aligned}$$

(66c)

similarly to the weak form of the balance equations (55) and (56). The element residuum vector (64) is then obtained by

$$\begin{aligned} \mathbf{r} ^{e} = \left. \frac{\partial {\tilde{\varPi }}^{e}}{\partial \mathbf{d} ^{e}} \right| _{\dot{T}, \rho , c_{{\varvec{\varepsilon }}}, \varvec{\sigma }, {\varvec{q}}, {\varvec{b}}, r , Q^{\text {m}}} \, . \end{aligned}$$

(67)

Therein, the quantities (AceGen: auxiliary variables) $\dot{T}$, $\rho$, $c_{{\varvec{\varepsilon }}}$, $\varvec{\sigma }$, ${\varvec{q}}$, ${\varvec{b}}$, r, and $Q^{\text {m}}$ are treated as constant in view of derivatives with respect to $\mathbf{d} ^e$. In the computation of the quadrature point contributions to the element tangent matrix (63)

$$\begin{aligned} \mathbf{J} ^{e} := \left. \frac{\partial \mathbf{r} ^{e}(\mathbf{d} ^e, {\varvec{z}} \left( \mathbf{d} ^e, {\varvec{z}}_n \right) , {\varvec{z}}_n)}{\partial \mathbf{d} ^{e}} \right| _{\frac{\partial {\varvec{z}}}{\partial \mathbf{d} ^{e}}={\frac{\partial {\varvec{z}}}{\partial \mathbf{d} ^{e}}}^*} \end{aligned}$$

(68a)

all entities are treated as functions of the element nodal degrees of freedom vector. Since AceGen only computes derivatives of explicit functions automatically, the derivative of the implicit relation ${\varvec{z}}$ $(\mathbf{d} ^e,{\varvec{z}}_n)$ must be provided, e.g. by means of the implicit function theorem

$$\begin{aligned} \left. \frac{\partial {\varvec{z}}(\mathbf{d} ^e, {\varvec{z}}_n)}{\partial \mathbf{d} ^{e}} \right. ^*= - \left[ \frac{\partial \mathbf{r} _{{\varvec{z}}}(\mathbf{d} ^e, {\varvec{z}}, {\varvec{z}}_n)}{\partial {\varvec{z}}}\right] ^{-1} : \frac{\partial \mathbf{r} _{{\varvec{z}}}(\mathbf{d} ^e, {\varvec{z}}, {\varvec{z}}_n)}{\partial \mathbf{d} ^e}\nonumber \\ \end{aligned}$$

(68b)

applied on the residuum vector of the evolution equation of the internal variables $\mathbf{r} _{{\varvec{z}}}$ as defined in Table 1 in Sect. 3.2 at the converged state, i.e. $\Vert \mathbf{r} _{{\varvec{z}}} \Vert \approx 0$.

3.2 Algorithmic treatment of the material model

Based on the finite element discretisation, the values of the temperature field T, its gradient $\nabla T$, the displacement gradient $\nabla {\varvec{u}}$, its rate $\nabla \dot{{\varvec{u}}}$, and the time increment $\Delta t = t - t_n$ are provided. In addition, the internal variables, i.e. the plastic strain tensor ${{\varvec{\varepsilon }}_\text {p}}_n$ and the isotropic hardening variable $k_n$ of the previous time step are known.

The implementation of the material model presented in Sect. 2.3 follows a predictor-corrector scheme as outlined in [33]. Therefore, in the predictor step all variables independent of the internal variables as well as trial values for those variables that depend on the internal state variables are computed based on which the yield condition can be evaluated. If the yield condition is fulfilled, the trial values are used as an update for the variables. If not, the internal variables are updated by using a Newton-Raphson scheme until the viscoplastic yield condition is fulfilled. The algorithmic box in Table 1 states the necessary steps for the implementation of the presented material model.

4 Parameter identification

In this section, the approximation functions for the temperature dependent parameters of the presented material model are given and the identification procedure of the model parameters based on experimental data is shown along with a table of the results for 16MnCr5 (1.7131) case hardening steel.

For the temperature dependency of the elastic bulk and shear moduli, K and G, as well as for the initial yield stress $y_0$, the relaxation time $\tau$ and the viscoplastic exponent m, the representation

$$\begin{aligned} X(T) = X_{0} \, \varphi _X(\Delta T_{\text {r}}) \quad \text {with} \quad \Delta T_{\text {r}} = T-T_{\text {r}}, \end{aligned}$$

(69)

is assumed which includes a continuous function $\varphi _X$. Therein, X and $X_0$ denote the respective temperature dependent quantity and its value at reference temperature $T=T_{\text {r}}$, respectively. For the continuous functions $\varphi _K$, $\varphi _G$, $\varphi _{y0}$, and $\varphi _\kappa$, the arctangent ansatz

$$\begin{aligned} \varphi ^{\arctan }_X(\Delta T_\text {r})= & {} 1 - \frac{2 \omega _X}{\pi -2 \phi _X} \Bigl [ \arctan ^{-1} \bigl ( \chi _X \Delta T_\text {r} \nonumber \\&+ \tan (\phi _X)\bigr ) - \phi _X \Bigr ] \end{aligned}$$

(70)

is assumed, where $\phi _X$ defines the initial ’angle’ of the arctangent curve at reference temperature $\Delta T_\text {r}=0$. Moreover, the function $\varphi _\tau$ is modelled by the exponential ansatz

$$\begin{aligned} \varphi ^{\exp }_X(\Delta T_\text {r}) = 1 - \omega _X \bigl [ \exp \bigl (- \chi _X \Delta T_\text {r} \bigr ) - 1 \bigr ] \, . \end{aligned}$$

(71)

Fig. 14

Comparison of force–displacement curves for shear simulation at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C with no viscosity ($\tau _0/\tau _0^\text {16MnCr5} = 0$) and different ratio of the heat conductivity $\varLambda _0/\varLambda _0^\text {16MnCr5}$ for different number of elements

Both functions (70) and (71) include scaling parameters $\omega _X$ and temperature dependencies are introduced by $\chi _X$. The function $\varphi _m$ is assumed to be linear according to the recursive formula for an n-th order polynomial

$$\begin{aligned} \varphi ^{\text {p}n}_X(\Delta T_\text {r})= \left[ 1 - w_{Xn} \, \Delta T_{\text {r}} \, \varphi ^{\text {p}n-1}_X \right] \end{aligned}$$

(72)

with $n \ge 1$ and $\varphi ^{\text {p}0}_X = 1$. In general, the coefficients $w_{Xi}$ with $i=1,\ldots ,n$, are included, whereas subsequent elaborations are restricted to $n=1$. The temperature dependencies of the mean coefficient of thermal expansion $\alpha _\text {m}$ and of the heat conductivity $\varLambda$ are described as piecewise continuous functions

(73)

Moreover, n-th order polynomial relations, as defined in (72), with degree $n=1$ are assumed for the functions $\varphi _{\alpha 1}$, $\varphi _{\alpha 2}$, $n=2$ for $\varphi _{c 1}$, $\varphi _{c 2}$, and $n=4$ for $\varphi _{\varLambda 1}$. The contribution $\varphi _{\varLambda 2}$ is modelled by the exponential relation given in (71).

For the identification of the material parameters, all parameters $\mathbf{p} _X$ describing the temperature dependent quantity $X(T,\mathbf{p} _X)$ are identified by minimising least squares functionals of the form

$$\begin{aligned} \min _\mathbf{p _X} \sum _{i=1}^{n_\text {data}} \left[ X(T_i,\mathbf{p} _X) - X^\text {exp}(T_i) \right] ^2 \, , \end{aligned}$$

(74)

where $X^\text {exp}(T_i)$ denotes experimental (literature) data of the quantity X at discrete temperatures $T_i$. For the minimisation, the MATLAB [26] implementation fminsearch of the Nelder-Mead simplex algorithm [24] is used. Since the simplex algorithm is an unconstrained optimisation method, special care has to be taken for those parameters which are defined only on an interval, such as $\phi _\bullet \in [-\frac{\pi }{2}, \ \frac{\pi }{2}]$ and $\{Y_{00}, \ \Delta Y_{\infty 0}, \ k_0, \ \tau _0, \ m\} \in \left( 0, \ \infty \right]$. During the identification procedure, these have been replaced by parameters $p_\bullet$ according to $\phi _\bullet = \text {arctan}(p_{\phi _\bullet })$ and $\{Y_{00}, \ \Delta Y_{\infty 0}, \ k_0, \ \tau _0, \ m_0\} = \{\exp (p_{Y_{00}}), \exp (p_{\Delta Y_{\infty 0}}), \exp (p_{k_0}), \ \exp (p_{\tau _0}), \ \exp (p_{m_0})\}$, respectively.

4.1 Thermo-elastic properties, G, K, and $\alpha _\text {m}$

This subsection presents the identification of the thermo-elasticity related parameters of the model.

To identify the parameters for the elastic moduli, the experimental data points for the Young’s modulus E and Poisson’s ratio $\nu$ are converted into values for the bulk modulus K and shear modulus G, respectively, according to

$$\begin{aligned} K = \frac{E}{3[1-2\nu ]} \quad \text {and} \quad G = \frac{E}{2[1+\nu ]} \, . \end{aligned}$$

(75)

The obtained values of the parameters of the arctangent model (70), $\mathbf{p _K = \left\{ K_{0},\omega _K,\chi _K,\phi _K \right\} }$ and $\mathbf{p} _G = \{G_{0},\omega _G, \chi _G,\phi _G \}$, are presented in Table 2. To show the quality of the approximation, the resulting curves for K(T), G(T), and $E=\frac{9KG}{3K+G}$ are presented in Fig. 2 along with the experimental data from [13, 38]. Therein, the solidus temperature of pure iron $T_\text {s}^\text {Fe}= 1538 \, ^\circ \text {C}$ [20] provides an estimate about the feasible temperature range of the model. For all moduli the model shows a good agreement with the experimental data but does not catch the relatively steep decline around room temperature of the bulk modulus, and thus as well of the Young’s modulus.

Fig. 15

Comparison of the normalised shear angle distribution $\gamma _{xy}(x) / {\bar{\gamma }}_{xy}$ at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C with no viscosity ($\tau _0/\tau _0^\text {16MnCr5} = 0$) and different ratios of the heat conductivity $\varLambda _0/\varLambda _0^\text {16MnCr5}$ for different number of elements. Only values of the bottom row of integration points are depicted

Fig. 16

Comparison of the temperature distribution $\Delta T(x)$ at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C with no viscosity ($\tau _0/\tau _0^\text {16MnCr5} = 0$) and different ratios of the heat conductivity $\varLambda _0/\varLambda _0^\text {16MnCr5}$ for different number of elements. Only values of the bottom row of integration points are depicted

Fig. 17

Comparison of force-displacement curves for shear simulation at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C without heat conduction ($\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$) for different number of elements $n_\text {el}$ and ratios of a the characteristic time $\tau _0/\tau _0^\text {16MnCr5}$ and b the viscous exponent $m_0/m_0^\text {16MnCr5}$

Fig. 18

Comparison of the normalised shear angle distribution $\gamma _{xy}(x) / {\bar{\gamma }}_{xy}$ at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C with no heat conduction ($\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$) for different number of elements and ratios of the characteristic time $\tau _0/\tau _0^\text {16MnCr5}$ and the viscous exponent $m_0/m_0^\text {16MnCr5}$. Only values of the bottom row of integration points are depicted

Fig. 19

Comparison of the temperature distribution $\Delta T(x)$ at averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and initial temperature $T_0=20 \, ^\circ$C with no heat conduction ($\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$) for different number of elements and ratios of the characteristic time $\tau _0/\tau _0^\text {16MnCr5}$ and the viscous exponent $m_0/m_0^\text {16MnCr5}$. Only values of the bottom row of integration points are depicted

The mean coefficient of thermal expansion $\alpha _{\text {m}}$ is modelled by piecewise continuous linear functions with a jump at the austenitisation temperature $T_\text {A}$. The obtained parameters $\mathbf{p} _\alpha = \{ \alpha _{01}, w_{\alpha \,1}, \alpha _{02}, w_{\alpha \,2},\}$ are given in Table 2. The good agreement of the resulting curve $\alpha _{\text {m}}(T)$ with the experimental data from [35] is shown in Fig. 3.

4.2 Thermal properties c and $\varLambda$

The model parameters for the heat capacity cannot be identified directly from experimental data, since in experiments the mean isobaric heat capacity (51) is determined, from which the real isobaric heat capacity (50) can be obtained by (52). For the specimen subjected to standard conditions ($p=p_\text {at}=1013\,\text {hPa}$) in an ideal setting with $\varvec{\sigma }= - p \, {\varvec{I}}$, the heat capacity at constant hydrostatic stress (37) with $n=1$ results in

$$\begin{aligned} \begin{aligned} c_{\varvec{\sigma }} =&\frac{T}{2 \rho } \Biggl [\frac{p^2}{K^2} \left[ \frac{2}{K} \left[ \frac{\text {d}K}{\text {d}T}\right] ^2 - \frac{\text {d}^2 K}{\text {d}T^2} \right] - 2 p \frac{\text {d}\gamma }{\text {d}T} \Biggr ]\\&+ c_0 + {w_c}_1 T + {w_c}_2 T [T-T_{\text {r}}] \, , \end{aligned} \end{aligned}$$

(76)

and thus depends on K(T) which has already been identified. Since the material considered, i.e. 16MnCr5 case hardening steel, undergoes a phase transformation, values for the model parameters $c_0, \ {w_c}_1$ and ${w_c}_2$ are identified independently below austenitisation temperature $T\le T_\text {A}$ as $c_{0\,1}, \ {w_c}_{1\, 1}$ and ${w_c}_{2 \, 1}$ with respect ot the reference temperature $T_\text {r}$, and above i.e. $T>T_\text {A}$ as $c_{0\,2}, \ {w_c}_{1\, 2}$ and ${w_c}_{2 \, 2}$ with respect to $T_\text {A}$ as reference temperature. The results of the identification of the parameters $\mathbf{p _c = \left\{ c_{0\,1}, \ {w_c}_{1\, 1}, \ {w_c}_{2 \, 1}, \ c_{0\,2}, \ {w_c}_{1\, 2}, \ {w_c}_{2 \, 2} \right\} }$ are given in Table 2. Inserting the condition ${\varvec{\varepsilon }}= {\varvec{0}}$ into (34) leads for the heat capacity at constant (zero) strain to

$$\begin{aligned} \begin{aligned} c_{{\varvec{\varepsilon }}} =&- \frac{T}{2\rho } \biggl [ \frac{\text {d}^2 K}{\text {d}T^2} \mathrm{tr}^2 {\varvec{\varepsilon }}_\text {e}- 4 \frac{\text {d}K}{\text {d}T} \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\gamma \\&2 K \! \left[ \gamma ^2 - \mathrm{tr}{\varvec{\varepsilon }}_\text {e}\frac{\text {d}\gamma }{\text {d}T} \right] \biggr ] + c_0 + {w_c}_1 T + {w_c}_2 T [T-T_{\text {r}}] \, , \end{aligned} \end{aligned}$$

(77)

where ${\mathrm{tr}{\varvec{\varepsilon }}_\text {e}= \gamma _{\text {m}}(T_0) \left[ T_0 - T_{0 \, ^\circ \text {C}} \right] - \gamma _{\text {m}}(T) \left[ T - T_{0 \, ^\circ \text {C}} \right] }$, cf. (22) and (23). Thus, $c_{{\varvec{\varepsilon }}}$ additionally depends on the ansatz $\gamma _{\text {m}}(T) = 3 \alpha _{\text {m}}(T)$ presented before, cf. (73) and (72). The results of the parameter identification are illustrated in Fig. 4. Therein, the real isobaric capacity $c_{\varvec{\sigma }}$, the resulting mean isobaric heat capacity $c_{\varvec{\sigma }\, \text {m}}$, and the isomorphic heat capacity $c_{{\varvec{\varepsilon }}}$ are plotted against the temperature. The plots of the real and mean isobaric heat capacity show good agreement between the model and the experimental data from [35]. Moreover, the differences between the values of the different heat capacities become visible.

The heat conductivity is approximated by piecewise continuous functions. To be specific, a fourth order polynomial below the austenitisation temperature $T_\text {A}$ and an exponential ansatz above $T_\text {A}$ are chosen. The obtained parameters $\mathbf{p} _\varLambda = \{ \varLambda _{01}, w_{\varLambda \,11}, w_{\varLambda \,21}, w_{\varLambda \,31}, w_{\varLambda \,41},$ $\varLambda _{02}, \omega _{\varLambda \,2}, \chi _{\varLambda \,2}\}$ are given in Table 2. To show the quality of the approximation, the resulting curve $\varLambda (T)$ is depicted in Fig. 5 together with the experimental data from [35].

4.3 Thermo-viscoplastic properties $y_0$, $\varphi _\kappa$, $r^\text {mix}$, $H_0$, $\Delta Y_ {\infty 0}$, $k_0$, $\tau$, and m

The identification of the parameters for the visco-plasticity related part of the model follows a staggered scheme: In a first step, exponentially saturating hardening, i.e. $r^\text {mix}=0$, is assumed. From yield curves obtained at different temperatures $T_i$ and different strain rates, found in [32], values of the initial yield stress $y_{0}(T_i)$, the saturation yield stress $\Delta y_\infty (T_i) = \varphi _\kappa (T_i) \Delta Y_\infty$, the saturation coefficient $k_0(T_i)$, the characteristic time $\tau (T_i)$ as well as the viscosity exponent $m(T_i)$ are identified for each of these temperatures individually. For the parameter identification, only the part of the yield curves with the effective strain $\varepsilon _\text {eff} = \sqrt{2/3} \Vert {\varvec{\varepsilon }}_{\mathrm{dev}}\Vert \le 0.1$ is considered.

In a second step, the parameters $\mathbf{p _{y_0} = \{ Y_{00}, \omega _{y_0}, \chi _{y_0}, \phi _{y_0} \}}$ as well as updated values of $\Delta y_\infty (T_i)$, $k_0(T_i)$, $\tau (T_i)$, $m(T_i)$ are identified from the data obtained in step 1 as well as from experimental data from [25].

In a third step, the parameters $\mathbf{p} _{\kappa }= \{\Delta Y_{\infty 0}, k_0, \omega _{\kappa }, \chi _{\kappa }, \phi _{\kappa } \}$, $\mathbf{p _{\tau }= \{ \tau _0, \omega _{\tau }, \chi _{\tau } \}}$, and $\mathbf{p _{m}= \{ m_0, w_{m} \}}$ are identified.

In a fourth step, linear hardening, i.e. $r^\text {mix}=1$, is assumed and the hardening modulus $H_0$ is identified. Finally, the mix parameter $r^\text {mix}$ is identified in a fifth step. It appears that purely exponential hardening fits best and thus $r^\text {mix}$ converges towards zero. All parameters of the presented model are provided in Table 2.

In Fig. 6, the resulting curve for the initial yield stress $y_0(T)$ and the experimental data are plotted. Both are in good agreement. The depicted saturation yield stress ${y_\infty =y_0(T)+\varphi _\kappa (T)\Delta Y_{\infty 0}}$ also shows distinct thermal softening.

Fig. 20

Discretised boundary value problem of the plate with hole

Fig. 21

Comparison of force-displacement-curves of the plate with a hole under tension at initial temperature $T_0=20 \, ^\circ$C and different average strain rates $\dot{\bar{\varepsilon }}_{yy}$

In Fig. 7, the viscous over-stress $\Delta \sigma$ is depicted for selected effective plastic strain rates ${\dot{\varepsilon }}_{\text {p}} = \sqrt{2/3}\Vert {\dot{{\varvec{\varepsilon }}}}_\text {p}\Vert$ in a logarithmic scale over the temperature range of interest. Due to the power-type ansatz for the viscous over-stress, a tenfold increase of the effective plastic strain rate leads to a constant spacing between the curves. It can be observed that for plastic strain rates $>1 / \text {s}$, the viscous over-stress may dominate the total yield stress with increasing temperature, whereas for low plastic strain rates it does not.

In Fig. 8, the stress–strain curves for a uniaxial stress state predicted by the material model at constant strain rates and temperatures are compared with experimental data from [32]. At room temperature $T=25 \, ^\circ \text {C}$ the initial yield stress as well as the saturation behaviour are captured well by the model for all strain rates. At $T=800 \, ^\circ \text {C}$ the initial yield stress overestimated by the model but the correct stress range is met. This over-estimation of the initial yield stress can be explained by comparably large derivations in the mechanical properties when comparing one batch to another and by a lack of experimental data performed on specimen from one batch. In addition, the increasing share of the viscous over-stress with increasing temperature is visible. The comparison of the curves obtained at $T=25 \, ^\circ \text {C}$ and $T=800 \, ^\circ \text {C}$ with the curves obtained at $T=600 \, ^\circ \text {C}$ shows the non-linearity of the thermal softening: Although the temperature difference between $25 \, ^\circ \text {C}$ and $600 \, ^\circ \text {C}$ is approximately three times larger as between $T=600 \, ^\circ \text {C}$ and $T=800 \, ^\circ \text {C}$, the curves obtained at $T=600 \, ^\circ \text {C}$ differ less to the ones obtained at $T=25 \, ^\circ \text {C}$ than to those obtained at $T=800 \, ^\circ \text {C}$.

5 Numerical examples

In this section, aspects of the localisation and regularisation behaviour of the representative initial boundary value problems are investigated by simulating shearing of a perturbed plate and a plate with a circular centric hole under tension.

5.1 Shearing of plate with perturbation

To investigate the effect of the model parameters on the localisation behaviour of the model, a perturbed shear problem as depicted in Fig. 9 is analysed. To be specific, simulations of a block with edge lengths $h=1\, \text {mm}$ subjected to shear loading are performed. The shear loading is applied in vertical direction ${\bar{u}}_y(t)$ on the left and right edges in opposite directions, the displacement in the remaining directions is inhibited on all nodes, ${\bar{u}}_x=0$ and ${\bar{u}}_z=0$. Since localisation is expected when hardening does not compensate thermal softening effects in this analysis, the applied magnitudes of shear loading are in general not within the usual range of a small-strain model. The boundaries are assumed to be adiabatic. For the investigation of the mesh-dependency of the problem, the block is discretised by ${n_\text {el} = 20, \ \ldots , \ 2000}$ eight-noded hexahedral Lagrangian elements along the horizontal x-direction and by 1 element along the other directions. The influence of the loading-rate, the viscous over-stress and the internal heat flux on the results is of special interest. Therefore, the problem is simulated at different loading rates, $\dot{\bar{u}}_y = 0.05\, \text {mm}/\text {s}$, $\dot{\bar{u}}_y = 0.5\, \text {mm}/\text {s}$ and $\dot{\bar{u}}_y = 5\, \text {mm}/\text {s}$, for different ratios of the heat conductivity $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$ (no heat conduction), $10^{-5}, \ 10^{-1}$ and 1, different ratios of the characteristic time $\tau _0/\tau _0^\text {16MnCr5} = 0$ (no viscosity), 0.1, 1 and 10, as well as different ratios of the visco-plastic exponent $m_0/m_0^\text {16MnCr5} = 1, \ 0.5$ and 0.2. These loading rates correspond to an averaged shear rate of $\dot{{\bar{\gamma }}}_{xy} = 0.1 \, / \text {s}$, $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ and $\dot{{\bar{\gamma }}}_{xy} = 10 \, / \text {s}$, respectively. The perturbation is applied as a cosine-shaped variation of the initial yield stress $Y_{00}(x) = Y_{00}\left[ 1 - 0.1 \cos \left( 2 \pi x/h \right) \right]$.

In Fig. 10, the resulting force-displacement curves are depicted for both problems, i.e. with, Fig. 10a, and without internal heat flux, Fig. 10b. In both cases the initial temperature is $T_0=20\,^\circ \text {C}$. Whereas the problem with internal heat flux does not show mesh dependency in the simulated regime, the problem without heat conduction does: At certain loading points in the considered range of applied displacement, the force-displacement curves observed at average shear rates of $\dot{{\bar{\gamma }}}_{xy} = 1\, /\text {s}$ and $\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$ drop, where their negative slope increases with increasing element-number $n_\text {el}$, i.e. decreasing mesh-size $h_\text {el} = h/n_\text {el}$. Also, with decreasing loading rate, the differences between the force-displacement curves of the different discretisations initiates at smaller magnitudes of the boundary displacements, e.g. at ${{\bar{u}}}_y \approx 0.2 \, \text {mm}$ for $\dot{{\bar{\gamma }}}_{xy} = 1\, /\text {s}$ and at ${{\bar{u}}}_y \approx 0.1 \, \text {mm}$ for $\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$.

The comparison of the averaged shear strain distributions $\bar{\gamma }_{xy}(x)$ at the integration points of the different discretisations depicted in Fig. 11, shows only minor localisation with decreasing loading rate for the simulations considering heat flux within the specimen, and all discretisations converge to the same solution. The relative differences of the averaged shear strains ${\bar{\gamma }}_{xy}$ at the centre of the specimen between the coarse (${{\,\mathrm{{n}_\text {el}}\,}}= 20$) and the finer discretisations are only $\approx 6.5 \, \%$ for the slowest loading rate ($\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$) and $\approx 2 \, \%$ for the fastest loading rate ($\dot{{\bar{\gamma }}}_{xy} = 10\, /\text {s}$). For the simulation neglecting heat flux, the comparison shows an obvious localisation with decreasing mesh size for the slowest loading rate $\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$. Its maximum values at $\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$ are 4.8 times the average for the coarse discretisation with $n_\text {el} = 20$, 17 times for $n_\text {el} = 200$, and 48 times for $n_\text {el} = 2000$. For the fast loading rate, $\dot{{\bar{\gamma }}}_{xy} = 10\, /\text {s}$, the shear strain distributions of the two fine discretisations do not show obvious differences in magnitude and converge to the same solution.

In Fig. 12 the resulting temperature distribution is shown. For both loading rates, the results of the simulations of considering heat flux converge to the same results. Due to the influence of the heat flux, a decreasing loading rate leads to a more uniform temperature distribution. Comparing the two plots of the simulations neglecting the influence of heat flux, a localisation in the temperature increase $\Delta T(x)$ caused by the localisation in strain and thus by the localisation of the mechanical heat production can be observed for the problem at slow loading rate $\dot{{\bar{\gamma }}}_{xy} = 0.1\, /\text {s}$. There, the maximum temperature change rises with the increasing number of elements from $122\,\text {K}$ for ${{\,\mathrm{{n}_\text {el}}\,}}=20$ up to $1330\,\text {K}$ for ${{\,\mathrm{{n}_\text {el}}\,}}=2000$. For the problem at fast loading rate, which in Fig. 10b does not show any divergence of the force-displacement curves obtained for the different discretisations in the investigated displacement range, the temperature increase converges also for the fine discretisations, $n_\text {el}=200$ and $n_\text {el}=2000$ to $213\, \text {K}$.

Figure 13 compares the strain rate dependency of the width of the shear zone b at different initial temperatures for simulations run with $\varLambda _0/\varLambda _0^\text {16MnCr5} = 1$, Fig. 13a, and $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$, Fig. 13b. The width of the shear zone b is identified by the relation $x \in [-b,\ b] \mid \gamma _{xy}(x) \ge {\bar{\gamma }}_{xy}$. It can be observed that for both cases, i.e. $\varLambda _0/\varLambda _0^\text {16MnCr5} = 1$ and $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$, with increasing strain rate, b seems to converge against values which are only little below the dimension of the imposed cosine-shaped perturbation $b^* = 0.25\, \text {mm}$. For low loading rates, however, the curves of the shear zone decline towards $b\approx 0.14 \, \text {mm}$ for $\varLambda _0/\varLambda _0^\text {16MnCr5} = 1$ and $b\approx 0.08 \, \text {mm}$ for $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$. This decline appears to show stronger saturation for $\varLambda _0/\varLambda _0^\text {16MnCr5} = 1$ than for $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$ which may indicate a regularising effect of the heat conduction. The tendency of an increasing width of the shear zone b with increasing initial temperature $T_0$ can be observed.

Figure 14 depicts the resulting force–displacement curves for different values of the heat conductivity for the case $\tau _0/\tau _0^\text {16MnCr5} = 0$ at $\dot{\bar{\gamma }}_{xy} = 1 \, / \text {s}$ for two different discretisations $n_\text {el}=200$ and $n_\text {el}=2000$. Up to $u_y \approx 0.06 \, \text {mm}$ all curves are congruent. Beginning at that point, the curves for low or no heat-conductivity show stronger softening behaviour than the curves at $\varLambda _0/\varLambda _0^\text {16MnCr5}=1$. This is caused by heat being more efficiently transported away from the centre of the specimen in the latter case ($\varLambda _0/\varLambda _0^\text {16MnCr5}=1$), see Fig. 16). The curves for the different discretisations for $\varLambda _0/\varLambda _0^\text {16MnCr5}=1$ and $\varLambda _0/\varLambda _0^\text {16MnCr5}=10^{-3}$ remain congruent in the sequel or show only minor deviations, whereas for lower or no heat conductivity, $\varLambda _0/\varLambda _0^\text {16MnCr5}\le 10^{-4}$, the force–displacement curves for both discretisations diverge from each other starting at $u_y \approx 0.15 \, \text {mm}$.

In Fig. 15, the resulting distributions of the normalised shear angle at $u_y \approx 0.16 \, \text {mm}$ are compared for both discretisations. Both figures show an increase of the maximum of the normalised shear angle $\gamma _{xy} / \bar{\gamma }_{xy}$ at $x=0$ with decreasing heat conductivity. The comparison of both discretisations shows an increase of the maximum values from $\gamma _{xy} / {\bar{\gamma }}_{xy}\approx 6.9$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=10^{-5}$) and $\gamma _{xy} / {\bar{\gamma }}_{xy}\approx 7.4$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=0$) for $n_\text {el}=200$, Fig. 15a, to $\gamma _{xy} / {\bar{\gamma }}_{xy}\approx 54$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=10^{-5}$) and $\gamma _{xy} / {\bar{\gamma }}_{xy}\approx 75$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=0$) for $n_\text {el}=2000$, Fig. 15b, which is an increase of the order of the reciprocal mesh size. For higher heat conductivity only minor deviations appear between the two discretisations.

Figure 16 shows the resulting temperature distribution $\Delta T(x)$. In contrast to the curves obtained for $\varLambda _0/\varLambda _0^\text {16MnCr5}=1$, which appears to be almost a homogeneous distribution, the curves at reduced heat conductivity ($\varLambda _0/\varLambda _0^\text {16MnCr5} \le 10^{-3}$) show a distinct peak at the centre of the specimen ($x=0$), which increases with decreasing heat conductivity. Similarly to the shear angle, the maximum values for low or no heat conductivity increase significantly with decreasing mesh size from $\Delta T\approx 119\, \text {K}$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=10^{-5}$) and $\Delta T\approx 126\, \text {K}$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=0$) for $n_\text {el}=200$ , Fig. 16a, to $\Delta T\approx 300 \, \text {K}$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=10^{-5}$) and $\Delta T\approx 690 \, \text {K}$ ($\varLambda _0/\varLambda _0^\text {16MnCr5}=0$) for $n_\text {el}=2000$, which is of the factors $\approx 2.5$ and $\approx 5.5$, respectively, larger for the finer mesh ($n_\text {el} = 2000$), Fig. 16b, than for the coarser mesh ($n_\text {el} = 200$), Fig. 16a.

Figure 17 compares the influence of the viscoplastic parameters $\tau _0$ (Fig. 17) and $m_0$ (Fig. 17b) on the stability of the solution. The simulations have been performed at an averaged shear rate $\dot{{\bar{\gamma }}}_{xy} = 1 \, / \text {s}$ starting at the initial temperature $T_0 = 20 \, ^\circ \text {C}$ and adiabatic conditions $\varLambda _0/\varLambda _0^\text {16MnCr5} = 0$ have been assumed. It can be denoted that a larger characteristic time $\tau _0$ has a stabilising effect, making the solution mesh-independent for a larger strain-range, whereas a smaller viscous exponent $m_0$ has the opposite effect, although both increase the current yield stress. For both cases, a variation of $\tau _0$ and a variation of $m_0$, the force displacement–curves obtained for both discretisations, $n_\text {el}=200$ and $n_\text {el}=2000$, diverge as soon as certain critical points have been reached and softening occurs.

The resulting distributions of the normalised shear angle $\gamma _{xy}(x)/{\bar{\gamma }}_{xy}$ are shown in Fig. 18. The comparison of the distributions depicted in Fig. 18a, b, obtained for both discretisations at different values of the characteristic time $\tau _0/\tau _0^\text {16MnCr5}$, shows increasing maximal values for decreasing ratio $\tau _0/\tau _0^\text {16MnCr5}$. The maxima obtained at $\tau _0/\tau _0^\text {16MnCr5}=0$ increase from $\gamma _{xy}/{\bar{\gamma }}_{xy}\approx 7.3$ for $n_\text {el}=200$ to $\gamma _{xy}/\bar{\gamma }_{xy}\approx 75$ for $n_\text {el}=2000$, which is an increase of the order of the reciprocal mesh size. For $\tau _0/\tau _0^\text {16MnCr5}>0$, no significant differences between both discretisations can be observed. The curves obtained for various values of $m_0/m_0^\text {16MnCr5}$ (Fig. 18c, d) show a localisation of the normalised shear angle at the centre of the specimen for $m_0/m_0^\text {16MnCr5}=0.2$ which increases from $\gamma _{xy}/{\bar{\gamma }}_{xy}\approx 3.9$ for $n_\text {el}=200$ to $\gamma _{xy}/\bar{\gamma }_{xy}\approx 16.6$ for $n_\text {el}=2000$ by $\approx 4.25\, \%$ when reducing the mesh size by the factor 10. The curves obtained for $m_0/m_0^\text {16MnCr5}=0.5$ and $m_0/m_0^\text {16MnCr5}=1$ show only minor deviations between both discretisations.

Fig. 22

Distribution of the isotropic hardening variable k at different average strain rates $\dot{\bar{\varepsilon }}_{yy}$ at ${\bar{\varepsilon }}_{yy} = 0.05$

Fig. 23

Temperature distribution $\Delta T$ at different average strain rates $\dot{\bar{\varepsilon }}_{yy}$ at $\bar{\varepsilon }_{yy} = 0.05$

The shape of the curves of the resulting temperature changes, depicted in Fig. 19, coincide with the curves of the normalised shear angle, depicted in Fig. 18. For decreasing characteristic time $\tau _0/\tau _0^\text {16MnCr5}$, the temperature difference at the centre of the specimen ($x=0$) increases. For $\tau _0/\tau _0^\text {16MnCr5}=0$ the temperature difference at the centre of the specimen increases with decreasing mesh size from $\Delta T = 126 \, \text {K}$ ($n_\text {el}=200$) to $\Delta T = 690 \, \text {K}$ ($n_\text {el}=2000$). For $\tau _0/\tau _0^\text {16MnCr5}\ge 0.1$ the maxima of the distributions of both discretisations show only minor deviations. The curves obtained for different ratios of the viscous exponent $m_0/m_0^\text {16MnCr5}$ also show a localisation of the temperature increase at $x=0$, which increases with decreasing ratio $m_0/m_0^\text {16MnCr5}$. For the case $m_0/m_0^\text {16MnCr5}=0.2$ this temperature change increases from $\Delta T = 65.5 \, \text {K}$ for $n_\text {el}=200$ to $\Delta T = 411 \, \text {K}$ for $n_\text {el}=2000$. The curves obtained for $m_0/m_0^\text {16MnCr5}=0.5$ and $m_0/m_0^\text {16MnCr5}=1$ only show minor differences between both discretisations. As for all investigated examples, a continuous differentiable perturbation has been imposed, and the distribution of the shear angle also seems to be continuous differentiable. This is in good agreement with analytical derivations found in, e.g. [2, 17].

5.2 Plate with a hole under tension

To investigate aspects of the regularisation behaviour of the model, a non-homogeneous problem of a plate with a circular centric hole, as depicted in Fig. 20, is considered. Starting at an initial temperature of $T_0 = 20\,^\circ \text {C}$, the plate is subjected to vertical displacement ${\bar{u}}_y$ in opposite directions along its upper and lower surfaces. The response of the system is investigated for three different constant loading rates $\dot{{\bar{u}}}_y = 2 \, \text {mm}/\text {s}$, $\dot{\bar{u}}_y = 20 \, \text {mm}/\text {s}$ and $\dot{{\bar{u}}}_y = 200 \, \text {mm}/\text {s}$, which are equivalent to $\dot{\bar{\varepsilon }}_{yy} = 0.1 \, /{\text {s}}$, $\dot{\bar{\varepsilon }}_{yy} = 1 \, /{\text {s}}$, and $\dot{\bar{\varepsilon }}_{yy} = 10 \, /{\text {s}}$, respectively. The remaining displacement components at both loaded surfaces are equal to zero, i.e. ${\bar{u}}_x=0$ and ${\bar{u}}_z=0$. All boundaries are assumed to be adiabatic. Based on the multiple symmetry of the problem, only the part of the plate located in the positive octant is considered. It is discretised by 10272 eight-noded hexahedral ${\bar{B}}$-elements, cf. [16, ch. 4.5.2], where four elements are considered in thickness direction z.

The resulting force-displacement curves, compared in Fig. 21, increase to maximum values which are between 5.1 and 5.2$\, \text {kN}$ for the three different loading rates considered. The maximum of the curve obtained at $\dot{\bar{\varepsilon }}_{yy} = 1 \, /{\text {s}}$ at $u_y\approx 2\, \text {mm}$, $F_y\approx 5.12\,\text {kN}$, is slightly below the maximum of the curve obtained at $\dot{{\bar{\varepsilon }}}_{yy} = 0.1 \, /{\text {s}}$ at $u_y\approx 1.8\, \text {mm}$, $F_y\approx 5.13\,\text {kN}$. The curve obtained for $\dot{\bar{\varepsilon }}_{yy} = 10 \, /{\text {s}}$ shows its maximum of $F_y\approx 5.2\,\text {kN}$ at $u_y\approx 2.3\, \text {mm}$. For displacements larger than at the force maxima, all three curves show a decreasing force $F_y$, where the magnitude of the negative slopes of the force-displacement curves increases with increasing strain rate.

Figure 22 shows the resulting distribution of the isotropic hardening variable k at ${{\bar{\varepsilon }}}_{yy} = 0.05$ which, for moderate temperature changes and monotonically increasing loading, gives a good approximation of the effective plastic strain. For all loading rates compared, the distribution of k shows a localisation at the hole under $45^\circ$ with respect to the overall loading direction. Since the maximum value of k is highest for $\dot{{\bar{\varepsilon }}}_{yy} = 1 \, /{\text {s}}$, the localisation seems to reach a maximum for a loading rate between $\dot{{\bar{\varepsilon }}} = 0.1 \, /{\text {s}}$ and $\dot{\bar{\varepsilon }} = 10 \, /{\text {s}}$.

Figure 23 compares the resulting temperature distribution for the considered loading rates at $\bar{\varepsilon }_{yy} = 0.05$. Like the hardening variable, the temperature increase $\Delta T$ also concentrates at the hole, whereas, with increasing loading rate, a more distinct localisation in direction of $45^\circ$ is observable.

6 Summary

In this paper, a material model for thermo-viscoplasticity has been established in the setting of thermodynamics with internal variables and implemented into a fully coupled finite-element framework. The model incorporates thermal softening of the thermal and thermo-elastic properties, as well as of the thermo-plastic properties. Mechanical heat production due to plastic deformation as well as the Gough-Joule effect are covered. The model parameters have been identified based on experimental data for 16MnCr5 (1.1731) case hardening steel.

The regularisation effects arising from heat conduction and strain-rate hardening (viscosity) on the localisation phenomena related to thermal softening and saturating strain hardening included in the model have been investigated for different strain rates and values of the heat conductivity, viscoplastic characteristic time and viscoplastic exponent. The examples show a regularising effect of the heat conduction as well as the viscoplastic characteristic time and the strain rate, whereas a decreasing viscoplastic exponent has a negative effect on the convergence of the finite element solution. It can be concluded that for the given parameter set and boundary conditions considered, the regularisation due to the heat conduction is more pronounced than due to viscoplasticity.

Since the model is formulated in a small strain setting, it does not cover geometric effects like, e.g. necking. Thus, for the investigation of such effects, a formulation in a finite strain framework is deemed necessary.