1 Introduction

Material interfaces can occur at different material length scales and can significantly influence the effective constitutive response of the material (system) under consideration. Typical examples for such interfaces are grain boundaries in polycrystalline materials and transition zones between different phases in multi-phase materials. In this regard, the unique properties of the interfaces may significantly differ from those of the surrounding continuum and can be accounted for in simulations by the introduction of interface models. In these approaches, the physical interface (of finite thickness) is not geometrically resolved but rather approximated as a lower-dimensional object (e.g. a surface in a three-dimensional setting).

Based on the assumed continuity of field quantities across the interface, different types of interface formulations may moreover be distinguished, see [15] and references cited therein. Elastic-interface models originate from the pioneering works of Gurtin and Murdoch on interface elasticity [11, 23], and assume the displacement-type fields to be continuous, whereas traction-type quantities may exhibit jump-discontinuities across the interface. Classic cohesive interface models that date back to the seminal works by Barenblatt on quasi-brittle materials [2] and by Dugdale on ductile materials [6] on the other hand, assume traction continuity across the interface and allow for the modelling of jump-discontinuities in the displacement-type fields. Although seemingly different, it has recently been shown that classic cohesive zone formulations and interface elasticity formulations can be regarded as two extremes of the unifying theory of generalised imperfect interfaces elaborated in [15, 16, 27, 31].

Since the works of Barenblatt and Dugdale [2, 6], classic cohesive zone models have been subject of intense research with many contributions focusing on the consistency of cohesive zone formulations with fundamental requirements of continuum mechanics (particularly for finite deformations), e.g. [22, 26, 35, 38], and on the elaboration of specific traction separation laws that account for irreversible processes such as damage and plasticity, e.g. [7, 12, 25, 30, 33, 39]. In this regard, a salient feature of cohesive zone damage formulations as compared to continuum damage formulations is that the fracture energy does not depend on the finite element size such that no sophisticated regularisation schemes are required [3, 24]. Moreover, cohesive zone formulations can conveniently be incorporated into finite element formulations by means of mixed-type boundary conditions or cohesive zone elements, see [24] and references cited therein.

In addition to the developments on cohesive zone formulations for purely mechanical problems, cohesive zone formulations for coupled multi-physics problems have been in the focus of intense research. In particular, thermo-mechanical coupling has been addressed in [8, 9, 28] and electro-mechanically coupled cohesive zone formulations for electro-active solids have been studied in [1, 18, 19, 34, 36, 37]. Focussing on piezo- and ferroelectric effects in dielectric solids, the latter formulations differ significantly from the present developments on electrical conductors. In this regard, the principal (electrical) material parameters in the established formulations for electro-active solids are the piezo- and dielectric moduli, whereas the present contribution is motivated by the influence of mechanically-induced interface damage processes on the electrical conductivity, as studied experimentally in, e.g., [4, 5, 10].

The contribution is organised as follows: Section 2 deals with the derivation of the fundamental set of balance equations and jump-conditions at material interfaces, with particular focus being on the electrical sub-problem. Based on these developments, a finite element-based implementation of the theory is discussed in Section 3. These fundamentals serve as the basis for the study of representative boundary value problems in Section 4 that show the applicability of the proposed formulation. In particular, the finite element implementation is validated by means of analytical solutions, and the influence of intergranular fracture processes on the electrical conductivity is studied numerically.

1.1 Notation

With \(\varvec{\alpha }\), \(\varvec{\beta }\), \(\varvec{\gamma }\), \(\varvec{\delta }\) denoting tensor-valued quantities of first order and with the standard dyadic product denoted by \(\otimes \), single and double tensor contractions take the form \( \left[ \varvec{\alpha }\otimes \varvec{\beta }\right] \cdot \left[ \varvec{\gamma }\otimes \varvec{\delta }\right] = \left[ \varvec{\beta }\cdot \varvec{\gamma }\right] \,\left[ \varvec{\alpha }\otimes \varvec{\delta }\right] \) and \( \left[ \varvec{\alpha }\otimes \varvec{\beta }\right] :\left[ \varvec{\gamma }\otimes \varvec{\delta }\right] = \left[ \varvec{\alpha }\cdot \varvec{\gamma }\right] \, \left[ \varvec{\beta }\cdot \varvec{\delta }\right] \). In addition, the non-standard dyadic products \( \left[ \varvec{\alpha }\otimes \varvec{\beta }\right] \overline{\otimes }\left[ \varvec{\gamma }\otimes \varvec{\delta }\right] = \left[ \varvec{\alpha }\otimes \varvec{\gamma }\right] \otimes \left[ \varvec{\beta }\otimes \varvec{\delta }\right] \) and \( \left[ \varvec{\alpha }\otimes \varvec{\beta }\right] \underline{\otimes } \left[ \varvec{\gamma }\otimes \varvec{\delta }\right] = \left[ \varvec{\alpha }\otimes \varvec{\gamma }\right] \otimes \left[ \varvec{\delta }\otimes \varvec{\beta }\right] \) are introduced to shorten notation. Moreover, \(\varvec{I}\) denotes the second order identity tensor, \(\varvec{\epsilon }\) the third order permutation tensor and \(\nabla \bullet \), \(\nabla \cdot \bullet \), \(\nabla \times \bullet \), indicate (right-)gradient, (right-)divergence and (right-)curl operations, respectively. Furthermore, quantities at the two opposing sides of an interface will be indicated by superscripts \(\bullet ^-\) and \(\bullet ^+\) such that the jump of a quantity across the interface follows as

$$\begin{aligned} \llbracket {\bullet }\rrbracket = \bullet ^+ - \bullet ^- , \end{aligned}$$
(1)

the interfacial mean value reads

$$\begin{aligned} \{\!\{ {{\bullet }} \}\!\} = \frac{1}{2}\left[ \bullet ^+ + \bullet ^- \right] , \end{aligned}$$
(2)

and the identity

$$\begin{aligned} \llbracket {\bullet *}\rrbracket = \llbracket {\bullet }\rrbracket \, \{\!\{ {*} \}\!\} + \{\!\{ {\bullet } \}\!\}\,\llbracket {*}\rrbracket , \end{aligned}$$
(3)

holds.

2 Continuum thermodynamics

This section deals with the thermodynamic fundamentals of a continuum with material interfaces that is subjected to mechanical and electrical loads, see Figure 1. For the convenience of the reader, and to show similarities and differences in the derivations of the local field equations, the mechanical sub-problem is briefly recapitulated in Section 2.1 before the electrical sub-problem is studied in detail in Section 2.2. Based on these fundamentals, an extended form of the balance equation of energy is proposed in Section 2.3, and constitutive restrictions that are posed by the extended dissipation inequality are discussed in Section 2.4. The ensuing derivations are based on the assumption of quasi-static deformation processes and of a quasi-stationary electrical problem.

Fig. 1
figure 1

Specification of quantities in the control volume \(\mathcal {V}\) and on the interface \(\mathcal {I}\). The interface is characterised by its unit surface normal vector \(\widetilde{\varvec{n}}\) and quantities at opposing sides of the interface are indicated by superscripts \(\bullet ^-\) and \(\bullet ^+\)

Full size image

2.1 Mechanical sub-problem

The control volume \(\mathcal {V}\) is assumed to be loaded by volume distributed forces \(\varvec{f}\) that scale in the mass density (per unit volume) \(\rho \), by surface distributed forces \(\widetilde{\varvec{f}}\) that act on the interface \(\mathcal {I}\) and scale in the mass density (per unit surface) \(\widetilde{\rho }\), and by tractions

$$\begin{aligned} \varvec{t}=\varvec{\sigma }\cdot \varvec{n}, \end{aligned}$$
(4)

that are related to the small strain stress tensor \(\varvec{\sigma }\) via the outward unit surface normal vector \(\varvec{n}\). Based on the latter assumptions, and by neglecting line-distributed (tangential) forces on \(\partial \mathcal {I}\), the extended integral form of the (quasi-static) balance equation of linear momentum reads

$$\begin{aligned} \varvec{0} =&\int _{\mathcal {V}}\rho \,\varvec{f}\, \mathrm {d}v+ \int _{\mathcal {I}}\widetilde{\rho }\, \widetilde{\varvec{f}}\, \mathrm {d}a+ \int _{\partial \mathcal {V}}\varvec{t}\, \mathrm {d}a. \end{aligned}$$
(5)

The third summand on the right-hand side of (5) can further be rewritten as

$$\begin{aligned} \begin{aligned} \int _{\partial \mathcal {V}}\varvec{t}\, \mathrm {d}a=&\int _{\partial \mathcal {V}}\varvec{t}\, \mathrm {d}a+\left[ -1+1\right] \, \int _{\mathcal {I}^+\,\cup \,\mathcal {I}^-}\varvec{t}\, \mathrm {d}a\\ =&\int _{\partial \mathcal {V}^+}\varvec{t}\, \mathrm {d}a+ \int _{\partial \mathcal {V}^-}\varvec{t}\, \mathrm {d}a+ \int _{\mathcal {I}}\llbracket {\widetilde{\varvec{t}}}\rrbracket \,\mathrm {d}a\\ =&\int _{\mathcal {V}^+}\nabla \cdot \varvec{\sigma }\, \mathrm {d}v+ \int _{\mathcal {V}^-}\nabla \cdot \varvec{\sigma }\, \mathrm {d}v+ \int _{\mathcal {I}}\llbracket {\widetilde{\varvec{t}}}\rrbracket \,\mathrm {d}a\end{aligned}\end{aligned}$$
(6)

where the classic divergence theorem was used along with the definitions

$$\begin{aligned} \llbracket {\widetilde{\varvec{t}}}\rrbracket = \widetilde{\varvec{t}}^+-\widetilde{\varvec{t}}^-, \quad \widetilde{\varvec{t}}^+= \varvec{\sigma }^+\cdot \widetilde{\varvec{n}}, \quad \widetilde{\varvec{t}}^-= \varvec{\sigma }^-\cdot \widetilde{\varvec{n}}\end{aligned}$$
(7)

and with the geometric constraint on the unit surface normal vectors at opposing sides of the interface

$$\begin{aligned} \varvec{n}^+= -\widetilde{\varvec{n}}, \quad \varvec{n}^-= \widetilde{\varvec{n}}. \end{aligned}$$
(8)

The localisation of the ensuing equation that results from the insertion of (6) into (5), i.e.,

$$\begin{aligned} \begin{aligned} \varvec{0} =&\int _{\mathcal {V}^+}\nabla \cdot \varvec{\sigma }+ \rho \,\varvec{f}\, \mathrm {d}v+ \int _{\mathcal {V}^-}\nabla \cdot \varvec{\sigma }\,+ \rho \, \varvec{f}\mathrm {d}v\\&+ \int _{\mathcal {I}}\llbracket {\widetilde{\varvec{t}}}\rrbracket + \widetilde{\rho }\, \widetilde{\varvec{f}}\, \mathrm {d}a, \end{aligned}\end{aligned}$$
(9)

for control volumes that contain and for control volumes that do not contain material interfaces, eventually gives rise to the local form of the balance equation of linear momentum in the bulk and at the interface, namely

$$\begin{aligned} \nabla \cdot \varvec{\sigma }&+ \rho \,\varvec{f}\, = \,\varvec{0} \qquad \text {(in the bulk)} , \end{aligned}$$
(10a)
$$\begin{aligned} \llbracket {\widetilde{\varvec{t}}}\rrbracket&+ \widetilde{\rho }\, \widetilde{\varvec{f}}\, = \,\varvec{0}\qquad \text {(at the interface)}. \end{aligned}$$
(10b)

Under the same assumptions that gave rise to (5), the extended integral form of the balance equation of angular momentum follows as

$$\begin{aligned} \begin{aligned} \varvec{0} =&\int _{\mathcal {V}}\varvec{x}_{\varDelta }\times \rho \,\varvec{f}\, \mathrm {d}v+ \int _{\mathcal {I}}\varvec{x}_{\varDelta }\times \widetilde{\rho }\widetilde{\varvec{f}}\, \mathrm {d}a+ \int _{\partial \mathcal {V}}\varvec{x}_{\varDelta }\times \varvec{t}\, \mathrm {d}a\,, \end{aligned}\end{aligned}$$
(11)

with \(\varvec{x}\) denoting the position vector of a particle and with \(\varvec{x}_{\varDelta }=\varvec{x}-\varvec{x}_\mathrm {ref}\) denoting the difference vector to a fixed but otherwise arbitrary reference point \(\varvec{x}_\mathrm {ref}\). In a small deformation setting, the balance equations are evaluated with regard to the undeformed configuration such that \(\widetilde{\varvec{x}}=\varvec{x}^-=\varvec{x}^+\). Accordingly (11), takes the form

$$\begin{aligned} \begin{aligned} \varvec{0} =&\int _{\mathcal {V}^+}\varvec{x}_{\varDelta }\times \left[ \nabla \cdot \varvec{\sigma }+\rho \,\varvec{f}\right] + \varvec{\epsilon }:\varvec{\sigma }^{\mathrm {t}} \, \mathrm {d}v\\ \quad&+\int _{\mathcal {V}^-}\varvec{x}_{\varDelta }\times \left[ \nabla \cdot \varvec{\sigma }+\rho \,\varvec{f}\right] + \varvec{\epsilon }:\varvec{\sigma }^{\mathrm {t}} \, \mathrm {d}v\\ \quad&+\int _{\mathcal {I}}~~\varvec{x}_{\varDelta }\times \left[ \llbracket {\widetilde{\varvec{t}}}\rrbracket +\widetilde{\rho }\widetilde{\varvec{f}}\right] \, \mathrm {d}a. \end{aligned}\end{aligned}$$
(12)

By invoking (10), the localisation of (12) further simplifies to the classic symmetry condition of the bulk stress tensor

$$\begin{aligned} \varvec{\sigma }=\varvec{\sigma }^{\mathrm {t}}\quad \text {(in the bulk)} . \end{aligned}$$
(13)

In a finite deformation setting, the balance equation of angular momentum additionally stipulates a coaxiality constraint between \(\{\!\{ {\widetilde{\varvec{t}}} \}\!\}\) and the jump in the displacement field across the interface \(\llbracket {\varvec{u}}\rrbracket \), see for instance [16] for a detailed derivation and the discussion in [26, 38].

2.2 Electrical sub-problem

The quasi-stationary processes of electrodynamics that are in the focus of this contribution are governed by the continuity equation for the electric current density

$$\begin{aligned} 0 = \int _{\partial \mathcal {V}}\varvec{j}\cdot \varvec{n}\, \mathrm {d}a, \end{aligned}$$
(14)

and by Faraday’s law of induction

$$\begin{aligned} 0 = \int _{\partial \mathcal {A}}\varvec{e}\cdot \mathrm {d}\varvec{s}, \end{aligned}$$
(15)

with \(\varvec{e}\) denoting the electric field vector, see e.g. [14, 17] for a derivation based on Maxwell’s equations of electromagnetism.

Following the same procedure that led to (10), the surface term in (14) is rewritten by making use of the classic divergence theorem

$$\begin{aligned} 0 =&\int _{\partial \mathcal {V}}\varvec{j}\cdot \varvec{n}\, \mathrm {d}a+\left[ -1+1\right] \, \int _{\mathcal {I}^+\,\cup \,\mathcal {I}^-}\varvec{j}\cdot \varvec{n}\, \mathrm {d}a\nonumber \\ =&\int _{\partial \mathcal {V}^+}\varvec{j}\cdot \varvec{n}\, \mathrm {d}a\, + \int _{\partial \mathcal {V}^-}\varvec{j}\cdot \varvec{n}\, \mathrm {d}a\, + \int _{\mathcal {I}}\llbracket {\widetilde{i}}\rrbracket \,\mathrm {d}a\nonumber \\ =&\int _{\mathcal {V}^+}\nabla \cdot \varvec{j}\, \mathrm {d}v+ \int _{\mathcal {V}^-}\nabla \cdot \varvec{j}\, \mathrm {d}v~\,+ \int _{\mathcal {I}}\llbracket {\widetilde{i}}\rrbracket \,\mathrm {d}a\end{aligned}$$
(16)

and by introducing the definitions

$$\begin{aligned} \llbracket {\widetilde{i}}\rrbracket = \widetilde{i}^+-\widetilde{i}^-\,, \quad \widetilde{i}^+= \varvec{j}^+\cdot \widetilde{\varvec{n}}\,,\quad \widetilde{i}^-= \varvec{j}^-\cdot \widetilde{\varvec{n}}. \end{aligned}$$
(17)

The localisation of (16) for control volumes that contain and for control volumes that do not contain material interfaces stipulates the local form of the continuity equation for the electric current in the bulk and at the interface, namely

$$\begin{aligned} \nabla \cdot \varvec{j}&= \,0\qquad \text {(in the bulk)} , \end{aligned}$$
(18a)
$$\begin{aligned} \llbracket {\widetilde{i}}\rrbracket&= \,0\qquad \text {(at the interface)}. \end{aligned}$$
(18b)

Equation (18b) states that the normal jump of the electric current density vector across a material interface vanishes. In the derivation of this continuity condition it has tacitly been assumed that the tangential component of the interfacial electric current density vector is negligible. The relaxation of this assumption would lead to a generalised formulation that includes contributions akin to those known from interface elasticity formulations in the mechanical case.

Fig. 2
figure 2

Detailed schematic sketch of the interface

Full size image

In order to localise Faraday’s law of induction (15) under the assumption of strong discontinuities in the electric field quantities, it is instructive to resolve the electrical processes at the interface as depicted in Figure 2. To this end, assume for now that it is possible to define the electric field as the (negative) gradient of an electric potential field \(\phi \), as is customary for quasi-stationary electrical problems. By integrating the electric field along a path \(\mathcal {T}\) connecting two opposing points of the interface one arrives at

$$\begin{aligned} \int _\mathcal {T}\varvec{e}\cdot \mathrm {d}\varvec{s}&= \int _\mathcal {T}-\nabla \phi \cdot \mathrm {d}\varvec{s}= \int _{\phi =\phi ^-}^{\phi ^+}-1 \, \mathrm {d}\phi = -\llbracket {\phi }\rrbracket . \end{aligned}$$
(19)

The mathematic analogue to the latter physically motivated derivation is the integration of a \(\delta \)-distribution since the electric field becomes infinite in the limit case of vanishing interface thickness. With (19) at hand, the evaluation of (15) for an arbitrary control surface \(\mathcal {A}\) that intersects the material interface, see Figure 3, yields

$$\begin{aligned} \int _{\partial \mathcal {A}}\varvec{e}\cdot \mathrm {d}\varvec{s}=&\int _{\mathcal {S}^+}\varvec{e}\cdot \mathrm {d}\varvec{s}+ \int _{\mathcal {S}^-}\varvec{e}\cdot \mathrm {d}\varvec{s}+ \llbracket {\phi }\rrbracket _{\mathrm {E}}- \llbracket {\phi }\rrbracket _{\mathrm {B}}\nonumber \\ =&\int _{\mathcal {S}^+}\varvec{e}\cdot \mathrm {d}\varvec{s}+ \int _{\mathcal {S}^-}\varvec{e}\cdot \mathrm {d}\varvec{s}+ \llbracket {\phi }\rrbracket _{\mathrm {E}}- \llbracket {\phi }\rrbracket _{\mathrm {B}}\nonumber \\&+ \left[ -1+1\right] \int _{\mathcal {S}^+_\mathcal {I}\, \cup \,\mathcal {S}^-_\mathcal {I}}\varvec{e}\cdot \mathrm {d}\varvec{s}\nonumber \\ =&\int _{\mathcal {A}^+}\nabla \times \varvec{e}\cdot \varvec{n}\, \mathrm {d}a+ \int _{\mathcal {A}^-}\nabla \times \varvec{e}\cdot \varvec{n}\, \mathrm {d}a\nonumber \\&+\int _{\mathcal {S}_\mathcal {I}}\left[ \varvec{e}^+-\varvec{e}^-\right] \cdot \mathrm {d}\varvec{s}+ \llbracket {\phi }\rrbracket _{\mathrm {E}}- \llbracket {\phi }\rrbracket _{\mathrm {B}}\end{aligned}$$
(20)

where the Kelvin-Stokes theorem in its classic form has been used. The localisation of (20) for a control surface that does not intersect a material interface yields the local version of Faraday’s law of induction in the bulk

$$\begin{aligned} \nabla \times \varvec{e}&= \varvec{0} \quad \text {(in the bulk)} , \end{aligned}$$
(21)

which can naturally be fulfilled by the introduction of an electric potential for the electric field vector. The localisation of (20) for a control surface that intersects the interface yields no additional condition for the studied cohesive zone formulation since, by invoking (21), the last three summands in (20) cancel out. It is noted that the latter statement tacitly assumes negligible tangential electric currents in the interface and hence neglects the tangential electric field in the interface. In an extended formulation that accounts for the latter quantities in the spirit of interface elasticity, an additional condition would occur that can be fulfilled by a proper definition of the interfacial electric potential. This discussion lies, however, beyond the scope of the present contribution.

Fig. 3
figure 3

Intersection of control surface \(\mathcal {A}=\mathcal {A}^- \cup \mathcal {A}^+\) and interface \(\mathcal {I}\). The beginning and end point of the intersection line are labelled with \(\mathrm {B}\) and \(\mathrm {E}\), respectively

Full size image

Remark 1

(Continuity condition in the case of weak discontinuities). In the derivation of (20), strong discontinuities, i.e. jumps in the electric potential across material interfaces, were considered. Due to this assumption, the classic continuity condition for the tangential component of the electric field vector

$$\begin{aligned} \llbracket {\varvec{e}}\rrbracket \cdot \widetilde{\varvec{h}}= 0 \quad \forall \, \widetilde{\varvec{h}}\perp \widetilde{\varvec{n}}\quad \text {(at the interface)} \end{aligned}$$
(22)

with \(\widetilde{\varvec{h}}\) denoting tangential vectors to the interface, was not recovered. If only weak discontinuities, i.e. jumps in the electric field vector, were considered, (20) would take the form

$$\begin{aligned} \int _{\partial \mathcal {A}}\varvec{e}\cdot \mathrm {d}\varvec{s}=&\int _{\mathcal {A}^+}\nabla \times \varvec{e}\cdot \varvec{n}\, \mathrm {d}a+ \int _{\mathcal {A}^-}\nabla \times \varvec{e}\cdot \varvec{n}\, \mathrm {d}a\nonumber \\ -&\int _{\mathcal {S}_\mathcal {I}}\left[ \varvec{e}^+-\varvec{e}^-\right] \cdot \mathrm {d}\varvec{s}, \end{aligned}$$
(23)

which would imply (22) in addition to (21).

2.3 Balance equation of energy

This section summarises the balance equation of energy for a continuum that is subjected to mechanical, thermal and electrical loads. The thermal problem is not in the focus of the present contribution but included in the presentation to highlight the fundamental differences between electrical and thermal cohesive zone formulations with regard to the evaluation of the dissipation inequality, cf. Section 2.4. By introducing the mass-specific internal energy densities of the bulk \(e\) and of the interface \(\widetilde{e}\), the (quasi-static) balance equation of energy reads

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\mathrm {t}} \int _{\mathcal {V}}\rho \, e\, \mathrm {d}v+ \frac{\mathrm {d}}{\mathrm {d}\mathrm {t}} \int _{\mathcal {I}}\widetilde{\rho }\, \widetilde{e}\, \mathrm {d}a= \mathcal {P}^{\varvec{u}}+ \mathcal {P}^{\theta }+ \mathcal {P}^{\phi }. \end{aligned}$$
(24)

The powers exerted by mechanical, thermal and electrical loads on the control volume are denoted by \(\mathcal {P}^{\varvec{u}}\), \(\mathcal {P}^{\theta }\) and \(\mathcal {P}^{\phi }\), respectively. In accordance with the assumptions made in Section 2.1, \(\mathcal {P}^{\varvec{u}}\) takes the form

$$\begin{aligned} \mathcal {P}^{\varvec{u}}=&\int _{\mathcal {V}}\dot{\varvec{u}}\cdot \rho \,\varvec{f}\, \mathrm {d}v+ \int _{\mathcal {I}}\dot{\widetilde{\varvec{u}}}\cdot \widetilde{\rho }\, \widetilde{\varvec{f}}\, \mathrm {d}a\,+ \int _{\partial \mathcal {V}}\dot{\varvec{u}}\cdot \varvec{t}\, \mathrm {d}a\nonumber \\ =&\int _{\mathcal {V}\setminus \mathcal {I}}\nabla \dot{\varvec{u}}:\varvec{\sigma }\, \mathrm {d}v+ \int _{\mathcal {V}\setminus \mathcal {I}}\dot{\varvec{u}}\cdot \left[ \nabla \cdot \varvec{\sigma }+ \rho \,\varvec{f}\right] \, \mathrm {d}v \nonumber \\&+\int _{\mathcal {I}}\llbracket {\dot{\varvec{u}}}\rrbracket \cdot \{\!\{ {\widetilde{\varvec{t}}} \}\!\} \, \mathrm {d}a+\int _{\mathcal {I}}\dot{\widetilde{\varvec{u}}}\cdot \widetilde{\rho }\, \widetilde{\varvec{f}}+\{\!\{ {\dot{\varvec{u}}} \}\!\} \cdot \llbracket {\widetilde{\varvec{t}}}\rrbracket \, \mathrm {d}a, \end{aligned}$$
(25)

with \(\dot{\varvec{u}}\) denoting the velocity field. By additionally assuming that the interface remains positioned in the middle of the two opposing surfaces, i.e. \(\dot{\widetilde{\varvec{u}}}=\{\!\{ {\dot{\varvec{u}}} \}\!\}\), and by invoking (10), (25) simplifies to

$$\begin{aligned} \mathcal {P}^{\varvec{u}}= \int _{\mathcal {V}\setminus \mathcal {I}}\nabla \dot{\varvec{u}}:\varvec{\sigma }\, \mathrm {d}v+\int _{\mathcal {I}}\llbracket {\dot{\varvec{u}}}\rrbracket \cdot \{\!\{ {\widetilde{\varvec{t}}} \}\!\} \, \mathrm {d}a. \end{aligned}$$
(26)

The thermal power is given by

$$\begin{aligned} \begin{aligned} \mathcal {P}^{\theta }&= \int _{\mathcal {V}}\rho \,r\, \mathrm {d}v- \int _{\partial \mathcal {V}}\varvec{q}\cdot \varvec{n}\, \mathrm {d}a\\&= \int _{\mathcal {V}\setminus \mathcal {I}}\rho \,r- \nabla \cdot \varvec{q}\, \mathrm {d}v+ \int _{\mathcal {I}}-\llbracket {\varvec{q}\cdot \widetilde{\varvec{n}}}\rrbracket \, \mathrm {d}a\end{aligned}\end{aligned}$$
(27)

with the classic heat flux vector \(\varvec{q}\) and with \(r\) denoting mass-specific heat sources in the bulk. It is noted that heat sources and the tangential heat flux vector in the interface have been neglected in (27) for the sake of simplicity.

The electrical contribution to (24) is of purely dissipative type if polarisation and magnetisation effects are neglected. In particular, the dissipation caused by the electric current in the bulk is assumed to take the classic form

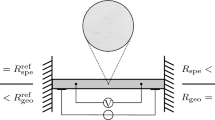
$$\begin{aligned} \mathcal {P}^{\phi }_{\mathcal {V}\setminus \mathcal {I}}= \int _{\mathcal {V}\setminus \mathcal {I}}\varvec{j}\cdot \varvec{e}\, \mathrm {d}v. \end{aligned}$$
(28)

In order to derive the energy contribution related to the electric current across the interface, a simple electrical resistor connecting the two opposing sides of the interface is analysed, as schematically depicted in Figure 2. According to (18b), the electric current density does not change across the interface, i.e. \(\widetilde{i}^+=\widetilde{i}^-=\{\!\{ {\widetilde{i}} \}\!\}\), such that

$$\begin{aligned} \mathcal {P}^{\phi }_{\mathcal {I}} = \int _{\mathcal {I}}\int _\mathcal {T}\varvec{e}\cdot \{\!\{ {\widetilde{i}} \}\!\}\, \mathrm {d}\varvec{s}\, \mathrm {d}a= \int _{\mathcal {I}}- \{\!\{ {\widetilde{i}} \}\!\}\, \llbracket {\phi }\rrbracket \, \mathrm {d}a, \end{aligned}$$
(29)

is proposed, see also Remark 2. It is noted that tangential electric currents in the interface are neglected in (29), in accordance with the derivations presented in Section 2.2.

By inserting (26)–(29) into (24) and by localising the ensuing equation in the bulk and at the interface one eventually arrives at

$$\begin{aligned} \rho \, \dot{e}&\!=\! \varvec{\sigma }:\dot{\varvec{\varepsilon }} \!+\!\rho \,r\!-\!\nabla \cdot \varvec{q}\!+\!\varvec{j}\cdot \varvec{e}\qquad \qquad \, \, \text {(in the bulk)}, \end{aligned}$$
(30a)
$$\begin{aligned} \widetilde{\rho }\, \dot{\widetilde{e}}&= \llbracket {\dot{\varvec{u}}}\rrbracket \cdot \{\!\{ {\widetilde{\varvec{t}}} \}\!\} \,-\llbracket {\varvec{q}\cdot \widetilde{\varvec{n}}}\rrbracket -\{\!\{ {\widetilde{i}} \}\!\}\, \llbracket {\phi }\rrbracket \quad \, \text {(at the int.)}\,, \end{aligned}$$
(30b)

where the definition of the small strain deformation tensor \(\varvec{\varepsilon }=\nabla ^{\mathrm {sym}} \varvec{u}\) was used.

Remark 2

(Alternative derivation of (29)). The specific form of the dissipation related to the electric current across the interface, (29), was motivated in Section 2.3 based on physical arguments. In this remark, a more elaborated way to derive (29) is shown. First when focusing on a control volume that does not contain interfaces, it is observed that by virtue of (18a), (28) can alternatively be expressed in terms of the electric current density and of the electric potential at the boundaries, namely

$$\begin{aligned} \int _{\mathcal {V}}\varvec{j}\cdot \varvec{e}\, \mathrm {d}v= - \int _{\partial \mathcal {V}}\varvec{j}\cdot \varvec{n}\, \phi \, \mathrm {d}v+ \int _{\mathcal {V}}\underbrace{\nabla \cdot \varvec{j}}_{=0} \,\phi \, \mathrm {d}v. \end{aligned}$$
(31)

Analogously to the mechanical sub-problem (25), the evaluation of the surface integral-based representation of the electric dissipation for a control volume that contains interfaces yields

$$\begin{aligned} - \int _{\partial \mathcal {V}}\varvec{j}\cdot \varvec{n}\, \phi \, \mathrm {d}v= \int _{\mathcal {V}\setminus \mathcal {I}}\varvec{j}\cdot \varvec{e}\, \mathrm {d}v- \int _{\mathcal {I}}\llbracket {\widetilde{i}\, \phi }\rrbracket \, \mathrm {d}a, \end{aligned}$$
(32)

where tangential electric currents in the interface have been neglected in accordance with Section 2.2. From a physics point of view, (32) states that two contributions are associated with the dissipation caused by the movement of electric charges from regions of high electric potential to regions of low electric potential. Whereas the first contribution is related to the classic electrical resistance of the bulk, the second contribution accounts for the electrical resistance of the interface. By additionally taking (3) and (18b) into account, the interface contribution in (32) can further be rewritten as

$$\begin{aligned} - \int _{\mathcal {I}}\llbracket {\widetilde{i}\, \phi }\rrbracket \, \mathrm {d}a= - \int _{\mathcal {I}}\underbrace{\llbracket {\widetilde{i}}\rrbracket }_{=0}\, \{\!\{ {\phi } \}\!\} + \{\!\{ {\widetilde{i}} \}\!\}\,\llbracket {\phi }\rrbracket \, \mathrm {d}a. \end{aligned}$$
(33)

2.4 Dissipation inequality

With \(\theta \) and \(s\) denoting the absolute temperature and the mass-specific entropy density of the bulk, and with \(\widetilde{s}\) denoting the mass-specific entropy density of the interface, the dissipation inequality reads

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\mathrm {t}} \int _{\mathcal {V}}\rho \, s\, \mathrm {d}v+ \int _{\mathcal {I}}\widetilde{\rho }\, \widetilde{s}\, \mathrm {d}a\ge \int _{\mathcal {V}}\frac{\rho \,r}{\theta } \, \mathrm {d}v- \int _{\partial \mathcal {V}}\frac{\varvec{q}\cdot \varvec{n}}{\theta } \, \mathrm {d}a. \end{aligned}$$
(34)

In order to localise (34), the volume integral on the right-hand side is rewritten in a first step. More specifically speaking

$$\begin{aligned} \begin{aligned} \int _{\partial \mathcal {V}}\frac{\varvec{q}\cdot \varvec{n}}{\theta } \, \mathrm {d}a=&\int _{\mathcal {V}\setminus \mathcal {I}}\frac{1}{\theta } \, \nabla \cdot \varvec{q}-\frac{1}{\theta ^2} \, \varvec{q}\cdot \nabla \theta \, \mathrm {d}v\\ +&\int _{\mathcal {I}}\llbracket {\varvec{q}\cdot \widetilde{\varvec{n}}}\rrbracket \, \{\!\{ {\theta ^{-1}} \}\!\} \!+\!\{\!\{ {\varvec{q}\cdot \widetilde{\varvec{n}}} \}\!\}\,\llbracket {\theta ^{-1}}\rrbracket \, \mathrm {d}a\end{aligned}\end{aligned}$$
(35)

holds, where (3) was used. To proceed, the convex-concave Legendre(-Fenchel) transformations

$$\begin{aligned} \psi \left( \theta , \bullet \right)&= \inf _s\left\{ e\left( s, \bullet \right) -\theta \, s\right\} {\!}, \end{aligned}$$
(36a)
$$\begin{aligned} \widetilde{\psi }\left( \widetilde{\theta }, \bullet \right)&=\inf _{\widetilde{s}} \left\{ \widetilde{e}\left( \widetilde{s}, \bullet \right) -\widetilde{\theta }\, \widetilde{s}\right\} {\!}, \end{aligned}$$
(36b)

with energetic duals

$$\begin{aligned} \theta&= \frac{\partial e}{\partial s} , \qquad s=-\frac{\partial \psi }{\partial \theta } , \end{aligned}$$
(37a)
$$\begin{aligned} \widetilde{\theta }&= \frac{\partial \widetilde{e}}{\partial \widetilde{s}} , \qquad \widetilde{s}=-\frac{\partial \widetilde{\psi }}{\partial \widetilde{\theta }} , \end{aligned}$$
(37b)

are invoked. In the latter set of equations, \(\psi \) and \(\widetilde{\psi }\) denote the mass-specific Helmholtz free energy density functions of the bulk and of the interface, and \(\widetilde{\theta }\) denotes the interface temperature.

By inserting (30) and (35) into (34), and by making use of (36) one eventually arrives at the local forms of the dissipation inequality

$$\begin{aligned}&\varvec{\sigma }:\dot{\varvec{\varepsilon }} - \rho \left[ \dot{\psi } + s\, \dot{\theta }\right] -\frac{1}{\theta } \,\varvec{q}\cdot \nabla \theta + \varvec{j}\cdot \varvec{e}\ge 0\, \nonumber \\&\text {(in the bulk)} \end{aligned}$$
(38a)

and

$$\begin{aligned}&\llbracket {\dot{\varvec{u}}}\rrbracket \cdot \{\!\{ {\widetilde{\varvec{t}}} \}\!\} -\widetilde{\rho }\left[ \dot{\widetilde{\psi }} + \widetilde{s}\, \dot{\widetilde{\theta }}\right] -\{\!\{ {\widetilde{i}} \}\!\}\, \llbracket {\phi }\rrbracket \nonumber \\&\qquad +\widetilde{\theta }\left[ \{\!\{ {\varvec{q}\cdot \widetilde{\varvec{n}}} \}\!\}\,\llbracket {\theta ^{-1}}\rrbracket + \left[ \{\!\{ {\theta ^{-1}} \}\!\} - \widetilde{\theta }^{-1}\right] \llbracket {\varvec{q}\cdot \widetilde{\varvec{n}}}\rrbracket \right] \ge 0 \nonumber \\&\text {(at the interface)}. \end{aligned}$$
(38b)

The application of a Coleman-Noll-type procedure to evaluate (38) naturally gives rise to the constitutive restrictions for the electrical sub-problem

$$\begin{aligned} \varvec{j}\cdot \varvec{e}\,&\ge 0 \qquad \text {(in the bulk)}, \end{aligned}$$
(39a)
$$\begin{aligned} -\{\!\{ {\widetilde{i}} \}\!\}\, \llbracket {\phi }\rrbracket \,&\ge 0\qquad \text {(at the interface)}. \end{aligned}$$
(39b)

From a physics point of view, (39) implies that the flow of electric charges is opposed to the electric potential gradient. In contrast to the electrical sub-problem, the thermal sub-problem at the interface

$$\begin{aligned}&\widetilde{\theta }\left[ \{\!\{ {\varvec{q}\cdot \widetilde{\varvec{n}}} \}\!\}\,\llbracket {\theta ^{-1}}\rrbracket + \left[ \{\!\{ {\theta ^{-1}} \}\!\} - \widetilde{\theta }^{-1}\right] \llbracket {\varvec{q}\cdot \widetilde{\varvec{n}}}\rrbracket \right] \, \ge 0\nonumber \\& \text {(at the interface)} \end{aligned}$$
(40)

cannot further be evaluated without additional assumptions on the relation between the bulk and the interface temperature.

3 Weak form of equilibrium

In order to derive the weak form of equilibrium for the electro-mechanically coupled continuum under consideration, field equations (10a) and (18a) are multiplied by test functions

$$\begin{aligned} \varvec{\eta }^{\varvec{u}}\,, \quad \text {respectively}\quad {\eta }^{\phi }\end{aligned}$$
(41)

and integrated over (the subdomains of) body \(\mathcal {B}\). Likewise, (10b) and (18b) are multiplied by test functions

$$\begin{aligned} \varvec{\eta }^{\widetilde{\varvec{u}}}=\{\!\{ {\varvec{\eta }^{\varvec{u}}} \}\!\}\,, \quad \text {respectively}\quad {\eta }^{\widetilde{\phi }}=\{\!\{ {{\eta }^{\phi }} \}\!\} \end{aligned}$$
(42)

and integrated over the interface(s) \(\mathcal {I}\). By additionally applying the classic divergence theorem and by making use of (3), the weak form of the balance equation of linear momentum (10), i.e.

$$\begin{aligned} 0 =&\int _{\mathcal {B}\setminus \mathcal {I}}\varvec{\eta }^{\varvec{u}}\cdot \left[ \nabla \cdot \varvec{\sigma }+ \rho \,\varvec{f}\right] \, \mathrm {d}v+ \int _{\mathcal {I}}\varvec{\eta }^{\widetilde{\varvec{u}}}\cdot \left[ \llbracket {\widetilde{\varvec{t}}}\rrbracket + \widetilde{\rho }\, \widetilde{\varvec{f}}\right] \, \mathrm {d}a\end{aligned}$$
(43)

takes the form

$$\begin{aligned} \begin{aligned} 0 =&- \int _{\mathcal {B}\setminus \mathcal {I}}\nabla \varvec{\eta }^{\varvec{u}}:\varvec{\sigma }\, \mathrm {d}v- \int _{\mathcal {I}}\llbracket {\varvec{\eta }^{\varvec{u}}}\rrbracket \cdot \{\!\{ {\widetilde{\varvec{t}}} \}\!\} \, \mathrm {d}a\\&+ \int _{\mathcal {B}\setminus \mathcal {I}}\varvec{\eta }^{\varvec{u}}\cdot \rho \, \varvec{f}\, \mathrm {d}v+ \int _{\mathcal {I}}\{\!\{ {\varvec{\eta }^{\varvec{u}}} \}\!\} \cdot \widetilde{\rho }\, \widetilde{\varvec{f}}\, \mathrm {d}a\\&+ \int _{\partial \mathcal {B}}\varvec{\eta }^{\varvec{u}}\cdot \varvec{t}\, \mathrm {d}a. \end{aligned}\end{aligned}$$
(44)

Following the same procedure, the weak form of the continuity equation for the electric current density

$$\begin{aligned} 0= \int _{\mathcal {B}\setminus \mathcal {I}}{\eta }^{\phi }\, \nabla \cdot \varvec{j}\, \mathrm {d}v+ \int _{\mathcal {I}}{\eta }^{\widetilde{\phi }}\, \llbracket {\widetilde{i}}\rrbracket \, \mathrm {d}a\end{aligned}$$
(45)

can be rewritten as

$$\begin{aligned} \begin{aligned} 0=&-\int _{\mathcal {B}\setminus \mathcal {I}}\nabla {\eta }^{\phi }\cdot \varvec{j}\, \mathrm {d}v- \int _{\mathcal {I}}\llbracket {{\eta }^{\phi }}\rrbracket \, \{\!\{ {\widetilde{i}} \}\!\} \, \mathrm {d}a\\&+ \int _{\partial \mathcal {B}}{\eta }^{\phi }\, \varvec{j}\cdot \varvec{n}\, \mathrm {d}a. \end{aligned}\end{aligned}$$
(46)

3.1 Finite element implementation

The finite element implementation of the proposed cohesive zone formulation is based on the discretisation of primary fields and test functions by means of Lagrange polynomials, namely,

$$\begin{aligned} \varvec{u}^{\mathrm {h}}&= \sum _{C=1}^{\mathrm {n}_{\mathrm {en}}}N_C \, \varvec{u}_C , \quad \varvec{\eta }^{\varvec{u}\, \mathrm {h}}\quad = \sum _{A=1}^{\mathrm {n}_{\mathrm {en}}}N_A \, \varvec{\eta }^{\varvec{u}}_A , \end{aligned}$$
(47a)
$$\begin{aligned} \phi ^{\mathrm {h}}&= \sum _{D=1}^{\mathrm {n}_{\mathrm {en}}}N_D \, \phi _D , \quad {\eta }^{\phi \, \mathrm {h}}\quad = \sum _{B=1}^{\mathrm {n}_{\mathrm {en}}}N_B \, {\eta }^{\phi }_B, \end{aligned}$$
(47b)

with \(\mathrm {n}_{\mathrm {en}}\) denoting the number of element nodes, with \(N_\bullet \) denoting shape functions and with nodal values being indicated by subscripts, e.g. \(\varvec{u}_C\). By inserting (47) into the weak forms of the field equations, (44) and (46), one arrives at the residual-type format

$$\begin{aligned} \left[ \begin{array}{l} \varvec{r}^{\varvec{u}\,\mathrm {h}}\\ \varvec{r}^{\phi \,\mathrm {h}} \end{array} \right] = \left[ \begin{array}{l} \varvec{f}_{\mathrm {int}}^{\varvec{u}\,\mathrm {h}}+ \tilde{\varvec{f}}_{\mathrm {int}}^{\varvec{u}\,\mathrm {h}}- \varvec{f}_{\mathrm {sur}}^{\varvec{u}\,\mathrm {h}}- \varvec{f}_{\mathrm {vol}}^{\varvec{u}\,\mathrm {h}}- \tilde{\varvec{f}}_{\mathrm {vol}}^{\varvec{u}\,\mathrm {h}}\\ \varvec{f}_{\mathrm {int}}^{\phi \,\mathrm {h}}+ \tilde{\varvec{f}}_{\mathrm {int}}^{\phi \,\mathrm {h}}- \varvec{f}_{\mathrm {sur}}^{\phi \,\mathrm {h}}\end{array} \right] \end{aligned}$$
(48)

that is based on the (generalised) internal, surface and volume forces vectors defined in Appendix A. The linearisation of (48) at some iteration step q in an iterative, gradient-based solution method moreover results in the update relation

$$\begin{aligned} \left[ \begin{array}{ll} \mathbf {K}^{\varvec{u}\varvec{u}}+\widetilde{\mathbf {K}}^{\varvec{u}\varvec{u}}~ &{} \mathbf {K}^{\varvec{u}\phi }+\widetilde{\mathbf {K}}^{\varvec{u}\phi } \\ \mathbf {K}^{\phi \varvec{u}}+\widetilde{\mathbf {K}}^{\phi \varvec{u}}~ &{} \mathbf {K}^{\phi \phi }+\widetilde{\mathbf {K}}^{\phi \phi } \end{array} \right] _q \cdot \left[ \begin{array}{l} \varDelta \widehat{\varvec{u}} \\ \varDelta \widehat{\phi } \end{array} \right] _q = - \left[ \begin{array}{l} \varvec{r}^{\varvec{u}\,\mathrm {h}}\\ \varvec{r}^{\phi \,\mathrm {h}} \end{array} \right] _{q} \end{aligned}$$
(49)

for the global lists of nodal degrees of freedom, \(\widehat{\varvec{u}}\) and \(\widehat{\phi }\). In (49), \(\mathbf {K}^{\bullet *}\) and \(\widetilde{\mathbf {K}}^{\bullet *}\) denote bulk and interface contributions to the generalised global stiffness matrix. The specific forms of these quantities are provided in Appendix B.

4 Representative simulation results

This section focuses on the study of representative boundary value problems. To this end, the electro-mechanical material behaviour is specified in Section 4.1 and Section 4.2. In particular, a coupling of the mechanical and electrical field equations due to the influence of deformation-induced interface damage processes on the electrical conductivity is considered. With the specific material model at hand, analytical solutions for a one-dimensional tensile problem are derived in Section 4.3 and compared with finite element-based simulation results in Section 4.4. Finally, tension and compression tests of a test specimen with geometrically resolved microstructure are studied in Section 4.5. It is emphasised that the boundary value problems studied in the proof of concept-type simulations are of academic nature and that, in particular, neither the material models nor the material parameters are adapted to a specific material (system). Moreover, it is noted that the derivations presented in Section 2 and Section 3 hold independently of the spatial dimensions such that the application of the proposed formulation to general three-dimensional boundary value problems is possible.

4.1 Mechanical material models

For the sake of simplicity, the mechanical response of the bulk is assumed to be isotropic, linear-elastic and to be governed by the Helmholtz free energy density function

$$\begin{aligned} \rho \, \psi =\varPsi \left( \varvec{\varepsilon }\right) = \frac{1}{2}\,\varvec{\varepsilon }:\varvec{\mathsf {E}}:\varvec{\varepsilon }, \end{aligned}$$
(50)

with the elasticity tensor

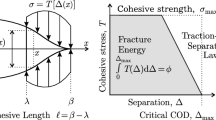
$$\begin{aligned} \varvec{\mathsf {E}}= \frac{E\,\nu }{\left[ 1+\nu \right] \left[ 1-2\,\nu \right] } \,\varvec{I}\otimes \varvec{I}+ \frac{E}{2\left[ 1+\nu \right] } \, \left[ \varvec{I}\, \overline{\otimes }\,\varvec{I}+ \varvec{I}\,\underline{\otimes }\, \varvec{I}\right] \end{aligned}$$
(51)

being parametrised in terms of Young’s modulus \(E\) and Poisson’s ratio \(\nu \). For the interface, a linear-elastic mechanical material response combined with a brittle damage formulation is used, which represents a direct extension of the model proposed in [29]. More specifically speaking, the area specific interface Helmholtz free energy density function \(\widetilde{\varPsi }=\widetilde{\rho }\, \widetilde{\psi }\) is formulated as a function of the displacement jump \(\llbracket {\varvec{u}}\rrbracket \) and of the interface damage variable \(\widetilde{d}\). Furthermore, it is assumed that interface damage processes manifest themselves in a reduction of the mechanical stiffness \(\widetilde{E}\) in the tensile region

$$\begin{aligned} \begin{aligned} \widetilde{\varPsi }\left( \llbracket {\varvec{u}}\rrbracket , \widetilde{d}\,\right)&= \left[ 1-\widetilde{d}\,\right] \, \widetilde{\varPsi }_{\mathrm {e}}\left( \llbracket {\varvec{u}}\rrbracket \,\right) \quad \text {with} \\ \widetilde{\varPsi }_{\mathrm {e}}\left( \llbracket {\varvec{u}}\rrbracket \,\right)&= \frac{1}{2}\widetilde{E}\,\llbracket {\varvec{u}}\rrbracket \cdot \varvec{I}\cdot \llbracket {\varvec{u}}\rrbracket \,, \quad \text {if } \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}>0 \,, \end{aligned}\end{aligned}$$
(52a)

whereas the interface is assumed to regain its normal stiffness under compressive loadings

$$\begin{aligned} \begin{aligned} \widetilde{\varPsi }\left( \!\llbracket {\varvec{u}}\rrbracket , \widetilde{d}\,\right) \!&= \frac{1}{2} \widetilde{E}\, \llbracket {\varvec{u}}\rrbracket \cdot \left[ 1-\widetilde{d}\,\right] \left[ \varvec{I}- \widetilde{\varvec{n}}\otimes \widetilde{\varvec{n}}\right] \cdot \llbracket {\varvec{u}}\rrbracket \\&{\!}{\!}{\!}+\frac{1}{2} \widetilde{E}\, \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}\otimes \widetilde{\varvec{n}}\cdot \llbracket {\varvec{u}}\rrbracket \,, \,\text {if } \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}\le \!0. \end{aligned}\end{aligned}$$
(52b)

With (50) and (52) at hand, the evaluation of (38) yields the specific form of the bulk stress tensor

$$\begin{aligned} \varvec{\sigma }= \frac{\partial \varPsi }{\partial \varvec{\varepsilon }}= \varvec{\mathsf {E}}:\varvec{\varepsilon }, \end{aligned}$$
(53)

and of the traction separation law under tensile loadings

$$\begin{aligned} \{\!\{ {\widetilde{\varvec{t}}} \}\!\}= \frac{\partial \widetilde{\varPsi }}{\partial \llbracket {\varvec{u}}\rrbracket } = \left[ 1-\widetilde{d}\,\right] \widetilde{E}\,\llbracket {\varvec{u}}\rrbracket \,, \quad \text {if }\llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}>0 , \end{aligned}$$
(54)

respectively under compressive loadings

$$\begin{aligned} \begin{aligned} \{\!\{ {\widetilde{\varvec{t}}} \}\!\}= \frac{\partial \widetilde{\varPsi }}{\partial \llbracket {\varvec{u}}\rrbracket }&= \widetilde{E}\, \left[ 1-\widetilde{d}\,\right] \left[ \varvec{I}- \widetilde{\varvec{n}}\otimes \widetilde{\varvec{n}}\right] \cdot \llbracket {\varvec{u}}\rrbracket \\&+ \widetilde{E}\, \widetilde{\varvec{n}}\otimes \widetilde{\varvec{n}}\cdot \llbracket {\varvec{u}}\rrbracket \,, \,\text {if } \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}\le 0. \end{aligned}\end{aligned}$$
(55)

By virtue of (38)-(40) and (52a), the reduced form of the interface dissipation inequality in the tensile region takes the form

$$\begin{aligned} \widetilde{\mathcal {D}}^{\mathrm {red}}= -\frac{\partial \widetilde{\varPsi }}{\partial \widetilde{d}}\, \dot{\widetilde{d}} = \widetilde{\varPsi }_{\mathrm {e}}\, \dot{\widetilde{d}}, \quad \quad \text {if }\llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}>0 , \end{aligned}$$
(56)

which stipulates that the damage process is intrinsically energy driven and that no self-healing occurs. By additionally assuming that damage evolution only takes place under tensile loadings (i.e. \(\dot{\widetilde{d}}=0\) if \(\llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}<0\)), the failure function

$$\begin{aligned} \widetilde{\mathcal {F}}=\mathrm {sgn}\left( {\llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}}\right) \,\sqrt{\frac{2\, \widetilde{\varPsi }_{\mathrm {e}}}{\widetilde{E}}} - \chi \end{aligned}$$
(57)

with admissibility conditions

$$\begin{aligned} \widetilde{\mathcal {F}}\le 0, \quad \dot{\widetilde{d}} \ge 0, \quad \widetilde{\mathcal {F}}\, \dot{\widetilde{d}} =0, \end{aligned}$$
(58)

is proposed. In accordance with the developments presented in [12, 29], \(\widetilde{d}\) is moreover assumed to be related to the displacement jump-type internal variable at time \(t^*\),

$$\begin{aligned} \chi = \max \left\{ \max _{0<t\le t^*} \left\{ \mathrm {sgn}\left( {\llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}}\right) \,\sqrt{\frac{2\, \widetilde{\varPsi }_{\mathrm {e}}}{\widetilde{E}}} \right\} , \chi _0\right\} , \end{aligned}$$
(59)

via

$$\begin{aligned} \widetilde{d}=1-\frac{\chi _0}{\chi } \exp \left( -\left[ \chi -\chi _0\right] \, \frac{\widetilde{E}\,\chi _0}{G_\mathrm {F}-\frac{1}{2}\,\widetilde{E}\, \chi _0^2} \right) . \end{aligned}$$
(60)

In the light of (57), \(\chi _0\) takes the interpretation of the critical interface opening that is related to the initial fracture strength \(Q_\mathrm {0}\) according to

$$\begin{aligned} Q_\mathrm {0}= \widetilde{E}\,\chi _0. \end{aligned}$$
(61)

Furthermore, \(G_\mathrm {F}\) can be interpreted as the fracture toughness, see [29] and Remark 3.

Remark 3

(Fracture toughness). The fracture toughness of the brittle material under consideration is defined by the dissipation that is associated with the crack formation. In particular, time integration of (56) yields

$$\begin{aligned} \int _{t=0}^{\infty } \widetilde{\mathcal {D}}^{\mathrm {red}}\mathrm {d}t=&\int _{\chi =\chi _0}^{\infty } \widetilde{\varPsi }_{\mathrm {e}}\, \frac{\mathrm {d}\widetilde{d}}{\mathrm {d}\chi } \, \mathrm {d}\chi = G_\mathrm {F}. \end{aligned}$$
(62)

4.2 Electrical material models

The electrical material models are chosen in accordance with the restrictions posed by the dissipation inequalities (39). In particular, a linear relation between the electric field vector and the electric current density vector, namely

$$\begin{aligned} \varvec{j}= \varvec{\mathcal {S}}\cdot \varvec{e}, \end{aligned}$$
(63)

is assumed in the bulk, with

$$\begin{aligned} \varvec{\mathcal {S}}=\kappa \, \varvec{I}, \end{aligned}$$
(64)

denoting the (positive definite) electrical conductivity tensor that is defined in terms of the scalar-valued electrical conductivity parameter \(\kappa \).

Moreover, the deformation-induced damage processes at the interface are assumed to influence the effective electrical conductivity. The specific form of the constitutive equation for the electric current density

$$\begin{aligned} \{\!\{ {\widetilde{i}} \}\!\}= {\left\{ \begin{array}{ll} -\left[ 1-\widetilde{d}\,\right] \widetilde{\kappa }\,\llbracket {\phi }\rrbracket \quad \,\,\,\text {if } \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}>0\\ \quad \qquad \quad \,\,\,- \widetilde{\kappa }\,\llbracket {\phi }\rrbracket \,\quad \text { if } \llbracket {\varvec{u}}\rrbracket \cdot \widetilde{\varvec{n}}\le 0 \end{array}\right. }, \end{aligned}$$
(65)

with \(\widetilde{\kappa }\) denoting the idealised conductivity of the interface, thus establishes a coupling between the electrical and mechanical field equations. Equation (65) is based on the assumption that the effective conducting interface area in the tensile region is reduced due to the damage processes, whereas the interface recovers its initial conductivity under compressive loads. Conceptually speaking, the electrical problem is thus treated similarly to the mechanical problem with the damage evolution being associated with a reduction in the number of springs, respectively a reduction in the number of wires, connecting the opposing sides of the interface, cf. Figure 2.

4.3 Analytical solution

This section deals with the derivation of an analytical solution for the one-dimensional sample boundary value problem sketched in Figure 4, subject to the assumption of monotonic tensile loadings. The total elongation of the bar

$$\begin{aligned} \overline{\varDelta u}= 2\, \varDelta u+ \llbracket {u}\rrbracket \end{aligned}$$
(66a)

results from the elongation of the regions \(\mathcal {B}^{-}\) and \(\mathcal {B}^{+}\), i.e. \(2\,\varDelta u\), and from the displacement jump across the interface \(\llbracket {u}\rrbracket \). Moreover, the latter kinematic quantities are related to the axial stress in the bulk via

$$\begin{aligned} \sigma = E\, \frac{\varDelta u}{l} \end{aligned}$$
(66b)

and determine the stresses at the interface

$$\begin{aligned} \sigma = \left[ 1-\widetilde{d}\,\right] \widetilde{E}\,\llbracket {u}\rrbracket , \end{aligned}$$
(66c)

such that by evaluating the set of equations (66) one eventually arrives at

$$\begin{aligned} \overline{\varDelta u}= \left[ 1+\frac{2\,l\, \widetilde{E}}{E}\right] \llbracket {u}\rrbracket - \widetilde{d}\left( \chi \right) \frac{2\,l\, \widetilde{E}}{E} \, \llbracket {u}\rrbracket . \end{aligned}$$
(67)

For monotonic loadings, \(\widetilde{d}\left( \chi \right) \) can equivalently been expressed as a function of the displacement jump \(\llbracket {u}\rrbracket \), such that (67) establishes an analytical relation between the displacement jump across the interface and the total elongation of the bar. In this regard, it is noted that, by virtue of (59) and (60), \(\dot{\widetilde{d}}>0\) implies \(\dot{\llbracket {u}\rrbracket }>0\).

Fig. 4
figure 4

Bar of length \(2\, l\) and cross-sectional area \(A\), subjected to mechanical and electrical loadings. A material interface is positioned in the middle of the bar as indicated by dark-grey colour

Full size image

Expressions for the effective mechanical and electrical properties of the bar may further be derived by interpreting the bar in Figure 4 as a series connection of springs and resistors. More specifically speaking, the axial stress \(\sigma \) as a function of the displacement jump takes the form

$$\begin{aligned} \sigma = \left[ \frac{2\,l}{E} + \frac{1}{\left[ 1-\widetilde{d}\left( \llbracket {u}\rrbracket \right) \,\right] \widetilde{E}} \right] ^{-1} \, \overline{\varDelta u}\left( \llbracket {u}\rrbracket \right) \end{aligned}$$
(68)

and the axial electric current density \(j\) as a function of the displacement jump and of the prescribed electric potential difference \(\overline{\varDelta \phi }\) reads

$$\begin{aligned} j=\left[ \frac{2\,l}{\kappa } + \frac{1}{\left[ 1-\widetilde{d}\left( \llbracket {u}\rrbracket \right) \,\right] \widetilde{\kappa }} \right] ^{-1}\, \overline{\varDelta \phi }. \end{aligned}$$
(69)

With parametrisations of the total elongation, of the axial stress and of the electric current density in terms of the displacement jump at hand, (implicit) relations between the total elongation and the axial stress, respectively between the total elongation and the electric current density, are established.

Fig. 5
figure 5

Evolution of the normalised (unloading) tensile stiffness and electrical conductance, according to (73), for various length scale ratios \(\ell _{\bullet }/l\)

Full size image

Remark 4

(Size effects). According to (69), the electrical conductance of the bar for a given deformation state reads

$$\begin{aligned} \mathcal {G}=\left[ \frac{2\,l}{\kappa } + \frac{1}{\left[ 1-\widetilde{d}\,\right] \widetilde{\kappa }} \right] ^{-1}\, A. \end{aligned}$$
(70)

Likewise, by taking (69) into account and by neglecting snap-back-type effects the mechanical (unloading) tensile stiffness is given by

$$\begin{aligned} \mathcal {K}_{\mathrm {ul}}= \left[ \frac{2\,l}{E} + \frac{1}{\left[ 1-\widetilde{d}\,\right] \widetilde{E}} \right] ^{-1}\, A. \end{aligned}$$
(71)

The specific forms of (70) and (71) indicate a size-dependent theory and motivate the introduction of internal length scales

$$\begin{aligned} \ell _{\varvec{u}}= & {} \frac{E}{\widetilde{E}} , \end{aligned}$$
(72a)
$$\begin{aligned} \ell _{\phi }= & {} \frac{\kappa }{\widetilde{\kappa }} , \end{aligned}$$
(72b)

which can be used to derive a unified form of (70) and (71). More specifically speaking, by indicating the reference (unloading) tensile stiffness and the reference conductance of the virgin material by subscripts \(\bullet _0\) one arrives at

$$\begin{aligned} \frac{\mathcal {G}}{\mathcal {G}_0} = \frac{\mathcal {K}_{\mathrm {ul}}}{{\mathcal {K}_{\mathrm {ul}}}_0} = \frac{2\,l+\ell _{\bullet }}{2\,l+\frac{\ell _{\bullet }}{1-\widetilde{d}}} = \frac{2+\frac{\ell _{\bullet }}{l}}{2+\frac{1}{1-\widetilde{d}} \frac{\ell _{\bullet }}{l}} . \end{aligned}$$
(73)

Relation (73) suggests a similar evolution of the mechanical (unloading) stiffness and of the electrical conductance with damage evolution, and is plotted in Figure 5 for various values of the length scale ratio \(\ell _\bullet /l\). In particular, it is observed that the extent to which interface damage processes manifest themselves in a reduction of the mechanical stiffness and of the electrical conductance significantly depends on the length scale ratio \(\ell _\bullet /l\) which may take different values for the mechanical and the electrical problem.

Fig. 6
figure 6

Axial stress \(\sigma \) and axial electric current density \(j\) as functions of deformation. The two-dimensional finite element simulations are based on the material parameters provided in Table 1 and assume a plane strain deformation setting. By virtue of (74), the analytical solution is evaluated for \(E_{\mathrm {ps}}\approx {230 769}{\hbox {N} \hbox {m}\hbox {m}^{-2}}\) and \(\widetilde{E}={210 000}{\hbox {N} \hbox {mm}^{-2}}\)

Full size image
Table 1 Material parameters used in the finite element-based simulations
Full size table
Fig. 7
figure 7

Sample of length 100mm, height 10mm and thickness 1mm with geometrically resolved microstructure. The circular notches in the centre region of the sample are of radius \({0.1}{\hbox {m}\hbox {m}}\)

Full size image
Fig. 8
figure 8

Axial reaction force \(\overline{\varvec{F}}\cdot \varvec{\mathrm {e}}_{1}\) and electric current \(\overline{I}\) as functions of prescribed elongation \(\overline{\varDelta u}\) and prescribed potential difference \(\overline{\varDelta \phi }\). The simulations of the test specimen with geometrically resolved microstructure according to Figure 7 are based on the set of material parameters provided in Table 1 and assume a plane strain deformation setting

Full size image

4.4 Comparisson of simulation results and analytical solutions

This section focuses on the validation of the finite element implementation proposed in Section 3 based on the analytical solution derived in Section 4.3. To this end, the elementary boundary value problem depicted in Figure 4 is discretised by means of four-node quadrilateral bulk and four-node (two nodes on each side) linear interface elements, e.g. [32, 33], with the same discretisation being used for the geometry and the primary electrical and mechanical field quantities. Occurring integrals are evaluated numerically by means of Gaussian quadrature schemes featuring four quadrature points, respectively one quadrature point. Since the two-dimensional finite element calculations are carried out subject to the simplifying assumption of a plane strain deformation setting, the material parameter \(E\) in the analytical solutions derived in Section 4.3 needs to be substituted by its plane strain equivalent \(E_{\mathrm {ps}}\), i.e.

$$\begin{aligned} E\leftarrow E_{\mathrm {ps}}= \frac{E}{1-\nu ^2} . \end{aligned}$$
(74)

The finite element results and the analytical solutions for the axial stress \(\sigma \) and for the axial electric current density \(j\) are provided in Figure 6 for a bar of length \(2\, l={100}{\hbox {m} \hbox {m}}\). The finite element simulations are based on the material parameters provided in Table 1, whereas, according to (74), \(E_{\mathrm {ps}}\approx {230 769}{\hbox {N} \hbox {mm}^{-2}}\) and \(\widetilde{E}={210 000}{\hbox {N} \hbox {mm}^{-2}}\) are used in the evaluation of the analytical solutions.

Fig. 9
figure 9

Electric potential field \(\phi \) at the centre region of the boundary value problem depicted in Figure 7 for deformation states according to Figure 8. In particular, state B resembles a sample in an undeformed state, state C a sample subjected to tensile loading and state E a sample subjected to compressive loading. It is noted that the material interface in state E is damaged due to the deformation history. Moreover, (normalised) electric current density vectors are indicated by black arrows

Full size image
Fig. 10
figure 10

Electric current density field \(\Vert \varvec{j}\Vert \) at the centre region of the boundary value problem depicted in Figure 7 for deformation states according to Figure 8. In particular, state B resembles a sample in an undeformed state, state C a sample subjected to tensile loading and state E a sample subjected to compressive loading. It is noted that the material interface in state E is damaged due to the deformation history. Moreover, (normalised) electric current density vectors are indicated by black arrows

Full size image
Fig. 11
figure 11

Comparison of axial reaction force \(\overline{\varvec{F}}\cdot \varvec{\mathrm {e}}_{1}\) and electric current \(\overline{I}\) as functions of prescribed elongation \(\overline{\varDelta u}\) and prescribed potential difference \(\overline{\varDelta \phi }\) for different finite element discretisations. The simulations of the test specimen with geometrically resolved microstructure according to Figure 7 are based on the set of material parameters provided in Table 1 and assume a plane strain deformation setting

Full size image

4.5 Intergranular crack propagation

Motivated by cracks that propagate along grain boundaries, the two-dimensional sample boundary value problem depicted in Figure 7 is studied in this section. In particular, the individual grains of the microstructure are resolved in the ensuing finite element calculations by making use of the proposed electro-mechanically coupled cohesive zone formulation. By doing so, transgranular fracture processes where cracks grow through the material grains are neglected for now and the set of admissible crack paths is significantly reduced. Furthermore, the material models are chosen according to Section 4.1 and Section 4.2, a plane strain setting is assumed and the set of material parameters provided in Table 1 is adopted. In accordance with Section 4.4, the finite element discretisation is based on four-node quadrilateral bulk and four-node (two nodes on each side) linear interface elements, and Gaussian quadrature schemes with four quadrature points, respectively one quadrature point, are used.

Whereas the vertical displacement at the two ends of the test sample is fixed in the simulations, a relative displacement in horizontal direction is prescribed that results in a total elongation \(\overline{\varDelta u}\). Moreover, an electric potential difference \(\overline{\varDelta \phi }\) between the two ends is prescribed and the electric potential at the left boundary is set to 0.0mV. The potential difference \(\overline{\varDelta \phi }={0.1}{\hbox {m} \hbox {V}}\) is applied in the first load step (A\(\rightarrow \)B) and kept constant during tensile loading (B\(\rightarrow \)C), unloading (C\(\rightarrow \)D) and compressive loading (D\(\rightarrow \)E).

For the latter load path, the horizontal reaction force \(\overline{\varvec{F}}\cdot \varvec{\mathrm {e}}_{1}\) and the electric current \(\overline{I}\) are depicted in Figure 8 as functions of deformation. Due to the evolution of interface damage, significant reductions in both the mechanical reaction force and the electric current are observed under tensile loading (B\(\rightarrow \)C). In the (purely elastic) unloading step (C\(\rightarrow \)D), no damage evolution occurs so that the overall mechanical stiffness and electrical conductance remain constant. Under compressive loading (D\(\rightarrow \)E), the damage evolution is suppressed and the interfaces are assumed to regain their normal stiffness and conductivity. Hence, jumps in the horizontal reaction force-elongation curve and in the electric current-elongation curve are observed at the end of the unloading step (C\(\rightarrow \)D). In addition to the generalised reaction force-displacement curves, the electric potential field and the electric current density field are depicted in Figs. 9 and  10 for various load steps. Since the material interfaces pose additional obstacles for the electric current, a complex, inhomogeneous electric current density distribution is observed. Moreover, due to the evolution of interface damage and its influence on the electrical conductivity, the electric current density distribution and the electric potential field significantly change with deformation.

Finally, an additional study of the influence of the finite element discretisation on the simulation results is provided in Appendix C.

Fig. 12
figure 12

Comparison of electric potential field \(\phi \) and electric current density field \(\Vert \varvec{j}\Vert \) at the centre region of the boundary value problem depicted in Figure 7 for different finite element discretisations and deformation states according to Figure 8, respectively Figure 11. In particular, state B resembles a sample in an undeformed state and state C a sample subjected to tensile loading

Full size image

5 Closure

Motivated by the influence of mechanically-induced interface damage processes on the electrical conductivity, this contribution dealt with the fundamentals of electro-mechanically coupled cohesive zone formulations for electrical conductors. At the outset of the theory, local forms and jump conditions of the governing set of balance equations for the electrical sub-problem, that reduced to Faraday’s law of induction and to the continuity equation for the electric current, were discussed. In addition, an extended form of the balance equation of energy that accounted for additional electrical interface contributions was proposed and the associated restrictions stipulated by the dissipation inequality were studied. Next, the electro-mechanically coupled cohesive zone formulation was implemented into a multi-field finite element framework. The coupling between the electrical and mechanical sub-problem was established by the constitutive equations at the material interface – i.e. mechanically-induced damage processes were assumed to reduce the interface conductivity in the sample boundary value problems studied. More specifically speaking, the finite element formulation was validated by means of analytical solutions in a first step, before the influence of intergranular crack propagation on the effective electrical properties was studied.

The sample boundary value problems have been of academic nature to show the principle applicability of the proposed formulation. However, to truly understand and predict the electro-mechanical interaction at material interfaces, tailored material models (including damage, plasticity and their influence on the electrical conductivity) need to be furnished for a specific material system in close relation to experiments. In this regard, sophisticated computational multiscale approaches for material interfaces, as elaborated for instance in [13, 20, 21], may be invoked to take detailed (lower scale) information of the material interfaces into account. Put into perspective, the general modelling framework for electro-mechanically coupled cohesive zone formulations that has been established in the present work provides a basis for these developments.

In conclusion, it is remarked that tangential electric currents in the interface have been neglected in the proposed formulation. From a modelling point of view, these processes share similarities with the theory of interface elasticity known from mechanical problems. An extension of the present formulation in the spirit of generalised imperfect interfaces is thus aspired in future works.