A new variational approach for the thermodynamic topology optimization of hyperelastic structures

Abstract

We present a novel approach to topology optimization based on thermodynamic extremal principles. This approach comprises three advantages: (1) it is valid for arbitrary hyperelastic material formulations while avoiding artificial procedures that were necessary in our previous approaches for topology optimization based on thermodynamic principles; (2) the important constraints of bounded relative density and total structure volume are fulfilled analytically which simplifies the numerical implementation significantly; (3) it possesses a mathematical structure that allows for a variety of numerical procedures to solve the problem of topology optimization without distinct optimization routines. We present a detailed model derivation including the chosen numerical discretization and show the validity of the approach by simulating two boundary value problems with large deformations.

1 Introduction

An important question in engineering is how to design a structure such that it fulfills the individual purpose in an ideal way. For instance, the purpose can be maximum stiffness for a restricted total structure volume [38]. There exist various methods to answer this question: size optimization alters the thickness of an existing design; shape optimization modulates the form; topology optimization searches for the best design without any preexisting requirements, see [15]. The direct applicability of topology optimization to various problems has rendered this strategy quite popular. Review papers can be found, e.g., in [16, 33, 41]. Additionally, the progress in rapid prototyping now provides the feasibility to realize even very complex topologies, cf. the review paper of [28].

To clearly identify the geometric boundaries of optimized structures, a so-called black–white solution has to be found where black indicates the (locally) full material and white the void material; the intermediate gray state has to be restricted to a minimum. One possibility to interpret the black–white solution is given by phase fractions such that the optimization problem can be reformulated as phase transformation problem. This approach is pursued, e.g., by phase field methods for topology optimization, cf. [9, 39, 47]. Here, the mixture energy between the phases “full” and “void” is a double well function such that the grey intermediate states are energetically less favorable. A comparable approach is used for continuum mechanical strategies for topology optimization as the popular solid isotropic material penalization (SIMP) method: instead of using a convex mixture energy of the form $\Psi =\rho \Psi _0$, a non-convex energy of the form $\Psi =\rho ^3 \Psi _0$ has become the standard. Here, $\rho \in \; ]0,1]$ denotes the relative density that identifies the full ($\rho =1$) and void ($\rho \approx 0$) state; thus, $\rho$ can be interpreted as volume fraction. As for phase field approaches, a distinct black–white solution is obtained. However, the usage of the non-convex energy has a drastic impact on the mathematical problem: the loss of ellipticity excludes existence of a (unique) solution of the optimization problem. Any numerical simulation finds a solution that strongly depends on the finite spatial discretization as e.g., employed by the finite element mesh. Consequently, strong mesh dependencies are present and numerical instabilities manifest in form of alternating black/white distributions which are referred to as checkerboarding. Topology optimization has therefore to be equipped with regularization strategies. A prominent class of such regularization are filter techniques of which a wide variety exists. Examples can be found, e.g., in [4, 26, 37, 44]. A different approach is gradient-enhancement for topology optimization, cf. e.g. [17], as also used in damage modeling, see [21].

A prominent subproblem of topology optimization is the treatment of hyperelastic structures, i.e. to optimize elastic structures undergoing large deformations. Works dealing with snap-through problems are given in [5] and [27], for instance; shape optimization including r-adaption is presented in [40]; finite deformations in combination with a homogenization design method are investigated in [30]; a fictitious domain technique for large deformations is employed in [46]. An important problem for topology optimization for finite deformations remains the treatment of buckling for which various approaches exist. Examples can be found, e.g., in [7, 25, 29]. Further examples are given, e.g., in [22] for hyperelastic bodies with prescribed, non-zero displacements, in [12] for geometrically non-linear structures, and in [8] which presents a method how to optimize structures at finite deformations using the finite element program ANSYS.

In a series of papers, we contributed to the topology optimization problem by making use of thermodynamic extremal principles, see e.g., [17]. The resultant equations transform the optimization problem to an evolutionary problem, cf. also [23, 24]. A comparison of the thermodynamical principle-based topology optimization to SIMP is given in [19]. An advantage of this approach is its origin to material modeling which directly gives access to include material non-linearities to the optimization problem as for fiber-reinforced materials in [18] and tension/compression hybrid material systems as steel/concrete in [11]. There, efficient regularization by gradient enhancement has been employed in combination with a fast numerical treatment, see [17].

A disadvantage of the topology optimization approaches based on thermodynamic principles presented so far in the literature is that an extension to hyperelastic structures is not yet available. For generalization, we now present a more fundamental approach to thermodynamic topology optimization which is indeed also valid for large deformations. We therefore start with some remarks on the previous formulation of the thermodynamic topology optimization and identify the related problems. We then present a generalized approach in combination with a novel representation of the relative density. This allows to analytically compute the Lagrange parameter for controlling the volume of the structure. Afterwards, we discuss the numerical treatment and apply our model to Neo–Hookean structures. We present the validity of our model based on the Messerschmitt–Bölkow–Blohm (MBB) beam problem and investigate the problem of buckling structures. To demonstrate the robustness of our model, we employ an arc-length control which allows topology optimization of the MBB beam for even unrealistically large deformations. Here, remarkably different structures are found optimal compared to results obtained for small deformations. Furthermore, we investigate a complex three-dimensional cantilever problem which indicates that strong tension/compression asymmetries are inherently included when optimizing hyperelastic structures.

2 Preliminaries to thermodynamic topology optimization

In a series of previous papers, we derived a novel approach to topology optimization. It was based on variational strategies that are usually applied to material modeling [17] such as Hamilton’s principle, cf. [13, 14]. Since the respective strategies are well-known from material modeling and route back to the thermodynamics and mechanics of materials, we referred these approaches to as thermodynamic topology optimization. Note that this does not imply that the evolution of the optimization process itself follows a real physical, thermodynamical process. It is rather the thermodynamical principles which are exploited to derive an efficient framework for topology optimization. A detailed comparison of these strategies with the SIMP approach has been presented in [19].

Hamilton’s principle states that the sum of Gibbs ${\mathcal {G}}$ energy and dissipation-related work ${\mathcal {D}}_{\varvec{y}}$ should become stationary. This can be recast as variational principle as

$$\begin{aligned} \delta {\mathcal {G}}[\varvec{u},{\varvec{y}}](\delta \varvec{u},\delta {\varvec{y}}) + \delta {\mathcal {D}}_{\varvec{y}}[{\varvec{y}}](\delta {\varvec{y}}) = 0 \quad \forall \; \delta \varvec{u}, \ \delta {\varvec{y}}\end{aligned}$$

(1)

with the Gibbs energy

$$\begin{aligned} {\mathcal {G}}[\varvec{u},{\varvec{y}}]:= & {} \int _\Omega \Psi (\nabla \varvec{u},{\varvec{y}}) \ \mathrm {d}V - \int _\Omega \varvec{b}^\star \cdot \varvec{u}\ \mathrm {d}V \nonumber \\&-\, \int _{\partial \Omega } \varvec{t}^\star \cdot \varvec{u}\ \mathrm {d}A \ . \end{aligned}$$

(2)

Herein, $\delta \varvec{u}$ and $\delta {\varvec{y}}$ are the test functions associated to the primal variables which are the displacements $\varvec{u}$ and the internal variables ${\varvec{y}}$. Whereas the displacements are searched in the standard Sobolev space $\hbox {H}^1$, the space for the internal variables depends on the specific choice of the functionals. Here, we assume ${\varvec{y}}$ to be a vectorial quantity. In case of ${\varvec{y}}$ having other dimensions, i.e., being scalar- or matrix-valued, the related scalar products have to be adopted. For instance, isotropic damage models usually make use of a scalar damage variable as internal variable; plasticity models, on the other hand, consider the second-order tensor of plastic strains as internal variable. The quantity $\Psi$ denotes the strain energy density defined per reference unit volume. The external forces can be split into the body forces $\varvec{b}^\star$ and the traction vector $\varvec{t}^\star$. The volume of the body is denoted by $\Omega$ with its surface $\partial \Omega$. The rate is indicated by $\mathrm {d}{\varvec{y}}/\mathrm {d}t=:{\dot{{\varvec{y}}}}$. The work due to dissipative processes is defined as

$$\begin{aligned} {\mathcal {D}}_{\varvec{y}}[{\varvec{y}}] := \int _\Omega \varvec{p}^\text {diss}_{\varvec{y}}\cdot {\varvec{y}}\ \mathrm {d}V \end{aligned}$$

(3)

with the non-conservative thermodynamic forces $\varvec{p}^\text {diss}_{\varvec{y}}$ which are assumed to be invariant regarding variations of ${\varvec{y}}$, i.e., $\delta \varvec{p}^\text {diss}_{\varvec{y}}={\varvec{0}}$, such that

$$\begin{aligned} \delta {\mathcal {D}}_{\varvec{y}}[{\varvec{y}}](\delta {\varvec{y}}) = \int _\Omega \varvec{p}^\text {diss}_{\varvec{y}}\cdot \delta {\varvec{y}}\ \mathrm {d}V \ . \end{aligned}$$

(4)

The non-conservative thermodynamic forces can be derived from a dissipation function $\Delta ^\text {diss}$ via the relation $\varvec{p}^\text {diss}_{\varvec{y}}= \partial \Delta ^\text {diss}_{\varvec{y}}/\partial {\dot{{\varvec{y}}}}$. The quantity $\Delta ^\text {diss}_{\varvec{y}}$ is also referred to as dissipation functional or dissipation distance when discretized in time, cf. [6, 31, 32]. The sole constraint of formulating a dissipation potential is $\Delta ^\text {diss}_{\varvec{y}}\ge 0$ which is fulfilled e.g., by functions that are homogeneous of order one or two. Consequently, for $\Delta ^\text {diss}_{\varvec{y}}= r |{\dot{{\varvec{y}}}}|$, rate-independent processes can be modeled with r being the yield criterion that indicates some threshold value that separates elastic and inelastic processes as e.g., the yield stress in plasticity ($r=\sigma _\text {y}$). A function that is homogeneous of order two, i.e., $\Delta ^\text {diss}_{\varvec{y}}=\eta |{\dot{{\varvec{y}}}}|^2/2$ can be used for modeling rate-dependent processes with the viscosity $\eta$. Then, Hamilton’s principle reads

$$\begin{aligned}&\delta {\mathcal {G}}[\varvec{u},{\varvec{y}}](\delta \varvec{u},\delta {\varvec{y}}) \nonumber \\&\quad + \int _\Omega \frac{\partial \Delta ^\text {diss}_{\varvec{y}}({\dot{{\varvec{y}}}})}{\partial {\dot{{\varvec{y}}}}} \cdot \delta {\varvec{y}}\ \mathrm {d}V = 0 \quad \forall \; \delta \varvec{u}, \ \delta {\varvec{y}}\ , \end{aligned}$$

(5)

wherein the internal variables and their test functions are searched in $\hbox {L}^2$ when we assume ${\mathcal {G}}={\mathcal {G}}[\varvec{u},\nabla \varvec{u},{\varvec{y}},\nabla {\varvec{y}}]$ and our specific choice of the dissipation functional ${\mathcal {D}}={\mathcal {D}}[{\varvec{y}}]$. Examples how this principle can be applied to material modeling, where internal variables might be plastic strains, damage parameters or volume fractions of crystallographic phases, are given, e.g., in [21, 45].

The key idea of thermodynamic topology optimization was to use the very same variational statement (5) also for structural optimization as has been done for material modeling. To this end, the strain energy density was replaced by $\Psi =\rho ^3 \Psi _0$ where the exponent of 3 for the relative density $\rho \in \; ]0,1]$ was adapted from classical optimization approaches, i.e. SIMP. Consequently, maximum stiffness is employed for $\rho =1$. Here, the density $\rho \leftarrow {\varvec{y}}$ is interpreted as internal variable whose adaption to external conditions is described in terms of an evolution equation. The strain energy density of the full material is denoted by $\Psi _0$. The evolution of the distribution of the relative density was accounted for by a dissipation function $\Delta ^\text {diss}:= \eta {\dot{\rho }}^2/2$ with some (numerical) viscosity $\eta$. Application of Hamilton’s principle yields then an evolution equation for the relative density of the form

$$\begin{aligned} {\dot{\rho }} = -\frac{3}{\eta } \rho ^2 \Psi _0 \ . \end{aligned}$$

(6)

Inspection of this equation revealed that the relative density is reduced more at those spatial coordinates with high loading, i.e. large values of $\Psi _0$, which, in turn, reduces the global stiffness. This is usually a characteristic of damage models and, obviously, stands in contrast to the aim of topology optimization: instead of a model for topology optimization, a damage model is the result by direct application of Hamilton’s principle. Therefore, a reformulation of the variational equations was necessary in order to obtain evolution equations of the appropriate form. With ${\varvec{y}}\rightarrow \rho$, it reads as follows:

$$\begin{aligned} \left\{ \begin{array}{rll} \delta {\mathcal {G}}[\varvec{u},\rho ](\delta \varvec{u}) &{}= 0 &{}\quad \forall \; \delta \varvec{u}\\ \delta {\mathcal {G}}[\varvec{\sigma },\rho ](\delta \varvec{u},\delta \rho ) + \displaystyle \int _\Omega \frac{\partial \Delta ^\text {diss}_{\rho }({\dot{\rho }})}{\partial {\dot{\rho }}} \delta \rho \ \mathrm {d}V &{}= 0 &{}\quad \forall \; \delta \rho \end{array}\right. \end{aligned}$$

(7)

Therefore, the strain energy density was used in the form proposed also by SIMP, reading $\Psi (\varvec{\varepsilon },\rho )=\rho ^3\Psi _0(\varvec{\varepsilon })$, for the derivation of the balance law of linear momentum, (7)${}_1$; however, for the evolution equation of the relative density in (7)${}_2$, Hookes law $\varvec{\sigma }= \rho ^3 {\mathbb {E}}_0\cdot \varvec{\varepsilon }$ had been inserted with the elastic constants for the full material ${\mathbb {E}}_0$. This results in the strain energy density $\Psi (\varvec{\sigma },\rho )= \rho ^{-3} \Psi _0(\varvec{\sigma }) = \rho ^{-3} \varvec{\sigma }\cdot {\mathbb {E}}_0^{-1}\cdot \varvec{\sigma }/2$ such that the evolution equation derived from (7)${}_2$ reads

$$\begin{aligned} {\dot{\rho }} = \frac{3}{\eta } \rho ^{-4} \Psi _0(\varvec{\sigma }) = \frac{3}{\eta } \rho ^2 \Psi _0(\varvec{\varepsilon }) \end{aligned}$$

(8)

which fulfills the purpose of topology optimization: the relative density is locally increased more at spatial coordinates with high values of the strain energy density. The benefit of this thermodynamically motivated procedure was the inclusion of material non-linearities of which examples can be found in [11, 18]. Furthermore, the classical optimization problem is reformulated as evolutionary problem. Therefore, no (additional) optimization procedures are necessary and implementations in any finite element subroutine with user elements or user materials is possible. The differential equation itself serves as update scheme.

Although this modeling principle is sound in the context of small deformations, a direct application for hyperelastic materials, i.e., in the context of large deformations is not possible since an analytic inversion of the constitutive relation between stress and strain measures is not available here. We therefore propose a novel variational model for topology optimization, inspired by (1).

3 A generalized approach to variational topology optimization

A variational approach to topology optimization possesses three principal benefits: (1) constraints can be easily included by simple addition to the functional; (2) the optimization problem can be reformulated as evolutionary problem for which no optimization routines are requested; (3) the evolutionary character of the resultant model for topology optimization allows for a immediate consideration of material microstructure evolution without using external mathematical optimizer. Thus, a generalized approach to thermodynamic topology optimization shall be formulated that can also be applied to hyperelastic structures undergoing large deformations.

An appropriate model for topology optimization is supposed to apply mass where locally the mechanical loads are high and, in turn, remove mass where locally mechanical loads are low. The intensity of the mechanical loads is measured by the strain energy density which enters the Gibbs energy serving as global measure. Furthermore, the rearrangement of relative density in terms of local and convective rates contributes to the energetic balancing. Since the rearrangement consumes partly the stored energy, it is the difference between the Gibbs energy plus dissipation-related work and the work related to rearrangement that is assumed to be stationary. Thereby, the goal to couple the local rearrangement of relative density to the intensity of mechanical loads is achieved. Constraints are included by the functional ${\mathcal {C}}$. These considerations can be recast in the Hamilton functional for both microstructure evolution and topology optimization as

$$\begin{aligned} {\mathcal {H}}[\varvec{u},{\varvec{\alpha }},\chi ]:= & {} {\mathcal {G}}[\varvec{u},{\varvec{\alpha }},\chi ] + {\mathcal {D}}_{\varvec{\alpha }}[{\varvec{\alpha }}] - {\mathcal {R}}[{\varvec{\alpha }},\chi ] \nonumber \\&+ {\mathcal {C}}[{\varvec{\alpha }},\chi ] \rightarrow \underset{\varvec{u},{\varvec{\alpha }},\chi }{\text {stat}} \end{aligned}$$

(9)

where the set of internal variables ${\varvec{y}}={\varvec{\alpha }}\cup \chi$ is decomposed into two parts: variables that account for the physical behavior, i.e., that are related to physical microstructure evolution, are indicated by ${\varvec{\alpha }}$; the variable that is used for the topology optimization is indicated by $\chi$ and referred to as density variable. It is worth mentioning that we do not formulate the variational approach directly in terms of the relative density $\rho$; instead, we use the density variable $\chi$. This enables us to chose a suitable mapping $\rho =\rho (\chi )$ such that constraints on the relative density can be fulfilled by construction of $\rho$. A specification is provided in Sect. 3.2.

A measure of the dissipation-related work due to local rearrangement is given by the part of ${\mathcal {D}}_{\varvec{y}}$ that is related to the topology. The energy due to convective rearrangement is measured by the functional ${\mathcal {F}}$. Thus, the total energy due to rearrangement is given by

$$\begin{aligned} {\mathcal {R}}[\chi ] := {\mathcal {D}}[\chi ] + {\mathcal {F}}[\chi ] \ . \end{aligned}$$

(10)

Thereby, a split of dissipation-related work according to ${\mathcal {D}}_{\varvec{y}}[{\varvec{y}}]={\mathcal {D}}_{\varvec{\alpha }}[{\varvec{\alpha }}]-{\mathcal {D}}[\chi ]$ is implied. Consequently, the stationary condition reads

$$\begin{aligned}&\delta {\mathcal {H}}[\varvec{u},{\varvec{\alpha }},\chi ](\delta \varvec{u},\delta {\varvec{\alpha }},\delta \chi ) \nonumber \\&\quad = \delta {\mathcal {G}}[\varvec{u},{\varvec{\alpha }},\chi ](\delta \varvec{u},\delta {\varvec{\alpha }},\delta \chi ) + \delta {\mathcal {D}}_{\varvec{\alpha }}[{\varvec{\alpha }}](\delta {\varvec{\alpha }}) - \delta {\mathcal {D}}[\chi ](\delta \chi ) \nonumber \\&\qquad - \delta {\mathcal {F}}[\chi ](\delta \chi ) + \delta {\mathcal {C}}[{\varvec{\alpha }},\chi ](\delta {\varvec{\alpha }},\delta \chi )\nonumber \\&\quad = 0 \quad \forall \; \delta \varvec{u}, \ \delta {\varvec{\alpha }}, \ \delta \chi \end{aligned}$$

(11)

with $\delta {\mathcal {D}}_{\varvec{\alpha }}[{\varvec{\alpha }}](\delta {\varvec{\alpha }})=\int _\Omega \varvec{p}^\text {diss}_{\varvec{\alpha }}\cdot \delta {\varvec{\alpha }}\ \mathrm {d}V$, cf. (4). This variational balance condition comprises microstructure evolution and topology optimization. Thus, the stationarity conditions enable us to derive the balance of linear momentum and the evolution equations for dissipative materials along with the variational condition for topology optimization:

$$\begin{aligned} \left\{ \begin{array}{rl} &{} \displaystyle \delta _u{\mathcal {G}}[\varvec{u},{\varvec{\alpha }},\chi ](\delta \varvec{u}) = 0 \quad \forall \; \delta \varvec{u}\\ &{} \displaystyle \delta _{\varvec{\alpha }}{\mathcal {G}}[\varvec{u},{\varvec{\alpha }},\chi ](\delta {\varvec{\alpha }}) + \int _\Omega \frac{\partial \Delta ^\text {diss}_{\varvec{\alpha }}({\dot{{\varvec{\alpha }}}})}{\partial {\dot{{\varvec{\alpha }}}}} \cdot \delta {\varvec{\alpha }}\ \mathrm {d}V \\ &{} \quad + \delta _{\varvec{\alpha }}{\mathcal {C}}[{\varvec{\alpha }},\chi ](\delta {\varvec{\alpha }}) = 0 \quad \forall \; \delta {\varvec{\alpha }}\\ &{} \quad \displaystyle \delta _\chi {\mathcal {G}}[\varvec{u},{\varvec{\alpha }},\chi ](\delta \chi ) - \delta _\chi {\mathcal {D}}[\chi ](\delta \chi ) \\ &{} \quad - \delta _\chi {\mathcal {F}}[\chi ](\delta \chi ) + \delta _\chi {\mathcal {C}}[{\varvec{\alpha }},\chi ](\delta \chi ) = 0 \quad \forall \; \delta \chi \end{array}\right. \nonumber \\ \end{aligned}$$

(12)

Here, we used $\varvec{p}^\text {diss}_{\varvec{\alpha }}=\partial \Delta ^\text {diss}_{\varvec{\alpha }}({\dot{{\varvec{\alpha }}}})/\partial {\dot{{\varvec{\alpha }}}}$. The displacements are searched in $\hbox {H}^1$; the spaces for the internal variables, i.e., ${\varvec{\alpha }}$ and $\chi$, still depend on the specific choice of the functionals. Again, dissipative effects of the material are modeled by the internal variable ${\varvec{\alpha }}$. This formulation is more general than the previous equations used for thermodynamic topology optimization. However, for the case of small deformations, the novel formulation yields identical evolution equations as the classical form. Examples for thermodynamic topology optimization including dissipative material behavior are given for tension/compression hybrid structures in [11] and for anisotropic materials in [18]. In the current work, we restrict ourselves to non-linear elastic materials such that (12)${}_2$ is not considered here.

3.1 Strain energy density and balance of linear momentum

Let us begin with the evaluation of (12)${}_1$ for which we need to define the strain energy density $\Psi$ in (2) to specify the Gibbs energy. In analogy to the SIMP approach in topology optimization, we use a multiplicative split of the energy into its elastic contribution $\Psi _0$ and a non-linear scaling. It thus reads

$$\begin{aligned} \Psi (\varvec{C},\chi ) = \rho (\chi )^3 \, \Psi _0(\varvec{C}) \end{aligned}$$

(13)

with the right Cauchy-Green tensor $\varvec{C}=\varvec{F}^\text {T} \varvec{F}$ and the deformation gradient

$$\begin{aligned} \varvec{F}= \frac{\partial \varvec{x}}{\partial \varvec{X}} = \varvec{I}+ \frac{\partial \varvec{u}}{\partial \varvec{X}} \ . \end{aligned}$$

(14)

Here, the spatial coordinates in the current configuration are indicated by $\varvec{x}$ while those of the reference configuration are given by $\varvec{x}(t=t_0)=\varvec{x}_0=:\varvec{X}$.

The balance of linear momentum results from the condition $\delta _u{\mathcal {G}}=0$:

$$\begin{aligned} \delta _u{\mathcal {G}}= & {} \int _\Omega \frac{\partial \Psi }{\partial \varvec{C}}\cdot \delta \varvec{C}\ \mathrm {d}V \nonumber \\&- \int _\Omega \varvec{b}^\star \cdot \delta \varvec{u}\ \mathrm {d}V - \int _{\partial \Omega } \varvec{t}^\star \cdot \delta \varvec{u}\ \mathrm {d}A = 0 \quad \forall \; \delta \varvec{u}\ . \end{aligned}$$

(15)

Note that we evaluate the integrals with respect to the reference configuration. Following the method of Coleman and Noll, we identify the 2nd Piola–Kirchhoff stress tensor $\varvec{S}=2\partial \Psi /\partial \varvec{C}$. The weak form of the balance of linear momentum (15) thus reads

$$\begin{aligned}&\int _\Omega \varvec{S}:\frac{1}{2}\delta \varvec{C}\ \mathrm {d}V - \int _\Omega \varvec{b}^\star \cdot \delta \varvec{u}\ \mathrm {d}V\nonumber \\&\qquad \qquad \qquad \qquad \ - \int _{\partial \Omega } \varvec{t}^\star \cdot \delta \varvec{u}\ \mathrm {d}A = 0 \quad \forall \; \delta \varvec{u}\ . \end{aligned}$$

(16)

3.2 Representation of the relative density

Before we evaluate (12)${}_3$, let us introduce a representation of the relative density $\rho$. Several constraints have to be fulfilled by models for topology optimization. For instance, the relative density has to be bounded from above and below, reading

$$\begin{aligned} \rho (\varvec{x}) \in \; ]\rho _\text {min},1] \quad \forall \; \varvec{x}\end{aligned}$$

(17)

with the minimal relative density $\rho _\text {min}>0$ which is introduced for numerical reasons. Usual values are $\rho _\text {min}<10^{-6}$. The bounds can be introduced by means of Kuhn–Tucker parameters into the constraint functional ${\mathcal {C}}$. However, they drastically complicate the numerical treatment since the constraint has to be fulfilled for each discretization point individually. Therefore, the goal is to avoid the complex constraint of bounds for the relative density. To this end, we make use of a mapping $\rho =\rho (\chi )$ which fulfills (17) directly. This mapping represents the relative density and is chosen as the sigmoid function

$$\begin{aligned} \rho (\chi ) = [1+e^{-\chi }]^{-1} \quad \text {with}\quad \rho '(\chi ) = e^{-\chi } [1+ e^{-\chi }]^{-2}\nonumber \\ \end{aligned}$$

(18)

where the quantity $\chi \in \;]-\infty ,+\infty [$ is termed density variable. The sigmoid function fulfills by construction $\displaystyle \rho (\chi )\in \;]0,1[$, $\displaystyle \lim _{\chi \rightarrow -\infty }\rho (\chi )=0$, and $\displaystyle \lim _{\chi \rightarrow +\infty }\rho (\chi )=1$. The initial value for the density variable $\chi$ is computed by the inverse function of $\rho$, thus

$$\begin{aligned} \chi _0 = - \log [\rho _0^{-1}-1] \ . \end{aligned}$$

(19)

3.3 Generalized approach for thermodynamic topology optimization

We make use of the variational balance condition in (12)${}_3$ and specify the individual functionals as follows:

$$\begin{aligned} {\mathcal {D}}[\chi ]= & {} \int _\Omega p^\text {diss} \chi \ \mathrm {d}V \ , \end{aligned}$$

(20)

$$\begin{aligned} {\mathcal {F}}[\chi ]= & {} \int _\Omega \frac{1}{2} \beta |\nabla \rho |^2 \ \mathrm {d}V \ , \end{aligned}$$

(21)

$$\begin{aligned} {\mathcal {G}}[\varvec{u},\chi ]= & {} \int _\Omega \rho (\chi )^3 \, \Psi _0(\varvec{C}(\varvec{u})) \ \mathrm {d}V \nonumber \\&- \int _\Omega \varvec{b}^\star \cdot \varvec{u}\ \mathrm {d}V - \int _{\partial \Omega } \varvec{t}^\star \cdot \varvec{u}\ \mathrm {d}A \ . \end{aligned}$$

(22)

It is worth to already mention that an appropriate choice of the parameter $\beta$ in the term for conevctive rearrangement ${\mathcal {F}}$ controls the member size, i.e. the minimum truss thickness. Thus, the topology optimization problem is regularized and for $\beta = c h^2$ with some constant $c>0$ the checkerboard phenomenon is not present where the finite element mesh size is given by h. Same choices for the respective terms have been made for thermodynamic topology optimization in the context of the linearized theory in [17].

Thanks to the representation of $\rho$ in Sect. 3.2, the only constraint that remains to be considered by the model for topology optimization is simply mass conservation which is given by

$$\begin{aligned} \int _\Omega \rho (\chi ) \ \mathrm {d}V = {\bar{\rho }} \, \Omega \quad \Leftrightarrow \quad \int _\Omega \rho ' \, {\dot{\chi }} \ \mathrm {d}V = 0 \end{aligned}$$

(23)

with the prescribed relative structure density ${\bar{\rho }}$. The initial condition for the density function is then $\rho _0 = \rho (\chi _0) = {\bar{\rho }}$. The constraint is taken into account by introducing a Lagrange parameter $\lambda$. Thus, the constraint functional reads

$$\begin{aligned} {\mathcal {C}}=\lambda \left( \int _\Omega \rho \ \mathrm {d}V - {\bar{\rho }} \, \Omega \right) \ . \end{aligned}$$

(24)

The variational balance condition in analogy to Hamilton’s principle according to (12)${}_3$ hence reads

$$\begin{aligned}&\delta _\chi \int _\Omega \Psi \ \mathrm {d}V -\int _\Omega \frac{\partial \Delta ^\text {diss}}{\partial {\dot{\chi }}}\delta \chi \ \mathrm {d}V - \delta _\chi \int _\Omega \frac{1}{2}\beta |\nabla \rho |^2 \ \mathrm {d}V \nonumber \\&\quad + \delta _\chi \left[ \lambda \left( \int _\Omega \rho \ \mathrm {d}V - {\bar{\rho }} \, \Omega \right) \right] = 0 \quad \forall \; \delta \chi \ . \end{aligned}$$

(25)

where we used the relation $p^\text {diss} = \partial \Delta ^\text {diss}/\partial {\dot{\chi }}$ and $\delta _\chi p^\text {diss}=0$, cf. (4). Computing the Gâteaux derivatives results in

$$\begin{aligned}&\int _\Omega \frac{\partial \Psi }{\partial \chi } \delta \chi \ \mathrm {d}V -\int _\Omega \eta {\dot{\chi }} \delta \chi \ \mathrm {d}V -\int _\Omega \beta \nabla \rho \nabla (\rho ' \ \delta \chi ) \ \mathrm {d}V \nonumber \\&\quad + \int _\Omega \lambda \rho ' \delta \chi \ \mathrm {d}V =0 \quad \forall \; \delta \chi \ . \end{aligned}$$

(26)

when $\Delta ^\text {diss}=\eta {\dot{\chi }}^2/2$ has been chosen. Integration by parts of the third term and consideration of the arbitrariness of $\delta \chi$ gives

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \ \ \quad \eta {\dot{\chi }} = -p + \beta \rho ' \mathop {}\!\mathbin \bigtriangleup \rho + \lambda \rho ' &{} \forall \; \varvec{x}\in \Omega \\ \displaystyle \varvec{n}\cdot \nabla \rho = 0 &{} \forall \; \varvec{x}\in \partial \Omega \end{array}\right. } \end{aligned}$$

(27)

where (27)${}_2$ implies zero mass fluxes across the boundaries. It is worth mentioning that (27)${}_2$ only holds on parts of the boundary where no Dirichlet boundary conditions are employed, i.e., $\partial \Omega _\rho =\emptyset$. In case of prescribed density at the boundary, e.g. due to a connection to an existing construction part, the Neumann condition (27)${}_2$ transforms to a Dirichlet condition $\rho =\rho ^\star \ \forall \varvec{x}\in \partial \Omega _\rho$ such that $\varvec{n}_0\nabla \rho$ does not apply on $\varvec{x}\in \partial \Omega _\rho$. In (27)${}_1$, the quantity $p:=-\partial \Psi /\partial \chi$ is defined in analogy to thermodynamic driving forces and serves as source for the density evolution. It reads with $\Psi =\rho (\chi )^3\Psi _0$

$$\begin{aligned} p = -3 \rho ^2\rho ^\prime \,\Psi _0 \ . \end{aligned}$$

(28)

For computing the Lagrange parameter $\lambda$, we multiply (27)${}_1$ by $\rho '$ and integrate over the volume $\Omega$. This gives

$$\begin{aligned}&\int _\Omega \eta \rho ' \, {\dot{\chi }} \ \mathrm {d}V \overset{(23)}{=} 0 \nonumber \\&\quad = \int _\Omega \rho ' [ -p + \beta \rho ' \mathop {}\!\mathbin \bigtriangleup \rho ] \ \mathrm {d}V + \lambda \int _\Omega (\rho ')^2 \ \mathrm {d}V \end{aligned}$$

(29)

from which we find

$$\begin{aligned} \lambda = \left[ \int _\Omega (\rho ')^2 \ \mathrm {d}V \right] ^{-1} \int _\Omega \rho ' [p - \beta \rho ' \mathop {}\!\mathbin \bigtriangleup \rho ] \ \mathrm {d}V \ . \end{aligned}$$

(30)

Concluding, the field equations (16) and (27) in combination with (30) describe the evolution of the displacements $\varvec{u}$ and the density variable $\chi$ in time and space. The relative density $\rho$ can be computed according to (18). In the following, we present a possible numerical treatment.

4 Numerical treatment

Summarizing, the following set of equations has to be solved for the displacement field $\varvec{u}$ and the density variable $\chi$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \quad 0 = \int _\Omega \varvec{S}(\varvec{C}(\varvec{u}),\chi )\cdot \frac{1}{2}\delta \varvec{C}\ \mathrm {d}V &{} \\ \quad \quad \quad - \displaystyle \int _\Omega \varvec{b}^\star \cdot \delta \varvec{u}\ \mathrm {d}V - \int _{\partial \Omega } \varvec{t}^\star \cdot \delta \varvec{u}\ \mathrm {d}A &{} \forall \; \delta \varvec{u}\\ \displaystyle \ \eta {\dot{\chi }} = -p(\varvec{C}(\varvec{u}),\chi ) + \beta \rho ^\prime (\chi ) \mathop {}\!\mathbin \bigtriangleup \rho (\chi )&{} \\ \qquad \qquad + \lambda \rho ^\prime (\chi ) &{}\forall \; \varvec{x}\in \Omega \end{array}\right. } \end{aligned}$$

(31)

with the Dirichlet and Neumann boundary conditions, i.e., $\varvec{u}=\varvec{u}^\star \;\forall \;\varvec{x}\in \partial \Omega _u$ and $\varvec{F}\varvec{S}\varvec{n}_0=\varvec{t}^\star \;\forall \;\varvec{x}\in \partial \Omega _u$, respectively, and $\Omega =\Omega _u\cup \Omega _t$. The quantity $\varvec{n}_0$ is the normal vector on $\partial \Omega$ in the reference configuration. The evolution of topology is given in terms of (31)$_2$ which is a partial differential equation in space and time. The initial condition is chosen as $\chi =\chi _0\;\forall \;\varvec{x}\in \Omega$. This naive choice corresponds to the usual homogeneously gray initial distribution which is also used for other methods for topology optimization. However, we show by numerical investigations that remarkably different optimal topologies only evolve when strong inhomogeneities are chosen as initial distribution, see Sect. 5.3.1. The Neumann condition is $\varvec{n}_0\nabla \rho = 0 \ \forall \; \varvec{x}\in \partial \Omega$, see (27)$_2$. According to (30), the equations are complemented by the Lagrange multiplier

$$\begin{aligned} \lambda= & {} \left[ \int _\Omega \rho ^\prime (\chi )^2 \ \mathrm {d}V \right] ^{-1} \int _\Omega \rho ' [p(\varvec{C}(\varvec{u}),\chi ) - \beta \rho ^\prime (\chi )\mathop {}\!\mathbin \bigtriangleup \rho (\chi )] \ \mathrm {d}V \ . \end{aligned}$$

(32)

The field equations in (31) constitute a coupled system of partial differential equations (PDEs). For standard systems of coupled PDEs, the finite element method can be employed for numerical solution. However, the Lagrange multiplier prevents a direct application of such a strategy in the present case: since the evaluation of $\lambda$ demands knowledge of the global fields of $\varvec{u}$ and $\chi$, a staggered solution scheme appears advantageous. In a first step, the updated displacement field is computed from (31)$_1$ by fixating the density variable; in a second step, the density variable is updated using (31)$_2$. This procedure is repeated until convergence. For the weak form of the balance of linear momentum (31)$_1$ the finite element method can be employed. For the field equation of the density variable (31)$_2$, we make use of a modified finite differences scheme that is also valid for irregular and unstructured grids and had been referred to as neighbored element method in e.g., [17, 21, 42]. Details for the numerical treatment are given in the following subsections. Of course, a different numerical treatment could be employed. For instance, using the weak form of (31)$_2$, as presented in (26), would enable us to solve it along with (31)$_1$ in a monolithic manner in which no operator split is necessary. A similar procedure has been presented in [20]. Unfortunately, the numerical effort in terms of computation times is higher by approximately one order of magnitude. Consequently, we prefer the staggered update scheme which, as shown later, is quite fast since the extra effort for optimization is quite small compared to the effort needed to compute the displacement field.

4.1 Balance of linear momentum

The weak form of the balance of linear momentum (16) is as usual numerically solved by means of the finite element method. To this end, the displacements are approximated by use of

$$\begin{aligned} u_k = N_o \ {\hat{u}}_o^{{(k)}} = \varvec{N}\cdot {\hat{\varvec{u}}}^{{(k)}} \end{aligned}$$

(33)

where the shape functions are denoted by $\varvec{N}$ and the nodal displacements in the spatial direction k are indicated by ${\hat{\varvec{u}}}^{(k)}$. Then, the weak form of the balance of linear momentum (16) can be reformulated in terms of the approximations as $\delta {\hat{\varvec{u}}}\cdot \varvec{r}= 0$ with the global column matrix of nodal virtual displacements $\delta {\hat{\varvec{u}}}$ and

(34)

Herein, $\varvec{r}$ is the global residual column-matrix that results from assembling and $\varvec{r}_e$ is the residual column-matrix of each finite element (e). The quantity $\varvec{s}$ denotes the matrix notation of the 2nd Piola–Kirchhoff stress tensor and $\varvec{B}_e$ an operator matrix including the derivatives of the shape functions. When the linear terms including body forces and the traction vector are not taken into account and Dirichlet boundary conditions are included in the variation, the nodal displacements are found from

$$\begin{aligned} \varvec{r}= {\varvec{0}} \ . \end{aligned}$$

(35)

Details for the derivation are deferred to Appendix A.

Note that both $\varvec{B}_e$ and $\varvec{s}$ depend on the nodal displacements such that (35) constitutes as a system of nonlinear algebraic equations for the global nodal displacements ${\hat{\varvec{u}}}$. Due to its nonlinearity, the Newton method is employed to solve (34). To this end, the tangent in each element

$$\begin{aligned} \frac{\mathrm {d}\varvec{r}_e}{\mathrm {d}}{{\hat{\varvec{u}}}_e} = \int _{\Omega _e} \varvec{B}_e^\text {T} \frac{\partial \varvec{s}}{\partial \hat{\varvec{u}}_e} \ \mathrm {d} V + \int _{\Omega _e} \frac{\partial \varvec{B}_e^\text {T}}{\partial {\hat{\varvec{u}}}_e} \varvec{s}\ \mathrm {d}V \end{aligned}$$

(36)

is mandatory. Here, ${\hat{\varvec{u}}}_e$ denotes the column-matrix of all nodal displacements in element (e). The tangent is given as

$$\begin{aligned} \frac{\mathrm {d}\varvec{r}_e}{\mathrm {d}{\hat{\mathbf{u}}}_e} = \int _{\Omega _e} \varvec{B}_e^\text {T} \varvec{E}_e \varvec{B}_e \ \mathrm {d} V + \int _{\Omega _e} \varvec{G}_e \ \mathrm {d}V \end{aligned}$$

(37)

with the material tangent matrix $\varvec{E}_e=2 \partial \varvec{s}/\partial \varvec{c}$ and the matrix form $\varvec{c}$ of the right Cauchy–Green tensor $\varvec{C}$. The geometrical part of the derivative is defined as $\varvec{G}_e:= (\partial \varvec{B}_e^\text {T}/\partial \hat{\varvec{u}_e}) \varvec{s}$, all in element ${{(e)}}$. Details are given in Appendix B and C .

Note that both the residual $\varvec{r}_e$ and its derivative in (37) have to be assembled to obtain the residual and its tangent for an entire finite element analysis.

4.2 Field equation for the relative density

We approximate the relative density field with one value for each finite element ${{(e)}}$, i.e., only one value for the relative density is used for all integration points in each finite element. Thus, for the approximation of the piece-wise constant relative density, we use $C^0$ shape functions. For the solution of (31)$_2$, we make use of the recently introduced neighbored element method (NEM). It was developed to discretize the Laplace operator in a model for topology optimization in [17]. However, it could also successfully be applied to a damage model in [21] and a generalized formulation was found in [42]. For convenience, we recall here the principal ideas of NEM.

The Laplace operator can be computed on regular and structured meshes by the finite difference method (FDM). Unfortunately, the standard FDM fails to compute sufficiently accurate values for the Laplace operator for meshes with even small irregularity. Therefore, the NEM makes use of a Taylor series expansion of order two to approximate the relative density between the midpoints of neighbored finite elements. The set of $n^{{(e)}}$ neighbored elements for element ${{(e)}}$ is given by ${\mathcal {N}}^{{(e)}}$ such that ${\mathcal {N}}^{{(e)}}_k$ returns the global element number for the kth neighbor. For elements that are located at the boundary of the design space, mirror (“ghost”) elements are introduced to increase ${\mathcal {N}}^{{(e)}}$ accordingly. In analogy to the FDM, we set $\rho ^\text {mirrored}=\rho ^{{(e)}}$ which fulfills (27)${}_2$ identically. The Taylor expansion for all neighbored elements ${(k)}$ with the expansion point of the investigated element ${{(e)}}$ can be written as

$$\begin{aligned} \rho ^{({\mathcal {N}}^{{(e)}}_k)} = \rho ^{{(e)}}+ \sum _o D^{{(i,k)}}_o \rho ^{{(e)}}_{\partial ,o} \ . \end{aligned}$$

(38)

Herein, $\rho ^{{({\mathcal {N}}^{{(e)}}_k)}}$ denotes the relative density at the midpoint of a neighboring element ${(k)}$ with the global element number ${\mathcal {N}}^{{(e)}}_k$; $\rho ^{{(e)}}$ is the relative density at the midpoint of element ${{(e)}}$.

The derivative terms of the Taylor series are collected in the vector

$$\begin{aligned} \varvec{\rho }_{\partial }^{{(e)}}:= \left( \begin{matrix} \displaystyle \frac{\partial \rho ^{{(e)}}}{\partial x}&\displaystyle \frac{\partial \rho ^{{(e)}}}{\partial y}&\displaystyle \frac{\partial \rho ^{{(e)}}}{\partial z}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial x \partial y}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial y \partial z}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial x \partial z}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial x^2}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial y^2}&\displaystyle \frac{\partial ^2 \rho ^{{(e)}}}{\partial z^2} \end{matrix} \right) \ . \end{aligned}$$

(39)

Finally, the matrix $\varvec{D}^{{(e)}}\in {\mathbb {R}}^{n\times d}$ stores the distances between the midpoint of the element of interest ${{(e)}}$ and those of all neighbored elements $k\in {\mathcal {N}}^{{(e)}}$ with varying powers. The value of d depends on the spatial dimension and for 3D, we find $d=9$ (in 2D $d=5$). The kth row in $\varvec{D}^{{(e)}}$ is given by

$$\begin{aligned} D^{{(k)}}:= & {} \Bigg ( x_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \quad y_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \quad z_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \quad (xy)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \quad (yz)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \quad (zx)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} \nonumber \\&\quad \frac{1}{2}\Big ( x_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}}\Big )^2 \quad \frac{1}{2}\Big ( y_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}}\Big )^2 \quad \frac{1}{2}\Big ( z_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}}\Big )^2 \Bigg ) \end{aligned}$$

(40)

with

$$\begin{aligned}&x_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := x^{({\mathcal {N}}^{{(e)}}_k)}-x^{{(e)}}\ , \,\, (xy)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := (x^{{({\mathcal {N}}^{{(e)}}_k)}}-x^{{(e)}})(y^{{({\mathcal {N}}^{{(e)}}_k)}}-y^{{(e)}}) \\&y_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := y^{({\mathcal {N}}^{{(e)}}_k)}-y^{{(e)}}\ ,\,\, (yz)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := (y^{{({\mathcal {N}}^{{(e)}}_k)}}-y^{{(e)}})(z^{{({\mathcal {N}}^{{(e)}}_k)}}-z^{{(e)}}) \\&z_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := z^{({\mathcal {N}}^{{(e)}}_k)}-z^{{(e)}}\ ,\,\, (zx)_{\Delta }^{{({\mathcal {N}}^{{(e)}}_k)}} := (z^{{({\mathcal {N}}^{{(e)}}_k)}}-z^{{(e)}})(x^{{({\mathcal {N}}^{{(e)}}_k)}}-x^{{(e)}}) \ . \end{aligned}$$

Similarly to the definition of the distances, let us introduce $\varvec{\rho }_{\Delta }^{{(e)}}\in {\mathbb {R}}^n$ be a column-matrix for element ${{(e)}}$, whose kth component reads

$$\begin{aligned} \rho ^{{(e)}}_{\Delta ,k} := \rho ^{({\mathcal {N}}^{{(e)}}_k)}-\rho ^{{(e)}}. \end{aligned}$$

(41)

Then, the Taylor series expansion up to order two can shortly be represented by

$$\begin{aligned} \varvec{\rho }_{\Delta }^{{(e)}}= \varvec{D}^{{(e)}}\varvec{\rho }_{\partial }^{{(e)}}\ . \end{aligned}$$

(42)

Due to the known values of the density variable in all elements, the differences $\varvec{\rho }_{\Delta }^{{(e)}}$ are known. Furthermore, the distance matrix $\varvec{D}^{{(e)}}$ is fixed for fixed grits. Consequently, we can solve (42) for the vector $\varvec{\rho }_{\partial }^{{(e)}}$ that stores the different derivatives according to (39). The value of the Laplace operator can subsequently be determined from $\varvec{\rho }_{\partial }^{{(e)}}$ by summation of the last three components. To obtain a convenient notation, we introduce

$$\begin{aligned} \varvec{a}:= \left( \begin{matrix} 0&0&0&0&0&0&1&1&1 \end{matrix} \right) \ , \end{aligned}$$

(43)

and we can thus write

$$\begin{aligned} \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}= \varvec{\rho }_{\partial }^{{(e)}}\cdot \varvec{a}\ . \end{aligned}$$

(44)

A necessary condition for the solvability of (42) is that $n\ge d$, i.e., the number of neighbored elements has to be at least as large as the number of derivative terms d. The set of neighbored elements ${\mathcal {N}}^{{(e)}}_k$ can be chosen in two different ways. One possibility is to select all neighbored elements that share the same vertices (stencil for structured, regular finite element meshes) plus three diagonal elements (two in 2D). For sufficiently regular meshes, $\varvec{D}^{{(e)}}$ contains full rank and $\varvec{D}^{{(e)}}$ is regular such that a solution to (42) exists. For this choice of ${\mathcal {N}}^{{(e)}}_k$, $n=d$ holds and we can invert (42) directly. We then obtain for the Laplace operator

$$\begin{aligned} \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}= \varvec{\rho }_{\partial }^{{(e)}}\cdot \varvec{a}= (\varvec{D}^{{{(e)}}\,-1}\varvec{\rho }_{\Delta }^{{(e)}}) \cdot \varvec{a}= \varvec{a}\varvec{D}^{{{(e)}}\,-1}\varvec{\rho }_{\Delta }^{{(e)}}\ . \end{aligned}$$

(45)

The other option to simply collect all neighbored elements, i.e., all elements with same vertices and all diagonal elements. Then, no special selection of surrounding elements for the neighbored elements must be performed. For this general case, $n>d$ holds but it was shown in [42] that the right-inverse can be taken such that the Laplace operator reads

$$\begin{aligned} \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}= \varvec{a}\varvec{D}^{{{(e)}}\,T} (\varvec{D}^{{(e)}}\varvec{D}^{{{(e)}}\,T})^{-1} \varvec{\rho }_{\Delta }^{{(e)}}\ . \end{aligned}$$

(46)

Here, we assumed full rank of all $\varvec{D}^{{(e)}}$ which is fulfilled for sufficiently undistorted finite elements. Note that we evaluate all equations in the reference configuration. Consequently, all $\varvec{D}^{{(e)}}$ maintain their rank throughout the entire computation.

For a unified notation, we introduce

$$\begin{aligned} \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}= \varvec{l}^{{(e)}}\cdot \varvec{\rho }_{\Delta }^{{(e)}}\end{aligned}$$

(47)

with

$$\begin{aligned} \varvec{l}^{{(e)}}:= {\left\{ \begin{array}{ll} \varvec{a}\varvec{D}^{{{(e)}}\,-1} &{} \text {for } n=d \\ \varvec{a}\varvec{D}^{{{(e)}}\,T} (\varvec{D}^{{(e)}}\varvec{D}^{{{(e)}}\,T})^{-1} &{} \text {for } n>d \end{array}\right. } \ . \end{aligned}$$

(48)

We emphasize that for fixed finite element meshes, i.e., when no adaptive finite element mesh is used, the values for each $\varvec{l}^{{(e)}}$ can be computed once in advance to the respective simulation.

4.3 Time integration

The evolution equation and the Lagrange parameter in (31)${}_2$ and (32), respectively, need to be discretized for numerical investigation. For simplicity, we perform an explicit Euler time integration along with the Neighbored Element Method for the approximation of the Laplace operator $\mathop {}\!\mathbin \bigtriangleup \rho$. The time incrementation is given by $\Delta t := t_{n+1}-t_n$ where $n+1$ indicates the current time step and n the previous time step. Of course, usage of an implicit time integration scheme would be beneficial and should be chosen rather than the explicit one we used. However, our intention is to provide an optimization approach that is suitable to be programmed into an existing finite element program with a minimum of extra effort or need of external libraries, e.g. for the solution of a system coupled nonlinear equations. We therefore make use of the most simple integration method and accept the related numerical disadvantages. However, an appropriate choice of the viscosity allows for a smooth numerical behavior which was observed for all numerical experiments we performed.

The target volume ${{\bar{\rho }}}$ is conserved by use of the Lagrange parameter $\lambda _n$. However, the representation of the relative density $\rho _{n+1}=\rho (\chi _{n+1})$ possesses only a small sensitivity on changes of $\chi _{n+1}$ when $\rho _{n+1}\approx 0$ or $\rho _{n+1}\approx 1$. Therefore, the evolutionary update of the density variable $\chi$ and thus of the relative density $\rho$ might be influenced by truncation errors that accumulate during the iteration process. We thus make use of the scaling as presented in Algorithm 1 to reduce the impact of truncation errors. The unscaled density variable is termed as ${\tilde{\chi }}$ and obtained from the discretized form of (31)${}_2$, reading

$$\begin{aligned} {{\tilde{\chi }}}^{{(e)}}_{n+1} = \chi ^{{(e)}}_n + \frac{\Delta t}{\eta } \left[ -{\bar{p}}^{{(e)}}_n + \beta \rho ^{{{(e)}}\,\prime }_n \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}_n + \lambda _n \rho ^{{{(e)}}\,\prime }_n \right] \end{aligned}$$

(49)

with the discretized form of (32)

$$\begin{aligned} \lambda _n = \left[ \sum _e \Omega ^{{(e)}} (\rho ^{{{(e)}}\,\prime }_n)^2 \right] ^{-1} \sum _e \Omega ^{{(e)}}\rho ^{{{(e)}}\,\prime }_n [p^{{(e)}}_n - \beta \rho ^{{{(e)}}\,\prime }_n \mathop {}\!\mathbin \bigtriangleup \rho _n^{{(e)}}] \ .\nonumber \\ \end{aligned}$$

(50)

Note that the precise numerical value of the driving forces is of minor importance; it is the relative fraction that determines whether the relative density in a specific finite element ${{(e)}}$ will increase or decrease. It is thus convenient to scale the driving forces by introducing ${\bar{p}}^{{(e)}}_n$ as

$$\begin{aligned} {\bar{p}}^{{(e)}}_n := p^{{(e)}}_n \left[ \sum _e \Omega ^{{(e)}}\rho ^{{(e)}}_n (1-\rho ^{{(e)}}_n) p^{{(e)}}_n \right] ^{-1} \sum _e \Omega ^{{(e)}}\rho ^{{(e)}}_n (1-\rho ^{{(e)}}_n)\nonumber \\ \end{aligned}$$

(51)

and to use these to update the density variable as presented in (49). The metric $\rho ^{{(e)}}_n (1-\rho ^{{(e)}}_n)$ ensures that only the driving forces of all “active”, grey states, i.e., $\rho \in \;]0,1[$, are considered for scaling. This procedure reduces strong local effects such as boundary conditions, cf. [17].

As mentioned, truncation errors might accumulate over the times steps if ${\tilde{\chi }}$ is used directly to compute the updated value for the relative density. Consequently, the unscaled values ${\tilde{\chi }}^{{(e)}}$ are taken to compute the unscaled relative density ${\tilde{\rho }}^{{(e)}}$ which might violate $\sum _e {\tilde{\rho }}^{{(e)}}\Omega ^{{(e)}}= \sum _e {\bar{\rho }} \Omega ^{{(e)}}$, i.e., the unscaled relative density does not cover the prescribed total volume given by $\int _\Omega {\bar{\rho }} \ \mathrm {d}V=\sum _e {\bar{\rho }} \Omega ^{{(e)}}$. We therefore compute a “trial” density $\rho _\text {t}^{{(e)}}$

$$\begin{aligned} \rho _\text {t}^{{(e)}}:= {\tilde{\rho }}^{{(e)}}\frac{\sum _{k}{\bar{\rho }} \ \Omega ^{(k)}}{\sum _k {\tilde{\rho }}^{(k)}\Omega ^{(k)}} \end{aligned}$$

(52)

which fulfills the constraint exactly. However, this procedure might result in local values for the trial density that exceed the admissible interval, i.e., it might be that $\rho _\text {t}^{(k)}>1$ for some elements ${(k)}$. We therefore perform a corrector step and set for each element ${{(e)}}$ the bounded $\rho ^{{(e)}}_\text {b}$ and unbounded $\rho ^{{(e)}}_\text {u}$ relative densities as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {if } \rho ^{{(e)}}_\text {t} \le \mathrm {tol}: \rho ^{{(e)}}_\text {b} = 0 , \quad \rho ^{{(e)}}_\text {u} = \rho ^{{(e)}}_\text {t} &{} \quad \text {(no local correction necessary)} \\ \text {if } \rho ^{{(e)}}_\text {t} > \mathrm {tol}: \rho ^{{(e)}}_\text {b} = \mathrm {tol} , \ \rho ^{{(e)}}_\text {u} = 0 &{} \quad \text {(local correction necessary)} \end{array}\right. } \end{aligned}$$

(53)

where $\text {tol}=0.999$ is chosen as maximum relative density for the numerical calculations presented later.

In a final step, the scaled relative density for the current time step can be found by combining the bounded values with the unbounded values, whereas the latter are weighted to the structure volume that remains after subtraction of the structure volume of all elements that contain locally the maximum value for the relative density, i.e., $\rho ^{{(e)}}_\text {b}=\text {tol}$, thus

$$\begin{aligned} \rho _{n+1}^{{(e)}}= \rho _\text {b}^{{(e)}}+ \frac{\sum _{k}{\bar{\rho }} \ \Omega ^{(k)}- \sum _k \rho ^{(k)}_\text {b} \Omega ^{(k)}}{\sum _k \rho ^{(k)}_\text {u} \Omega ^{(k)}} \rho _\text {u}^{{(e)}}\ . \end{aligned}$$

(54)

This procedure ensures that both constraints, prescribed total structure volume and admissible bounds, are fulfilled by the scaled relative density $\rho _{n+1}^{{(e)}}$. A summary of the scaling process is given in Algorithm 1.

Before closing this section regarding the time integration and update scheme of the density variable, let us present the discretized form of the driving forces. They read locally for each element ${{(e)}}$

$$\begin{aligned} p^{{(e)}}_n = -3 (\rho _n^{{(e)}})^2 \rho _n^{{{(e)}}\,\prime } \; {\bar{\Psi }}_{0,n+1}^{{(e)}}\ . \end{aligned}$$

(55)

Note that only one value for the density variable is used per finite element. Therefore, we make use of an averaged value for the free energy density which is given by

$$\begin{aligned} {\bar{\Psi }}_{0,n+1}^{{(e)}}:= \frac{1}{\Omega ^{{(e)}}} \int _{\Omega ^{{(e)}}} \Psi _{0,n+1} \ \mathrm {d}V \ . \end{aligned}$$

(56)

Then, Eq. (49) is written in short form as

$$\begin{aligned} {{\tilde{\chi }}}^{{(e)}}_{n+1} = \chi ^{{(e)}}_n + \frac{\Delta t}{\eta } \tau ^{{(e)}}_n \end{aligned}$$

(57)

with the total driving force

$$\begin{aligned} \tau ^{{(e)}}_n := -{\bar{p}}^{{(e)}}_n + \beta \rho ^{{{(e)}}\,\prime }_n \mathop {}\!\mathbin \bigtriangleup \rho ^{{(e)}}_n + \lambda _n \rho ^{{{(e)}}\,\prime }_n \ . \end{aligned}$$

(58)

Fig. 1

Flowchart for the proposed method

Remark

The choice of the time increment $\Delta t$ in combination with the viscosity $\eta$ controls the convergence speed. The time increment, on the other hand, also controls the load increment. Due to the inherent non-linearities in the context of finite deformations, the maximum load has to be applied within several time steps whose increments have to be limited. Therefore, the time increment cannot be chosen arbitrarily. The choice of $\eta$ thus dominates the convergence speed of the density field. Obviously, smaller values increase this speed whereas larger values decrease the convergence velocity. It is thus advantageous to use small values for $\eta$. However, small values can cause instabilities which is well-known from the Neumann stability condition, e.g. for the transient heat conduction equation that has a similar mathematical structure as our model when non-linearities are neglected. We thus adapt the strategy in [17] and evaluate (57) $n_\text {loop}$ times with modified viscosity, i.e., the effective velocity is $n_\text {loop}\eta$. Then, the value of $\eta$ can be chosen relatively small which results in a small number of time steps until the optimal structure has been found. In case of instabilities, the value for $\eta$ does not have to be modified whereas just the value of $n_\text {loop}$ can be increased. Of course, this demands an evaluation of the update for the density variable more often. However, this procedure is computationally very cheap, particularly as compared to the update for the displacement field. It is thus advantageous to increase $n_\text {loop}$ while keeping the time increment $\Delta t$ and thus the number of necessary updates of the displacement field fixated. The final update scheme for the density variable $\chi$ and the relative density $\rho$ is presented in Algorithm 2.

Remark

The optimal topology has been found when no further update is performed from one iteration step to the next one. This can be expressed by ${\dot{\chi }}=0 \ \forall \varvec{x}\in \Omega$. Inserting this relation directly into (31)$_2$ removes the transient term and gives a partial differential equation that only includes spatial derivatives. A solution of this reduced equation would result in the optimal topology without the need of an update scheme in time. However, numerical investigations show that attempts to directly solving the reduced equation fail due to severe numerical instabilities. As a consequence, the time-dependent term adds a viscous contribution and allows for an evolutionary solution scheme which converges smoothly. A—preferably mathematical—analysis why a direct solution is not obtainable is highly appreciated.

4.4 Combined update of the displacement and density field

The update of the density field is given in terms of a transient partial differential equation. Thus, each update step corresponds to a time step during which the boundary conditions of the boundary value problem may change. Due to the explicit Euler integration for the density field, the displacement field can be solved in standard manner, i.e., no additional nodal unknowns enter the finite element procedure.

Furthermore, the computation of the stress for the residual and the material derivative for the tangent is evaluated with the elementwise discretized relative density; then, the system of non-linear algebraic equations for the displacement field can be solved without taking adaptions of the density field into account. The entire procedure can be interpreted—when the boundary conditions are fixated—as staggered approach to solve both field equations for the displacements and the relative density. The algorithmic procedure can be equipped with an exit criterion based on the energy ${\mathcal {S}}:=\varvec{r}^\star {\hat{\varvec{u}}}^\star$ stored in the boundary with prescribed displacements, with the reaction forces $\varvec{r}^\star$ at the nodes with prescribed displacements ${\hat{\varvec{u}}}^\star \not \in {\varvec{0}}$: if the increment of stored energy between two time steps is below some tolerance, the solution is converged. The amount of stored energy ${\mathcal {S}}$ is, as usual, identified as measure for the stiffness of the structure. A flowchart of the numerical treatment is presented in Fig. 1.

Table 1 Model parameters for the MBB beam

5 Numerical analysis of proposed approach

5.1 Specification of the considered material model

The method presented here can be used for arbitrary hyperelastic structures, i.e., arbitrary ansatzes for the strain energy density can be used for the presented generalized approach to thermodynamic topology optimization. However, in order to ensure minimizers of the potential energy and to automatically guarantee material stability [35], polyconvex strain energy densities in the sense of [2] should be considered. Extensions to anisotropic materials are found in e.g., [3, 34, 36]. Postponing more complex materials to future investigations, we concentrate on isotropic materials and make use of the polyconvex Neo–Hooke energy in the current work. This choice for the material model ensures that all non-linearities are due to finite deformations and do not route back to material non-linearities. This simplifies comparison of the results to those obtained for a small-deformation setting. The free energy density is thus chosen as

$$\begin{aligned} \Psi _0(I_1, J) = \frac{1}{2} \mu (I_1-3) + \frac{\lambda }{4} (J^2-1) - \frac{\lambda }{2} \ln [J] - \mu \ln [J] \nonumber \\ \end{aligned}$$

(59)

where $I_1=\mathrm {tr}[\varvec{C}]$, $J=\det [\varvec{F}]$, $\lambda = E \nu (1-\nu -2\nu ^2)^{-1}$, and $\mu =E(2+2\nu )^{-1}$ with Young’s modulus E and Poisson’s ratio $\nu$, cf. e.g., [48]. The 2nd Piola–Kirchhoff stress tensor $\varvec{S}$ is then given in tensor form by

$$\begin{aligned} \varvec{S}= & {} 2\frac{\partial \Psi }{\partial \varvec{C}} = 2\rho ^3\frac{\partial \Psi _0}{\partial \varvec{C}} = \rho ^3\left[ \mu \frac{\partial I_1}{\partial \varvec{C}} \right. \nonumber \\&\left. + \lambda J \frac{\partial J}{\partial \varvec{C}} - \lambda J^{-1} \frac{\partial J}{\partial \varvec{C}} - 2 \mu J^{-1} \frac{\partial J}{\partial \varvec{C}} \right] \end{aligned}$$

(60)

which can be transformed by aid of Jacobi’s formula and the identity matrix $\varvec{I}$ to

$$\begin{aligned} \varvec{S}= \rho ^3 \left[ \frac{\lambda }{2} (J^2 - 1) \varvec{C}^{-1}+ \mu (\varvec{I}- \varvec{C}^{-1}) \right] \ . \end{aligned}$$

(61)

The derivative of the 2nd Piola–Kirchhoff stress tensor is then given in component form by

$$\begin{aligned} E_{ijxy}=4\frac{\partial ^2\Psi }{\partial C_{ij}\partial C_{xy}}=2\frac{\partial S_{ij}}{\partial C_{xy}} =k_1 C^{-1}_{ij} C^{-1}_{xy} - k_2 C_{ix}^{-1}C_{jy}^{-1} \ .\nonumber \\ \end{aligned}$$

(62)

with $k_1=\rho ^3\lambda J^2$ and $k_2=\rho ^3[\lambda (J^2-1)-2\mu ]$. The associated matrix representation of the material tangent $\varvec{E}$ is given in Appendix C.

Fig. 2

Dimensions, boundary conditions and symmetry plane for the MBB beam

5.2 Preliminaries to the simulation results

We present numerical results for two different boundary value problems: the classical benchmark problem given by the Messerschmitt–Bölkow–Blohm (MBB) beam and a complex cantilever problem that demonstrates the behavior of the optimization model for a truly three-dimensional problem. The material parameters, e.g., Young’s modulus and Poisson’s ratio of the full material, are the same for all computations. The energy scales proportionally with the Young’s modulus for which we can follow the usual choice in topology optimization and set $E=1$ MPa. Since we are interested to optimize structures that behave hyperelastically, e.g. polymers or rubber, we set $\nu =0.45$. All simulations are obtained by an implementation of the model into FEAP [10] where we used tri-linear hexahedral finite elements.

Table 2 Finite element meshes for the MBB beam: dimensions (length/height/thickness in mm) and number of subdivisions

Fig. 3

MBB beam: optimized structures for tension (top) and compression loading (bottom) in the deformed configuration. Center: comparison of the optimized structures for compression (left) and tension loading (right)

We emphasize that no amplification of the deformed configuration of the structures has been performed, i.e., the shown deformed structures represent the true deformation state. The structures are all obtained by using the isovolume filter for the relative density $\rho$ in Paraview [1] where the minimum threshold is set to 0.5 if not stated differently; this is the average value between void and full material in a structured finite element mesh. This implies that full material is assumed everywhere where the threshold is exceeded and otherwise void material is obtained. Furthermore, all simulations, except of the arc-length controlled simulations, are performed for prescribed displacements which facilitates the generation of comparative numerical results.

5.3 Messerschmitt–Bölkow–Blohm (MBB) beam

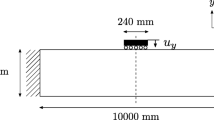
All necessary data regarding mesh information and model parameters are given for the MBB beam in Table 1. The dimensions, boundary conditions and symmetry plane are plotted in Fig. 2. All simulations are performed for thick, three-dimensional computations. The thickness is given in Table 2.

5.3.1 Displacement-controlled simulations

As first example, we compute the MBB beam with a maximum displacement of $u_\text {max}^\star =0.25$ mm, prescribed at the top center point of the beam. The structure resulting from the topology optimization is depicted in the deformed state at top of Fig. 3. The resultant structure is quite similar to classical optimization results for linear elastic structures: there are no dramatic differences between the results obtained for the linearized and the finite theory. Although the deflection is already quite large (25% of the height), the deformations are not large enough to trigger a distinct tension–compression asymmetry of the optimized structures. However, the chosen Neo–Hookean energy for the hyperelastic materials includes non-quadratic terms. It thus might be expected that a different result for the MBB beam is present when the displacement is pointing in opposite direction, which would be differing to the results from the linearized strain framework. This difference results from a tension-compression asymmetry in the considered material response. We therefore present the result for $u_\text {max}^\star =-0.25$ mm at bottom of Fig. 3. However, the differences between the two loading states are limited. This observation is also supported by the centered picture in Fig. 3: here, the optimized result in reference configuration for $u_\text {max}^\star =-0.25$ mm is given at the left-hand side. On the right hand side, the result for $u_\text {max}^\star =0.25$ mm is given. Only small deviations are present. As already indicated in the theoretical derivation, cf. (20), the gradient enhancement ensures that the model is well-posed if the parameter $\beta$ is sufficiently large for a specific element size, i.e., no checkerboard should be present and numerical results should be independent of the respective finite element mesh. To investigate this point, the result for the MBB beam is presented using two different meshes in Fig. 4: at the left-hand side, a coarse mesh is used with 2562 nodes that form 1200 elements; at the right-hand side, a fine mesh is employed with 15,402 nodes that form 7500 elements; both the side view and an isometric perspective are presented. Here, cubic elements are used, i.e., the element length is identical for all three spatial directions. However, for both quasi-2D results, only one row of finite elements is used. Therefore, the boundary value problems differ in thickness. As can be seen from Fig. 4, the optimal structure is identical, though. This shows that (1) the thickness does not influence the result, i.e., the MBB beam is indeed a two-dimensional problem, and (2) the results are mesh-independent. In Fig. 5, the influence of the regularization parameter $\beta$ is investigated for the MBB beam for tension loading with $u^\star _\text {max}=0.25$ mm. The values are $\beta =0.01~\hbox {MPa mm}^2$ (left) and $\beta =0.08~\hbox {MPa mm}^2$ (right), respectively. The fine finite element mesh with 7500 elements has been used. It is obvious that the choice of $\beta$ influences two aspects: (1) the minimal member size, i.e., the minimum truss thickness, and (2) the transition between void and full material distribution. Whereas thin members with a steep gradient of the relative density result for a small value of $\beta =0.01$ MPa mm$^2$ (left), thick members with a smooth gradient result for a large value of $\beta =0.08$ MPa mm$^2$ (right). Finally, we investigate the influence of the initial distribution of the relative density $\rho _0$ on the final result of the topology optimization. To this end, we present in Fig. 6 results for four inhomogeneous initial distributions of the initial relative density: the initial value for the density is set for the lower vertical half of the design space to $\rho _0=\rho _{0,\text {inhom}} \forall \varvec{x}| y \le 0.5$ mm and to $\rho _0={\bar{\rho }}-\rho _{0,\text {inhom}} \forall \varvec{x}| y > 0.5$ mm for the upper vertical half of the design space such that $\int _\Omega \rho _{0}\mathrm {d} V={\bar{\rho }}$ holds. The homogeneous initial condition corresponds to $\rho _{0,\text {inhom}}=0.5{\bar{\rho }}$. The numerical experiments reveal that the impact of an inhomogeneous inital distribution is small even for distinctly inhomogeneous initial distributions ($\rho _{0,\text {inhom}}=0.825{\bar{\rho }})$. However, for even larger values, i.e., $\rho _{0,\text {inhom}}=0.850{\bar{\rho }}$, remarkable different structures are obtained, see lower line in Fig. 6. The maximum stiffnesses after convergence of the respective optimized structures are ${\mathcal {S}}_\text {max}(\rho _{0,\text {inhom}}=0.800{{\bar{\rho }}})=1.56\times 10^{-5}$ Nmm, ${\mathcal {S}}_\text {max}(\rho _{0,\text {inhom}}=0.825{{\bar{\rho }}})=1.53\times 10^{-5}$ Nmm, ${\mathcal {S}}_\text {max}(\rho _{0,\text {inhom}}=0.850{{\bar{\rho }}})=1.27\times 10^{-5}$ Nmm, and ${\mathcal {S}}_\text {max}(\rho _{0,\text {inhom}}=0.900{{\bar{\rho }}})=0.91\times 10^{-5}$ Nmm. These results are computed using the coarse finite element mesh with 1200 elements for which the stiffness of the optimized topology with homogeneous initial condition is ${\mathcal {S}}_\text {max}(\rho _{0}={{\bar{\rho }}})=1.60\times 10^{-5}$ Nmm. This indicates that the homogeneously gray initial distribution for the relative density provides, at least for this example, best results since here ${\mathcal {S}}_\text {max}$ reaches its highest value. This can be explained since the evolutionary character of the topology update does not ensure that the global minimum is found; in contrast, once stuck in a local minimum, the method is not capable of finding lower minima which is demonstrated by the results with remarkably different topology in Fig. 6.

Fig. 4

MBB beam: comparison of two different finite element discretizations. Left: 1200 elements with 2562 nodes; right: 7500 elements with 15,402 nodes

Fig. 5

MBB beam: investigation of the influence of the regularization parameter $\beta$ for tension loading with $u^\star _\text {max}=0.25$ mm. Left: result for $\beta =0.01$ MPa mm$^2$; right: result for $\beta =0.08$ MPa mm$^2$. The fine finite element mesh with 7500 elements has been used

Fig. 6

MBB beam: investigation of the influence of the initial distribution of the relative density $\rho _0$ from which the initial $\chi _0$ is computed. In all cases, we assign $\rho _0=\rho _{0,\text {inhom}} \forall \varvec{x}| y \le 0.5$ mm and $\rho _0={\bar{\rho }}-\rho _{0,\text {inhom}} \forall \varvec{x}| y > 0.5$ mm, respectively

5.3.2 Performance analysis

Let us investigate the performance of the novel variational approach to topology optimization in this paragraph. To be more precise, we present here the numerical effort and the stiffness measured in terms of the stored energy. All simulations were performed on a system consisting of 40 Intel Xeon CPUs with 2.20 GHz and 64 GB memory. Minimal parallelization was only applied for solving the non-linear system of algebraic equations for the displacements using 4 cores; to be more precise, assembling and updating the density field was performed without any parallelization. On purporse, we did not use more cores or apply a parallel assembling in order to show the efficiency of the method enabling it to be used on standard computers. Exemplarily, we present the computation times for the MBB beam under compression. Here, the simulation of 300 time steps with $n_\text {loop}=8$ needed approximately 700 sec for completion. This number includes the computation of the matrices $\varvec{l}^{{(e)}}$ for all finite elements prior to the optimization process. Furthermore, for each time step, the results were written to the hard drive disk as vtk file each of which has a size of 4.4 MB; this effort is also included in the 700 sec. The consumption of computation time of the optimization algorithm is negligible to the time needed for convergence of the displacement field: doubling of the number of updates of the density variable, i.e., doubling the number of updates of the density field by setting $n_\text {loop}=16$ increased the total simulation time to 709 sec which is an increase of less than $1.3\%$. Keeping in mind that parallelization was not excessively used, the computation effort demonstrates that our novel approach to topology optimization is indeed quite fast. This impression is confirmed by comparing our results to other approaches: [22] report 3–5 finite element iteration steps for convergence. In all numerical examples we present, 3 iteration steps were necessary during loading; this number reduced to 2 when the maximum load was kept constant. Furthermore, we can conclude from the presented computation times that a purely elastic computation without optimization would need around 690 s. Thus, the additional time effort for the optimization (between 10 and 20 s in total) is very limited and the finite element computation of the displacement field is the expensive part. Same observation has been made by [22]. Summarizing, our presented approach for topology optimization of hyperelastic structures can compete with other approaches. A same statement could be drawn for the linear version of thermodynamic topology optimization, cf. [19].

The number of iterations varied between three, when the prescribed load continues to increase, and two, when the boundary conditions do not change anymore. This shows empirically that the novel approach to topology optimization does not alter the number of Newton iterations.

Fig. 7

Evolution of the stiffness for the MBB beam problem using the fine finite element mesh. Left: compression loading; right: tension loading. The plots are scaled to the maximum value which is $5.38\times 10^{-6}$ Nmm (left) and $6.14\times 10^{-6}$ Nmm (right)

As can be seen from Fig. 7, the stored energy evolves quite similarly for both loading cases: at the left-hand side, the stored energy of the MBB beam for the tension cases is plotted over time; at the right-hand side, the stored energy for the compression loading is depicted. The final values differ to some extent since the structure for tension stores approximately 14.1% more energy. Furthermore, a distinct kink in the graph can be observed at time step $n=50$: this results from the load that is linearly ramped up within the first 50 time steps. After 100 time steps, i.e., 50 time steps after the maximum load has been applied, no remarkable increase in stiffness is present. Consequently, it can be concluded that basically 50 iteration steps are needed for convergence of the pure topology optimization algorithm which is comparable to the computation effort for the MBB beam for both thermodynamic topology optimization and SIMP approaches for linear elastic structures, [19]. Figure 7 furthermore reveals that the stored energy which also serves as measure of the structure’s stiffness increases monotonically. This is of particular interest since we did not formulate an appropriate goal function (directly): this result empirically shows that the novel approach to thermodynamic topology optimization as given in (12) appears to indeed give structures with optimized stiffness.

Fig. 8

MBB beam with the last converged time step with a current tension load of $u^\star =0.358$ mm. Contour plot of the relative density $\rho$ with finite element mesh at the left-hand side and the extracted isovolume at the right hand side. Severe buckling in the horizontal compression bar is present

5.3.3 Arc-length-controlled simulations for the MBB beam

Although a prescribed deformation of $|u_\text {max}^\star |=0.25$ mm yields results with already large deflections which lie outside the validity of the linearized theory, our goal is to study the behavior of the model for even larger deformations. We thus increase the maximum displacement further. However, here it might happen that the Newton iteration for computing the displacement field is terminated if the determinant of the deformation gradient becomes negative. This is, of course, an unphysical result whose origin can be investigated from Fig. 8.

At the left-hand side of Fig. 8, the deformed mesh including the spatial distribution of $\rho$ is presented, and the extracted structure is given at the right-hand side. This result corresponds to the last time step that has converged; during the next time step, the Newton scheme was terminated due to $\det [\varvec{F}]<0$. Inspection of Fig. 8 reveals that the physical reason for the termination of the Newton scheme is the buckling of the outer lower bar. Due to its horizontal orientation, mainly compression loads are present that exceed at some point the critical load for buckling. Consequently, a snap-through problem is present which is known to constitute an ill-posed problem when no numerical control schemes are applied, see also the review paper [28].

Fig. 9

Zoomed plot of the deformed contour plot of the last converged time step from Fig. 8 in isometric perspective. Distinct deformations of the finite element with void material in the vicinity of the inner edge of the outer triangle truss section are present

In principal, it cannot be estimated in advance in which element the error of a negative determinant of $\varvec{F}$ will be present. To be more precise, the problem can both arise in elements with full or void material. In the exemplarily shown problem in Fig. 8, a void element is deformed in an unphysical way. This is more obvious by the isometric zoom of the deformed mesh in Fig. 9: the deformation forces the elements to become over-distorted which is mathematically expressed by $\det [\varvec{F}]<0$. Since buckling phenomena are accompanied by localization effects, it is appreciated to resolve these spatial areas with higher accuracy, i.e., remove possible mesh-sensitivities. Unfortunately, the spatial regions with buckling cannot be anticipated for problems of topology optimization (simply because the topology, which includes severe jumps of coefficients due to the distribution of relative density, is unknown in advance). This issue could be resolved in a most elegant and efficient manner when mesh adaptations are performed during the computation as presented, e.g., in [43] for thermodynamic topology optimization. This aspect, however, is beyond the scope of the current work. To still analyze the model behavior for extreme deformations, we thus apply the arc-length control which is a built-in function in FEAP. Here, it is possible to control neither force or displacement; in contrast, only the increment of both can be controlled. In FEAP, the increment is given in terms of the time increment $\Delta t$ which hence looses its physical interpretation. However, to avoid modifications in the numerical implementation of the model, we still use the same parameter $\Delta t$ and adapt the viscosity $\eta$. Since we are using a different finite element mesh, the value of $n_\text {loop}$ is also adapted, see Tables 1 and 2.

Fig. 10

MBB beam with arc-length control, tension loading, at various time steps. Undeformed design space is printed in gray. Deformed configurations in side view and and isometric perspective

The arc-length control continues to increase the increment of forces and displacements, i.e., the loading increases throughout the entire simulation process. Then, of course, we cannot expect the model to converge in the sense that the topology will not change anymore. However, this problem is also present in comparable form, e.g., for classical SIMP approaches where it manifests by trusses that continue to slowly move and slightly adapt the angle for the MBB beam.

The result for the model for the MBB beam under tension loading with arc-length control is given in Fig. 10 for the time steps $n=\{400,2000,6000,9000\}$ with respective maximum deflections of $u_\text {max}=\{0.007, 0.087, 0.588, 0.923 \}$ mm. Note that here again the deformed structures are depicted. Since the arc-length scheme in FEAP uses the time increment $\Delta t$ as control parameter, very small values for $\Delta t$ have to be chosen even for a purely linear elastic computation without any optimization. Therefore, it takes much more time steps for pursuing the computation. A future implementation of our model into a finite element program with combined arc-length and time step control is hence feasible. However, we see that after 400 load steps the maximum deflection is quite small and the ”classical“ optimal MBB structure has developed, cf. Fig. 10 (top left).

After 2000 time steps, remarkable modifications in the topology are present which are in agreement to severe buckling effects in thickness direction, see Fig. 10 (top right). Increasing the load steps further, results in a complete remodeling of the topology, cf. time step $n=6000$ in Fig. 10 (bottom left). This topology does not change anymore. However, very large deformations in z-direction are present as presented for the time step $n=9000$ in Fig. 10 (bottom right).

Fig. 11

MBB beam with arc-length control, compression loading, at various time steps. Undeformed design space is printed in gray. Deformed configurations in side view and and isometric perspective

Table 3 Model parameters for the 3D cantilever beam

Figure 11 shows the result for the arc-length control for compression loading. Here, we present the results for the time steps $n=\{200,1000,2000,8000\}$ and respective maximum deflections of $u_\text {max}=\{-0.021, -0.045, -0.171, -1.200 \}$mm. In general, similar effects are present as for the case of tension loading: in the beginning, the optimal topology is comparable to the classical MBB beam result, see the result for $n=200$ in Fig. 11 (top left). As for the tension loading, buckling of the topology is present at larger deformation states, however, at different locations, cf. time step $n=1000$ in Fig. 11 (top right). The buckling, which also increases for increased time steps, triggers remarkable remodeling. After the minor modifications that are already present for $n=1000$ in Fig. 11 (top right), more distinct remodeling is observed for later time steps: evolving through intermediate states, cf. time step $n=2000$ in Fig. 11 (bottom left), the topology continues to adapt to the severe deformations as presented for time step $n=8000$ in Fig. 11 (bottom right). As for the case of positive prescribed displacements, severe buckling is observed which serves as beads that affect the stiffness of the structure.

Concluding, the presented optimization model possesses a high level of numerical stability which allows to compute and remodel structures for severe finite deformations even undergoing buckling.

5.4 3D cantilever

5.4.1 Displacement-controlled simulations for the 3D cantilever

After analyzing the model for the classical MBB beam benchmark problem, the model is now applied to the complex boundary value problem of a cantilever that is indeed three-dimensional. Again, we present results for displacement-controlled boundary conditions which simplifies the investigation of the model for different maximum loads. The maximum displacement is applied within the first 50 time steps of modeling time for all results discussed here. All model parameters are collected in Table 3. The dimensions, boundary conditions and symmetry plane are presented in Fig. 12. The mesh consists of 32,307 nodes and 28,160 tri-linear, hexahedral elements.

Fig. 12

Dimensions, boundary conditions and symmetry plane for the 3D cantilever

Fig. 13

3D cantilever problem, “tension” load case: evolving optimal structures at discrete time steps ($n=\{200,1200,2000\}$, respectively) and for varying maximum prescribed displacements

As first example, the prescribed displacement is positive, thus inducing “tension” loading. Figure 13 shows the resulting structures in the reference configuration for various time steps and for different maximum displacement. To be more precise, the maximum displacement takes values in $u_\text {max}^\star =\{0.4,0.8,2.0\}$ mm. After 200 time steps, the resultant topologies have a comparable shape for all different maximum displacements (first row in Fig. 13). However, the structures continue to evolve in time and the final design is given approximately at $n=1200$, cf. second row in Fig. 13. Only minor modifications are observed when time continues as can be seen in the last row in Fig. 13. The deformed configurations of the topologies at $n=2000$ are given in side view and in isometric perspective in Fig. 14. In this example, the effect of the anisotropic character of the $\log$ term in the strain energy density is clearly visible: for moderate loading, i.e. $u_\text {max}^\star =0.4$ mm, strong bending moments are present in the deformed state, see Fig. 14 at the left-hand side. To compensate this, the arc-like structure is established. For higher loading, i.e. $u_\text {max}=0.8$ mm, smaller bending moments are present in the deformed configuration, cf. center column in Fig. 14. Thus, the arc-like structure is thinner but occupies larger dimensions. Increasing the maximum load to be five times the reference maximum displacement, no bending moments at all are present. Consequently, the optimal structure is a “tension sheet” as can be seen in Fig. 14 at the right-hand side.

Fig. 14

3D cantilever problem, “tension” load case: deformed configuration of the respective optimal structures for $n=2000$. Side view above, isometric view below

Remark

Optimizing hyperelastic structures undergoing large deformations may result for sufficiently large loads in structures that cover a deformed configuration that exceeds the design space $\Omega$, cf. Fig. 14. This would be in line with topology optimization problems where the limitations regarding the design space are governed by the manufacturing process rather than the operation status. Enforcing optimal structures that lie within $\Omega$ also in the deformed configuration demands more sophisticated constraints than the ones used here. Furthermore, in this case prescribed deformations have to be limited such that the constraint is even possible to achieve, i.e., a deformation of $u_\text {max}^\star =2.0$ mm as employed in Fig. 14 already violates the constraint. The maximum admissible displacement that fulfills this constraint would be $u_\text {max}^\star =1.0$ mm, cf. the geometric dimensions of the boundary value problem as depicted in Fig. 12.

Fig. 15

Evolution of the stored energy for a maximum displacement of $u_\text {max}^\star =0.4$ mm (left), $u_\text {max}^\star =0.8$ mm (center), $u_\text {max}^\star =2.0$ mm (right) over time. The plots are scaled to their respective maximum values which are $2.46\times 10^{-5}$ Nmm, $6.22\times 10^{-4}$ Nmm, and $5.87\times 10^{-3}$ Nmm

The stored energies over time are plotted in Fig. 15. Interestingly, the convergence rate increases for higher loading. Due to the nonlinearities in the energy, the fractions are 1 : 25.28 : 238.62 for the maximum displacements of $u_\text {max}^\star =\{0.4,0.8,2.0\}$ mm, respectively.

Fig. 16

3D cantilever problem, “compression” load case: evolving optimal structures for for different time steps, i.e. $n=\{200,1200,200\}$

As final example, we present in Fig. 16 the evolution of the optimal topology when the maximum displacement is pointing downwards, thus implying a “compression” load case. The character of the evolution of the structure shares some similarities to that for the tension load case: only minor deviations are observable at $n=200$, cf. left-hand side in Fig. 16. However, the optimal structure that has evolved after 1200 time steps (center in Fig. 16) possesses a remarkably different shape than the structures for the tension load case and reminds of optimal structures for linear elasticity. Almost no modifications are visible when time continues, cf. $n=2000$ at the right-hand side in Fig. 16. Finally, the deformed configurations are presented in Fig. 17 and the evolution of the stored energy in Fig. 18.

Fig. 17

3D cantilever problem, “compression” load case: deformed configuration of the optimal structures for $n=2000$. Side view at the left-hand side, isometric view at the right-hand side

Fig. 18

3D cantilever problem, “compression” load case: evolution of stored energy over time. The plot is scaled to its maximum value ${\mathcal {S}}_\text {max}=6.76\times 10^{-5}$ Nmm

5.4.2 Arc-length control simulations for the 3D cantilever problem

Concluding, we also apply the arc-length control to the 3D cantilever. The model parameters are given in Table 3. The results are given in the undeformed configuration in Fig. 19, and those in the deformed configuration are given for the “tension” load case in Fig. 20 and for the “compression” load case in Fig. 21, respectively. Here, again, the boundary conditions have to be provided by traction forces to apply arc-length control in FEAP. Accordingly, displacements in all three spacial directions are possible. These modifications in the boundary conditions lead to different optimal structures than for the examples presented above.

Fig. 19

3D cantilever problem, arc-length control, undeformed configurations: “tension” load case (left) and “compression” load case (right) in different perspectives, minimum value for the iso-volume filter 0.33

The results represent the last load steps that converged with a minimum value for the iso-volume filter of 0.33. Interestingly, here much faster evolution can be observed as for the MBB beam: maximum possible deformations are reached for $n=771$ and $n=1024$, respectively. As can be seen from Figs. 20 and 21, strong bending and buckling is present. This is, of course, associated by severe mesh distortion such that the error for termination is, again, a negative determinant of the deformation gradient. To avoid this, a remeshing would be a suitable strategy. Additionally, possible self-contact has to be taken into account. However, for the current investigation, we emphasize that the model for thermodynamic topology optimization is robust enough to compute structures with extreme deformations including buckling.

Fig. 20

3D cantilever problem, “tension” load case, arc-length control: deformed configuration of the optimal structures for $n=771$ in different perspectives, minimum value for the iso-volume filter 0.33

Fig. 21

3D cantilever problem, “compression” load case, arc-length control: deformed configuration of the optimal structures for $n=1024$ in different perspectives, minimum value for the iso-volume filter 0.33

6 Conclusions

We presented a novel approach to thermodynamic topology optimization that is valid for hyperelastic structures, but in principle also applicable to linear elastic structures. This approach does not need to make use of the strain energy density expressed in stress measures. In contrast, the usual definition in terms of strains or the right Cauchy-Green tensor can be applied. Regularization is employed by introducing a gradient enhancement of the energy which yields mesh-independent finite element results; no checkerboarding is present. Furthermore, including a sigmoid function for the description of relative density allows for an analytical computation of the Lagrange parameter that accounts for mass conservation. An algorithmic treatment is presented enabling a straightforward numerical implementation. For the case of Neo–Hookean structures, numerical results for two boundary value problems are investigated. Moderate loading of the MBB beam gives structures that resemble to those obtained for linear-elastic structures. Severe loading causes buckling effects that terminate the standard simulations. However, the model shows to be robust enough to be evaluated also when arc-length control is applied. In this case, the “standard” solution for the MBB beam is obtained for small loads. For higher loads, however, buckling is present which causes strong remodeling such that the later optimal structures possess a unique topology. It is emphasized that the approach for topoplogy optimization itself needs only a negligible amount of computation power. The total simulation time is dominated by the time needed for computation of the displacements, i.e., for the finite element method to converge. Furthermore, we compute thick, three-dimensional problems and show that the effect of tension/compression asymmetry is obvious in this case. Finally, we also see that optimizing for the deformed configuration leads to significantly different topologies and arc-length controlled simulations give access to optimized structures for complex and severe buckling in various spatial directions. It is thus inevitable to make use of optimization in the context of finite deformations if the loading of the final structure is not “small” for which the linearized theory can be applied.

Appendices

Derivation of the numerical discretization of weak form

For the derivation of the numerical discretization of the weak form of the balance of linear momentum, we first mention in (16)

$$\begin{aligned} \frac{1}{2} \delta \varvec{C}= \frac{1}{2} \frac{\partial \varvec{C}}{\partial \varvec{F}} \cdot \cdot \frac{\partial \varvec{F}}{\partial \varvec{u}} \delta \varvec{u}\ . \end{aligned}$$

(63)

Let us introduce the column matrix notation for the 2nd Piola–Kirchhoff tensor $\varvec{S}$ by

$$\begin{aligned} \varvec{s}:= \left( \begin{matrix} S_{11} \\ S_{22} \\ S_{33} \\ S_{12} \\ S_{23} \\ S_{13} \end{matrix} \right) \end{aligned}$$

(64)

and similarly the right Cauchy–Green tensor $\varvec{C}$ by

$$\begin{aligned} \varvec{c}:= & {} \left( \begin{matrix} C_{11} \\ C_{22} \\ C_{33} \\ 2 C_{12} \\ 2 C_{23} \\ 2 C_{13} \end{matrix}\right) = \left( \begin{matrix} F_{k1}F_{k1} \\ F_{k2}F_{k2} \\ F_{k3}F_{k3} \\ 2 F_{k1}F_{k2} \\ 2 F_{k2}F_{k3} \\ 2 F_{k1}F_{k3} \end{matrix}\right) \nonumber \\= & {} \left( \begin{matrix} F_{11}F_{11} + F_{21}F_{21} + F_{31}F_{31} \\ F_{12}F_{12} + F_{22}F_{22} + F_{32}F_{32} \\ F_{13}F_{13} + F_{23}F_{23} + F_{33}F_{33} \\ 2 F_{11}F_{12} + 2 F_{21}F_{22} + 2 F_{31}F_{32} \\ 2 F_{12}F_{13} + 2 F_{22}F_{23} + 2 F_{32}F_{33} \\ 2 F_{11}F_{13} + 2 F_{21}F_{23} + 2 F_{31}F_{33} \end{matrix}\right) \ . \end{aligned}$$

(65)

The matrix form of the deformation gradient $\varvec{F}$ can be defined by

$$\begin{aligned} \varvec{f}&:= \left( \begin{matrix} F_{11}&F_{22}&F_{33}&F_{12}&F_{23}&F_{13}&F_{21}&F_{32}&F_{31} \end{matrix}\right) ^\text {T} \nonumber \\&= \left( \begin{matrix} \displaystyle 1 + \frac{\partial u_1}{\partial X_1}&\displaystyle 1 + \frac{\partial u_2}{\partial X_2}&\displaystyle 1 + \frac{\partial u_3}{\partial X_3}&\displaystyle \frac{\partial u_1}{\partial X_2}&\displaystyle \frac{\partial u_2}{\partial X_3}&\displaystyle \frac{\partial u_1}{\partial X_3}&\displaystyle \frac{\partial u_2}{\partial X_1}&\displaystyle \frac{\partial u_3}{\partial X_2}&\displaystyle \frac{\partial u_3}{\partial X_1} \end{matrix}\right) ^\text {T} \nonumber \\&= \left( \begin{matrix} \displaystyle 1 + u_{1,1}&\displaystyle 1 + u_{2,2}&\displaystyle 1 + u_{3,3}&\displaystyle u_{1,2}&\displaystyle u_{2,3}&\displaystyle u_{1,3}&\displaystyle u_{2,1}&\displaystyle u_{3,2}&\displaystyle u_{3,1} \end{matrix}\right) ^\text {T} \ . \end{aligned}$$

(66)

Then, (63) is given in matrix notation for each finite element (e) by

$$\begin{aligned} \frac{1}{2} \delta \varvec{c}= \frac{1}{2} \frac{\partial \varvec{c}}{\partial \varvec{f}} \frac{\partial \varvec{f}}{\partial {{\hat{\varvec{u}}}}} \delta {{\hat{\varvec{u}}}} =: \varvec{B}_e \delta {\hat{\varvec{u}}}_e \end{aligned}$$

(67)

where we introduced the well-known $\varvec{B}_e$ operator matrix; the vector $\delta {\hat{\varvec{u}}}_e$ in (67) stores all of the three $\delta {\hat{\varvec{u}}}^{(k)}$ introduced in (33). Computing the derivatives

$$\begin{aligned} \left( \frac{\partial c_i}{\partial f_j}\right) = \left( \begin{matrix} 2F_{11} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 F_{21} &{} 0 &{} 2 F_{31} \\ 0 &{} 2 F_{22} &{} 0 &{} 2 F_{12} &{} 0 &{} 0 &{} 0 &{} 2 F_{32} &{} 0 \\ 0 &{} 0 &{} 2 F_{33} &{} 0 &{} 2F_{23} &{} 2 F_{13} &{} 0 &{} 0 &{} 0 \\ 2 F_{12} &{} 2 F_{21} &{} 0 &{} 2 F_{11} &{} 0 &{} 0 &{} 2 F_{22} &{} 2 F_{31} &{} 2 F_{32} \\ 0 &{} 2 F_{23} &{} 2 F_{32} &{} 2 F_{13} &{} 2 F_{22} &{} 2 F_{12} &{} 0 &{} 2 F_{33} &{} 0 \\ 2 F_{13} &{} 0 &{} 2 F_{31} &{} 0 &{} 2 F_{21} &{} 2 F_{11} &{} 2 F_{23} &{} 0 &{} 2 F_{33} \end{matrix}\right) \nonumber \\ \end{aligned}$$

(68)

and

$$\begin{aligned} \left( \frac{\partial f_j}{\partial {{\hat{u}}}_o^{{(k)}}}\right) = \left( \begin{matrix} N_{o,1} &{} 0 &{} 0 \\ 0 &{} N_{o,2} &{} 0 \\ 0 &{} 0 &{} N_{o,3} \\ N_{o,2} &{} 0 &{} 0 \\ 0 &{} N_{o,3} &{} 0 \\ N_{o,3} &{} 0 &{} 0 \\ 0 &{} N_{o,1} &{} 0 \\ 0 &{} 0 &{} N_{o,2} \\ 0 &{} 0 &{} N_{o,1} \end{matrix}\right) \ , \end{aligned}$$

(69)

the $\varvec{B}_e$ matrix in (67) can be constructed from the submatrices

$$\begin{aligned} \varvec{B}^{{(o)}}_e = \left( \begin{matrix} F_{11} N_{o,1} &{} F_{21} N_{o,1} &{} F_{31} N_{o,1} \\ F_{12} N_{o,2} &{} F_{22} N_{o,2} &{} F_{32} N_{o,2} \\ F_{13} N_{o,3} &{} F_{23} N_{o,3} &{} F_{33} N_{o,3} \\ F_{12} N_{o,1} + F_{11} N_{o,2} &{} F_{21} N_{o,2} + F_{22} N_{o,1} &{} F_{31} N_{o,2} + F_{32} N_{o,1} \\ F_{13} N_{o,2} + F_{12} N_{o,3} &{} F_{23} N_{o,2} + F_{22} N_{o,3} &{} F_{32} N_{o,3} + F_{33} N_{o,2} \\ F_{13} N_{o,1} + F_{11} N_{o,3} &{} F_{21} N_{o,3} + F_{23} N_{o,1} &{} F_{31} N_{o,3} + F_{33} N_{o,1} \end{matrix}\right) \nonumber \\ \end{aligned}$$

(70)

such that $\varvec{B}_e = (\varvec{B}^{{(o)}}_e)$.

Since $\varvec{S}:\delta \varvec{C}\equiv \varvec{s}\delta \varvec{c}$ by construction, the integral over a finite element (e) in the weak form of the linear momentum (16) can thus be approximated by

$$\begin{aligned} \int _{\Omega } \frac{1}{2}\varvec{S}: \delta \varvec{C}\ \mathrm {d}V= & {} \sum _e \int _{\Omega _e} \varvec{s}^\text {T}\frac{1}{2}\delta \varvec{c}\ \mathrm {d}V \nonumber \\= & {} \sum _e \delta {\hat{\varvec{u}}}_e^\text {T} \int _{\Omega _e} \varvec{B}_e^\text {T} \varvec{s}\ \mathrm {d}V \nonumber \\=: & {} \sum _e \delta {\hat{\varvec{u}}}_e^\text {T} \varvec{r}_e = \delta {\hat{\varvec{u}}}^\text {T}\varvec{r}\end{aligned}$$

(71)

with the residual vector for each element

$$\begin{aligned} \varvec{r}_e := \int _{\Omega _e} \varvec{B}_e^\text {T} \varvec{s}\ \mathrm {d}V \end{aligned}$$

(72)

and the global displacement vector $\delta {\hat{\varvec{u}}}:= \underset{e}{\cup } \delta {\hat{\varvec{u}}}_e$ and global residual vector $\varvec{r}$. This is exactly (34), see also [48].

Tangent for the Newton scheme

For the computation of the tangent

$$\begin{aligned} \frac{\mathrm {d}\varvec{r}_e}{\mathrm {d}{\hat{\varvec{u}}}_e} = \int _{\Omega _e} \varvec{B}_e^\text {T} \frac{\partial \varvec{s}}{\partial {\hat{\varvec{u}}}_e} \ \mathrm {d} V + \int _{\Omega _e} \frac{\partial \varvec{B}_e^\text {T}}{\partial {\hat{\varvec{u}}}_e} \varvec{s}\ \mathrm {d}V \ , \end{aligned}$$

(73)

we start with the investigation of the first integral which is the material tangent. It is given by

$$\begin{aligned} \frac{\partial \varvec{s}}{\partial {\hat{\varvec{u}}}_e} = \frac{\partial \varvec{s}}{\partial \varvec{c}} \frac{\partial \varvec{c}}{\partial \varvec{f}} \frac{\partial \varvec{f}}{\partial {\hat{\varvec{u}}}_e} = \varvec{E}\varvec{B}_e \end{aligned}$$

(74)

where we introduced the material stiffness $\varvec{E}:=2\partial \varvec{s}/\partial \varvec{c}=2\partial \varvec{s}/\partial \varvec{C}\cdot \cdot \partial \varvec{C}/\partial \varvec{c}$. The second integral is termed geometric tangent for which we compute

$$\begin{aligned} \frac{\partial \varvec{B}_e^\text {T}}{\partial {\hat{\varvec{u}}}_e} = \frac{\partial \varvec{B}_e^\text {T}}{\partial \varvec{f}} \frac{\partial \varvec{f}}{\partial {\hat{\varvec{u}}}_e} \ . \end{aligned}$$

(75)

Keeping in mind that $\varvec{s}$ remains fixed for this derivative, we find

$$\begin{aligned} \left( \frac{\partial (\varvec{B}^{{(k)}}_e)^\text {T} \varvec{s}}{\partial \varvec{f}}\right) ^\text {T}= \left( \begin{matrix} N_{k,1} s_1 + N_{k,2} s_4 + N_{k,3} s_6 &{} 0 &{} 0 \\ 0 &{} N_{k,2} s_2 + N_{k,1} s_4 + N_{k,3} s_5 &{} 0 \\ 0 &{} 0&{} N_{k,3} s_3 + N_{k,2} s_5 + N_{k,1} s_6 \\ N_{k,2} s_2 + N_{k,1} s_4 + N_{k,3} s_5 &{} 0 &{} 0 \\ 0 &{} N_{k,3} s_3 + N_{k,2} s_5 + N_{k,1} s_6 &{} 0 \\ N_{k,3} s_3 + N_{k,2} s_5 + N_{k,1} s_6 &{} 0 &{} 0 \\ 0 &{} N_{k,1} s_1 + N_{k,2} s_4 + N_{k,3} s_6 &{} 0 \\ 0 &{} 0 &{} N_{k,2} s_2 + N_{k,1} s_4 + N_{k,3} s_5 \\ 0 &{} 0 &{} N_{k,1} s_1 + N_{k,2} s_4 + N_{k,3} s_6 \end{matrix}\right) \end{aligned}$$

(76)

and by use of (69) we arrive at

$$\begin{aligned} \varvec{G}^{{(op)}}_e := \frac{\partial (\varvec{B}^{{(0)}}_e)^\text {T} \varvec{s}}{\partial \varvec{f}} \frac{\partial \varvec{f}}{\partial {\hat{\varvec{u}}}_e} = \left( \begin{matrix} k_3^{(op)} &{} 0 &{} 0 \\ 0 &{} k_3^{(op)} &{} 0 \\ 0 &{} 0 &{} k_3^{(op)} \end{matrix}\right) \end{aligned}$$

(77)

with

$$\begin{aligned} k_3^{(op)}= & {} N_{o,1}\left( N_{p,1} s_1 + N_{p,2} s_4 + N_{p,3} s_6\right) \nonumber \\&+ N_{o,2}\left( N_{p,2} s_2 + N_{p,1} s_4 + N_{p,3} s_5 \right) \nonumber \\&+ N_{o,3}\left( N_{p,3} s_3 + N_{p,2} s_5 + N_{p,1} s_6\right) \ . \end{aligned}$$

(78)

The geometric tangent for element (e) is obtained by assembling .

Component of the material stiffness

The components of the symmetric material stiffness $\varvec{E}$ are computed to be

$$\begin{aligned} E_{11}= & {} k_1 C^{-1}_{11} C^{-1}_{11} - k_2 C_{11}^{-1} C_{11}^{-1}\\ E_{21}= & {} k_1 C^{-1}_{22} C^{-1}_{11} - k_2 C_{21}^{-1} C_{21}^{-1} = E_{12} \\ E_{31}= & {} k_1 C^{-1}_{33} C^{-1}_{11} - k_2 C_{31}^{-1} C_{31}^{-1} = E_{13}\\ E_{41}= & {} k_1 C^{-1}_{12} C^{-1}_{11} - k_2 C_{11}^{-1} C_{21}^{-1} = E_{14}\\ E_{51}= & {} k_1 C^{-1}_{23} C^{-1}_{11} - k_2 C_{21}^{-1} C_{31}^{-1} = E_{15}\\ E_{61}= & {} k_1 C^{-1}_{13} C^{-1}_{11} - k_2 C_{11}^{-1} C_{31}^{-1} = E_{16} \\ E_{22}= & {} k_1 C^{-1}_{22} C^{-1}_{22} - k_2 C_{22}^{-1} C_{22}^{-1} \\ E_{32}= & {} k_1 C^{-1}_{33} C^{-1}_{22} - k_2 C_{32}^{-1} C_{32}^{-1} = E_{23}\\ E_{42}= & {} k_1 C^{-1}_{12} C^{-1}_{22} - k_2 C_{12}^{-1} C_{22}^{-1} = E_{24} \\ E_{52}= & {} k_1 C^{-1}_{23} C^{-1}_{22} - k_2 C_{22}^{-1} C_{32}^{-1} = E_{25}\\ E_{62}= & {} k_1 C^{-1}_{13} C^{-1}_{22} - k_2 C_{12}^{-1} C_{32}^{-1} = E_{26} \\ E_{33}= & {} k_1 C^{-1}_{33} C^{-1}_{33} - k_2 C_{33}^{-1} C_{33}^{-1} \\ E_{43}= & {} k_1 C^{-1}_{12} C^{-1}_{33} - k_2 C_{13}^{-1} C_{23}^{-1} = E_{34}\\ E_{53}= & {} k_1 C^{-1}_{23} C^{-1}_{33} - k_2 C_{23}^{-1} C_{33}^{-1} = E_{35}\\ E_{63}= & {} k_1 C^{-1}_{13} C^{-1}_{33} - k_2 C_{13}^{-1} C_{33}^{-1} = E_{36} \\ E_{44}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{12} C^{-1}_{12} - \frac{k_2}{2} C_{11}^{-1} C_{22}^{-1} \\ E_{54}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{23} C^{-1}_{12} - \frac{k_2}{2} C_{13}^{-1} C_{22}^{-1} = E_{45}\\ E_{64}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{13} C^{-1}_{12} - \frac{k_2}{2} C_{11}^{-1} C_{32}^{-1} = E_{46} \\ E_{55}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{23} C^{-1}_{23} - \frac{k_2}{2} C_{22}^{-1} C_{33}^{-1}\\ E_{65}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{13} C^{-1}_{23} - \frac{k_2}{2} C_{12}^{-1} C_{33}^{-1} = E_{56} \\ E_{66}= & {} \left( k_1-\frac{k_2}{2}\right) C^{-1}_{13} C^{-1}_{13} - \frac{k_2}{2} C_{11}^{-1} C_{33}^{-1} \end{aligned}$$

with the above introduced parameters $k_1=\rho ^3\lambda J^2$ and $k_2=\rho ^3[\lambda (J^2-1)-2\mu ]$.