Wavelet based reduced order models for microstructural analyses

Abstract

This paper proposes a novel method to accurately and efficiently reduce a microstructural mechanical model using a wavelet based discretisation. The model enriches a standard reduced order modelling (ROM) approach with a wavelet representation. Although the ROM approach reduces the dimensionality of the system of equations, the computational complexity of the integration of the weak form remains problematic. Using a sparse wavelet representation of the required integrands, the computational cost of the assembly of the system of equations is reduced significantly. This wavelet-reduced order model (W-ROM) is applied to the mechanical equilibrium of a microstructural volume as used in a computational homogenisation framework. The reduction technique however is not limited to micro-scale models and can also be applied to macroscopic problems to reduce the computational costs of the integration. For the sake of clarity, the W-ROM will be demonstrated using a one-dimensional example, providing full insight in the underlying steps taken.

1 Introduction

An increasing amount of engineering applications rely on materials with complex microstructures to achieve desired material properties that are tailored to the application [25]. Computational homogenisation provides an accurate and efficient framework to investigate the macroscopic properties arising from the microstructure using the Hill–Mandel conditions [22] to establish the scale transition. An overview of recent advances in computational homogenisation is presented by Geers et al. [16].

Advanced microstructural models enable the analysis of highly nonlinear materials, which are strongly path and history dependent. This naturally entails models necessitating the computation and storage of internal variables, so-called history variables. Such microstructural models become computationally demanding in terms of CPU-time and memory usage due to the large number of degrees of freedom and history variables involved. The complexity propagates from the array of microstructural models (to be solved repeatedly) to the considered macroscopic problem. The term FE${}^2$, coined by Feyel and Chaboche [13] for the nested solution of the two resulting boundary value problems, illustrates the nature of the complexity of a computational homogenisation framework [29].

The Reduced Order Modelling (ROM) technique, proposed by Almroth et al. [1] and Noor et al. [31], is applied to reduce the dimensionality and computational costs of solving the microstructural model, i.e. PDE. For nonlinear problems however, the computational complexity of the constitutive equations in the reduced problem remains unaffected, i.e. ODE, as pointed out by Rathinam and Petzold [34], since the integration scheme itself is not reduced. For the nonlinear reduced order models, the achieved speed-up is marginal compared to the reduction in number of degrees of freedom. Furthermore, the use of constitutive equations that involve internal variables describing the constitutive behaviour of the material on each integration point in the model imposes strong requirements on the available memory.

To remedy this, several methods have been proposed in the literature to reduce the computational costs of the assembly, such as the Missing Point Estimation approach (MPE) [2], the Discrete Empirical Interpolation Method (DEIM) [5], hyper reduction with reduced internal variables [35], Transformation Field Analysis (TFA) [11], Nonuniform Transformation Field Analysis (NTFA) [28], potential-based Reduced Basis Model Order Reduction (pRBMOR) [15], High-Performance Reduced Order Modelling (HP-ROM) [21], Energy-Conserving mesh Sampling and Weighting (ECSW) [12] and the Empirical Cubature Method (ECM) [20], among many others.

Following Hernández et al. [20], the hyper-reduction methods can be divided into two classes. On the one hand the nodal vector approximations that approximate the integral by introducing a global basis to represent the integrand. This allows the basis to be evaluated only once (offline), thereby reducing costs of the subsequent evaluations of the integral. This basis is weighted using coefficients that minimise the interpolation error between the nonlinear integrand and its modal approximation on a set of sampled points in the least-squares sense. Examples of this class are DEIM and MPE [2, 5]. On the other hand the integral (quadrature) approaches approximate the integral using a reduced set of integration points which have empirically determined weights in the methods ECM or ECSW [12, 20]. A comparison of the Empirical Interpolation Method, in particular High-Performance Reduced Order Modelling [21], and the Empirical Cubature Method [20] for solving micromechanical equilibrium problems is presented in [38].

Besides Reduced Order Models, the computational costs have also been reduced using numerically efficient solvers, e.g. the Fast Fourier Transform [30] or wavelet bases to reduce the number of equations by projecting a fully discretised multi-scale problem onto a lower dimensional space, e.g. [3, 9, 17, 19]. Some alternative wavelet-based reduction methods can be found in literature. The wavelet-based MOR [14] has been proposed to provide an alternative subspace, for those problems where there is no time to build a POD basis or when a global POD basis cannot adequately represent the local behaviour. However, this alternative approach does not attain significant compression ratios that are characteristic for POD. In this work, we will therefore still rely on a POD for the first reduction.

In this paper, the dimensionality of the problem is first tackled using the classical Reduced Order Modelling approach. Next, a novel integration scheme is proposed to limit the number of function evaluations by adaptively selecting the quadrature points using a sparse wavelet representation of the integrand. Due to the hierarchical nature of the wavelet bases, local refinement comes naturally with a wavelet representation. This approach can be considered as a form of multi-resolution analysis (MRA) used to perform the local refinement similar to Meyer [27] and Mallat [24]. The multi-resolution analysis provides control over the approximation accuracy of local phenomena [3] using a pre-defined tolerance.

A combined approach of ROM and MRA reduces the computational costs of both the assembly and solution of the microstructural models. Furthermore, it requires only a tolerance to indicate the required accuracy of the approximation, allowing to bound introduced errors. The introduction of an a priori determined reduced integration scheme for the high-dimensional parameter space is thereby omitted, greatly reducing the dimensionality of the snapshot space.

This paper is outlined as follows. First, the mechanical problem and the corresponding standard Reduced Order Model are introduced in Sects. 2 and 3 respectively. In Sect. 4, a one-dimensional mechanical model is introduced, aiming for a comprehensive analysis of the proposed method. Evidently, a 1D problem may not be as convincing in reproducing a state not captured in the snapshot space as a 2D problem might. Therefore, more convincing examples will be provided in 2D in forthcoming work. The section shortly outlines Reduced Order Modelling, after which the wavelet reduced model using MRA is introduced. As no assumptions are made with respect to the spatial dimensionality of the problem and multi-dimensional adaptive wavelet transforms are available in literature [32], the method can be readily extended to two or three dimensional problems. The presentation in a 1D context however, allows the reader to fully comprehend the underlying principles and added value of the method. The extension to a wavelet reduced multi-dimensional model will be discussed in a following publication. Section 5 presents the results of the wavelet reduced analysis of two one-dimensional elasto-plastic microstructural models, whereby the accuracy and the reduction in computational costs are discussed. The paper closes with the conclusions in Sect. 6.

Fig. 1

Schematic outline of a two-scale mechanical model for a macroscopic cantilever beam loaded with force $\mathbf {F}$ composed of a material with inclusions on the micro-scale

1.1 Notation

First the mechanical model is described in general context using a tensorial notation. Vectors and tensors are typeset using a boldface symbol, e.g. $\mathbf {w}$, ${\varvec{\varepsilon }}$, ${\varvec{\sigma }}$ etc. Spaces are noted using a calligraphic font $\mathcal {S}$ and columns and matrices are denoted by single and double underlined symbols, e.g. column vector $\underline{c}$ and matrix $\underline{\underline{M}}$.

Single and double contractions between vector or tensor valued quantities are denoted with a dot or a double dot respectively, e.g. $\mathbf {a} \cdot \mathbf {b} = s$ and $\nabla \mathbf {q}(\mathbf {x}) : {\varvec{\sigma }}= s$ where s represents a scalar quantity.

Furthermore all basis functions $\underline{N}(\mathbf {x})$ and $\underline{R}(\mathbf {x})$ are denoted in uppercase. The corresponding coefficients that are not reduced are denoted with lowercase characters, e.g. $\underline{\mathbf {w}}$. Their reduced equivalent coefficients are written in uppercase, e.g. $\underline{\mathbf {W}}$.

Scaling function coefficients are denoted with $s^j_i\left[ f(x) \right]$ where $i$ indicates the index and $j$ the level of the scaling function. The shorthand notation $f^j_i$ is used to denote the scaling function coefficient $s^j_i\left[ f(x) \right]$. The grid point of the corresponding scaling function on a dyadic wavelet grid is denoted by $x^j_i$ in the wavelet coefficients, the notation $d^j_i\left[ f(x) \right]$ is introduced where $i$ and $j$ are the index and the level of the wavelet function. The integrands occurring in the weak form of the linear momentum balance are denoted using Greek symbols, e.g. the force and stiffness integrands are denoted by $\underline{\varphi }$ and $\underline{\underline{\kappa }}$ respectively.

A short-hand notation is employed for time discretised parameters, such as the history parameters. The time-step on which the parameter is sampled is denoted by a superscript $t$ for the current time step and $t+ \varDelta t$ for the next time step, e.g. $\underline{\xi }^{t} = \underline{\xi }(t)$ and $\underline{\xi }^{t+\varDelta t} = \underline{\xi }(t+\varDelta t)$.

2 Mechanical model

To outline the principles of W-ROM, this work considers a two-scale model similar to those presented in [13, 16, 29]. The model is comprised of a macro-mechanical model and a micro-mechanical model representing the topological and material information on the corresponding macro- and micro-scale. The subscript $\mathrm{M}$ and $\mathrm{m}$ are introduced to distinguish between macro- and micro-scale quantities respectively. The loading in the macro-scale model is transferred to the micro-scale model via periodic boundary conditions and the stress state in the macro-scale model is given by the volume averaged stress in the micro-scale model, conforming to the Hill-Mandel condition [23]. This procedure is schematically depicted in Fig. 1.

Fig. 2

Outline of the micro-mechanical model

The reduced order approach is illustrated using a micro-scale mechanical model depicted in Fig. 2, where a Lagrangian description is employed with $\mathbf {x}$ the position vector of a material point $\mathbf {x}(t)$ at time $t$, $\mathcal {V}$ and $\mathcal {S}$ denote the microstructural domain and its boundary respectively and $O$ is the origin. Neglecting the inertia and body-forces, the linear momentum balance for this problem is given by

$$\begin{aligned} \nabla \cdot {\varvec{\sigma }}({\varvec{\varepsilon }}, \underline{\xi }) = \mathbf {0} \quad \text { in } \mathcal {V}\end{aligned}$$

(1)

where ${\varvec{\sigma }}$ is the Cauchy stress tensor and $\underline{\xi }$ are the history parameters describing the local material state. The model is formulated in a small strain framework. The local micro-scale strain tensor ${\varvec{\varepsilon }}$ consists of a contribution of the macroscopic strain ${\varvec{\varepsilon }}_\mathrm{M}$ and the symmetric gradient of the micro-fluctuations $\mathbf {w}(\mathbf {x})$. This leads to the following definition of the micro-scale strain ${\varvec{\varepsilon }}({\varvec{\varepsilon }}_\mathrm{M}, \mathbf {x}, t)$

$$\begin{aligned} {\varvec{\varepsilon }}({\varvec{\varepsilon }}_\mathrm{M}, \mathbf {x}, t)&= {\varvec{\varepsilon }}_\mathrm{M}(t) + \nabla ^\mathrm{s}\mathbf {w}(\mathbf {x}, t)&\text { in } \mathcal {V}\end{aligned}$$

(2)

2.1 Weak formulation

After multiplication of Eq. (1) with weighting function $\mathbf {q}(\mathbf {x})$ and integration by parts, the standard Bubnov–Galerkin weak form is obtained

$$\begin{aligned} \underbrace{\int _{\mathcal {V}} \nabla \mathbf {q}(\mathbf {x}) \cdot {\varvec{\sigma }}({\varvec{\varepsilon }}, \underline{\xi }) \, \mathrm{d}{\mathcal {V}}}_{\underline{\mathbf {f}}^{ \mathrm int}(\underline{\mathbf {w}})} = \underbrace{\int _\mathcal {S}\mathbf {q}(\mathbf {x}) \cdot \mathbf {t}(\mathbf {x}) \, \mathrm{d}{\mathcal {S}}}_{\underline{\mathbf {f}}^{ \mathrm ext}} \end{aligned}$$

(3)

where $\mathcal {V}$ is the domain of the microstructural model with boundary $\mathcal {S}$, on which an outward pointing unit normal $\mathbf {n}$ is defined. The traction $\mathbf {t}$ is defined as $\mathbf {t} = \mathbf {n} \cdot {\varvec{\sigma }}$. The internal and external forces are denoted by $\underline{\mathbf {f}}^{{ \mathrm int}}(\underline{\mathbf {w}})$ and $\underline{\mathbf {f}}^{{ \mathrm ext}}$ respectively.

The micro-fluctuation field $\mathbf {w}(\mathbf {x})$ is constrained using periodic boundary conditions at the boundary $\mathcal {S}$ and the macroscopic strain ${\varvec{\varepsilon }}_\mathrm{M}(t)$ results from the macro-scale kinematics. Using Hill–Mandel, the macroscopic stress is obtained by volume averaging the microstructural stress ${\varvec{\sigma }}({\varvec{\varepsilon }}, \underline{\xi })$, i.e.

$$\begin{aligned} {\varvec{\sigma }}_\mathrm{M}({\varvec{\varepsilon }}_\mathrm{M}) = \frac{1}{|\mathcal {V}|} \int _\mathcal {V}{\varvec{\sigma }}({\varvec{\varepsilon }}, \underline{\xi }) \, \mathrm{d}{\mathcal {V}} \end{aligned}$$

(4)

where $|\mathcal {V}|$ denotes the volume of the microstructure.

2.2 Spatial discretisation

The microstructural model is discretised using a standard Lagrangian finite element basis. The weighting and trial functions $\mathbf {q}$ and $\mathbf {w}$ in the weak form of the linear momentum balance (3) are approximated using the discretised weighting and trial functions $\mathbf {q}^{h}$ and $\mathbf {w}^{h}$ respectively.

$$\begin{aligned} \mathbf {q}^{h}(\mathbf {x})&= \sum _i N_i(\mathbf {x}) \mathbf {q}_i \end{aligned}$$

(5)

$$\begin{aligned} \mathbf {w}^{h}(\mathbf {x})&= \sum _j N_j(\mathbf {x}) \mathbf {w}_j \end{aligned}$$

(6)

where $\underline{N}(\mathbf {x})$ is a set of Lagrangian interpolation functions. After substitution of the discretised weighting and trial functions, the finite element problem can be solved for different macroscopic strains ${\varvec{\varepsilon }}_\mathrm{M}(t)$ using the Newton–Raphson procedure.

3 Reduced order modelling

To reduce the dimensionality of the finite element discretisation, the microstructural model is reformulated using a set of reduced basis functions. In the traditional FE discretisation, the spatial accuracy of the model is proportional to $h^{-p}$ for $p> 0$, where $h$ and $p$ are the element size and order respectively. The number of physical deformation modes present in the microstructure is often much lower than the number of FE shape functions required to accurately capture the deformation field. Therefore, the number of degrees of freedom can be reduced using a set of global shape functions which are sufficiently detailed to capture the local phenomena occurring in the microstructural model. The number of degrees of freedom required for the discretisation is thereby no longer proportional to the spatial accuracy of the basis.

3.1 Proper orthogonal decomposition

The applied Reduced Order Modelling technique makes use of the Proper Orthogonal Decomposition (POD) by Pearson [33] and Schmidt [36] to extract essential physical modes from a set of solutions constructed using the original discretisation. Snapshots of the discretised micro-fluctuation coefficients $\underline{\mathbf {w}}$ are collected in a snapshot-matrix $\underline{\underline{\mathfrak {X}}}$. The snapshot matrix is then decomposed into proper orthogonal modes and corresponding eigenvalues $\lambda$ using the POD. The normalised eigenvalues represent the contribution of the corresponding mode to the snapshot matrix and are used to truncate the reduced basis to $\underline{\underline{V}}$ , consisting of the first $n^\mathrm{m}$ modes with a contribution above the predetermined tolerance $\delta ^\mathrm{RB}$. This process is schematically depicted in Fig. 3.

Fig. 3

Extraction of the reduced basis using POD

3.2 Construction of the reduced basis

The snapshot matrix $\underline{\underline{\mathfrak {X}}}$ is obtained by collecting snapshots of the micro-fluctuation coefficients $\underline{\mathbf {w}}$ under $n^\mathrm{s}$ different macroscopic strains ${\varvec{\varepsilon }}_\mathrm{M}$ as columns in a snapshot matrix $\underline{\underline{\mathfrak {X}}} = \left[ \underline{\mathbf {w}}({\varvec{\varepsilon }}_\mathrm{M}^1),\underline{\mathbf {w}}({\varvec{\varepsilon }}_\mathrm{M}^2), \ldots , \underline{\mathbf {w}} ({\varvec{\varepsilon }}_\mathrm{M}^{n^\mathrm{s}}) \right]$, after which the POD yields the modal coefficients $\underline{v}_j$ and corresponding eigenvalues $\lambda _j$. The reduced basis functions $\underline{R}(\mathbf {x})$ are then constructed out of a linear combination of the Lagrangian basis

$$\begin{aligned} \mathbf {R}_j(\mathbf {x})&= \sum _i v_{ij} N_i(\mathbf {x}) \end{aligned}$$

(7)

The weighting and trial functions are then discretised using the reduced basis functions only.

$$\begin{aligned}&\mathbf {q}^{h}(\mathbf {x}) = \sum _i \mathbf {R}_i(\mathbf {x}) Q_i&\mathbf {w}^{h}(\mathbf {x}) = \sum _j \mathbf {R}_j(\mathbf {x}) W_j \end{aligned}$$

(8)

Substitution of the reduced weighting and trial functions (8) into the weak form (3) yields the ROM [41]:

$$\begin{aligned} \hat{\underline{\mathbf {f}}}^{ \mathrm int}(\underline{W}) = \int _\mathcal {V}\nabla ^\mathrm{s}\underline{\mathbf {R}}(x) : {\varvec{\sigma }}({\varvec{\varepsilon }}(\underline{\mathbf {W}}), \underline{\xi }) \, \mathrm{d}{\mathcal {V}} \end{aligned}$$

(9)

From the equations it is clear that the integration can not be performed a priori since the internal force $\hat{\underline{\mathbf {f}}}^{{ \mathrm int}}(\underline{W})$ is non-linearly dependent on the reduced micro-fluctuations. The integration scheme requires the stresses ${\varvec{\sigma }}$ at every integration point in the microstructure. Therefore the integration procedure is still proportional to the number of elements used to discretise the microstructural problem and the reduction in memory usage and floating point operations (FLOPs) required to assemble and solve the microstructural problem is only marginal.

This problem can be resolved using, for example, hyper-reduction techniques such as HP-ROM [21] or ECM [20]. In the first approach, not only the displacement-field but also the stress-field is projected onto a reduced basis. The modal contributions are determined in a least-squares sense by sampling the stresses in a reduced set of integration points. The latter approach reduces the integration scheme itself directly by choosing a subset of integration points and optimising the quadrature weights based on snapshots of the integrands. Both schemes rely on snapshots of either the stress-field or the complete integrand to reduce the integration.

4 Wavelet-Reduced Order Model

The Wavelet-Reduced Order Modelling technique will be demonstrated on a one-dimensional microstructural model. The 1D setting provides a transparent view of all underlying principles and implementation aspects, which assists the reader in getting a full comprehensive view of the method proposed. To obtain the 1D model, all previous equations are simplified to scalar expressions, e.g $\mathbf {x}$ becomes $x$, ${\varvec{\varepsilon }}$ becomes $\varepsilon$, ${\varvec{\sigma }}$ becomes $\sigma$ etc. The homogenisation of the 1D micro-structural problem leads to a homogenised force instead of a homogenised stress. This model with length $\ell$ and spatially varying cross-sectional area $A(x)$ is schematically depicted in Fig. 4. An elasto-plastic model is used to describe the material behaviour. The microstructure is loaded with a macroscopic strain $\varepsilon _\mathrm{M}= \frac{\varDelta \ell }{\ell }$ with $\varDelta \ell$ the increase in length of the microstructure.

Fig. 4

Microstructure of length $\ell$ with a varying cross-sectional area $A(x)$

Fig. 5

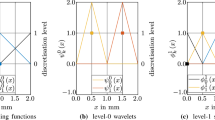
Schematically depicted finite element grid and dyadic wavelet grid used for the integration of internal force and stiffness. The integrand is projected onto the dyadic grid and expressed in terms of coefficients $s_{i}^{0}$ and $d_{i}^{j}$ using basis functions $\phi _{i}^{0}(x)$ and $\psi _{i}^{j}(x)$ on resolution levels $j= 0$ to $j_\mathrm{max}$

To reduce the computational integration costs, the integrands in the reduced order model are approximated using wavelets. In this case, the approximation is performed using Deslauriers–Dubuc interpolating wavelets [7, 8, 10]. This wavelet family was chosen because it yields a compact interpolating scheme. Furthermore the basis functions are smooth and therefore compatible with the smooth fields often present in mechanical problems.

The W-ROM relies on several wavelet techniques, such as wavelet synthesis, wavelet analysis, MRA and data compression. These concepts are briefly explained in Appendix A. The interested reader is also referred to the book by Goedecker [18].

4.1 Wavelet representation of the integrand

The Reduced Order Model requires an integration step to determine the reduced internal forces $\underline{\hat{f}}^{{ \mathrm int}}$ and the corresponding tangent stiffness $\underline{\underline{\hat{K}}}$. To approximate these integrals efficiently, the integrands are projected on the wavelet grid using MRA. The MRA automatically determines the sampling points for interpolation, and the integration is performed on the wavelet approximation of the reduced integrand.

$$\begin{aligned} \underline{\hat{f}}^{{ \mathrm int}}(\underline{W})&= \int _{\mathcal {V}} \underline{\varphi }(\varepsilon , \underline{\xi }) \, \mathrm{d}{\mathcal {V}} \end{aligned}$$

(10)

$$\begin{aligned} \underline{\underline{\hat{K}}}^{{ \mathrm int}}(\underline{W})&= \int _{\mathcal {V}} \underline{\underline{\kappa }}(\varepsilon , \underline{\xi }) \, \mathrm{d}{\mathcal {V}} \end{aligned}$$

(11)

The integrands $\underline{\varphi }(\varepsilon , \underline{\xi })$ and $\underline{\underline{\kappa }}(\varepsilon , \underline{\xi })$ for the internal force and stiffness are defined in (12) and (13) respectively.

$$\begin{aligned} \underline{\varphi }(\varepsilon , \underline{\xi })&= \partial _{x} \underline{R}(x) \sigma (\varepsilon , \underline{\xi }) \end{aligned}$$

(12)

$$\begin{aligned} \underline{\underline{\kappa }}(\varepsilon , \underline{\xi })&= \partial _{x} \underline{R}(x) \frac{\partial \sigma }{\partial \varepsilon }(\varepsilon , \underline{\xi }) \left( \partial _{x} \underline{R}(x)\right) ^\mathrm{T} \end{aligned}$$

(13)

For the present analysis, periodicity of the microstructural model is used to approximate the function values at the boundary of the domain. Note, however, that wavelets are not limited to periodic boundary conditions. For the treatment of general boundary conditions using a wavelet basis, the reader is referred to Vasilyev et al. [40].

In order to approximate the integrand $\underline{\varphi }(\varepsilon , \underline{\xi })$ of the internal force using wavelets, the gradients of the reduced basis functions $\partial _{x} \underline{R}(x)$ are required on the points in the dyadic wavelet grid. The gradients are found by sampling the finite element discretised gradient at every dyadic grid point in the wavelet basis using an inverse mapping of the physical to the isoparametric coordinate. Both discretisations are schematically depicted in Fig. 5.

In this work, second order Lagrangian finite elements are used to obtain the full-order finite element solution yielding a piecewise linear approximation of the strain field. This finite element basis is sufficiently smooth to be sampled directly using the Deslauriers–Dubuc interpolating wavelets. When discontinuous strain fields are required to capture the homogenised behaviour accurately, a discontinuous wavelet transform [39] could be used to interpolate the stress and strain fields.

4.2 Multi-resolution wavelet approximation

The integrands $\underline{\varphi }(\varepsilon , \underline{\xi })$ and $\underline{\underline{\kappa }}(\varepsilon , \underline{\xi })$ are projected onto Deslauriers–Dubuc interpolating wavelet basis. The basis is constructed out of multiple grid levels $j= 0, 1, \ldots , j_\mathrm{max}$. Each level contains a set of scaling functions $\phi ^j_i(x)$ and wavelets $\psi ^j_i(x)$ with index $i= 0, 1, \ldots , 2^jn$ and grid level $j= 0, 1, \ldots , j_\mathrm{max}$. The scaling functions and wavelets are derived from the scaling function $\phi (x)$ and mother wavelet $\psi (x)$ by scaling their width by a factor 1 / 2 at each increasing level and translating them with a step of the grid size $\varDelta x^j$ corresponding to the level $j$. The scaling function and wavelet coefficients are found by projecting the integrands onto the corresponding scaling function $\phi ^j_i(x)$ or wavelet $\psi ^j_i(x)$. They are denoted by $s^j_i[f(x)]$ and $d^j_i[f(x)]$ respectively. Note that the Deslauriers–Dubuc scaling functions are interpolating. Therefore, the scaling function coefficient is given directly by the function values sampled on the wavelet grid point, i.e. $s^j_i\left[ f(x) \right] = f(x^j_i)$.

Using the reduced basis gradient $\partial _{x} \underline{R}(x^j_i)$ sampled on the dyadic wavelet grid, the local strain in each grid point is computed using $\varepsilon ^j_i= \varepsilon _\mathrm{M}+ \partial _{x} \underline{R}(x^j_i) \cdot \underline{W}$. The history coefficients $\underline{\xi }^j_i= \underline{\xi }^{t}(x^j_i)$ are discretised using the same multi-resolution sparse wavelet grid. This allows for the wavelet interpolation of the history parameters on newly added grid points avoiding the need to store the history coefficients of every dyadic wavelet grid point. Using the strain $\varepsilon ^j_i$ and the history $\underline{\xi }^j_i$, the stress $\sigma ^j_i= \sigma (\varepsilon ^j_i, \underline{\xi }^j_i)$, the internal force integrand $\underline{\varphi }^j_i= \underline{\varphi }(\varepsilon ^j_i, \underline{\xi }^j_i)$ and the tangent stiffness integrand $\underline{\underline{\kappa }}^j_i= \underline{\underline{\kappa }}(\varepsilon ^j_i, \underline{\xi }^j_i)$ are computed on the wavelet grid. This enables a MRA of the internal force integrand $\underline{\varphi }(\varepsilon , \underline{\xi })$ associated with the reduced micro-fluctuations $\underline{W}$ on the wavelet-grid. During the MRA, the analysis of the grid points is conducted on each level in the hierarchy. The analysis of subsequent levels by evaluating and wavelet transforming the neighbouring points of current level grid points enables the error control, which other hyper-reduction methods ignore.

$$\begin{aligned} s^j_i[\underline{\varphi }(\varepsilon ^j_i, \underline{\xi }^j_i)] = s^j_i\left[ \partial _{x} \underline{R}(x^j_i) \sigma (\varepsilon ^j_i, \underline{\xi }^j_i) \right] \end{aligned}$$

(14)

Note that for an accurate approximation of the internal force and tangent stiffness integrands the initial wavelet grid needs to be sufficiently fine such that the adaptive refinement scheme detects regions requiring local refinement. In principle the initial grid should be as coarse as possible, yet still resolving the presence of fine-scale features, e.g. in a heterogeneous microstructure there need to be grid points in the neighbourhood of the microstructural features to pick up their influence on the initial grid, even if this is still very inaccurate.

4.3 Integration of the wavelet representation

The internal force and tangent stiffness matrix required for the Newton–Raphson procedure result from integrating the wavelet representations of the internal force integrand $\underline{\varphi }(\varepsilon ^j_i, \underline{\xi }^j_i)$ and stiffness integrand $\underline{\underline{\kappa }}(\varepsilon ^j_i, \underline{\xi }^j_i)$. The MRA approximation of an integrand approximation $\tilde{f}(x)$ is defined using a set of coarse scaling coefficients and a sparse set of wavelet coefficients, $s^0_{i}[f(x)]$ and $d^{j}_{i}[f(x)]$ respectively. The field $\tilde{f}(x)$ is then given by:

$$\begin{aligned} \tilde{f}(x) = \sum _{i=0}^ns^0_{i}[f(x)] \phi ^0_i(x) + \sum _{j=0}^{j_\mathrm{max}} \sum _{i} d^{j}_{i}[f(x)] \psi ^{j}_i(x) \end{aligned}$$

(15)

To evaluate the integral of the weak form the unit-integral property of the Deslauriers–Dubuc interpolating wavelets is used [37]. The integral of the mother scaling function $\phi (\theta )$ constructed on a dyadic wavelet grid with sufficient grid points ($\ge 2m-1$), coordinate $\theta$ and a grid spacing $\varDelta \theta =1$ is given by [4].

$$\begin{aligned} \int _{-\infty }^{\infty } \phi (\theta ) \, \mathrm{d}{\theta } = 1 \end{aligned}$$

(16)

Using the biorthogonal refinement relations [18] the mother wavelet function is expressed as a function of the scaling function.

$$\begin{aligned} \psi (\theta ) = \sum _{i=-m}^{m} g_{i} \phi (2\theta - i) \end{aligned}$$

(17)

For Deslauriers–Dubuc interpolating wavelets this simplifies to the following expression.

$$\begin{aligned} \psi (\theta ) = -\phi (2\theta - 1) \end{aligned}$$

(18)

Mapping the coordinate $\theta$ onto the physical coordinate $x$, the integrals of the Deslauriers–Dubuc scaling functions and wavelets on an equidistant dyadic grid, with $\varDelta x_{j}$ the grid spacing on level $j$, are given by:

$$\begin{aligned} \int _{x} \phi ^{j}_{i}(x) \, \mathrm{d}{x}&= \varDelta x_j\end{aligned}$$

(19a)

$$\begin{aligned} \int _{x} \psi ^{j}_{i}(x) \, \mathrm{d}{x}&= -\tfrac{1}{2} \varDelta x_j\end{aligned}$$

(19b)

Substitution yields the following simple summation of the coefficients times the grid size at the coefficient level.

$$\begin{aligned} \int _{\mathcal {V}} \tilde{f}(x) \, \mathrm{d}{\mathcal {V}}= & {} \sum _{i=0}^ns^0_{i}[f(x) A(x^j_i) ] \varDelta x_0\nonumber \\&\quad -\,\sum _{j=0}^{j_\mathrm{max}} \sum _{i} \tfrac{1}{2} d^{j}_{i}[f(x) A(x^j_i) ] \varDelta x_{j} \end{aligned}$$

(20)

Combining the wavelet approximation of the integrands $\underline{\varphi }$ and $\underline{\underline{\kappa }}$ and the integration and substitution into a Newton–Raphson procedure to solve the linear momentum balance leads to the W-ROM outlined in Algorithm 1. Note that the integration grid is rebuilt within every iteration. When the history coefficients from the previous increment or iteration are required, the wavelet representation thereof is stored. Upon refinement, the history variables need to be interpolated between the available grid points when the history is required on newly added grid points. The Deslauriers–Dubuc basis functions used to discretise the integrands are also used to interpolate the history variables.

Fig. 6

Example I: microstructural domain with length $\ell$ and varying cross-sectional area $A(x)$

Fig. 7

Corresponding strains of micro-fluctuation modes and singular values extracted from the snapshots $\underline{\underline{\mathfrak {X}}}$ for the microstructure loaded with a macroscopic strain $\varepsilon _\mathrm{M}= 0.1$ in 10 equivalent increments

5 Numerical examples

To evaluate the performance of the W-ROM, a one-dimensional microstructure with elasto-plastic material behaviour is modelled. The required integration points are monitored to assess the computational costs. The accuracy of the resulting macroscopic forces $f_\mathrm{M}(\varepsilon _\mathrm{M})$ of the full order model (FOM), the ROM and the W-ROM are compared. The accuracy with respect to the standard ROM is evaluated by comparing the micro-fluctuation coefficients $\underline{W}$. To demonstrate the flexibility of the wavelet integration a second microstructure consisting of two domains with different material parameters is modelled. The spatially dependent cross-sectional area given by Eq. (21) is used for both models. An average cross-sectional area of $A_\mathrm{avg} = 0.1 \, \mathrm{mm}^2$ and an area fluctuation of $\varDelta A= 0.02 \, \mathrm{mm}^2$ are used for both examples. A wavelength of $L= 0.5\, \mathrm{mm}$ is selected for a microstructure with length $\ell = 1 \, \mathrm{mm}$. The cross-sectional area is then given by:

$$\begin{aligned} A(x) = A_\mathrm{avg} + \varDelta A\cos \left( 2\pi \frac{x}{L} \right) \end{aligned}$$

(21)

To homogenise the one-dimensional problem, the following relation between the macroscopic strain $\varepsilon _\mathrm{M}$ and the macroscopic force $f_\mathrm{M}$ is introduced.

$$\begin{aligned} f_\mathrm{M}(\varepsilon _\mathrm{M}) = \frac{1}{\ell } \int _{0}^{\ell } \sigma (x; \varepsilon _\mathrm{M}) A(x) \, \mathrm{d}{x} \end{aligned}$$

(22)

The full-order model is discretised with 1000 quadratic Lagrangian elements and the weak form is integrated using 2 Gauss-Legendre quadrature points per element. The dyadic wavelet grid has 9 points at level $j= 0$ such that the 4th degree Deslauriers–Dubuc scaling functions and wavelets are fully supported within the domain. Note however that a finer initial grid may be used when this is required. Periodic boundary conditions are employed for both the finite element and the wavelet discretisations.

5.1 Example I: Micro-structural model with one material

The first example consists of a unit-cell, schematically depicted in Fig. 6, with an elasto-plastic material having a Young’s modulus of $E= 1.0$ GPa, a yield-stress of $\sigma _\mathrm{y}= 0.02$ GPa, and a hardening coefficient of $K= 0.4$ GPa.

The model is loaded with a macroscopic strain $\varepsilon _\mathrm{M}$ increasing from 0 to 0.1 in 10 equidistant increments. Snapshots of the resulting micro-fluctuation fields $w(x)$ are stored in the snapshot-matrix $\underline{\underline{\mathfrak {X}}}$ to extract the modes constituting the reduced basis $\underline{R}(x)$. Using the POD, the modes and their corresponding eigenvalues required to formulate the reduced basis $\underline{R}(x)$ are retrieved. The modes and singular values are plotted in Fig. 7. In this example, 3 modes are used to capture the micro-fluctuation field. After the derivation of a reduced basis, it is projected onto the dyadic wavelet grid to complete the W-ROM.

The accuracy of the reduced models is assessed by comparing the reduced micro-fluctuation coefficients and the resulting integrated macroscopic force obtained using the ROM and W-ROM (using Algorithm 1) with the results obtained using the FOM. The relation between computational cost and accuracy of the W-ROM is investigated by adopting different tolerances and comparing the corresponding sparse wavelet grids.

5.1.1 Accuracy

To assess the accuracy, the macroscopic strain $\varepsilon _\mathrm{M}$ is increased from 0 to 0.1 in 20 equal increments. Note that the macroscopic strain is applied in twice the number of increments, i.e. every odd strain increment lies in the middle of two strains used to generate the snapshots $\underline{\underline{\mathfrak {X}}}$ such that the ROM needs to interpolate between the available modes. The resulting micro-scale stress and strain fields obtained with the FOM, ROM, and W-ROM are plotted in Fig. 8 for load increments 5, 7 and 20 (using a tolerance $\delta ^\mathrm{w}= 10^{-2}$).

Fig. 8

Microscopic stress, strain and force fields for the FOM, ROM and W-ROM ($\delta ^\mathrm{w}= 10^{-2}$). A section of the force curve is enlarged $5\times$ to visualise the small deviations in the force equilibrium

Due to the limited number of snapshots and modes used, the ROM is not able to represent the force equilibrium exactly close to the plastic deformation front. Small deviations of the force equilibrium are visible between the ROM and FOM results. Since the W-ROM relies on the same basis, these small deviations are also present here. In order to obtain a more accurate representation of the strain field close to the plastic deformation front, more snapshots are required to obtain the missing modes to construct the ROM. Moreover, if the ROM problem would be solved with a wavelet approximation as well, this concern would be completely alleviated. This will be explored in future work.

Note, however, that the W-ROM approximates the reduced order model accurately using only a reduced set of integration points. The strains of the W-ROM are compared to the lossless integrated result of the ROM. Since both models make use of the same basis (in the wavelet representation the strains are sampled from the reduced basis directly), it suffices to compare the reduced coefficients. The evolution of the coefficients over the load increments is plotted in Fig. 9, where the integration error in the coefficients of the W-ROM model is defined with respect to the ROM model as follows.

$$\begin{aligned} \epsilon _{W} = \frac{ \Vert \underline{W}^\mathrm{W-ROM} - \underline{W}^\mathrm{ROM}\Vert _2}{\Vert \underline{W}^\mathrm{ROM}\Vert _2} \end{aligned}$$

(23)

Fig. 9

The evolution of the reduced strain coefficients $W$ of the ROM and W-ROM ($\delta ^\mathrm{w}= 10^{-4}$) and the integration error $\epsilon _{W}$ of the W-ROM relative to the fully integrated ROM

Fig. 10

The macroscopic force–strain curve of the FOM, ROM and W-ROM ($\delta ^\mathrm{w}= 10^{-4}$) of the microstructure and the relative error $\epsilon _{\sigma _{\mathrm{M}}}$ using ROM and W-ROM

Fig. 11

The error in the macroscopic force–strain curves approximated using W-ROM

Fig. 12

Sparse dyadic grids used for the wavelet representation using various tolerances $\delta ^\mathrm{w}$

To investigate the influence of the wavelet representation on the macroscopic force $f_{\mathrm{M}}$, the macroscopic force–strain curve for the FOM, ROM and W-ROM is shown in Fig. 10. The error $\epsilon _{f_\mathrm{M}}$ in the approximation of the macroscopic force $f_\mathrm{M}$ using the ROM and W-ROM model with respect to the FOM model is defined as

$$\begin{aligned} \epsilon _{f_{\mathrm{M}}} = \frac{|f_\mathrm{M}^* - f_\mathrm{M}^\mathrm{FOM}|}{|f_\mathrm{M}^\mathrm{FOM}|} \end{aligned}$$

(24)

where $f_\mathrm{M}^*$ is the macroscopic force approximated with either the fully integrated ROM or W-ROM model.

Even though the tolerance $\delta ^\mathrm{w}= 10^{-4}$ only applies to the approximation of the internal force, the error in the wavelet representation of the macroscopic force remains of approximately the same order. The ROM captures the macroscopic force $f_{\mathrm{M}}$ exactly up to numerical precision in the linear regime and in the post-yielding regime up to the given tolerance. In this regime, the wavelet representation proves sufficiently accurate to maintain the ROM accuracy.

The influence of the applied tolerance on the macroscopic force $f_\mathrm{M}$ is investigated by approximating the internal forces in the W-ROM model using different tolerances $\delta ^\mathrm{w}= 10^{-2}, 10^{-3}, \ldots , 10^{-6}$. The resulting errors of the ROM and W-ROM with respect to the FOM case are plotted in Fig. 11.

A stricter tolerance consistently leads to a better force approximation. The errors for the tolerances $\delta ^\mathrm{w}= 10^{-5}$ and $\delta ^\mathrm{w}= 10^{-6}$ are plotted in dashed lines since the wavelet representation reached the maximum level (here set to $j_\mathrm{max}= 12$) and accordingly the reduction in error stagnates. A larger $j_\mathrm{max}$ would allow to capture more details, through which the approximation of the internal force integrand $\varphi (x_0)$ becomes even more accurate resulting in a more accurate force integral.

This becomes clear by considering the sparse wavelet grids for the various tolerances $\delta ^\mathrm{w}$, as depicted in Fig. 12. At tolerance $\delta ^\mathrm{w}= 10^{-4}$ the maximum level is reached and the grid starts to fill in. The accuracy of the approximation can be enhanced using a higher maximum level $j_\mathrm{max}$, or by increasing the order of the bases.

5.1.2 Reduction

The sparsity of the wavelet representation allows the approximation of the micro-scale stress and internal force integrand fields using a limited number of sample points. Depending on the tolerance, the algorithm automatically identifies points at locations where refinement is needed, thereby eliminating the need for an a priori determined set of integration points [20] or modal reconstruction of the micro-scale stress field [21]. The wavelet basis enables an approximation up until a pre-set tolerance picking up local phenomena in high detail while using few sample points in regions without significant fluctuations. When the maximum level is reached, the wavelet coefficient gives an indication of the order of magnitude of the remaining approximation error.

Fig. 13

The number of points in the sparse wavelet grid for various tolerances $\delta ^\mathrm{w}$. The dashed line denotes the number of integration points used in the FOM model

Fig. 14

Example II: Two-phase microstructural composite rod with length $\ell$ and varying cross-sectional area $A(x)$. The Young’s modulus of the elasto-plastic material is $E= 1$ GPa. The left side (red) has a yield stress $\sigma _\mathrm{y}= 0.04$ GPa and hardening rate of $K= 0.2$ GPa. The right side (blue) has a yield stress of $\sigma _\mathrm{y}= 0.02$ GPa and hardening rate of $K= 0.4$ GPa

Fig. 15

The evolution of the micro-scale strain (left-hand side), stress (middle) force (right-hand side) approximated with a FOM, ROM and W-ROM model for increments 5, 7 and 20. A section of the force curve is enlarged $\times \,5$ to visualise the small deviations in the force equilibrium

The number of points required for an approximation with tolerance $\delta ^\mathrm{w}$ is depicted in Fig. 13. For a tolerance of $\delta ^\mathrm{w}= 10^{-2}$ in the internal force integrand only 76 integration points are required, compared to the original FEM problem with 2000 integration points. The method gains on the full order model up to a tolerance $\delta ^\mathrm{w}= 10^{-5}$, which is remarkable considering there are only limited regions without strong fluctuations in the force integrand field in the one-dimensional example model.

Note, that for a tolerance $\delta ^\mathrm{w}\le 10^{-5}$ the wavelet representation of the integrand requires more integration points than the original Gauss scheme to project the integrand onto the wavelet basis. The accuracy of the integrand in the FOM however is also limited by the element size of order $\mathcal {O}\left( {10^{-3}}\right)$. When using a tolerance $\delta ^\mathrm{w}$ lower than the accuracy of the FOM the wavelet representation will approximate the artefacts of the original Lagrangian discretisation of the finite element problem. This locally requires extra sampling points which do not yield extra accuracy of the physical solution, but merely in the discretised solution. If a higher accuracy is desired a finer finite element mesh discretisation for the FOM needs to be employed first.

Evidently, this emphasises again that the tolerance used in the wavelet reduction/approximation should be balanced with respect to the underlying discretisation error of the FOM. Note that this problem will no longer exist if wavelets are used to solve the BVP for the FOM/ROM as will be done in future work.

5.2 Example II: Two-phase microstructural composite rod

Next, a somewhat more complex microstructure is considered. Similar to the first case, this problem consists of an expanding plastically deformed zone. However, this microstructure consists of two phases of elasto-plastic material which yield at different stress-levels with a different hardening rate, resulting in a discontinuous micro-scale strain field. The microstructure is schematically depicted in Fig. 14.

The resulting micro-scale stresses and strains are plotted in Fig. 15 for the load increments 5, 7 and 20. At increment 5 the onset of plastic deformation is visible on the right hand side of the microstructure, at increment 7 the right phase shows a significant plastically deformed zone and at the final increment 20 both phases reveal plasticity. When both phases are deforming plastically, a strain discontinuity originates due to the difference in yield stress and hardening parameters. Here one can see a small approximation error in the ROM and the W-ROM stress, strain and force field. This error is however localised due to the (automatically) refined wavelet grid near the discontinuity and hardly influences the integrated macroscopic stress. As stated before, this problem can be solved by adopting a wavelet family which allows for discontinuities [39].

Fig. 16

The evolution of the reduced micro fluctuation coefficients $\underline{W}$ of the ROM and W-ROM model over the increments (left). Integration error in the W-ROM model relative to the fully integrated ROM (right)

Fig. 17

Macroscopic force resulting from the microstructure loaded with $\varepsilon _{\mathrm{M}}$ approximated using FOM, ROM and W-ROM. The error in the ROM and W-ROM models with respect to the FOM model $\epsilon _{f_{\mathrm{M}}}$ are plotted on the right

Figure 16 shows the resulting micro-fluctuations resolved with ROM and W-ROM. Comparing the W-ROM method relative to the fully integrated ROM method, the errors in the reduced micro-fluctuation parameters $\underline{W}$ are of the order $\mathcal {O}\left( {10^{-4}}\right)$, which is much smaller than the imposed tolerance of $\delta ^\mathrm{w}= 10^{-3}$.

Fig. 18

The sparse wavelet grid used to approximate the micro-scale variables in the microstructural problem

When looking at the macroscopic force–strain curve in Fig. 17 of the FOM, ROM and W-ROM models, a similar trend is observed. In the plastic regime, the error in the ROM and W-ROM with respect to the FOM are of order $\mathcal {O}\left( {10^{-4}}\right)$ using approximately 300 integration points. This is considerably smaller than the imposed tolerance.

The wavelet grid used for the W-ROM approximation presented in Fig. 18 shows that the discontinuities at the boundaries and centre of the domain are adequately picked up by the automatic refinement strategy until the maximum wavelet level $j_\mathrm{max}$ is used. The W-ROM model uses $\sim \,300$ integration points to integrate the internal force vector, stiffness matrix and macroscopic force. The FOM and ROM are integrated using a Gaussian quadrature with 2000 integration points.

Due to the $C^{0}$ kinks originating at the plastic front, the refinement algorithm locally uses a lot of sampling points. In this work it is shown that the local high accuracy can be obtained. If a high reduction factor is favoured, the user has several options to fine tune the compression: (i) choosing the maximum wavelet level lower; (ii) a less strict tolerance; (iii) using higher order bases. This implies that (i) the minimum width of the wavelets increases or (ii) the approximation does not refine that much in narrow regions around kinks and discontinuities; (iii) fine scale details are approximated using less sampling points. Options (i) and (ii) will give a locally less accurate microscale solution. Note however, that the error defined locally is quite strict when one is interested in the homogenised stresses or forces, since the error made in the homogenised result is often lower than the local error.

6 Conclusions

This paper presents a novel hyper-reduced method by introducing a wavelet basis and a MRA to integrate the weak form up to a pre-set tolerance. The innovative aspects of the proposed method are:

• The wavelet reduced integration does not require an offline calibration step using a second set of (stress-based) snapshots to construct the reduced integration scheme. This reduces the input parameters required to construct the integration scheme to the strain modes only (projected on the dyadic wavelet grid) and a tolerance to control the level of approximation.

• The reduced integration uses the wavelet-based MRA to enable an adaptive and local refinement of the dyadic grid used to integrate the stress, internal forces and stiffness. Conversely, the adaptive dyadic grid will also coarsen when smooth functions are to be approximated.

• The error in the integration is controlled using a pre-set tolerance. This is verified by quantifying the microfluctuation error of the W-ROM relative to the FOM. The resulting error in micro-fluctuation coefficients is typically bounded by the imposed tolerance.

The reduction of the number of stress evaluations to perform the integration with respect to the original Gauss integration scheme used in the ROM is demonstrated and the compression is shown to be inversely proportional to the tolerance.

Hyper-reduced models such as Empirical Interpolation Methods and Empirical Cubature Methods rely on offline determined integration points, and sometimes a basis for the integrand. This allows for a higher compression ratio, but requires a detailed sampling of the high-dimensional snapshot space including the history parameters for path dependent materials, to ensure that no physical modes are missing since the integration scheme is constructed a priori. Many hyper-reduction techniques combine the sampling of the non-linear terms, such as the stress field ${\varvec{\sigma }}$ or the internal force integrand $\underline{\varphi }$, with the sampling of the kinematics. Therefore no additional computations are required for the construction of the snapshots of the nonlinear term. The accuracy of the reduced integration of history dependent material models however, requires extensive sampling of both the kinetics and the kinematics present in the parameter space.

The Wavelet-Reduced Order Model, on the other hand, adaptively determines the points required for accurate integration in-situ and only requires prior accurate sampling of the kinematics. The sampled kinematics are required to construct the symmetric gradient of the reduced basis $\nabla ^2$R$(\mathbf {x})$ and is therefore less sensitive to the sampled snapshots, and algorithmic choices to select integration points.

Fig. 19

The scaled and translated Haar scaling functions and wavelets

Note that there is no theoretical limitation to expand W-ROM to two or three dimensional microstructural models. This 1D model provides a transparent view of all underlying principles and implementation aspects of the method proposed. Expanding the method to multiple dimensions will however require multi-dimensional adaptive wavelet transforms as presented by Paolucci et al. in [32] and more elaborate storage solutions for the internal variables and modes by approximating each variable independently on a separate wavelet grid to allow fast wavelet transforms while still limiting the memory usage.

Wavelet analysis and synthesis

1.1 Multi resolution analysis using wavelets

Wavelet families are constructed using a mother wavelet $\psi (x)$ and scaling function $\phi (x)$. The wavelet basis is spanned by scaling functions and wavelets formed by scaling and translation the scaling function $\phi _i^j(x) = \phi \left( \frac{2^j}{\varDelta x_0} x- i\right)$ and mother wavelet $\psi ^j_i(x) = \psi \left( \frac{2^j}{\varDelta x_0} x- i\right)$, respectively. This process is illustrated for the Haar scaling functions and wavelets in Fig. 19.

Fig. 20

Schematically depicted hierarchical relations between the Haar scaling functions and wavelets on level $j$ and $j+1$

To approximate the integrands, a sequence of approximation spaces is used, $\mathcal {V}^j$ containing the scaling functions $\phi _i^j(x)$. The scaling function spaces in the sequence are subspaces of their successors, i.e. $\mathcal {V}^{j} \subset \mathcal {V}^{j+1}$. The wavelet spaces $\mathcal {W}^{j}$ complement the scaling function spaces $\mathcal {V}^{j}$ such that the combination of both spaces $\mathcal {V}^j\oplus \mathcal {W}^{j}$ are spanning the (more detailed) space $\mathcal {V}^{j+1}$. This hierarchical relation between the wavelets and scaling functions on different levels is schematically depicted in Fig. 20.

Fig. 21

A schematic representation of the multi-resolution analysis of function $f(x)$ using Haar scaling functions and wavelets

In this work, the wavelets are translated along grid points on level $j$ spaced $\varDelta x_j$ apart. At each level the wavelet is scaled down using a factor $\tfrac{1}{2}$ in width for each subsequent level forming a dyadic wavelet grid. The basis consisting of coarse scaling functions and increasingly fine wavelet functions living on multiple levels is formed. In each subsequent level $j$, the wavelet functions $\psi ^j_i(x) \in \mathcal {W}^j$ and scaling functions $\phi ^j_i\in \mathcal {V}^j$ are respectively scaled by a factor $\tfrac{1}{2}$ in width and translated, allowing each new level to capture higher frequency components in the field. The union of all the approximation spaces $\cup _{k=1}^\infty \mathcal {V}^{j}$ spans the complete Lebesgue space $\mathcal {L}^{2}(\mathbb {R})$.

To perform a MRA on a function $f(x)$, without considering the computational efficiency, the function can be projected onto the fine level scaling functions $\phi ^{j_\mathrm{max}}_i(x)$. The scaling function representation can be decomposed into a combination of scaling functions and wavelets at the lower level $j_\mathrm{max}-1$. The projection of the function $f(x)$ on the scaling functions $\phi ^{j_\mathrm{max}-1}_i(x)$ can be analysed again using the wavelet analysis to obtain a representation in terms of level $j= j_\mathrm{max}-2$ scaling functions $\phi ^{j_\mathrm{max}-2}_i(x)$ and wavelets $\psi ^{j_\mathrm{max}-2}_i(x)$. In the multi-resolution analysis the wavelet transform is applied hierarchically to decompose the different frequency components in the function $f(x)$. The multi-resolution analysis is schematically shown for the Haar wavelet family in Fig. 21.

On a dyadic wavelet grid the wavelet analysis and synthesis can be performed discretely using a set of filter coefficients hierarchically relating the scaling function coefficients and wavelet coefficients. The level $j$ scaling function and wavelet coefficients are related to the level $j+1$ scaling function coefficients via the analysis filter coefficients denoted by $\tilde{h}_k$ and $\tilde{g}_k$. The synthesis of the level $j$ scaling function and wavelet coefficients to the level $j+1$ scaling function coefficients is performed using the synthesis filter coefficients $h_{k}$ and $g_{k}$. For a more detailed explanation of multi-resolution analysis the reader is referred to the books [6, 26].

Table 1 The wavelet coefficients used to generate the 4th degree interpolating Deslauriers–Dubuc wavelet and scaling functions

Fig. 22

The 4th degree Deslauriers–Dubuc interpolating scaling functions and wavelets forming the basis on level $j= 0$

Fig. 23

Interpolation using the MRA for the 4th degree interpolating Deslauriers–Dubuc wavelet

1.1.1 Wavelet synthesis

Starting from a coarse representation of the function $f(x)$ comprising of 0th level scaling functions $\phi ^0_i(x)$, an increasingly detailed reconstruction of the function $f(x)$ is obtained by adding higher level wavelets. This reconstruction relies on the wavelet synthesis relations to interpolate intermediate points on finer grid levels $j+ 1$. The synthesis of the discretised field is performed using the synthesis relations for bi-orthogonal wavelets (25).

$$\begin{aligned} s^{j+1}_{2i}&= \sum _{k=-\tfrac{m}{2}}^{\tfrac{m}{2}} h_{2 k} s^{j}_{i- k} + g_{2k} d^{j}_{i- k} \end{aligned}$$

(25a)

$$\begin{aligned} s^{j+1}_{2i+1}&= \sum _{k=-\tfrac{m}{2}}^{\tfrac{m}{2}} h_{2 k+1} s^{j}_{i- k} + g_{2k+1} d^{j}_{i- k} \end{aligned}$$

(25b)

Here, $m$ is the degree of the current filter, and $h_{k}$ and $g_{k}$ are the synthesis filter coefficients listed in Table 1 used to perform the synthesis. The analysis filter coefficients are denoted by $\tilde{h}_k$ and $\tilde{g}_k$.

The 4th degree Deslauriers–Dubuc level $j= 0$ scaling functions $\phi ^0_i(x)$ and wavelets $\psi ^0_i(x)$ are depicted in Fig. 22. When using these Deslauriers–Dubuc interpolating wavelets, the wavelet coefficients $d_i^{j+1}$ on the fine level are given directly by the difference between the level $j$ wavelet interpolation and the sampled function value $f(x^j_i)$¹. This is shown for wavelet synthesis on a dyadic grid using the 4th degree ($m=4$) bi-orthogonal Deslauriers–Dubuc scaling function coefficients $h_k$ and wavelet coefficients $g_k$. A schematic overview of the synthesis is depicted in Fig. 23.

Fig. 24

Schematically depicted compression by truncating the MRA with 4th order Deslauriers–Dubuc (DD4) wavelets using a tolerance $\delta ^\mathrm{w}= 10^{-5}$, where $f(x/\ell )$ is the exact solution and $\tilde{f}(x/\ell )$ is the wavelet representation

The interpolated (or approximated) values on the intermediate grid points can be found by interpolating wavelets assuming that the wavelet coefficients $d^{j}_{k} = 0$. This yields the relation for the approximated function value $\tilde{f}(x_{2i+1}) = s^{j+1}_{2i+1}$, i.e.

$$\begin{aligned} \tilde{f}(x_{2i+1})&= \sum _{k=-\tfrac{m}{2}}^{\tfrac{m}{2}} h_{2 k+1} f^{j}_{i- k} \end{aligned}$$

(26)

For Deslauriers–Dubuc wavelets the filter coefficient $g_{k}$ is described using the Kronecker-delta function $-\delta ^1_{k}$. Therefore the only value $d^j_{i-k}$ contributing to approximation $\tilde{f}^{j+1}_{2i+1}$ is $k= 0$. This coefficient represents the error between the interpolated function value $\tilde{f}^{j+1}_{2i+1}$ and the exact function value $f(x_{2i+1})$

$$\begin{aligned} d^{j}_{i} = \sum _{k= -\tfrac{m}{2}}^{\tfrac{m}{2}} h_{2 k+1} f^{j}_{i- k} - f(x_{2i+1}) \end{aligned}$$

(27)

Note that relation (27) is specific for the Deslauriers–Dubuc interpolating wavelet. For other wavelets the general synthesis relations for bi-orthogonal wavelets (25) can be applied to find the wavelet coefficients.

1.2 Data compression

Using the Deslauriers–Dubuc wavelet family allows the wavelet representation of the function $f(x)$ to be constructed from the coarse level up. By hierarchically applying equation (27) over each level, the correcting wavelet coefficients $d_{i}^{j}$ are computed.

Only the points for which the error $|d_{i}^{j}|/|f_\mathrm{avg}| \ge \delta ^\mathrm{w}$, in which $\delta ^\mathrm{w}$ is the tolerance on the approximation error relative to the absolute average of the function values on the initial grid $|f_\mathrm{avg}|$, are marked for further refinement. When a point $x^j_i$ is marked for further refinement the surrounding grid points on level $j+1$, $x^{j+1}_{2i}$ and $x^{j+1}_{2i+1}$ are approximated in the next level, providing a systematic refinement scheme. The MRA approximation $\tilde{f}(x/\ell )$ is proven to converge to the function $f(x/\ell )$ as the number of levels tends to infinity [6].

The process of truncating wavelets is schematically depicted for the Deslauriers–Dubuc wavelet family in Fig. 24. In this example several wavelets have coefficients $d^{j}_{i}$ that are below the imposed tolerance at level $j= 3$. These wavelets are no longer considered for further refinement in higher levels. At level $j= 4$ all coefficients are below the imposed tolerance $\delta ^\mathrm{w}$. The wavelet representation is sufficiently accurate and all contributions of higher level wavelets can be neglected.