Force sensing using 3D displacement measurements in linear elastic bodies

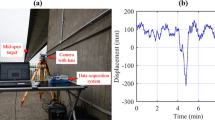
Abstract

In cell traction microscopy, the mechanical forces exerted by a cell on its environment is usually determined from experimentally measured displacement by solving an inverse problem in elasticity. In this paper, an innovative numerical method is proposed which finds the “optimal” traction to the inverse problem. When sufficient regularization is applied, we demonstrate that the proposed method significantly improves the widely used approach using Green’s functions. Motivated by real cell experiments, the equilibrium condition of a slowly migrating cell is imposed as a set of equality constraints on the unknown traction. Our validation benchmarks demonstrate that the numeric solution to the constrained inverse problem well recovers the actual traction when the optimal regularization parameter is used. The proposed method can thus be applied to study general force sensing problems, which utilize displacement measurements to sense inaccessible forces in linear elastic bodies with a priori constraints.

Appendix

1.1 General cases

In this part, we extend our discussion to general boundary value problem in linear elasticity:

$$\begin{aligned} \nabla \cdot {\varvec{\sigma }} +{\varvec{f}}=0,\quad \hbox { in }\Omega ,\quad {\varvec{u}}|_{\Gamma _{u} } =\bar{{\varvec{u}}},\quad {\varvec{\sigma }}\cdot {\varvec{n}}|_{\Gamma _{t} } =\bar{{\varvec{t}}} \end{aligned}$$

(45)

where ${\varvec{f}}$ is the body force density, $\bar{{\varvec{u}}}$ is the prescribed displacements on $\Gamma _{u}$ and $\bar{{\varvec{t}}}$ is the unknown traction on $\Gamma _{t}$.

Denote the solution to (45) as ${\varvec{u}}\left[ {\bar{{\varvec{t}}}} \right]$. According to the principle of superposition,

$$\begin{aligned} {\varvec{u}}\left[ {\bar{{\varvec{t}}}} \right] ={\varvec{u}}_{0} +{\varvec{u}}^{\circ }\left[ {\bar{{\varvec{t}}}} \right] \end{aligned}$$

(46)

where ${\varvec{u}}_{0}$ is the solution to problem

$$\begin{aligned} \nabla \cdot {\varvec{\sigma }} +{\varvec{f}}=0,\quad \hbox { in }\Omega ,\quad {\varvec{u}}|_{\Gamma _{u} } =\bar{{\varvec{u}}},\quad {\varvec{\sigma }}\cdot {\varvec{n}}|_{\Gamma _{t} } =0 \end{aligned}$$

(47)

and ${\varvec{u}}^{\circ }\left[ {\bar{{\varvec{t}}}} \right]$ is the solution to problem

$$\begin{aligned} \nabla \cdot {\varvec{\sigma }}=0,\quad \hbox { in }\Omega ,\quad {\varvec{u}}|_{\Gamma _{u} } =0,\quad {\varvec{\sigma }}\cdot {\varvec{n}}|_{\Gamma _{t} } =\bar{{\varvec{t}}}. \end{aligned}$$

(48)

The maps of prediction to (45) and (48) are respectively $T\left( {\bar{{\varvec{t}}}} \right) =T_{m} \left( {{\varvec{u}}\left[ {\bar{{\varvec{t}}}} \right] } \right)$ and $T^{\circ }\left( {\bar{{\varvec{t}}}} \right) =T_{m} \left( {{\varvec{u}}^{\circ }\left[ {\bar{{\varvec{t}}}} \right] } \right)$, where $T_{m}$ is the map of sampling defined by

$$\begin{aligned} T_{m} \left( {{\varvec{w}}} \right) \equiv \left[ {{\begin{array}{l} {{\varvec{w}}({{\varvec{p}}}_{1} )} \\ \vdots \\ {{\varvec{w}}({{\varvec{p}}}_{M} )} \\ \end{array} }} \right] ,\quad \forall {\varvec{w}}\in {{\varvec{C}}}\left( \Omega \right) . \end{aligned}$$

(49)

Therefore, (46) leads to

$$\begin{aligned} T\left( {\bar{{\varvec{t}}}} \right) =T_{m} \left( {{\varvec{u}}_{0} } \right) +T^{o}\left( {\bar{{\varvec{t}}}} \right) \end{aligned}$$

(50)

with which the original inverse problem $T\left( {\bar{{\varvec{t}}}} \right) =\hat{{\varvec{U}}}_{m}$ is found to be equivalent to

$$\begin{aligned} T^{\circ }\left( {\bar{{\varvec{t}}}} \right) =\hat{{\varvec{U}}}_{m} -T_{m} \left( {{\varvec{u}}_{0} } \right) . \end{aligned}$$

(51)

1.2 Proof of Theorem in Sect. 2

Consider the boundary value problem (48) with homogeneous displacement boundary and vanishing body force. Denote the measurement points in the interior of $\Omega$ as ${\varvec{p}}_{i} ,i=1,\ldots , M$ and the corresponding map of prediction as T. Since T is a continuous linear transformation between Hilbert spaces ${\varvec{W}}_{f}$, i.e. ${\varvec{L}}\left( {\Gamma _{t} } \right)$, and $R^{3M}$, there exists a unique adjoint transformation $T^{*}:R^{3M}\rightarrow {\varvec{W}}_{f}$ which is also linear and continuous. By definition, $\forall {\varvec{v}}_{m} \in R^{3M},\bar{{\varvec{t}}}\in {{\varvec{W}}}_{f}$, $T^{*}$ satisfies

$$\begin{aligned} T\left( {\bar{{\varvec{t}}}} \right) \cdot {\varvec{v}}_{m} =\int \limits _{\Gamma _{t} } {\bar{{\varvec{t}}}\cdot T^{*}\left( {{\varvec{v}}_{m} } \right) dA}. \end{aligned}$$

(52)

On the other hand, the solution to (48) is given by

$$\begin{aligned} {\varvec{u}}[\bar{{\varvec{t}}}]\left( {{\varvec{x}}} \right) =\int \limits _{\Gamma _{t} } {{\varvec{G}}\left( {{\varvec{x}},{{\varvec{y}}}} \right) \bar{{\varvec{t}}}\left( {{\varvec{y}}} \right) dA} \end{aligned}$$

(53)

where the $i{-}j$ component of matrix ${\varvec{G}}\left( {{\varvec{x}},{{\varvec{y}}}} \right)$ gives the displacement at point ${\varvec{x}}$ in the $i^{{\textit{th}}}$ direction caused by a unit force in the $j^{{\textit{th}}}$ direction at point ${\varvec{y}}$ on $\Gamma _{t}$, which we denote as $G_{ij} \left( {{\varvec{x}},{{\varvec{y}}}} \right)$.

Notice $T\left( {\bar{{\varvec{t}}}} \right) =T_{m} \left( {{\varvec{u}}\left[ {\bar{{\varvec{t}}}} \right] } \right)$, (53) leads to

$$\begin{aligned} T\left( {\bar{{\varvec{t}}}} \right) \cdot {\varvec{v}}_{m}= & {} \int \limits _{\Gamma _{t} } {T_{m} \left( {{\varvec{G}}\left( {\cdot , {\varvec{y}}} \right) \bar{{\varvec{t}}}\left( {{\varvec{y}}} \right) } \right) \cdot {\varvec{v}}_{m} dA} \nonumber \\= & {} \int \limits _{\Gamma _{t} } {\bar{{\varvec{t}}}\left( {{\varvec{y}}} \right) \cdot \left( {\sum _{i=1}^M {{\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \cdot {\varvec{u}}_{i} } } \right) dA.} \end{aligned}$$

(54)

where ${\varvec{v}}_{m} =\left( {{\varvec{u}}_{1}^{T},\ldots ,{\varvec{u}}_{M}^{T} } \right) \in R^{3M}$.

Due to the uniqueness of the adjoint operator, (52) and (54) gives

$$\begin{aligned} T^{*}\left( {{\varvec{v}}_{m} ;{\varvec{y}}} \right) =\sum _{i=1}^M {{\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \cdot {\varvec{u}}_{i} },\quad \forall {\varvec{y}}\in \Gamma _{t}. \end{aligned}$$

(55)

Here $T^{*}\left( {{\varvec{v}}_{m} ;{\varvec{y}}} \right)$ denotes the evaluation of $T^{*}\left( {{\varvec{v}}_{m} } \right)$ at point ${\varvec{y}}\in \Gamma _{t}$. The range of $T^{*}$ is therefore given by

$$\begin{aligned} {\mathcal {R}}\left( {T}^{*} \right) =span\left\{ {\bar{{\varvec{t}}}_{ij}, j=1,2,3} \right\} _{i=1}^{M} \end{aligned}$$

(56)

where

$$\begin{aligned} \bar{{\varvec{t}}}_{ij} \left( {{\varvec{y}}} \right) ={\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \cdot {\varvec{e}}_{j}. \end{aligned}$$

(57)

According to [22], the error function vanishes for any traction in ${\mathcal {R}}\left( {T}^{*} \right)$, i.e.

$$\begin{aligned} E\left( {\bar{{\varvec{t}}}} \right) \equiv \bar{{\varvec{t}}}-T^{\dag }\left( {T\left( {\bar{{\varvec{t}}}} \right) } \right) =0,\quad \forall \bar{{\varvec{t}}}\in {\mathcal {R}}\left( {T}^{*} \right) \end{aligned}$$

(58)

More generally, knowing that ${\mathcal {R}}\left( {T}^{*} \right)$ is closed in ${\varvec{W}}_{f}$, for any $\bar{{\varvec{t}}}\in {{\varvec{W}}}_{f}$, there exists a unique decomposition $\bar{{\varvec{t}}}=\bar{{\varvec{t}}}_{1} +\bar{{\varvec{t}}}_{2}$ where $\bar{{\varvec{t}}}_{1} \in {\mathcal {R}}\left( {T}^{*} \right)$ and $\bar{{\varvec{t}}}_{2} \in {\mathcal {R}}\left( {T}^{*} \right) ^{\perp }=Ker\left( T \right)$. Therefore, $T\left( {\bar{{\varvec{t}}}} \right) =T\left( {\bar{{\varvec{t}}}_{1} } \right)$ and

$$\begin{aligned} E\left( {\bar{{\varvec{t}}}} \right) =\bar{{\varvec{t}}}-T\left( {T\left( {\bar{{\varvec{t}}}_{1} } \right) } \right) =\bar{{\varvec{t}}}_{2}. \end{aligned}$$

(59)

Since $\left\| {\bar{{\varvec{t}}}} \right\| _{L^{2}}^{2} =\left\| {\bar{{\varvec{t}}}_{1} } \right\| _{L^{2}}^{2} +\left\| {\bar{{\varvec{t}}}_{2} } \right\| _{L^{2}}^{2}$, it is known from (59) that E is a bounded linear transformation with $\left\| E \right\| \le 1$.

Now consider an infinite series of measurement points $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$. We call $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ to be locally dense in $\Omega$ if $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ is dense in a sub-domain $\Omega _{0} \subset \Omega$ with positive measure, i.e. the closure $\overline{\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty } }$ of $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ contains $\Omega _{0}$ and $meas\left( {\Omega _{0} } \right) >0$.

For any given $M>0$, we denote the map of prediction of the inverse problem given partial measurement points $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{M}$ as $T_{M}$ and the corresponding error function as $E_{M} \left( {\bar{{\varvec{t}}}} \right) \equiv \left( {I-T_{M}^{\dagger } \circ T_{M} } \right) \left( {\bar{{\varvec{t}}}} \right)$. We claim that if $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ is locally dense in $\Omega$, then

$$\begin{aligned} \left\| {E_{M} \left( {\bar{{\varvec{t}}}} \right) } \right\| _{L^{2}} \rightarrow 0,\quad \hbox {as }M\rightarrow \infty . \end{aligned}$$

(60)

In order to prove (60), we need the following lemmas:

Lemma 1

If a real analytic function ${\varvec{u}}$ on $\Omega$ vanishes on a set of positive measure, then ${\varvec{u}}$ is identically zero [52].

Lemma 2

If $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ is locally dense in $\Omega$, then ${\mathcal {R}}_{\infty }^{\bot } =\left\{ {\mathbf {0}} \right\}$. Here ${\mathcal {R}}_{\infty } \equiv span\left\{ {\bar{{\varvec{t}}}_{ij}, j=1,2,3} \right\} _{i=1}^{\infty }$ where $\bar{{\varvec{t}}}_{ij}$ is defined in (57).

Proof

Consider an arbitrary element $\bar{{\varvec{t}}}^{\prime }\in {\mathcal {R}}_{\infty }^{\bot }$ which by definition satisfies

$$\begin{aligned} \int \limits _{\Gamma _{t} } {\bar{{\varvec{t}}}^{\prime }\cdot \bar{{\varvec{t}}}_{ij} dA} =0, \quad \forall i\ge 1,\quad j=1,2,3 \end{aligned}$$

(61)

Notice

$$\begin{aligned} \int \limits _{\Gamma _{t} } {\bar{{\varvec{t}}}^{\prime }\cdot \bar{{\varvec{t}}}_{ij} dA}= & {} \int \limits _{\Gamma _{t} } {\bar{{\varvec{t}}}^{\prime }\left( {{\varvec{y}}} \right) \cdot {\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \cdot {\varvec{e}}_{j} dA} \end{aligned}$$

(62)

$$\begin{aligned}= & {} {\varvec{e}}_{j} \cdot \int \limits _{\Gamma _{t} } {{\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \bar{{\varvec{t}}}^{\prime }\left( {{\varvec{y}}} \right) dA} ={\varvec{e}}_{j} \cdot {\varvec{u}}\left[ \bar{{\varvec{t}}}^{\prime } \right] ({\varvec{p}}_{i} ).\nonumber \\ \end{aligned}$$

(63)

(61) indicates that the elastic displacement ${\varvec{u}}\left[ \bar{{\varvec{t}}}^{\prime } \right]$ to (48) vanishes at ${\varvec{p}}_{i}$ for $i\ge 1$. On the other hand, according to Gurtin [21], ${\varvec{u}}\left[ \bar{{\varvec{t}}}^{\prime } \right]$ is a real analytic function in $\Omega$. Due to lemma 1, therefore, the elastic solution vanishes everywhere in $\Omega$, i.e. ${\varvec{u}}\left[ \bar{{\varvec{t}}}^{\prime } \right] =\mathbf {0}$. Further, notice that the material is assumed to be compressible, we have ${\varvec{\sigma }}\left[ \bar{{\varvec{t}}}^{\prime } \right] =\mathbf {0}$ and hence $\bar{{\varvec{t}}}^{\prime }={\varvec{\sigma }}\left[ \bar{{\varvec{t}}}^{\prime } \right] \cdot {\varvec{n}}=\mathbf {0}$ on $\Gamma _{t}$.

Corollary

$\overline{{\mathcal {R}}_{\infty } } =\left\{ \mathbf{0} \right\} ^{\bot }={\varvec{W}}_{f}$, i.e., $\left\{ {\bar{{\varvec{t}}}_{ij} ,j=1,2,3,i\ge 1} \right\}$ is dense in ${\varvec{W}}_{f}$.

We are now in a position to prove (60), which is summarized in the following theorem:

Theorem

If $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ is locally dense in $\Omega$, then $\forall \bar{{\varvec{t}}}\in {{\varvec{W}}}_{f}$, $\left\| {E_{M} \left( {\bar{{\varvec{t}}}} \right) } \right\| _{L^{2}} \rightarrow 0$ as $M\rightarrow \infty$.

Proof

According to the above corollary, $\left\{ \bar{{\varvec{t}}}_{ij}, j=1,2,3,\right. \left. i\ge 1 \right\}$ is dense in ${\varvec{W}}_{f}$ given that $\left\{ {{\varvec{p}}_{i} } \right\} _{i=1}^{\infty }$ is locally dense in $\Omega$. As a result, for any $\bar{{\varvec{t}}}\in {{\varvec{W}}}_{f}$ and $\varepsilon >0$, there exists $\left\{ {{\varvec{u}}_{i} } \right\} _{i=1}^{\infty }$ and $M_{\varepsilon }$ such that $\left\| {\bar{{\varvec{t}}}-\bar{{\varvec{t}}}_{p}^{M} } \right\| _{L^{2}} <\varepsilon$ for $\forall M>M_{\varepsilon }$ where $\bar{{\varvec{t}}}_{p}^{M} =\sum \limits _{i=1}^M {{\varvec{G}}\left( {{\varvec{p}}_{i}, {\varvec{y}}} \right) \cdot {\varvec{u}}_{i} }$. Note $\bar{{\varvec{t}}}_{p}^{M} \in {\mathcal {R}}\left( {T_{M}^{{*}} } \right)$, we have $E_{M} \left( {\bar{{\varvec{t}}}_{p}^{M} } \right) =0$ and further, due to linearity of the error function,

$$\begin{aligned} E_{M} \left( {\bar{{\varvec{t}}}} \right) =E_{M} \left( {\bar{{\varvec{t}}}-\bar{{\varvec{t}}}_{p}^{M} } \right) . \end{aligned}$$

(64)

From our earlier discussion, $\left\| {E_{M} } \right\| \le 1$ is uniformly bounded. Therefore, (64) leads to that $\left\| {E_{M} \left( {\bar{{\varvec{t}}}} \right) } \right\| _{L^{2}} \le \left\| {\bar{{\varvec{t}}}-\bar{{\varvec{t}}}_{p}^{M} } \right\| _{L^{2}} <\varepsilon$, which is true for any $M>M_{\varepsilon }$.

To this end, we’ve proved that $\forall \bar{{\varvec{t}}}\in {{\varvec{W}}}_{f}$, $\left\| {E_{M} \left( {\bar{{\varvec{t}}}} \right) } \right\| _{L^{2}} \rightarrow 0$, as $M\rightarrow \infty$.