A variational formulation with rigid-body constraints for finite elasticity: theory, finite element implementation, and applications

Abstract

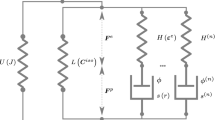
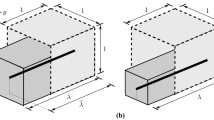
This paper presents a new variational principle in finite elastostatics applicable to arbitrary elastic solids that may contain constitutively rigid spatial domains (e.g., rigid inclusions). The basic idea consists in describing the constitutive rigid behavior of a given spatial domain as a set of kinematic constraints over the boundary of the domain. From a computational perspective, the proposed formulation is shown to reduce to a set of algebraic constraints that can be implemented efficiently in terms of both single-field and mixed finite elements of arbitrary order. For demonstration purposes, applications of the proposed rigid-body-constraint formulation are illustrated within the context of elastomers, reinforced with periodic and random distributions of rigid filler particles, undergoing finite deformations.

Appendix: On the FE implementation in 3D

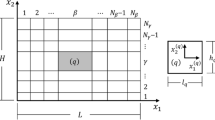
This appendix briefly describes the generalization of the FE implementation of the proposed rigid-body-constraint formulation to 3D. In this case, a set of four non-coplanar “reference” nodes is needed for each interface $\Gamma ^i_h$ (in 3D, $\Gamma ^i_h$ is the boundary of a polyhedral $\Omega _{i h}^{(2)}$). Assuming that we have four non-coplanar “reference” nodes for the interface $\Gamma ^i_h$, denoted as $\widetilde{\mathbf{X }}^i_r=\left\{ \tilde{x}^i_r,\tilde{y}^i_r,\tilde{z}^i_r\right\} ^T, r=1,2,3,4$, any linear field $g\left( \mathbf X \right)$ can be interpolated exactly via

$$\begin{aligned} g\left( \mathbf X \right) =\sum _{r=1}^4\phi ^i_r\left( \mathbf X \right) \widetilde{g}^i_{,r}, \end{aligned}$$

(81)

where the interpolation functions are of the form

$$\begin{aligned} \phi ^i_1\left( \mathbf X \right)= & {} \frac{ \begin{vmatrix} 1&\quad x&\quad y&\quad z\\ 1&\quad \widetilde{x}^i_2&\quad \widetilde{y}^i_2&\quad \widetilde{z}^i_2\\ 1&\quad \widetilde{x}^i_3&\quad \widetilde{y}^i_3&\quad \widetilde{z}^i_3\\ 1&\quad \widetilde{x}^i_4&\quad \widetilde{y}^i_4&\quad \widetilde{z}^i_4\\ \end{vmatrix}}{\widetilde{\phi }^i},\quad \phi ^i_2\left( \mathbf X \right) =\frac{ \begin{vmatrix} 1&\quad \widetilde{x}^i_1&\quad \widetilde{y}^i_1&\quad \widetilde{z}^i_1\\ 1&\quad x&\quad y&\quad z\\ 1&\quad \widetilde{x}^i_3&\quad \widetilde{y}^i_3&\quad \widetilde{z}^i_3\\ 1&\quad \widetilde{x}^i_4&\quad \widetilde{y}^i_4&\quad \widetilde{z}^i_4\\ \end{vmatrix}}{\widetilde{\phi }^i}, \nonumber \\ \end{aligned}$$

(82)

$$\begin{aligned} \phi ^i_3\left( \mathbf X \right)= & {} \frac{ \begin{vmatrix} 1&\quad \widetilde{x}^i_1&\quad \widetilde{y}^i_1&\quad \widetilde{z}^i_1\\ 1&\quad \widetilde{x}^i_2&\quad \widetilde{y}^i_2&\quad \widetilde{z}^i_2\\ 1&\quad x&\quad y&\quad z\\ 1&\quad \widetilde{x}^i_4&\quad \widetilde{y}^i_4&\quad \widetilde{z}^i_4\\ \end{vmatrix}}{\widetilde{\phi }^i},\quad \phi ^i_4\left( \mathbf X \right) =\frac{ \begin{vmatrix} 1&\quad \widetilde{x}^i_1&\quad \widetilde{y}^i_1&\quad \widetilde{z}^i_1\\ 1&\quad \widetilde{x}^i_2&\quad \widetilde{y}^i_2&\quad \widetilde{z}^i_2\\ 1&\quad \widetilde{x}^i_3&\quad \widetilde{y}^i_3&\quad \widetilde{z}^i_3\\ 1&\quad x&\quad y&\quad z\\ \end{vmatrix}}{\widetilde{\phi }^i}\nonumber \\ \end{aligned}$$

(83)

with

$$\begin{aligned} \widetilde{\phi }^i= \begin{vmatrix} 1&\quad \widetilde{x}^i_1&\quad \widetilde{y}^i_1&\quad \widetilde{z}^i_1\\ 1&\quad \widetilde{x}^i_2&\quad \widetilde{y}^i_2&\quad \widetilde{z}^i_2\\ 1&\quad \widetilde{x}^i_3&\quad \widetilde{y}^i_3&\quad \widetilde{z}^i_3\\ 1&\quad \widetilde{x}^i_4&\quad \widetilde{y}^i_4&\quad \widetilde{z}^i_4\\ \end{vmatrix}, \end{aligned}$$

(84)

and $\mathbf X =\left\{ x,y,z\right\} ^T$. With help of (81), the unknown fields $\mathbf u ^i_0$ and $\mathbf H ^i$ can be written as

$$\begin{aligned} \mathbf u ^i_0+\mathbf H ^i\mathbf X =\sum _{r=1}^4\phi ^i_k \left( \mathbf X \right) \widetilde{\mathbf{u }}^i_{,r} \end{aligned}$$

(85)

with $\widetilde{\mathbf{u }}^i_{,r}=\left\{ \widetilde{u}^i_{x,r},\widetilde{u}^i_{y,r},\widetilde{u}^i_{z,r}\right\} ^T$. The remainder of the generalizations for both displacement-based and mixed approximations can be obtained by simply expanding the dimensions of nodal variables (and consequently, the corresponding arrays and matrices), and following the same procedure described for the 2D case. For conciseness, they are not presented here. As a final remark, we note that there is a total of $3n-6$ constraining equations for a given interface $\Gamma ^i_h$ with n boundary nodes in 3D. Moreover, $3n-12$ of the constraining equations are linear on the displacement DOFs (corresponding to Eqs. (71), (75) in 2D), and the remaining 6 are quadratic on the displacement DOFs of the “reference” nodes (corresponding to Eqs. (70), (74) in 2D).