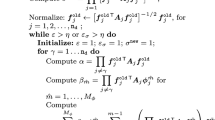Arlequin based PGD domain decomposition

Abstract

Problems defined in fully or partially separable domains can be solved by considering a space separated representation of the unknown fields. Thus three-dimensional problems can be solved from the solution of some one-dimensional problems in the case of fully separated representations involving the three space coordinates or as a sequence of 2D and 1D problems in the case of partially separated representations (plates, shells or extruded geometries). When the domains become more complex, sometimes they can be simplified by using appropriate mappings. When it is not possible or such a transformation becomes too complex, the use of domain decomposition could facilitate the use of separated representations. However, domain coupling in the context of space separated representations have never been analyzed. In this paper we propose a domain decomposition strategy based on the use of space separated representations and the Arlequin coupling strategy. First we consider separated representations of the physical space that will be then extended to address parametric solutions.

Appendices

Separated representation constructor: alternating direction strategy

Each iteration of the alternating direction scheme consists in the following two steps:

• Calculating $X_n^{p}(x)$ from $Y_n^{p-1}(y)$ In this case, the approximation reads

  $$\begin{aligned} u^{n,p} (x,y) = \sum \limits _{i=1}^{n-1} X_i (x) \cdot Y_i (y) + X_n^p(x) \cdot Y_n^{p-1}(y) , \end{aligned}$$

  (53)

  where all functions are known except $X_n^p(x)$. The simplest choice for the weight function $u^*$ in the weighted residual formulation (7) is

  $$\begin{aligned} u^*(x,y) = X_n^*(x) \cdot Y_n^{p-1}(y), \end{aligned}$$

  (54)

  which amounts to select the Galerkin weighted residual form of the Poisson equation. Injecting (53) and (54) into (7), we obtain

  $$\begin{aligned}&\int \limits _{\varOmega _x \times \varOmega _y} X_n^*\cdot Y_n^{p-1} \cdot \Bigg ( \frac{d^2 X_n^p}{d x^2} \cdot Y_n^{p-1}\nonumber \\&\quad + X_n^p \cdot \frac{d^2 Y_n^{p-1}}{d y^2} \Bigg ) \ dx \cdot dy \ = \nonumber \\&\quad - \int \limits _{\varOmega _x \times \varOmega _y} X_n^*\cdot Y_n^{p-1} \cdot \sum \limits _{i=1}^{n-1} \Bigg ( \frac{d^2 X_i}{d x^2} \cdot Y_i \nonumber \\&\quad + X_i \cdot \frac{d^2 Y_i}{d y^2} \Bigg ) \ dx \cdot dy \ \nonumber \\&\quad + \ \int \limits _{\varOmega _x \times \varOmega _y} X_n^*\cdot Y_n^{p-1} \cdot f \ dx \cdot dy . \end{aligned}$$

  (55)

  Here comes a crucial point: since all functions of $y$ are known in the above expression, we can compute the following one-dimensional integrals over $\varOmega _y$:

  $$\begin{aligned} \left\{ \begin{array}{l} \alpha ^x = \int \limits _{\varOmega _y} \left( Y_n^{p-1}(y) \right) ^2 \ dy \\ \beta ^x = \int _{\varOmega _y} Y_n^{p-1}(y) \cdot \displaystyle {\frac{d^2 Y_n^{p-1}(y)}{d y^2}} \ dy \\ \gamma ^x_i = \int \limits _{\varOmega _y} Y_n^{p-1}(y) \cdot Y_i(y) \ dy \\ \delta ^x_i = \int \limits _{\varOmega _y} Y_n^{p-1}(y) \cdot \displaystyle {\frac{d^2 Y_i(y)}{d y^2}} \ dy \\ \xi ^x = \int \limits _{\varOmega _y} Y_n^{p-1}(y) \cdot f \ dy \end{array} \right. . \end{aligned}$$

  (56)

  Equation (55) becomes

  $$\begin{aligned}&\int \limits _{\varOmega _x } X_n^*\cdot \left( \alpha ^x \cdot \frac{d^2 X_n^p}{d x^2} + \beta ^x \cdot X_n^p \right) \ dx \ =\nonumber \\&- \int \limits _{\varOmega _x} X_n^*\cdot \sum \limits _{i=1}^{n-1} \left( \gamma ^x_i \cdot \frac{d^2 X_i}{d x^2} + \delta ^x_i \cdot X_i \right) \ dx \ \nonumber \\&\quad +\int \limits _{\varOmega _x} X_n^*\cdot \xi ^x \ dx .\nonumber \\ \end{aligned}$$

  (57)

  We have thus obtained the weighted residual form of a one-dimensional problem defined over $\varOmega _x$ that can be solved (e.g. by the finite element method) to obtain the function $X_n^{p}$ we are looking for. Alternatively, we can return to the corresponding strong formulation

  $$\begin{aligned}&\alpha ^x \cdot \frac{d^2 X_n^p}{d x^2} \!+\! \beta ^x \cdot X_n^p \ \!=\! \!-\!\ \sum \limits _{i\!=\!1}^{n-1} \left( \gamma ^x_i \cdot \frac{d^2 X_i}{d x^2} \!+\! \delta ^x_i \cdot X_i \right) \ \nonumber \\&\quad + \ \xi ^x , \end{aligned}$$

  (58)

  and solve it numerically by means of any suitable numerical method (e.g. finite differences, pseudo-spectral techniques, ...). The strong form (57) is a second-order ordinary differential equation for $X_n^{p}$. This is due to the fact that the original Poisson equation involves a second-order $x$-derivative of the unknown field $u$. With either the weighted residual or strong formulations, the homogeneous Dirichlet boundary conditions $X_n^p(x=0)=X_n^p(x=L)=0$ are readily specified. Having thus computed $X_n^p(x)$, we are now ready to proceed with the second step of iteration $p$.

• Calculating $Y_n^{p}(y)$ from the just-computed $X_n^p(x)$ The procedure exactly mirrors what we have done above. Indeed, we simply exchange the roles played by all relevant functions of $x$ and $y$. The current PGD approximation reads

  $$\begin{aligned} u^{n,p} (x,y) = \sum \limits _{i=1}^{n-1} X_i (x) \cdot Y_i (y) + X_n^p(x) \cdot Y_n^{p}(y), \end{aligned}$$

  (59)

  where all functions are known except $Y_n^p(y)$ . The Galerkin formulation of (7) is obtained with the particular choice

  $$\begin{aligned} u^*(x,y) = X_n^p(x) \cdot Y_n^*(y) . \end{aligned}$$

  (60)

  Then, by introducing (59) and (60) into (7), we get

  $$\begin{aligned}&\int \limits _{\varOmega _x \times \varOmega _y} X_n^p \cdot Y_n^*\cdot \left( \frac{d^2 X_n^p}{d x^2} \cdot Y_n^p + X_n^p \cdot \frac{d^2 Y_n^p}{d y^2} \right) \ dx \cdot dy \nonumber \\&\quad =-\, \int \limits _{\varOmega _x \times \varOmega _y} X_n^p \cdot Y_n^*\cdot \sum \limits _{i=1}^{n-1} \left( \frac{d^2 X_i}{d x^2} \cdot Y_i \!+\! X_i \cdot \frac{d^2 Y_i}{d y^2} \right) \ dx \cdot dy\nonumber \\&\quad + \, \int \limits _{\varOmega _x \times \varOmega _y} X_n^p \cdot Y_n^*\cdot f \ dx \cdot dy . \end{aligned}$$

  (61)

  As all functions of $x$ are known, the integrals over $\varOmega _x$ can be computed to obtain

  $$\begin{aligned} \left\{ \begin{array}{l} \alpha ^y = \int \limits _{\varOmega _x} \left( X_n^p(x) \right) ^2 \ dx \\ \beta ^y = \int \limits _{\varOmega _x} X_n^p(x) \cdot \displaystyle {\frac{d^2 X_n^p(x)}{d x^2}} \ dx \\ \gamma ^y_i = \int \limits _{\varOmega _x} X_n^p(x) \cdot X_i(x) \ dx \\ \delta ^y_i = \int \limits _{\varOmega _x} X_n^p(x) \cdot \displaystyle {\frac{d^2 X_i(x)}{d x^2} } \ dx \\ \xi ^y = \int \limits _{\varOmega _x} X_n^p(x) \cdot f \ dx \end{array} \right. . \end{aligned}$$

  (62)

  Equation (61) becomes

  $$\begin{aligned}&\int \limits _{\varOmega _y } Y_n^*\cdot \left( \alpha ^y \cdot \frac{d^2 Y_n^p}{d y^2} + \beta ^y \cdot Y_n^p \right) \ dy = \nonumber \\&\quad - \int \limits _{\varOmega _y} Y_n^*\cdot \sum \limits _{i=1}^{n-1} \left( \gamma ^y_i \cdot \frac{d^2 Y_i}{d y^2} + \delta ^y_i \cdot Y_i \right) \ dy \ \nonumber \\&\quad + \, \int \limits _{\varOmega _y} Y_n^*\cdot \xi ^y \ dy. \end{aligned}$$

  (63)

  As before, we have thus obtained the weighted residual form of an elliptic problem defined over $\varOmega _y$ whose solution is the function $Y_n^{p}(y)$. Alternatively, the corresponding strong formulation of this one-dimensional problem reads

  $$\begin{aligned}&\alpha ^y \cdot \frac{d^2 Y_n^p}{d y^2} + \beta ^y \cdot Y_n^p \nonumber \\&\quad = \ -\sum \limits _{i=1}^{n-1} \left( \gamma ^y_i \cdot \frac{d^2 Y_i}{d y^2} + \delta ^y_i \cdot Y_i \right) + \, \xi ^y . \end{aligned}$$

  (64)

  This again is an ordinary differential equation of the second order, due to the fact that the original Poisson equation involves second-order derivatives of the unknown field with respect to $y$. With both the weighted residual and strong formulations, the homogeneous Dirichlet boundary conditions $Y_n^p(y=0)=Y_n^p(y=L)=0$ are readily specified.

We have thus completed iteration $p$ at enrichment step $n$.

Separated representation of the transformation Jacobians

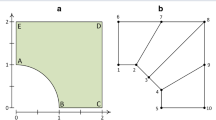
The different Jacobian $\mathcal {J}_1^j$ related to the mapping $\mathcal {D}_1^j \rightarrow \mathcal {V}_1^j$ can be in the present example easily obtained for $j=1, \ldots , 6$:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {J}_1^1 = \left( \begin{array}{cc} 1&{} 0 \\ 0&{}0.5 \end{array} \right) , &{} \mathbf {x} \in (0, 1.5) \times (0, 1) \\ \\ \mathcal {J}_1^2 = \left( \begin{array}{cc} 1&{} 0 \\ 0&{} 1 \end{array}\right) , &{} \mathbf {x} \in (0,1.5) \times (1,2) \\ \\ \mathcal {J}_1^3 = \left( \begin{array}{cc} 1&{}0 \\ 0&{}1.5 \end{array}\right) , &{} \mathbf {x} \in (0,1.5) \times (2,3) \\ \\ \mathcal {J}_1^4 =\left( \begin{array}{cc} 1&{} y \\ 0&{} x-1 \end{array}\right) , &{} \mathbf {x} \in (1.5,2) \times (0,1) \\ \\ \mathcal {J}_1^5 =\left( \begin{array}{cc} 1&{} 1 \\ 0&{} 1 \end{array}\right) , &{} \mathbf {x} \in (1.5,2) \times (1,2) \\ \\ \mathcal {J}_1^6 =\left( \begin{array}{cc} 1&{} 3-y \\ 0&{} 3-x \end{array}\right) ,&\mathbf {x} \in (1.5,2) \times (2,3) \end{array}\right. \end{aligned}$$

(65)

and similarly for the mapping $\mathcal {D}_2^k \rightarrow \mathcal {V}_2^k$, $k=1,2$.

The associated determinants result:

$$\begin{aligned} \left\{ \begin{array}{l} \det (\mathcal {J}_1^1) = 0.5 \\ \\ \det (\mathcal {J}_1^2) = 1 \\ \\ \det (\mathcal {J}_1^3) = 1.5 \\ \\ \det (\mathcal {J}_1^4) = x-1\\ \\ \det (\mathcal {J}_1^5) = 1 \\ \\ \det (\mathcal {J}_1^6) = 3-x \end{array}\right. \end{aligned}$$

(66)

The Jacobian of the inverse transformations also accepts a fully separated representation because as just proved the determinant of the Jacobian only involves functions of $x$. For example, when considering $(\mathcal {J}_1^6)^{-1}$

$$\begin{aligned} (\mathcal {J}_1^6)^{-1} = \frac{1}{\det (\mathcal {J}_1^6)} \ \left( \begin{array}{cc} 3-x &{} y-3 \\ 0 &{} 1 \end{array} \right) = \left( \begin{array}{cc} 1 &{} \frac{y-3}{3-x} \\ 0 &{} \frac{1}{3-x} \end{array} \right) \end{aligned}$$

(67)

that proves its fully separability.

In the most general case in which the determinant involves a two-terms sum where each term consists of the product of a function of $x$ times a function of $y$, the components of $(\mathcal {J}_1^j)$ have not a direct separated representation [4]. Approximated separated representations can be obtained by invoking the SVD (or the HOSVD) as indicated before.

After being calculated the Jacobian of the direct and inverse transformations of each quadrilateral we can compact the notation by introducing the characteristic function of each quadrilateral $\mathcal {V}_1^j$ and $\mathcal {V}_2^k$:

$$\begin{aligned} \chi _1^j(\mathbf {x}) = \left\{ \begin{array}{ll} 1 &{}\quad if \ \mathbf {x} \in \mathcal {V}_1^j = \left( x_1^{j-},x_1^{j+}\right) \times \left( y_1^{j-},y_1^{j+}\right) \\ 0 &{}\quad elsewhere \end{array} \right. \end{aligned}$$

(68)

and

$$\begin{aligned} \chi _2^k(\mathbf {x}) = \left\{ \begin{array}{ll} 1 &{}\quad if \ \mathbf {x} \in \mathcal {V}_2^k = \left( x_2^{k-},x_2^{k+}\right) \times \left( y_2^{k-},y_2^{k+}\right) \\ 0 &{}\quad elsewhere \end{array} \right. \end{aligned}$$

(69)

from which we can write the Jacobian of the mappings $\varOmega _1 \rightarrow \mathcal {T}_1$ and $\varOmega _2 \rightarrow \mathcal {T}_2$, respectively $\mathcal {J}_1$ and $\mathcal {J}_2$:

$$\begin{aligned} \mathcal {J}_1(\mathbf {x} \in \mathcal {T}_1) = \sum \limits _{j=1}^{6} \chi _1^j(\mathbf {x}) \cdot \mathcal {J}_1^j(\mathbf {x}) \end{aligned}$$

(70)

and

$$\begin{aligned} \mathcal {J}_2(\mathbf {x} \in \mathcal {T}_2) = \sum \limits _{k=1}^{2} \chi _2^k(\mathbf {x}) \cdot \mathcal {J}_2^k(\mathbf {x}) \end{aligned}$$

(71)

and similarly for the inverse transformations

$$\begin{aligned} (\mathcal {J}_1)^{-1}(\mathbf {x} \in \mathcal {T}_1) = \sum \limits _{j=1}^{6} \chi _1^j(\mathbf {x}) \cdot \left( \mathcal {J}_1^j(\mathbf {x})\right) ^{-1} \end{aligned}$$

(72)

and

$$\begin{aligned} (\mathcal {J}_2)^{-1}(\mathbf {x} \in \mathcal {T}_2) = \sum \limits _{k=1}^{2} \chi _2^k(\mathbf {x}) \cdot \left( \mathcal {J}_2^k(\mathbf {x})\right) ^{-1} \end{aligned}$$

(73)

The mapping determinants can be also expressed in the compact form

$$\begin{aligned} \det (\mathcal {J}_1(\mathbf {x} \in \mathcal {T}_1)) = \sum \limits _{j=1}^{6} \chi _1^j(\mathbf {x}) \cdot \ \det \left( \mathcal {J}_1^j(\mathbf {x})\right) \end{aligned}$$

(74)

and

$$\begin{aligned} \det (\mathcal {J}_2(\mathbf {x} \in \mathcal {T}_2)) = \sum \limits _{k=1}^{2} \chi _2^k(\mathbf {x}) \cdot \ \det \left( \mathcal {J}_2^k(\mathbf {x})\right) \end{aligned}$$

(75)