Implicit yield function formulation for granular and rock-like materials

Abstract

The constitutive modelling of granular, porous and quasi-brittle materials is based on yield (or damage) functions, which may exhibit features (for instance, lack of convexity, or branches where the values go to infinity, or ‘false elastic domains’) preventing the use of efficient return-mapping integration schemes. This problem is solved by proposing a general construction strategy to define an implicitly defined convex yield function starting from any convex yield surface. Based on this implicit definition of the yield function, a return-mapping integration scheme is implemented and tested for elastic–plastic (or -damaging) rate equations. The scheme is general and, although it introduces a numerical cost when compared to situations where the scheme is not needed, is demonstrated to perform correctly and accurately.

1 Introduction

The pressure-sensitive yielding of granular, porous, and quasi-brittle materials (such as ceramic or metallic powders, porous metals, rocks and concretes), or the Lode’s angle dependence of high-strength and shape memory alloys, forces the use of complex yield functions in the plastic or damaging constitutive modelling. These yield functions (three examples are those introduced by Jeremic et al. [7], by Foster et al. [5] and by Bigoni and Piccolroaz [2], the last called ‘BP’ in the following) often display ‘undesidered features’, such as for instance lack of convexity, or regions where they blow up to infinity or, as indicated by Brannon and Leelavanichkul [4], ‘false elastic domains’ (in which negative values are associated to stress states external to the ‘true’ elastic domain), preventing the use of standard return-mapping integration algorithms. Moreover, these yield functions often describe high-curvature surfaces and nearly sharp vertices, which are difficult to treat with the necessary accuracy and definitely slow down numerical procedures. Remedies to these problems have been proposed in [4] and [12], but the former technique, based on a multi-stage algorithm, is very complex, while the latter, based on a cutoff-substepping return algorithm, is applicable only to the BP yield function.

The purpose of the present article is to introduce a new approach to the problem, where a general procedure to construct an implicit definition of a convex yield function starting from a convex yield surface is proposed and the related application within a standard return-mapping scheme is explained and tested. The method is general, simple to be implemented, and applies to every convex yield surface. It is shown to be, on the one hand, associated to a computational cost (which has to be regarded as the counterpart of the complexity of the employed yield function), but on the other hand, to be robust and to provide accurate and stable results.

The paper is organized as follows. The general setting of the implicit yield function formulation is presented in Sect. 2. The original BP yield function [2] is recalled, and its undesired features are illustrated in Sect. 3. In Sect. 4, the general formulation is specified for the BP yield surface: the implicit yield function is formulated in the $(p,q)$-space, and the presentation style is oriented towards computer implementation employing an automatic differentiation (AD) technique and AceGen, an automatic code generation system [8, 9]. The complete AceGen input is also provided as a supplementary material accompanying the paper along with ready-to-use subroutines in C, Fortran, Mathematica and Matlab. Feasibility of the implicit yield function concept in incremental elastoplasticity is finally illustrated in Sect. 5.

2 Implicit yield function: general setting

Consider a yield function $F(\varvec{\sigma },\varvec{\eta })$, depending on stress $\varvec{\sigma }$ and hardening variables $\varvec{\eta }$, that defines a convex elastic domain $\mathcal{E}$ such that the boundary $\partial \mathcal{E}$ of the elastic domain, i.e., the yield surface, is specified by the zero level set, $F(\varvec{\sigma },\varvec{\eta })=0$. As discussed in the introduction, the yield function $F$ may be non-convex or defined infinity in some regions, see Sect. 3 for the illustration of those features in the case of the BP yield function.

The strategy proposed in the present paper to overcome the difficulties mentioned above is to introduce an alternative yield function $F^*(\varvec{\sigma },\varvec{\eta })$ that is defined for an arbitrary stress, and such that its zero level set $F^*=0$ (i.e., the yield surface) is identical to that of the original yield function, $F=0$. In this way, the elastic domain $\mathcal{E}$ and its closure, which are the only two relevant quantities from the mechanical point of view, will remain the same as for the original yield function $F(\varvec{\sigma },\varvec{\eta })$, but convexity and finiteness will be enforced.

Note that the yield surface may be non-convex with respect to the hardening or damage variables $\varvec{\eta }$ which could result in convergence problems in an incremental computational scheme, e.g., [16]. However, such non-convexity would be a constitutive feature of a specific hardening/softening law that cannot be removed by reformulating the yield function itself. For the sake of a compact notation, we will skip the dependence of $F$ on $\varvec{\eta }$ in this section, because only the dependency on $\varvec{\sigma }$ is relevant in the following.

The main idea is to use the so-called convex distance function $d_\mathcal{E}(\varvec{\sigma })$ of the zero level set $F=0$, i.e., the boundary of the elastic domain $\partial \mathcal{E}$, of the original yield function. The convex distance function is defined as

$$\begin{aligned} d_\mathcal{E}(\varvec{\sigma }) := \frac{\Vert \varvec{\sigma } - \mathbf o \Vert }{\Vert \varvec{\sigma }_0(\varvec{\sigma }) - \mathbf o \Vert } \end{aligned}$$

(1)

with $\Vert \cdot \Vert$ being the 2-norm, $\mathbf o \in \mathcal{E}{\setminus }\partial \mathcal{E}$ representing a fixed reference point inside the elastic domain, and we define $d_\mathcal{E}(\mathbf o ) = 0$. The convex distance function has the property

$$\begin{aligned} d_\mathcal{E}(\varvec{\sigma }) = {\left\{ \begin{array}{ll} [0, 1)&{} \text {if}\quad \varvec{\sigma } \in \mathcal{E} {\setminus } \partial \mathcal{E} \\ 1 &{} \text {if}\quad \varvec{\sigma } \in \partial \mathcal{E} \\ > 1 &{} \text {if}\quad \varvec{\sigma } \not \in \mathcal{E} \end{array}\right. } \end{aligned}$$

(2)

and it is a convex function, see [3, 6] for a proof. In this definition, $\varvec{\sigma }_0(\varvec{\sigma })$ is the unique intersection of a ray from $\mathbf o$ in the direction of $\varvec{\sigma }$ with the boundary $\partial \mathcal{E}$ of the elastic domain as depicted in Fig. 1.

Fig. 1

Convex distance function

To compute the unique intersection point $\varvec{\sigma }_0(\varvec{\sigma })$ we define a ray from the reference point $\mathbf o$ in the direction of $\varvec{\sigma }$ by

$$\begin{aligned} \mathbf r (\varvec{\sigma }, \hat{\varrho }) = \mathbf o + \hat{\varrho } \mathbf e _r \end{aligned}$$

(3)

with

$$\begin{aligned} \mathbf e _r = \frac{\varvec{\sigma } - \mathbf o }{\Vert \varvec{\sigma } - \mathbf o \Vert } , \quad \hat{\varrho } > 0 \quad \mathrm{and} \quad \varvec{\sigma } \ne \mathbf o , \end{aligned}$$

(4)

and introduce the following abbreviations

$$\begin{aligned} \varvec{\varrho } = \varvec{\sigma }-\mathbf o , \quad \varvec{\varrho }_0 = \varvec{\sigma }_0-\mathbf o , \quad \varrho = \Vert \varvec{\varrho }\Vert , \quad \varrho _0=\Vert \varvec{\varrho }_0\Vert , \end{aligned}$$

(5)

so that $\mathbf r (\varvec{\sigma },\varrho )=\varvec{\sigma }$ and $\mathbf r (\varvec{\sigma },\varrho _0)=\varvec{\sigma }_0$.

The intersection of the ray with the boundary $\partial \mathcal{E}$ of the elastic domain, i.e. the original yield surface, is computed by

$$\begin{aligned} F_0(\varrho _0,\varvec{\sigma }) = F(\mathbf r (\varvec{\sigma }, \varrho _0)) = 0 , \end{aligned}$$

(6)

which, for a fixed $\varvec{\sigma }$, is in general a nonlinear equation for $\varrho _0$. One would solve this nonlinear equation, e.g., by a Newton-type or a regula falsi method. If $\varrho _0$ is the unique solution of Eq. 6, then the intersection point is given by

$$\begin{aligned} \varvec{\sigma }_0(\varvec{\sigma }) = \mathbf r (\varvec{\sigma }, \varrho _0(\varvec{\sigma })) , \end{aligned}$$

(7)

where we indicate that the solution $\varrho _0$ depends (implicitly) on $\varvec{\sigma }$ through Eq. (6).

With this at hand, we can implicitly define a new convex yield function $F^*$ based only on the yield surface $F = 0$ of the original yield function by

$$\begin{aligned} F^*(\varvec{\sigma }) = d_\mathcal{E}(\varvec{\sigma }) - 1 = \frac{\varrho (\varvec{\sigma })}{\varrho _0(\varvec{\sigma })} - 1 , \end{aligned}$$

(8)

where the term $-1$ is introduced such that we obtain the common property $F^*=0$ on the yield surface. One should observe that the zero level sets $F^*=0$ and $F=0$ are identical but that the new yield function $F^*$ inherits the convexity from the convex distance function $d_\mathcal{E}$.

In plasticity, we usually need the first derivative of the yield function with respect the the stress $\varvec{\sigma }$, e.g., to define the flow direction in the case of an associated flow rule, and with respect to the hardening variables $\varvec{\eta }$, and often also the second derivative, e.g., to compute the consistent tangent. By differentiating Eq. (8)$_2$, we have

$$\begin{aligned} \frac{\partial F^*}{\partial \varvec{\sigma }} = \frac{1}{\varrho _0} \frac{\partial \varrho }{\partial \varvec{\sigma }} - \frac{\varrho }{\varrho _0^2} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} , \end{aligned}$$

(9)

where the explicit derivative $\partial \varrho /\partial \varvec{\sigma }$ reads

$$\begin{aligned} \frac{\partial \varrho }{\partial \varvec{\sigma }} = \mathbf e _r . \end{aligned}$$

(10)

The dependence of $\varrho _0$ on $\varvec{\sigma }$ is implicit through Eq. (6). To compute the derivative of this implicit dependence, the total derivative of Eq. (6) with respect to $\varvec{\sigma }$ is computed,

$$\begin{aligned}&\frac{\partial }{\partial \varvec{\sigma }} F(\mathbf o + \varrho _0(\varvec{\sigma }) \mathbf e _r(\varvec{\sigma })) \nonumber \\&\quad = \left( \varrho _0 \frac{\partial \mathbf e _r}{\partial \varvec{\sigma }} + \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \otimes \mathbf e _r \right) \left[ \left. \frac{\partial F}{\partial \varvec{\sigma }} \right| _{\varvec{\sigma }_0} \right] = 0 , \end{aligned}$$

(11)

where the gradient of the original yield function $\partial F/\partial \varvec{\sigma }$ is evaluated at $\varvec{\sigma }_0$, and we have

(12)

with denoting the symmetrizing fourth order tensor. In Eq. (11) and in the following, the square brackets indicate double contraction of the second order tensor enclosed within the brackets with the fourth order tensor preceding the brackets. Equation (11) is solved for the implicit derivative $\partial \varrho _0/\partial \varvec{\sigma }$, thus yielding

$$\begin{aligned} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} = \frac{\varrho _0}{\varrho } \mathbf e _r - \frac{\varrho _0}{\varrho } \left( \mathbf e _r \cdot \left. \frac{\partial F}{\partial \varvec{\sigma }} \right| _{\varvec{\sigma }_0} \right) ^{-1} \left. \frac{\partial F}{\partial \varvec{\sigma }} \right| _{\varvec{\sigma }_0} . \end{aligned}$$

(13)

Finally, combing Eqs. (9), (10) and (13), the first derivative of $F^*$ with respect to $\varvec{\sigma }$ is obtained as

$$\begin{aligned} \frac{\partial F^*}{\partial \varvec{\sigma }} = \frac{1}{\varrho _0} \left( \mathbf e _r \cdot \left. \frac{\partial F}{\partial \varvec{\sigma }} \right| _{\varvec{\sigma }_0} \right) ^{-1} \left. \frac{\partial F}{\partial \varvec{\sigma }} \right| _{\varvec{\sigma }_0} . \end{aligned}$$

(14)

The main ingredient of $\partial F^*/\partial \varvec{\sigma }$ is the gradient of the original yield function $\partial F/\partial \varvec{\sigma }$ evaluated at the intersection point $\varvec{\sigma }_0$, and it is seen that the former is equal to the latter multiplied by a scalar.

For completeness, the second derivative of $F^*$ with respect to $\varvec{\sigma }$ is provided in “Appendix”. The derivatives with respect to the hardening variables $\varvec{\eta }$ and the mixed second derivatives can be obtained analogously. In the implementation approach adopted in the present work, the necessary derivatives of the implicit yield function $F^*$ are obtained using an automatic differentiation technique, hence the explicit formulae are, in fact, not needed. The corresponding formulation, with application to the BP yield function, is presented in Sect. 4.

3 Original BP yield function

In this section, the original Bigoni–Piccolroaz (BP) yield function [2] is briefly introduced, and its deficiencies concerning its practical application in computational plasticity are illustrated.

Introduce first the following invariants of the stress tensor $\varvec{\sigma }$:

$$\begin{aligned} p = -\frac{1}{3} \, \text{ tr }\varvec{\sigma } , \quad q = \sqrt{3 J_2} , \quad \theta = \frac{1}{3} \, \cos ^{-1} \left( \frac{3\sqrt{3}}{2} \, \frac{J_3}{J_2^{3/2}} \right) ,\nonumber \\ \end{aligned}$$

(15)

where $\theta$ is the Lode angle, and $J_2=\frac{1}{2}\varvec{\sigma }'\cdot \varvec{\sigma }'$ and $J_3=\det \varvec{\sigma }'$ are the usual invariants of the stress deviator $\varvec{\sigma }'=\varvec{\sigma }+\frac{1}{3}p\mathbf I$, see, for instance, [1].

The original BP yield function is defined by the following equations:

$$\begin{aligned} F(\varvec{\sigma },\varvec{\eta }) = \hat{F}(p,q,\theta ,\varvec{\eta }) = f(p) + \frac{q}{g(\theta )} , \end{aligned}$$

(16)

where

$$\begin{aligned} f(p)&= \left\{ \begin{array}{ll} -M p_c \sqrt{(\Phi -\Phi ^m)[2(1-\alpha )\Phi +\alpha ]} \;\; &{} \text{ if } \; \Phi \in [0,1], \\ +\infty &{} \text{ otherwise }, \end{array} \right. \nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned} \Phi&= \frac{p+c}{p_c+c} , \end{aligned}$$

(18)

and

$$\begin{aligned} g(\theta ) = \frac{1}{\cos [\beta \pi /6 - (1/3) \cos ^{-1}(\gamma \cos 3\theta )]} . \end{aligned}$$

(19)

Here, $p_c$ and $c$ define the size and position of the yield surface along the hydrostatic axis, and $M$, $m$, $\alpha$, $\beta$ and $\gamma$ are parameters that define the shape of the yield surface in the stress space. All these parameters may depend on the hardening variables that are here left unspecified and collectively denoted by $\varvec{\eta }$. For instance, in the model for ceramic powder compaction [14, 15], the forming pressure $p_c$ is adopted as the only hardening variable that is related to the volumetric plastic deformation, cohesion $c$ is assumed to depend on $p_c$, while the remaining parameters are assumed constant.

To enforce convexity, the BP yield function in its original version (16) is defined infinity for stress states for which $\Phi \notin [0,1]$, indicated as white zones in Fig. 2a. This is an inconvenience for numerical implementation, as virtually any stress state can be encountered during iterative solution of the incremental constitutive equations resulting, for instance, from application of the return mapping algorithm.

Fig. 2

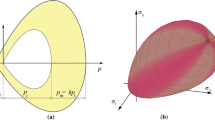
Iso-lines of the BP yield function in the $(p,q)$–space: a original yield function $F$ is defined infinity in the white regions, b the squared yield function $F_2$, Eq. (20), is not convex ($F$ is normalized by $p_c$ and $F_2$ is normalized by $p_c^2$). Parameters of the yield function correspond to alumina powder, see Sect. 5, and Lode angle is assumed as $\theta =0$

One way to overcome this problem is to use a ‘squared version’ of the yield function (16) defined by

$$\begin{aligned} F_2(\varvec{\sigma },\varvec{\eta }) = -f^2(p) + \frac{q^2}{g^2(\theta )} , \end{aligned}$$

(20)

which corresponds to the same BP yield surface and is defined for arbitrary stress, but looses convexity,¹ as illustrated in Fig. 2b. Here, the squared function $f^2(p)$ is defined for arbitrary $p$ by the first branch in Eq. (17). The nonconvex yield function shows, in the terminology introduced by Brannon and Leelavanichkul [4], a ‘false elastic domain’ so that, employing a return mapping algorithm it may happen (for certain trial stresses) that convergence is reached at a wrong stress state. Nonconvexity may also lead to divergence of the corresponding iterative scheme.

4 Implicit yield function in the $(p,q)$-space

In the special case of the BP yield function defined by Eq. (16), one can use the general formulation of the implicit yield function, as presented in Sect. 2. However, as only the pressure-dependent part $f(p)$ specified by Eq. (17) is inconvenient for numerical implementation, it is simpler and thus numerically more efficient to apply the implicit yield function formulation in the $(p,q)$-space, as shown below.

Compared to Sect. 2, a somewhat different presentation style is adopted here, which is oriented towards computer implementation using an automatic differentiation (AD) technique and AceGen, an automatic code generation system [8, 9]. Accordingly, the specific formulae, such as that in Eq. (14) are not provided, as they are not needed, and the focus is on indicating the actual dependencies and on defining the implicit derivatives of $\varrho _0$.

Consider the $(p,q)$-space and the yield surface $F=0$ corresponding to a fixed Lode angle $\theta$, see Fig. 3. The implicit yield function $F^*$ is given by, see Eq. (8),

$$\begin{aligned} F^*(\varvec{\sigma },\varvec{\eta }) = \frac{\varrho }{\varrho _0} - 1 , \end{aligned}$$

(21)

where $\varrho$ is now the distance between the current stress point $(p,q)$ in the $(p,q)$–plane and a reference point $(p_r,0)$ taken inside the yield surface,

$$\begin{aligned} \varrho = \Vert \varvec{\varrho } \Vert , \quad \varvec{\varrho } = (p-p_r,q) , \end{aligned}$$

(22)

and $\varrho _0$ is the distance between the reference point $(p_r,0)$ and the image $(p_0,q_0)$ of the current stress point $(p,q)$,

$$\begin{aligned} \varrho _0 = \Vert \varvec{\varrho }_0 \Vert , \quad \varvec{\varrho }_0 = (p_0-p_r,q_0) , \quad \varvec{\varrho } = (1+F^*) \varvec{\varrho }_0 . \end{aligned}$$

(23)

The image point $(p_0,q_0)$, which is the counterpart of $\varvec{\sigma }_0$ of Sect. 2, lies on the yield surface, thus

$$\begin{aligned} \hat{F}(p_0,q_0,\theta ,\varvec{\eta }) = 0 , \end{aligned}$$

(24)

$\hat{F}$ being the yield function expressed in terms of the invariants, cf. Eq. (16). In the present implementation, the squared version of the yield function, Eq. (20), is actually used instead of the original version (16), as the former is more convenient for practical application.

Fig. 3

Construction of the implicit yield function $F^*$ in the $(p,q)$-space

By construction, the yield function $F^*$ defined by Eq. (21) generates a family of self-similar surfaces $F^*=\text{ const }$ that are scaled with respect to the reference point $(p_r,0)$, as Fig. 3 illustrates. Self-similarity implies that the implicit yield function is convex if the generating yield surface $F=0$ is convex.

The iso-lines of the implicit BP yield function in the $(p,q)$-plane are shown in Fig. 4a (the model parameters are equal to those adopted in Fig. 2). Figure 4b shows the iso-surfaces of the implicit BP yield function in the principal stress space. Here and in the following, the position of the reference point has been assumed as $p_r=(p_c+c)/2$, although other choices (for instance, the center of mass of the yield surface [12]) can be made.

Fig. 4

The iso-lines (iso-surfaces) of the implicit BP yield function: a in the $(p,q)$-space, b in the principal stress space

The value of the yield function $F^*$ is defined implicitly by Eq. (24), i.e., by the condition that the image point lies on the yield surface. This can be formulated as a nonlinear equation for $\varrho _0$ (at fixed $\varvec{\sigma }$ and $\varvec{\eta }$),

$$\begin{aligned} F_0 ( \varrho _0, \varvec{\sigma }, \varvec{\eta } ) = 0 , \end{aligned}$$

(25)

which is solved using the iterative Newton method,

$$\begin{aligned} \varrho _0^{i+1} = \varrho _0^i + \varDelta \varrho _0^i , \quad \varDelta \varrho _0^i = - \left( \frac{\partial F_0}{\partial \varrho _0} \right) ^{-1} F_0 (\varrho _0^i) . \end{aligned}$$

(26)

The solution $\varrho _0$ implicitly depends on the stress $\varvec{\sigma }$ and hardening variables $\varvec{\eta }$ through Eq. (25). The derivative of $\varrho _0$ with respect to $\varvec{\sigma }$ is obtained by taking the total derivative of Eq. (25) with respect to $\varvec{\sigma }$,

$$\begin{aligned} \frac{\partial F_0}{\partial \varrho _0} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} + \frac{\partial F_0}{\partial \varvec{\sigma }} = 0 , \end{aligned}$$

(27)

so that

$$\begin{aligned} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} = - \left( \frac{\partial F_0}{\partial \varrho _0} \right) ^{-1} \frac{\partial F_0}{\partial \varvec{\sigma }} . \end{aligned}$$

(28)

The second derivative, which is also needed, is obtained by differentiating (27) with respect to $\varvec{\sigma }$ again, which gives

$$\begin{aligned} \frac{\partial ^2 \varrho _0}{\partial \varvec{\sigma }\partial \varvec{\sigma }}&= - \left( \frac{\partial F_0}{\partial \varrho _0} \right) ^{-1} \Bigg ( \frac{\partial ^2 F_0}{\partial \varrho _0\partial \varrho _0} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \otimes \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \nonumber \\&+ \frac{\partial ^2 F_0}{\partial \varvec{\sigma }\partial \varvec{\sigma }} + 2 \left( \frac{\partial ^2 F_0}{\partial \varvec{\sigma }\partial \varrho _0} \otimes \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \right) _{ sym} \Bigg ) . \end{aligned}$$

(29)

Derivatives of $\varrho _0$ with respect to hardening variables $\varvec{\eta }$, as well as mixed second derivatives, are obtained analogously. In fact, the formulae for the implicit derivatives of $\varrho _0$ with respect to $\varvec{\eta }$ are obtained by simply replacing $\varvec{\sigma }$ by $\varvec{\eta }$ in Eqs. (28) and (29), with the adequate redefinition of the tensor product in Eq. (29).

The first derivative $\partial \varrho _0/\partial \varvec{\sigma }$, Eq. (28), is needed, for instance, to compute the gradient of the implicit yield function, see Eq. (9). The second derivative comes into play when the constitutive update problem is solved and when the incremental constitutive equations are linearized, see Sect. 5.1.

Computer implementation of the above implicit BP yield function has been performed using AceGen, a code generation system that combines the symbolic algebra capabilities of Mathematica (www.wolfram.com) with an automatic differentiation technique and a stochastic expression optimization technique [8, 9]. In particular, all the necessary explicit derivatives are directly derived by automatic differentiation, while the implicit derivatives of $\varrho _0$, i.e., those specified by Eqs. (28) and (29), are introduced using the so-called AD exceptions implemented in AceGen [9].

The AceGen implementation of the implicit BP yield function is provided as a supplementary material accompanying this paper. Specifically, the complete AceGen input is provided for generating the numerical code that computes the implicit BP yield function $F^*$ and its first and second derivatives with respect to the stress $\varvec{\sigma }$ and with respect to all the parameters defining the yield surface. The AceGen code, as well as the corresponding ready-to-use subroutines in C, Fortran, Mathematica and Matlab, are also available at our web sites.²

5 Application to return mapping algorithm

In this section, feasibility of the implicit yield function concept is illustrated in the context of time integration algorithms in elastoplasticity. The classical return mapping algorithm is first recalled and its performance is subsequently evaluated in the case when the implicit BP yield function is used in an elastoplastic model based on perfect plasticity.

5.1 Return mapping algorithm

The return mapping algorithm is here introduced for the possibly simplest model of elastoplasticity. Specifically, ideal plasticity (no hardening) and the associated flow rule are assumed. No restrictions are introduced for the yield surface, except the usual assumptions of convexity and smoothness. The goal is to apply the return mapping algorithm to a yield surface that is defined by an implicit yield function, such as the BP yield surface, and this can be sufficiently accomplished for the present simple model. For more general formulations of elastoplasticity and their computational treatment, the reader is referred, for instance, to the monographs [17, 18].

Upon backward-Euler integration of the flow rule, the incremental constitutive equations can be written in the form of the following constitutive update problem:

Constitutive update problem Given the strain $\varvec{\varepsilon }_{n+1}$ at the current time step $t=t_{n+1}$ and the plastic strain $\varvec{\varepsilon }^p_n$ at the previous time step $t=t_n$, find the current plastic strain $\varvec{\varepsilon }^p_{n+1}$ and the plastic multiplier $\varDelta \gamma$ that satisfy the elastic constitutive equation

(30)

the incremental flow rule

$$\begin{aligned} \varvec{\varepsilon }^p_{n+1} = \varvec{\varepsilon }^p_n + \varDelta \gamma \, \mathbf n (\varvec{\sigma }_{n+1}) , \quad \mathbf n = \frac{\partial F}{\partial \varvec{\sigma }} , \end{aligned}$$

(31)

and the complementarity conditions

$$\begin{aligned} F(\varvec{\sigma }_{n+1}) \le 0 , \quad \varDelta \gamma \ge 0 , \quad \varDelta \gamma F(\varvec{\sigma }_{n+1}) = 0 , \end{aligned}$$

(32)

where $F(\varvec{\sigma })$ is a given yield function with a convex and smooth zero level set $F(\varvec{\sigma })=0$, and denotes the fourth-order elastic moduli tensor.

The constitutive update problem is solved using the return mapping algorithm which involves the following steps:

• 1. Compute the trial elastic state

  

  (33)

• 2. Check the yield condition: if $F^{ trial}\le 0$ then the step is elastic and

  $$\begin{aligned} \varvec{\varepsilon }^p_{n+1} = \varvec{\varepsilon }^p_n , \quad \varDelta \gamma = 0 . \end{aligned}$$

  (34)

• 3. If $F^{ trial}>0$ then the step is plastic and the following nonlinear algebraic equations are solved for $\varvec{\varepsilon }^p_{n+1}$ and $\varDelta \gamma$:

  $$\begin{aligned} \begin{array}{l} 0 = \varvec{\varepsilon }^p_{n+1} - \varvec{\varepsilon }^p_n - \varDelta \gamma \, \mathbf n (\varvec{\sigma }_{n+1}) , \\ [0.5ex] 0 = F(\varvec{\sigma }_{n+1}) , \end{array} \end{aligned}$$

  (35)

  where the stress $\varvec{\sigma }_{n+1}$ is given by the constitutive equation (30).

Denote the vector of unknowns and the residual vector corresponding to the nonlinear equations (35) by $\mathbf{h}=\{\varvec{\varepsilon }^p_{n+1},\varDelta \gamma \}$ and $\mathbf{Q}(\mathbf{h})$, respectively. Equation $\mathbf{Q}(\mathbf{h})=\mathbf{0}$ is then solved using the Newton method which employs the following iterative scheme:

$$\begin{aligned} \mathbf{h}^{i+1} = \mathbf{h}^i + \varDelta \mathbf{h}^i , \quad \varDelta \mathbf{h}^i = - \left( \frac{\partial \mathbf{Q}}{\partial \mathbf{h}} \right) ^{-1} \mathbf{Q}(\mathbf{h}^i) , \end{aligned}$$

(36)

with the typical initial guess $\mathbf{h}^0=\{\varvec{\varepsilon }^p_n,0\}$.

At the solution of the constitutive update problem, the current stress $\varvec{\sigma }_{n+1}$ belongs to the elastic domain $F(\varvec{\sigma })\le 0$. However, the trial stress $\varvec{\sigma }_{n+1}^{ trial}$ and the stresses $\varvec{\sigma }_{n+1}^i$ at subsequent iterations may lie well outside the elastic domain. It is thus crucial for the direct application of the return mapping algorithm that the yield function $F(\varvec{\sigma })$ be defined and differentiable for arbitrary stress. The original BP yield function (but also many other yield functions, for instance, those of Jeremic et al. [7] and Foster et al. [5]) is thus not suitable for the return mapping algorithm, while the implicit one introduced in Sect. 4 is fully suitable.

Note that the flow rule (31) involves the gradient of the yield function. The tangent matrix $\partial \mathbf{Q}/\partial \mathbf{h}$ used in the Newton scheme (36) involves thus the second derivative of the yield function. In the case of the implicit yield function, those derivatives cannot be obtained directly, so that the implicit derivatives discussed in Sect. 4 must be used instead.

Convergence of the iterative Newton scheme (36) is not guaranteed in general. This difficulty can be circumvented (at least partially) by applying a globally convergent scheme, for instance, by enhancing the Newton scheme with a suitable line search strategy. The iterative update (36)$_1$ would then be replaced by the following one: $\mathbf{h}^{i+1}=\mathbf{h}^i+\alpha ^i\varDelta \mathbf{h}^i$, where the line search parameter $0<\alpha ^i\le 1$ is determined by requiring that the iterative update results in a sufficient decrease of an appropriate merit function, see, for instance, [11]. In the numerical study reported in Sect. 5.3, the Newton method combined with the line search scheme specified in Box A.1 of [13] has been used in addition to the pure Newton method specified by Eq. (36). More elaborate, globally convergent schemes employing primal and dual algorithms for the solution of the closest-point projection problems in incremental elastoplasticity are discussed in [13].

5.2 Implementation and computational efficiency

For the purpose of testing of the proposed implicit yield function formulation, a simple computer code has been developed that implements the return mapping algorithm described in the previous section. The code solves the constitutive update problem (30)–(32) in a format that exactly corresponds to the constitutive model implementation in a displacement-based finite element code. Specifically, for a given total strain $\varvec{\varepsilon }_{n+1}$ and previous plastic strain $\varvec{\varepsilon }^p_n$, the current plastic strain $\varvec{\varepsilon }^p_{n+1}$ is computed along with the current stress $\varvec{\sigma }_{n+1}$ and consistent tangent moduli

(37)

While the code developed to test the proposed formulation is limited for simplicity to material-point computations and small-strain ideal elastoplasticity, the implicit yield function formulation has already been successfully implemented in a finite-element framework and for a much more general class of constitutive models. In particular, the model for ceramic powder compaction [14, 15] has been implemented in its finite-strain version including effects such as nonlinear hardening, elastoplastic coupling, and non-associated flow rule. Some examples of the corresponding finite-element simulations of ceramic powder forming processes, but without details of algorithmic treatment, are reported in [19].

Computer implementation of the incremental constitutive equations has been performed using the AceGen system [8, 9]. The formulation of incremental elastoplasticity that is appropriate for an automated implementation using AceGen is introduced in [9]; a concise presentation of the formulation can also be found in [10]. As an essential part of this formulation, an automatic differentiation technique is used to automatically derive the consistent tangent moduli and other relevant quantities such as the dependent tangent $\partial \mathbf{Q}/\partial \mathbf{h}$ involved in the Newton scheme (36). In the context of the present implicit yield function formulation, the automatic differentiation technique is also used to efficiently implement the implicit derivatives (28) and (29), representing an important ‘ingredient’ in the formulation. This part of AceGen implementation is available as a supplementary material, see Sect. 4.

It is obvious that the use of an implicitly defined yield function, as introduced in Sect. 4, in incremental algorithms of elastoplasticity is necessarily associated with an extra computational cost due to the nonlinear equation (25), that must be solved at each evaluation of the yield function. Furthermore, evaluation of the gradient and second derivative of the yield function requires evaluation of the implicit derivatives (28) and (29), and this also has a computational price. Therefore, it is worthwhile to assess the computational efficiency of the implicit yield function formulation, and this is done below with reference to the Cam-clay model.

The original Cam-clay yield function is defined as $F_{cc}=(q/M)^2+p(p-p_c)$, but instead than this, the transformed Cam-clay yield function $F_{cc}^*$ will now be used,

$$\begin{aligned} F_{cc}^*(\varvec{\sigma }) = \sqrt{ \left( \frac{2q}{M p_c} \right) ^2 + \left( \frac{2p}{p_c} -1 \right) ^2 } - 1 , \end{aligned}$$

(38)

which specifies the same yield surface $F_{cc}^*=0$ as the original Cam-clay yield function, $F_{cc}=0$. At the same time, the transformed yield function $F_{cc}^*$ is equivalent to the implicit BP yield function $F^*$, Eq. (21), obtained in the special case corresponding to the Cam-clay yield surface, by setting $c=0$, $m=2$, $\alpha =1$, $\beta =1$, and $\gamma =0$, cf. [2].

Being numerically equivalent, the two yield functions exhibit identical convergence behavior in the return mapping algorithm, but they differ in computational efficiency: $F_{cc}^*$ is an explicit analytical function while $F^*$ is implicit and thus is associated with an additional computational cost, as described above.

Table 1 presents the results of a study of computational efficiency of the implicit BP yield function $F^*$. The constitutive update problem has been repeatedly solved for several values of input variables, and the corresponding overall evaluation time has been determined. That procedure has been applied for the Cam-clay yield function $F_{cc}^*$ and for the implicit BP yield function $F^*$, with parameters adjusted such that the response of the two is identical. The specific model parameters ($E$, $\nu$, $p_c$, $M$) used in the present study are given in Table 2 (and are typical of alumina powder), while the remaining parameters of the BP yield function assume the special values that define the Cam-clay yield surface (see above).

Table 1 Normalized evaluation time and code size for the solution of the constitutive update problem for the Cam-clay yield function

Table 2 Model parameters used in the convergence study

In addition to the computation of both the stress and the consistent tangent moduli (marked “$\varvec{\sigma }_{n+1}$ & ” in Table 1), the code has also been tested when computing only the stress (marked “$\varvec{\sigma }_{n+1}$” in Table 1). The evaluation times, normalized by the evaluation time needed for the computation of the stress using the Cam-clay yield function $F_{cc}^*$, are reported in Table 1.

The return mapping algorithm based on the implicit yield function $F^*$ has been found to be approximately four times less efficient than that employing the explicit Cam-clay yield function $F_{cc}^*$. It is reminded here that the convergence behavior, including the number of Newton iterations, of both formulations is identical, so that the difference is solely due to the extra cost of evaluation of the implicit yield function and its derivatives. Though the factor of four might at a first glance seem significant, two aspects have to be considered. Firstly, a very simple elastoplastic model has been used in the present study, so that the evaluation of the yield function and its derivatives constitutes a significant part of the complete formulation. In more complex models (involving, for instance, hardening, elastoplastic coupling, or finite-strain effects), the extra cost of evaluation of the implicit yield function related to the (increased) overall cost of the constitutive update problem becomes significantly lower. Secondly, the remarkable flexibility of the meridian and deviatoric shape of the BP yield surface must be associated to some ‘computational cost’.

Interestingly, the additional computing cost for the consistent tangent moduli is surprisingly small, when compared to the computing cost of the stress only, as it is well below 10 % for both formulations. This is probably due to the highly efficient treatment of implicit dependencies through the so-called AD exceptions that are implemented in AceGen, see [9].

Table 1 shows also the normalized size of the generated C code. As expected, the use of the implicit yield function $F^*$ results in an increase of the code size by a factor of 2–3, with respect to the code corresponding to the explicit yield function $F_\mathrm{cc}^*$. The code size is in some way related to the evaluation time, so that the remarks concerning the latter apply also here.

5.3 Convergence of the return mapping algorithm

In this section, convergence of the return mapping algorithm is analyzed for two sets of model parameters that correspond to alumina powder [14] and concrete [12]. The model parameters are provided in Table 2, and the corresponding yield surfaces are shown in Fig. 5.

Fig. 5

Yield surfaces in the principal stress space: a alumina powder, b concrete

In the present study, the number of iterations needed for the convergence of the return mapping algorithm has been evaluated as a function of the elastic trial state. Due to isotropy, the trial stress $\varvec{\sigma }^{ trial}$ is fully characterized by its invariants $p^{ trial}$, $q^{ trial}$ and $\theta ^{ trial}$, and Figs. 6 and 7 show the number of iterations as a function of $p^{ trial}$ and $q^{ trial}$ for three selected values of $\theta ^{ trial}$. Note that $p^{ trial}$ and $q^{ trial}$ have been normalized by $p_c$ so that the elastic range (in which the number of iterations is obviously equal to zero) occupies a very small region corresponding to $0\le p^{ trial}/p_c\le 1$ and $q^{ trial}/p_c$ close to zero. Each contour plot shown in Figs. 6 and 7 has been obtained by sampling the trial $(p,q)$-space using 200$\times$200 points.

Fig. 6

Number of iterations needed for convergence of the return mapping algorithm using the Newton method (top row) and the Newton method with line search (bottom row) for a $\theta ^{ trial}=0$, b $\theta ^{ trial}=\pi /6$, c $\theta ^{ trial}=\pi /3$. White regions indicate lack of convergence (defined as more than 50 iterations). The parameters of the yield function correspond to alumina powder

Fig. 7

Number of iterations needed for convergence of the return mapping algorithm using the Newton method (top row) and the Newton method with line search (bottom row) for a $\theta ^{ trial}=0$, b $\theta ^{ trial}=\pi /6$, c $\theta ^{ trial}=\pi /3$. White regions indicate lack of convergence (defined as more than 50 iterations). The parameters of the yield function correspond to concrete

The maximum number of iterations has been set to 50, and the white regions in Figs. 6 and 7 indicate the regions where the maximum number of iterations has been reached and which are thus considered ‘no-convergence regions’. It has been checked that, in the case of the pure Newton method (reported in the top rows in Figs. 6 and 7), no-convergence regions do not noticeably decrease with an increase of the maximum number of iterations. The figures corresponding to the Newton method with line search (reported in the bottom rows in Figs. 6 and 7), show only isolated spots of lack of convergence, and it has been checked that these regions vanish when the maximum number of iterations is further increased.

The main purpose of the present numerical example is to show that the implicit yield surface formulation can be effectively applied to develop incremental schemes for elastoplasticity. This goal has been achieved by showing that the implicit BP yield function can be evaluated for arbitrary stresses, so that the standard return mapping algorithm can be applied directly, while this is not the case of the original BP yield function, as illustrated in Sect. 3. Further, by construction, the implicit yield function is convex (provided that the generating yield surface is convex), which is beneficial for the convergence of the return mapping algorithm. This is illustrated by the excellent convergence properties of the return mapping algorithm, employing the Newton method combined with a standard line search strategy.

Note that the two yield surfaces used in the present study pose difficulties in their computational treatment as they locally exhibit very high curvature. Especially the yield surface representative of concrete features sharp edges in the deviatoric section ($\gamma =0.98$) and nearly a vertex on the hydrostatic axis located at high pressure ($\alpha =1.99$). Those features are responsible for the poor convergence of the pure Newton method, particularly for $\theta ^{ trial}=\pi /6$, both for the model for alumina powder and for the model for concrete, see Figs. 6b and 7b (in the latter case, the no-convergence region spans the whole plot).

It should be noted here that the simple return mapping algorithm enhanced with a line search strategy performs so well because the elastoplastic model is rather simple, so that the only difficulty lies in the complexity of the yield surface, as related, in particular, to its high curvature. Effects such as strain hardening and elastoplastic coupling, which are crucial in applications involving granular and rock-like materials, would definitely deteriorate convergence of the return mapping algorithm. Anyway, the implicit yield function formulation may offer significant advantages in the development of more advanced incremental formulations of elastoplasticity.

6 Conclusions

A technique has been introduced to integrate elastoplastic (or elastodamaging) rate equations based on pressure-sensitive and $J_3$-dependent yield functions that often exhibit undesired features such as lack of convexity or ‘false elastic domains’. The technique is based on a re-definition of the yield function in an implicit form, that can be subsequently treated with standard numerical tools. Although associated to a numerical cost, the proposed technique is shown to be efficient, general and accurate.

Appendix: Second derivative of \(F^*\)

The second derivative of the implicit yield function is obtained by differentiating Eq. (9), viz.

$$\begin{aligned} \frac{\partial ^2 F^*}{\partial \varvec{\sigma }\partial \varvec{\sigma }}&= \frac{1}{\varrho _0} \frac{\partial ^2 \varrho }{\partial \varvec{\sigma }\partial \varvec{\sigma }} -\frac{\varrho }{\varrho _0^2} \frac{\partial ^2 \varrho _0}{\partial \varvec{\sigma }\partial \varvec{\sigma }} \nonumber \\&+\frac{2\varrho }{\varrho _0^3} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \otimes \frac{\partial \varrho _0}{\partial \varvec{\sigma }} -\frac{2}{\varrho _0^2} \left( \frac{\partial \varrho }{\partial \varvec{\sigma }} \otimes \frac{\partial \varrho _0}{\partial \varvec{\sigma }} \right) _{ sym} . \end{aligned}$$

(39)

The above formula involves the explicit first and second derivatives of $\varrho$ and the implicit first and second derivatives of $\varrho _0$. The first derivative of $\varrho$ is given by Eq. (10), the second derivative is given by

(40)

in view of Eq. (12). The implicit first derivative of $\varrho _0$ has been derived in Sect. 2, see Eq. (13), and the second derivative is obtained below.

For future use, we introduce the following notation for the derivatives of the original yield function evaluated at $\varvec{\sigma }_0$,

(41)

With this notation, the first derivatives of $\varrho _0$ and $F^*$, Eqs. (13) and (14), respectively, are written as

$$\begin{aligned} \frac{\partial \varrho _0}{\partial \varvec{\sigma }} = \frac{\varrho _0}{\varrho } \big ( \mathbf e _r - n_r^{-1} \mathbf n _0 \big ) , \quad \frac{\partial F^*}{\partial \varvec{\sigma }} = \frac{1}{\varrho _0} \big ( n_r^{-1} \mathbf n _0 \big ) . \end{aligned}$$

(42)

As discussed in Sect. 2, the implicit dependence of $\varrho _0$ on $\varvec{\sigma }$ is introduced by the condition that $\varvec{\sigma _0}$ lies on the yield surface, i.e., $F(\mathbf o +\varrho _0(\varvec{\sigma })\mathbf e _r(\varvec{\sigma }))=0$. This equation is differentiated with respect to $\varvec{\sigma }$ twice, and the resulting equation is solved for the unknown second derivative of $\varrho _0$, just like in the case of the first derivative in Sect. 2, and the following formula is obtained:

(43)

With this at hand, the second derivative of $F^*$ is finally obtained in a remarkably simple form,

(44)