1 Introduction

The crossing number \(\textsc {cr}(G)\) of a graph G is the minimum number of edge crossings over all drawings of G in the plane. In the optimal drawing of G, crossings are not necessarily distributed uniformly on the edges. Some edges can be more “responsible” for the crossing number than others. For any positive integer k, there exists a graph G whose crossing number is k, but it has an edge e such that \(G-e\) is planar. On the other hand, Richter and Thomassen [6, Sect. 3] conjectured that if \(\textsc {cr}(G)=k\), then G contains an edge e such that \({\textsc {cr}}\,(G-e)\ge k-c\sqrt{k}\) for some constant c. They observed that this bound would be optimal, as shown, e.g., by the graph \(K_{3,n}\). They managed to prove a much weaker bound, namely, if \(\textsc {cr}(G)=k\), then G contains an edge e such that \({\textsc {cr}}\,(G-e)\ge 2k/5-8\).

A graph G is k-crossing-critical if \(\textsc {cr}(G)\ge k\), but \({\textsc {cr}}\,(G-e)<k\) for any edge e of G. The structure and properties of crossing-critical graphs are fundamental in the study of crossing numbers. It is easy to describe 1-crossing-critical graphs, and there is an almost complete description of 2-crossing-critical graphs [3]. For \(k>2\), a description of k-crossing-critical graphs seems hopeless at the moment. It has been proven recently, that the bounded maximum degree conjecture for k-crossing-critical graphs holds for \(k\le 12\) and does not hold for \(k>12\) [2]. More precisely, there is a constant D with the property that for every \(k\le 12\), every k-crossing-critical graph has maximum degree at most D, and for every \(k>12\), \(d\ge 1\), there is a k-crossing-critical graph with maximum degree at least d.

We rephrase the result and conjecture of Richter and Thomassen [6] as follows. They conjectured that if G is k-crossing-critical, then \(\textsc {cr}(G)\le k+c'\sqrt{k}\) for some \(c'>0\) and this bound would be optimal. They proved that if G is k-crossing-critical, then \(\textsc {cr}(G)\le 2.5\, k+16\). This result has been improved in two special cases. Lomelí and Salazar [5] proved that for any k there is an n(k) such that if G is k-crossing-critical and has at least n(k) vertices, then \(\textsc {cr}(G)\le 2k+23\). Salazar [7] proved that if G is k-crossing-critical and all vertices of G have degree at least 4, then \(\textsc {cr}(G)\le 2k+35\). It is an easy consequence of the Crossing Lemma [1] that if the average degree in a k-crossing-critical graph is large, then its crossing number is close to k [4]. That is, if G is k-crossing critical and it has at least cn edges, where \(c\ge 7\), then \(\textsc {cr}(G)\le kc^2/(c^2-29)\). In this note, we obtain a general improvement.

Theorem 1.1

For any \(k>0\), if G is a k-crossing-critical multigraph, then \(\textsc {cr}(G)\le 2k+8\sqrt{k}+47\).

We need a few definitions and introduce now several parameters for the proof. We also list them at the end of the paper.

Let G be a graph. If C is a cycle of G and v is a vertex of C, then we call the pair (C, v) the cycle C with special vertex v. The special vertex is meant to be a vertex with large degree. When it is clear from the context, which vertex is the special one, we just write C instead of (C, v). Suppose C is a cycle with special vertex v. Let x be a vertex of C. An edge, adjacent to x but not in C, is hanging from x in short. Let \(l(C)=l(C, v)\) be the length of C, that is, the number of its edges. For any vertex x, let d(x) denote the degree of x. Let \(h(C)=h(C, v)=\sum _{u\in C, u\ne v}(d(u)-2)\), that is, the total number of hanging edges from all non-special vertices of C (with multiplicity). A set of edges is independent if no two of them have a common endvertex.

2 The Proof of Richter and Thomassen

In [6], the most important tool in the proof was the following technical result. In this section we review and analyze its proof. The algorithmic argument recursively finds an induced cycle C such that h(C) is small.

Theorem 2.1

([6])   Let H be a simple graph with minimum degree at least 3. Assume that H has a set E of t edges such that \(H-E\) is planar. Then H has an induced cycle K with special vertex v such that \(h(K)\le t+36\).

Proof

The proof is by induction on t. The induction step can be considered as a process, which constructs a graph \(H^*\) from the graph H, and a cycle K of H, either directly, or from a cycle \(K^*\) in \(H^*\). For convenience, for any planar graph H, define \(H^*=\emptyset \). In the rest of the paper we refer to this as the Richter–Thomassen procedure. The statement of Theorem 2.1 for \(t=0\) is the following.

Lemma 2.2

([6])    Let H be a simple planar graph with minimum degree at least 3. Then H has an induced cycle K with special vertex v such that \(l(K)\le 5\) and \(h(K)\le 36\).

Here we omit the proof of Lemma 2.2. Suppose now that \(t>0\) and we have already shown Theorem 2.1 for smaller values of t. Let H be a simple graph with minimum degree at least 3. Assume that H has a set E of t edges such that \(H-E\) is planar and let \(e=uw\in E\). Let \(H'=H-e\). We distinguish several cases.

  • 1. \(H'\) has no vertex of degree 2. By the induction hypothesis, \(H'\) has a cycle \(K^*\) with a special vertex v such that \(h(K^*)\le t+35\). In H, if e is not a chord of \(K^*\), then \(K=K^*\) with the same special vertex satisfying the conditions for H. Let \(H^*=H'\). If e is a chord of \(K^*\), then \(K^*+e\) determines two cycles, and it is easy to see that either one satisfies the conditions. So, let K be one of them. If K contains v, then v remains the special vertex. If K does not contain v, then we can choose the special vertex of K arbitrarily. Let \(H^*=H'\).

  • 2. \(H'\) has a vertex of degree 2. Clearly, only u and w can have degree 2. Suppress vertices of degree 2. That is, for each vertex of degree 2, remove the vertex and connect its neighbors by an edge. Let \(H''\) be the resulting graph. It can have at most two sets of parallel edges.

    • 2.1. \(H''\) has no parallel edges. By the induction hypothesis, \(H''\) contains a cycle \(K^*\) with a special vertex v such that \(h(K^*)\le t+35\). It corresponds to a cycle \(K'\) in H. Let \(H^*=H''\).

      • 2.1.1. The edge e is not incident with \(K'\). In this case, \(K=K'\) satisfies the conditions, with the same special vertex as \(H^*\).

      • 2.1.2. The edge e has exactly one endvertex on \(K'\). In this case, let \(K=K'\) with the same special vertex. Now \(h(K)=h(K^*)+1\le t+36\) and we are done.

      • 2.1.3. The edge e has both endvertices on \(K'\). Now, just like in case 1., \(K'+e\) determines two cycles and it is easy to see that either one satisfies the conditions. If the new cycle contains v, the special vertex, then it will remain the special vertex; if not, then we can choose the special vertex arbitrarily.

    • 2.2. \(H''\) has one set of parallel edges. Let x and y be the endvertices of the parallel edges. We can assume that one of the xy edges in \(H''\) corresponds to the path xuy in H and \(H'\). Clearly, \(d(u)=3\).

      • 2.2.1. Another xy edge in \(H''\) corresponds to the path xwy in H and \(H'\). In this case \(d(u)=d(w)=3\), so for the cycle \(K=uxw\) with special vertex x we have \(h(K)\le 2\) and we are done. Let \(H^*=\emptyset \). We do not define \(K^*\) in this case.

      • 2.2.2. No xy edge in \(H''\) corresponds to the path xwy in H and \(H'\), and either \(d(x)\le 37+t\) or \(d(y)\le 37+t\). Assume that \(d(x)\le 37+t\), the other case is treated analogously. Since there were at least two xy edges in \(H''\), H contains the edge xy. For the cycle \(K=uxy\), with special vertex y, we have \(h(K)\le 35+t+1\), so we are done. Let \(H^*=\emptyset \).

      • 2.2.3. No xy edge in \(H''\) corresponds to the path xwy in H and \(H'\), and both \(d(x), d(y) > 37+t\). Replace the parallel edges by a single xy edge in \(H''\). In the resulting graph \(H^*\), we can apply the induction hypothesis and get a cycle \(K^*\) with special vertex v such that \(h(K^*)\le 35+t\). Now \(K^*\) cannot contain both x and y and if it contains either one, then it has to be the special vertex. Therefore, the cycle K in H, corresponding to \(K^*\), with the same special vertex, satisfies the conditions, since the only edge that can increase h(K) is e, and e is not a chord of K.

    • 2.3. \(H''\) has two sets of parallel edges, xy and ab say. Now H contains the edges xy and ab. We can assume by symmetry that H contains the paths xuy and awb. Also \(d(u)=d(w)=3\) in H.

      • 2.3.1. At least one of a, b, x, y has degree at most \(37+t\) in H. Assume that \(d(x)\le 37+t\), the other cases are treated analogously. For the cycle \(K=uxy\) with special vertex y, we have \(h(K)\le 35+t+1\), so we are done. Let \(H^*=\emptyset \).

      • 2.3.2. \(d(x),d(y),d(a),d(b)>37+t\). Replace the parallel edges by single edges xy and ab in \(H''\). In the resulting graph \(H^*\), we can apply the induction hypothesis and get a cycle \(K^*\) with special vertex v such that \(h(K^*)\le 35+t\). However, \(K^*\) can contain at most one of x, y, a, and b, and if it contains one, then it has to be the special vertex. Therefore, the cycle K in H, corresponding to \(K^*\), with the same special vertex satisfies the conditions.

It is clear from the procedure that K does not have a chord in H since we always choose K as a minimal cycle. This finishes the proof of Theorem 2.1.\(\square \)

3 Proof of Theorem 1.1

The main idea in the proof of Richter and Thomassen [6] is the following. Suppose that G is k-crossing-critical. Then it has at most k edges whose removal makes G planar. Then by Theorem 2.1, we find a cycle C with special vertex v such that \(h(C)\le k+36\). Let e be an edge of C adjacent to v. We can draw \(G-e\) with at most \(k-1\) crossings. Now we add the edge e, along \(C-e\), on the “better” side. We get additional crossings from the crossings on \(C-e\) and from the hanging edges, and we can bound both.

Our contribution is the following. Take a “minimal” set of edges, whose removal makes G planar. Clearly, this set would contain at most k edges. However, we have to define “minimal” in a slightly more complicated way, but still our set contains at most \(k+\sqrt{k}\) edges. We carefully analyze the proof of Richter and Thomassen, extend it with some operations, and find a cycle C with special vertex v such that (roughly) \(l(C)+h(C)/2\le k+6\sqrt{k}\). Now, do the redrawing step. If h(C) or the number of crossings on \(C-e\) is small, then we get an improvement immediately. If both of them are large, then l(C) is much smaller than the number of crossings on \(C-e\). But in this case, we can remove the edges of C, and get rid of many crossings. This way, we can get a bound on the “minimal” set of edges whose removal makes G planar.

As we will see, for the proof we can assume that G is simple and all vertices have degree at least 3. But if we want to prove a better bound, say, \(\textsc {cr}(G)\le (2-\varepsilon )\, k+o(k)\), then we cannot prove that the result for simple graphs implies the result for multigraphs. Therefore, the whole proof collapses. Moreover, even if we could assume without loss of generality that G is simple, we still cannot go below the constant 2 with our method. We cannot rule out the possibility that all (or most of the) \(k-1\) crossings are on \(C-e\).

Proof of Theorem 1.1

Suppose that G is k-crossing-critical. Just like in the paper of Richter and Thomassen [6], we can assume that G is simple and all vertices have degree at least 3. We sketch the argument.

If G has an isolated vertex, then we can remove it from G. Suppose that a vertex v of G has degree 1. Then \(\textsc {cr}(G)={\textsc {cr}}\,(G-v)\), contradicting crossing criticality. Suppose now that v has degree 2. We can suppress v (remove it and connect its neighbors by an edge). The resulting (multi)graph is still k-crossing-critical and has the same crossing number as G. Clearly, G cannot contain loops, as adding or removing a loop does not change the crossing number. Finally, suppose that e and f are parallel edges, both connecting x and y. Since G is k-crossing-critical, we have \({\textsc {cr}}\,(G-e)\le k-1\). Take a drawing of the graph \(G-e\) with at most \(k-1\) crossings. Add the edge e, drawn very close to f. The obtained drawing of G has at most \(2k-2\) crossings, consequently \(\textsc {cr}(G)\le 2k-2<2k+6\sqrt{k}+47\) and we are done. So, we assume in the sequel that G is simple and all vertices have degree at least 3.

Let \(k'\) be the smallest integer with the property that we can remove \(k'\) edges from G so that the remaining graph is planar. Define the function \(f(x,y)=x\sqrt{k}+y\). Let \((t,t')\) be the pair of numbers that minimizes the function \(f(t, t')=\sqrt{k}t+t'\) subject to the following property: There exists a set E of t edges such that \(G-E\) is planar, and the set E contains at most \(t'\) independent edges. In the next lemma, (i) is from [6]; we repeat it here for completeness.

Lemma 3.1

The following two statements hold: (i) \(k'\le k\) and (ii) \(t\le k'+\sqrt{k}\).

Proof

(i) Since G is k-crossing-critical, \(G-e\) can be drawn with at most \(k-1\) crossings for any edge e. Remove one of the edges from each crossing in such a drawing. We removed from G at most k edges in total and got a planar graph. (ii) Let \(E'\) be a set of \(k'\) edges in G such that \(G-E'\) is planar. Suppose that \(E'\) contains at most \(k''\) independent edges. Now \(k''\le k'\). By the choice of \((t,t')\), \(f(t,t')\le f(k',k'')\). Consequently, \(t\sqrt{k}\le t\sqrt{k}+t'=f(t,t')\le f(k',k'')\le k'\sqrt{k}+k'\). Therefore, \(t\le k'+k'/\sqrt{k}\le k'+\sqrt{k}\) by part (i). \(\square \)

Now set \(E=\{ e_1, e_2, \ldots , e_t \}\subseteq E(G)\), where E contains at most \(t'\) independent edges and \(G-E\) is planar. Apply the Richter–Thomassen procedure recursively starting with \(H_0=G\). We obtain a sequence of graphs \(H_0, H_1, \ldots , H_s\), \(s\le t\), such that for \(0\le i\le s-1\), \(H_i^*=H_{i+1}\), and \(H_s^*=\emptyset \). The procedure stops with graph \(H_s\), where we obtain a cycle \(C_s\) either directly, in cases 2.2.1, 2.2.2, and 2.3.1, or by Lemma 2.2, when \(H_s\) is planar. In all cases, \(l(C_s)\le 5\). Following the procedure again, we also obtain cycles \(C_{s-1}, \ldots , C_0\) of \(H_{s-1}, \ldots , H_0\), respectively, such that for \(0\le i\le s-1\), \(C_i^*=C_{i+1}\). Let \(C_0=C\) with special vertex v.

Lemma 3.2

There is a cycle K of G such that \(l(K)+h(K)/2\le t+7\sqrt{k}+48\).

Proof

The cycle K will be either C, or a slightly modified version of C. Recall that C is an induced cycle so it does not have a chord in G. Consider the moment of the procedure when we get cycle C. We get it either directly, when we apply Lemma 2.2, and in cases 2.2.1, 2.2.2, or 2.3.1, or we get it from \(C^*\). In the latter case, all hanging edges of C correspond to a hanging edge of \(C^*\), with the possible exception of \(e=uw\). Therefore, if we get a new hanging edge e, then \(e\in E\). Taking into account the initial cases in the procedure, that is, when we apply Lemma 2.2, or we have cases 2.2.1, 2.2.2, or 2.3.1, we get the following easy observations. We omit the proofs.

Observation 3.3

  1. (i)

    All but at most 36 edges of \(G-C\) adjacent to a non-special vertex of C are in E.

  2. (ii)

    For all but at most four non-special vertices \(z'\) of C, all edges of \(G-C\) incident to \(z'\) are in E.

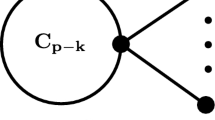
Suppose that \(l(C)>t'+6\). Consider \(t'+5\) consecutive vertices on C, none of them being the special vertex v. By Observation 3.3 (ii), for at least \(t'+1\) of them, all hanging edges are in E. Consider one of these hanging edges at each of these \(t'+1\) vertices. By the definition of \(t'\), \(t'>0\) and these \(t'+1\ge 2\) edges cannot be independent: at least two of them have a common endvertex, which is not on C. Suppose that \(x, y\in C\), \(z\notin C\), \(xz,yz\in E\). Let a be the xy arc (path) of C, which does not contain the special vertex v. Take two consecutive neighbors of z in a. Assume for simplicity, that they are x and y. Let the cycle \((C',z)\) be formed by the arc a of C, together with the path xzy. See Fig. 1. The cycle \(C'\) does not have a chord in G. We have \(l(C')\le t'+6\), \(h(C')\le h(C)\). The edges zx and zy are the only new hanging edges of \(C'\) from a non-special vertex. They might not be in E, therefore, the statement of Observation 3.3 holds in a slightly weaker form.

Observation 3.4

  1. (i)

    All but at most 38 edges of \(G-C'\) adjacent to a non-special vertex of \(C'\) are in E.

  2. (ii)

    For all but at most six non-special vertices \(z'\) of \(C'\), all edges of \(G-C'\) incident to \(z'\) are in E.

Let cycle \(K=C\), if \(l(C)\le t'+6\), and let \(K=C'\), if \(l(C)> t'+6\). In both cases, for the rest of the proof, let v denote the special vertex of K. Let \(h=h(K)\), \(l=l(K)\). We have

$$\begin{aligned} l\le t'+6. \end{aligned}$$
(1)

The cycle K does not have a chord. In particular, none of \(e_1,e_2, \ldots , e_t\) can be a chord of K. Now we partition E into three sets, \(E=E_p\cup E_q\cup E_m\), where \(E_p\) is the subset of edges of E that have exactly one endvertex on K (these are the hanging edges in E), \(E_q=E\cap K\), and \(E_m\) is the subset of edges of E that do not have an endvertex on K. Let \(p=|E_p|\), \(q=|E_q|\), \(m=|E_m|\). Let \(p'\) denote the number of edges of \(E_p\) hanging from the special vertex v. By definition,

$$\begin{aligned} t=p+q+m \end{aligned}$$
(2)

and \(p\ge p'\). It follows from Observations 3.3 (i) and 3.4 (i) that

Fig. 1
figure 1

Cycles C and \(C'\)

Full size image
$$\begin{aligned} h\ge p-p'\ge h-38. \end{aligned}$$
(3)

Therefore,

$$\begin{aligned} h+q+m\le p+q+m+38=t+38. \end{aligned}$$

Since all vertices have degree at least 3, and K does not have a chord, \(h\ge l-1\).

Now, at each vertex x of K, where all hanging edges belong to \(E_p\), take one such edge. The set of these edges is \(E'\). By Observations 3.3 (ii) and 3.4 (ii), \(|E'|\ge l-7\). See Fig. 2. Let \(F=E_p\cup E(K)\cup E_m- E'\) where E(K) is the set of edges of K. Since \(F\cup E'\supseteq E\), \(G'=G- (F\cup E')\) is a planar graph. Let \(G''=G'\cup E'=G- F\). In \(G''\), each edge of \(E'\) has an endvertex of degree one. Therefore, we can add all edges of \(E'\) to \(G'\) without losing planarity. Consequently, the graph \(G''=G'\cup E'=G- F\) is planar. Since \(|E'|\ge l-7\), we have \(|F|=|E_p|+|E(K)|+|E_m|-|E'|\le p+l+m-(l-7)=p+7+m\le t+7\) by (2). That is,

Fig. 2
figure 2

The edge set \(E'\)

Full size image
$$\begin{aligned} |F|\le t+7. \end{aligned}$$
(4)

Let \(F'\subseteq F\) be a maximal set of independent edges in F. We have \(|F'|=|F'\cap E_m|+|F'\cap E_p|+|F'\cap E(K)|\). The edges in \(F'\cap E_m\) are disjoint from K and clearly \(|F'\cap E_m|\le |E_m|=m\). The edges in \(|F'\cap E_p|\) have exactly one vertex on K. There are \(p-p'\) hanging edges of K from non-special vertices, and \(E'\) contains at least \(l-7\) of them, so \(F'\) contains at most \(p-p'-(l-7)\) hanging edges from non-special vertices. Clearly, \(F'\) can contain at most one hanging edge from the special vertex v. Consequently, \(|F'\cap E_p|\le p-p'-(l-7)+1\). Finally, each edge in \(|F'\cap E(K)|\) “occupies” two vertices of K. Summarizing,

$$\begin{aligned} |F'|&= |F'\cap E_m|+|F'\cap E_p|+|F'\cap E(K)|\\&\le |F'\cap E_m|+|F'\cap E_p|+\frac{l-|F'\cap E_p|}{2}\\&\le m+ p-p'-(l-7)+1+\frac{l-(p-p'-l+8)}{2}=\frac{p-p'}{2}+4+m. \end{aligned}$$

By the choice of the pair \((t,t')\), \(t\sqrt{k}+t'\le |F|\sqrt{k}+|F'|\). Therefore,

$$\begin{aligned} \frac{p-p'}{2}+4+m\ge |F'|\ge t \sqrt{k}+t'-|F|\sqrt{k}\ge t'-7\sqrt{k}, \end{aligned}$$

using (4). Now by (3) we obtain \(h/2+4+m\ge (p-p')/2+4+m\ge t'-7\sqrt{k}\). Therefore, \(h/2+m\ge t'-4-7\sqrt{k}\ge l-10-7\sqrt{k}\) by (1). Summarizing, we have

$$\begin{aligned} h+m\le t+38,\qquad \frac{h}{2}+m\ge l-10-7\sqrt{k}, \end{aligned}$$

which implies

$$\begin{aligned} m\le t-h+38, \qquad \frac{h}{2}+t-h+38\ge l-10-7\sqrt{k}, \end{aligned}$$

and finally \(t+7\sqrt{k}+48\ge l+h/2\). This concludes the proof of Lemma 3.2. \(\square \)

Now we can finish the proof of Theorem 1.1. By Lemma 3.2, we have a cycle K in G with special vertex v such that \(h(K)/2+l(K)\le t+7\sqrt{k}+48\). Let e be an edge of K adjacent to v. Since G was k-crossing-critical, the graph \(G-e\) can be drawn with at most \(k-1\) crossings. Let us consider such a drawing D. Let \(h=h(K)\), \(l=l(K)\). Suppose the path \(K- e\) has cr crossings in D. Remove the edges of K from the drawing, and one edge from each crossing not on \(K-e\). Together with e, we removed at most \(k+l-cr\) edges from G to get a planar graph. Therefore, \(l+k-cr\ge k'\). Combining this with Lemma 3.1 (ii) we have

$$\begin{aligned} l+k-cr\ge t-\sqrt{k}. \end{aligned}$$

Consequently, \(l+k-cr\ge t-\sqrt{k}\ge l+h/2-48-8\sqrt{k}\) by Lemma 3.2. That is,

$$\begin{aligned} k+8\sqrt{k}+48\ge cr+\frac{h}{2}. \end{aligned}$$
Fig. 3
figure 3

Adding the missing edge e

Full size image

Consider the drawing D of \(G-e\). We can add the missing edge e drawn along the path \(K- e\) on either side. See Fig. 3. The two possibilities together create at most \(h+2cr\) crossings. Choose the one which creates fewer crossings. That makes at most \(h/2+cr\) crossings. Since \(k+8\sqrt{k}+48\ge cr+h/2\), we can add e with at most \(k+8\sqrt{k}+48\) additional crossings. Hence \(\textsc {cr}(G)\le 2k+8\sqrt{k}+47\). \(\square \)

4 Notations

Here we give a list of the parameters and their definitions, used in the proof.

k::

G is k-crossing-critical.

\(k'\)::

the smallest integer with the property that we can remove \(k'\) edges from G so that the remaining graph is planar.

\((t,t')\)::

the pair of numbers that minimizes the function \(f(t, t')=t\sqrt{k}+t'\) subject to the following property: There exists a set E of t edges such that \(G-E\) is planar and the set E contains at most \(t'\) independent edges.

\(p=|E_p|\)::

the number of edges in E that have exactly one endvertex on C.

\(q=|E_q|\)::

the number of edges in \(E\cap C\).

\(m=|E_m|\)::

the number of edges in E that do not have an endvertex on C.

\(p'\)::

the number of edges of \(E_p\) hanging from the special vertex v of C.

\(h=h(C)\)::

the total number of hanging edges from all non-special vertices of C (with multiplicity); \(h(C)=h(C, v)=\sum _{u\in C, u\ne v}(d(u)-2)\).

\(l=l(C)\)::

the length of C.