Geometric Multicut: Shortest Fences for Separating Groups of Objects in the Plane

Abstract

We study the following separation problem: Given a collection of pairwise disjoint coloured objects in the plane with k different colours, compute a shortest “fence” F, i.e., a union of curves of minimum total length, that separates every pair of objects of different colours. Two objects are separated if F contains a simple closed curve that has one object in the interior and the other in the exterior. We refer to the problem as geometric k-cut, as it is a geometric analog to the well-studied multicut problem on graphs. We first give an $O(n^4\log ^3\!n)$-time algorithm that computes an optimal fence for the case where the input consists of polygons of two colours with n corners in total. We then show that the problem is NP-hard for the case of three colours. Finally, we give a randomised $4/3\cdot 1.2965$-approximation algorithm for polygons and any number of colours.

1 Introduction

Problem Statement We are given k pairwise interior-disjoint sets $B_1,B_2,\ldots ,B_k$ in the plane, not necessarily connected. We want to find a covering of the plane ${\mathbb {R}}^2 = {{\bar{B}}}_1\cup {{\bar{B}}}_2 \cup \cdots \cup {{\bar{B}}}_k$ such that the sets ${{\bar{B}}}_i$ are closed and interior-disjoint, $B_i\subseteq {{\bar{B}}}_i$, and the total length of the boundary $F=\bigcup _{i=1}^k \partial {{\bar{B}}}_i$ between the different sets ${{\bar{B}}}_i$ is minimized.

We think of the k sets $B_i$ as having k different colours and each set $B_i$ as a union of simple geometric objects like circular disks or simple polygons. We call ${{\bar{B}}}_i$ the territory of colour i. Examples are shown in Figs. 1 and 2. The “fence” F consists of the boundaries that separate the territories, or alternatively, F is the set of points belonging to more than one territory. As we can see, the fence does not have to be connected, and a territory can have more than one connected component.

Fig. 1

An instance with $k=2$ sets, red and green, with two disks each; the big green disk is only partially shown. The optimal covering has a hippodrome-shaped red territory, with the small green disk as a hole, and an additional unbounded part of the green territory. The fence F has two components: the boundary of the hippodrome and the boundary of the small green disk

Fig. 2

An instance of geometric 3-cut and a fence in black. The fence contains a cycle that does not touch any object. The grey fence shows how such a cycle can be shrunk without changing the total length of the fence (Lemma 2.2). We believe this to be the optimal fence. In any case, we can ensure that this fence is optimal by filling the territories more densely with objects of the appropriate colour

An alternative view of the problem concentrates on the fence: A fence is defined as a union of curves F such that each connected component of ${\mathbb {R}}^2\setminus F$ intersects at most one set $B_i$. An interior-disjoint covering as defined above gives, by definition, such a fence. Likewise, a fence F induces such a covering, by assigning each connected component of ${\mathbb {R}}^2\setminus F$ to an appropriate territory ${{\bar{B}}}_i$. The total length of a fence F is also called the cost of F and is denoted as |F|.

In this paper, we will focus on the case where the input consists of simple polygons with disjoint interiors. We refer to this problem as geometric k-cut. Each input polygon is called an object. The results can be extended to more general shapes of objects as long as they are reasonably well behaved, but we refrain from trying to achieve greater generality. We use n to denote the total number of corners of the input polygons, counted with multiplicity.

Even in this simple setting, the problem poses both geometric and combinatorial difficulties. A set $B_i$ can consist of several objects, and the combinatorial challenge is to choose which of the objects should be grouped into the same component of ${{\bar{B}}}_i$. The geometric task is to construct a network of curves that surrounds the given groups of objects and thus separates the groups from each other. For $k=2$ colours, optimal fences consist of geodesic curves around obstacles, which are well understood. As soon as the number k of colours exceeds 2, the geometry becomes more complicated, and the problem acquires traits of the geometric Steiner tree problem, as shown in the example in Fig. 2.

Our Results In Sect. 3, we show how to solve the case with $k=2$ colours in time $O(n^4\log ^3\!n)$. (The running time is actually a tiny bit smaller, see Theorem 3.2.) The crucial observation is that the optimal fence must consist of line segments between corners of input polygons (Lemma 3.1). The algorithm is then straightforward. We consider the arrangement ${{\mathcal {A}}}$ formed by all these line segments. The shortest fence corresponds to a minimum cut in the dual graph of this arrangement. This is a planar graph, and for solving the multiple-source multiple-sink maximum flow problem in this graph, we can apply results from the literature.

The case with $k=3$ colours is already NP-hard, as we show in Sect. 4 by a reduction from planar positive 1-in-3-sat (Theorem 4.7). The main feature of the gadgets in our reduction is that they have different optimal solutions (in a local sense) of equal length, thus allowing logical values to be represented and propagated. The analysis of our clause gadget, which captures the logical core of the reduction, is unfortunately quite involved and requires a large case distinction over several pages.

It is not known whether the decision version of geometric k-cut is in NP or not. Indeed, this seems to depend on the complexity of other problems such as the sum of square roots problem [17] and the Euclidean Steiner tree problem [11], both of which are not known to be in NP. See the remarks after Theorem 3.2.

In Sect. 5, we discuss an approximation algorithm. We first compare the optimal fence $F_{{\mathcal {A}}}$ consisting of line segments between corners of input polygons to the unrestricted optimal fence $F^*$, and in Theorem 5.1 we show that $|F_{{\mathcal {A}}}|\le 4|F^*|/3$. The proof requires topological arguments (Lemma 5.2) as well as combinatorial arguments (Lemma 5.4). As in Sect. 3, restricting the solution to the arrangement ${{\mathcal {A}}}$ allows us to view the problem as a graph-theoretic problem. By applying a 1.2965-approximation algorithm for the k-terminal multiway cut problem [21], we obtain a polynomial-time $4/3\cdot 1.2965$-approximation algorithm for geometric k-cut (Theorem 5.6).

Related Work Despite the fact that the problem is natural and fundamental, there is little previous work. The problem of enclosing a set of objects by a shortest system of fences has recently been considered with a single set $B_1$ by Abrahamsen et al. [1]. The task is to “enclose” the components of $B_1$ by a shortest system of fences. This can be formulated as a special case of our problem with $k=2$ colours: We add an additional set $B_2$, far away from $B_1$ and large enough so that it is never optimal to surround $B_2$. Thus, we have to enclose all components of $B_1$ and separate them from the unbounded region. In this setting, there will be no nested fences. Abrahamsen et al. gave an algorithm with running time $O(n{\text {polylog}}n)$ for the case where the input consists of n unit disks.

Some variations with additional constraints on the fence become NP-hard already for point objects with two colours. For example, if we require the fence to be a single closed curve, it has been observed by Eades and Rappaport [10] already in 1993 that one can model the Euclidean Travelling Salesman Problem of computing the shortest tour through a given set of sites by placing two tiny objects of opposite colour next to each site. If we require the fence to be connected, the same construction will lead to the Euclidean Steiner Tree Problem, which was shown to be NP-hard by Garey, Graham, and Johnson in 1977 [11].

Applications Besides being a natural problem in its own right, the geometric multicut problem may well find applications in image processing and computer vision. As we describe in Sect. 3, a problem closely related to the case $k=2$ has been studied from the perspective of image segmentation. Simplified slightly, we are given a picture with some pixels known to be black or white, and we have to choose colours for the remaining pixels so as to minimize the boundary between black and white regions. The problem for $k>2$ is equally well motivated in this context, although we have not found any explicit references to it (perhaps because of the NP-hardness which we will prove in this case).

2 Structure of Optimal Fences

Lemma 2.1

An optimal fence $F^*$ is a union of (not necessarily disjoint) closed curves, disjoint from the interior of the objects. Furthermore, if the objects are polygons, $F^*$ is the union of straight line segments of positive length. If two non-collinear line segments in $F^*$ have a common endpoint p that is not a corner of an object, then exactly three line segments meet at p, forming angles of $2\pi /3$ with each other.

Proof

We first prove that the curves in $F^*$ are disjoint from the interior of each object. To this end, consider any fence F in which some open curve $\pi \subset F$ is contained in the interior of an object $O\subset B_i$. Then the connected components of ${\mathbb {R}}^2\setminus F$ on both sides of $\pi$ must be part of the territory $\bar{B}_i$. Hence, $\pi$ can be removed from F while the fence remains feasible. That operation reduces the length, so F is not optimal.

We next show that $F^*$ is the union of a set of closed curves. Suppose not. Let $F'\subset F^*$ be the union of all closed curves contained in $F^*$ and let $\pi$ be a connected component in $F^*\setminus F'$. Then $\pi$ is the (not necessarily disjoint) union of a set of open curves, which do not contribute to the separation of any objects. Hence, $F^*\setminus \pi$ is a fence of smaller length than $F^*$, so $F^*$ is not optimal.

In a similar way, one can consider the union L of all line segments of positive length contained in $F^*$, and if $F^*\setminus L$ is non-empty, a curve $\pi$ in $F^*\setminus L$ can be replaced by a shortest path homotopic to it, which consists of a sequence of line segments. (See the proof of Lemma 5.2.)

The last claimed property is shared with the Euclidean Steiner minimal tree on a set of points in the plane, and it can be proved in the same way, see for example Gilbert and Pollak [13]: suppose that the fence F contains two non-collinear line segments $\ell _1$ and $\ell _2$ sharing an endpoint p that is not a corner of an object. If the angle between $\ell _1$ and $\ell _2$ at p is less than $2\pi /3$, then parts of $\ell _1$ and $\ell _2$ can be replaced by three shorter segments. Hence, the angle between segments meeting at p is at least $2\pi /3$, and there can be at most three such line segments. If there are only two, one can make a shortcut. Therefore, there are exactly three segments, and they form angles of $2\pi /3$. $\square$

As can be seen in Fig. 2, optimal fences may contain cycles that do not touch any object. By the following lemma, such cycles can be eliminated without increasing the length. This will be useful for the design of our approximation algorithm (Sect. 5).

Lemma 2.2

Let N be the set of corners of the objects in an instance of geometric k-cut. There exists an optimal fence $F^*$ with the property that $F^*\setminus N$ contains no cycles.

Proof

Let us look at a connected component T of $F^*\setminus N$. Since $F^*$ is a union of closed curves by Lemma 2.1, it follows that the leaves of $F^*\setminus N$ are in N. All other vertices have degree 3, and the incident edges meet at angles of $2\pi /3$. If T contains a cycle C, we can push the edges of C in a parallel fashion (forming an offset curve), as shown in Fig. 2. This operation does not change the total length of T. This can be seen by looking at each degree-3 vertex v individually: We enclose v in a small equilateral triangle whose sides cut the edges at right angles, see Fig. 3. It is a well-known geometric fact that the sum of the distances from a point v inside an equilateral triangle to the three sides is constant. (This can be seen by observing that each distance is proportional to one of the barycentric coordinates of v, and that the three proportionality factors are the same in case of an equilateral triangle.) This implies that the length of the fence inside the triangle is unchanged by the offset operation. The portions of C outside the triangles are just translated and do not change their lengths either.

Fig. 3

Offsetting the cycle does not change the total length of the fence inside the triangle

As we offset the cycle C, an edge of C must eventually hit a corner of an object. Another conceivable possibility is that an edge of C between two degree-3 vertices is reduced to a point, but this would lead to an optimal fence with two non-collinear segments sharing an endpoint and forming an angle of $\pi /3$, violating Lemma 2.1. In this way, the cycles of T can be eliminated one by one. $\square$

We mention that the restriction of objects to polygonal shapes is not crucial for Lemmas 2.1 and 2.2. If objects have curved boundaries, the fence consists of straight segments that are disjoint from the interior of the objects, plus portions of object boundaries.

3 The Bicoloured Case

In this section we consider the case of $k=2$ colours. Let N be the set of all corners of the objects. A line segment is said to be free if it is disjoint from the interior of every object. A vertex v of an optimal fence cannot have degree 3 or more unless $v\in N$, as otherwise two of the regions meeting at v would be part of the same territory and could be merged, thus reducing the length of the fence. We therefore get the following consequence of Lemma 2.1.

Lemma 3.1

An optimal fence consists of free line segments with endpoints in N.

Fig. 4

Left: the arrangement ${\mathcal {A}}$ induced by an instance of geometric 2-cut with two green and two red objects. The dual graph G is blue. Right: the optimal solution

Let S be the set of all free segments with endpoints in N. S includes all edges of the objects. Let ${\mathcal {A}}$ be the arrangement induced by S, see Fig. 4. Consider an optimal fence $F^*$ and the associated territories ${\bar{B}}_1$ and ${\bar{B}}_2$. Lemma 3.1 implies that $F^*$ is contained in the edges and vertices of ${\mathcal {A}}$. Thus, each cell of ${\mathcal {A}}$ belongs entirely either to ${\bar{B}}_1$ or ${\bar{B}}_2$. The objects are cells of ${\mathcal {A}}$ whose classification (i.e., membership of ${\bar{B}}_1$ versus ${\bar{B}}_2$) is fixed. In order to find $F^*$, we need to select the territory that each of the other cells belongs to. Since $|S|=O(n^2)$, ${\mathcal {A}}$ has size $O(|S|^2)=O(n^4)$ and can be computed in $O(|{\mathcal {A}}|)= O(n^4)$ time [7]. For simplicity, we stick with the worst-case bounds. In practice, set S can be pruned by observing that the edges of an optimal fence must be bitangents that touch the objects in a certain way, because the curves of the fence are locally shortest.

Finding an optimal fence amounts to minimising the boundary between ${\bar{B}}_1$ and ${\bar{B}}_2$. This can be formulated as a minimum-cut problem in the dual graph G(V, E) of the arrangement ${\mathcal {A}}$. There is a node in V for each cell and a weighted edge in E for each pair of adjacent cells: the weight of the edge is the length of the cells’ common boundary. Let $S_1,S_2\subset V$ be the sets of cells that contain the objects of $B_1,B_2$, respectively. We need to find the minimum cut that separates $S_1$ from $S_2$. This can be obtained by finding the maximum flow in G from the sources $S_1$ to the sinks $S_2$, where the capacities are the weights. Such a maximum flow can be computed in strongly polynomial time. As G is a planar graph, we can use the algorithm by Borradaile et al. [4] with running time $O(|V|\log ^3|V|)$. The running time has since then been improved to $O({|V|\log ^3|V|}/{\log ^2\log |V|})$ by Gawrychowski and Karczmarz [12]. As $|V|=O(|S|^2)=O(n^4)$, we obtain the following theorem.

Theorem 3.2

geometric 2-cut can be solved in time $O({n^4\log ^3\!n}/{\log ^2\log n})$, where n is the total number of corners of the objects.

A Note on the Machine Model Theorem 3.2 assumes that edge weights can be added and subtracted in constant time. As the edge weights are Euclidean distances, whose computation involves square roots, this is only warranted if we work in the real-ram model of computation, which is appropriate for geometric algorithms [19]. In the Turing machine model, the exact comparison of sums of square roots is difficult [17], and geometric 2-cut is not known to be even in NP, a property that it shares with many other geometric optimisation problems such as the Euclidean Travelling Salesman Problem or the Euclidean Minimum Spanning Tree Problem [11].

Related Algorithms A similar algorithm has been described before in a slightly different context: image segmentation [14], see also [4]. Here, we have a rectangular grid of pixels, each having a given gray-scale value. Some pixels are known to be either black or white. The remaining pixels have to be assigned either the black or the white colour. Each pixel has edges to its (at most four) neighbours. The weights of these edges can be chosen in such a way that the minimum cut problem corresponds to minimising a cost function consisting of two parts: One part, the data component, has a term for each pixel, and it measures the discrepancy between the gray-value of the pixel and the assigned value. The other part, the smoothing component, penalises neighbouring pixels with similar gray-values that are assigned different colours.

Alternative Approaches The running time of roughly $n^4$ in Theorem 3.2 is rather high. In many instances, the arrangement ${\mathcal {A}}$ might be much smaller than the worst case, and then the algorithm will of course benefit. The $O(n^4)$ complexity is due to the inclusion of all intersections between the $O(n^2)$ potential line segments. We are rewarded because this turns the problem into a problem on a planar graph, and therefore the effort for obtaining a maximum flow adds only a polylogarithmic factor. On the other hand, finding the minimum cut in the arrangement ${\mathcal {A}}$ is some sort of overkill, since it optimises also weird types of fences that zigzag through the arrangement, while we know that optimal fences can only bend at object corners.

It would be nice to work only with the $O(n^2)$ line segments without their crossings. We have considered an incremental approach that turns red objects into green objects one by one and determines the green territories that should be merged, by computing the boundary cycle of the resulting larger territory. However, a preliminary estimate indicated that this approach would not be competitive with the algorithm of Theorem 3.2, unless it is combined with new ideas.

4 Hardness of the Tricoloured Case

We show how to construct an instance I of geometric 3-cut from an instance $\Phi$ of planar positive 1-in-3-sat. For ease of presentation, we first describe the reduction geometrically, allowing irrational coordinates. We prove that if $\Phi$ is satisfiable, then I has a fence of a certain cost $M^*$, whereas if $\Phi$ is not satisfiable, then the cost is at least $M^*+1/50$. This gap of 1/50 allows us to slightly move the corners into a new instance $I'$ with rational coordinates, while still being able to distinguish whether $\Phi$ is satisfiable or not, based on the cost of an optimal fence.

In order to make the geometric part of the proof as simple as possible, we introduce a new specialised problem, coloured trigrid positive 1-in-3-sat, by endowing the instances with additional geometric and combinatorial structure (in the form of a double edge colouring).

4.1 Auxiliary NP-Complete Problems

Definition 4.1

• 1. In the positive 1-in-3-sat problem, we are given a collection $\Phi$ of clauses, each consisting of exactly three distinct variables. (There are no negated variables.) The problem is to decide whether there exists an assignment of truth values to the variables of $\Phi$ such that exactly one variable in each clause is true.

• 2. The trigrid positive 1-in-3-sat problem is the same, except that the input has some additional geometric structure: We are given an instance $\Phi$ of positive 1-in-3-sat together with a planar embedding of an associated graph $G(\Phi )$ with the following properties, see Fig. 5:

  • $G(\Phi )$ is a subgraph of the infinite regular triangular grid in the plane, which is composed of equilateral triangles of side length 1.

  • For each variable x, there is a simple cycle $v_x$.

  • For each clause $C=\{x,y,z\}$, there is a path $P_C$ and three vertical paths $\ell ^C_x,\ell ^C_y,\ell ^C_z$ with one endpoint at a vertex of $P_C$ and one at a vertex of each of $v_x,v_y,v_z$.

  • Except for the described incidences, no edges share a vertex.

  • All vertices have degree 2 or 3.

  • Any two adjacent edges form an angle of $\pi$ or $2\pi /3$.

  • The number of vertices is bounded by a quadratic function of the size of $\Phi$.

Fig. 5

Left: an instance of planar positive 1-in-3-sat for the formula $\Phi =C_1\wedge C_2\wedge C_3$ with three clauses $C_1=\{x_1 , x_3 , x_5\}$, $C_2=\{x_1 , x_2 , x_3\}$, and $C_3=\{x_2 , x_4 , x_5\}$, which are represented as rotated E-shapes. Right: a corresponding instance of trigrid positive 1-in-3-sat. The paths representing the three clauses are highlighted. Clause vertices are drawn as dots and branch vertices as boxes

Mulzer and Rote [20] showed that another problem, planar positive 1-in-3-sat, is NP-complete, which is similar but uses a slightly different plane embedding with axis-parallel segments: The variables are represented by disjoint line segments on a horizontal line $\ell$; and each three-legged clause looks like a rotated E-shape and lies above or below $\ell$. Figure 5 shows how such an instance can be easily converted to follow the conventions of Definition 4.1. It follows that trigrid positive 1-in-3-sat is also NP-complete.

The idea of our reduction to geometric 3-cut is to thicken the edges of $G(\Phi )$ into channels of width 1/2, as illustrated in Fig. 6. A channel contains small inner objects and is bounded by larger outer objects of another colour. There will be two equally good ways to separate the inner and outer objects, namely long fences along the boundaries of the channel and individual fences around the inner objects. Any other way of separating the inner from the outer objects will turn out to require more fence. These two optimal ways of separating the colours are used to represent the truth values.

Fig. 6

Illustration of a section of a channel with red outer objects and six green inner objects, centred around an edge of the graph $G(\Phi )$ (the dashed line), and two ways of separating the different colours. The solution on the left will be called the inner solution because the empty part inside the channel is assigned to the same territory as the inner objects. The solution on the right is called the outer solution

We will now be more specific. Consider an instance $(\Phi ,G(\Phi ))$ of trigrid positive 1-in-3-sat. There are some vertices of degree three on the cycles $v_x$ corresponding to each variable x in $\Phi$, and these are denoted as branch vertices. There is also one vertex of degree three on the path $P_C$ corresponding to each clause C in $\Phi$, which we denote as a clause vertex. These are the only vertices of degree 3.

We consider $G(\Phi )$ as a subset of the plane and remove all clause vertices. This splits $G(\Phi )$ into one connected component $E_x$ for each variable x of $\Phi$. We build one channel around each set $E_x$, including the bends and branch vertices, and we will ensure that there are two equally good ways to separate the inner and outer objects throughout the whole channel. These two choices, along the boundaries or around each inner object individually, play the roles of x being false and true, respectively.

At the clause vertices where three regions $E_x,E_y,E_z$ meet, we make a clause gadget that connects the three channels of x, y, z. The objects in the clause gadget can be separated using the least amount of fence if and only if one of the channels is in the state corresponding to true and the other two are in the false state. Therefore, this corresponds to the clause being satisfied in the sense that exactly one variable is true.

In order to make this idea work, we first assign two colours to every edge of $G(\Phi )$: an inner and an outer colour from the set $\{\text {red},\text {green},\text {blue}\}$. These will be used as the colours of the inner and outer objects of the channel. The colouring must have the following properties:

• 1. The inner and outer colours of every edge are distinct.

• 2. Any two adjacent collinear edges have the same inner or the same outer colour (or both).

• 3. Any two adjacent edges that meet at an angle of $2\pi /3$ at a non-clause vertex have the same inner and the same outer colour.

• 4. The inner colours of the three edges meeting at a clause vertex are red, green, blue in clockwise order, while the outer colours of the same edges are blue, red, green, respectively.

We now introduce the problem coloured trigrid positive 1-in-3-sat, which we will reduce to geometric 3-cut, see Fig. 7.

Fig. 7

An instance of coloured trigrid positive 1-in-3-sat based on the instance from Fig. 5

Definition 4.2

In coloured trigrid positive 1-in-3-sat, we are given an instance $(\Phi ,G(\Phi ))$ of trigrid positive 1-in-3-sat together with a colouring of the edges of $G(\Phi )$ satisfying the above four requirements. We want to decide whether $\Phi$ has a satisfying assignment in the sense of positive 1-in-3-sat (Definition 4.1).

Lemma 4.3

The problem coloured trigrid positive 1-in-3-sat is NP-complete.

Proof

Membership in NP is obvious. For NP-hardness, we reduce from trigrid positive 1-in-3-sat. Let $(\Phi ,G(\Phi ))$ be an instance of the latter. We assume that all vertical paths $\ell ^C_x$ have length at least 4. This can be achieved by stretching them vertically, as shown in Fig. 7, or simply by scaling the whole graph by a factor of 4.

We colour each triple of edges meeting at a clause vertex according to requirement 4. Then, in each clause path $P_C$, we simply continue the colouring from the edges incident to the clause vertices in both directions, and also to the first edge of the vertical paths $\ell ^C_x$ incident to the endpoints. For all branch vertices and all cycles $v_x$ we choose red as the outer colour and blue as the inner colour, and this colouring is also used for the first edge on each incident vertical path $\ell ^C_x$.

It remains to colour the “interior” edges of the vertical paths $\ell ^C_x$. Since each vertical path has at least four edges and only the colours of the first and last edges have been fixed, it is possible to change inner or outer colour three times. It is easy to check that this is sufficient to interpolate between any combination of colours at the boundary edges. There are six possible combinations of inner and outer colours: (R, B), (B, R), (R, G), (G, R), (B, G), and (G, B), denoting the three colours by R, B, G. These combinations can be arranged in a cycle of length six, so that it is possible to get from one combination to an adjacent one by changing the inner or the outer colour:

Each colour change is denoted by a vertical bar. It follows that one can get from any combination to any other in at most three steps. The maximum number of changes is needed when the inner and outer colours have to be swapped.

Therefore, it is possible to adjust the colours so that the entire path gets coloured. We have hence constructed an instance of coloured trigrid positive 1-in-3-sat.    $\square$

4.2 Building a geometric 3-sat Instance from Tiles

Consider an instance $(\Phi ,G(\Phi ))$ of coloured trigrid positive 1-in-3-sat that we want to reduce to geometric 3-cut. We use hexagonal tiles of six different types, namely straight, inner colour change, outer colour change, bend, branch, and clause tiles. Each tile is a regular hexagon with side length $1/\sqrt{3}$ and hence has distance 1 between opposite sides.

Every tile is placed with its centre at a vertex p of $G(\Phi )$, and rotated so that it has two horizontal edges. Thus, each edge of $G(\Phi )$, which has length 1, connects the centres of two adjacent tiles. Let $G_p$ be the part of the graph $G(\Phi )$ within distance 1/2 from p. Figure 8 shows the tiles and how they are placed according to the shape and colours of $G_p$.

Fig. 8

The six kinds of tiles used in the reduction to geometric 3-cut. The dashed coloured lines show the edges of $G_p$ and their inner and outer colours. The tiles are coloured accordingly. The points in the clause tile are defined so that $\Vert ab\Vert =\Vert a'b'\Vert =0.24$ and $\Vert bc\Vert =\Vert b'c\Vert =1/4=0.25$. The point c has coordinates $(x,x/\sqrt{3})$, where $x= 13\sqrt{3}/200+3/16-\sqrt{3900\sqrt{3}-459}/400\approx 0.1017$ is a solution to $10000x^2+(-1300\sqrt{3}-3750)x+507=0$. Rotations by $\pm 2\pi /3$ around p give the remaining points in the tile. The point c and its images $c_1,c_2$ form an equilateral triangle with side length $2x\approx 0.2034$

In order to define the objects of a tile, we take the offsets of the edges of $G_p$ at distance 1/4 on both sides, as shown in Fig. 8. Such an offset is obtained by translating each edge of $G_p$ parallel to itself. The moving edges are shortened or extended to meet adjacent moving edges in common endpoints. The region between the offset curves contains all points at distance at most 1/4 from the edges of $G_p$. In the bend tile, this region contains also some points of larger distance because an offset of a reflex angle is formed. The largest distance occurs for the vertex q: it has distance $1/\sqrt{12}$ from p.

The offset polygons partition the tile into an inner and an outer region. The outer objects cover the outer region completely. Every point in the outer region is coloured with the outer colour of the closest edge in $G_p$. The inner region is mostly empty, except for the inner objects described in each case below.

We place the origin at the centre $p=(0,0)$. We describe each tile in one selected orientation, as shown in Fig. 8; the tiles can be rotated by multiples of $\pi /3$. In each case, we assume that $G_p$ contains the vertical segment from p upwards to (0, 1/2).

The Straight Tile: This is used when two collinear edges meet at p with the same inner and outer colour. There are four axis-parallel squares of the inner colour of $G_p$ with side length 1/8 centred at $(\pm (1/4-1/16),\pm 1/4)$. This size is chosen so that their total perimeter is 2 and equals the length of the boundary between the inner and outer regions.

The Inner Colour Change Tile: This is used when two consecutive collinear edges have different inner colours. In addition to the four squares of the previous case, there are four smaller axis-parallel squares with side length 1/28 centred at $(\pm (1/4-1/56),\pm 1/56)$. Each square is coloured in the inner colour of the closest point in $G_p$. The size of the small squares is chosen so that they can be individually enclosed using fences of total length $2\times 7\times 1/28=1/2$, which is the width of the inner region.

The Outer Colour Change Tile: This is used when two consecutive collinear edges have different outer colours. There are four axis-parallel squares of the inner colour of $G_p$ with side length 3/32. Their centres are $(\pm (1/4-3/64),\pm 1/4)$. The size of these squares is chosen so that their total perimeter is $2-1/2=3/2$.

The Bend Tile: If two non-collinear edges meet at p, we use a bend tile. We place an axis-parallel square with side length $x=({6+\sqrt{3}})/{72}$ and centre $(-(1/4-x/2),1/4)$ and another with side length $y=({6-\sqrt{3}})/{48}$ and centre $(1/4-y/2, 3/8)$. We place symmetric squares across the symmetry line b. One of the outer objects has a concave corner q with exterior angle $2\pi /3$. We place a parallelogram at this corner, of side length x, with two edges running along the edges of the outer object. The boundary between the inner and the outer region has a total length of $(1-{\sqrt{3}}/6)+(1+{\sqrt{3}}/6)=2$. The inner objects are chosen so that the total perimeter of the two small squares, $8y=1-{\sqrt{3}}/6$, as well as the total perimeter of the three larger objects, $12x=1+{\sqrt{3}}/6$, equals the length of the respective boundary on which these objects abut.

The Branch Tile: This is used when p is a branch vertex. We place axis-parallel squares of side length $y=({6-\sqrt{3}})/{48}$ centred at $(\pm (1/4-y/2),3/8)$ and their rotations around p by angles $2\pi /3$ and $4\pi /3$. The boundary between the inner and the outer regions has total length of $({6-\sqrt{3}})/{2}$, and the total perimeter of the inner objects is also $24y=({6-\sqrt{3}})/{2}$.

The Clause Tile: It is used for a clause vertex, and it is described in the caption of Fig. 8.

4.3 Solving the Tiles Locally

Let an instance I of geometric 3-sat be given together with a fence ${\mathcal {F}}$. We will consider the restriction of I to a polygon P, which is a tile or a part of a tile. In this way, we only have to look at problems of constant size. The part of the fence ${\mathcal {F}}\cap P$ inside P can be expressed as a union of (not necessarily disjoint) closed curves and open curves with endpoints on the boundary $\partial P$. An open curve must be contained in a larger closed curve of ${\mathcal {F}}$ that continues outside P.

Note that ${\mathcal {F}}\cap P$ has the property that if a path $\pi \subset P$ connects two objects in P of different colour, then $\pi$ intersects ${\mathcal {F}}\cap P$. We call a union of closed and open curves in P with this property a solution to $I\cap P$. Clearly, this is a necessary condition for a set of curves to be extensible to a fence ${\mathcal {F}}$ for the full instance. In the following, we analyse the solutions to the tiles defined in Sect. 4.2, and we characterise the solutions of minimum cost. We say that two closed curves (disjoint from the interiors of the objects) are homotopic if one can be continuously deformed into the other without entering the interiors of the objects. Two open curves with endpoints on the boundary of the tile are homotopic if they can be extended outside the tile to two homotopic closed curves.

Fig. 9

The optimal solutions to each type of tile. The edges in $G_p$ are shown in dashed grey. The left solution to each of the first five types of tiles is the outer solution, and the right solution is the inner solution, as explained in Fig. 6. For the clause tile, we call the solutions the z-outer, x-outer, and y-outer solutions from left to right, according to the dominant territory

The following lemma characterises the optimal solutions to each type of tile. The statement is that if a solution is not too much more expensive than the solutions shown in Fig. 9, then it will contain curves homotopic to each curve in one of the solutions in the figure.

Lemma 4.4

Figure 9 shows optimal solutions to each kind of tile. The cost in each case is:

• Straight tile: 2.

• Inner colour change tile: 5/2.

• Outer colour change tile: $2+(2/{\sqrt{3}}-1/2)\approx 2.65$.

• Bend tile: 2.

• Branch tile: $({6-\sqrt{3}})/2\approx 2.13$.

• Clause tile: $M\approx 3.51$. (The value M is specified in Lemma 4.5. The exact algebraic expression is complicated and of no importance.)

Moreover, if the cost of a solution ${\mathcal {F}}$ to a tile T exceeds the optimum by less than 1/50, then ${\mathcal {F}}$ is homotopic to one of the optimal solutions ${\mathcal {F}}^*$ of T in the following sense: For each curve $\pi ^*$ in ${\mathcal {F}}^*$, there is a curve $\pi$ in ${\mathcal {F}}$ homotopic to $\pi ^*$. If $\pi ^*$ is a closed curve, the distance from any point on $\pi$ to the closest point on $\pi ^*$ is less than $\sqrt{(1/8+1/100)^2-(1/8)^2}<0.06$. If $\pi ^*$ is an open curve and $\pi ^*$ has an endpoint $f^*$, there is a corresponding endpoint f of $\pi$ with $\Vert f^*f\Vert < 1/10$.

Proof

We assume again that the origin is at the centre $p= (0,0)$ of the tile T, and we assume that the orientation and colours are as in Fig. 8.

For each tile T, $G_p$ consists of the two or three half-edges of $G(\Phi )$ meeting at p, and it separates T into two or three pieces. The pieces are two pentagons for the straight, inner colour change, and outer colour change tiles; a pentagon and a non-convex heptagon for the bend tile; and three pentagons for the branch and the clause tiles.

For each tile type except the clause tile, we consider each such piece $T'$ separately and check the minimum cost of a solution to $T'$. Since these pieces contain few objects, it is easy to compute the optimal solutions. For example, consider the simplest instance: the left half-tile $T'$ of the straight tile. The fence runs inside a $1/4\times 1$ rectangle containing two small blue squares. There are two possibilities: The two blue squares can be in the same connected component of the blue territory or in two different components. These components may be disjoint from the boundary or touch the boundary of $T'$. In the first case, the fence must contain a closed curve surrounding the blue object(s) in it. In the second case, the fence is a curve between two boundary points. In each case, it is easy to calculate (or even to see) what the optimal solution is and, by comparing all possibilities, one finds that there are the two optimal solutions shown in the first two pictures of Fig. 9. The solution in the right half must be symmetric to the left half in order to produce a solution to the whole tile T. In a similar way, one can treat the other tiles. We omit the details, but we will give the full proof for the most complicated case: the clause tile. Here, it is not true that a solution to the complete tile can be obtained by combining optimal solutions of the three smaller pieces. As this proof requires an extensive case analysis, it is deferred to Lemma 4.5.

It turns out that for each piece $T'$ of the first five tile types, there are two solutions, and they are as shown in Fig. 9. One solution corresponds to the outer state and the other to the inner state. In order to be combined to a solution for all of T, each of the two or three pieces $T'$ needs to be in the same state. Thus, the solutions shown in Fig. 9 are all the optimal solutions.

Fig. 10

Left: a square of side length 1/8. The red curve encloses all curves of length at most $1/2+1/50$ that enclose the square. One such curve with maximum deviation from the boundary of the square is drawn in black. The red curve consists of eight elliptic arcs. Middle and right: a solution to the straight tile in the outer resp. inner state with a cost that exceeds the optimum by 1/50

By analysing the cases more carefully, one obtains a stronger claim that any solution ${\mathcal {F}}$ that is not homotopic to an optimal solution has a cost that exceeds the optimal cost by more than 1/50. (Again, we give the detailed analysis only for the clause tile in Lemma 4.5 below.) Consider therefore a solution ${\mathcal {F}}$ whose cost exceeds the cost of a homotopic optimal solution ${\mathcal {F}}^*$ by less than 1/50. In order to decide how much ${\mathcal {F}}$ can deviate from ${\mathcal {F}}^*$, consider the straight tile as an example, see Fig. 10. In the outer state, each curve enclosing an inner object has length at least 1/2. Since the total cost is less than $2+1/50$, each curve has length less than $1/2+1/50$. An elementary analysis gives that a closed curve of length at most $1/2+1/50$ which encloses a square of side length 1/8 is within distance $\sqrt{(1/16+1/100)^2-(1/16)^2}<0.04$ from the boundary of the square. For the inner state, consider the curve $\pi \subset {\mathcal {F}}$ in the right side of the tile that has the inner objects to the left. The length of $\pi$ has to be less than $1+1/50$ in order for the total cost to be less than $2+1/50$. Note that $\pi$ has to pass through the upper right corner (1/4, 5/16) of the upper right square. Therefore, $\pi$ has to meet the top edge of T at a point within distance $\sqrt{(3/16+1/50)^2-(3/16)^2}<0.09$ from the corresponding endpoint (1/4, 1/2) of $\pi ^*$. The other non-clause tiles are analysed in a similar way.

The largest possible deviation between a closed curve in ${\mathcal {F}}$ and ${\mathcal {F}}^*$ appears for the clause tile, since it contains an inner object with the longest edge of all tiles, namely a triangle with an edge of length 1/4. This leads to a deviation of less than $\sqrt{(1/8+1/100)^2-(1/8)^2}<0.06$. Likewise, the largest possible deviation between open curves is 1/10, as realised in the clause tile and described in Lemma 4.5. $\square$

It remains to analyse the optimal solutions of the clause tile. We name objects in the clause tile as shown in Fig. 11. Indices are taken modulo 3. The optimal solutions are covered by Case 2.3 in the proof.

Fig. 11

Labels used in Lemma 4.5 and illustrations for Case 1

Lemma 4.5

The optimal cost of a solution ${\mathcal {F}}$ to a clause tile is $M:=3\Vert d_0c_0\Vert +6\Vert e_0b_0\Vert +4\Vert a_0b_0\Vert +2\Vert b_0c_0\Vert +\Vert c_0c_1\Vert \approx 3.51$. Moreover, if the cost is less than $M+1/50$, then there is $i\in \{0,1,2\}$ such that ${\mathcal {F}}$ contains the following, not necessarily disjoint parts (see Fig. 13, Case 2.3 for an illustration of the case $i=0$):

• a curve from $f_i\in a_ia'_i$ to $b_i$, where $\Vert f_ia_i\Vert <1/10$,

• a curve from $f'_i\in a_ia'_i$ to $b'_i$, where $\Vert f'_ia'_i\Vert <1/10$,

• a curve from $f_{i+1}\in a_{i+1}a'_{i+1}$ to $b_{i+1}$, where $\Vert f_{i+1}a_{i+1}\Vert <1/10$,

• a curve from $f'_{i+1}\in a_{i+1}a'_{i+1}$ to $b'_{i+1}$, where $\Vert f'_{i+1}a'_{i+1}\Vert <1/10$,

• a curve from $c_{i+1}$ to $c_{i+2}$,

• a curve from $c_i$ to $b'_{i+2}$,

• a curve from $c_{i+2}$ to $b_{i+2}$.

Proof

Clearly, ${\mathcal {F}}$ must contain segments $d_ic_i$, $e_ib_i$, and $e_ib'_{i+2}$ on the shared boundary of two objects of different colour, for $i=0,1,2$. In total, this amounts to $3\Vert d_0c_0\Vert +6\Vert e_0b_0\Vert$. In the following, we argue about the fence needed in addition to that, i.e., the part of ${\mathcal {F}}$ contained in the closed 15-gon $T'=a_0a'_0b'_0c_1b_1a_1a'_1b'_1c_2b_2a_2a'_2b'_2c_0b_0$. We characterise how the solution looks when the additional cost in $T'$ is at most the critical threshold

$$\begin{aligned} 4\Vert a_0b_0\Vert +2\Vert b_0c_0\Vert +\Vert c_0c_1\Vert +0.02=4\times 0.24 + 2\times 0.25 + 2x + 0.02<1.684, \end{aligned}$$

with the quantity x that was defined in Fig. 8. When we say that the solution must contain a curve or a tree with certain properties (such as connecting two specific points), we mean such a curve or tree inside $T'$.

We define a domain as a connected component of a territory inside a tile. Two different domains might conceivably be connected outside the tile, but we are interested only in the local situation. For this definition, we also do not consider the common point $e_{i+1}$ of objects $O'_i$ and $I_{i+1}$ as providing a connection between them. We only consider connections in $T'$. Since a territory is a closed set by definition, the interior of a domain might be disconnected.

We define the cases by specifying which objects are in the same domain. After making enough assumptions in one branch of the case analysis, we will conclude that the solution must connect certain groups of points. In most cases, this allows us to derive a lower bound on the cheapest solution, which is above 1.684. In the case that contains the optimal solution, all objects of different colours will be separated, and then we state what the solutions satisfying the specific assumptions are.

The shortest connection network for a specified set of terminal points is a geodesic variation of the geometric Steiner tree problem, where the network is constrained to lie in the region $T'$. It is usually easy to restrict the structure of the shortest connection network to a few possibilities, using geometric criteria such as that an angle less than $2\pi /3$ between incident edges is forbidden unless it is blocked by an object. We will often refer to the Fermat point F of three given points A, B, C: the point minimising the sum of distances to the tree points. If all angles in the triangle ABC are less than $2\pi /3$, F lies in the interior of this triangle. The three segments to FA, FB, FC make equal angles $2\pi /3$ at F and they form the minimal Steiner tree of A, B, C.

Once the combinatorial structure of a potential solution was specified, we have used the Geogebra software [15] to construct the solution from the geometric constraints and to estimate its costs numerically, and also for producing the illustrations. We will report the costs rounded to three digits; this precision is sufficient for the comparisons.

Note first that for $i=0,1,2$, in order to separate $O_i$ from $I_i$, the solution must contain a curve (in $T'$) starting at $b_i$ that has a length of at least 0.24, and similarly one from $b'_i$ in order to separate $O'_i$ from $I'_i$. The prefixes of length 0.24 of these six curves are disjoint. We can therefore charge 0.24 to each $b_i$ and $b'_i$, unless this point is already connected otherwise. The shortest possible cost of 0.24 arises when $b_i$ is connected to $a_i$ and $b'_i$ to $a'_i$. All possibilities of a different structure (for example, connecting $b_i,b_i'$ with each other or to $c_i$ and $c_{i+1}$, respectively) cost at least 0.25.

In the discussion of the cases it will often happen that an object $I_i$ or $I'_i$ is in a different domain than all other objects of the same colour. In this case, we say that $I_i$ or $I'_i$ is isolated.

Proposition 4.6

   

• If the object $I_i$ is isolated, the solution must contain a curve from $b_i$ to $c_i$ inside the tile.

• If the object $I'_i$ is isolated, the solution must contain a curve from $b'_i$ to $c_{i+1}$ inside the tile.

Proof

If $I_i$ is isolated, it is separated from all other objects in the tile, of whatever colour. Thus there must be curve between $b_i$ and $c_i$within the tile, or two curves that go from $b_i$ and $c_i$ to the boundary and continue outside. The second case is excluded by the following calculation: The shortest connection from $c_i$ to the boundary has length $\approx 0.441$. To this, we have to add $6\times 0.24=1.44$ for connecting $b_0,b'_0,b_1,b'_1,b_2,b'_2$, and this is far more than 1.684 in total. The statement about $I_i'$ is analogous. $\square$

We now start the case distinction.

Case 1: For some i, neither $O_i$and $O'_i$nor $I_i$and $I'_i$are in a domain together. Without loss of generality, suppose that the condition holds for $i=0$. We consider the solution ${\mathcal {F}}$ restricted to the hexagon $H=a_0a'_0b'_0c_1c_0b_0$. The condition implies that the left side $a'_0b'_0c_1$ must be separated from the right side $a_0b_0c_0$, and therefore there must be a connected component F of ${\mathcal {F}}\cap H$ that connects $a_0a'_0$ and $c_0c_1$. The individual cases are shown in Fig. 11.

Case 1.1: F also separates $O_0$from $I_0$and $O'_0$from $I'_0$inside H. Then F contains $b_0$ and $b'_0$. The shortest connected system of curves that connects $b_0$, $b'_0$, $a_0a'_0$, and $c_0c_1$ is a Steiner minimal tree with vertical edges meeting $a_0a'_0$ and $c_0c_1$. There are two infinite families of such minimal trees: In the tree F shown in Fig. 11, the two Steiner vertices can be simultaneously shifted along the edges incident to $b_0$ and $b_0'$. There is also a symmetric version of these trees. The optimal cost is $\approx 0.874$. Adding the $4\times 0.24=0.96$ charged to $b_1,b'_1,b_2,b'_2$, we get significantly more than 1.684.

Case 1.2: F separates $O_0$from $I_0$inside H, but not $O'_0$from $I'_0$ . Then F must contain $b_0$, and it has minimal length if $F=a_0b_0\cup b_0c_0$, which costs exactly 0.49. In addition to that, we have $5\times 0.24=1.2$ charged to $b'_0,b_1,b'_1,b_2,b'_2$, and the total is $1.69>1.684$.

Case 1.3: F separates $O'_0$from $I'_0$inside H, but not $O_0$from $I_0$ . This is symmetric to Case 1.2.

Case 1.4: F separates neither $O_0$from $I_0$, nor $O'_0$from $I'_0$inside H . In this case, F has cost at least $\approx 0.441$, which is the distance between $a_0a'_0$ and $c_0c_{1}$, and F contains neither $b_0$ nor $b'_0$. In addition, $6\times 0.24=1.44$ is charged to $b_i,b'_i,\ldots$, which in total is far more than 1.684.

Fig. 12

Case 2.1. Each pair $O_i,O'_i$ is in the same domain, and $I_i,I'_i$ are in different domains

Case 2: For every i, $O_i$and $O'_i$or $I_i$and $I'_i$are in a domain together. We divide into subcases according to the number c of values of i for which $I_i$ and $I'_i$ are in the same domain.

Case 2.1: $c=0$. In this case, $O_i$ and $O'_i$ are in the same domain for each i, and $I_i$ and $I'_i$ are in different domains. The subcases are shown in Fig. 12.

Case 2.1.1: For no i, $O_i\cup O'_i$is in a domain with $I_{i+1}$or $I'_{i+1}$. In this case, each object $I_i$ and $I'_i$ is isolated. Therefore, by Proposition 4.6, the solution contains curves from $b_i$ to $c_i$ and from $b'_i$ to $c_{i+1}$ for each i. Furthermore, there must be a curve from $b_i$ to $b'_i$ bounding the domain containing $O_i\cup O'_i$. It follows that the solution connects any two of the nine points $\bigcup _{i=0}^2\{b_i,b'_i,c_i\}$. The cheapest solution that satisfies this is $\bigcup _{i=0}^2(b_ic_i\cup b'_ic_{i+1}\cup c_ip)$, which has cost $\approx 1.852>1.684$. This is in fact the most expensive of all cases. All other solutions provide only a subset of these connections.

Case 2.1.2: For some i, $O_i\cup O'_i$is in a domain with $I'_{i+1}$. Assume without loss of generality that $O_0\cup O'_0$ is in a domain with $I'_1$. The boundary of this domain contains

• (a) a curve connecting $b'_0$ and $b'_1$, and

• (b) a curve connecting $b_0$ and $c_2$.

The mentioned domain separates $I'_0$ from the remaining green objects, and $I_2$ and $I'_2$ from the remaining blue objects. For this reason, these objects are isolated, and the solution contains

• (c) a curve connecting $b'_0$ and $c_1$,

• (d) a curve connecting $b_2$ and $c_2$, and

• (e) a curve connecting $b'_2$ and $c_0$.

By the combined assumptions of Case 2.1 and 2.1.2, $I_1$ is isolated, and therefore the solution contains

• (f) a curve connecting $b_1$ and $c_1$.

Summarising, it follows that the solution contains

• a component connecting $b'_0,c_1,b_1,b'_1$, by (a), (c), and (f),

• a component connecting $b_0,c_2,b_2$, by (b) and (d), and

• a component connecting $b'_2$ and $c_0$, by (e).

These components are not necessarily three distinct components. The optimal solution under these constraints consists of segments from $b_1,b'_1,c_1$ to their Fermat point and the segments $b_0c_0,b'_0c_1, b'_2c_0, c_0c_2, b_2c_2$, and it has cost $\approx 1.848>1.684$.

Case 2.1.3: For no i, $O_i\cup O'_i$is in a domain with $I'_{i+1}$, but for some i, $O_i\cup O'_i$is in a domain with $I_{i+1}$. Since each $I'_i$ is isolated, the solution must connect each pair $b'_i, c_{i+1}$. Assume without loss of generality that $O_0\cup O'_0$ is in a domain with $I_1$. There must be a curve connecting $b_0$ and $b_1$ on the boundary of this domain.

Case 2.1.3.1: $O_1\cup O'_1$is in a domain with $I_2$. There is a curve bounding this domain connecting $b_1$ and $b_2$. There is thus a component connecting the three points $b_0,b_1,b_2$. The shortest solution that also contains curves between all pairs $b'_i,c_{i+1}$ is $\bigcup _{i=0}^2 (b_ip\cup b'_ic_{i+1})$, which has total cost $\approx 1.832>1.684$.

Case 2.1.3.2: $O_1\cup O'_1$is not in a domain with $I_2$(and with $I'_2$). There is a curve from $b_1$ to $b'_1$, bounding the domain of $O_1\cup O'_1$, and this curve can be continued from $b'_1$ to $c_2$, and from $c_2$ to $b_2$ (because of the isolated object $I_2$). Thus, as in the previous Case 2.1.3.1, but for a different reason, we must have a curve connecting $b_1$ and $b_2$, and therefore the solution cannot be better than that solution.

The shortest solution that has all necessary connections consists of segments from $b_0,b_1,c_2$ to their Fermat point and the segments $b'_0c_1,b'_1c_2,b_2c_2,b'_2c_0$, and it has cost $\approx 1.835>1.684$. This “optimal solution” violates the assumptions defining this case, as the domain containing $O_1\cup O'_1$ intersects $I_2$ at the point $c_2$, so they are in the same domain. This solution actually falls under Case 2.1.3.1. Thus, properly speaking, there is no optimal solution for Case 2.1.3.2. By modifying the solution near $c_2$, one can obtain solutions for this case that are arbitrarily close to the infimum, but the infimum is not attained.

Fig. 13

Cases 2.2.1–2.4: $I_0$ and $I'_0$ are in the same domain

Case 2.2: $c=1$. Assume without loss of generality that $I_0$ and $I'_0$ are in the same domain, but $I_1$ and $I'_1$ are in different domains, and so are $I_2$ and $I'_2$. By the assumption of Case 2, we also know that $O_1$ and $O'_1$ are in the same domain, as are $O_2$ and $O'_2$. The domain of $I_0\cup I'_0$ separates $O_0$ and $O'_0$ from $I_1$ and $I'_1$, so $I_1$ and $I'_1$ are isolated, and the solution must contain a curve connecting $b_1$ and $c_1$ and one connecting $b'_1$ and $c_2$.

In order to separate $I_0\cup I'_0$ from $O_0$ and $O'_0$, the solution either contains a curve from $b_0$ to $b'_0$ or curves from $b_0$ and $b'_0$ to the boundary segment $a_0a'_0$. We consider the latter option, which is 0.02 cheaper. It will follow from the analysis that even this is too expensive to get below $M+0.02$. The alternative choices of connecting $b_0$ and $b'_0$ also do not interfere with the optimal connections between the remaining points.

The individual cases are shown in Fig. 13.

Case 2.2.1: $O_1\cup O'_1$is not in a domain with $I_2$or $I'_2$. The solution contains a curve from $b_1$ to $b'_1$ bounding the domain containing $O_1\cup O'_1$. In addition, since $I_2$ and $I'_2$ are isolated, there must be curves between $b_2$ and $c_2$ and between $b'_2$ and $c_0$. It follows that the solution contains a tree connecting $b_1,c_1,c_2,b'_1,b_2$. The cheapest such solution is $a_0b_0\cup a'_0b'_0\cup b_1c_1\cup c_1c_2\cup b'_1c_2\cup b_2c_2\cup b'_2c_0$, which has cost $M+0.02$. The difference to the optimal solution of Case 2.3 is that the two segments $b_1a_1$ and $b_1'a'_1$ of length 0.24 are replaced by $b_1c_1$ and $b_1'c_2$, each of length 0.25. This “second-best” solution is the reason we have chosen the threshold 0.02 in the lemma.

Note that the domain containing $O_1\cup O'_1$ intersects $I_2$ at the point $c_2$. We have the same situation as above in Case 2.1.3.2: The “optimal solution” can be obtained as a limit of solutions that fall under Case 2.2.1, but the limit itself violates the assumptions defining this case. This solution actually belongs to Case 2.2.3, and we will revisit it there.

Case 2.2.2: $O_1\cup O'_1$is in a domain with $I'_2$. The solution contains a curve connecting $b_1$ and $c_0$ and one connecting $b'_1$ and $b'_2$ bounding that domain. It also contains a curve connecting $b_2$ and $c_2$, since $I_2$ is isolated. The optimal solution consists of segments from $b_2,b'_2,c_2$ to their Fermat point and segments $a_0b_0, a'_0b'_0,b_1c_1,b'_1c_2,c_0c_1$, and it has cost $\approx 1.831>1.684$.

Case 2.2.3: $O_1\cup O'_1$is in a domain with $I_2$. The solution contains a curve connecting $b_1$ and $b_2$, and one connecting $b'_2$ and $c_0$, since $I'_2$ is isolated. In the cheapest solution, the domain containing $O_1\cup O'_1\cup I_2$ collapses to zero width at $c_2$, and the solution was described in Case 2.2.1.

Case 2.3: $c=2$. Assume without loss of generality that $I_0$ and $I'_0$ are in the same domain, as are $I_1$ and $I'_1$. Furthermore, $I_2$ and $I'_2$ are separated, but $O_2$ and $O'_2$ are together. As in Case 2.2, we assume that $b_0,b_0',b_1,b_1'$ are all connected to the boundary. Otherwise, the cost of the solution will increase by at least 0.02, and as the analysis will show, that is too much to stay below $M+0.02$. The domain containing $I_1\cup I'_1$ separates $O_1$ and $O'_1$ from $I_2$ and $I'_2$. It follows that $I_2$ and $I'_2$ are isolated, and the solution connects $b_2$ with $c_2$ and $b'_2$ with $c_0$. Likewise, the domain containing $I_0\cup I'_0$ separates $O_0$ and $O'_0$ from $I_1$ and $I'_1$. Hence, the boundary of the domain containing $I_1\cup I'_1$ contains a curve connecting $c_1$ and $c_2$. The cheapest solution is $a_0b_0\cup a'_0b'_0\cup a_1b_1\cup a'_1b'_1\cup b_2c_2\cup b'_2c'_0\cup c_1c_2$, as shown in Fig. 13, and the cost is M. This is the best solution among all cases.

The segment $a_0b_0$ can be substituted by a curve from $f_0\in a_0a'_0$ to $b_0$, while keeping the cost below $M+0.02$, if and only if $\Vert f_0a_0\Vert <\sqrt{(0.24+0.02)^2-0.24^2}=0.1$. Likewise for the other segments with an endpoint on the boundary of T. These are exactly the solutions described in the lemma.

Case 2.4: $c=3$. The cheapest way to connect the points $b_i$ and $b_i'$ is to connect all of them to the boundary. Furthermore, the solution contains a curve connecting $c_i$ and $c_{i+1}$ for each i, bounding the domain containing $I_i\cup I'_i$. The cheapest such solution is $\bigcup _{i=0}^2 (a_ib_i\cup a'_ib'_i\cup c_ip)$ as shown in Fig. 13, which has cost $1.792>1.684$. $\square$

Theorem 4.7

The problem geometric 3-cut is NP-hard.

Proof

Let an instance $(\Phi ,G(\Phi ))$ of coloured trigid positive 1-in-3-sat be given and construct the tiles on top of $G(\Phi )$ as described. Let ${\mathcal {T}}$ be the set of tiles and ${\mathcal {A}}$ the area that the tiles cover (i.e., ${\mathcal {A}}$ is a union of the hexagons). We will cover any holes in ${\mathcal {A}}$ with completely red tiles, and place red tiles all the way along the exterior boundary of ${\mathcal {A}}$. Let ${\mathcal {R}}$ be the set of these added red tiles and let I be the resulting instance of geometric 3-cut. It is now trivial how to place the fences in I everywhere except in the interior of ${\mathcal {A}}$.

Consider a fence ${\mathcal {F}}$ to the obtained instance with cost M. Let $M^*$ be the sum of the cost of an optimal solution to each tile in ${\mathcal {T}}$ plus the cost of the fence that must be placed along the boundaries of the added red tiles in ${\mathcal {R}}$. We claim that if $\Phi$ is satisfiable, then a solution realising the minimum $M^*$ exists. Furthermore, if $M< M^*+1/50$, then $\Phi$ is satisfiable.

Suppose that $\Phi$ is satisfiable and fix a satisfying assignment. Consider a clause tile where $E_x$, $E_y$, and $E_z$ meet. Now, we choose the v-outer state, where $v\in \{x,y,z\}$ is the variable that is true. For each non-clause tile that covers a part of $E_w$ for a variable w of $\Phi$, we choose the outer state if w is true and the inner otherwise. It is now easy to see that the curves form a fence of the desired cost.

On the other hand, suppose that $M<M^*+1/50$. It follows that in each tile in ${\mathcal {T}}$, the cost exceeds the optimum by at most 1/50. Hence, the solution in each tile is homotopic to one of the optimal states as described in Lemma 4.4. We now claim that the states of all tiles representing one variable must agree on either the inner or outer state. Consider two adjacent tiles where one is in the inner state. There are open curves with endpoints on the shared edge of the two tiles with a distance of more than $1/2-2\cdot 1/10=3/10$. The other tile cannot be in the outer state, because then there would have to be an extra open curve of length at least 3/10 to connect those endpoints. It follows that the other tile must also be in the inner state. Thus, both tiles are either in the inner or in the outer state, as desired.

We now describe how to obtain a satisfying assignment of $\Phi$. Consider a clause tile where $E_x$, $E_y$, and $E_z$ meet and suppose the tile is in the x-outer state. It follows from the above that each tile covering $E_x$ is in the outer state or, in the case of the clause tile, in the x-outer state. Similarly, each non-clause tile covering only $E_y$ (resp. $E_z$) is in the inner state and each clause tile covering a part of $E_y$ (resp. $E_z$) is not in the y-outer (resp. z-outer) state. We now set x to true and y and z to false and do similarly with the other clause tiles, and it follows that we get a solution to $\Phi$.

Fig. 14

An object O and an inner approximation $O'\subset O$

So far, we have described the construction geometrically. Since regular hexagons are involved, this requires irrational coordinates. We will now approximate each object O from inside by an object $O'$ with rational coordinates. For this purpose, we replace every corner v by a substitute $v'\in O$ with $\Vert vv'\Vert <1/({200n})$. See Fig. 14 for an example. If v is a concave corner, like $v_3$ in the example, we require that the closest point to $v'$ on the boundary should be the point v. This restricts $v'$ to an angular region between two normals to the edges incident to v.

Since the objects in our instance have no sharp angles (the smallest angle $b_0c_0e_0\approx 24^\circ$ occurs in the clause tile) and there is only one concave angle of size $2\pi /3$, namely in the bend tile, there is plenty of room for choosing the points $v'$, and it is easy to find points with small rational coordinates. In fact, we can choose all coordinates be multiples of $1/({2000n})$, so that they require only logarithmically many bits.

This results in an instance $I'$ where all objects are subsets of corresponding objects in I. Let C and $C'$ be the cost of the optimal solutions to I and $I'$, respectively, and note that $C'\le C$, as any solution to I is also a solution to $I'$. We claim that $C< C'+1/100$. To prove this, consider a solution ${\mathcal {F}}'$ to $I'$. If ${\mathcal {F}}'$ contains parts in the interior of an object O of I, we move these parts to the boundary of O as follows.

Let $O'\subseteq O$ be the object in $I'$ corresponding to O, see Fig. 14. Let $v_0,\ldots ,v_{k-1}$ be the vertices of O in clockwise order and $v'_0,\ldots ,v'_{k-1}$ the corresponding vertices of $O'$. In the following, indices will be taken modulo k. For each point $v'_i$, define the closest point $p_i$ on $v_{i-1}v_i$ and the closest point $q_i$ on $v_iv_{i+1}$. With these points, we form quadrilateral edge regions $E_i:=v_iv_{i+1}p_{i+1}q_{i+1}$.

We now describe the modification we make on ${\mathcal {F}}'$ in order to avoid O. If ${\mathcal {F}}'$ intersects some edge region $E_i$, we project each point in ${\mathcal {F}}'\cap E_i$ to the closest point on $v_iv_{i+1}$. This does not increase the length of the curve. However, this may disconnect the fence when it winds around a corner between $v'_i$ and $v_i$. For this purpose, we add a cap $p_iv_i\cup v_iq_i$ around each convex vertex $v_i$. Parts of the fence ${\mathcal {F}}'$ close to the corners which are inside O but not in one of the edge regions $E_i$ are simply discarded. The caps ensure that no connectivity is lost. We perform these operations for every object.

The modifications of ${\mathcal {F}}'$ made to avoid the objects of I do not increase the length, except for the added caps, which have total length less than $n\times 1/({100n})=1/{100}$. Hence, $C<C'+1/100$.

Let $M':={\lceil 100M^*\rceil }/{100}$, so that $M'$ is rational and $M^*\le M'< M^*+1/100$. We conclude by observing that if $C'\le M'$, then $C<C'+1/100< M'+1/100<M^*+1/50$, and thus $\Phi$ is satisfiable. On the other hand, if $\Phi$ is satisfiable, then $C'\le C=M^*\le M'$. We can thus tell whether $\Phi$ is satisfiable or not by evaluating whether $C'\le M'$. $\square$

5 Approximation Algorithm

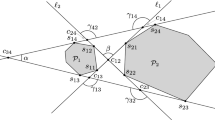
The approach for $k=2$ from Sect. 3 does not extend to $k\ge 3$ because Lemma 3.1 does not apply: The arrangement ${\mathcal {A}}$ (formed by the free segments between the corners N of the input objects) is no longer guaranteed to contain an optimal fence, see Fig. 2. However, we can follow the approach of Sect. 3 and still hope to get an approximate solution in ${\mathcal {A}}$: We show that the optimal fence $F_{\mathcal {A}}$ contained in ${\mathcal {A}}$ has a cost which is at most 4/3 times higher than the true optimal fence $F^*$ (Sect. 5.1). We construct a corresponding lower-bound example with $|F_{\mathcal {A}}|> 1.15\cdot |F^*|$. (This factor is the conjectured Steiner ratio, see Sect. 5.2.)

This reduces the problem to a graph-theoretic problem: the coloured multiterminal cut problem in the weighted dual graph $G=(V,E)$ of ${\mathcal {A}}$. We have terminals of $k\ge 3$ different colours and want to make a cut that separates every pair of terminals of different colours. This problem is NP-hard, but we can use approximation algorithms, see Sect. 5.3.

5.1 Upper Bound $|F_{\mathcal {A}}|/|F^*|\le 4/3$

Theorem 5.1

$|F_{\mathcal {A}}|\le 4/3\cdot |F^*|$.

Proof

By Lemmas 2.1 and 2.2, we know that after cutting an optimal fence $F^*$ at all points of N, the remaining components are Steiner minimal trees with leaves in N and internal Steiner vertices of degree 3, where three segments make angles of $2\pi /3$. Consider such a Steiner tree T (Fig. 15 a). Since T is embedded in the plane, the leaves can be enumerated in cyclic order as $v_1,\ldots ,v_m$. We will replace T by a connected system ${\bar{T}}$ of fences that connects the same set of leaves $v_1,\ldots ,v_m$, but contains only segments from the arrangement ${\mathcal {A}}$. Furthermore, we prove that the total length of ${\bar{T}}$ is bounded as $|{\bar{T}}|\le 4|T|/3$. Thus, carrying out this replacement for every Steiner tree leads to the fence $F_{\mathcal {A}}$ of the desired cost. If T consists of a single segment, we define ${\bar{T}}$ to be the same segment, in which case trivially $|{\bar{T}}|\le 4|T|/3$. Assume therefore that T has at least one Steiner vertex.

Let $T_{ij}$ be the path in T from $v_i$ to $v_j$. For each pair $\{i,j\}$, we define the path ${\bar{T}}_{ij}$ as the shortest path with the properties that

• (a) ${\bar{T}}_{ij}$ has endpoints $v_i$ and $v_j$, and

• (b) ${\bar{T}}_{ij}$ is homotopic to $T_{ij}$: this means that $T_{ij}$ can be continuously deformed into ${\bar{T}}_{ij}$ while keeping the endpoints fixed at $v_i$ and $v_j$, without entering the interiors of the objects.

It is clear that

• (c) ${\bar{T}}_{ij}$ is contained in the arrangement ${\mathcal {A}}$, and

• (d) ${\bar{T}}_{ij}$ is at most as long as $T_{ij}$.

We will construct ${\bar{T}}$ as the union of paths ${\bar{T}}_{ij}$ that are specified by a certain set S of leaf pairs $\{i,j\}$, and we will show that its total length is bounded, $|{\bar{T}}|\le 4|T|/3$. The fact that $F_{\mathcal {A}}$ is a valid fence is ensured by our choice of the set S, which we will now discuss.

Fig. 15

a Steiner tree T with five terminals $v_1,\ldots ,v_5$, which is part of a larger fence system $F^*$. Steiner vertices are white, leaves are black. b The transformed graph ${\bar{T}}$, formed as the union of three shortest homotopic paths ${\bar{T}}_{15}$, ${\bar{T}}_{24}$, and ${\bar{T}}_{35}$

If we overlay all paths $T_{ij}$ for $\{i,j\}\in S$, we get a multigraph ${{\widetilde{T}}}$, which has the same vertices as T and uses the edges of T, some of them multiple times. We require these three properties:

• 1. Every edge of T is used once or twice in ${{\widetilde{T}}}$.

• 2. Every Steiner vertex of T has even degree (4 or 6) in ${{\widetilde{T}}}$. (By contrast, the degree in T is always 3.)

• 3. Any two paths $T_{ij}$ and $T_{i'j'}$ with $\{i,j\},\{i',j'\}\in S$ that have a point of T in common must cross in the following sense: If we assume, by relabelling if necessary, that $i<j$ and $i'<j'$, then $i\le i'\le j\le j'$ or $i'\le i\le j'\le j$.

If the multigraph ${{\widetilde{T}}}$ is indeed constructed as the overlay of paths $T_{ij}$, property 2. is a consequence of 1. We will in fact construct the set S of pairs indirectly, through the multigraph ${{\widetilde{T}}}$. We will show that, once properties 1. and 2 . are fulfilled by ${{\widetilde{T}}}$, we can represent ${{\widetilde{T}}}$ as a union of a family of paths $T_{ij}$ for which 3. holds.

Let us discuss property 3. Two paths that share a common endpoint cross always. Thus, 3. poses a constraint only when the two paths have four distinct endpoints altogether. Property 3. is important to ensure that ${\bar{T}}$ is indeed connected, and that replacing T by ${\bar{T}}$ results in a valid fence. Although this is intuitively obvious, we could not come up with a short and elegant argument. We use the following lemma and its corollary, whose proofs are given later on. For a path P and points $x,y\in P$, we denote by P[x, y] the subpath of P from x to y. To make this notation unambiguous even if P is not simple, we will assume that the points x, y are associated to particular parameter values along the parameterisation of P.

Lemma 5.2

Suppose that the paths $T_{ij}$ and $T_{i'j'}$ cross in the sense of 3. Then there exists a point ${\bar{x}}\in {\bar{T}}_{ij}\cap {\bar{T}}_{i'j'}$ such that the path

$$\begin{aligned} {\bar{T}}_{ij}[v_j,{\bar{x}}]\cup {\bar{T}}_{i'j'}[{\bar{x}},v_{i'}] \end{aligned}$$

is homotopic to the path $T_{ji'}$.

Corollary 5.3

For any two leaves $v_i$ and $v_j$, where the pair $\{i,j\}$ is not necessarily in S, the set ${\bar{T}}$ contains a path from $v_i$ to $v_j$ that is homotopic to the path $T_{ij}$.

As a consequence, after replacing T by ${\bar{T}}$ in $F^*$, we get a system of fences $F'$ that encloses and separates the same objects as $F^*$, and thus we have indeed produced a valid fence.

Proof of Corollary 5.3

Let the vertices of $T_{ij}$ be $x_0,x_1,\ldots ,x_{p+1}$ in order such that $x_0:=v_i$ and $x_{p+1}:=v_j$. For each $m=0,1,\ldots ,p$, we select, by property 1., a path $T_{k_ml_m}$ with $\{k_m,l_m\}\in S$ that goes through the directed edge $x_mx_{m+1}$ on the way from $v_{k_m}$ to $v_{l_m}$. This leads to a sequence of paths $T_{k_0l_0},T_{k_1l_1},\ldots ,T_{k_pl_p}$, where $k_0=i$, $l_p=j$, and any two successive paths $T_{k_{m-1}l_{m-1}}$ and $T_{k_ml_m}$ have the point $x_m$ in common, and hence cross, by property 3. Lemma 5.2 implies that also the corresponding paths ${\bar{T}}_{k_{m-1}l_{m-1}}$ and ${\bar{T}}_{k_ml_m}$ have a common point ${\bar{x}}_m$ such that

$$\begin{aligned} {\bar{U}}_m :={\bar{T}}_{k_{m-1}l_{m-1}}[v_{l_{m-1}},{\bar{x}}_m]\cup {\bar{T}}_{k_ml_m}[{\bar{x}}_m,v_{k_m}] \end{aligned}$$

is homotopic to $U_m := T_{{l_{m-1}}{k_m}}$. Now, define the paths

$$\begin{aligned}&W:=T_{k_0l_0}\cup U_1\cup T_{k_1l_1}\cup U_2\cup \ldots \cup U_p\cup T_{k_pl_p}\quad \text { and}\\&{\bar{W}}:={\bar{T}}_{k_0l_0}\cup {\bar{U}}_1\cup {\bar{T}}_{k_1l_1}\cup {\bar{U}}_2\cup \ldots \cup {\bar{U}}_p\cup {\bar{T}}_{k_p l_p}. \end{aligned}$$

The path W is homotopic to $T_{ij}$, as it has the same endpoints and is obtained by joining paths in the simple tree T. Also, W and ${\bar{W}}$ are homotopic, as the corresponding subpaths are homotopic. The path ${\bar{W}}$ is thus homotopic to $T_{ij}$, and ${\bar{W}}$ is contained in ${\bar{T}}$, so we are done. $\square$

Proof of Lemma 5.2

We first describe how $T_{ij}$ can be continuously deformed into ${\bar{T}}_{ij}$ while remaining a polygonal path, moving one vertex at a time. We denote by ${\hat{T}}_{ij}$ the current path during this deformation procedure.

Consider the case that ${\hat{T}}_{ij}$ has a vertex b which is not in the set of corners N. Let a and c be the neighbouring vertices. We then move b towards c, thus shortening the edge bc while the edge ab sweeps over a region in the plane. If ab hits the corner of an object, ${\hat{T}}_{ij}$ gets a new vertex $a'$ at this point. The segment $aa'$ will then remain static, and we continue the movement of b with $a'$ taking the role of a. When b eventually reaches c, the number of vertices of ${\hat{T}}_{ij}$ that are not in N has decreased by 1. We repeat this process of contracting edges as long as there is a vertex not in N. Note that it is possible that the path crosses itself during the deformation, or it may have a vertex where it turns $180^\circ$ back on itself. Such a vertex is known as a spur, and it can be easily eliminated by moving it to the closest adjacent vertex.

(For establishing Theorem 5.1, we could already stop the deformation procedure as soon as all vertices of ${\hat{T}}_{ij}$ are in N and ${\hat{T}}_{ij}$ is free of spurs, because ${\hat{T}}_{ij}$ is contained in ${\mathcal {A}}$ and is at most as long as $T_{ij}$, thus satisfying properties (c) and (d).) If ${\hat{T}}_{ij}$ is not yet the shortest homotopic path, it must contain three consecutive vertices abc such that the angle at b contains no object. In this case we can start the same deformation move from b towards c as above. Temporarily, the vertex b is an additional vertex not in N, but after the move, ${\hat{T}}_{ij}$ is again a path connecting vertices of N. Since the number of such paths that are not longer than the initial path $T_{ij}$ is finite, the procedure must eventually terminate with the shortest homotopic path ${\bar{T}}_{ij}$.

We successively apply this procedure to the pairs ij and ${i'j'}$. We still have to prove the existence of a point ${\bar{x}}\in {\bar{T}}_{ij}\cap {\bar{T}}_{i'j'}$ with the property stated in the lemma. We assume that the four corners $v_{i},v_{j},v_{i'},v_{j'}$ are distinct because otherwise the statement follows easily if we choose a shared endpoint as ${\bar{x}}$.

The proof uses that fact that the number of crossings between the paths ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$ can only change by an even number during a deformation. The definition of a crossing requires some care, as the paths may share segments. Assume that ${\hat{T}}_{ij}$ is the path that is currently being deformed, while ${\hat{T}}_{i'j'}$ is either the initial path $T_{i'j'}$ or the final deformed path ${\bar{T}}_{i'j'}$.

Orient the paths ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$ arbitrarily. Consider a maximal subpath Q that is shared between ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$, possibly in opposite directions. If ${\hat{T}}_{ij}$ enters and leaves Q on the same side of ${\hat{T}}_{i'j'}$, we say that ${\hat{T}}_{ij}$touches ${\hat{T}}_{i'j'}$ at Q. Otherwise, ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$ form a crossing at Q. Here it is important that ${\hat{T}}_{i'j'}$ has no spurs, since at a spur, the side on which ${\hat{T}}_{ij}$ enters or leaves ${\hat{T}}_{i'j'}$ is ill-defined. If Q contains an endpoint q of one of the paths, we extend this path into the interior of the object in order to determine the side of ${\hat{T}}_{i'j'}$ on which ${\hat{T}}_{ij}$ enters or leaves Q at q.

A crossing Q of ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$ is a homotopic crossing if it has the desired property for the lemma, namely that ${\hat{T}}_{ij}[v_j,{\hat{x}}]\cup {\hat{T}}_{i'j'}[{\hat{x}},v_{i'}]$ for ${\hat{x}}\in Q$ is homotopic to $T_{ji'}$. Clearly, this does not depend on the choice of ${\hat{x}}\in Q$, because Q is represented by a connected interval of parameters, both on ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$.

When ${\hat{T}}_{ij}$ is deformed by moving one vertex at a time, as described above, it is easy to see that crossings can only appear or disappear in pairs: It is not possible for a crossing Q to appear or disappear by ${\hat{T}}_{ij}$ sliding over an endpoint $q'$ of ${\hat{T}}_{i'j'}$, since that would require ${\hat{T}}_{ij}$ to enter the interior of the object with $q'$ on the boundary.

Furthermore, a pair of crossings $Q_1,Q_2$ that appear or disappear will either both be homotopic crossings or non-homotopic crossings: At the moment when the pair appears or disappears, the loop formed by the subpaths of ${\hat{T}}_{ij}$ and ${\hat{T}}_{i'j'}$ between $Q_1$ and $Q_2$ is empty and thus contains no objects. Therefore, if ${\hat{x}}_1\in Q_1$ and ${\hat{x}}_2\in Q_2$, the paths ${\hat{T}}_{ij}[v_j,{\hat{x}}_1]\cup {\hat{T}}_{i'j'}[{\hat{x}}_1,v_{i'}]$ and ${\hat{T}}_{ij}[v_j,{\hat{x}}_2]\cup {\hat{T}}_{i'j'}[{\hat{x}}_2,v_{i'}]$ are homotopic.

During the deformation of ${\hat{T}}_{ij}$, each crossing Q can move back and forth on ${\hat{T}}_{i'j'}$, expand and shrink. However, it is clear that its character (homotopic versus non-homotopic) does not change during the deformation.

The initial number of crossings is 1, and the single crossing Q is a homotopic crossing, since $T_{ji'}$ can be realized as a path ${\hat{T}}_{ij}[v_j,{\hat{x}}]\cup {\hat{T}}_{i'j'}[{\hat{x}},v_{i'}]$ for ${\hat{x}}\in Q$. Hence the number of homotopic crossings of ${\bar{T}}_{ij}$ and ${\bar{T}}_{i'j'}$ is odd, and in particular positive, which establishes the claim. $\square$

To bound the length of ${\bar{T}}$, we bound each path ${\bar{T}}_{ij}$, $\{i,j\}\in S$, by the corresponding path $T_{ij}$ in T. This upper estimate is simply the total length of T plus the length of the duplicated edges of T.

As mentioned above, we start by constructing the multigraph ${{\widetilde{T}}}$. By property 1., this boils down to selecting which edges of T to duplicate. In order to fulfil property 2., we require that the degree of every inner vertex of ${{\widetilde{T}}}$ becomes even. We now analyse this task from a purely combinatorial viewpoint. We show in the end that this is sufficient to ensure that the edges of ${{\widetilde{T}}}$ can be partitioned into paths $T_{ij}$ such that 3. holds.

Lemma 5.4

The edges that should be duplicated can be chosen so that their total length is at most |T|/3.

Proof

For a particular tree, the optimum can be computed easily by dynamic programming, as follows. We root T at some arbitrary leaf. Consider a subtree U rooted at some vertex u of T such that u has one child v in U, see Fig. 16. We define $U_1$ and $U_2$ as the cost of the optimal set of duplicated edges in U, under the constraint that the multiplicity of the edge uv in ${{\widetilde{T}}}$ is 1 and 2, respectively. By induction, we will establish that

$$\begin{aligned} 2U_1+U_2 \le |U|. \end{aligned}$$

(1)

This gives $\min {\{U_1,U_2\}}\le |U|/3$ and proves the lemma, since this also holds for $U=T$. In the base case, U has only one edge. Then $U_1=0$ and $U_2=\Vert uv\Vert =|U|$, and (1) holds.

Fig. 16

A subtree U rooted at u and two possible solutions. The first solution is considered for computing $U_1$ and the second one for $U_2$

If U is larger, v has degree 3, and two subtrees L and R are attached there. If uv is not duplicated, then exactly one of the other edges incident to v has to be duplicated in order for v to get even degree in ${{\widetilde{T}}}$. On the other hand, if uv is duplicated, then either both or none of the other edges should be duplicated. Hence, we can compute $U_1$ and $U_2$ by the following recursion:

$$\begin{aligned} U_1&= \min {\{ L_1+R_2, L_2+R_1 \}}, \end{aligned}$$

(2)

$$\begin{aligned} U_2&= \min {\{ L_1+R_1, L_2+R_2 \}} + \Vert uv\Vert . \end{aligned}$$

(3)

We therefore get

$$\begin{aligned} U_1\le L_2+R_1,\qquad U_1\le L_1+R_2, \end{aligned}$$

(4)

from (2) and

$$\begin{aligned} U_2 \le L_1+R_1 + \Vert uv\Vert \end{aligned}$$

(5)

from (3). Adding inequalities (4) and (5) and using the inductive hypothesis (1) for L and R gives

$$\begin{aligned} 2U_1+U_2 \le 2L_1+L_2+2R_1+R_2+\Vert uv\Vert \le |L|+|R|+\Vert uv\Vert = |U|. \end{aligned}$$

The bound |T|/3 in Lemma 5.4 cannot be improved, as shown by the graph $K_{1,3}$ with 3 edges of unit length. This graph can appear as a Steiner tree in an optimal fence, see Fig. 17. (But this does not mean that the factor 4/3 in Theorem 5.1 cannot be improved.)

We now have a multigraph ${{\widetilde{T}}}$ where every internal vertex has even degree. It follows that the edges of ${{\widetilde{T}}}$ can be partitioned into leaf-to-leaf paths, much like when creating an Eulerian tour in a graph where all vertices have even degree. The endpoint pairs of these paths constitute the set S of leaf pairs.

We still need to satisfy property 3. Whenever two paths $P_1$ and $P_2$ violate this property, we repair this by swapping parts of the paths, without changing the number of remaining violating pairs, as follows: The paths $P_1$ and $P_2$ have a common vertex, and thus also a common edge uv, because the maximum degree in T is 3. Orient $P_1$ and $P_2$ so that they use this edge in the direction uv, and cut them at v into $P_1=Q_1\cdot R_1$ and $P_2=Q_2\cdot R_2$. We now make a cross-over at v, forming the new paths $Q_1\cdot R_2$ and $Q_2\cdot R_1$. These new paths satisfy 3. To check that we did not create any new violations, we observe that, by property 1., no other path can use the edge uv, because the capacity of 2 is already used up by $P_1$ and $P_2$. Thus, all other paths can either interact with $Q_1$ and $Q_2$, or with $R_1$ and $R_2$. Swapping the parts of $P_1$ and $P_2$ in the other half of the tree T does not affect property 3. We have thus established Theorem 5.1. $\square$

5.2 Lower Bound on $|F_{\mathcal {A}}|/|F^*|$

We believe that the bound 4/3 of Theorem 5.1 on the approximation factor can be improved: We have bounded $|{\bar{T}}_{ij}|$ crudely by $|T_{ij}|$, using only the triangle inequality, and we did not use at all the fact that edges meet at angles of $2\pi /3$.

We establish a lower bound of roughly 1.15 by constructing an example. Gilbert and Pollak [13] conjectured that for any set of points in the plane, the ratio between the length of a minimum spanning tree and the length of a minimum Steiner tree is at most ${2}/{\sqrt{3}}\approx 1.15$, which is realised by the corners of an equilateral triangle. The current best upper bound is 1.21 by Chung and Graham [8]. We show a lower bound on the ratio $|F_{\mathcal {A}}|/|F^*|$ that corresponds to the conjectured Steiner ratio.

Fig. 17

The core (left) and repeated (right) construction for the proof of Lemma 5.5

Lemma 5.5

For every $\varepsilon >0$, there is an instance of geometric 3-cut for which

$$\begin{aligned} \frac{|F_\mathcal{A}|}{|F^*|} \ge \frac{2}{\sqrt{3}} - \varepsilon > 1.15-\varepsilon . \end{aligned}$$

Proof

The core idea is shown in Fig. 17: Three very thin rectangles in different colours form an equilateral triangle with side length $\sqrt{3}$. The optimal fence uses the centre of the triangle as a Steiner vertex, whereas the fence $F_\mathcal{A}$ is restricted to follow the triangle edges. Considered in isolation, this example gives only a ratio ${|F_\mathcal{A}|}/{|F^*|} \approx {4\sqrt{3}}/({3+2\sqrt{3}}) \approx 1.07$, because the outer boundary edges, which are common to both fences, “dilute” the ratio. So we set $k = 1/\varepsilon$, and repeat the construction $k\times k$ times. We get $|F^*| = 2k^2 \cdot 3 + 2k \cdot \sqrt{3}$, versus $|F_\mathcal{A}| = 2k^2 \cdot 2 \sqrt{3} + 2k \cdot \sqrt{3}$. $\square$

5.3 Finding a Good Fence in ${\mathcal {A}}$

As in Sect. 3, the restriction to ${\mathcal {A}}$ reduces the optimal fence problem to a graph-theoretic problem of finding a best multicut in a planar graph. We apply results from the literature.

The problem of finding a small cut in a planar graph $G=(V,E)$ that separates k different classes $T_1,\ldots ,T_k\subset V$ of terminals was mentioned as a suggestion for future work by Dahlhaus et al. [9], but we have not found any subsequent work on that except for the case $k=2$ [4]. We can, however, reduce the problem to the multiway cut problem in general graphs (also known as the multiterminal cut problem): For each class $T_i$, we add an “apex vertex” $t_i$ which is connected to all vertices in $T_i$ by edges of infinite weight. We then ask for the cut of minimum total weight that separates each pair $t_i,t_j$. Dahlhaus et al. showed the problem to be APX-hard for $k\ge 3$ and gave a simple $(2-2/k)$-approximation algorithm. The approximation ratio was later improved to $3/2-1/k$ (expected) by Călinescu et al. [6]. Their algorithm is based on a geometric LP relaxation of the problem and an appropriate randomised rounding scheme. Successive refinements of the rounding scheme have brought down the ratio further: the currently best one is 1.2965, due to Sharma and Vondrák [21], and it has been verified only by computer. A slightly worse hand-verified ratio of $297/229\approx 1.29694$ was given by Buchbinder et al. [5]. For specific values of k the best known ratios are due to Karger et al. [16]. Finally, it is worth noting that, under the Unique Games Conjecture, the integrality gap of the LP of Călinescu et al. has been shown to be a lower bound for the approximation ratio for the multiway cut problem by Manokaran et al. [18]; the best known value for the integrality gap is $1.20016 - \varepsilon$, for any $\varepsilon > 0$, due to Bérczi, Chandrasekaran et al. [3].

Together with Theorem 5.1, we obtain the following result.

Theorem 5.6

There is a polynomial-time randomised $4/3\cdot 1.2965$-approximation algorithm for geometric k-cut.

6 Concluding Remarks

We have initiated the study of the geometric multicut problem. As our NP-hardness reduction does not imply APX-hardness, an interesting open question is whether there exists a $(1+\varepsilon )$-approximation algorithm for any $\varepsilon >0$.

There are other versions of the problem which could also be interesting to study. For example, apart from considering shortest paths in the plane, much attention has also been paid to minimum-link paths, i.e., paths connecting two points and consisting of a minimum number of line segments. The analogous problem in our setup is likewise interesting: Compute a simplest possible fence, i.e., one that is the union of as few line segments as possible. The fence can be required to be disjoint from the object interiors, or it can be allowed to pass through the objects, leading to two different problems.