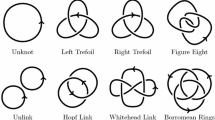
Abstract
We study random knots and links in \(\mathbb {R}^3\) using the Petaluma model, which is based on the petal projections developed in [2]. In this model we obtain a formula for the limiting distribution of the linking number of a random two-component link. We also obtain formulas for the expectations and the higher moments of the Casson invariant and the order-3 knot invariant \(v_3\). These are the first precise formulas given for the distributions and higher moments of invariants in any model for random knots or links. We also use numerical computation to compare these to other random knot and link models, such as those based on grid diagrams.








Similar content being viewed by others
References
Adams, C., Capovilla-Searle, O., Freeman, J., Irvine, D., Petti, S., Vitek, D., Weber, A., Zhang, S.: Bounds on übercrossing and petal numbers for knots. (2013) http://arxiv.org/abs/1311.0526
Adams, C., Crawford, T., DeMeo, B., Landry, M., Lin, A.T., Montee, M., Park, S., Venkatesh, S., Yhee, F.: Knot projections with a single multi-crossing. (2012) http://arxiv.org/abs/1208.5742
Adams, C.C.: The Knot Book. American Mathematical Society, Providence (1994)
Alvarez, M., Labastida, J.: Vassiliev invariants for torus knots. J. Knot Theory Ramif. 5(06), 779–803 (1996)
Arsuaga, J., Blackstone, T., Diao, Y., Karadayi, E., Saito, M.: Linking of uniform random polygons in confined spaces. J. Phys. A 40(9), 1925 (2007)
Ball, R., Mehta, M.: Sequence of invariants for knots and links. J. Phys. 42(9), 1193–1199 (1981)
Bellissard, J., Camacho, C.J., Barelli, A., Claro, F.: Exact random walk distributions using noncommutative geometry. J. Phys. A 30(21), L707 (1997)
Breiman, L.: Probability. Classics in Applied Mathematics, vol. 7. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (1992)
Brunn, H.: Über verknotete Kurven, pp. 256–259. Verhandlungen des ersten Internationalen Mathematiker-Kongresses in Zürich (1897). http://www.mathunion.org/ICM/ICM1897/Main/icm1897.0256.0259.ocr.pdf
Buck, G.R.: Random knots and energy: Elementary considerations. J. Knot Theory Ramif. 3(03), 355–363 (1994)
Chmutov, S., Duzhin, S., Mostovoy, J.: Introduction to Vassiliev Knot Invariants. Cambridge University Press, Cambridge (2012)
Cromwell, P.R.: Arc presentations of knots and links. Banach Cent. Publ. 42, 57–64 (1998)
Dunfield, N.M., Thurston, W.P.: Finite covers of random 3-manifolds. Invent. Math. 166(3), 457–521 (2006)
Duplantier, B.: Areas of planar Brownian curves. J. Phys. A 22(15), 3033 (1989)
Even-Zohar, C., Hass, J., Linial, N., Nowik, T.: Invariants of random knots and links. Ancillary files (2014). http://arxiv.org/abs/1411.3308
Goussarov, M., Polyak, M., Viro, O.: Finite-type invariants of classical and virtual knots. Topology 39(5), 1045–1068 (2000)
Gradshteyn, I., Jeffrey, A., Ryzhik, I., Zwillinger, D.: Table of Integrals, Series, and Products. Academic Press, New York (2007)
Harper, P.: The general motion of conduction electrons in a uniform magnetic field, with application to the diamagnetism of metals. Proc. Phys. Soc. Sect. A 68(10), 879 (1955)
Hoste, J., Thistlethwaite, M., Weeks, J.: The first 1,701,936 knots. Math. Intell. 20(4), 33–48 (1998)
Kauffman, L.H.: The Conway polynomial. Topology 20(1), 101–108 (1981)
Kauffman, L.H.: On Knots, vol. 115. Princeton University Press, Princeton (1987)
Khandekar, D., Wiegel, F.: Distribution of the area enclosed by a plane random walk. J. Phys. A 21(10), L563 (1988)
Kowalski, E.: On the complexity of Dunfield–Thurston random 3-manifolds. (2010) www.math.ethz.ch/~kowalski/complexity-dunfield-thurston.pdf
Lévy, P.: Wiener’s random function, and other laplacian random functions. In: Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 171–187. University of California Press, Berkeley (1951)
Linial, N., Meshulam, R.: Homological connectivity of random 2-complexes. Combinatorica 26(4), 475–487 (2006)
Lubotzky, A., Maher, J., Wu, C.: Random methods in 3-manifold theory. (2014) http://arxiv.org/abs/1405.6410
Lutz, F.H.: Combinatorial 3-manifolds with 10 vertices. Beiträge Algebra Geom. 49(1), 97–106 (2008)
Maher, J.: Random Heegaard splittings. J. Topol. 3(4), 997–1025 (2010)
Mashkevich, S., Ouvry, S.: Area distribution of two-dimensional random walks on a square lattice. J. Stat. Phys. 137(1), 71–78 (2009)
Micheletti, C., Marenduzzo, D., Orlandini, E.: Polymers with spatial or topological constraints: theoretical and computational results. Phys. Rep. 504(1), 1–73 (2011)
Milman, V.D., Schechtman, G.: Asymptotic Theory of Finite Dimensional Normed Spaces: Isoperimetric Inequalities in Riemannian Manifolds, vol. 1200. Springer, Berlin (1986)
Mingo, J.A., Nica, A.: On the distribution of the area enclosed by a random walk on \(\mathbb{Z}^2\). J. Comb. Theory Ser. A 84(1), 55–86 (1998)
Mohammad-Noori, M.: Enumeration of closed random walks in the square lattice according to their areas. (2010) http://arxiv.org/abs/1012.3720
Pippenger, N.: Knots in random walks. Discrete Appl. Math. 25(3), 273–278 (1989)
Polyak, M., Viro, O.: Gauss diagram formulas for Vassiliev invariants. Int. Math. Res. Not. 1994(11), 445–453 (1994)
Sumners, D., Whittington, S.: Knots in self-avoiding walks. J. Phys. A 21(7), 1689 (1988)
Vassiliev, V.A.: Cohomology of knot spaces. Theory Singul. Its Appl. 1, 23–69 (1990)
Willerton, S.: On the Vassiliev invariants for knots and for pure braids. Ph.D. thesis, University of Edinburgh (1997)
Acknowledgments
This project was supported by BSF Grant 2012188.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Günter M. Ziegler
Rights and permissions
About this article
Cite this article
Even-Zohar, C., Hass, J., Linial, N. et al. Invariants of Random Knots and Links. Discrete Comput Geom 56, 274–314 (2016). https://doi.org/10.1007/s00454-016-9798-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-016-9798-y