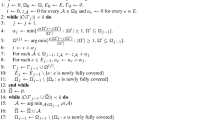Online Multiset Submodular Cover

Abstract

We study the Online Multiset Submodular Cover problem (OMSC), where we are given a universe U of elements and a collection of subsets $\mathcal {S}\subseteq 2^U$. Each element $u_j \in U$ is associated with a nonnegative, nondecreasing, submodular polynomially computable set function $f_j$. Initially, the elements are uncovered, and therefore we pay a penalty per each unit of uncovered element. Subsets with various coverage and cost arrive online. Upon arrival of a new subset, the online algorithm must decide how many copies of the arriving subset to add to the solution. This decision is irrevocable, in the sense that the algorithm will not be able to add more copies of this subset in the future. On the other hand, the algorithm can drop copies of a subset, but such copies cannot be retrieved later. The goal is to minimize the total cost of subsets taken plus penalties for uncovered elements. We present an $O(\sqrt{\rho _{\max }})$-competitive algorithm for OMSC that does not dismiss subset copies that were taken into the solution, but relies on prior knowledge of the value of $\rho _{\max }$, where $\rho _{\max }$ is the maximum ratio, over all subsets, between the penalties covered by a subset and its cost. We provide an $O\left( \log (\rho _{\max }) \sqrt{\rho _{\max }} \right)$-competitive algorithm for OMSC that does not rely on advance knowledge of $\rho _{\max }$ but uses dismissals of previously taken subsets. Finally, for the capacitated versions of the Online Multiset Multicover problem, we obtain an $O(\sqrt{\rho _{\max }'})$-competitive algorithm when $\rho _{\max }'$ is known and an $O\left( \log (\rho _{\max }') \sqrt{\rho _{\max }'} \right)$-competitive algorithm when $\rho _{\max }'$ is unknown, where $\rho _{\max }'$ is the maximum ratio over all subset incarnations between the penalties covered by this incarnation and its cost.

1 Introduction

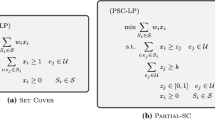
We study the Multiset Multicover problem, in which we are given a universe U with n elements, where element $u_j$ has a covering requirement $b_j \in \mathbb {N}$ and a penalty $p_j \in \mathbb {R}_+$. There is a collection $\mathcal {S}$ of m subsets, where the coverage of subset $S_i$ of element $u_j$ is $a_{ij} \in \mathbb {N}$ and its cost is $c_i$. Without loss of generality, we assume that $a_{ij} \le b_j$, for every i and j. (Note that a subset $S_i$ is actually a multiset if $a_{ij}>1$, for some element j, but we misuse the term “subset” for simplicity.) A solution is a multicollection $\mathcal {C}$ of the subsets, where multiple copies of subsets are allowed. The cost of a solution is the cost of selected subsets plus the penalties for unsatisfied covering requirements. One may formulate Multiset Multicover using the following integer linear program:

$$\begin{aligned} \begin{array}{lll} \min &{} \displaystyle \sum _{i=1}^m c_i x_i + \sum _{j=1}^n p_j z_j \\ \text {s.t.} &{} \displaystyle \sum _{i=1}^m a_{ij} x_i + z_j \ge b_j &{} \forall u_j \in U \\ &{} x_i \in \mathbb {N}&{} \forall S_i \in \mathcal {S}\\ &{} z_j \in \mathbb {N}&{} \forall u_j \in U \end{array} \qquad \qquad \qquad \qquad \mathrm{{(MM)}} \end{aligned}$$

where the value of $x_i$ represents the number of copies of subset $S_i$ taken into the solution $\mathcal {C}$, and $z_j$ is the amount of unsatisfied coverage by $\mathcal {C}$ of element $u_j$ (for which we pay a penalty per unit). Notice that, given a solution $\mathcal {C}$ one can easily obtain the corresponding pair (x, z). We define:

$$\begin{aligned} \textsc {cost} (\mathcal {C}) \triangleq \sum _i c_i x_i + \sum _j p_j z_j ~. \end{aligned}$$

The above formulation is unconstrained in the sense that each subset can be used any number of times. In the constrained variant a subset can be used at most once, i.e., $x_i \in \left\{ 0,1 \right\}$, for every i.

We study (generalizations of) the following online version of the Multiset Multicover problem, called Online Multiset Multicover (OMM), that was introduced by Fraigniaud et al. [15]. Initially, the elements are uncovered—and hence incur a penalty per each unit of uncovered element. That is, initially we pay $\sum _j p_j b_j$. Subsets with various coverage and cost arrive online. In each time step, a new subset arrives, and the online algorithm must decide how many copies of the arriving subset to add to the solution. This decision is irrevocable, in the sense that the algorithm will not be able to add more copies of this subset in the future. On the other hand, the algorithm is allowed to drop copies of a subset, but such copies cannot be retrieved later. The goal is to minimize the total cost of subsets taken plus penalties for uncovered elements. As usual with online algorithms we measure an online algorithm by its competitive ratio: in this case, the maximum ratio of cost incurred by the algorithm to the best possible cost for any given instance. We consider expected cost if the algorithm is randomized.

OMM is an abstraction of the following team formation scenario (corresponding to a binary matrix A and binary requirements b). Suppose we are embarking on a new project that is composed of n tasks. A task j can be satisfied by outsourcing at cost $p_j$, or by hiring an employee who possesses the ability or skill to perform task j. The goal is to minimize the project cost under the following procedure: We interview candidates one by one. After each interview we know the skills and the hiring cost of the candidate and must decide irrevocably whether to hire the candidate or not. In the more general setting, a task may require more effort, and this is captured by element requirements. A candidate i may be able to contribute more that one unit of effort to a task j and this is captured by the coverage $a_{ij}$. Finally, the unconstrained case is more appropriate when a candidate corresponds to a technology that may be purchased more than once.

As shown in [15], even randomized algorithms cannot have competitive ratio better than $\Omega (\sqrt{\rho _{\max }})$, where $\rho _{\max }$ is the maximum ratio, over all subsets, between the penalties covered by a subset and its cost (see Sect. 2 for an exact definition). The lower bound holds even in the binary case and even if $\rho _{\max }$ is known and one is allowed to drop previously selected subsets. On the other hand, they presented a deterministic algorithm with a competitive ratio of $O(\sqrt{\rho _{\max }})$ that does not dismiss subsets that were taken into the solution. This algorithm works for both the constrained and unconstrained cases. However, this algorithm relies on prior knowledge of the value of $\rho _{\max }$. It was also shown that without dismissals and without such knowledge only the trivial $O(\rho _{\max })$ bound is possible. It remained an open question whether there is an $o(\rho _{\max })$-competitive algorithm that has no knowledge of $\rho _{\max }$ but allows dismissals.

We note that in online algorithms the initial solution is typically empty and its value increases with time. In contrast, the algorithm from [15] is unique in the sense that a solution get progressively cheaper with time. This is a natural dimension that is worth exploring more widely. We contribute to this by treating (just about) the most general forms of covering problems known. We consider two extensions of OMM in this paper.

First, we consider OMM with submodular coverage. Assume that each element $u_j$ is associated with a nonnegative, nondecreasing, submodular polynomially computable set function $f_j$, whose domain consists of multi-collection of subsets and its range is $[0,b_j]$. Recall that a function g is nondecreasing if $g(\mathcal {A}) \le g(\mathcal {B})$, for all $\mathcal {A}\subseteq \mathcal {B}$, and g is submodular if $g(\mathcal {A}) + g(\mathcal {B}) \ge g(\mathcal {A}\cup \mathcal {B}) + g(\mathcal {A}\cap \mathcal {B})$, for every two subcollections $\mathcal {A}$ and $\mathcal {B}$. Assume that $f_j(\emptyset ) = 0$, for every j. Also, note that the domain of $f_j$ is revealed in an online manner. Given a multicollection $\mathcal {C}$ of $\mathcal {S}$, let $x_i$ be the multiplicity of $S_i$ in $\mathcal {C}$ (as defined above). Also, let $z_j = b_j - f_j(\mathcal {C})$. Going back to the team formation scenario, a submodular function captures the case where several employees that work together on a task need to spend some effort on maintaining team work, and thus their combined productivity is less than the sum of their productivities. We refer to this problem as Online Multiset Submodular Cover (abbreviated OMSC).

In another extension of OMM each subset $S_i$ has a capacity $\text {cap} (S_i)$ that limits the amount of coverage of a single copy of $S_i$. More specifically, when a subset $S_i$ arrives, it can potentially cover $a_{ij}$ of element j, for every j, but it can only cover at most $\text {cap} (S_i)$ out of this potential coverage. In this case a solution can be described as a pair $(\mathcal {C},y)$, where $\mathcal {C}$ is a multicollection and y satisfies the following conditions: (i) $y_{ij} \le a_{ij}$, for every i and j, (ii) $\sum _i y_{ij} \le b_j$, for every j, and (iii) $\sum _j y_{ij} \le \text {cap} (S_i)$, for every i. We refer to y as an incarnation function, since it determines the actual coverage of each subset $S_i$. This capacitated version of OMM has two flavors. In the soft capacities case (unconstrained) one is allowed to use multiple copies of any subset $S_i$, provided that one pays for each such copy. One the other hand, in the hard capacities case (constrained) one is allowed to use each subset at most once.

Capacities may describe the setting where a candidate has the potential to work on many tasks, but has a limited workload capacity. For example, there may be two task that require six hours a day, each. That is, $b_1 = b_2 = 6$. Assume that there is a candidate who can work eight hours per day, but at most five hours per task. In addition, this person may be assigned to both tasks, as long as each assignment is for at most five hours. In this case, $a_{11} = a_{12} = 5$ and $\text {cap} (S_1) = 8$. If this person is assigned to work five hours on task 1 and three on task 2, then we are using the incarnation $y_{11} = 5$ and $y_{12} = 3$.

1.1 Our Contribution

We present an $O(\sqrt{\rho _{\max }})$-competitive algorithm for OMSC that does not dismiss subsets that were taken into the solution, but relies on prior knowledge of the value of $\rho _{\max }$. It works for both the constrained and unconstrained cases. This competitive ratio is tight for the setting where $\rho _{\max }$ is known, since there is an $\Omega (\sqrt{\rho _{\max }})$ lower bound on the competitive ratio of randomized algorithms even for the special case of OMM with $b=1$ [15] and even if dismissals are possible. Our algorithm is an extension of the one for OMM from [15], and it is based on two upper bounds, one for the total cost of the subsets and one for the penalties. The next result required a parameterized version of the former bound.

Our main result is an $O\left( \log (\rho _{\max }) \sqrt{\rho _{\max }} \right)$-competitive algorithm for OMSC that does not rely on advance knowledge of $\rho _{\max }$. This result is new also for OMM. In contrast to the first algorithm, this one uses dismissals of previously taken subsets. Our algorithm does not use standard online methods, like Doubling or Classify & Select. Instead, it executes the above mentioned algorithm, for every power of 2 in parallel. We show that it is sufficient to maintain $O(\log (\rho _{\max }))$ executions at any given time. As a result, throughout the execution covers may be dropped completely, while others emerge. This algorithm also works for both the constrained and unconstrained cases. Specifically, in the constrained case, a subset used by several solutions is taken by the algorithm only once.

Finally, for the capacitated versions of OMM, we obtain an $O(\sqrt{\rho _{\max }'})$-competitive algorithm when $\rho _{\max }'$ is known and an $O\left( \log (\rho _{\max }') \sqrt{\rho _{\max }'} \right)$-competitive algorithm when $\rho _{\max }'$ is unknown, where $\rho _{\max }'$ is the maximum ratio over all subset incarnations between the penalties covered by this incarnation and its cost. For soft capacities this is a straightforward corollary from the OMM results. However, in the hard capacities case, we show a lower bound of $\Omega (\rho _{\max })$ if element reassignments are disallowed. If one may reassign elements, then we show that OMM with hard capacities can be reduced to OMSC. Submodularity is shown using a reduction to submodularity of partial maximum weight matching functions [3].

1.2 Related Work

In the most basic covering problem, Set Cover, the input consists of a universe U of n elements, a collection $\mathcal {S}\subseteq 2^U$ of subsets of U, and a non-negative cost function $c:\mathcal {S}\rightarrow \mathbb {N}$. The instance is called unweighted, if $c(S)=1$, for every $S \in \mathcal {S}$. A sub-collection $\mathcal {C}\subseteq \mathcal {S}$ is a set cover if $\cup _{S \in \mathcal {C}} S = U$. The goal is to find a minimum weight set cover, i.e., a sub-collection $\mathcal {C}$ that minimizes $c(\mathcal {C}) \triangleq \sum _{S \in \mathcal {C}} c(S)$. There are several $\Omega (\log n)$ lower bounds [2, 14, 26, 28] on the approximation ratio of Set Cover. Dinur and Steurer [12] gave an optimal inapproximability result by showing that Set Cover is not approximable within $(1-o(1)) \ln n$, unless P$=$NP. On the other hand, it is well known that the approximation ratio of the greedy algorithm is bounded by $H_n$, where $H_n$ is the nth Harmonic number [9, 22, 25]. Set Cover can be approximated within $\Delta \triangleq \max _u \left| \left\{ S: u \in S \right\} \right|$ [5, 21]. On the other hand, it is NP-hard to approximate Set Cover within a factor of $\Delta - 1 - \varepsilon$, for any $\varepsilon >0$, assuming $\Delta > 2$ is a constant [10]. The case where $\Delta = 2$ (i.e., Vertex Cover) is NP-hard to approximate within a factor of $10\sqrt{5}-21 \approx 1.36$ [11].

In the Set Multi-Cover problem each element $u_j$ is associated with a covering requirement $b_j \in \mathbb {N}$. A feasible solution is required to cover an element $u_j$ using $b_j$ sets, i.e., it is a sub-collection $\mathcal {C}\subseteq \mathcal {S}$ such that $\left| \left\{ S: u \in S \right\} \cap \mathcal {C} \right| \ge b_j)$, for every $u_j \in U$. As in Set Cover, the goal in Set Multi-Cover is to minimize $c(\mathcal {C})$. There are two versions on Set Multi-Cover. In the unconstrained version $\mathcal {C}$ is a multi-set that may contain any number of copies of a subset S, and in the constrained version each set may be picked at most once. We revert to Set Cover by setting $b_j = 1$, for every $u_j$, therefore the hardness results of Set Cover apply to both versions. On the positive side, both versions of Set Multi-Cover can be approximated with $O(\log n)$ using the natural greedy algorithm [29]. Constrained Set Multi-Cover admits a $\Delta$-approximation algorithm [20]. In the unweighted case there is a deterministic $(\Delta - b_{\min } + 1)$-approximation algorithm [31] and a randomized $(\Delta - b_{\min } + 1)(1 - o(1))$-approximation algorithm [27], where $b_{\min } = \min _j b_j$. Finally, it is known that a $(\Delta - b_{\min } + 1)$-approximation algorithm for the weighted case can be obtained using primal-dual or local ratio.

Multi-Set Multi-Cover (MM) is an extension of Set Multi-Cover in which the input also contains a coverage $a_{ij} \in \mathbb {N}$, for every $S_i \in \mathcal {S}$ and $u_j \in S_i$. Hence, $S_i$ can be viewed is a multi-set having $a_{ij}$ copies of $u_j$, for each $u_j$. As in Set Multi-Cover, the MM problem has two variants, unconstrained and constrained. Even the special case of constrained MM with one element is already NP-hard, since it is equivalent to Minimum Knapsack. Unconstrained MM can be approximated within an $O(\log n)$ ratio by greedy [29]. Dobson [13] showed that greedy is an $H(\max _i \sum _j a_{ij})$-approximation algorithm for constrained MM. Carr et al. [7] gave an LP-based p-approximation algorithm, where $p \triangleq \max _j \left| \left\{ S_i: a_{ij} > 0 \right\} \right|$. Kolliopoulos and Young [23] obtained an $O(\log n)$-approximation algorithm for constrained MM that uses LP-rounding.

Wolsey [30] studied Submodular Set Cover, where the goal is to find a minimum cost collection $\mathcal {C}\subseteq \mathcal {S}$ which covers all elements in U. Wolsey showed that the approximation ratio of the greedy algorithm is $1 + O(\log f_{\max })$, where $f_{\max } = \max _{S \in \mathcal {S}} f(\left\{ S \right\} )$. As mentioned in [8], Capacitated Set Cover can be seen a special case of Submodular Set Cover by defining $f(\mathcal {C})$ as the maximum number of elements that a subcollection $\mathcal {C}$ can cover.

Guha et al. [18] presented a primal-dual 2-approximation algorithm for Vertex Cover with soft capacities (a local ratio interpretation was given in [4]) and a 3-approximation algorithm for capacitated Vertex Cover with edge requirements. Both algorithms can be extended to Set Cover and the resulting approximation ratios are $\Delta$ and $\Delta +1$, respectively. Gandhi et al. [17] presented a 2-approximation algorithm for Vertex Cover with soft capacities using an LP-rounding method called dependent rounding. Chuzhoy and Naor [8] presented a 3-approximation algorithm for unweighted Vertex Cover with hard capacities, which is based on randomized rounding with alterations. They also proved that the weighted version of this problem is as hard to approximate as set cover. Gandhi et al. [16] improved the approximation ratio for unweighted Vertex Cover with hard capacities to 2.

In the standard approach to online covering, it is the elements that arrive overtime as opposed to the subsets. Alon et al. [1] defined Online Set Cover as follows (see also [6]). A collection of sets is known in advance. Elements arrive online, and the algorithm is required to maintain a cover of the elements that arrived: if the arriving element is not already covered, then some set from the given collection must be added to the solution. They presented an $O(\log n\log m)$-competitive algorithm, which is the best possible unless $\text {NP} \subseteq \text {BPP}$ [24]. Observe that our problem has the complementary view of what is known in advance and what arrives online. Recently, Gupta and Levin [19] considered a problem called Online Submodular Cover, which extends Online Set Cover. In this problem the subsets are known and the submodular functions (elements) arrive in an online manner. They presented a polylogarithmic competitive algorithm whose ratio matches the one from [1] in the special case of Online Set Cover.

1.3 Paper Organization

The remainder of this paper is organized as follows. In Sect. 2 we introduce some notation. In Sect. 3 we present the $O(\sqrt{\rho _{\max }})$-competitive algorithm for OMSC which relies on prior knowledge of the value of $\rho _{\max }$. Section 4 contains our $O\left( \log (\rho _{\max }) \sqrt{\rho _{\max }} \right)$-competitive algorithm for OMSC that does not rely on advance knowledge of $\rho _{\max }$. Section 5 studies the capacitated versions of OMM. We conclude in Sect. 6.

2 Preliminaries

When considering multicollections of subsets one should define set operations, such as union or intersection, on multicollections. If one implicitly assumes that each copy of a subset $S_i$ have a unique serial number, then multicollections become collections and set operations are properly defined. Let $\mathcal {A}$ and $\mathcal {B}$ be multi-collections. We assume that the operation $\mathcal {A}\cup \mathcal {B}$ is done on two multicollections whose subset serial numbers may or may not match. Moreover, we assume that the disjoint union operation $\mathcal {A}\uplus \mathcal {B}$ is done on two multicollections whose subset serial numbers do not match. Hence, the outcome of $\mathcal {A}\uplus \mathcal {B}$ can be represented by the vector $x^{\mathcal {A}} + x^{\mathcal {B}}$, where $x^{\mathcal {A}}$ and $x^{\mathcal {B}}$ are the corresponding vectors that indicate the number of copies of each subset in the multicollections.

As mentioned earlier, g is submodular if $g(\mathcal {A}) + g(\mathcal {B}) \ge g(\mathcal {A}\cup \mathcal {B}) + g(\mathcal {A}\cap \mathcal {B})$, for every two multicollections $\mathcal {A}$ and $\mathcal {B}$. An equivalent definition is that g is submodular if $g(\mathcal {A}\cup \{S\}) - g(\mathcal {A}) \ge g(\mathcal {B}\cup \{S\}) - g(\mathcal {B})$, for every $\mathcal {A}\subseteq \mathcal {B}$ and $S \in \mathcal {S}$.

Given a multicollection $\mathcal {C}$, let $F(\mathcal {C})$ be the weighted coverage (or, penalty savings) of $\mathcal {C}$, namely $F(\mathcal {C}) = \sum _j p_j f_j(\mathcal {C})$. Observe that F is submodular, since the class of submodular functions is closed under non-negative linear combinations. F is monotone as well.

For a subset $S_i$ let $\kappa (i)$ be the weighted coverage of a single copy of the subset $S_i$ by itself, i.e.,

$$\begin{aligned} \kappa (i) \triangleq F(\left\{ S_i \right\} ) = \sum _{j \in S_i} p_j f_j(\left\{ S_i \right\} ) ~. \end{aligned}$$

$\kappa (i)$ is the potential savings in penalties of a single copy of subset $S_i$. Observe that since the $f_j$s are submodular, $\kappa (i)$ is the maximum amount of penalties that can be saved by a single copy of $S_i$. More formally, for any multicollection $\mathcal {C}$, we have that

$$\begin{aligned}\textstyle \kappa (i) = \sum _j p_j f_j(\left\{ S_i \right\} ) \ge \sum _j p_j \left( f_j(\mathcal {C}\uplus \left\{ S_i \right\} ) - \sum _j f_j(\mathcal {C}) \right) = F(\mathcal {C}\uplus \left\{ S_i \right\} ) - F(\mathcal {C}) ~. \end{aligned}$$

In addition, define $\rho (i) \triangleq \kappa (i)/c_i$, for every i, and $\rho _{\max }\triangleq \max _i \rho (i)$. Hence, $\rho (i)$ is the ratio between the maximum potential savings and the cost of the subset $S_i$, namely it is the cost effectiveness of subset $S_i$. Observe that if $\kappa (i) \le c_i$ for some i, then the subset is redundant. It follows that we may assume, without loss of generality, that $\kappa (i) > c_i$ for every i, which means that $\rho (i) > 1$, for every i, and that $\rho _{\max }> 1$.

Intuitively, the cheapest possible way to cover the elements is by subsets with maximum cost effectiveness. Ignoring the sets and simply paying the penalties (i.e., the solution $x=0$ and $z=b$) gives a $\rho _{\max }$-approximate solution.

In the capacitated version of OMM each subset $S_i$ has a capacity $\text {cap} (S_i)$. This means that a single copy of $S_i$ may cover a total of at most $\text {cap} (S_i)$ units of the covering requirements of elements contained in $S_i$. Given $S_i \in \mathcal {C}$, we refer to $a_i$ as the potential coverage vector of $S_i$. A vector $a'_i \in \mathbb {R}_+^n$ is called an incarnation of $S_i$ if (i) $a'_{ij} \le a_{ij}$, for every j, (ii) $\sum _j a'_{ij} \le \text {cap} (S_i)$, and (iii) $\sum _i a'_{ij} \le b_j$. We use $a'_i \trianglelefteq a_i$ to denote that $a'_i$ is an incarnation of $S_i$. In the capacitated case it is not enough to provide a multicollection $\mathcal {C}$ as a solution, but rather one needs to assign an incarnation to every subset in $\mathcal {C}$. Hence, a solution can be described as a pair $(\mathcal {C},y)$, where $\mathcal {C}$ is a multicollection and $y(S_i)$ is an incarnation of $S_i$, i.e., $y(S_i) \trianglelefteq a_i$. In the soft capacities case, one may use multiple incarnations of a subset $S_i$, provided that one pays $c_i$ for each one. In the hard capacities case, one may use only one incarnation of $S_i$. In the capacitated case, the maximum weighted coverage of a subset $S_i$ depend on the incarnation of $S_i$. Hence, we define $\kappa '(i) = \max _{a'_i \trianglelefteq a_i} \sum _j p_j a'_{ij}$. Also, define $\rho '(i) \triangleq \kappa '(i)/c_i$, for every i, and $\rho _{\max }' \triangleq \max _i \rho '(i)$.

3 Competitive Submodular Coverage

In this section we provide a deterministic online algorithm for OMSC that relies on the advance knowledge of $\rho _{\max }$. The section mainly focuses on unconstrained OMSC, but a similar approach would work for constrained OMSC.

Our algorithm is called Threshold (Algorithm 1) and it generates a monotonically growing multicollection $\mathcal {C}$ of subsets based on a simple deterministic threshold rule. (Initially, $\mathcal {C}= \emptyset$.) It is assumed that Threshold has knowledge of an upper bound $\sigma$ on $\rho _{\max }$ (the maximum cost effectiveness over all subsets) and works as follows: Upon arrival of a new subset $S_i$, we add $x_i$ copies of $S_i$ to $\mathcal {C}$, where $x_i$ is the largest integer satisfying satisfying (1)

$$\begin{aligned} x_i \cdot c_i \le \left( F(\mathcal {C}\uplus S_i^{x_i}) - F(\mathcal {C}) \right) /\sqrt{\sigma } ~, \end{aligned}$$

(1)

where $S_i^q$ denotes the multicollection with q copies of S. Intuitively, we take the maximum possible number of copies of subset $S_i$ that allows us to save a factor of at least $\sqrt{\sigma }$ over the penalties avoided. Notice that $x_i$ is well-defined because Inequality (1) is always satisfied by $x_i = 0$. Also, let $z_j$ be the requirement of j that is uncovered by the current solution $\mathcal {C}$, namely let $z_j = b_j - f_j(\mathcal {C})$.

Algorithm 1

– Threshold

We show that the competitive ratio of Threshold is at most $2\sqrt{\rho _{\max }}$, if $\sigma = \rho _{\max }$. We assume that Threshold is executed with a parameter $\sigma$ such that $\sigma \ge \rho _{\max }$, since we shall need this extension in the next section.

Let $\mathcal {C}_i$ be the solution that is constructed after the arrival of subset $S_i$, and let $z^i_j$ be the corresponding value of $z_j$, for every i.

We first bound the cost $\sum _i c_i x_i$ of the selected sets.

Lemma 1

Let $\mathcal {C}$ be the solution computed by Threshold with parameter $\sigma$, where $\sigma \ge \rho _{\max }$. Also, let $\mathcal {C}^*$ be an optimal solution. Then,

$$\begin{aligned}\sum _i c_i x_i \le \frac{\rho _{\max }}{\sqrt{\sigma }} \sum _i c_i x^*_i + \frac{1}{\sqrt{\sigma }} \sum _j p_j (z^*_j - z_j) ~. \end{aligned}$$

Proof

By condition (1), we have that

$$\begin{aligned}{} & {} \sqrt{\sigma } \sum _i c_i x_i \le \sum _i \left( F(\mathcal {C}_{i-1} \uplus S_i^{x_i}) - F(\mathcal {C}_{i-1}) \right) \\{} & {} = \sum _i \left( F(\mathcal {C}_i) - F(\mathcal {C}_{i-1}) \right) = F(\mathcal {C}) = \sum _j p_j (b_j-z_j) ~. \end{aligned}$$

On the other hand, since $\rho (i) = \kappa (i)/c_i$, for every i, we have that

$$\begin{aligned} \sum _i c_i x^*_i&= \sum _i \frac{F(\left\{ S_i \right\} )}{\rho (i)} x^*_i \\&\ge \frac{1}{\rho _{\max }} \sum _i x^*_i F(\left\{ S_i \right\} ) \\&\ge \frac{1}{\rho _{\max }} \sum _i \left( F(\mathcal {C}^*_i) - F(\mathcal {C}^*_{i-1}) \right) \\&= \frac{1}{\rho _{\max }} \sum _j p_j (b_j - z^*_j) ~. \end{aligned}$$

It follows that

$$\begin{aligned} \sqrt{\sigma } \sum _i c_i x_i \le \sum _j p_j (b_j-z_j) = \sum _j p_j (b_j - z^*_j) + \sum _j p_j (z^*_j - z_j)\\ \le \rho _{\max }\sum _i c_i x^*_i + \sum _j p_j (z^*_j - z_j) ~, \end{aligned}$$

as required. $\square$

Theorem 1

Let $\mathcal {C}$ be the solution computed by Algorithm Threshold, and let $\mathcal {C}^*$ be an optimal solution. Then,

$$\begin{aligned} \textsc {cost} (\mathcal {C}) = \sum _i c_i x_i + \sum _j p_j z_j ~\le ~ 2 \left( \sqrt{\rho _{\max }} \sum _i c_i x^*_i + \sum _j p_j z^*_j \right) ~. \end{aligned}$$

Proof

Due to Lemma 1, with $\sigma = \rho _{\max }$, we have that

$$\begin{aligned} \sum _i c_i x_i \le \sqrt{\rho _{\max }} \sum _i c_i x^*_i + \frac{1}{\sqrt{\rho _{\max }}} \sum _j p_j (z^*_j - z_j) ~. \end{aligned}$$

The next step is to bound the total sum of penalties that $\mathcal {C}$ pays and $\mathcal {C}^*$ does not pay, namely to bound

$$\begin{aligned} \sum _j p_j \max \left\{ z_j-z^*_j,0 \right\} ~. \end{aligned}$$

Define

$$\begin{aligned} \Delta _i \triangleq \max \left\{ x^*_i - x_i,0 \right\} ~. \end{aligned}$$

If $\Delta _i = 0$, for all i, then $\mathcal {C}^* \subseteq \mathcal {C}$ and $z_j \le z^*_j$, for every j, and we are done. Otherwise, let i be an index such that $\Delta _i>0$. Due to condition (1) in the ith step, we have that

$$\begin{aligned} c_i x_i \le \left( F(\mathcal {C}_i) - F(\mathcal {C}_{i-1}) \right) /\sqrt{\rho _{\max }} ~, \end{aligned}$$

where $\mathcal {C}_i = \mathcal {C}_{i-1} \uplus S_i^{x_i}$, while

$$\begin{aligned} c_i x^*_i > \left( F \left( \mathcal {C}_{i-1} \uplus S_i^{x^*_i} \right) - F(\mathcal {C}_{i-1}) \right) /\sqrt{\rho _{\max }} ~. \end{aligned}$$

Hence,

$$\begin{aligned}{} & {} c_i \Delta _i ~=~ c_i x^*_i - c_i x_i ~>~ \left( F \left( \mathcal {C}_i \uplus S_i^{\Delta _i} \right) - F(\mathcal {C}_i) \right) /\sqrt{\rho _{\max }}\\{} & {} ~\ge ~ \left( F \left( \mathcal {C}\uplus S_i^{\Delta _i} \right) - F(\mathcal {C}) \right) /\sqrt{\rho _{\max }} ~, \end{aligned}$$

where the second inequality is due to the submodularity of F. It follows that

$$\begin{aligned} \sqrt{\rho _{\max }} \sum _i c_i \Delta _i&> \sum _i \left( F \left( \mathcal {C}\uplus S_i^{\Delta _i} \right) - F(\mathcal {C}) \right) \\&\ge F \left( \mathcal {C}\uplus \biguplus _i S_i^{\Delta _i} \right) - F(\mathcal {C}) \\&\ge F(\mathcal {C}^*) - F(\mathcal {C}) \\&\ge \sum _j p_j \max \{z_j - z^*_j,0\} ~, \end{aligned}$$

where the second inequality is due to the submodularity of F, and the third is due to the monotonicity of F. Since $x^* \ge \Delta$, we have that

$$\begin{aligned} \sum _j p_j \max \{z_j - z^*_j,0\} ~<~ \sqrt{\rho _{\max }} \sum _i c_i \Delta _i ~\le ~ \sqrt{\rho _{\max }} \sum _i c_i x^*_i ~. \end{aligned}$$

Putting it all together, we have that

$$\begin{aligned}&\sum _i c_i x_i + \sum _j p_j z_j \\&~~~\le \sum _i c_i x_i + \sum _j p_j z^*_j + \sum _j p_j \max \{z_j - z^*_j,0\} \\&~~~\le \sqrt{\rho _{\max }} \sum _i c_i x^*_i + \frac{1}{\sqrt{\rho _{\max }}} \sum _j p_j (z^*_j - z_j) + \sum _j p_j z^*_j + \sum _j p_j \max \{z_j - z^*_j,0\} \\&~~~= \sqrt{\rho _{\max }} \sum _i c_i x^*_i + \frac{1}{\sqrt{\rho _{\max }}} \sum _j p_j \max \left\{ z^*_j - z_j,0 \right\} - \frac{1}{\sqrt{\rho _{\max }}} \sum _j p_j \max \left\{ z_j - z^*_j,0 \right\} \\&~~~~~~~~~ + \sum _j p_j z^*_j + \sum _j p_j \max \{z_j - z^*_j,0\} \\&~~~\le \sqrt{\rho _{\max }} \sum _i c_i x^*_i + \left( 1 + \frac{1}{\sqrt{\rho _{\max }}} \right) \sum _j p_j z^*_j - \left( 1 - \frac{1}{\sqrt{\rho _{\max }}} \right) \sum _j p_j \max \{z_j - z^*_j,0\} \\&~~~\le (2\sqrt{\rho _{\max }}-1) \sum _i c_i x^*_i + \left( 1 + \frac{1}{\sqrt{\rho _{\max }}} \right) \sum _j p_j z^*_j ~, \end{aligned}$$

as required. $\square$

Theorem 1 leads us to an upper bound on the competitive ratio of Algorithm Threshold.

Corollary 2

Algorithm Threshold is $2\sqrt{\rho _{\max }}$-competitive for unconstrained OMSC, assuming prior knowledge of $\rho _{\max }$.

The same approach would work for the constrained variant of OMSC. In this case the value of $x_i$ in the Condition described by (1) is also bounded by 1.

Corollary 3

Algorithm Threshold is $2\sqrt{\rho _{\max }}$-competitive for constrained OMSC, assuming prior knowledge of $\rho _{\max }$.

4 Algorithm Without Prior Knowledge of $\rho _{\max }$

In this section we provide a deterministic online algorithm for OMSC that does not rely on advance knowledge of $\rho _{\max }$. This algorithm is based on Algorithm Threshold, but as opposed to algorithm Threshold, it uses dismissals. Recall that is was shown that dismissals are necessary in order to obtain an $o(\rho _{\max })$-competitive ratio [15] even for OMM. The competitive ratio of the algorithm is $O(\log (\rho _{\max }) \sqrt{\rho _{\max }})$.

Algorithm Multi-Threshold maintains a variable ${\bar{\rho }}$ that holds, at any given moment, $\rho _{\max }$ of the instance that it has seen so far. In addition, it computes in parallel, using Threshold, a solution $\mathcal {C}^k$, with the parameter $\sigma = 2^k$, for all k such that $2^k \in [{\bar{\rho }},{\bar{\rho }}^2]$ (initially, ${\bar{\rho }} = 1$). Each invocation of Threshold is run independently. That is, each copy of Threshold makes its decisions without taking into account the decisions of other copies. Let $(x^k,z^k)$ be the pair of variable vectors that correspond to $\mathcal {C}^k$.

Upon arrival of subset $S_i$, the Algorithm Multi-Threshold updates ${\bar{\rho }}$, if need be. If ${\bar{\rho }}$ is updated, then the algorithm terminates the invocations of Threshold for all parameters that are smaller than ${\bar{\rho }}$. That includes dismissing all subsets that were taken by those invocations. The algorithm then executes a step of Threshold for each power of 2 in the interval $[{\bar{\rho }},{\bar{\rho }}^2]$.

Algorithm 2

Multi-Threshold

Consider such an execution of Threshold with parameter $\sigma = 2^4 = 16$. As long as ${\bar{\rho }} < \sqrt{16} = 4$, then this execution does nothing. Hence, it is safe to activate it only upon arrival of a subset $S_i$ such that $\rho (i) \ge 4$.

The next lemma generalizes this argument in order to justify the fact that Multi-Threshold executes Threshold only on parameters in the interval $[{\bar{\rho }},{\bar{\rho }}^2]$. In other words, we show that one may assume that Multi-Threshold actually executes Threshold with parameter $2^k$, for all $k \ge \ell$, where $\ell = \min \left\{ k: 2^k \ge {\bar{\rho }} \right\}$, on the whole instance.

Lemma 2

Let k be such that $2^k > {\bar{\rho }}^2$, and assume that we execute Threshold with parameter $\sigma = 2^k$ starting at the arrival of the first subset. Then, $\mathcal {C}_k = \emptyset$.

Proof

When Threshold is run with parameter $\sigma = 2^k$, the algorithm adds a copy of a subset $S_i$ to the solution only if (1) is satisfied with (at least) $x_i^k = 1$. If $\sigma = 2^k > {\bar{\rho }}^2$, then no set will be included. $\square$

The multicollection which is computed by Multi-Threshold is:

$$\begin{aligned} \mathcal {C}&= \biguplus _{k : 2^k \in [{\bar{\rho }},{\bar{\rho }}^2]} C^k&\text{ or }{} & {} x&= \sum _{k : 2^k \in [{\bar{\rho }},{\bar{\rho }}^2]} x^k ~. \end{aligned}$$

Let $z_j = b_j - f_j(\mathcal {C})$, for every j. (We note that we need not hold a separate set of copies of each subset for each Threshold execution – it suffices to hold the maximum number of copies required.)

We observe that the penalties that are paid by the combined solution is smaller than the penalty that any invocation would have to pay.

Observation 1

$z \le z^k$, for every k such that $2^k \in [{\bar{\rho }},{\bar{\rho }}^2]$.

Next, we bound the competitive ratio of Multi-Threshold. We first show that the cost of subsets (without penalties) taken by invocation with parameter $\sigma = 2^k$, for $k > \ell$, is bounded by the optimal cost.

Lemma 3

Let $k > \ell$ such that $2^k \le {\bar{\rho }}^2$. Then, $\sum _i c_i x^k_i \le \sqrt{{\bar{\rho }}} \cdot \textsc {cost} (\mathcal {C}^*)$.

Proof

Due to Lemma 2 one may assume that the invocation of Threshold with parameter $2^k$ is run on the whole instance. Define a new instance similar to the original instance but with coverage requirements $b^k_j = f_j(\mathcal {C}^k)$, for every j. The solution $\mathcal {C}^k$ covers all of the requirements in the new instance by definition. Moreover, notice that Threshold would compute $\mathcal {C}^k$ if executed on the new instance with parameter $2^k$. Let $\mathcal {C}'$ be an optimal solution for the new instance.

Lemma 1 applied to Threshold with parameter $2^k$ and the new instance implies that

$$\begin{aligned}\sum _i c_i x^k_i \le \frac{{\bar{\rho }}}{\sqrt{2^k}} \sum _i c_i x'_i + \frac{1}{\sqrt{2^k}} \sum _j p_j z'_j ~. \end{aligned}$$

Since $2^k > {\bar{\rho }}$, we have that

$$\begin{aligned} \sum _i c_i x^k_i \le \sqrt{{\bar{\rho }}} \sum _i c_i x'_i + \frac{1}{\sqrt{{\bar{\rho }}}} \sum _j p_j z'_j \le \sqrt{{\bar{\rho }}} \cdot \textsc {cost} (\mathcal {C}') ~. \end{aligned}$$

The lemma follows, since $\textsc {cost} (\mathcal {C}') \le \textsc {cost} (\mathcal {C}^*)$. $\square$

We bound the total cost of the solution using Lemma 3 and the fact that the solution computed by invocation with parameter $\sigma = 2^\ell$ is $O(\sqrt{\rho _{\max }})$-competitive.

Theorem 4

There exists an $O(\log (\rho _{\max }) \sqrt{\rho _{\max }} )$-competitive algorithm for unconstrained OMSC.

Proof

Consider the solution $\mathcal {C}$ at termination of Multi-Threshold. Since ${\bar{\rho }} = \rho _{\max }$ at termination, we have that $x_i = \sum _{k: 2^k \in [\rho _{\max },\rho _{\max }^2]} x^k_i$, for every i. By Lemma 2 we may assume that the invocation of Threshold with parameter $2^\ell$ run on the whole instance. Also, by Observation 1 it follows that $z_j \le z^k_j$, for every j, and in particular for $k = \ell$. Hence,

$$\begin{aligned} \textsc {cost} (\mathcal {C})&= \sum _i c_i x_i + \sum _j p_j z_j \\&\le \sum _i c_i \sum _{k : 2^k \in [\rho _{\max },\rho _{\max }^2]} x^k_i + \sum _j p_j z_j \\&\le \sum _i c_i \sum _{k \ne \ell : 2^k \in [\rho _{\max },\rho _{\max }^2]} x^k_i + \sum _i c_i x^\ell _i + \sum _j p_j z^\ell _j \\&\le \log (\rho _{\max }) \sqrt{\rho _{\max }} \cdot \textsc {cost} (\mathcal {C}^*) + 2\sqrt{2\rho _{\max }} \cdot \textsc {cost} (\mathcal {C}^*) ~, \end{aligned}$$

where the second inequality follows from Lemma 3 and Corollary 2. $\square$

By replacing Corollary 2 with Corollary 3, we have that:

Theorem 5

There exists an $O(\log (\rho _{\max }) \sqrt{\rho _{\max }} )$-competitive algorithm for constrained OMSC.

5 Capacitated Online Multiset Multicover

In this section we consider the capacitated versions of Online Multiset Multicover. We deal with soft capacities using a straightforward reduction to uncapacited OMM. As for hard capacities, we show a lower bound of $\Omega (\rho _{\max })$, if subset reassignments are not allowed. If reassignments are allowed, we show that the capacitated coverage is submodular, and this paves the way to a reduction to OMSC.

5.1 Soft Capacities

We first show that our results extend to soft capacities.

Theorem 6

There exists an $O(\sqrt{\rho _{\max }'})$-competitive algorithm for OMM with soft capacities, assuming prior knowledge of $\rho _{\max }'$.

Proof

Consider a subset $S_i$. One can simulate the arrival of $S_i$ with the arrival of all its possible incarnations, namely with the arrival of $\mathcal {S}_i = \left\{ S'_i \subseteq S_i: \left| S'_i \right| = \text {cap} (S_i) \right\}$. The theorem follows, since the maximum cost effectiveness is $\rho _{\max }'$. $\square$

Theorems  4 and 6 lead to the following result:

Theorem 7

There exists an $O(\log (\rho _{\max }') \sqrt{\rho _{\max }'})$-competitive algorithm for OMM with soft capacities.

5.2 Hard Capacities Without Reassignments

The following construction shows a lower bound of $\Omega (\rho _{\max }')$, for the case where elements cannot be reassigned to other subsets.

Theorem 8

The competitive ratio of any randomized online algorithm for OMM with hard capacities is $\Omega (\rho _{\max })$ if reassignments are disallowed. This bound holds even if the algorithm is allowed to discard sets, and for inputs with unit penalties and costs, and subsets of size at most two.

Proof

Let alg be a randomized algorithm. Consider an instance with two unit penalty elements $u_1, u_2$. The coverage requirements of both elements is $\beta$. The sequence consists of two unit cost subsets with capacity $\beta$. It starts with $S_1 = \left\{ u_1,u_2 \right\}$, $a_{11} = a_{12} = \beta$. The second subset $S_2$ has two options, each with probability 0.5: (i) $S_2 = \left\{ u_1 \right\}$, $a_{11} = \beta$, and $a_{12} = 0$, and (ii) $S'_2 = \left\{ u_2 \right\}$, $a_{12} = \beta$, and $a_{11} = 0$. Clearly, the optimal cost is 2. Also, $\rho _{\max }= \rho _{\max }' = \beta$.

Let A be the event that $\textsc {alg}$ uses at least $\beta /2$ units of the capacity of $S_1$ to cover $u_1$. If A occurs and the adversary presents the subset $S_2$, then at least $\beta /2$ units of the cover requirements of $u_2$ are unsatisfied, for a penalty of at least $\beta /2$. Similarly, if A does not occur and the adversary presents the subset $S'_2$, the same $\beta /2$ penalty applies to $u_1$. In either case, with probability $\frac{1}{2}$, the cost is at least $\beta /2$. Hence, the expected cost of alg is at least $\beta /4$, for a competitive ratio of at least $\beta /8$. $\square$

5.3 Hard Capacities with Reassignments

Now consider the version of OMM, where reassignments are allowed. In this case, it is only natural to have the best possible assignment with respect to the current multicollection $\mathcal {C}$ at any time. Formally, given $\mathcal {C}\subseteq \mathcal {S}$, let $\tilde{y}$ be an incarnation function that maximizes the weighted coverage of $\mathcal {C}$, i.e., $\tilde{y}_{\mathcal {C}} = \textrm{argmax}_y F(y(\mathcal {C})) ~.$ Also, denote $\tilde{F}(\mathcal {C}) = F(\tilde{y}_{\mathcal {C}}) ~.$

The next natural step is to modify Algorithm Threshold by using $\tilde{F}$ instead of F. Hence, we would like to prove that $\tilde{F}$ is submodular. Before dealing with submodularity we reduce the problem of finding the best cover of a universe U using a capacitated collection $\mathcal {C}$ of subsets to an instance of the Maximum Weighted Matching problem in a bipartite graph.

Given a multicollection $\mathcal {S}$, we define the following bipartite graph $G = (L,R,E)$, where

$$\begin{aligned} L&= \left\{ \ell _i^s : S_i \in \mathcal {C}, s \in \left\{ 1,\ldots ,\text {cap} (S_i) \right\} \right\} \\ R&= \left\{ r_j^t : u_j \in U, t \in \left\{ 1,\ldots ,b_j \right\} \right\} \\ E&= \left\{ (\ell _i^s,r_j^t) : u_j \in S_i, s \in \left\{ 1,\ldots ,\text {cap} (S_i) \right\} , t \in \left\{ 1,\ldots ,b_j \right\} \right\} ~. \end{aligned}$$

The weight of an edge $(\ell _i^s,r_j^t)$ is defined as $p_j$, i.e., $w(\ell _i^s,r_j^t) = p_j$. A depiction is given in Fig. 1.

Fig. 1

A bipartite graph $G = (L,R,E)$ for the instance $U = \left\{ 1,2,3 \right\}$, where $b = (2,2,1)$ and $\mathcal {S}= \left\{ \left\{ 1 \right\} , \left\{ 1,2 \right\} , \left\{ 2,3 \right\} \right\}$, where $\text {cap} (S_1) = \text {cap} (S_3) = 2$ and $\text {cap} (S_2) = 1$

Given a multicollection $\mathcal {C}$, let $L_{\mathcal {C}}$ be the vertices in L that correspond to subsets in $\mathcal {C}$, i.e., $L_{\mathcal {C}} = \left\{ \ell _i^s \in L: S_i \in \mathcal {C} \right\}$. The graph $G[L_{\mathcal {C}} \times R]$ is an induced subgraph of G that contains that all element vertices on the right side, but only vertices that correspond to subsets in $\mathcal {C}$ on the left side.

Lemma 4

Consider an instance of capacitated Multiset Multicover and a multicollection $\mathcal {C}\subseteq \mathcal {S}$. Then, an incarnation function y induces a fractional matching M in $G[L_{\mathcal {C}} \times R]$, such that the weight of the matching is equal to the total penalty that is covered by y, and vice versa.

Proof

Given an incarnation y, let $y'$ be the following fractional matching:

$$\begin{aligned} y'(\ell _i^s,r_j^t) = \frac{y(S_i,u_j)}{\text {cap} (S_i) \cdot b_j} ~. \end{aligned}$$

$y'$ is a fractional matching, since

$$\begin{aligned} \sum _{\ell _i^s: u_j \in S_i} y'(\ell _i^s,r_j^t) = \sum _{\ell _i^s: u_j \in S_i} \frac{y(S_i,u_j)}{\text {cap} (S_i) \cdot b_j} = \sum _{u_j \in S_i} b_j \cdot \frac{y(S_i,u_j)}{\text {cap} (S_i) \cdot b_j} = \sum _{u_j \in S_i} \frac{y(S_i,u_j)}{\text {cap} (S_i)} \le 1 ~, \end{aligned}$$

for every $r_j^t$, and similarly

$$\begin{aligned}{} & {} \sum _{r_j^t: u_j \in S_i} y'(\ell _i^s,r_j^t) = \sum _{r_j^t: u_j \in S_i} \frac{y(S_i,u_j)}{\text {cap} (S_i) \cdot b_j}\\{} & {} = \sum _{S_i: u_j \in S_i} \text {cap} (S_i) \cdot \frac{y(S_i,u_j)}{\text {cap} (S_i) \cdot b_j} = \sum _{S_i: u_j \in S_i} \frac{y(S_i,u_j)}{b_j} \le 1 ~, \end{aligned}$$

for every $\ell _i^s$.

For the other direction, let $y'$ be a fractional matching. Define the following incarnation function:

$$\begin{aligned} y(S_i,u_j) = \sum _s \sum _t y'(\ell _i^s,r_j^t). \end{aligned}$$

We have that

$$\begin{aligned} \sum _j y(S_i,u_j) = \sum _j \sum _s \sum _t y'(\ell _i^s,r_j^t) = \sum _s \sum _{\ell _i^s: u_j \in S_i} y'(\ell _i^s,r_j^t) \le \sum _s 1 = \text {cap} (S_i) ~, \end{aligned}$$

and

$$\begin{aligned} \sum _i y(S_i,u_j) = \sum _i \sum _s \sum _t y'(\ell _i^s,r_j^t) = \sum _t \sum _{r_j^t: u_j \in S_i} y'(\ell _i^s,r_j^t) \le \sum _t 1 = b_j ~, \end{aligned}$$

Finally, it is not hard to verify that the total sum of covered penalties is equal to the weight of the matching. $\square$

Since the polytope of bipartite Maximum Weighted Matching is known to have integral optimal solutions, Lemma 4 implies that:

Corollary 9

Consider an instance of capacitated Multiset Multicover and a multicollection $\mathcal {C}\subseteq \mathcal {S}$. Then, there exists an optimal integral incarnation function y.

Now we move to proving that $\tilde{F}$ is submodular. To do that we use a result by Bar-Noy and Rabanca [3] that showed submodularity of partial maximum weight matching functions.

Definition 1

[3] Let $G = (L,R,E)$ be a bipartite graph and let $w:E \rightarrow \mathbb {R}_+$ be a non-negative weight function on the edges. The partial maximum weight matching function $f: 2^A \rightarrow \mathbb {R}$ maps any subset $U \subseteq L$ to the value of a maximum weight matching in $G[U \cup R]$.

Lemma 5

[3] Let f be a partial maximum weight matching function for a bipartite graph G with non-negative edge weights. Then, f is submodular.

By Lemmas 4, 5, and Corollary 9, we have that:

Lemma 6

Given an instance of capacitated Multiset Multicover, $\tilde{F}$ is submodular.

Since $\tilde{F}$ is submodular one may use the algorithms from the previous sections.

Theorem 10

There exists an $O(\sqrt{\rho _{\max }'})$-competitive algorithm for OMM with hard capacities, assuming prior knowledge of $\rho _{\max }'$.

Proof

We use Algorithm Threshold with $\tilde{F}$ instead of F. We assume that Algorithm Threshold uses the bipartite graph G in order to compute its solution. If this is done using an augmenting path algorithm, then $z_j$ can only decrease, for every $u_j$, throughout execution.

By Lemma 6, $\tilde{F}$ is submodular and $\tilde{F}$ is also monotone. Therefore the analysis of the Algorithm Threshold applies with $\rho _{\max }'$ replacing $\rho _{\max }$. $\square$

Theorems 4 and 10 lead to the following result:

Theorem 11

There exists an $O(\log (\rho _{\max }') \sqrt{\rho _{\max }'})$-competitive algorithm for OMM with hard capacities.

6 Conclusion

It was shown in [15] that randomized algorithms cannot have competitive ratio better than $\Omega (\sqrt{\rho }_{\max })$, even for OMM. This lower bound holds even if $\rho _{\max }$ is known, and even if one is allowed to drop previously selected subsets. We gave a matching upper bound for OMSC, but the corresponding algorithm is based on the prior knowledge of $\rho _{\max }$. The competitive ratio of our second algorithm is $O(\log (\rho _{\max }) \sqrt{\rho }_{\max })$, and this leaves a multiplicative gap of $O(\log (\rho _{\max }))$. It remains an open question whether there is an $O(\sqrt{\rho _{\max }})$-competitive algorithm that has no knowledge of $\rho _{\max }$, even for OMM.