On Structural Parameterizations of the Bounded-Degree Vertex Deletion Problem

Abstract

We study the parameterized complexity of the Bounded-Degree Vertex Deletion problem (BDD), where the aim is to find a maximum induced subgraph whose maximum degree is below a given degree bound. Our focus lies on parameters that measure the structural properties of the input instance. We first show that the problem is W[1]-hard parameterized by a wide range of fairly restrictive structural parameters such as the feedback vertex set number, pathwidth, treedepth, and even the size of a minimum vertex deletion set into graphs of pathwidth and treedepth at most three. We thereby resolve an open question stated in Betzler, Bredereck, Niedermeier and Uhlmann (2012) concerning the complexity of BDD parameterized by the feedback vertex set number. On the positive side, we obtain fixed-parameter algorithms for the problem with respect to the decompositional parameter treecut width and a novel problem-specific parameter called the core fracture number.

1 Introduction

This paper studies the Bounded-Degree Vertex Deletion problem (BDD): given an undirected graph G, a degree bound d, and a limit $\ell$, determine whether it is possible to delete at most $\ell$ vertices from G in order to obtain a graph of maximum degree at most d. Aside from being a natural generalization of the classical Vertex Cover problem, BDD has found applications in areas such as computational biology [19] and is the dual problem of the so-called s-Plex Detection problem in social network analysis [3, 38, 39, 44]. Finally, related problems on directed as well as undirected graphs which model problems in voting theory and social network analysis have also been studied in the literature [5, 7].

It is not surprising that the complexity of BDD and several of its variants has been studied extensively by the theory community in the past years [4, 6, 9, 10, 13, 34, 42, 44]. Since the problem is NP-complete in general, it is natural to ask under which conditions does the problem become tractable. In this direction, the parameterized complexity paradigm [12, 15, 41] allows a more refined analysis of the problem’s complexity than classical complexity. In the parameterized setting, we associate each instance with a numerical parameter k and are most often interested in the existence of a fixed-parameter algorithm, i.e., an algorithm solving the problem in time $f(k)\cdot |V(G)|^{{{\mathcal {O}}}(1)}$ for some computable function f. Parameterized problems admitting such an algorithm belong to the class FPT; on the other hand, parameterized problems that are hard for the complexity class W[1] or W[2] do not admit fixed-parameter algorithms (under standard complexity assumptions).

In general, there exist two notable approaches for selecting parameters: a parameter may either originate from the formulation of the problem itself (often called natural parameters), or rather from the structure of the input graph (so-called structural parameters, most prominently represented by the decomposition-based parameter treewidth ${\mathbf {tw}}$). The parameterized complexity of BDD has already been studied extensively through the lens of natural parameters (especially d and $\ell$). In particular, BDD is known to be FPT when parameterized by $d+\ell$ [19, 39, 42], W[2]-hard when parameterized only by $\ell$ [19], and NP-complete when parameterized only by d (as witnessed by the case of $d=0$, i.e., Vertex Cover). The complexity of BDD is also fairly well understood when considering combinations of natural and structural parameters: it is FPT when parameterized by ${\mathbf {tw}}+d$ due to Courcelle’s Theorem [11] and has been shown to be FPT when parameterized by ${\mathbf {tw}}+\ell$ [6].

Given the above, it is fairly surprising that the problem has remained fairly unexplored when viewed through the lens of structural parameters only, i.e., in the case where we impose no restrictions on the problem formulation itself but only on the structure of the graph. BDD was shown W[1]-hard when parameterized by treewidth [6], complementing the previous ${{\mathcal {O}}}(n^{{\mathbf {tw}}+1})$ algorithm of Dessmark et al. [13]. The only structural parameter which is known to make the problem fixed-parameter tractable is the feedback edge set number, i.e., the minimum number of edges whose deletion results in a forest [6].

Contribution The goal of this paper is to provide new insight into the complexity of BDD parameterized by the structure of the input graph. Our first main result shows that BDD is ${{{\textsf {W}}}}{ {[1]}}$-hard parameterized by the feedback vertex set number, i.e., the minimum number of vertices whose deletion results in a forest. This resolves an open question in [6]. Interestingly, our result is significantly stronger since we show that hardness even applies in the case that the remaining parts, after deleting the feedback vertex set, are trees of height three. This rules out fixed-parameter algorithms w.r.t. most of the remaining “classical” decomposition-based structural parameters such as pathwidth and treedepth [40] as well as w.r.t. the vertex deletion distance [23, 40] to bounded pathwidth, treedepth, and treewidth. On the way to our hardness result we show hardness for several multidimensional variants of the classical subset sum problem parameterized by the number of dimensions, which we believe are interesting on their own.

In light of the above, it is natural to ask whether there exist natural decomposition-based parameters for which BDD is fixed-parameter tractable. Our main algorithmic result answers this question affirmatively: we obtain a fixed-parameter algorithm utilizing the recently introduced structural parameter called treecut width. The importance of treecut width is that it plays a similar role with respect to the fundamental graph operation of immersion as the graph parameter treewidth plays with respect to the minor operation [32, 37, 45]. Up to now, only a handful of problems are known to be FPT when parameterized by treecut width but W[1]-hard when parameterized by treewidth [24]; recent work on treecut width also included new algorithmic lower bounds [27] and experimental evaluations [26]. We note that unlike previous algorithms exploiting treecut width, ours does not make use of an Integer Linear Programming formulation but instead relies purely on combinatorial arguments.

Our second algorithmic result focuses on structural parameters which are not based on any particular decomposition of the graph, but instead measure the “vertex-deletion distance” to a certain graph property. Such structural parameters have been successfully used in the past for a plethora of other difficult problems [16, 17, 23, 28, 29, 35]. In this context and taking into account the strong lower bounds obtained in Sect. 3, we introduce a structural parameter which is specifically tailored to BDD and which we call the core fracture number. Roughly speaking, the core fracture number k is the vertex deletion distance to a graph where each connected component only contains at most k vertices which exceed the degree bound d. We show that computing the core fracture number is FPT which in turn gives rise to a fixed-parameter algorithm for BDD; the latter is achieved by identifying and formalizing a type-aggregation condition, allowing for an encoding of the problem into an Integer Linear Program with a controlled number of integer variables. Since core fracture number generalizes vertex cover, this also resolves the question from [6] if BDD is FPT parameterized by vertex cover.

Finally, we exclude the existence of a polynomial kernel [12, 15] for BDD parameterized by the treecut width and core fracture number, and compare the two parameters in Sect. 5.

2 Preliminaries

2.1 Basic Notation

We use standard terminology for graph theory, see for instance [14]. All graphs except for those used to compute the torso-size in Sect. 2.4 are simple; the multigraphs used in Sect. 2.4 have loops, and each loop increases the degree of the vertex by 2.

Let G be a graph. We denote by V(G) and E(G) its vertex and edge set, respectively. For a vertex $v \in V(G)$, let $N_G(v)=\{y\in V(G):vy\in E(G)\}$, $N_G[v]=N_G(v)\cup \{v\}$, and $\deg _G(v)$ denote its open neighborhood, closed neighborhood, and degree, respectively. For a subset $X \subseteq V(G)$, the (open) neighborhood $N_G(X)$ of X is defined as $\bigcup _{x\in X} N(x) \setminus X$. The set $N_G[X]$ refers to the closed neighborhood of X defined as $N_G(X)\cup X$. We refer to the set $N_G(V(G)\setminus X)$ as $\partial _G(X)$; this is the set of vertices in X which have a neighbor in $V(G)\setminus X$. We omit the lower index G, if G is clear from the context. For a vertex set A, we use $G-A$ to denote the graph obtained from G by deleting all vertices in A. We use [i] to denote the set $\{0,1,\dots ,i\}$; note that [i] includes 0. For completeness, we provide a formal definition of our problem of interest below.

2.2 Parameterized Complexity

A parameterized problem ${\mathcal {P}}$ is a subset of $\varSigma ^* \times {\mathbb {N}}$ for some finite alphabet $\varSigma$. Let $L\subseteq \varSigma ^*$ be a classical decision problem for a finite alphabet, and let p be a non-negative integer-valued function defined on $\varSigma ^*$. Then L parameterized by $\kappa$ denotes the parameterized problem $\{\,(x,\kappa (x)) \;{|}\;x\in L \,\}$ where $x\in \varSigma ^*$. For a problem instance $(x,k) \in \varSigma ^* \times {\mathbb {N}}$ we call x the main part and k the parameter. A parameterized problem ${\mathcal {P}}$ is fixed-parameter tractable (FPT in short) if a given instance (x, k) can be solved in time ${{\mathcal {O}}}(f(k) \cdot p(|x|))$ where f is an arbitrary computable function of k and p is a polynomial function; we call algorithms running in this time fixed-parameter algorithms. We refer the reader to [15] for more details on parameterized complexity.

Parameterized complexity classes are defined with respect to fpt-reducibility. A parameterized problem ${\mathcal {P}}$ is fpt-reducible to ${\mathcal {Q}}$ if in time $f(k)\cdot |x|^{O(1)}$, one can transform an instance (x, k) of ${\mathcal {P}}$ into an instance $(x',k')$ of ${\mathcal {Q}}$ such that $(x,k)\in {\mathcal {P}}$ if and only if $(x',k')\in {\mathcal {Q}}$, and $k'\le g(k)$, where f and g are computable functions depending only on k. Owing to the definition, if ${\mathcal {P}}$ fpt-reduces to ${\mathcal {Q}}$ and ${\mathcal {Q}}$ is fixed-parameter tractable then ${\mathcal {P}}$ is fixed-parameter tractable as well.

Central to parameterized complexity is the following hierarchy of complexity classes, defined by the closure of canonical problems under fpt-reductions: ${\textsf {FPT}} \subseteq {{{\textsf {W}}}}{ {[1]}} \subseteq {{{\textsf {W}}}}{ {[2]}} \subseteq \cdots \subseteq {\textsf {XP}}.$ All inclusions are believed to be strict. In particular, ${\textsf {FPT}} \ne {{{\textsf {W}}}}{ {[1]}}$ under the Exponential Time Hypothesis [30].

The class ${{{\textsf {W}}}}{ {[1]}}$ is the analog of ${\textsf {NP}}$ in parameterized complexity. A major goal in parameterized complexity is to distinguish between parameterized problems which are in ${\textsf {FPT}}$ and those which are ${{{\textsf {W}}}}{ {[1]}}$-hard, i.e., those to which every problem in ${{{\textsf {W}}}}{ {[1]}}$ is fpt-reducible. There are many problems shown to be complete for ${{{\textsf {W}}}}{ {[1]}}$, or equivalently ${{{\textsf {W}}}}{ {[1]}}$-complete, including the MultiColored Clique (MCC) problem [15].

Closely related to the search for fixed-parameter algorithms is the search for efficient preprocessing techniques. The goal here is to find an equivalent instance (the so-called kernel) in polynomial time whose size can be bounded by a function of the parameter. A kernelization algorithm transforms in polynomial time a problem instance (x, k) of a parameterized problem L into an instance $(x', k')$ of L such that (i) $(x, k)\in L$ iff $(x', k')\in L$, (ii) $k' \le f(k)$, and (iii) the size of $x'$ can be bounded above by g(k), for functions f and g depending only on k. It is easy to show that a parameterized problem is in FPT if and only if there is kernelization algorithm. A polynomial kernel is a kernel, whose size can be bounded by a polynomial in the parameter.

A polynomial parameter transformation from a parameterized problem ${\mathcal {P}}$ to a parameterized problem ${\mathcal {Q}}$ is a parameterized reduction from ${\mathcal {P}}$ to ${\mathcal {Q}}$ that maps instances $({\mathcal {I}},k)$ of ${\mathcal {P}}$ to instances $({\mathcal {I}}',k')$ of ${\mathcal {Q}}$ with the additional property that

• 1. $({\mathcal {I}}',k')$ can be computed in time that is polynomial in $|{\mathcal {I}}|+k$, and

• 2. $k'$ is bounded by some polynomial p of k.

Proposition 1

[2, Proposition 1] Let ${\mathcal {P}}$ and ${\mathcal {Q}}$ be two parameterized problems such that there is a polynomial parameter transformation from ${\mathcal {P}}$ to ${\mathcal {Q}}$. Then, if ${\mathcal {Q}}$ has a polynomial kernel also ${\mathcal {P}}$ has a polynomial kernel.

In the following we will introduce another tool called cross-compositions, introduced by [8], for showing lower bounds for the size of kernels. An equivalence relation ${\mathcal {R}}$ on $\varSigma ^*$ is called a polynomial equivalence relation if the following two conditions hold:

• 1. There is an algorithm that given two strings $x,y \in \varSigma ^*$ decides whether x and y belong to the same equivalence class in $(|x|+|y|)^{O(1)}$ time.

• 2. For any finite set $S \subseteq \varSigma ^*$ the equivalence relation ${\mathcal {R}}$ partitions the elements of S into at most $(\max _{s \in S}|s|)^{O(1)}$ classes.

Let $L \subseteq \varSigma ^*$ be an (unparameterized) problem and let ${\mathcal {P}}\subseteq \varSigma ^* \times {\mathbb {N}}$ be a parameterized problem. We say that L AND-cross-composes into ${\mathcal {P}}$ if there is a polynomial equivalence relation ${\mathcal {R}}$ and an algorithm which, given t instances $(x_1,\dotsc ,x_t)$ of L belonging to the same equivalence class of ${\mathcal {R}}$, computes an instance $(x,k) \in \varSigma ^* \times {\mathbb {N}}$ of ${\mathcal {P}}$ in time polynomial in $\sum _{i=1}^t|x_i|$ such that:

• 1. $(x,k) \in {\mathcal {P}}$ if and only if $x_i \in L$ for every i with $1 \le i \le t$,

• 2. k is bounded by a polynomial in $(\max _{i=1}^t|x_i|)+\log t$.

Proposition 2

[8, Corollary 3.6] If an NP-hard language L AND-cross-composes into the parameterized problem ${\mathcal {P}}$, then ${\mathcal {P}}$ does not admit a polynomial kernel unless ${{\textsf {coNP}} \subseteq {\textsf {NP}}/poly }$.

2.3 Integer Linear Programming

Our algorithms use an Integer Linear Programming (ILP) subroutine. ILP is a well-known framework for formulating problems and a powerful tool for the development of fixed-parameter algorithms for optimization problems.

Definition 1

(p-Variable Integer Linear Programming Optimization) Let $A\in {\mathbb {Z}}^{q\times p}, b\in {\mathbb {Z}}^{q\times 1}$ and $c\in {\mathbb {Z}}^{1\times p}$. The task is to find a vector $x\in {\mathbb {Z}}^{p\times 1}$ which minimizes the objective function $c\times {\bar{x}}$ and satisfies all q inequalities given by A and b, specifically satisfies $A\cdot {\bar{x}}\ge b$. The number of variables p is the parameter (Fig. 1).

Fig. 1

A graph G and a width-3 treecut decomposition of G, including the torso-size (left value) and adhesion (right value) of each node

Lenstra [36] showed that p -ILP, together with its optimization variant p -OPT-ILP (defined above), are in FPT. His running time was subsequently improved by Kannan [31] and Frank and Tardos [21] (see also [20]).

Proposition 3

([20, 21, 31, 36]) p-OPT-ILP can be solved in time $O(p^{2.5p+o(p)}\cdot L)$, where L is the number of bits in the input.

2.4 Treecut Width

The notion of treecut decompositions was first proposed by Wollan [45], see also [37]. A family of subsets $X_1, \ldots , X_{k}$ of X is a near-partition of X if they are pairwise disjoint and $\bigcup _{i=1}^{k} X_i=X$, allowing the possibility of $X_i=\emptyset$.

Definition 2

A treecut decomposition of G is a pair $(T,{\mathcal {X}})$ which consists of a rooted tree T and a near-partition ${\mathcal {X}}=\{X_t\subseteq V(G): t\in V(T)\}$ of V(G). A set in the family ${\mathcal {X}}$ is called a bag of the treecut decomposition.

For any node t of T other than the root r, let $e(t)=ut$ be the unique edge incident to t on the path to r. Let $T^u$ and $T^t$ be the two connected components in $T-e(t)$ which contain u and t, respectively. Note that $(\bigcup _{q\in T^u} X_q, \bigcup _{q\in T^t} X_q)$ is a near-partition of V(G), and we use ${\mathbf {cut}}(t)$ to denote the set of edges with one endpoint in each part. We define the adhesion of t (${\mathbf {adh}}_T(t)$ or ${\mathbf {adh}}(t)$ in brief) as $|{\mathbf {cut}}(t)|$; if t is the root, we set ${\mathbf {adh}}_T(t)=0$ and ${\mathbf {cut}}(t)=\emptyset$.

The torso of a treecut decomposition $(T,{\mathcal {X}})$ at a node t, written as $H_t$, is the graph obtained from G as follows. If T consists of a single node t, then the torso of $(T,{\mathcal {X}})$ at t is G. Otherwise let $T_1, \ldots , T_{\ell }$ be the connected components of $T-t$. For each $i=1,\ldots , \ell$, the vertex set $Z_i\subseteq V(G)$ is defined as the set $\bigcup _{b\in V(T_i)}X_b$. The torso $H_t$ at t is obtained from G by consolidating each vertex set $Z_i$ into a single vertex $z_i$ (this is also called shrinking in the literature). Here, the operation of consolidating a vertex set Z into z is to substitute Z by z in G, and for each edge e between Z and $v\in V(G)\setminus Z$, adding an edge zv in the new graph. We note that this may create parallel edges.

The operation of suppressing (also called dissolving in the literature) a vertex v of degree at most 2 consists of deleting v, and when the degree is two, adding an edge between the neighbors of v. Given a connected graph G and $X\subseteq V(G)$, let the 3-center of (G, X) be the unique graph obtained from G by exhaustively suppressing vertices in $V(G) \setminus X$ of degree at most two. Finally, for a node t of T, we denote by ${\tilde{H}}_t$ the 3-center of $(H_t,X_t)$, where $H_t$ is the torso of $(T,{\mathcal {X}})$ at t. Let the torso-size ${\mathbf {tor}}(t)$ denote $|{\tilde{H}}_t|$.

Definition 3

The width of a treecut decomposition $(T,{\mathcal {X}})$ of G is defined as $\max _{t\in V(T)}\{ {\mathbf {adh}}(t), {\mathbf {tor}}(t) \}$. The treecut width of G, or ${\mathbf {tcw}}(G)$ in short, is the minimum width of $(T,{\mathcal {X}})$ over all treecut decompositions $(T,{\mathcal {X}})$ of G.

We conclude this subsection with some notation related to treecut decompositions. Given a tree node t, let $T_t$ be the subtree of T rooted at t. Let $Y_t=\bigcup _{b\in V(T_t)} X_b$, and let $G_t$ denote the induced subgraph $G[Y_t]$. The depth of a node t in T is the distance of t from the root r. The vertices of $\partial _t=\partial _G(Y_t)$ are called the border at node t.

A node $t\ne r$ in a rooted treecut decomposition is thin if ${\mathbf {adh}}(t)\le 2$ and bold otherwise. For a node t, we let $B_t=\{\,b{\text { is a child of}}\,t\;{|}\;|N(Y_b)|\le 2\wedge N(Y_b)\subseteq X_t \,\}$ denote the set of thin children of t whose neighborhood is a subset of $X_t$, and we let $A_t=\{\,a{\text { is a child of} }\,t\;{|}\;a\not \in B_t \,\}$ be the set of all other children of t.

While it is not known how to compute optimal treecut decompositions efficiently, there exists a fixed-parameter 2-approximation algorithm which fully suffices for our purposes.

Theorem 1

([32]) There exists an algorithm that takes as input an n-vertex graph G and integer k, runs in time $2^{{{\mathcal {O}}}(k^2)} n^2$, and either outputs a treecut decomposition of G of width at most 2k or correctly reports that ${\mathbf {tcw}}(G)> k$.

A treecut decomposition $(T,{\mathcal {X}})$ is nice if it satisfies the following condition for every thin node $t\in V(T)$: $N(Y_t)\cap \bigcup _{b{\textit{ is a sibling of}}\,t}Y_b=\emptyset$. The intuition behind nice treecut decompositions is that we restrict the neighborhood of thin nodes in a way which facilitates dynamic programming.

Lemma 1

([24]) There exists a cubic-time algorithm which transforms any rooted treecut decomposition $(T,{\mathcal {X}})$ of G into a nice treecut decomposition of the same graph, without increasing its width or number of nodes.

The following property of nice treecut decompositions will be crucial for our algorithm.

Lemma 2

([24]) Let t be a node in a nice treecut decomposition of width k. Then $|A_t|\le 2k+1$.

For completeness and self-containedness, we also provide the proofs of the previous two lemmata in an appendix. We refer to previous work [24, 32, 37, 45] for a more detailed comparison of treecut width to other parameters. Here, we mention only that treecut width lies “between” treewidth and treewidth plus maximum degree.

Proposition 4

[24, 37, 45] Let ${\mathbf {tw}}(G)$ denote the treewidth of G and ${\mathbf {degtw}}(G)$ denote the maximum over ${\mathbf {tw}}(G)$ and the maximum degree of a vertex in G. Then ${\mathbf {tw}}(G)\le 2{\mathbf {tcw}}(G)^2+3{\mathbf {tcw}}(G)$, and ${\mathbf {tcw}}(G)\le 4{\mathbf {degtw}}(G)^2$.

3 Hardness Results

In this section we show that BDD is W[1]-hard parameterized by a vertex deletion set to trees of height at most three, i.e., a subset D of the vertices of the graph such that every component in the graph, after removing D, is a tree of height at most three. On the way towards this result, we provide hardness results for several interesting versions of the multidimensional subset sum problem (parameterized by the number of dimensions) which we believe are interesting in their own right. In particular, we note that the hardness results also hold for the well-known and more general multidimensional knapsack problem [22].

Our first auxiliary result shows hardness for the following problem.

Lemma 3

MSS is W[1]-hard even if all integers in the input are given in unary.

Proof

We prove the lemma by a parameterized reduction from Multicolored Clique, which is well-known to be W[1]-complete [43]. Given an integer k and a k-partite graph G with partition $V_1,\dotsc ,V_k$, the Multicolored Clique problem asks whether G contains a k-clique. In the following we denote by $E_{i,j}$ the set of all edges in G with one endpoint in $V_i$ and the other endpoint in $V_j$, for every i and j with $1\le i < j \le k$. To show the lemma, we will construct an instance ${\mathcal {I}}=(k',S,t)$ of MSS in polynomial time with $k'=2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k$ and all integers in ${\mathcal {I}}$ are bounded by a polynomial in |V(G)| such that G has a k-clique if and only if ${\mathcal {I}}$ has a solution.

For our reduction we will employ so called Sidon sequences of natural numbers. A Sidon sequence is a sequence of natural numbers such that the sum of every two distinct numbers in the sequence is unique. For our reduction we will need a Sidon sequence of |V(G)| natural numbers, i.e., containing one number for each vertex of G. Since the numbers in the Sidon sequence will be used as numbers in ${\mathcal {I}}$, we need to ensure that the largest of these numbers is bounded by a polynomial in |V(G)|. Indeed [18] shows that a Sidon sequence containing n elements and whose largest element is at most $2p^2$, where p is the smallest prime number larger or equal to n, can be constructed in polynomial time. Together with Bertrand’s postulate [1], which states that for every natural number n there is a prime number between n and 2n, we obtain that a Sidon sequence containing |V(G)| numbers and whose largest element is at most $8|V(G)|^2$ can be found in polynomial time. In the following we will assume that we are given such a Sidon sequence ${\mathcal {S}}$ and we denote by ${\mathcal {S}}(i)$ the i-th element of ${\mathcal {S}}$ for any i with $1 \le i \le |V(G)|$. Moreover, we denote by $\max ({\mathcal {S}})$ and $\max _2({\mathcal {S}})$ the largest element of ${\mathcal {S}}$ and the maximum sum of any two numbers in ${\mathcal {S}}$, respectively. We will furthermore assume that the vertices of G are identified by numbers between 1 and |V(G)| and therefore ${\mathcal {S}}(v)$ is properly defined for every $v \in V(G)$.

We are now ready to construct the instance ${\mathcal {I}}=(k',S,t)$. We set $k'=2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k$ and t is the vector whose first $\left( {\begin{array}{c}k\\ 2\end{array}}\right)$ entries are all equal to $\max _2({\mathcal {S}})+1$ and whose remaining $\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k$ entries are all equal to 1. For every i and j with $1 \le i < j \le k$, we will use I(i, j) as a means of enumerating the indices in a sequence of two-element tuples; formally, $I(i,j)=(\sum _{l=1}^{l<i}(k-l))+(j-1)$. Note that the vector t and its indices can then be visualized as follows:

$$\begin{aligned} t=(\underbrace{{\max _2}({\mathcal {S}})+1, \dotsc , \max _2({\mathcal {S}})+1}_{I(1,2), I(1,3), \dotsc , I(k-1,k)}, \underbrace{1, \dotsc , 1}_{\left( {\begin{array}{c}k\\ 2\end{array}}\right) +I(1,2), \dotsc , \left( {\begin{array}{c}k\\ 2\end{array}}\right) +I(k-1,k)}, \underbrace{1, \dotsc , 1}_{2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +1,\dotsc , 2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k)}) \end{aligned}$$

We now proceed to the construction of S, which will contain one element for each edge and for each vertex in G. In particular, the set S of item-vectors contains the following elements:

• for every i with $1 \le i \le k$ and every $v \in V_i$, a vector $s_v$ such that all entries with index in $\{\,I(l,r) \;{|}\;1 \le l< r \le k \wedge l=i \,\}\cup \{\,I(l,r) \;{|}\;1\le l < r \le k \wedge r=i\,\}$ are equal to ${\mathcal {S}}(v)$ (informally, this corresponds to all indices where at least one element of the tuple (l, r) is equal to i), the $2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +i$-th entry is equal to 1, and all other entries are equal to 0. The following illustrates $s_v$ for the case that $k=4$ and $i=2$:

  $$\begin{aligned} s_v=(\underbrace{{\mathcal {S}}(v),0,0,{\mathcal {S}}(v),{\mathcal {S}}(v),0}_{I(1,2), I(1,3), \dotsc ,I(3,4)}, \underbrace{0, \dotsc , 0}_{I(1,2), I(1,3), \dotsc ,I(3,4)}, \underbrace{0,1,0,0}_{2\left( {\begin{array}{c}4\\ 2\end{array}}\right) +1,\dotsc , 2\left( {\begin{array}{c}4\\ 2\end{array}}\right) +4)}) \end{aligned}$$

• for every i and j with $1\le i < j \le k$ and every $e=\{u,v\} \in E(i,j)$, a vector $s_e$ such that the entry I(i, j) is equal to $(\max _2({\mathcal {S}})+1)-({\mathcal {S}}(u)+{\mathcal {S}}(v))$, the $\left( {\begin{array}{c}k\\ 2\end{array}}\right) +I(i,j)$-th entry is equal to 1, and all other entries are equal to 0. The following illustrates the vector $s_e$ for the case that $k=4$, $i=2$, and $j=3$:

  $$\begin{aligned} s_e=(\underbrace{0,0,0,\max _{2}({\mathcal {S}})+1-({\mathcal {S}}(u)+{\mathcal {S}}(v)),0,0}_{I(1,2), I(1,3), \dotsc ,I(3,4)}, \underbrace{0,0,0,1,0, 0}_{I(1,2), \dotsc ,I(3,4)}, \underbrace{0,\dotsc ,0}_{2\left( {\begin{array}{c}4\\ 2\end{array}}\right) +1,\dotsc , 2\left( {\begin{array}{c}4\\ 2\end{array}}\right) +4)}) \end{aligned}$$

This completes the construction of ${\mathcal {I}}$. It is clear that ${\mathcal {I}}$ can be constructed in polynomial time and moreover every integer in ${\mathcal {I}}$ is at most $\max _2({\mathcal {S}})+1$ and hence polynomially bounded in |V(G)|. Intuitively, the construction relies on the fact that since the sum of each pair of vertices is unique, we can uniquely associate each pair with an edge between these vertices whose value will then be the remainder to the global upper-bound of $\max _2({\mathcal {S}})$.

It remains to show that G has k-clique if and only if ${\mathcal {I}}$ has a solution. Towards showing the forward direction, let C be a k-clique in G with vertices $v_1,\dotsc ,v_k$ such that $v_i \in V_i$ for every i with $1\le i \le k$. We claim that the subset $S'=\{\,s_v \;{|}\;v \in V(C) \,\}\cup \{\,s_e \;{|}\;e \in E(C) \,\}$ of S is a solution for ${\mathcal {I}}$. Let $t'$ be the vector $\sum _{s \in S'}s$. Because C contains exactly one vertex from every $V_i$ and exactly one edge from every $E_{i,j}$, it holds that $t'[l]=t[l]=1$ for every index l with $\left( {\begin{array}{c}k\\ 2\end{array}}\right) < l \le 2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k$. Moreover, for every i and j with $1 \le i < j \le k$, the vectors $s_{v_i}$, $s_{v_j}$, and $s_{e_{i,j}}$ are the only vectors in $S'$ with a non-zero entry at the I(i, j)-th position. Hence $t'[I(i,j)]=s_{v_i}[I(i,j)]+s_{v_j}[I(i,j)]+s_{e_{i,j}}[I(i,j)]$, which because $s_{v_i}[I(i,j)]={\mathcal {S}}(v_i)$, $s_{v_j}[I(i,j)]={\mathcal {S}}(v_j)$, and $s_{e_{i,j}}[I(i,j)]=(\max _2({\mathcal {S}})+1)-({\mathcal {S}}(v_i)+{\mathcal {S}}(v_j))$ is equal to ${\mathcal {S}}(v_i)+{\mathcal {S}}(v_j)+(\max _2({\mathcal {S}})+1)-({\mathcal {S}}(v_i)+{\mathcal {S}}(v_j))=\max _2({\mathcal {S}})+1=t[I(i,j)]$, as required.

Towards showing the reverse direction, let $S'$ be a subset of S such that $\sum _{s \in S'}s=t$. Because the last k entries of t are equal to 1 and for every i with $1 \le i \le k$, it holds that the only vectors in S that have a non-zero entry at the i-th last position are the vectors in $\{\,s_v \;{|}\;v \in V_i\,\}$, it follows that $S'$ contains exactly one vector say $s_{v_i}$ in $\{\,s_v \;{|}\;v \in V_i\,\}$ for every i with $1 \le i \le k$. Using a similar argument for the entries of t with indices between $\left( {\begin{array}{c}k\\ 2\end{array}}\right) +1$ and $2\left( {\begin{array}{c}k\\ 2\end{array}}\right)$, we obtain that $S'$ contains exactly one vector say $e_{i,j}$ in $\{\,s_e \;{|}\;e \in E_{i,j}\,\}$ for every i and j with $1 \le i < j \le k$. Consequently, $S'=\{s_{v_1},\dotsc ,s_{v_k}\}\cup \{\,e_{i,j} \;{|}\;1 \le i < j \le k \,\}$. We claim that $\{v_1,\dotsc ,v_k\}$ forms a k-clique in G, i.e., for every i and j with $1 \le i < j \le k$, it holds that $e_{i,j}=\{v_i,v_j\}$. To see this consider the I(i, j)-th entry of $t'=\sum _{s\in S'}s$. The only vectors in $S'$ having a non-zero contribution towards $t'[I(i,j)]$ are the vectors $s_{v_i}$, $s_{v_j}$, and $s_{e_{i,j}}$. Because $s_{v_i}[I(i,j)]={\mathcal {S}}(v_i)$, $s_{v_j}[I(i,j)]={\mathcal {S}}(v_j)$, and $t'[I(i,j)]=t[I(i,j)]=\max _2({\mathcal {S}})+1$, we obtain that $s_{e_{i,j}}[I(i,j)]=(\max _2({\mathcal {S}})+1)-({\mathcal {S}}(v_i)+{\mathcal {S}}(v_j))$. Because ${\mathcal {S}}$ is Sidon sequence and thus the sum $({\mathcal {S}}(v_i)+{\mathcal {S}}(v_j))$ is unique, we obtain that $e_{i,j}=\{v_i,v_j\}$, as required. $\square$

Observe that because any solution $S'$ of the constructed instance in the previous lemma must be of size exactly $k'=2\left( {\begin{array}{c}k\\ 2\end{array}}\right) +k$, it follows that the above proof also shows W[1]-hardness of the following problem.

Corollary 1

RMSS is W[1]-hard even if all integers in the input are given in unary.

Using an fpt-reduction from the above problem, we will now show that also the following more relaxed version is W[1]-hard.

Lemma 4

MRSS is W[1]-hard even if all integers in the input are given in unary.

Proof

We prove the lemma by a parameterized reduction from RMSS, which is W[1]-hard even if all integers in the input are given in unary because of Corollary 1. Namely, given an instance ${\mathcal {I}}=(k,S,t,k')$ of RMSS we construct an equivalent instance ${\overline{{\mathcal {I}}}}=(2k,{\overline{S}},{\overline{t}},k')$ of MRSS in polynomial time such that all integers in ${\overline{{\mathcal {I}}}}$ are bounded by a polynomial of the integers in ${\mathcal {I}}$.

The set ${\overline{S}}$ contains one vector ${\overline{s}}$ for every vector $s \in S$ with ${\overline{s}}[i]=s[i]$ and ${\overline{s}}[k+i]=t[i]-s[i]$ for every i with $1\le i \le k$. Finally, the target vector ${\overline{t}}$ is defined by setting ${\overline{t}}[i]=t[i]$ and ${\overline{t}}[k+i]=(k'-1)\cdot t[i]$ for every i with $1 \le i \le k$. This concludes the construction of ${\overline{{\mathcal {I}}}}$. Clearly, ${\overline{{\mathcal {I}}}}$ can be constructed in polynomial time and the values of all numbers in ${\overline{{\mathcal {I}}}}$ are bounded by a polynomial of the maximum number in ${\mathcal {I}}$. It remains to show that ${\mathcal {I}}$ has a solution if and only if ${\overline{{\mathcal {I}}}}$ has a solution.

Towards showing the forward direction, let $S' \subseteq S$ be a solution for ${\mathcal {I}}$, i.e., $|S'|=k'$ and $\sum _{s\in S'}s=t$. We claim that the set ${\overline{S}}'=\{\,{\overline{s}} \;{|}\;s\in S'\,\}$ is a solution for ${\overline{{\mathcal {I}}}}$. Because ${\overline{s}}[i]=s[i]$ and ${\overline{t}}[i]=t[i]$ for every $s \in S$ and i with $1 \le i \le k$, it follows that $\sum _{{\overline{s}}\in {\overline{S}}'}{\overline{s}}[i]={\overline{t}}[i]$ for every i as above. Moreover, for every i with $1 \le i \le k$, it holds that $\sum _{{\overline{s}}\in {\overline{S}}'}{\overline{s}}[k+i]=k'\cdot t[i] - \sum _{{\overline{s}}\in {\overline{S}}'}{\overline{s}}[i]=k'\cdot t[i] - t[i]=(k'-1)t[i]={\overline{t}}[k+i]$, showing that ${\overline{S}}$ is a solution for ${\overline{{\mathcal {I}}}}$.

Towards showing the reverse direction, let ${\overline{S}}' \subseteq {\overline{S}}$ be a solution for ${\mathcal {I}}'$, i.e., $|{\overline{S}}'|\le k'$ and $\sum _{{\overline{s}}\in {\overline{S}}'}{\overline{s}}\ge {\overline{t}}$. We claim that the set $S'=\{\,s \;{|}\;{\overline{s}}\in {\overline{S}}'\,\}$ is a solution for ${\mathcal {I}}$.

Because ${\overline{S}}'$ is a solution for ${\mathcal {I}}'$, we obtain for every i with $1 \le i \le k$ that:

• (1) $\sum _{s \in {\overline{S}}'}{\overline{s}}[i]\ge t[i]$, which because $s[i]={\overline{s}}[i]$ implies that $\sum _{s \in S'}s[i]\ge t[i]$,

• (2) $\sum _{{\overline{s}} \in {\overline{S}}'}{\overline{s}}[k+i]\ge (k-1)t[i]$, which because ${\overline{s}}[k+i]=t[i]-s[i]$ implies that $|S'|t[i]-\sum _{s\in S'}s[i]\ge (k'-1)t[i]$. First, since we can assume that $t[i]>0$ and therefore also $\sum _{s\in S'}s[i]>0$ by (1), observe that $|S'|> k'-1$ and in particular $|S'|=k'$. Then by using this, we obtain that $k't[i]-\sum _{s\in S'}s[i]\ge (k'-1)t[i]$ which implies $t[i]\ge \sum _{s\in S'}s[i]$.

It follows from (1) and (2) that $\sum _{s\in S'}s[i]=t[i]$ and hence $S'$ is a solution for ${\mathcal {I}}$ of size $k'$, as required. $\square$

We are now ready to show our main hardness result for BDD using a reduction from MRSS.

Theorem 2

BDD is W[1]-hard parameterized by the size of a vertex deletion set into trees of height at most 3.

Proof

We prove the theorem by a parameterized reduction from MRSS. Namely, given an instance ${\mathcal {I}}=(k,S,t,k')$ of MRSS we construct an equivalent instance ${\mathcal {I}}'=(G,d,\ell )$ of BDD such that G has a FVS D of size $k\cdot (k'+1)$. The core idea of the reduction relies on transforming the decision of whether to select a vector into a solution $S'$ for ${\mathcal {I}}$ into the decision of whether to resolve a tree gadget in G in one of two possible ways.

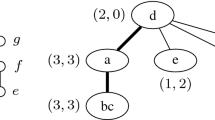
See Fig. 2, which provides an illustration of the construction. The set D consists of $(k'+1)$ vertices $d_i^1,\dotsc ,d_i^{k'+1}$ for every i with $1\le i \le k$. Moreover, for every $s \in S$ we introduce the gadget G(s) defined as follows. G(s) consists of $\max (s)$, where $\max (s)$ is the value of the largest coordinate of s, stars with centers $c_1^s,\dotsc ,c_{\max (s)}^s$. For now we attach one leaf denoted $l_i^s$ to every such center $c_i^s$; we will later attach additional “unnamed” leaves to ensure that every center has exactly $d+1$ leaves, however, d is to be determined later.

Fig. 2

Example of the gadget in Theorem 2

Additionally, G(s) has a root vertex, denoted by $r^s$, that has an edge to every center vertex $c_i^s$. Finally, we add edges between the leaves $l_1^s,\dotsc ,l_{\max (s)}^s$ and the vertices in D such that for every i and j with $1 \le i \le k$ and $1 \le j \le k'+1$, it holds that $d_i^j$ has s[i] neighbors among the leaves $l_1^s,\dotsc ,l_{\max (s)}^s$ of G(s). Clearly this is always possible and can be done in an arbitrary manner.

We set d to be the maximum degree of the part of G constructed so far (note that this maximum is reached by one of the vertices in D). We now add d leaves to each center $c_i^s$ ensuring that every such center has exactly $d+1$ leaves. Moreover, we now ensure that for every i and j with $1\le i \le k$ and $1\le j \le k'+1$, the vertex $d_i^j$ has degree $d+t[i]$ in G by attaching a appropriate number of leaves to $d_i^j$. Finally, we set $\ell$ to be $(\sum _{s \in S}\max (s))+k'$. This completes the construction of ${\mathcal {I}}'$. Clearly, ${\mathcal {I}}'$ can be constructed in polynomial time. Moreover, $|D|\le k\cdot (k'+1)$ and each component of $G - D$ is a tree with height at most 3. It remains to show the equivalence between ${\mathcal {I}}$ and ${\mathcal {I}}'$.

Towards showing the forward direction, let $S' \subseteq S$ be a solution for ${\mathcal {I}}$, i.e., $|S'|\le k'$ and $\sum _{s \in S'}s\ge t$. We construct a solution $V' \subseteq V(G)$ from $S'$ as follows. For every $s \in S\setminus S'$, $V'$ contains the center vertices $c_1^s,\dotsc ,c_{\max (s)}^s$ from G(s) and for every $s \in S'$, $V'$ contains the root vertex $r^s$ and the leaf vertices $l_1^s,\dotsc ,l_{\max (s)}^s$ from G(s). Clearly, $|V'|=\sum _{s\in S}\max (s)+|S'|\le \sum _{s\in S}\max (s)+k'=\ell$. Moreover, since for every $s \in S$, the only vertices in G(s), whose degree exceeds d in G, are the centers of the stars, we obtain that the degree of the vertices in G(s) w.r.t. $G- V'$ is at most d. Finally, for every i and j with $1 \le i \le k$ and $1\le j \le k'$, the degree of the vertex $d_i^j$ in $G - V'$ is equal to $d+t[i]-\sum _{s\in S'}s[i]\le d$, as required.

Before we continue with the proof for the reverse direction, we will prove a crucial property of the gadget G(s) for any $s \in S$. $\square$

Claim 1

If ${\mathcal {I}}=(G,d,\ell )$ has a solution, then there is a solution $V' \subseteq V(G)$ such that for every $s \in S$, it holds that either:

• (G1) $V'\cap G(s)=\{c_1^s,\ldots ,c_{\max (s)}^s\}$, or

• (G2) $V'\cap G(s)=\{r^s, l_1^s,\ldots ,l_{\max (s)}^s\}$.

Proof

Let $V' \subseteq V(G)$ be a solution for ${\mathcal {I}}$ and let $s \in S$. It is easy to see that if $|V'\cap G(s)|=\max (s)$ then $V' \cap G(s)$ must be equal to $\{c_1^s,\ldots ,c_{\max (s)}^s\}$. So suppose that $|V'\cap G(s)|> \max (s)$. We claim that then $V''=(V'\setminus G(s)) \cup \{r^s, l_1^s,\ldots ,l_{\max (s)}^s\}$ is also a solution for ${\mathcal {I}}$. Clearly, $|V''|\le |V'|\le \ell$ and every vertex in G(s) has degree at most d in $G - V''$. Finally, since the leaf vertices $l_1^s,\ldots ,l_{\max (s)}^s$ are the only vertices in G(s) with neighbors in D, it holds that the degree of any vertex in $D- V''$ in $G - V''$ is at most equal to its degree in $G - V'$ and since $V'$ is a solution so is $V''$. $\square$

Towards showing the reverse direction of the claim, let $V' \subseteq V(G)$ be a solution for ${\mathcal {I}}'$, i.e., $|V'|\le \ell$ and every vertex in $G - V'$ has degree at most d. Because of Claim 1, we can assume that $V'$ satisfies (G1) or (G2) for every $s \in S$. We claim that the set $S' \subseteq S$ containing all $s \in S$ such that $V'$ satisfies (G2) is a solution for ${\mathcal {I}}$. Because $|V'|\le \ell =\sum _{s\in S}\max (s)+k'$ and $V'$ contains at least $\max (s)$ vertices from every gadget G(s) for any $s \in S$, we obtain that $|S'|\le k'$. It hence only remains to show that $\sum _{s\in S'}s\ge t$. Because $|V'|\le \ell =\sum _{s\in S}\max (s)+k'$ and $V'$ contains at least $\max (s)$ vertices from every gadget G(s) for any $s \in S$, it follows that $|D\cap V'|\le k'$. Hence for every i with $1 \le i \le k$, there is a j with $1 \le j \le k'+1$ such that $d_i^j \notin V'$. Consequently, $V'$ must contain at least t[i] neighbors of $d_i^j$. Since the only neighbors of a vertex $d_i^j$ (other than leaves, which we can assume are not contained in $V'$) are the leaf vertices of the gadgets G(s), all these neighbors must lie in the gadgets G(s) for some $s \in S'$. Since the number of neighbors of $d_i^j$ in $V' \cap G(s)$ for such an $s \in S'$ is equal to s[i], we obtain that $\sum _{s\in S'}s[i]\ge t[i]$. Because the same argument applies to every i with $1 \le i \le k$, we obtain that $\sum _{s\in S'}s\ge t$ and hence $S'$ is a solution for ${\mathcal {I}}$. $\square$

Clearly trees of height at most three are trivially acyclic. Moreover, it is easy to verify that such trees have pathwidth [33] and treedepth [40] at most three, which implies:

Corollary 2

BDD is W[1]-hard parameterized by any of the following parameters:

• the size of a feedback vertex set,

• the pathwidth and treedepth of the input graph,

• the size of a minimum set of vertices whose deletion results in components of pathwidth/treedepth at most three.

4 Solving BDD using Treecut Width

The goal of this section is to provide a fixed-parameter algorithm for BDD parameterized by treecut width. The core of the algorithm is a dynamic programming procedure which runs on a nice treecut decomposition $(T,{\mathcal {X}})$ of the input graph G. Recall that for $t \in V(T)$, $G[Y_t]=G_t$ denotes the subgraph of G induced on all vertices that appear below t, i.e., in a bag in the subtree rooted at t. Moreover, recall that $\partial _t$ denotes the border of $G[Y_t]$, i.e., the vertices which have a neighbor outside of $G[Y_t]$.

4.1 Overview

First we define the data table the algorithm is going to dynamically compute for individual nodes of the treecut decomposition. For each node $t\in V(T)$, the table is going to contain two components, which we will call the universal cost $u_t$ and the specific cost $s_t$. Informally, the universal cost captures the minimum number of vertices which need to be deleted from $Y_t$ to satisfy the degree bound in $G_t$. The specific cost captures how many more vertices (than the universal cost) we need to delete in order to satisfy the degree bound in $G_t$ when we also place restrictions on how $G_t$ will interact with the rest of the graph. We formalize these notions below.

Let us fix an instance $(G,d,\ell )$ of BDD and a treecut decomposition $(T,{\mathcal {X}})$ of G of width at most k and rooted at r. A configuration $\delta$ of a graph H with a designated vertex-subset Z is a mapping $Z\mapsto [k]\cup \{\text {del}\}$, i.e., each vertex in Z receives a value up to the treecut width or “del”. Intuitively, configurations are going to be used to place additional restrictions on the deletion sets we are interested in. We let ${\mathbf {bdd}}(H,Z,\delta )$ denote the minimum size of a vertex set $W\subseteq V(H)$ such that:

• (A) $v\in W\cap Z$ if and only if $\delta (v)={\text {del}}$, and

• (B) for each $v\in Z\setminus W$, the degree of v in $H-W$ is at most $d-\delta (v)$,

• (C) for each $v\in V(H)\setminus (Z\cup W)$, the degree of v in $H-W$ is at most d.

Figure 3 depicts an illustration of ${\mathbf {bdd}}(H,Z,\delta )$. Informally, bdd captures the size of a minimum deletion set which intersects the designated subset precisely in the vertices specified by $\delta$, and for the remainder of the designated subset it overshoots the degree bound by a buffer specified by $\delta$. If ${\mathbf {bdd}}(H,Z,\delta )$ is not defined (which may happen, e.g., if $d<|Z|$), we formally set ${\mathbf {bdd}}(H,Z,\delta )=\infty$. For each node $t\in V(T)$, we can now define:

• $u_t={\mathbf {bdd}}(G_t,\emptyset ,\emptyset )$, and

• for each $\delta :\partial _t \rightarrow [k]\cup \{\text {del}\}$ such that each $v\in \partial _t$ is mapped to ${\text {del}}$ or to an integer $i\le |N(v)\setminus Y_t|$, we let $s'_t(\delta )={\mathbf {bdd}}(G_t,\partial _t,\delta )-u_t$.

We proceed with a few observations. Naturally, the value of $u_t$ can be much larger than k (as an example, consider a collection of disjoint stars), and this is not an issue for our algorithm. Furthermore, for every $\delta$ it holds that $0\le s'_t(\delta )$, since $u_t\le {\mathbf {bdd}}(G_t,\partial _t,\delta )$; notice that $u_t$ attains the value of the smallest deletion set for $G_t$, while ${\mathbf {bdd}}(G_t,\partial _t,\delta )$ attains the value of a smallest deletion set for $G_t$ which satisfies certain additional restrictions.

Crucially, the value of $s'_t(\delta )$ can be much larger than k, and this represents a significant obstacle for our algorithm. The role of the specific cost in the dynamic programming procedure is to capture how a node may interact with the solution and how such interactions affect the size of a deletion set. The algorithm relies heavily on having only a bounded number of possible interactions in order to achieve its run-time bounds. Luckily, we will prove that any value of $s'_t(\delta )$ exceeding k must lead to a dead end and can be disregarded. Note that Lemma 5 also showcases how $s'_t$ relates to a solution in G, and the introduced notion of $\delta ^t_S$ defined in the statement of the lemma is also useful later on.

Fig. 3

Illustration of the set ${\mathbf {bdd}}(H,Z,\delta )$. The dotted edges are not considered for the degree of a node v

Lemma 5

Let S be a minimum-size bounded degree deletion set in G. Let $\delta ^t_S$ be defined over $\partial _t$ as follows: $\delta ^t_S(v)= {\text {del}}$ if $v\in S$, and otherwise $\delta ^t_S(v)= |(N(v)\setminus Y_t)\setminus S|$. Then $s'_t(\delta ^t_S)\le |N(Y_t)|\le k$.

Proof

For brevity, let $q=|N(Y_t)|$. The fact that $q\le k$ follows immediately from the bound on the adhesion of t, hence we only need to prove that $s'_t(\delta ^t_S)\le q$. So, assume for a contradiction that $s'_t(\delta ^t_S)> q$. Let P be a witness for the value of $u_t$, i.e., let P be a minimum-cardinality vertex subset of $G_t$ such that the maximum degree in $G_t-P$ is at most d. Observe that $|P\cup N(Y_t)|=u_t+q$. Now consider the set $S'=(S\setminus Y_t)\cup P\cup N(Y_t)$. First of all, note that $|S'|<|S|$, since we obtained $S'$ from S by removing more than $u_t+q$ vertices (recall that, by our assumption, $s'_t(\delta ^t_S)> q$) and then adding back at most $u_t+q$ vertices. Second, we claim that $S'$ is also a bounded degree deletion set in G. Indeed, consider for a contradiction that $G-S'$ contains a vertex v of degree higher than d. Such a v cannot lie in $Y_t$ since P was a solution in $G_t$ and $N(Y_t)$ separates $G_t$ from the rest of G. On the other hand, v cannot lie outside of $Y_t$ due to the fact that S itself was a solution in $G[V(G)-Y_t]$. So the claim holds, and $S'$ contradicts the optimality of S. $\square$

Thanks to Lemma 5, we can safely focus our attention on those configurations $\delta$ where $s'_t(\delta )\le |N(Y_t)|$. In particular, let $s_t(\delta )$ be defined as follows.

$$\begin{aligned} s_t(\delta ) = {\left\{ \begin{array}{ll} s'_t(\delta ) &{} {\text { if} } s'_t(\delta )\le |N(Y_t)| \\ \infty &{} {\text { otherwise. }} \end{array}\right. } \end{aligned}$$

Observe that, unlike $s'_t$, the number of distinct possibilities of what a specific cost $s_t$ may look like is bounded by a function of k. The high-level strategy for the algorithm is now the following:

• 1. Compute $(u_t,s_t)$ when t is a leaf,

• 2. Compute $(u_t,s_t)$ when t is not a leaf, but the universal and specific costs are known for all of its children, and

• 3. Use the values $(u_r,s_r)$ at the root node $r \in T$.

As we will see below, points 1. and 3. are straightforward.

Observation 3

$(u_t,s_t)$ can be computed in time at most $2^{{{\mathcal {O}}}(k\cdot \log k)}$ if t is a leaf.

Proof

Recall that $|X_t|\le k$. To compute $u_t$ it suffices to exhaustively loop through all vertex subsets $L\subseteq X_t$ and check whether $G_t-L$ has degree at most d. Then $u_t$ is equal to the minimum size of such a subset. To compute $s_t$, we proceed similarly: for each configuration $\delta$ such that each $v\in \partial _t$ is mapped to ${\text {del}}$ or to an integer $i\le |N(v)\setminus Y_t|$, we exhaustively loop through all $L\subseteq X_t\setminus \partial _t$ in order to determine the value of ${\mathbf {bdd}}(G_t,\partial _t,\delta )$, and we then use that value and $u_t$ to determine $s_t(\delta )$. $\square$

Observation 4

$(G,d,\ell )$ is a YES-instance of BDD if and only if $u_r\le \ell$.

Given the above, the last remaining obstacle is handling point 2, i.e., the dynamic propagation of information from leaves to the root. This is also the by far most challenging part of the algorithm, and we will deal with it in the next subsection.

4.2 The Dynamic Step

Recalling that $u_t$ is an integer and $s_t$ a mapping from configurations to integers, we summarize the subproblem that corresponds to handling point 2:

Our strategy for dealing with BDD Join is to apply a 2-step approach. Figure 4 shows an illustration of the upcoming branching sets for a node t. Recall that $A_t$ and $B_t$ denote the set of all children of t which are bold and thin, respectively. First, we exhaustively loop over all options of how a deletion set candidate intersects with $X_t$ and the borders of nodes in $A_t$, resulting in a set of “templates” which provide us with additional information about a potential solution. Here the bound on $|A_t|$ provided in Lemma 2 will be crucial. Second, we use branching and network flows to find an optimal way of extending such a template to a solution which deals with $B_t$. In this step, we overcome the fact that there may be an unbounded number of children p in $B_t$ by “aggregating” them into types based on their $s_p$ component. Lemma 5 along with our definition of specific costs then guarantees that the number of aggregated types will depend only on k. Informally, if two nodes $p_1$, $p_2$ in $B_t$ have the same specific cost, then their behavior (“contribution”) to any solution is fully interchangeable. In particular, even if $p_1$, $p_2$ have different universal costs, both of these costs will need to be “paid” by every solution regardless of how the solution handles the borders of these nodes. We proceed by formalizing the algorithm for BDD Join.

Fig. 4

The three branching sets for a node $t \in V(T)$, first branch on $\partial _t$ (green), then on the boundaries of the bold nodes $A_t$ together with the “interior” of t (orange) and finally on the equivalence classes of $B_t$ (gray)

Lemma 6

BDD Join can be solved in time $2^{{{\mathcal {O}}}(k^2)}\cdot |B_t|^2$, where $|B_t|$ is upper-bounded by the number of children of t.

Proof

For technical reasons, we will show how to compute the value ${\mathbf {bdd}}(G_t,\partial _t,\delta )$ for each configuration $\delta$; clearly, this is sufficient to determine $(u_t,s_t)$, as $u_t$ is the minimum of ${\mathbf {bdd}}(G_t,\partial _t, \delta )$ over all choices of $\delta$. For our presentation, let us now consider an arbitrary fixed choice of $\delta$.

Dealing with Bold Nodes  Let $Q=(Y_t\cap (X_t\cup \bigcup _{p\in A_t} \partial _p))\setminus \partial _t$. In other words, Q contains vertices in $X_t$ as well as the endpoints (in $Y_t$) of any edge which contributes to the adhesion of $p\in A_t$, but not vertices in $\partial _t$. The idea underlying the choice of Q is that we want it to act as our branching set extending our initial choice of $\delta$ (which already provides us with full information on $\partial _t$). See Fig. 5 for an illustration of Q. Since $|A_t|\le 2k+1$ by Lemma 2 and the adhesion of each node in $A_t$ is upper-bounded by k, we see that $|Q|\le k+(2k+1)\cdot k=2k^2+2k$. In the first phase of the algorithm, we will exhaustively loop through all possible intersections of a deletion set with Q. For the following, let us consider one such intersection $R\subseteq Q$. $\square$

Fig. 5

Illustration of the set Q. The orange parts are exactly the sets Q consists of (Color figure online)

At this point, a fixed choice of R and $\delta$ together with the records for nodes in $A_t$ give us sufficient information to determine the size of the intersection between (1) any minimum deletion set corresponding to our choice of $\delta$ and R, and (2) $Y_p$ for any $p\in A_t$. Our next order of business is to formally establish this claim. For the rest of the proof, we will use the term global solution as shorthand for “a minimum-cardinality vertex subset of G such that the maximum degree in the graph after its deletion is at most d”. Furthermore, let $C_t=Y_t\setminus (\bigcup _{b\in B_t}Y_b)$, $\delta _{\text {del}}=\{\,v \;{|}\;\delta (v)={\text {del}}\,\}$ and $\gamma (R,\delta )= |X_t\cap (R\cup \delta _{\text {del}})| +\sum _{p\in A_t}(u_p+s_p(\delta '))$, where $\delta '$ is the configuration of p which corresponds to our choices of R and $\delta$. Formally, $\delta '$ is defined for each p and each $w\in \partial _p$ as follows:

• if $w\in R$ or $\delta (w)={\text {del}}$ then we set $\delta '(w)={\text {del}}$, and otherwise

• if $w\in \partial _t$ then we set $\delta '(w)=|N(w)\setminus (Y_p\cup R\cup \delta _{\text {del}})|+\delta (w)$.

• if $w\not \in \partial _t$ then we set $\delta '(w)=|N(w)\setminus (Y_p\cup R\cup \delta _{\text {del}})|$, and otherwise

Intuitively, $C_t$ refers to the part of $Y_t$ that we can deal with thanks to having fixed R and $\delta$, and $\gamma (R,\delta )$ denotes the size of a global solution in $C_t$ as we prove below.

Claim 2

Let S be a global solution such that $S\cap Q= R$ and $S\cap \partial _t=\delta _{\text {del}}$. Then $|S\cap C_t|=\gamma (R,\delta )$.

Proof

(Claim) Assume for a contradiction that $|S\cap C_t|< \gamma (R,\delta )$. This implies that there must exist a child $p\in A_t$ such that $|S\cap Y_p|< u_p+s_p(\delta ')$, where $\delta '$ is defined as above. However, note that $S\cap Y_p$ satisfies all the conditions stipulated by ${\mathbf {bdd}}(G_p,Y_p,\delta ')$, which are:

• $v\in S\cap \partial _p$ if and only if $\delta '(v)={\text {del}}$, and

• for each $v\in \partial _p\setminus S$, the degree of v in $G_p-S$ is at most $d-\delta '(v)$,

• for each $v\in Y_p\setminus (\partial _p\cup S)$, the degree of v in $H-S$ is at most d.

In particular, this implies that ${\mathbf {bdd}}(G_p,Y_p,\delta ')\le |S\cap Y_p|$; since we assumed that $|S\cap Y_p|< u_p+s_p(\delta ')={\mathbf {bdd}}(G_p,Y_p,\delta ')$, we arrive at a contradiction.

On the other hand, assume that $|S\cap C_t|> \gamma (R,\delta )$. Then there must exist a child $p\in A_t$ such that $|S\cap Y_p|> u_p+s_p(\delta ')$. By the definition of $s_p$, we know that there exists a vertex set $W\subseteq Y_p$ of size $u_p+s_p(\delta ')$ which satisfies all the conditions imposed on W by ${\mathbf {bdd}}(G_p,Y_p,\delta ')$. Let us now consider the vertex set $S'$ obtained by replacing its part in $Y_p$ with W; formally, let $S'=(S\setminus Y_p)\cup W$. By our assumption that $|S\cap Y_p|> u_p+s_p(\delta ')$, it follows that $|S'|<|S|$. Moreover, we claim that $S'$ is also a bounded degree deletion set in G. Indeed, each vertex $v\not \in (Y_p\cup S)$ has the same neighborhood in S as in $S'$ (Condition (A)). On the other hand, each vertex $v\in (Y_p\setminus S')$ has degree at most d by the properties of W; in particular, if v has no neighbors outside of $Y_p$ then it suffices to realize that W is a solution in $G_p$ (Condition (C)), and if v has neighbors outside of $Y_p$ then these are accounted for by the more restrictive degree bounds placed on vertices in $\partial _p$ (Condition (B)).

Since $S'$ is a bounded degree deletion set in G that is smaller than S, we have reached a contradiction with our assumption that S is a global solution. $\square$

Since $\gamma (R,\delta )$ can be readily computed for each choice of R and $\delta$ using the information we have for children in $A_t$, it remains to determine how to best extend a particular choice of R and $\delta$ into a deletion set for $B_t$; in particular, we need to determine $|S\cap \bigcup _{b\in B_t}Y_b|$ for a global solution S that corresponds to R and $\delta$. Note that, unlike $A_t$, the cardinality of $B_t$ is not bounded by a function of k, but instead we have strong restrictions on the neighborhood of each $G_b$.

Dealing with Thin Nodes  Our first goal will be to show that any global solution only “expends” a total of at most k from all the specific costs of all nodes in $B_t$.

Claim 3

Let S be a global solution. Then $|S\cap \bigcup _{b\in B_t}Y_b|\le k+\sum _{b\in B_t}u_b$.

Proof

(of Claim) Assume for a contradiction that $|S\cap \bigcup _{b\in B_t}Y_b|> k+\sum _{b\in B_t}u_b$. For each $b\in B_t$, let $P_b$ be a solution realizing $u_b$, i.e., let $P_b$ be a vertex subset of $G_b$ such that $|P_b|=u_b$ and $G_b-P_b$ has maximum degree at most d. Now consider the set obtained from S by replacing its intersection with $B_t$ with the union of all the sets $P_b$ and by adding $X_t$; formally, let $S'=((S \setminus \bigcup _{b\in B_t} Y_b) \cup X_t) \cup \bigcup _{b\in B_t}P_b$. Since $S'$ is obtained by removing $S\cap \bigcup _{b\in B_t}Y_b$ (of cardinality greater than $k+\sum _{b\in B_t}u_b$) and then adding $X_t \cup \bigcup _{b\in B_t}P_b$ (of cardinality at most $k+\sum _{b\in B_t}u_b$), it follows that $|S'|<|S|$. We claim that $S'$ is a global solution, contradicting the initial choice of S (specifically, its optimality).

To see that $S'$ is indeed a global solution, consider an arbitrary vertex $v\in V(G)-S'$. If v lies in some $Y_b$, then v cannot have degree greater than d by our choice of $P_b$. Otherwise, v is separated from every $Y_b$ by $X_t\subseteq S'$ and hence $N(v)\setminus S'\subseteq N(v)\setminus S$. So $S'$ is indeed a global solution and the claim holds. $\square$

As an immediate consequence of Claim 3, every optimal solution S has the property that there are at most k nodes $b\in B_t$ such that $|S\cap Y_b|>u_b$. However, since the cardinality of $B_t$ is not bounded by a function of k, exhaustively looping through all possible k-tuples of nodes in $B_t$ to “guess” where S exceeds $u_b$ would be too expensive. Instead, we will identify a bounded number of equivalence classes of nodes in $B_t$, and show that nodes in $B_t$ are interchangeable as far as determining where S exceeds the universal cost.

Let us define the following relation $\equiv$ on $B_t$. Two nodes $p,q\in B_t$ satisfy $p\equiv q$ if there exists a bijective function $\tau :\partial _p\rightarrow \partial _q$ (called the renaming function) such that

• 1. $\forall v\in \partial _p: N(v)\cap X_t= N(\tau (v))\cap X_t$, and

• 2. $\forall \delta \in \big \{ \partial _p\rightarrow \{\text {del},0,1,2\}\big \}: s_p(\delta )=s_q(\tau (\delta ))$, where $\tau (\delta )$ is the mapping obtained from $\delta$ by renaming vertices in $\partial _p$ according to $\tau$.

Since $\tau$ is bijective, $\equiv$ is clearly an equivalence relation. Let $\langle \equiv \rangle$ denote the set of equivalence classes of $\equiv$. We claim that $|\langle \equiv \rangle |\le {{\mathcal {O}}}(k^2)$: indeed, since the borders in $B_t$ have size at most 2, there are ${{\mathcal {O}}}(k^2)$ different possibilities of selecting neighbors of border vertices in $X_t$, and thanks to Lemma 5 there are at most $|\{\text {del},0,1,2\}|^2=16$ many different options for the specific costs. Furthermore, we can determine whether $p\equiv q$ in constant time: indeed, there are only constantly many renaming functions to consider, and checking each renaming function only requires constant time. In turn, this means that we can arrange all elements of $B_t$ into equivalence classes in time at most ${{\mathcal {O}}}(|B_t|^2)$.

As explained earlier, the goal of $\equiv$ is to partition $B_t$ into boundedly-many equivalence classes which group nodes that are fully interchangeable as far as their interactions with any global solution are concerned. We will formalize this in the next claim. It will be useful to recall the definition of $\delta ^p_S$ from Lemma 5.

Claim 4

Let S be a global solution and let p, q be two nodes of $B_t$ such that $p\equiv q$ and $\tau (\delta ^p_S)\ne \delta ^q_S$. Then there exists a global solution $S'$ satisfying:

• $S'\setminus (Y_p\cup Y_q)=S\setminus (Y_p\cup Y_q)$, and

• $\tau (\delta ^p_S)= \delta ^q_{S'}$, and

• $\tau (\delta ^p_{S'})= \delta ^q_S$.

Proof

(of Claim) Let $W_p$ be a minimum-cardinality bounded degree deletion set for $G_p$ satisfying the conditions imposed by ${\mathbf {bdd}}(G_p,\partial _p,\delta ^p_{S'})$, and similarly for $W_q$ on $G_q$ and $\delta ^q_{S'}$; in other words, $W_p$ is a solution on $G_p$ which has the “same properties” as $S\cap Y_q$ (since $\tau (\delta ^p_{S'})= \delta ^q_S$), and similarly $W_q$ is a solution on $G_q$ which has the “same properties” as $S\cap Y_p$ (since $\tau (\delta ^p_S)= \delta ^q_{S'}$). Consider the set $S'=(S\setminus (Y_q\cup Y_p))\cup W_p\cup W_q$. The set $S'$ satisfies the itemized properties by construction, and so it remains to argue that $S'$ is a global solution. Since $p\equiv q$, it follows that $|W_p\cup W_q|=u_p+u_q+s_p(\delta ^p_{S'})+s_q(\delta ^q_{S'})= u_p+u_q+s_p(\delta ^p_{S})+s_q(\delta ^q_{S})=|S\cap (Y_p\cup Y_q)|$; in particular, $|S'|=|S|$.

Now we only need to argue that $S'$ is indeed a bounded degree deletion set of G. It will be useful to recall that $N(Y_q)=N(Y_p)$. Observe that $S\setminus (Y_p\cup Y_q)=S'\setminus (Y_p\cup Y_q)$, and so every vertex $v\in V(G)\setminus (Y_p\cup Y_q\cup N(Y_q))$ satisfies $N(v)\setminus S=N(v)\setminus S'$ and so has degree at most d in $S'$. Now consider a vertex $v\in N(Y_q)$; such a vertex will also have the same degree in $G-S$ as in $G-S'$; since the configurations of q and p were swapped, any change of the number of edges between v and $Y_q$ is precisely compensated by the opposite change of the number of edges between v and $Y_p$. Next, let us consider (w.l.o.g. based on symmetry between p and q) a vertex $v\in Y_p\setminus \partial _p$: here, v must have degree at most d in $G-S'$ because $W_p$ was a bounded degree deletion set in $G_p$.

Finally, we consider (w.l.o.g.) $v\in \partial _p\setminus S'$. The existence of such v means that, due to the construction of our configuration $\delta ^q_{S'}$, the vertex $\tau (v)\in \partial _q$ is not in S. Since S is a solution, $\tau (v)$ has degree at most d in $G-S$, and in particular has degree at most $d-\delta ^q_S(\tau (v))$ in $G_q-S$ and has $\delta ^q_S(\tau (v))$ neighbors in $X_t$. Moreover, since $N(v)\cap X_t=N(\tau (v))\cap X_t$ it holds that v also has $\delta ^q_S(\tau (v))$ neighbors in $X_t\setminus S'$. And since $\delta ^q_S(\tau (v))=\delta ^p_{S'}(v)$, v must have at most $d-\delta ^q_S(\tau (v))$ neighbors in $Y_p\setminus S'$. All in all, the degree of v in $G-S'$ is at most d.

We have shown that $S'$ has the same cardinality as S and is also a bounded degree deletion set, meaning that $S'$ is a global solution satisfying the desired properties. $\square$

As a consequence of Claim 3 and 4 , when looking for a global solution consistent with our choice of $\delta$ and R, we may exhaustively branch over:

• 1. how many nodes in $B_t$ have a specific cost greater than 0 ($k+1$ many options),

• 2. which equivalence classes of $\equiv$ are these nodes located in (at most $k^{{{\mathcal {O}}}(k)}$ many options after considering point 4.2),

• 3. which configuration do these nodes have in a global solution (also at most $k^{{{\mathcal {O}}}(k)}$ many options after considering point 4.2).

Let us consider the procedure for one specific branch as above, denoted $\alpha$; formally, $\alpha$ is a tuple of the form $(i,([\equiv ]_1,\dots ,[\equiv ]_i),(\delta _1,\dots ,\delta _i))$. Let $B_t^\alpha$ be obtained from $B_t$ after removing i arbitrary choices of nodes from the equivalence classes specified in $\alpha$. Having fixed $\alpha$, R and $\delta$, we can already determine the value of ${\mathbf {bdd}}(G_t,\partial _t,\delta )$ for any bounded degree deletion set consistent with $\alpha$ and R. In particular, if such a deletion set exists then it must have size ${\text {val}}(\alpha ,R,\delta )=\gamma (R,\delta )+\sum _{b\in B_t}u_b+\sum _{j\in [i]}s_{[\equiv ]_j}(\delta _j)$, where $s_{[\equiv ]_j}$ is the specific cost of an arbitrary node in $[\equiv ]_j$.

All that remains now is to determine whether there in fact exists a bounded degree deletion set in $G_t$ (a t-solution) consistent with $\alpha$, R and $\delta$. To be precise, a t-solution S is a bounded degree deletion set in $G_t$ such that:

• 1. $S\cap Q=R$,

• 2. $v\in S\cap \partial _t$ if and only if $\delta (v)={\text {del}}$,

• 3. for each $v\in \partial _t\setminus S$, $|(N(v)\cap Y_t)\setminus S|\le d-\delta (v)$, and

• 4. for each $b\in B_t$ such that $|S\cap Y_b|>u_b$, there exists a unique $j\in \alpha$ such that equivalence class of b is $[\equiv ]_j$, $|S\cap Y_b|=u_b+s_b(\delta _j)$, and $S\cap Y_b$ satisfies the conditions of $\delta _j$.

Clearly, if ${\text {val}}(\alpha ,R,\delta )=\infty$, then the answer is no. On the other hand, if ${\text {val}}(\alpha ,R,\delta )\ne \infty$, then we only need to make sure that the degree bounds are met for nodes in $X=X_t\setminus (R\cup \delta _{\text {del}})$. Furthermore, for each vertex $x\in X$, we can straightforwardly determine the maximum number of neighbors it can accommodate from nodes in $B_t^\alpha$: this is done by subtracting from d the “buffer” required by $\delta$, the number of its neighbors in X, the number of its neighbors in $\bigcup _{a\in A_t}Y_a\setminus R$, and the number of its neighbors in $\bigcup _{b\in B_t\setminus B_t^\alpha }Y_b$ based on the configurations in $\alpha$. Let us denote the maximum number of neighbors x can still accommodate from $B_t^\alpha$ by c(x), i.e., $c(x)=d-\delta (x)-|N(x) \cap (X \cup (\bigcup _{a\in A_t}Y_a\setminus R)\cup (\bigcup _{b\in B_t\setminus B_t^\alpha }Y_b))|$.

Before solving this final problem and moving onward to arguing the correctness of our algorithm, we will need a few final considerations. First of all, it may happen that our choice of R and $\delta$ means that the sought-after t-solution will leave some nodes in $X_t$ undeleted, and these nodes may prevent the use of a configuration achieving $u_b$ for some node $b\in B^\alpha _t$. To give a concrete example, consider an undeleted vertex $x\in X_t$ and a node $b\in B^\alpha _t$ with $\partial _b=\{b_1\}$ and $x\in N(b_1)$; it could happen that $s_b(b_1\mapsto 0)$ is the only specific cost that is equal to 0, but the presence of x means that $s_b(b_1\mapsto 1)$ would need to be used instead. Naturally, it can be checked in time $|B_t|$ whether each node in $B^\alpha _t$ can still achieve a specific cost of 0; if not, then we discard our choice of $\alpha$ and proceed to the next branch.

Next, for any node $b\in B_t^\alpha$ such that $\partial _b=\{b_1\}$, a t-solution could in principle either contain $b_1$ or not. If $s_b(b_1\mapsto {\text {del}})\ne 0$ then the sought after t-solution must (based on our choice of $\alpha$) not intersect $b_1$; this means that any such node b will reduce the value $c(N(b_1)\cap X_t)$ by 1. On the other hand, if $s_b(b_1\mapsto {\text {del}})= 0$, then we may assume w.l.o.g. that the t-solution contains $b_1$ (as this comes at no additional “cost”); such nodes b will not reduce the value of c(x) for any x.

Let us now consider a node $b\in B_t^\alpha$ such that $\partial _b=\{b_1,b_2\}$. By the same considerations as above (and always while respecting the condition that the specific cost must remain 0):

• if we can add both $b_1$ and $b_2$ into the t-solution, we can safely do so, and we do not change the values of c(x);

• otherwise, if it is only possible to have a t-solution that intersects $b_1$ but not $b_2$, then we will reduce the value of $c(N(b_2))$ by 1;

• otherwise, if it is only possible to have a t-solution that intersects $b_2$ but not $b_1$, then we will reduce the value of $c(N(b_1))$ by 1;

• otherwise, if it is only possible to have a t-solution that intersects neither $b_1$ nor $b_2$, then we need to reduce the values of c(x) accordingly (resulting in a total decrease of 2).

The last remaining case is that we can choose between a t-solution that intersects $b_2$ but not $b_1$ and a t-solution that intersects $b_1$ but not $b_2$; in one case, we will reduce the value of $c(N_1)$ by 1, and in the other case we will reduce the value of $c(N_2)$ by 1. Let $\omega$ be the subset of nodes in $B_t$ which have this property. Our final task is to determine whether it is possible to delete one of the two border vertices in the nodes of $\omega$ while maintaining non-negative values of c(x). We will encode this task into a network flow instance $\kappa$, which we construct below.

We begin by adding a universal source and a universal sink. Next, we add one vertex for each $w\in \omega$, and one vertex for each $x\in X$. We add an arc from each $x\in X$ to the sink with the remaining capacity c(x) (after all the updates of c(x) carried out above). We add an arc from the universal source to each $w\in \omega$ of capacity 1. Finally, we add arcs from each w to its two neighbors in X, each arc of capacity 1.

Claim 5

$\kappa$ admits a network flow of size $|\omega |$ if and only if there exists a t-solution consistent with $\alpha$, R and $\delta$.

Proof

(of Claim) Consider a t-solution S consistent with $\alpha$, R and $\delta$. Let us consider the intersection between S and a node $b\in B_t^\alpha$. For all nodes b which do not force us to make a choice between deleting one of its border vertices or the other, either S behaves “optimally” as per our considerations above, or we can locally replace $S\cap Y_b$ by a different t-solution for $G_b$ which intersects more vertices from the border than S. After performing all such local replacements, we are left with a new t-solution $S'$.

Let us now consider a node $b\in \omega$, and recall that $|\partial _b|=2$. Since S is consistent with $\alpha$, it can only intersect at most one vertex from $\partial _b$; let us set $z\in \partial _b\setminus S$. Now, let us route the flow in $\kappa$ from b to $N(z)\cap X$, and observe that this cannot exceed the capacity bound on the edges from X to the sink because the number of neighbors of each $x\in X$ to $\bigcup _{b\in \omega }Y_b\setminus S$ is upper-bounded by c(x).

On the other hand, consider a flow in $\kappa$ of size $|\omega |$. From the definition of t-solutions consistent with $\alpha$, R and $\delta$, it follows that we merely need to determine how S interacts with $B_t^\alpha$, i.e., its intersection with each $\partial _b$ for $b\in B_t^\alpha$. For all nodes in $B_t^\alpha \setminus \omega$, we determine the intersection based on our considerations above. For $\omega$, we use the flow in $\kappa$ of size $|\omega |$: for each $b\in \omega$ the flow must go to some $x\in X$, and so we select an arbitrary $z\in N(x)\cap Y_b$ and set $S\cap \partial _b=\partial _b\setminus \{z\}$. This guarantees that the degree bound is never exceeded by any $x\in X$, while the existence of a bounded degree deletion set in $G_b$ of size $u_b$ that intersects $\partial _b$ in $\partial _b\setminus \{z\}$ is guaranteed by the fact that $b\in \omega$. $\square$

Let us now summarize the whole algorithm. We begin by branching over all configurations $\delta$ of $G_t$ with the goal of computing ${\mathbf {bdd}}(G_t,\partial _t,\delta )$ for each choice of $\delta$. Next, we construct the branching set Q and apply a second round of branching by exhaustively selecting $R\subseteq Q$. We then construct the equivalence classes $[\equiv ]$, and apply our third (and final) round of branching by selecting $\alpha$. In the resulting branch, we have full information about how we want our solution to intersect all borders except for those in $B_t^\alpha$. For the remaining nodes in $B_t^\alpha$, we either determine this intersection greedily, or apply network flows. If we did not reach a conflict up to this point (e.g., by constructing an instance $\kappa$ with a negative capacity of some edge, or by having ${\text {val}}(\alpha ,R,\delta )=\infty$), then we are guaranteed the existence of a solution consistent with $\alpha$, R and $\delta$ and can set ${\mathbf {bdd}}(G_t,\partial _t,\delta )={\text {val}}(\alpha ,R,\delta )$; otherwise, we set ${\text {val}}(\alpha ,R,\delta )=\infty$.

We conclude the proof by arguing the running time of the above algorithm. The number of choices of $\delta$ is upper-bounded by ${{\mathcal {O}}}(k^k)$. Since $|Q|\le {{\mathcal {O}}}(k^2)$, the number of choices of R is upper-bounded by $2^{{{\mathcal {O}}}(k^2)}$. For our third branching, the number of choices of $\alpha$ can be upper-bounded by $k\cdot k^{2k}=k^{{{\mathcal {O}}}(k)}$. The network flow instance can be constructed in time ${{\mathcal {O}}}(|B_t|)$ and can be solved by the Ford-Fulkerson algorithm in time ${{\mathcal {O}}}(|B_t|^2)$. Hence we can upper-bound the total running time of the algorithm by $2^{{{\mathcal {O}}}(k^2)}\cdot |B_t|^2$. $\square$

Theorem 5

BDD can be solved in time $n^3+2^{{{\mathcal {O}}}(k^2)}\cdot n^2$, where k and n are the treecut width and number of vertices of the input graph, respectively.

Proof

We begin by applying Theorem 1 followed by Lemma 1 to obtain a nice treecut decomposition $(T,{\mathcal {X}})$ of width at most 2k. We then use a dynamic programming algorithm to compute the values $u_t$ and $s_t$ at every node $t\in V(T)$. For leaves, this is carried out by Observation 3, while for non-leaves we invoke Lemma 6. Finally, once we compute $u_r$ for the root r, we can determine the answer to a BDD instance using Observation 4. $\square$

Theorem 6

BDD parameterized by treecut width has no polynomial kernel unless ${{\textsf {coNP}} \subseteq {\textsf {NP}}/poly }$.

Proof

We will show that the well-known NP -complete Vertex Cover problem, i.e., given a graph G and an integer k, decide whether G has a vertex cover of size at most k, AND-cross-composes into BDD parameterized by treecut width. This then shows the theorem due to Proposition 2.

Note that, by employing the polynomial equivalence relation that maps two instances (G, k) and $(G',k')$ of Vertex Cover to the same equivalence class if $|V(G)|=|V(G')|$ and $k=k'$, we can assume that the t instances come with the same number of vertices and the same value for k.

Hence, assume that we are given t instances $(G_1,k),\dotsc ,(G_t,k)$ of Vertex Cover, where $n=|V(G_i)|$. Note that simply taking a disjoint union of the t instances and then asking for a vertex cover of size kt is not sufficient, since some of the instances might have a vertex cover using less than k vertices and could therefore compensate for instances whose vertex cover is larger than k.

Hence, before taking the disjoint union, we need to adapt the instances in such a way that the original instance has a vertex cover of size at most k if and only if the modified instance has a deletion set of size exactly k.

Given the instance $(G_i,k)$ of Vertex Cover, we construct an instance $(G_i',n-k, k)$ of BDD as follows:

• we add $k+1$ apex vertices $a_1,\dotsc ,a_{k+1}$ to $G_i$ and make them adjacent to every vertex in $G_i$,

• we add $n-2k-1$ leaves to every vertex in $G_i$.

The following claim now shows that the constructed instance has the desired properties. $\square$

Claim 6

$(G_i,k)$ has a vertex cover of size at most k if and only if $(G_i',n-k,k)$ has no deletion set of size at most $k-1$ and $(G_i',n-k,k)$ has a deletion set D of size exactly k such that $G_i'\setminus D$ has maximum degree $n-k$.

Proof

(of Claim) Towards showing the forward direction let C be a vertex cover of size at most k for $G_i$ and let A be an arbitrary set of exactly $k-|C|$ vertices in $G_i\setminus C$. We claim that $D=C\cup A$ is the required deletion set for $G_i'$, for which it suffices to show that every vertex in $G_i'\setminus D$ has degree at most $n-k$. This clearly holds for the apex vertices $a_1,\dotsc ,a_{k+1}$, since each of these vertices has degree exactly n in $G_i'$ of which exactly k are in D. Moreover, since C is a vertex cover for $G_i$, every other vertex in $G_i'$ is only adjacent to the $n-2k-1$ leaves and the $k+1$ apex vertices and hence has degree at most $n-k$, as required.

Towards showing the reverse direction, let D be a deletion set of size exactly k for $G_i'$. Because $|D|\le k$, there is at least one apex vertex, say $a_i$, that is not in D. Moreover, since the degree of $a_i$ in $G_i'$ is exactly k more than the required degree (of $n-k$) and $a_i$ is only adjacent to the (original) vertices in $G_i$, it follows that $D \subseteq V(G_i)$. We now claim that D is a vertex cover for $G_i$. This is because every vertex in $G_i$ has at least $n-k$ neighbors in $G_i'\setminus D$, i.e., the $k+1$ apex vertices plus the $n-2k-1$ leaf vertices. $\square$

We now obtain the required instance (G, d, l) of BDD by taking the disjoint union of the graphs $G_i$ and setting $d=n-k$ and $l=tk$. Clearly, (G, d, l) can be constructed in time polynomial in $\sum _{i=1}^t|x_i|$ and moreover it satisfies Property 1 of an AND-cross-composition, because of Claim 6. Finally, the instance also satisfies Property 2, because the treecut width of G is equal to the maximum treecut width of any of the t instances, which in turn is at most $n=\max _{i=1}^t|V(G_i)|$. $\square$

5 Core Fracture Number

In this section we introduce the new structural parameter core fracture number and provide a fixed-parameter algorithm for BDD parameterized by this parameter. An important prerequisite for the introduction of this parameter is the following simple preprocessing procedure that can be applied to any BDD instance. Given an instance ${\mathcal {I}}=(G,d,\ell )$ of BDD, the core of ${\mathcal {I}}$, denoted by $\mathbf{c }({\mathcal {I}})=(\mathbf{c }(G),d,\ell )$, is the BDD instance obtained from ${\mathcal {I}}$ after removing all edges whose both endpoints have degree at most d from G.

Observation 7

Let ${\mathcal {I}}=(G,d,\ell )$ be a BDD instance. Then ${\mathcal {I}}$ and ${\mathbf{c}}({\mathcal {I}})$ are equivalent instances of BDD in the sense that any solution for ${\mathcal {I}}$ is also a solution for ${\mathbf{c}}({\mathcal {I}})$ and vice versa. Moreover, ${\mathbf{c}}({\mathcal {I}})$ can be computed in linear time w.r.t. the number of edges of G.

In the following we will assume that we have already applied the above preprocessing procedure to any BDD instance and hence the graph of the instance does not contain any edges between vertices whose degree is already below the given degree bound. The core fracture number of a BDD instance ${\mathcal {I}}=(G,d,\ell )$, denoted by ${\mathbf{cfn}} ({\mathcal {I}})$, is the minimum integer k such that there is a deletion set $D \subseteq V(G)$ with $|D|\le k$ and the number of vertices in any component C of $G \setminus D$ of degree larger than d in G is at most k. In other words, each connected component of $G-D$ may contain only at most k vertices of degree greater than d. We start by showing that this parameter is orthogonal to treecut width.

Theorem 8

For every $d \in {\mathbb {N}}$, there are classes ${\mathcal {C}}_1^d$ and ${\mathcal {C}}_2^d$ of BDD instances ${\mathcal {I}}=(G,d,\ell )$ with ${\mathbf{c}}({\mathcal {I}})={\mathcal {I}}$ such that:

• all instances in ${\mathcal {C}}_1^d$ have core fracture number at most 1 and for every $n>1$ there is a graph in ${\mathcal {C}}_1^d$ with treecut width n,

• all graphs in ${\mathcal {C}}_2^d$ have treecut width at most 1 and and for every $n>1$ there is an instance in ${\mathcal {C}}_2^d$ with core fracture number n,

Proof

For the class ${\mathcal {C}}_1^d$ we make use of the class ${\mathcal {H}}_2$ that was used in previous work on treecut width [24, Proposition 3]. In particular, ${\mathcal {H}}_2$ is the class of graphs $S_n$ obtained from a star with n leaves $l_1,\ldots , l_n$ by replacing each edge with n subdivided edges; Fig. 6 illustrates the graph $S_3$. Following the arguments used in previous work [24, Proposition 3], we can verify that ${\mathbf {tcw}}(S_n)\ge n$: suppose for a contradiction that ${\mathbf {tcw}}(S_n)\le n-1$. Then any two leaves $z_i$ and $z_j$, $i\ne j$, must be contained in the same bag in any tree-cut decomposition of width at most $n-1$ as they are connected by n edge-disjoint paths. This means there exists a bag t containing all $z_i$’s in any such tree-cut decomposition, which however implies that ${\mathbf {tor}}(t)\ge n$.

Towards defining the class ${\mathcal {C}}_1^d$ of BDD instances, we need to ensure that graphs do not change after the core operation is applied. We do so by introducing the graphs $S_n^d$, which are obtained from $S_n$ after attaching $d-1$ novel leaf vertices to every $l_i$. Then ${\mathcal {C}}_1^d$ contains all BDD instances $(S_n^d,d,\ell )$ for any $n,\ell \in {\mathbb {N}}$. Because $S_n$ is a subgraph of $S_n^d$, we still have that ${\mathbf {tcw}}(S_n^d)\ge n$. Moreover, for every $d>1$ it holds that after deleting the center vertex of $S_n^d$ every component has only one vertex with degree larger than d and hence ${\mathbf{cfn}} (S_n^d)\le 1$.

Fig. 6

The graph $S_3$

Towards the definition of the class ${\mathcal {C}}_2^d$, let $P_n^d$ be the path on n vertices after attaching d novel leaf vertices to every vertex in the path. Then ${\mathcal {C}}_2^d$ is the class of all BDD instance $(P_n^d,d,\ell )$ for any $n, \ell \in {\mathbb {N}}$. Note that ${\mathbf{c}}({\mathcal {I}})={\mathcal {I}}$ for every ${\mathcal {I}}\in {\mathcal {C}}_2^d$. Because the treecut width of any tree is at most one (simple take the tree itself as the treecut decomposition), we have that ${\mathbf {tcw}}({\mathcal {I}})\le 1$ for every ${\mathcal {I}}\in {\mathcal {C}}_2^d$. Towards showing that the core fracture number of the instances in ${\mathcal {C}}_2^d$ is unbounded, assume for a contradiction that this is not the case, i.e., there is $k \in {\mathbb {N}}$ such that ${\mathbf{cfn}} ({\mathcal {I}})\le k$ for every ${\mathcal {I}}\in {\mathcal {C}}_2^d$. Consider the BDD instance ${\mathcal {I}}=(P_{(k+1)^2}^d,d,\ell ) \in {\mathcal {C}}_2^d$. Then any vertex set $D \subseteq V(G)$ witnessing ${\mathbf{cfn}} ({\mathcal {I}})$ must contain at least one vertex from every subpath of $P_{(k+1)^2}$ of length $k+1$. Since $P_{(k+1)^2}$ contains $k+1$ such subpaths, which are pairwise disjoint, this is not possible if $|D|\le k$. Hence ${\mathbf{cfn}} ({\mathcal {I}})>k$, a contradiction to our initial assumption. $\square$

For completeness, we note that the treedepth (and hence also treewidth) of the core is always upper-bounded by a function of the core fracture number. Indeed, observe that deleting k vertices from a graph with core fracture number k leads to a graph where every connected component has at most k vertices; from this and the definition of treedepth [40], it is easy to show that the graph has treedepth at most $2k+1$. On the other hand, the core fracture number is upper bounded by the vertex cover number (i.e., the size of a minimum vertex cover). Hence our tractability results for core fracture number also imply analogous results for the vertex cover number.

We are now ready to present our fixed-parameter algorithm for BDD parameterized by the core fracture number. The algorithm consists of two steps: (1) it computes a deletion set D of size at most k, witnessing that ${\mathbf{cfn}} ({\mathcal {I}})\le k$ and (2) it solves ${\mathcal {I}}$ with the help of the deletion set D. Namely, our algorithm will consists of fixed-parameter algorithms for the following two parameterized problems.

Theorem 9

CFND can be solved in time ${{\mathcal {O}}}((2k+1)^k|E(G)|)$ and is hence fixed-parameter tractable.

Proof

Let ${\mathcal {I}}=(G,d,\ell ,k)$ be any instance of CFND and let M be the set of all vertices in G that have degree larger than d. We will show the lemma by providing a depth-bounded search tree algorithm, which is based on the following observations.

• O1 If G is not connected then a solution for ${\mathcal {I}}$ can be obtained as the disjoint union of solutions for every component of G.

• O2 If G is connected and C is any subset of V(G) such that G[C] is connected and $|C\cap M|> k$, then any solution for ${\mathcal {I}}$ has to contain at least one vertex from C.

These observations lead directly to the following recursive algorithm that given the instance ${\mathcal {I}}$ either determines that the instance is a No-instance or outputs a solution $D \subseteq V(G)$ of minimum size for ${\mathcal {I}}$. The algorithm first checks whether G is connected. If G is not connected the algorithm calls itself recursively on the instance $(C,d,\ell , k)$ for each component C of G. If one of the recursive calls returns No or if the size of the union of the solutions returned for each component exceeds k, the algorithm returns that ${\mathcal {I}}$ is a No-instance. Otherwise the algorithm returns the union of the solutions returned for each component of G.

If G is connected and $|V(G)\cap M|\le k$, the algorithm returns the empty set as a solution. Otherwise, i.e., if G is connected but $|V(G)\cap M|>k$ the algorithm first computes a set C of at most $2(k+1)-1$ vertices of G such that G[C] is connected and $|C\cap M|>k$. This can for instance be achieved by a depth-first search that starts at any vertex in M and stops as soon as $k+1$ vertices of M have been visited. Then $|C|\le 2(k+1)-1$ because at most every second vertex that is visited by the depth-first search can be a vertex in $V(G)\setminus M$; this is because $G - M$ is an independent set (recall that we assume ${\mathbf{c}}(G)=G$ and hence G contains no edges between vertices of degree at most d). The algorithm then branches on the vertices in C, i.e., for every $v \in C$ the algorithm recursively computes a solution for the instance $(G - \{v\},d,\ell ,k-1)$. It then returns the solution of minimum size returned by any of those recursive calls, or No-if none of those calls returns a solution. This completes the description of the algorithm. The correctness of the algorithm follows immediately from the above observations. Moreover the running time of the algorithm is easily seen to be dominated by the maximum time required for the case that at each step of the algorithm G is connected.

In this case the running time can be obtained as the product of the number of branching steps times the time spent on each of those. Because at each recursive call the parameter k is decreased by at least one and the number of branching choices is at most $2(k+1)-1$, we obtain that there are at most $(2(k+1)-1)^k=(2k+1)^k$ branching steps. Furthermore, the time at each branching step is dominated by the time required to check whether G is connected, which is linear in the number of edges of G. Putting everything together, we obtain ${{\mathcal {O}}}((2k+1)^k|E(G)|)$ as the total time required by the algorithm, which completes the proof of the lemma. $\square$

We note that the depth-first search algorithm in the above proof can be easily transformed into a polynomial time approximation algorithm for CFND that exhibits an approximation ratio of $2k+1$. In particular, instead of branching on the vertices of a connected subgraph C of G with at most $2k+1$ vertices, this algorithm would simply add all the vertices of C into the current solution. This way we obtain:

Theorem 10

CFND can be approximated in polynomial time within a factor of $2k+1$.

Let ${\mathcal {I}}=(G,d,\ell ,D)$ be an instance of CFNE and assume w.l.o.g. that ${\mathbf{c}}(G)=G$ and $k=|D|$. We start by showing that we do not need to consider solutions $V' \subseteq V(G)$ for ${\mathcal {I}}$ that contain more than $2k-1$ vertices from any component C of $G - D$.

Lemma 7

If ${\mathcal {I}}$ has a solution, then it has a solution $V'$ such that $|V'\cap V(C)|< 2k$ for every component C of $G - D$.

Proof

Let $V'$ be a solution for ${\mathcal {I}}$ and C be a component of $G - D$ with $|V'\cap V(C)|\ge 2k$; if no such component exists, then we are done. Let M be the set of all vertices in C, whose degree is larger than d in G. Then $(V' \setminus V(C))\cup M \cup D$ is also a solution for ${\mathcal {I}}$ and moreover $|(V' \setminus V(C))\cup M \cup D|\le |V'|-2k+k+k\le |V'|$. By iterating the same process for every component C with $|V'\cap V(C)|\ge 2k$, one obtains the desired solution for ${\mathcal {I}}$. $\square$

Let C be a component of $G - D$ and let $M \subseteq V(C)$ be the set of all vertices with degree larger than d in G. Then the signature of C, denoted by ${\mathcal {S}}(C)$, contains all pairs $(D', \varGamma )$ such that:

• $D' \subseteq D$,

• $\varGamma$ is the set of all pairs $(o,\gamma )$ such that:

  • o is an integer with $0 \le o < 2k$, and

  • $\gamma : D\setminus D' \rightarrow \{0,\dotsc ,2k-1\}$ is a mapping such that there is a set $V' \subseteq V(C)$ with $|V'|= o$ satisfying the following conditions:

• (S1) every vertex in $M \setminus V'$ has degree at most d in $G- (V'\cup D')$ and

• (S2) for every vertex v in $D\setminus D'$, $V'$ contains exactly $\gamma (v)$ neighbors of v.

Informally, for every subset $D'$ of vertices that we decide to delete from D, the signature tells us how many vertices in C we need to delete and how their deletion affects the degrees of the remaining vertices in $D - D'$. Because we only need to consider solutions containing less than 2k vertices from C (Lemma 7), the number of ways in which different solutions effect the degrees of vertices in D is bounded (in terms of k), which allows us to compute the signatures.

Lemma 8

The signature ${\mathcal {S}}(C)$ can be computed in time $O(|V(C)|+|E(C)|+2^k(2k)^{2^{2k}})$ for any component C of $G - D$.

Proof

Let ${\mathcal {I}}=(G,d,\ell ,D)$ be the given instance of CFNE, let C be any component of $G - D$, and let M be the set of all vertices in C that have degree more than d in G. Note that $|M|\le k$ and because $G={\mathbf{c}}(G)$ also $C - M$ is an independent set. The main idea behind the algorithm to compute ${\mathcal {S}}(C)$ is that even though there can be many vertices in $V(C) \setminus M$ the vertices can only behave in a limited number of ways towards the vertices of high degree, i.e., the vertices in $D \cup M$. Namely, let $D'$ be an arbitrary subset of D. Then we say that two vertices $v,v' \in V(C)\setminus M$ have the same type if both have the same neighborhood in $M \cup (D\setminus D')$. Let $NT$ be the set of types of vertices in $V(C) \setminus M$ and for a type $t \in NT$ we denote by $\#(t)$ the number of vertices in C having type t. Because $|D\cup M|\le 2k$, it holds that $|NT | \le 2^{2k}$. For a vertex $v \in D \setminus D'$ let $NT (v)$ be the set of all types having v as a neighbor. Observe that if two vertices u and v have the same type then the effect of removing u is the same as the effect of removing v, i.e., the resulting graphs will be isomorphic. Hence for the computation of ${\mathcal {S}}(C)$ it is not necessary to distinguish between vertices of the same type. Namely, there is a pair $(o,\gamma )$ satisfying (S1) and (S2) if and only if there is a subset $M' \subseteq M$ together with a mapping $\beta : NT \rightarrow \{0,\dotsc ,2k-1\}$ such that:

• (S0’) $\beta (t)\le \#(t)$ for every $t \in NT$ and $|M'|+\sum _{t \in NT }\beta (t) =o$,

• (S1’) every vertex in $M \setminus M'$ has degree at most d in the graph obtained from $G[(D\setminus D') \cup V(C)]- M'$ after deleting $\beta (t)$ vertices of type t for every $t \in NT$, and

• (S2’) for every vertex v in $D\setminus D'$, $\gamma (v)=|N(v,M')|+\sum _{t \in NT (v)}\beta (t)$.

Hence for a given $D'$ we can compute $\varGamma$ by enumerating all pairs $(M',\beta )$ and for each pair testing whether it satisfies (S0’)–(S2’). If it does then we add the pair $(o,\gamma )$, where $o=|M'|+\sum _{t \in NT }\beta (t)$ and $\gamma (v)=|N(v,M')|+\sum _{t \in NT (v)}\beta (t)$ for every $v \in D\setminus D'$ to $\varGamma$, otherwise we do not.

The total running time of the algorithm is obtained as follows. To compute $NT$ and $\#(t)$ for every $t \in NT$ it is sufficient to make one pass through the vertices in $V(C) \setminus M$; since one also needs to store the values the total running time of this step is at most $O(|V(C)|+|E(C)|+2^{2k})$. Moreover, the time needed to enumerate all pairs $(M',\beta )$ and verify that the pair satisfies Conditions (S0’)–(S2’), is dominated by the number of these pairs, i.e., $O(2^k(2k)^{2^{2k}})$. The same holds for calculating the pair $(o,\gamma )$ from $(M',\beta )$ in the case that all conditions were met. Hence the total running time of the algorithm is $O(|V(C)|+|E(C)|+2^k(2k)^{2^{2k}})$. $\square$

Let $D'\subseteq D$ and let C and $C'$ be two distinct components of $G - D$. We say that C and $C'$ are equivalent w.r.t. $D'$ if $(D',\varGamma ) \in {\mathcal {S}}(C) \cap {\mathcal {S}}(C')$ for some $\varGamma$. Let ${\mathcal {P}}(D')$ be the partition of all components of $G - D$ into equivalence classes and for an equivalence class ${\mathcal {C}}\in {\mathcal {P}}(D')$ let $\varGamma ({\mathcal {C}})$ denote the set $\varGamma$ such that $(D',\varGamma ) \in {\mathcal {S}}(C)$ for every $C \in {\mathcal {C}}$. Note that $|{\mathcal {P}}(D')|\le 2^{2k(2k)^k}$.

Lemma 9

An instance ${\mathcal {I}}=(G,d,\ell ,D)$ has a solution if and only if there is a subset $D'$ of D and a mapping $\alpha$ that assigns to every ${\mathcal {C}}\in {\mathcal {P}}(D')$ and every $(o,\gamma ) \in \varGamma ({\mathcal {C}})$ a natural number satisfying the following conditions:

• (C1) $(\sum _{{\mathcal {C}}\in {\mathcal {P}}(D') \wedge (o,\gamma ) \in \varGamma ({\mathcal {C}})}o\cdot \alpha ({\mathcal {C}},(o,\gamma )))+|D'|\le \ell$, i.e., the budget $\ell$ is not exceeded,

• (C2) $\sum _{(o,\gamma ) \in \varGamma ({\mathcal {C}})}\alpha ({\mathcal {C}},(o,\gamma )) = |{\mathcal {C}}|$ for every ${\mathcal {C}}\in {\mathcal {P}}(D')$, i.e., all components are considered,

• (C3) $\sum _{{\mathcal {C}}\in {\mathcal {P}}(D') \wedge (o,\gamma ) \in \varGamma ({\mathcal {C}})} \gamma (v)\cdot \alpha ({\mathcal {C}},(o,\gamma ) \ge |N_{G- D'}(v)|-d$ for every $v\in D\setminus D'$, i.e., the degree conditions for the vertices in $D\setminus D'$ are satisfied.

Informally, for ${\mathcal {C}}\in {\mathcal {P}}(D')$ and every $(o,\gamma ) \in \varGamma ({\mathcal {C}})$, $\alpha$ gives the number of components in ${\mathcal {C}}$ that use the configuration $(o,\gamma )$.

Proof

Towards showing the forward direction let $V'$ be a solution for ${\mathcal {I}}$. We start by setting $D'=D \cap V'$. Consider a component C of $G - D$ and let $\varGamma$ be the set such that $(D',\varGamma ) \in {\mathcal {S}}(C)$. Because of Lemma 7, we can assume that $|V'\cap V(C)|< 2k$. Hence $\varGamma$ contains a pair $(|V'\cap V(C)|,\gamma )$, which we denote by A(C), such that for every $v \in D \setminus D'$, it holds that v has exactly $\gamma (v)$ neighbors in $V'\cap V(C)$. For every ${\mathcal {C}}\in {\mathcal {P}}(D')$ and $(o,\gamma )\in \varGamma ({\mathcal {C}})$, we now set $\alpha ({\mathcal {C}},(o,\gamma ))$ to be the number of components C in ${\mathcal {C}}$ with $A(C)=(o,\gamma )$ and claim that $\alpha$ satisfies the conditions (C1)–(C3). Because $(\sum _{{\mathcal {C}}\in {\mathcal {P}}(D') \wedge (o,\gamma ) \in \varGamma ({\mathcal {C}})}o\cdot \alpha ({\mathcal {C}},(o,\gamma )))+|D'|=|V'|$ and $|V'|\le \ell$, we obtain that $\alpha$ satisfies (C1). Condition (C2) follows immediately from the definition of $\alpha$. Finally, Condition (C3) follows because for every $v \in D \setminus D'$ it holds that $\sum _{{\mathcal {C}}\in {\mathcal {P}}(D') \wedge (o,\gamma ) \in \varGamma ({\mathcal {C}})} \gamma (v)\cdot \alpha ({\mathcal {C}},(o,\gamma ))$ is equal to the number of neighbors of v in $V'\setminus D$ and the fact that v can have at most d neighbors in $G - V'$.

Towards showing the reverse direction let $D' \subseteq D$ and $\alpha$ be a mapping satisfying (C1)–(C3). For a component $C \in {\mathcal {C}}$ and $(o,\gamma ) \in \varGamma$, where ${\mathcal {C}}\in {\mathcal {P}}(D')$ and $(D',\varGamma ) \in {\mathcal {S}}(C)$, we denote by $V(C,(o,\gamma ))$ a subset of V(C) of size o satisfying the conditions (S1) and (S2) in the definition of a signature. Then a solution $V'$ for ${\mathcal {I}}$ is obtained as follows. For any ${\mathcal {C}}\in {\mathcal {P}}(D')$ we take the union of $V(C,(o,\gamma ))$ for exactly $\alpha ({\mathcal {C}},(o,\gamma ))$ components $C \in {\mathcal {C}}$. Condition (C2) ensures that there are enough components in ${\mathcal {C}}$ and moreover that this way we use every component exactly once. Finally, we add $D'$ to $V'$. Because of Condition (C1), we have that $|V'|\le \ell$. Moreover, because of Condition (C3), we obtain that every vertex in $D\setminus D'$ has degree at most d in $G - V'$. The same holds for every vertex in any component C of $G - D$, because of Property (S1). Hence $V'$ is a solution for ${\mathcal {I}}$ of size at most $\ell$. $\square$

With the help of the above lemma, we can express the existence of a solution in terms of the solution of an integer linear program with a bounded number of variables, which in turn can be solved in fpt-time w.r.t. the number of variables (Proposition 3).

Theorem 11

CFNE is fixed-parameter tractable.

Proof

Let ${\mathcal {I}}=(G,d,\ell ,D)$ be the given instance of CFNE. The algorithm first computes the signature ${\mathcal {S}}(C)$ for every component C of $G - D$ according to Lemma 8. It then uses the characterization given in Lemma 9 to decide whether ${\mathcal {I}}$ has a solution. Namely, for every $D'\subseteq D$ the algorithm constructs an ILP instance ${\mathcal {I}}'$ whose optimum is at most $\ell -|D'|$ if and only if the BDD instance ${\mathcal {I}}$ has a solution $V'$ with $V' \cap D=D'$. In accordance with Lemma 9 the ILP instance ${\mathcal {I}}'$ has one variable, denote by $x_{{\mathcal {C}},(o,\gamma )}$, for every ${\mathcal {C}}\in {\mathcal {P}}(D')$ and $(o,\gamma ) \in \varGamma ({\mathcal {C}})$ and consists of the following constraints:

$$ \begin{array}{*{20}c} {{\text{minimize}}} & {\sum\limits_{{{\mathcal{C}} \in {\mathcal{P}}(D^{\prime}),(o,\gamma ) \in \Gamma ({\mathcal{C}})}} o \cdot x_{{{\mathcal{C}},(o,\gamma )}} } & \\ {{\text{subject}}\;{\text{to}}} & {\sum\limits_{{(o,\gamma ) \in \Gamma ({\mathcal{C}})}} {x_{{{\mathcal{C}},(o,\gamma )}} } = |{\mathcal{C}}|} & {\forall {\mathcal{C}} \in {\mathcal{P}}(D^{\prime})} \\ & {\sum\limits_{{{\mathcal{C}} \in {\mathcal{P}}(D^{\prime}) \wedge (o,\gamma ) \in \Gamma ({\mathcal{C}})}} \gamma (v) \cdot x_{{{\mathcal{C}},(o,\gamma )}} \ge |N_{{G - D^{\prime}}} (v)| - d} & {\forall v \in D{ \setminus }D^{\prime}} \\ \end{array} $$

Observe that there is a one-to-one correspondence between assignments $\beta$ for the variables in ${\mathcal {I}}'$ and the assignment $\alpha$ defined in Lemma 9. Moreover, the constraints of ${\mathcal {I}}'$ ensure Condition (C2) and (C3) and Condition (C1) can be satisfied if and only if the optimum value of ${\mathcal {I}}'$ is at most $\ell -|D'|$. This completes the description of the algorithm and the running time of the algorithm is obtained as follows.

Apart from constructing the ILP instance, the main task of the algorithm are to compute the signature for every component C of $G - D$ and to compute ${\mathcal {P}}(D')$ for every $D' \subseteq D$. The first task can be achieved in time $O(|E(G)|+|V(G)|2^k(2k)^{2^{2k}})$ due to Lemma 8. The second task can be achieved by going over all of the at most $|V(G)|^2$ pairs of components of $G - D$ and checking for each such pair whether the signatures are the same. Hence the total time required for the second step is at most $O(2^k|V(G)|^2k(2k)^k)$. Finally, constructing and solving the ILP instance ${\mathcal {I}}'$ for every $D' \subseteq D$ is dominated by the time required to solve ${\mathcal {I}}'$, which because of Proposition 3 takes time at most $O(p^{2.5p+o(p)}\cdot L)$, where p is the number of variables and L is the size of ${\mathcal {I}}'$ in bits. Now the number of variables p of ${\mathcal {I}}'$ is at most $|{\mathcal {P}}(D')|\max _\varGamma$, where $\max _\varGamma =\max _{{\mathcal {C}}\in {\mathcal {P}}(D')}|\varGamma ({\mathcal {C}})|$. Moreover, the size of ${\mathcal {I}}'$ in bits is dominated by the size of the last row of constraints in ${\mathcal {I}}'$, which is at most $O((\log (k)|{\mathcal {P}}(D')|\max _\varGamma )+\log (|V(G)|)k)$. Since $|{\mathcal {P}}(D')|\le 2^{k(2k)^k}$ and $\max _\varGamma \le k(2k)^k$, we obtain that $p \in O(2^{k(2k)^k}k(2k)^k)$ and $L \in O((\log (k)2^{k(2k)^k}k(2k)^k)+\log (|V(G)|)k)$, which shows that constructing and solving ${\mathcal {I}}'$ is fixed-parameter tractable parameterized by k. Taking everything together, we obtain $O(2^k(|V(G)|^2k(2k)^k+p^{2.5p+o(p)}L)$, where $p \in O(2^{k(2k)^k}k(2k)^k)$ and $L \in O((\log (k)2^{k(2k)^k}k(2k)^k)+\log (|V(G)|)k)$, as the total running time of the algorithm. $\square$

As our final result, we show a kernel lower bound for CFNE.

Theorem 12

CFNE has no polynomial kernel unless ${{\textsf {coNP}} \subseteq {\textsf {NP}}/poly }$.

Proof

We give a polynomial parameter transformation from the well-known Set Cover parameterized by the size of the universe. The result then follows from Proposition 1.

It is known that Set Cover does not admit a polynomial kernel under standard complexity assumptions, notably, unless ${{\textsf {coNP}} \subseteq {\textsf {NP}}/poly }$ [12]. Given an instance ${\mathcal {I}}=(U,{\mathcal {F}},k)$ of Set Cover, we construct an instance ${\mathcal {I}}'=(G,d,\ell ,D)$ of CFNE as follows. G has one vertex $v_u$ for every $u \in U$ as well as one vertex $w_F$ for every $F \in {\mathcal {F}}$. Moreover, G has an edge between a vertex $v_u$ and a vertex $w_F$ if and only if $u \in F$. We set $D=\{\,v_u \;{|}\;u \in U \,\}$. Let $\varDelta$ be the maximum degree of any vertex in G. Then we attach to every vertex in D new leaf vertices such that the degree of every vertex in D becomes $\varDelta +1$. This completes the construction of G. Finally, we set $d=\varDelta$ and $\ell =k$. Because $G - D$ is an independent set, it shows that $\mathbf{cfn} (G)\le |U|=|D|$. It remains to show that ${\mathcal {I}}$ has a solution if and only if so does ${\mathcal {I}}'$.

Towards showing the forward direction let ${\mathcal {F}}' \subseteq {\mathcal {F}}$ be a solution for ${\mathcal {I}}$. Then it is straightforward to verify that $\{\,w_F \;{|}\;F \in {\mathcal {F}}'\,\}$ is a solution for ${\mathcal {I}}'$.

Towards establishing the reverse direction let $V' \subseteq V(G)$ be a solution for ${\mathcal {I}}'$. We first show that w.l.o.g. we can assume that $V' \subseteq \{\,w_F \;{|}\;F \in {\mathcal {F}}\,\}$. Suppose not then $V'$ either contains a vertex in D or a leaf attached to a vertex in D. If $V'$ contains a leaf, then we can replace the leaf with the vertex in D that it is attached to. Hence it only remains to deal with the case that $V'$ contains a vertex in D. In this case we can replace the vertex say $v_u$ in D with any vertex $w_F$ such that $u \in F$ and $F \in {\mathcal {F}}$. Note that such a vertex $w_F$ exists since otherwise ${\mathcal {I}}$ is a No-instance. This works because all vertices in $\{\,w_F \;{|}\;F \in {\mathcal {F}}\,\}$ already have degree at most d in G and moreover v has degree at most $d+1$ in G. Thus let $V'$ be a solution for ${\mathcal {I}}'$ with $V' \subseteq \{\,w_F \;{|}\;F \in {\mathcal {F}}\,\}$. Then it is straightforward to verify that $\{\,F \;{|}\;w_F \in V'\,\}$ is a solution for ${\mathcal {I}}$. $\square$

6 Concluding Notes

Our results close a wide gap in the understanding of the complexity landscape of BDD parameterized by structural parameters. In particular, they not only resolve an open question from previous work in the area [6], but push the lower bounds significantly further, specifically to deletion distance to trees of bounded depth. Moreover, we identified structural parameterizations which are better suited for the problem at hand and used these to obtain two novel fixed-parameter algorithms for BDD. In particular, it is interesting that treecut width is the only known decompositional parameter that allows for an fixed-parameter algorithm. Moreover, the core fracture number is a natural and quite significant generalization of the vertex cover number.

For future work it would be interesting to empirically evaluate how large the considered parameters are on practical instances, and whether the ideas used in our exact algorithms can be used to improve heuristic approaches commonly used to solve the problem.

Appendix

1.1 Proof of Lemma 1

The proof of Lemma 1 is based on the following considerations. Let $(T,{\mathcal {X}})$ be a rooted tree-cut decomposition of G whose width is at most w. We say that a node t, $t \ne r$, is bad if ${\mathbf {adh}}(t)\le 2$ and there is a sibling b of t such that $N(Y_t)\cap Y_b\ne \emptyset$. For a bad node t, we say that b is a bad neighbor of t if $N(Y_t) \cap X_b\ne \emptyset$ and b is either a sibling of t or a descendant of a sibling of t.

Rerouting(t): let t be a bad node and let b be a bad neighbor of t of maximum depth (resolve ties arbitrarily). Then remove the tree edge e(t) from T and add a new tree edge $\{b,t\}$.

Top-down Rerouting: as long as $(T,{\mathcal {X}})$ is not a nice tree-cut decomposition, pick any bad node t of minimum depth. Perform Rerouting(t).

For the following proof, we will use ${\mathbf {tor}}_T(z)$ to denote the torso-size of a node z in the tree T; ${\mathbf {adh}}_T$ and ${\mathbf {cut}}_T$ are defined analogously, but for ${\mathbf {adh}}$ and ${\mathbf {cut}}$. This will be useful when comparing adhesion and torso-size between two different tree-cut decompositions.

Lemma 10

Rerouting(t) does not increase the width of the tree-cut decomposition.

Proof

Let b be the bad neighbor of t chosen by Rerouting(t), and let $(T',{\mathcal {X}})$ be the tree-cut decomposition obtained from the tree-cut decomposition $(T,{\mathcal {X}})$ by Rerouting(t). We will show that for each $z\in V(T)$, it holds that

• (1) ${\mathbf {adh}}_T(z)\ge {\mathbf {adh}}_{T'}(z)$, and

• (2) ${\mathbf {tor}}_T(z)={\mathbf {tor}}_{T'}(z)$,

from which the lemma follows.

Let us first consider Claim (1). Let P be the set of edges on the path in T between b and the parent a(t) of t. Then for any edge $p\not \in P$ it holds that ${\mathbf {cut}}_T(p)={\mathbf {cut}}_{T'}(p)$, and hence Claim (1) holds for all vertices z which are not incident to P and also for $z=a(t)$. As for the remaining choices of z, it holds that the edge between $X_b$ and t lies in ${\mathbf {cut}}_T(e(z))\setminus {\mathbf {cut}}_{T'}(e(z))$. Furthermore, by thinness of t there may exist at most one edge $e'$ such that $e' \in {\mathbf {cut}}_{T'}(e(z))\setminus {\mathbf {cut}}_T(e(z))$, and hence either ${\mathbf {adh}}_T(z)= {\mathbf {adh}}_{T'}(z)$ or ${\mathbf {adh}}_T(z)= {\mathbf {adh}}_{T'}(z)+1$. Thus Claim (1) holds.

Now we consider Claim (2). Since the contents of the bags did not change and the adhesion did not increase (Claim (1)) it follows that Claim (2) may only be violated if $N_T(z)\subset N_{T'}(z)$, which is only the case for $z=b$. However, it is easy to verify that ${\mathbf {tor}}_T(b)={\mathbf {tor}}_{T'}(b)$ since $\{t\}=N_{T'}(b)\setminus N_{T}(b)$ and t is thin. $\square$

Lemma 11

Top-down Rerouting terminates after performing Rerouting at most $|T|^2$ times, where $(T,{\mathcal {X}})$ is the initial tree-cut decomposition.

Proof

Let $(T,{\mathcal {X}})$ be a rooted tree-cut decomposition with a bad node t at depth d such that all nodes at depth at most $d-1$ are not bad, and let $(T',{\mathcal {X}})$ be the rooted tree-cut decomposition obtained from $(T,{\mathcal {X}})$ by Rerouting(t). Let $dep_T(i)$ denote the number of nodes at depth i in T. It is easy to see that $dep_T(d)=dep_{T'}(d)+1$. Furthermore, for any tree-cut decomposition $(T'',{\mathcal {X}}'')$, if $dep_{T''}(i)=1$ then the single node at depth i cannot be bad. From these two observations it follows that Rerouting(t) can only be called at most |T| times at each depth d, and since d is bounded by |T|, the proof is finished. $\square$

Proof

(of Lemma 1) By definition, the output of Top-down Rerouting is a nice tree-cut decomposition. The lemma then follows from Lemma 11 and Lemma 10. $\square$

1.2 Proof of Lemma 2

We partition the nodes in $A_t$ into two sets: $A'_t$ contains all thin nodes in $A_t$ and $A''_t$ contains all the bold nodes in $A_t$. We claim that $|A'_t|\le k$ and $|A''_t|\le k+1$, which will establish the statement. The inequality $|A'_t|\le k$ is easy to see. Indeed, recall that $N(Y_b)\subseteq X_t \cup (V(G)\setminus Y_t)$ for every $b \in A'_t$ since $(T,{\mathcal {X}})$ is nice. Furthermore, each $b\in A'_t$ satisfies $N(Y_{b})\cap (V(G)\setminus Y_t)\ne \emptyset$ since otherwise, b would have been included in $B_t$. Therefore, each $b \in A'_t$ contributes at least one to the value ${\mathbf {adh}}(t)$. From ${\mathbf {adh}}(t)\le k$, the inequality follows.

To prove $|A''_t|\le k+1$, suppose $|A''_t|=\ell \ge k+2$ for the sake of contradiction. Consider the torso $H_t$ at t. For each $b\in A_t \cup B_t$, let $z_b$ be the vertex of $H_t$ obtained by consolidating the vertex set $Y_b$ in G and let $z_{top}$ be the vertex of $H_t$ obtained by consolidating the vertex set $V(G)\setminus Y_t$. Fix a sequence of suppressing vertices of degree at most two which yields a sequence of intermediate graphs $H_t=H_t^{(0)}, H_t^{(1)}, \cdots , H_t^{(m)}={\tilde{H}}_t$ with the following property: whenever it is possible to suppress $z_{top}$ as well as some other vertex, we always prioritize suppressing a vertex different from $z_{top}$.

Let us choose $b',b'' \in A''_t$ so that $z_{b'}$ and $z_{b''}$ are the first and the second (distinct) vertex among $z_b$ for all $b\in A''_t$ whose degree strictly decreases in this sequence. Such $b'$ and $b''$ must exist since at least two vertices $z_b$, where $b\in A''_t$, do not appear in ${\tilde{H}}_t$, and any $z_b$ may only be removed by suppression. Let $a',a'' \in A_t\cup B_t\cup \{top\}$ and $0\le i < j \le m$ be such that the first decrease in the degrees of $z_{b'}$ and $z_{b''}$ is due to suppressing of $z_{a'}\in V(H^{(i)}_t)$ and of $z_{a''}\in V(H^{(j)}_t)$. We observe that the respective degree of $z_{a'}$ and $z_{a''}$ are exactly one in $V(H^{(i)}_t)$ and in $V(H^{(j)}_t)$ since otherwise, the degree of $z_{b'}$ and $z_{b''}$ would not decrease.

We first argue that $a', a'' \in A''_t \cup \{top\}$. Notice that $z_{b'}$ and $z_{a'}$ are adjacent in $H_t^{(i)}$ and also, $z_{b''}$ and $z_{a''}$ are adjacent in $H_t^{(j)}$. This means that $z_{b'}z_{a'}$ and $z_{b''}z_{a''}$ are edges in $H_t$ as well. For the sake of contradiction, suppose $a' \in A'_t\cup B_t$. This means that $a'$ is a thin node. The property of a nice tree-cut decomposition implies $N(Y_{a'}) \cap Y_{b'}=\emptyset$ and thus $z_{b'}$ and $z_{a'}$ are non-adjacent in $H_t$. In particular, this implies that $z_{a'}$ must have been adjacent to $z_{top}$ in $H_t$ and $z_{top}$ must have been suppressed as a degree-2 vertex at some step $f<i$ to create an edge between $z_{a'}$ and $z_{b'}$. However, observe that in this case it would also have been possible to suppress $z_{top}$ immediately after suppressing $z_{a'}$, contradicting our assumption about the sequence of suppressions. The same argument applies to $a''$. It follows that $a',a''\in A''_t\cup \{top\}$. Furthermore, as a suppressing of a vertex removes it from the considered graph, either $a'$ or $a''$ belongs to $A''_t$. Since we pick $b'$ as the first $b \in A''_t$ such that the degree $z_{b}$ strictly decreases, it cannot be $a'\in A''_t$. Hence, we have $a'=top$ and $a''\in A''_t$. By a similar argument, we know that $a''=b'$.

Notice that the suppressing of $z_{a'}$, namely $z_{top}$, decreases the degree of $z_{b'}$ by one. That is, the degree of $z_{b'}$ in $H^{(i+1)}_t$ remains at least two. Now that the suppressing of $z_{b'}$ in $H^{(j)}_t$ strictly decreases the degree of $z_{b''}$, the degree of $z_{b'}$ in $H^{(j)}$ equals to one. This implies that there is a suppressing of a vertex, say $z_{a^*}$, which further decreases the degree of $z_{b'}$ between the sequence of $H^{(i+1)}_t$ and $H^{(j)}_t$. However, then $a^*\in A''_t$, which contradicts our choice of $b''$ and $H^{(j)}_t$. This proves $|A''_t|=\ell \le k+1$.