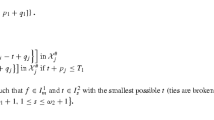Approximation Schemes for Minimizing the Maximum Lateness on a Single Machine with Release Times Under Non-availability or Deadline Constraints

Abstract

In this paper, we consider four single-machine scheduling problems with release times, with the aim of minimizing the maximum lateness. In the first problem we have a common deadline for all the jobs. The second problem looks for the Pareto frontier with respect to the two objective functions maximum lateness and makespan. The third problem is associated with a non-availability constraint. In the fourth one, the non-availability interval is related to the operator who is organizing the execution of jobs on the machine (no job can start, and neither can complete during the operator non-availability period). For each of the four problems, we establish the existence of a polynomial time approximation scheme.

1 Introduction

The problem we consider is the one-machine scheduling problem with release dates and delivery times. The objective is to minimize the maximum lateness. Formally, the problem is defined in the following way. We have to schedule a set $J=\{1,2,\ldots ,n\}$ of n jobs on a single machine. Each job $j\in J$ has a processing time $p_{j}$, a release time (or head) $r_{j}$ and a delivery time (or tail) $q_{j}$. The machine can only perform one job at a given time. Preemption is not allowed. The problem is to find a sequence of jobs, with the objective of minimizing the maximum lateness $L_{\max }=\max _{1\le j\le n}\left\{ C_{j}+q_{j}\right\}$ where $C_{j}$ is the completion time of job j. We also define $s_{j}$ as the starting time of job j, i.e., $C_{j}=s_{j}+p_{j}$, then $P=\sum _{j=1}^{n}p_{j}$ as the total processing time and $p(H)=\sum _{j\in H}p_{j}$ as the total processing time for a subset of jobs $H\subset J$. Four scenarios are considered:

• Scenario 1: Every job should be completed before a deadline d, i.e., $C_{\max }=\max _{1\le j\le n}\{C_{j}\}\le d$. This scenario is denoted as $1|r_{j},C_{\max }\le d|L_{\max }$. For a simpler notation, this variant is also abbreviated as $\Pi _{1}$.

• Scenario 2: We are given the one-machine bicriteria scheduling problem with the two objectives $L_{\max }$ and $C_{\max }$, denoted by $1|r_{j}|L_{\max }, C_{\max }$. We will speak shortly of problem $\Pi _{2}$.

• Scenario 3: The machine is not available during a given time interval $]T_{1},T_{2}[$. This scenario is denoted by $1,h_{1}|r_{j}|L_{\max }$. We will speak shortly of problem $\Pi _{3}$. Here, $]T_{1},T_{2}[$ is a machine non-availability (MNA) interval.

• Scenario 4: In this case, the non-availability interval $]T_{1},T_{2}[$ is related to the operator who is organizing the execution of jobs on the machine. An operator non-availability (ONA) period is an open time interval in which no job can start, and neither can complete. Using an extended notation as in [11], this scenario is denoted by $1,ONA|r_{j}|L_{\max }$. We will speak shortly of problem $\Pi _{4}$.

Note that the main difference between machine non-availability and operator non-availability consists in the fact that a job can be processed but can neither start nor finish during the ONA period. However, the MNA interval is a completely forbidden period.

All four presented scenarios are generalizations of the well-known problem $1|r_{j},q_{j}|L_{max}$ which has been widely studied in the literature. For the sake of simplicity, this problem will be denoted by $\Pi _{0}$. According to Lenstra et al. [16] problem $1|r_{j},q_{j}|L_{max}$ is NP-hard in the strong sense. Therefore, we are interested in the design of efficient approximation algorithms for our problems. Note that the four studied scenarios are strongly related and as a consequence the different algorithms we will propose later are linked. For example, we will see in the remainder of the paper that the algorithm elaborated for problem $\Pi _{4}$ uses the one developed for problem $\Pi _{3}$, which recalls the algorithm proposed for problem $\Pi _{1}$. All these links are carefully explained in the different proofs of our algorithms.

For self-consistency, we recall some necessary definitions related to the approximation area. A $\rho$-approximation algorithm for a problem of minimizing an objective function $\mathcal {\varphi }$ is an algorithm such that for every instance $\pi$ of the problem it gives a solution $S_{\pi }$ verifying $\mathcal {\varphi }\left( S_{\pi }\right) /\mathcal {\varphi }\left( OPT_{\pi }\right) \le \rho$ where $OPT_{\pi }$ is an optimal solution of $\pi$ . The value $\rho$ is also called the worst-case bound of the above algorithm.

A class of $\left( 1+\varepsilon \right)$-approximation algorithms is called a Polynomial Time Approximation Scheme (PTAS), if its running time is polynomial with respect to the length of the problem input for every $\varepsilon >0$. A class of $\left( 1+\varepsilon \right)$ -approximation algorithms is called a Fully Polynomial Time Approximation Scheme (FPTAS), if its running time is polynomial with respect to both the length of the problem input and $1/\varepsilon$ for every $\varepsilon >0$.

Given the aim of this paper, we summarize briefly related results on scheduling problems with non-availability constraints but no release times. A huge number of papers is devoted to such problems in the literature. This has been motivated by practical and real industrial problems, like maintenance problems or the occurrence of breakdown periods. For a survey we refer to the article by [15]. However, to the best of our knowledge, there is only a limited number of references related to the design of approximation algorithms in the case of maximum lateness minimization. Yuan et al [26] developed a PTAS for the problem without release dates. The paper by Kacem et al. [11] contains an FPTAS for $1,h_{1}||L_{\max }$ and $1,ONA||L_{\max }$. Kacem and Kellerer [9] consider different close semi-online variants ($1,h_{1}||C_{\max }$, $1,h_{1}|r_{j}|C_{\max }$ and $1,h_{1}||L_{\max }$) and propose approximation algorithms with effective competitive ratios.

Numerous works address problems with release times but without unavailability constraints. Most of the exact algorithms are based on enumeration techniques. See for instance the papers by Dessouky and Margenthaler [3], Carlier et al. [2], Larson et al. [14], Yin et al. [24, 25] and Grabowski et al. [6].

Various approximation algorithms were also proposed. Most of these algorithms are based on variations of the extended Jackson’s rule, also called Schrage’s algorithm. Schrage’s algorithm consists in scheduling ready jobs on the machine by giving priority to the one having the greatest tail. It is well-known that the Schrage sequence yields a worst-case performance ratio of 2. This was first observed by Kise et al. [13]. Potts [21] improves this result by running Schrage’s algorithm at most n times to slightly varied instances. The algorithm of Potts has a worst-case performance ratio of $\frac{3}{2}$ and it runs in $O(n^{2}\log n)$ time. Hall and Shmoys [7] showed that a modification of the algorithm of Potts has the same worst-case performance ratio under precedence constraints. Nowicki and Smutnicki [19] proposed a faster $\frac{3 }{2}$-approximation algorithm with $O(n\log n)$ running time. By performing the algorithm of Potts for the original and the inverse problem and taking the best solution Hall and Shmoys [7] established the existence of a $\frac{4}{3}$-approximation. They also proposed two polynomial time approximation schemes. A more effective PTAS has been proposed by Mastrolilli [18] for the single-machine and parallel-machine cases. For more details the reader is invited to consult the survey by Kellerer [12].

There are only a few papers which treat the problem with both release times and non-availability intervals. Leon and Wu [17] present a branch-and-bound algorithm for the problem with release times and several machine non-availability intervals. Gharbi et al. [5] investigate the single machine scheduling problem with job release dates, due dates and multiple planned unavailability time periods. They propose a new lower bound and an exact algorithm for that problem. A 2-approximation has been established by Kacem and Haouari [8] for $1,h_{1}|r_{j}|L_{\max }$.

Rapine et al. [22] have described some applications of operator non-availability problems in the planning of a chemical experiments. Brauner et al. [1] have studied single-machine problems under the operator non-availability constraint. Finally, we refer to the book by T’kindt and Billaut [23] for an introduction on multicriteria scheduling.

For each of the four problems $\Pi _{1}$, $\Pi _{2}$, $\Pi _{3}$ and $\Pi _{4}$ we will present a polynomial time approximation scheme. Notice, that the PTAS’s in [7] and [18] for $1|r_{j},q_{j}|L_{max}$ use modified instances with only a constant number of release dates. This is not possible in the presence of deadlines or non-availability periods since the feasibility of a solution would not be guaranteed. Notice that the four investigated scenarios are strongly NP-hard since already the problem $1|r_{j}|L_{\max }$ is strongly NP-hard. Consequently, no FPTAS can be derived unless P = NP and we limit our investigation to the existence of an PTAS.

The paper is organized as follows. Section 2 repeats some notations and results for Schrage’s sequence. Section 3 contains the PTAS for problem $\Pi _{1}$, Sect. 4 is devoted to the bicriteria scheduling problem $\Pi _{2}$, Sects. 5 and 6 deal with problems $\Pi _{3}$ and $\Pi _{4}$, respectively. Finally, Sect. 7 concludes the paper.

2 Schrage’s Algorithm

For self-consistency we repeat in this section some notations and results for the Schrage’s sequence, initially designed for problem $\Pi _{0}$ and later exploited for other extensions (see for instance Kacem and Kellerer [10]). Recall that Schrage’s algorithm schedules the job with the greatest tail from the available jobs at each step. At the completion of such a job, the subset of the available jobs is updated and a new job is selected. The procedure is repeated until all jobs are scheduled. For a given instance I the sequence obtained by Schrage shall be denoted by $\sigma _{Sc}(I)$. Assume that jobs are indexed such that $\sigma _{Sc}(I)=(1,2,\ldots ,n)$. The job c which attains the maximum lateness in Schrage’s schedule, is called the critical job. Then the maximum lateness of $\sigma _{Sc}(I)$ can be given as follows:

$$\begin{aligned} L_{max}(\sigma _{Sc}(I))=\min _{j\in \Lambda }\{r_{j}\}+\sum _{j\in \Lambda }{p_{j}} +q_{c}=r_{a}+\sum _{j=a}^{c}{p_{j}}+q_{c}, \end{aligned}$$

where job a is the first job so that there is no idle time between the processing of jobs a and c, i.e., either there is idle time before a or a is the first job to be scheduled. The sequence of jobs $a,a+1,\ldots ,c$ is called the critical path in the Schrage schedule (or the critical bloc $\Lambda$). It is obvious that all jobs j in the critical path have release dates $r_{j}\ge r_{a}$.

Let $L^{*}_{max}(I)$ denote the optimal maximum lateness for a given instance I. We will write briefly $L^{*}_{max}$ if it is clear from the context. For every subset of jobs $F \subset J$ the following useful lower bound is valid.

$$\begin{aligned} L^{*}_{max} \ge \min _{j \in F}\{r_{j}\} + \sum _{j \in F}{p_{j}} + \min _{j \in F}\{q_{j}\} \end{aligned}$$

(1)

If c has the smallest tail in $\Lambda =\{a,a+1,\ldots ,c\}$, sequence $\sigma _{Sc}(I)$ is optimal by inequality (1). Otherwise, there exists an interference job $b\in \Lambda$ such that

$$\begin{aligned} q_{b} < q_{c} \ \text{ and }\ q_{j}\ge q_{c}\ \text{ for } \text{ all } \ j \in \{b + 1, b + 2,\ldots , c-1\}. \end{aligned}$$

(2)

Let $\Lambda _{b}:=\{b+1,b+2,\ldots ,c\}$ be the jobs in $\Lambda$ processed after the interference job b. Clearly, $q_{j}\ge q_{c}>q_{b}$ and $r_{j}>s_{b}$ hold for all $j\in \Lambda _{b}$, where $s_{b}$ denotes the starting time of the interference job b. Inequality (1) applied to $\Lambda _{b}$ gives with (2) the lower bound

$$\begin{aligned} L_{max}^{*}\ge \min _{j\in \Lambda _{b}}r_{j}+p(\Lambda _{b})+\min _{j\in \Lambda _{b}}q_{j}>s_{b}+p(\Lambda _{b})+q_{c}. \end{aligned}$$

(3)

where $p(\Lambda _{b})$ is the sum of processing times of jobs in $\Lambda _{b}$.

Since there is no idle time during the execution of the jobs of the critical sequence, the maximum lateness of Schrage’s schedule is $L_{\max }(\sigma _{Sc}(I))=s_{b}+p_{b}+p(\Lambda _{b})+q_{c}$. Subtracting this equation from (3) we get the following upper bound for the absolute error in terms of the processing time $p_{b}$ of the interference job b

$$\begin{aligned} L_{max}(\sigma _{Sc}(I))-L_{max}^{*}<p_{b}. \end{aligned}$$

(4)

Notice that using $L^{*}_{max}\ge p_{b}$ and applying inequality (4) shows that Schrage yields a relative performance guarantee of 2.

It is well-known that Schrage’s sequence is optimal with respect to the makespan, i.e.,

$$\begin{aligned} C_{\max }(\sigma _{Sc}(I))=C_{max}^{*}. \end{aligned}$$

(5)

3 PTAS for the First Scenario: $1|r_{j},C_{j}\le d|L_{\max }$

In this section, we consider problem $\Pi _{1}$ with a common deadline d for the jobs. By (5) the Schrage sequence shows whether a feasible solution for $\Pi _{1}$ exists or not. If $C_{\max }(\sigma _{Sc}(I))>d$, then the problem has no feasible solution. Hence, we will assume in the following that

$$\begin{aligned} C_{\max }(\sigma _{Sc}(I))\le d \end{aligned}$$

(6)

Let $\varepsilon >0$. A job j is called large if $p_{j}\ge \varepsilon L_{\max }(\sigma _{Sc}(I))/2$, otherwise it is called small. Let L be the subset of large jobs. Since $L_{\max }(\sigma _{Sc}(I))\le 2L_{\max }^{*}$ (see [13]), it can be observed that $|L|\le 2/\varepsilon$. Let $k=|L|$. We assume that jobs are indexed such that $L=\{1,2,\ldots ,k\}$.

Our PTAS is based on the construction of a set of modified instances starting from the original instance I. Set $R=\{r_{1},\ldots ,r_{n}\}$ and $Q=\{q_{1},\ldots ,q_{n}\}$. Let us define the following sets of heads and tails:

$$\begin{aligned} R\left( i\right)&=\{r_{j}\in R|r_{j}\ge r_{i}\},\quad i=1,2,\ldots ,k, \\ Q(i)&=\{q_{j}\in Q|q_{j}\ge q_{i}\}, \quad i=1,2,\ldots ,k. \end{aligned}$$

Now, we define the set of all the combinations of couples $(r,q)\in R\left( i\right) \times Q(i)$ for every $i=1,2,\ldots ,k$:

$$\begin{aligned} W=\{(\widetilde{r}_{1},\widetilde{q}_{1},\widetilde{r}_{2},\widetilde{q} _{2},\ldots ,\widetilde{r}_{k},\widetilde{q}_{k})|\widetilde{r}_{i}\in R\left( i\right) ,\widetilde{q}_{i}\in Q\left( i\right) ,\quad i=1,2,\dots , k\} \end{aligned}$$

Clearly, the cardinality of W is bounded as follows:

$$\begin{aligned} |W|\le n^{2k}=O(n^{4/\varepsilon }). \end{aligned}$$

Let $w\in W$ with $w=(\widetilde{r}_{1},\widetilde{q}_{1},\widetilde{r}_{2}, \widetilde{q}_{2},\ldots ,\widetilde{r}_{k},\widetilde{q}_{k})$. Instance $I_{w}$ is a slight modification of instance I and is defined as follows. $I_{w}$ consists of large and small jobs. The k large jobs have modified release times $\widetilde{r}_{1},\widetilde{r}_{2},\ldots ,\widetilde{r}_{k}$ and delivery times $\widetilde{q}_{1},\widetilde{q}_{2},\ldots ,\widetilde{q} _{k}$. All processing times and the $n-k$ small jobs remain unchanged. Let ${\mathcal {I}}$ be the set of all possible instances $I_{w}$, i.e.,

$$\begin{aligned} {\mathcal {I}}=\{I_{w}|w\in W\}. \end{aligned}$$

It is clear that $|{\mathcal {I}}|$ is in $O(n^{4/\varepsilon })$. By the modification, the processing times of instances in ${\mathcal {I}}$ are not changed and release times and delivery times are not decreased.

Let $\widetilde{{\mathcal {I}}}\subseteq {\mathcal {I}}$. An instance $I^{\prime }\in \widetilde{{\mathcal {I}}}$ is called maximal if there is no other instance $I^{\prime \prime }\in \widetilde{{\mathcal {I}}}$ such that for every $i=1,2,\ldots ,k$, we have $r_{i}^{\prime }\le r_{i}^{\prime \prime }$, $q_{i}^{\prime }\le q_{i}^{\prime \prime }$ and at least one inequality is strict. Here, $r_{i}^{\prime }, q_{i}^{\prime }$ denote the heads and tails in $I^{\prime }$ and $r_{i}^{\prime \prime }, q_{i}^{\prime \prime }$ the heads and tails in $I^{\prime \prime }$, respectively.

Now, we can introduce our procedure PTAS1 which depends on the instance I, the deadline d and the accuracy $\varepsilon$.

Algorithm $PTAS1(I,d,\varepsilon )$

Input: :

An instance I of n jobs, a deadline d and an accuracy $\varepsilon$.

Output: :

A sequence $\sigma (I)$ with $L_{\max }(\sigma (I))\le (1+\varepsilon )L_{\max }^{*}$ and $C_{\max }(\sigma (I))\le d$.

1.:

Run Schrage’s algorithm for all instances in ${\mathcal {I}}$.

2.:

Select the best feasible solution, i.e., the best solution with $C_{\max }\le d$. Apply the corresponding sequence to the original instance I.

Let $\sigma ^{*}\left( I\right)$ be a sequence for instance I which is optimal for $L_{\max }$ under the constraint $C_{\max }(\sigma ^{*}(I))\le d$. Let $\widetilde{I}\in {\mathcal {I}}$ be an instance which is compatible with $\sigma ^{*}\left( I\right)$, i.e.,

$$\begin{aligned}&C_{\max }(\sigma ^{*}(\widetilde{I}))\le d, \end{aligned}$$

(7)

$$\begin{aligned}&\widetilde{r}_{j}\le s_{j}(\sigma ^{*}\left( I\right) ) \text { for } j=1,2,\ldots ,k, \end{aligned}$$

(8)

$$\begin{aligned}&L_{\max }( \sigma ^{*}(\widetilde{I})) = L_{\max }(\sigma ^{*}(I)). \end{aligned}$$

(9)

The set of all instances $\widetilde{I}\in {\mathcal {I}}$ which are compatible with $\sigma ^{*}$ is denoted as ${\mathcal {I}}_{\sigma ^{*}}$. By (6) instance I fulfills the conditions (7)–(9). Thus, ${\mathcal {I}}_{\sigma ^{*}}$ is nonempty.

Theorem 1

Algorithm PTAS1 yields a $(1+\varepsilon )$-approximation for $\Pi _{1}$ and has polynomial running time for fixed $\varepsilon$. It can be implemented in $O\left( \ln \left( n\right) \cdot n^{\left( 1+4/\varepsilon \right) }\right)$.

Proof

Let $I_{\max }$ be a maximal instance in ${\mathcal {I}}_{\sigma ^{*}}$. Applying Schrage’s algorithm to $I_{\max }$ gives the sequence $\sigma _{Sc}(I_{\max })$. We show

$$\begin{aligned} C_{\max }(\sigma _{Sc}(I_{\max }))\le d \end{aligned}$$

(10)

and

$$\begin{aligned} L_{\max }(\sigma _{Sc}(I_{\max }))\le (1+\varepsilon )L_{\max }(\sigma ^{*}(I)). \end{aligned}$$

(11)

From (5) and (7) we conclude that $C_{\max }(\sigma _{Sc}(I_{\max }))\le C_{\max }(\sigma ^{*}(I_{\max }))\le d$ and (10) follows.

Several cases are distinguished:

• Case 1: $\sigma _{Sc}(I_{\max })$ is optimal, i.e., $L_{\max }(\sigma _{Sc}(I_{\max }))=L_{\max }(\sigma ^{*}(I))$ and by (9) we get (11).

• Case 2: $\sigma _{Sc}(I_{\max })$ is not optimal. Thus, there is an interference job b. Recall that $\Lambda _{b}=\{b,b+1,\ldots ,c\}$ is the set of jobs processed after the interference job until the critical job c. By (4) $L_{\max }(\sigma _{Sc}(I_{\max }))-L_{\max }(\sigma ^{*}(I_{ \max }))<p_{b}$. If b is not large, then (11) follows immediately with (4). Otherwise, two subcases occur.

Subcase 2a: $\sigma _{Sc}(I_{\max })$ is not optimal and at least one job of $\Lambda _{b}$ is processed before b in the optimal solution. Thus, b cannot start before $r_{\min }=\min _{i\in \Lambda _{b}}\{r_{i}\}>s_{b}$. Consequently, $r_{b}$ can be increased to $r_{\min }$ and the new instance fulfills the conditions (7)–(9), which contradicts the maximality of $I_{\max }$.

Subcase 2b: $\sigma _{Sc}(I_{\max })$ is not optimal and all the jobs of $\Lambda _{b}$ are processed after b in the optimal solution. Thus, $q_{b}$ can be increased to $q_{c}$ and the new instance fulfills the conditions (7)–(9), which again contradicts the maximality of $I_{\max }$.

Thus, we have found a sequence which is a $(1+\varepsilon )$-approximation for $\Pi _{1}$. Since ${\mathcal {I}}$ has at most $O(n^{4/\varepsilon })$ elements and Schrage’s sequence can be computed in $O(n\ln \left( n\right) )$, algorithm PTAS1 runs in polynomial time. Its overall running time is in $O\left( \ln \left( n\right) \cdot n^{\left( 1+4/\varepsilon \right) }\right)$. $\square$

4 PTAS for the Second Scenario: $1|r_{j}|L_{\max }, C_{\max }$

Computing a set of solutions which covers all possible trade-offs between different objectives can be understood in different ways. We will define this (as most commonly done) as searching for “efficient” solutions. Given an instance I a sequence $\sigma (I)$ dominates another sequence $\sigma ^{\prime }(I)$ if

$$\begin{aligned} L_{\max }(\sigma (I))\le L_{\max }(\sigma ^{\prime }(I)) \text{ and } C_{\max }(\sigma (I))\le C_{\max }(\sigma ^{\prime }(I)) \end{aligned}$$

(12)

and at least one of the inequalities (12) is strict. The sequence $\sigma (I)$ is called efficient or Pareto optimal if there is no other sequence which dominates $\sigma (I)$. The set ${\mathcal {P}}$ of efficient sequence for I is called Pareto frontier.

We have also to define what we mean by an approximation algorithm with relative performance guarantee for our bicriteria scheduling problem. A sequence $\sigma (I)$ is called a $(1+\varepsilon )$-approximation algorithm of a sequence $\sigma ^{\prime }(I)$ if

$$\begin{aligned} L_{\max }(\sigma (I))\le (1+\varepsilon ) L_{\max }(\sigma ^{\prime }(I)) \end{aligned}$$

(13)

and

$$\begin{aligned} C_{\max }(\sigma (I))\le (1+\varepsilon ) C_{\max }(\sigma ^{\prime }(I)) \end{aligned}$$

(14)

hold.

A set $\mathcal {F_{\varepsilon }}$ of schedules for I is called a $(1+\varepsilon )$-approximation of the Pareto frontier if, for every sequence $\sigma ^{\prime }(I)\in {\mathcal {P}}$, the set $\mathcal { F_{\varepsilon }}$ contains at least one sequence $\sigma (I)$ that is a $(1+\varepsilon )$-approximation of $\sigma ^{\prime }(I)$.

A PTAS for the Pareto frontier is an algorithm which outputs for every $\varepsilon >0$, a $(1+\varepsilon )$-approximation of the Pareto frontier and runs in polynomial time in the size of the input.

The Pareto frontier of an instance of a multiobjective optimization problem may contain an arbitrarily large number of solutions. On the contrary, for every $\varepsilon >0$ there exists a $(1+\varepsilon )$-approximation of the Pareto frontier that consists of a number of solutions that is polynomial in the size of the instance and in $\frac{1}{\varepsilon }$ (under reasonable assumptions). An explicit proof for this observation was given by Papadimitriou and Yannakakis [20]. Consequently, a PTAS for a multiobjective optimization problem does not only have the advantage of computing a provably good approximation in polynomial time, but also has a good chance of presenting a reasonably small set of solutions.

Our PTAS for the Pareto frontier of problem $\Pi _{2}$ has even the stronger property that for every sequence $\sigma ^{\prime }(I)\in {\mathcal {P}}$, the set $\mathcal {F_{\varepsilon }}$ contains a sequence such that (13) holds and (14) is replaced by the inequality

$$\begin{aligned} C_{\max }(\sigma (I)) \le C_{\max } (\sigma ^{\prime }(I)). \end{aligned}$$

(15)

Algorithm $PTAS2(I,\varepsilon )$

Input: :

An instance I of n jobs and an accuracy $\varepsilon$.

Output: :

A PTAS for the Pareto frontier of problem $\Pi _{2}$.

1.:

Run Schrage’s algorithm for all instances in ${\mathcal {I}}$ and store the solutions in set $\mathcal {F_{\varepsilon }}$.

2.:

Remove all sequences from $\mathcal {F_{\varepsilon }}$ which are dominated by other sequences in $\mathcal {F_{\varepsilon }}$.

Theorem 2

Algorithm PTAS2 yields a PTAS for problem $\Pi _{2}$ such that for every sequence $\sigma ^{\prime }(I)\in {\mathcal {P}}$, the set $\mathcal { F_{\varepsilon }}$ contains a sequence $\sigma (I)$ such that (13) and (15) hold. PTAS2 has polynomial running time for fixed $\varepsilon$. It can be implemented in $O\left( \ln \left( n\right) \cdot n^{\left( 1+4/\varepsilon \right) }\right)$.

Proof

The running time of PTAS2 is polynomial because the set ${\mathcal {I}}$ contains only a polynomial number of instances. More precisely, PTAS2 has the same running time as PTAS1. Let $\sigma ^{\prime }(I)$ be a Pareto optimal sequence for problem $\Pi _{2}$ with $C_{\max }(\sigma ^{ \prime }(I))=d$. Algorithm $PTAS1(I,d,\varepsilon )$ of Sect. 3 outputs a sequence $\sigma (I)$ which fulfills both (13) and (15). Since sequence $\sigma (I)$ is also found in Step 1 of Algorithm PTAS2, the theorem follows. $\square$

5 PTAS for the Third Scenario: $1,h_{1}|r_{j}|L_{\max }$

The third scenario $1,h_{1}|r_{j}|L_{\max }$, denoted as $\Pi _{3}$, is studied in this section. The proposed PTAS for this scenario is related to the first one and it is based on several steps. In the remainder of this section, I denotes a given instance of $\Pi _{3}$ and $\varepsilon$ is the desired accuracy. Since a 2-approximation for $1,h_{1}|r_{j}|L_{\max }$ has been established in [8], we consider only $\varepsilon <1$. Without loss of generality, in any instance I of problem $\Pi _{3}$, we assume that $r_{j}\notin [T_{1},T_{2}[$ for $j\in J$ and that if $r_{j}<T_{1}$, then the inequality $r_{j}+p_{j}\le T_{1}$ should hold. Otherwise, in both cases, $r_{j}$ would be set equal to $T_{2}$. Thus, jobs in J can be partitioned in two disjoint subsets X and Y:

$$\begin{aligned} X&=\{j\in J|r_{j}+p_{j}\le T_{1}\}\nonumber \\ Y&=\{j\in J|r_{j}\ge T_{2}\} \end{aligned}$$

(16)

Finally, we assume that $1/\varepsilon$ is integer ($1/\varepsilon =f$) and that every instance I of problem $\Pi _{3}$ respects the conditions expressed in the following proposition.

Proposition 3

With no ($1+\varepsilon$)-loss, every instance I of $\Pi _{3}$ contains at most f different tails from the set $\{\varepsilon \overline{q},2\varepsilon \overline{q},3\varepsilon \overline{q},\ldots ,\overline{q}\}$, where $\overline{q }=\max _{j\in J}\{q_{j}\}$.

Proof

We simplify the instance I as follows. Split the interval $[0,\max _{j\in J}\{q_{j}\}]$ into $1/\varepsilon$ equal length intervals and round up every tail $q_{j}$ to the next multiple of $\varepsilon \overline{q}$. Clearly, every tail will not be increased by more than $\varepsilon \overline{q} \le \varepsilon L_{\max }^{*}(I)$. Then, we obtain that the modified instance has an optimal solution of a maximum lateness less than or equal to $\left( 1+\varepsilon \right) L_{\max }^{*}(I)$. $\square$

Since all the jobs of Y should be scheduled after $T_{2}$ in any feasible solution of I, our PTAS will focus on subset X. More precisely, this PTAS will be based on guessing the disjoint subsets $X_{1}$ and $X_{2}$ ($X_{1}\subset X$, $X_{2}\subset X$ and $X_{1}\cup X_{2}=X$) such that $X_{1}$ (respectively $X_{2}$) contains the jobs to be scheduled before $T_{1}$ (respectively after $T_{2}$). In the optimal solution, we will denote the jobs of X to be scheduled before $T_{1}$ (respectively after $T_{2}$) by $X_{1}^{*}$ (respectively by $X_{2}^{*}$). It is clear that if we are able to guess correctly $X_{1}^{*}$ in polynomial time, then it is possible to construct a PTAS for $\Pi _{3}$. Indeed, we can associate the scheduling of the jobs in $X_{1}^{*}$ before $T_{1}$ with a special instance $I_{1}^{*}$ of $\Pi _{1}$ where the jobs to be scheduled are those in subset $X_{1}^{*}$ and the deadline is equal to $T_{1}$. On the other hand, the scheduling of the other jobs in $X_{2}^{*}\cup Y$ after $T_{2}$ can be seen as a special instance $I_{2}^{*}$ of problem $\Pi _{0}$ , with all release times greater or equal to $T_{2}$. Consequently,

$$\begin{aligned} L_{\max }^{*}(I)=\max \{L_{\max }^{*}(I_{1}^{*}),L_{\max }^{ *}(I_{2}^{*})\} \end{aligned}$$

(17)

Clearly, the optimal sequence $\sigma _{1}^{*}$ of $I_{1}^{*}$ should satisfy the feasibility condition

$$\begin{aligned} C_{\max }(\sigma _{1}^{*}(I_{1}^{*}))\le T_{1}. \end{aligned}$$

(18)

As a consequence, by applying PTAS1 with $d=T_{1}$ or another existing PTAS for $\Pi _{0}$ (for example PTAS1 with d set to $\infty$ or the PTAS by Hall and Shmoys [7]), we would get a PTAS for problem $\Pi _{3}$. Unfortunately, it is not possible to guess the exact subset $X_{1}^{*}$ in a polynomial time, since the potential number of the candidate subsets $X_{1}$ is exponential. Nevertheless, we will show later that we can guess in a polynomial time another close/approximate subset $X_{1}^{\#}$ for which the associated instance $I_{1}^{\#}$ of $\Pi _{1}$ and its optimal solution $\sigma _{1}^{\#}$ verify the following relations:

$$\begin{aligned} L_{\max }(\sigma _{1}^{\#}(I_{1}^{\#}))\le \left( 1+\varepsilon \right) L_{\max }(\sigma _{1}^{*}(I_{1}^{*})), \end{aligned}$$

(19)

$$\begin{aligned} C_{\max }(\sigma _{1}^{\#}(I_{1}^{\#}))\le C_{\max }(\sigma _{1}^{*}(I_{1}^{*})). \end{aligned}$$

(20)

As the core of our problem of designing a PTAS for $\Pi _{3}$ is to schedule correctly the jobs of X, our guessing approach will be based on a specific structure on X. In the next paragraph, we will describe such a structure. Then, we present our PTAS and its proof.

5.1 Defining a Structure for the Jobs in X

In this section, we will focus on the jobs of X and partition them into subsets. Recall that $P=\sum _{j=1}^{n}p_{j}$. Set

$$\begin{aligned} \delta =\frac{\varepsilon ^{2}P}{4}. \end{aligned}$$

A job $j\in X$ is called a big job if $p_{j}>\delta$. Let $B\subset X$ denote the set of big jobs. Obviously, $|B|< 4/\varepsilon ^{2}$. The set $S = X\backslash B$ represents the subset of small jobs. We partition S into f subsets S(k), $1\le k\le f$, where jobs in S(k) have identical tails of length $k\varepsilon \overline{q}$.

In the next step, jobs in S(k) are sorted in non-decreasing order of release times. In other words, jobs in S(k) are encoded by pairs of integers

$$\begin{aligned} (k,1),(k,2),\ldots ,(k,|S(k)|) \end{aligned}$$

such that

$$\begin{aligned} r_{(k,1)}\le r_{(k,2)}\le \cdots \le r_{(k,|S(k)|)}. \end{aligned}$$

(21)

Set $m(k)=\lceil p(S(k))/\delta \rceil$. Hence, m(k) is in $O(4/\varepsilon ^{2})$. For every k and z with $1\le k\le f$ and $1\le z\le m(k)$, the subset $S_{k,z}=\{(k,1),(k,2),\ldots ,(k,e(z))\}$ is composed of the e(z) jobs of S(k) with the smallest release times, such that its total processing time $p\left( S_{k,z}\right) =\sum _{l=1}^{e(z)}p_{(k,l)}$ fulfills

$$\begin{aligned} (z-1)\delta <p\left( S_{k,z}\right) \le z\delta , \end{aligned}$$

(22)

and e(z) is the largest integer for which (22) holds. Moreover, define $S_{k,0}=\emptyset$ and $e(0)=0$. Note that $S_{k,m(k)}=S(k)$.

5.2 Description of the PTAS for $\Pi _{3}$

As we mentioned before, our proposed PTAS for problem $\Pi _{3}$ is based on guessing the subset of jobs $X_{1}\subset X$ to be scheduled before $T_{1}$ (Subset $X_{2}=X\backslash X_{1}$ will be scheduled after $T_{2}$). For every guessed subset $X_{1}\subset X$ in our PTAS, we associate an instance $I_{1}$ of $\Pi _{1}$ with $d=T_{1}$. To the complementary subset $X_{2}\cup Y$ we associate an instance $I_{2}$ of $\Pi _{0}$ after setting all the release times in $X_{2}$ to $T_{2}$. In order to solve the generated instances $I_{2}$, we use PTAS1 with $d=\infty$. (Alternatively, we could also use the existing PTAS by Hall and Shmoys for $\Pi _{0}$. More details on this PTAS are available in [7]). We will abbreviate $PTAS1(I,\infty , \varepsilon )$ by $PTAS0(I,\varepsilon )$. For instances $I_{1}$ we apply $PTAS1(I_{1},T_{1},3\varepsilon /5)$ and for instances $I_{2}$, we apply $PTAS0(I_{2},\varepsilon /3)$. The guessing of $X_{1}$ and the details of our PTAS are described in procedure PTAS3.

Algorithm $PTAS3(I,T_{1},T_{2},\varepsilon )$

Input: :

An instance I of n jobs, integers $T_{1}, T_{2}$ with $T_{1}\le T_{2}$ and an accuracy $\varepsilon$.

Output: :

A sequence $\sigma (I)$ with $L_{\max }(\sigma (I))\le (1+\varepsilon )L_{\max }^{*}\left( I\right)$ respecting the non-availability interval $]T_{1},T_{2}[$.

1.:

The big jobs $B_{1}$ to be included in $X_{1}$ are guessed from B by complete enumeration. For every guess of $B_{1}$, the jobs $B\backslash B_{1}$ will be a part of $X_{2}$.

2.:

The small jobs to be included in $X_{1}$ are guessed for each subset S(k), $1\le k\le f$, by choosing one of the $m(k)+1$ possible subsets $S_{k,z}$, $0\le z\le m(k)$. Thus, $X_{1}=B_{1}\cup _{k=1}^{f}S_{k,z}$ and $X_{2}=\left( B\backslash B_{1}\right) \cup _{k=1}^{f}\left( S(k)\backslash S_{k,z}\right)$. Set all the release times of jobs in $X_{2}$ to $T_{2}$.

3.:

With every guessed subset $X_{1}$ in Step 2, we associate an instance $I_{1}$ of $\Pi _{1}$ with $d=T_{1}$. With the complementary subset $X_{2}\cup Y$ we associate an instance $I_{2}$ of $\Pi _{0}$. Apply $PTAS1(I_{1} ,T_{1},3\varepsilon /5)$ for solving instance $I_{1}$ of $\Pi _{1}$ and $PTAS0(I_{2},\varepsilon /3)$ for solving instance $I_{2}$ of $\Pi _{0}$. Let $\sigma _{1}$ and $\sigma _{2}$ be the obtained schedules from $PTAS1(I_{1} ,T_{1},3\varepsilon /5)$ and $PTAS0(I_{2},\varepsilon /3)$, respectively. If they are feasible, then merge $\sigma _{1}$ and $\sigma _{2}$ to get $\sigma$, which represents a feasible solution for instance I of $\Pi _{3}$.

4.:

Return $\sigma (I)$, the best feasible schedule from all the complete merged schedules for I in Step 3.

5.3 Proof of the PTAS for $\Pi _{3}$

Denote the jobs from S(k) which are scheduled before $T_{1}$ in the optimal solution by $S_{k,*}$. If

$$\begin{aligned} 0\le p\left( S_{k,*}\right) <p(S_{k})=p\left( S_{k,m(k)}\right) , \end{aligned}$$

there is an integer $z_{k}\in \{0,1,\ldots ,m(k)-1\}$ such that

$$\begin{aligned} z_{k}\delta \le p\left( S_{k,*}\right) < (z_{k}+1)\delta . \end{aligned}$$

(23)

We will see in the following lemma that we can get a sufficient approximation by taking the jobs of $S_{k,z_{k}}$, $z_{k}=0,1,\ldots , m(k)$, instead of those in $S_{k,*}$. In particular, we will see that it is possible to schedule heuristically before $T_{1}$ the jobs in $S_{k,z_{k}}$ instead of those in $S_{k,*}$ without altering the optimal performance too much. By selecting jobs with minimal release times we maintain the feasibility of inserting these jobs before $T_{1}$ instead of $S_{k,*}$. Inequalities (22) and (23) imply that there is an integer $z_{k}\in \{0,1,\ldots ,m(k)-1\}$ such that

$$\begin{aligned} p\left( S_{k,z_{k}}\right) \le p\left( S_{k,*}\right) \le p\left( S_{k,z_{k}}\right) +2\delta \end{aligned}$$

(24)

holds for $0\le p\left( S_{k,*}\right) <p\left( S_{k}\right)$.

Note that if $S_{k,*}=S(k)$ holds, the guessing procedure ensures that for $z_{k}=m(k)$ we get $S_{k,m(k)}=S(k)$. The choice of $S_{k,z_{k}}$ is illustrated in Fig. 1.

Fig. 1

Relation between $S_{k,z_{k}}$ and $S_{k,*}$

Recall that $X_{1}^{*}$ (respectively $X_{2}^{*}\cup Y$) is the subset of jobs to be scheduled before $T_{1}$ (respectively after $T_{2}$) in the optimal schedule $\sigma ^{*}(I)$ of a given instance I of $\Pi _{3}$. Let $I_{1}^{*}$, $I_{2}^{*}$ denote the corresponding instances of problems $\Pi _{1}$ and $\Pi _{0}$, and $\sigma _{1}^{*}(I_{1}^{*})$, $\sigma _{2}^{*}(I_{2}^{*})$ the associated optimal schedules, respectively. Then, we get.

Lemma 4

There is a subset $X_{1}^{\#}\subset X$, generated in Step 2 of PTAS3, for which we can construct two feasible schedules $\sigma _{1}^{\#}(I_{1}^{\#})$ and $\sigma _{2}^{\#}(I_{2}^{\#})$ such that:

$$\begin{aligned} L_{\max }(\sigma _{1}^{\#}(I_{1}^{\#}))\le L_{\max }(\sigma _{1}^{*}(I_{1}^{*}))+f\delta , \end{aligned}$$

(25)

$$\begin{aligned} C_{\max }(\sigma _{1}^{\#}(I_{1}^{\#}))\le C_{\max }(\sigma _{1}^{*}(I_{1}^{*})), \end{aligned}$$

(26)

$$\begin{aligned} L_{\max }(\sigma _{2}^{\#}(I_{2}^{\#}))\le L_{\max }(\sigma _{2}^{*}(I_{2}^{*}))+2f\delta , \end{aligned}$$

(27)

where $I_{1}^{\#}$ is an instance of $\Pi _{1}$ where we have to schedule the jobs of $X_{1}^{\#}$ before $T_{1}$ and $I_{2}^{\#}$ is an instance of $\Pi _{0}$ where we have to schedule the jobs of $(X\backslash X_{1}^{\#})\cup Y$ after $T_{2}$.

Proof

Let $B_{1}^{*}$ be the subset of big jobs contained in $X_{1}^{*}$. The other jobs of $X_{1}^{*}$ are small and belong to $\cup _{k=1}^{f}S(k)$ . Hence,

$$\begin{aligned} X_{1}^{*}=B_{1}^{*}\cup \bigcup \limits _{k=1}^{f}S_{k,*} \end{aligned}$$

and $X_{1}^{\#}$ will have the following structure:

$$\begin{aligned} X_{1}^{\#}=B_{1}^{*}\cup \bigcup \limits _{k=1}^{f}S_{k,z_{k}}. \end{aligned}$$

Obviously, subset $B_{1}^{*}$ can be guessed correctly in Step 2 of PTAS3 since PTAS3 considers all possible subsets of B. Therefore, for proving that subset $X_{1}^{\#}$ is a good guess, we need to prove that the guessing of each subset $S_{k,z_{k}}$ is close enough to $S_{k,*}$, but with smaller total processing time.

First, we observe that if $S_{k,*}=\varnothing$ or $S_{k,*}=S(k)$, then the guessing is perfect, i.e. $S_{k,*}=S_{k,z}$.

If $S_{k,*}\not =\varnothing$, we can determine intervals where only jobs of $S_{k,*}$ are scheduled in the optimal schedule $\sigma _{1}^{ *}(I_{1}^{*})$ and which contain no idle time. Denote those intervals by

$$\begin{aligned} G_{1,k} = [a_{1,k}^{*},b_{1,k}^{*}], G_{2,k} = [a_{2,k}^{*},b_{2,k}^{*}], \ldots , G_{\gamma _{k},k} = [a_{\gamma _{k},k}^{*},b_{\gamma _{k},k }^{*}],\quad k=1,\ldots ,f, \end{aligned}$$

where $\gamma _{k}$ is a certain finite integer. Set

$$\begin{aligned} G_{k} =\bigcup _{u=1}^{\gamma _{k}}G_{u,k}, \quad k=1,\ldots ,f. \end{aligned}$$

Otherwise, in case $S_{k,*}=\varnothing$, we set $G_{k}=\emptyset$. Finally, define

$$\begin{aligned} G =\bigcup _{k=1}^{f}G_{k}. \end{aligned}$$

In addition, we recall that $S_{k,z_{k}}=\{(k,1),(k,2),\ldots ,(k,e(z_{k}))\}$. In our feasible schedule $\sigma _{1}^{\#}(I_{1}^{\#})$, we will schedule the jobs of this subset $S_{k,z_{k}}$ according to the following heuristic procedure Schedule$^{\mathbf {\#}}$. It assigns the jobs to the intervals $G_{u,k}$ but throughout the procedure starting and finish times of these intervals may be changed (e.g. when there is some overload of jobs) or they are simply shifted to the right.

Procedure Schedule$^{\mathbf {\#}}$

• 1. For $k=1$ to f do:

• 2. $\alpha _{0}:=0;$

• 3. For $u=1$ to $u=\gamma _{k}$ do:

  • 3.1 Process remaining jobs from $S_{k,z_{k}}$ (in non-decreasing order of release dates) starting at time $a_{u,k}^{*}+\alpha _{u-1}$ until the first job finishes at time $t\ge b_{u,k}^{*}$ or all jobs from $S_{k,z_{k}}$ are assigned. Let job (k, l) be the last scheduled job from this set with completion time $C_{(k,l)}$.

  • 3.2 If $l=e(z_{k})$ set $G_{u,k}=[a_{u,k}^{*}+\alpha _{u-1},\,b_{u,k}^{*}]$ and Stop: All items from $S_{k,z_{k}}$ are assigned.

  • 3.3 Else set $\alpha _{u}=C_{(k,l)}-b_{u,k}^{*}$ and $G_{u,k}=[a_{u,k}^{*}+\alpha _{u-1},\,b_{u,k}^{*}+\alpha _{u}]=[a_{u,k}^{ *}+\alpha _{u-1},\,C_{(k,l)}]$.

  • 3.4 Shift intervals from G which are located between $b_{u,k}^{*}$ and $a_{u+1,k}^{*}$ without any modification of their lengths by $\alpha _{u+1}$ to the right.

  • 3.5 End If/Else

• 4. End For

• 5. End For

Notice that the value $\alpha _{u}$ represents the “overload” of the uth interval $G_{u,k}$ in a given set $G_{k}$. The next interval $G_{u+1,k}$ is then shortened by the same amount $\alpha _{u}$. Consequently, only the intervals between $G_{u,k}$ and $G_{u+1,k}$ are shifted to the right, but no others. Moreover, the total processing time assigned until $b_{u+1,k}^{*}$ in the kth iteration of Schedule$^{\#}$ is not greater than the original total length of the intervals $G_{1,k}, G_{2,k},\ldots , G_{u+1,k}$. Since for every family k the jobs in $S_{k,z_{k}}$ have the smallest release times and since by (21) these jobs are sorted in non-decreasing order of release times, no idle time is created during Step 3. Together with the first inequality of (24) this guarantees that all jobs of family k are processed without changing the right endpoint of the last interval $G_{\gamma _{k},k}$, i.e., creating no overload in this interval. That ensures the feasibility of the schedule yielded by Schedule$^{\mathbf {\#}}$ and that $G_{\gamma _{k},k}=[a_{ \gamma _{k},k}^{*}+\alpha _{\gamma _{k}-1},\,b_{\gamma _{k},k}^{*}]$.

In each iteration of the procedure the jobs will be delayed by at most $\max _{u\le \gamma _{k}}\{\alpha _{u}\}\le \delta$. Since this possible delay may occur for every family k, $k=1,2,\ldots ,f$, the possible overall delay for every job, after the f applications of procedure Schedule$^{\#}$ is therefore bounded by $f\delta$. Hence, (25) follows.

The finishing time of the last interval among the intervals $G_{\gamma _{k},k}, k=1,\ldots , f$, generated by Schedule$^{\#}$ determines the makespan of instance $I_{1}^{\#}$. But this interval is never shifted to the right and we obtain (26).

Recall that if $S_{k,*}=S(k)$, we get with $z_{k}=m(k)$ that $S_{k,m(k)}=S(k)$. Hence, in the case that no jobs of family k are scheduled after $T_{2}$ in $\sigma _{2}^{*}(I_{2}^{*})$, also $\sigma _{2}^{\#}(I_{2}^{\#})$ contains no jobs of family f.

Hence, assume in the following that $S(k)\backslash S_{k,*}\not =\emptyset$ and let $[c_{1,k}^{*},d_{1,k}^{*}],[c_{2,k}^{ *},d_{2,k}^{*}],\ldots ,[c_{\lambda _{k},k}^{*},d_{\lambda _{k},k}^{*}]$ be the intervals in which the jobs of $S(k)\backslash S_{k,*}$ are scheduled in the optimal schedule $\sigma _{2}^{*}(I_{2}^{*})$. The schedule $\sigma _{2}^{\#}(I_{2}^{\#})$ will be created similarly to procedure Schedule$^{\#}$.

As a consequence of performing possibly less amount of jobs from every S(k) before $T_{1}$ in the feasible schedule $\sigma _{1}^{\#}(I_{1}^{\#})$, an additional small quantity of processing time must be scheduled after $T_{2}$ compared to the optimal solution. This amount is bounded by $2\delta$ by the second inequality of (24). Therefore, in each iteration k we start by enlarging the last interval by $2\delta$, i.e., $[c_{\lambda _{k},k}^{*},d_{\lambda _{k},k}^{*}+2\delta ]$ instead of $[c_{\lambda _{k},k}^{*},d_{\lambda _{k},k}^{*}]$, and shifting those jobs starting after $d_{\lambda _{k},k}^{*}$ in $\sigma _{2}^{*}(I_{2}^{ *})$ by the same distance $2\delta$ to the right. Then, all what we have to do in order to continue the construction of our feasible schedule $\sigma _{2}^{\#}(I_{2}^{\#})$ is to insert the remaining jobs from every $S(k)\backslash S_{k,z_{k}}$ in the corresponding intervals $[c_{1,k}^{*},d_{1,k}^{*}],[c_{2,k}^{*},d_{2,k}^{*}],\ldots ,[c_{ \lambda _{k},k}^{*},d_{\lambda _{k},k}^{*}+2\delta ]$ like in iteration k of procedure Schedule$^{\#}$.

Analogously to Schedule$^{\#}$ intervals between $d_{u,k}^{*}$ and $c_{u+1,k}^{*}$ are shifted to the right by some distance bounded by $\delta$. Thus, in a certain iteration k jobs are shifted to the right by not more than $\max \{2\delta ,\delta \}=2\delta$. Since the possible delay may occur for every job family k, the possible overall delay for every job scheduled in $\sigma _{2}^{\#}(I_{2}^{\#})$ is bounded by $2f\delta$. This shows that inequality (27) is valid. $\square$

Theorem 5

Algorithm PTAS3 is a PTAS for problem $\Pi _{3}$. The running time of this algorithm is in $O\left( 2^{4/\varepsilon ^{2}}\cdot \left( 4/\varepsilon ^{2}\right) ^{1/\varepsilon }\cdot \ln \left( n\right) \cdot \left( n^{\left( 1+20/3\varepsilon \right) } +n^{\left( 1+12/\varepsilon \right) }\right) \right)$.

Proof

The big jobs $B_{1}$ to be included in $X_{1}$ are completely guessed from B in $O(2^{4/\varepsilon ^{2}})$. The small jobs to be included in $X_{1}$ are guessed from every subset S(k) by considering only the $m(k)+1$ possible subsets $S_{k,z}$. This can be done for every guessed $B_{1}$ in $O(\left( m(k)+1\right) ^{f})=O(\left( 4/\varepsilon ^{2}\right) ^{1/\varepsilon })$ time. In overall, the guessing of all the subsets $X_{1}$ will be done in $O(2^{4/\varepsilon ^{2}}.\left( 4/\varepsilon ^{2}\right) ^{1/\varepsilon })$. Hence, from the computational analysis of the different steps of PTAS3, it is clear that this algorithm runs polynomially in the size of instance I of $\Pi _{3}$ for a fixed accuracy $\varepsilon >0$.

Let us now consider the result of Lemma 4. We established that a subset $X_{1}^{\#}\subset X$ is generated in Step 2 of PTAS3 and that two feasible schedules $\sigma _{1}^{\#}(I_{1}^{\#})$ and $\sigma _{2}^{\#}(I_{2}^{\#})$ exist such that (25), (26) and (27) hold. By Theorem 1 we have

$$\begin{aligned} L_{\max }\left( PTAS1(I_{1}^{\#},T_{1},3\varepsilon /5)\right) \le \left( 1+3\varepsilon /5\right) L_{\max }(\sigma _{1}^{\#}(I_{1}^{\#})). \end{aligned}$$

From (25), we then deduce that

$$\begin{aligned} L_{\max }\left( PTAS1(I_{1}^{\#},T_{1},3\varepsilon /5)\right) \le \left( 1+3\varepsilon /5\right) \left( L_{\max }(\sigma _{1}^{*}(I_{1}^{*}))+f\delta \right) . \end{aligned}$$

(28)

Moreover, we have

$$\begin{aligned} L_{\max }\left( PTAS0(I_{2}^{\#},\varepsilon /3)\right) \le \left( 1+\varepsilon /3\right) L_{\max }(\sigma _{2}^{\#}(I_{2}^{\#})). \end{aligned}$$

From (27) we establish that

$$\begin{aligned} L_{\max }\left( PTAS0(I_{2}^{\#},\varepsilon /3)\right) \le \left( 1+\varepsilon /3\right) \left( L_{\max }(\sigma _{2}^{*}(I_{2}^{*}))+2f\delta \right) . \end{aligned}$$

(29)

By using (26) we get

$$\begin{aligned} C_{\max }(\sigma _{1}^{\#}(I_{1}^{\#}))\le C_{\max }(\sigma _{1}^{*}(I_{1}^{*}))\le T_{1}. \end{aligned}$$

(30)

Inequality (30) implies that the algorithm $PTAS1(I_{1}^{\#},T_{1},3 \varepsilon /5)$ yields a feasible solution with $C_{\max }(PTAS1(I_{1}^{ \#},T_{1},3\varepsilon /5))\le T_{1}$.

Let us now define the global solution $\sigma ^{\#}(I)$ for instance I (of $\Pi _{3}$) as the union of the two feasible subsolutions $PTAS1(I_{1}^{ \#},T_{1},3\varepsilon /5)$ and $PTAS0(I_{2}^{\#},\varepsilon /3)$. The following relation holds

$$\begin{aligned} L_{\max }\left( \sigma ^{\#}(I)\right) =\max \left\{ L_{\max }(PTAS1(I_{1}^{\#},T_{1},3\varepsilon /5)),L_{\max }\left( PTAS0(I_{2}^{\#},\varepsilon /3)\right) \right\} . \end{aligned}$$

Thus, by applying (28) and (29), we deduce that

$$\begin{aligned} L_{\max }\left( \sigma ^{\#}(I)\right)\le & {} \max \{\left( 1+3\varepsilon /5\right) \left( L_{\max }(\sigma _{1}^{*}(I_{1}^{*}))\right. \nonumber \\&\left. +\,f\delta \right) ,\left( 1+\varepsilon /3\right) \left( L_{\max }(\sigma _{2}^{*}(I_{2}^{*}))+2f\delta \right) \}. \end{aligned}$$

(31)

From (31) and by observing that $f\delta \le \varepsilon L_{\max }^{*}(I)/4$, we obtain for $\varepsilon \le 1$ the final relations

$$\begin{aligned} L_{\max }\left( \sigma ^{\#}(I)\right)&\le \max \{L_{\max }(\sigma _{1}^{*}(I_{1}^{*}))+\varepsilon L_{\max }^{*}(I),L_{\max }(\sigma _{2}^{*}(I_{2}^{*}))+\varepsilon L_{\max }^{*}(I)\} \\&=\max \{L_{\max }(\sigma _{1}^{*}(I_{1}^{*})),L_{\max }(\sigma _{2}^{*}(I_{2}^{*}))\}+\varepsilon L_{\max }^{*}(I)=(1+\varepsilon )L_{\max }^{*}(I). \end{aligned}$$

This finishes the proof of Theorem 5. $\square$

6 PTAS for the Fourth Scenario: $1,ONA|r_{j}|L_{\max }$

The studied scenario $\Pi _{4}$ can be formulated as follows. An operator has to schedule a set J of n jobs on a single machine, where every job j has a processing time $p_{j}$, a release date $r_{j}$ and a tail $q_{j}$. The machine can process at most one job at a time if the operator is available at the starting time and the completion time of such a job. The operator is unavailable during $]T_{1},T_{2}[$. Preemption of jobs is not allowed (jobs have to be performed under the non-resumable scenario). As in the previous scenarios, we aim to minimize the maximum lateness.

If for every $j\in J$ we have $p_{j}<T_{2}-T_{1}$ or $r_{j}\geqslant T_{2}$, it can be easily checked that $\Pi _{4}$ is equivalent to an instance of $\Pi _{3}$ for which we can apply the PTAS described in the previous section. Hence, in the remainder we assume that there are some jobs which have processing times greater than $T_{2}-T_{1}$ and can complete before $T_{1}$. Let ${\mathcal {K}}$ denote the subset of these jobs. Similarly to the transformation proposed in [11], the following theorem on the existence of the PTAS for Scenario $\Pi _{4}$ can be proved.

Theorem 6

Scenario $\Pi _{4}$ admits a PTAS. The running time of this approximation scheme is in $O\left( \left( n/\varepsilon \right) \cdot 2^{4/\varepsilon ^{2}}\cdot \left( 4/\varepsilon ^{2}\right) ^{1/\varepsilon }\cdot \ln \left( n\right) \cdot \left( n^{\left( 1+20/3\varepsilon \right) } +n^{\left( 1+12/\varepsilon \right) }\right) \right)$.

Proof

We distinguish two subcases:

• Subcase 1: There exists a job $s\in {\mathcal {K}}$, called straddling job, such that in the optimal solution it starts not later than $T_{1}$ and completes not before $T_{2}$.

• Subcase 2: There is no straddling job in the optimal solution.

It is obvious that Subcase 2 is equivalent to an instance of $\Pi _{3}$ for which we have established the existence of a PTAS. Thus, the last step necessary to prove the existence of a PTAS for an instance of $\Pi _{4}$ is to construct a special scheme for Subcase 1. Without loss of generality, we assume that Subcase 1 holds and that the straddling job s is known (indeed, it can be guessed in O(n) time among the jobs of ${\mathcal {K}}$). Moreover, the time-window of the starting time $t_{s}^{*}$ of this job s in the optimal solution fulfills

$$\begin{aligned} t_{s}^{*}\in [T_{2}-p_{s},T_{1}]. \end{aligned}$$

If $T_{2}-p_{s}= T_{1}$, i.e., the interval $[T_{2}-p_{s},T_{1}]$ consists of a single point $T_{1}$, we can apply $PTAS3(I,T_{1},T_{1},\varepsilon )$. Otherwise, set

$$\begin{aligned} t_{s}^{h}=T_{2}-p_{s}+h \frac{T_{1}-T_{2}+p_{s}}{\left\lceil 1/\varepsilon \right\rceil }\quad h=0,1,\ldots , \left\lceil 1/\varepsilon \right\rceil . \end{aligned}$$

We consider a set of $\left\lceil 1/\varepsilon \right\rceil +1$ instances $\{ {\mathcal {I}}_{0},{\mathcal {I}}_{1},\ldots ,{\mathcal {I}}_{\left\lceil 1/\varepsilon \right\rceil }\}$ of $\Pi _{4}$ where in ${\mathcal {I}}_{h}$ the straddling job s starts at time $t_{s}^{h}$. Each such instance is equivalent to an instance of $\Pi _{3}$ with a set of jobs $J-\{s\}$ and a machine non-availability interval $\Delta _{h}$ with

$$\begin{aligned} \Delta _{h}=\left] T_{2}-p_{s}+h\frac{T_{1}-T_{2}+p_{s}}{\left\lceil 1/\varepsilon \right\rceil },T_{2}+h\frac{T_{1}-T_{2}+p_{s}}{\left\lceil 1/\varepsilon \right\rceil }\right[ . \end{aligned}$$

For every instance from $\{{\mathcal {I}}_{0},{\mathcal {I}}_{1},\ldots ,{\mathcal {I}}_{\left\lceil 1/\varepsilon \right\rceil } \}$, we apply PTAS3 and select the best solution among all the $\left\lceil 1/\varepsilon \right\rceil +1$ instances.

If $t_{s}^{*} = T_{2}-p_{s}$, PTAS3 applied to ${\mathcal {I}}_{0}$ is the right choice. In all other cases, there is an $h\in \{0,1,\ldots , \lceil 1/\varepsilon \rceil \}$ with $t_{s}^{*}\in ]t_{s}^{h},t_{s}^{h+1}]$. Delaying s and the next jobs in the optimal schedule of ${\mathcal {I}}_{h+1}$ , $h=0,1,\ldots ,\left\lceil 1/\varepsilon \right\rceil -1$, will not cost more than

$$\begin{aligned} \frac{T_{1}-T_{2}+p_{s}}{\left\lceil 1/\varepsilon \right\rceil } \le \varepsilon \left( T_{1}-T_{2}+p_{s}\right) \le \varepsilon p_{s}. \end{aligned}$$

Thus, the solution $\Omega _{h}$ obtained by PTAS3 for ${\mathcal {I}}_{h}$, $h=1,2,\ldots ,\left\lceil 1/\varepsilon \right\rceil$) is sufficiently close to an optimal schedule for Subcase 1 if s is the straddling job and $t_{s}^{*}\in ] t_{s}^{h},t_{s}^{h+1}]$. As a conclusion, Subcase 1 has a PTAS. $\square$

7 Conclusions

In this paper, we considered important single-machine scheduling problems under release times and tails assumptions, with the aim of minimizing the maximum lateness. Four variants have been studied under different scenarios. In the first scenario, all the jobs are constrained by a common deadline. The second scenario consists in finding the Pareto front where the considered criteria are the makespan and the maximum lateness. In the third scenario, a non-availability interval constraint is considered (breakdown period, fixed job or a planned maintenance duration). In the fourth scenario, the non-availability interval is related to the operator who is organizing the execution of jobs on the machine, which implies that no job can start, and neither can complete during the operator non-availability period. For each of these four open problems, we establish the existence of a PTAS.

As a perspective, the study of min-sum scheduling problems in a similar context seems to be a challenging subject.