Reconstructing Phylogenetic Level-1 Networks from Nondense Binet and Trinet Sets

Abstract

Binets and trinets are phylogenetic networks with two and three leaves, respectively. Here we consider the problem of deciding if there exists a binary level-1 phylogenetic network displaying a given set $\mathbb {T}$ of binary binets or trinets over a taxon set X, and constructing such a network whenever it exists. We show that this is NP-hard for trinets but polynomial-time solvable for binets. Moreover, we show that the problem is still polynomial-time solvable for inputs consisting of binets and trinets as long as the cycles in the trinets have size three. Finally, we present an $O(3^{|X|} poly(|X|))$ time algorithm for general sets of binets and trinets. The latter two algorithms generalise to instances containing level-1 networks with arbitrarily many leaves, and thus provide some of the first supernetwork algorithms for computing networks from a set of rooted phylogenetic networks.

1 Introduction

A key problem in biology is to reconstruct the evolutionary history of a set of taxa using data such as DNA sequences or morphological features. These histories are commonly represented by phylogenetic trees, and can be used, for example, to inform genomics studies, analyse virus epidemics and understand the origins of humans [23]. Even so, in case evolutionary processes such as recombination and hybridization are involved, it can be more appropriate to represent histories using phylogenetic networks instead of trees [2].

Generally speaking, a phylogenetic network is any type of graph with a subset of its vertices labelled by the set of taxa that in some way represents evolutionary relationships between the taxa [13]. Here, however, we focus on a special type of phylogenetic network called a level-1 network. We present the formal definition for this type of network in the next section but, essentially, it is a binary, directed acyclic graph with a single root, whose leaves correspond to the taxa, and in which any two cycles are disjoint (for example, see Fig. 2 below). This type of network was first considered in [20] and is closely related to so-called galled-trees [3, 7]. Level-1 networks have been used to, for example, analyse virus evolution [10], and are of practical importance since their simple structure allows for efficient construction [7, 10, 15] and comparison [17].

One of the main approaches that have been used to construct level-1 networks is from triplet sets, that is, sets of rooted binary trees with three leaves (see e.g. [10, 18, 19, 22]). Even so, it has been observed that the set of triplets displayed by a level-1 network does not necessarily provide all of the information required to uniquely define or encode the network [5]. Motivated by this observation, in [11] an algorithm was developed for constructing level-1 networks from a network analogue of triplets: rooted binary networks with three leaves, or trinets. This algorithm relies on the fact that the trinets displayed by a level-1 network do indeed encode the network [11]. Even so, the algorithm was developed for dense trinet sets only, i.e. sets in which there is a trinet associated to each combination of three taxa.

In this paper, we consider the problem of constructing level-1 networks from arbitrary sets of level-1 trinets and binets, where a binet is an even simpler building block than a trinet, consisting of a rooted binary network with just two leaves. We consider binets as well as trinets since they can provide important information to help piece together sets of trinets. Our approach can be regarded as a generalisation of the well-known supertree algorithm called Build [1, 23] for checking whether or not a set of triplets is displayed by a phylogenetic tree and constructing such a tree if this is the case. In particular, the algorithm we present in Sect. 4 is one of the first supernetwork algorithms for constructing a phylogenetic network from a set of networks. Note that some algorithms have already been developed for computing unrooted supernetworks—see, for example [8, 12].

We expect that our algorithm could be useful in practice as there are programs which can be used to compute trinets from biological data [14, 25] (and also binets as subnets of the computed trinets). Some of these programs use optimisation criteria such as likelihood which can be very computationally expensive for large datasets, but which are much more practical for small datasets. Note that a similar strategy was used in the quartet puzzling [24] approach for computing phylogenetic trees from four-leaved trees or quartets based on likelihood, before likelihood became more practical for larger data sets. It should be noted, however, that most of the current programs for computing phylogenetic networks are based on the trees embedded within a network, and so they might not be able to distinguish between different types of trinets [21]. Hopefully the development of new models will make it possible to deal with potential difficulties in this respect. Also, it could be of interest to build networks from networks on slightly larger subsets (such as size-four and size-five subets) and try to merge these instead of or as well as trinets, as such subsets may be more informative than size-three ones.

We now summarize the contents of the paper. After introducing some basic notation in the next section, in Sect. 3 we begin by presenting a polynomial-time algorithm for deciding whether or not there exists some level-1 network that displays a given set of level-1 binets, and for constructing such a network if it actually exists (see Theorem 1). Then, in Sect. 4, we present an exponential-time algorithm for an arbitrary set consisting of binets and trinets (see Theorem 2). This algorithm uses a top-down approach that is somewhat similar in nature to the Build algorithm [1, 23] but it is considerably more intricate. The algorithm can be generalised to instances containing level-1 networks with arbitrarily many leaves since trinets encode level-1 networks [11].

In Sect. 5 we show that for the special instance where each cycle in the input trinets has size three our exponential-time algorithm is actually guaranteed to work in polynomial time. This is still the case when the input consists of binary level-1 networks with arbitrarily many leaves as long as all their cycles have length three. However, in Sect. 6 we prove that in general it is NP-hard to decide whether or not there exists a binary level-1 network that displays an arbitrary set of trinets (see Theorem 4). We also show that this problem remains NP-hard if we insist that the network contains only one cycle. Our proof is similar to the proof that it is NP-hard to decide the same question for an arbitrary set of triplets given in [18], but the reduction is more complicated. In Sect. 7, we conclude with a discussion of some directions for future work.

2 Preliminaries

Let X be some finite set of labels. We will refer to the elements of X as taxa. A rooted phylogenetic network N on X is a simple directed acyclic graph which has a single indegree-0 vertex (the root, denoted by $\rho (N)$), no indegree-1 outdegree-1 vertices and its outdegree-0 vertices (the leaves) bijectively labelled by the elements of X. We will refer to rooted phylogenetic networks as networks for short. In addition, we will identify each leaf with its label and denote the set of leaves of a network N by $\mathcal {L}(N)$. For a set $\mathcal {N}$ of networks, $\mathcal {L}(\mathcal {N})$ is defined to be $\cup _{N\in \mathcal {N}} \mathcal {L}(N)$. A network is called binary if all vertices have indegree and outdegree at most two and all vertices with indegree two (the reticulations) have outdegree one. Refining a vertex with outdegree $d>2$ means replacing the vertex by a path of $d-1$ vertices of outdegree 2. A cycle of a network is the union of two non-identical, internally-vertex-disjoint, directed s-t paths, for any two distinct vertices s, t. The size of the cycle is the number of vertices that are on at least one of these paths. A cycle is tiny if it has size three and large otherwise. A network is said to be a tiny cycle network if all its cycles are tiny. A binary network is said to be a binary level-1 network if all its cycles are disjoint. We only consider binary level-1 networks in this paper, see Fig. 2 for an example containing one tiny and two large cycles. Note that, when $|X| = 1$, there exists a unique binary level-1 network on X consisting of a single vertex labelled by the only element of X.

If N is a network on X and $X'\subseteq X$ nonempty, then a vertex v of N is a stable ancestor of $X'$ (in N) if every directed path from the root of N to a leaf in $X'$ contains v. The lowest stable ancestor of $X'$ is the unique vertex $LSA(X')$ that is a stable ancestor of $X'$ and such that there is no directed path from $LSA(X')$ to any of the other stable ancestors of $X'$.

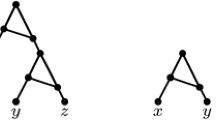
A binet is a network with exactly two leaves and a trinet is a network with exactly three leaves. In this paper, we only consider binary level-1 binets and trinets. There exist two binary level-1 binets and eight binary level-1 trinets (up to relabelling) [11], all presented in Fig. 1. In the following, we will use the names of the trinets and binets indicated in that figure. For example, $T_1(x,y;z)$ denotes the only rooted tree on $\{x,y,z\}$ where $\{x,y\}$ is a cluster, where a cluster is the entire set of leaf descendants of a node. Trinet $T_1(x,y;z)$ is also called a triplet.

A set $\mathbb {B}$ of binets on a set X of taxa is called dense if for each pair of taxa from X there is at least one binet in $\mathbb {B}$ on those taxa. A set $\mathbb {T}$ of (binets and) trinets on X is dense if for each combination of three taxa from X there is at least one trinet in $\mathbb {T}$ on those taxa.

Fig. 1

The two binary level-1 binets and the eight binary level-1 trinets

Given a phylogenetic network N on X and a subset $X'\subseteq X$, we define the network $N|X'$ as the network obtained from N by deleting all vertices and arcs that are not on a directed path from the lowest stable ancestor of $X'$ to a leaf in $X'$ and repeatedly suppressing indegree-1 outdegree-1 vertices and replacing parallel arcs by single arcs until neither operation is applicable.

Two networks $N,N'$ on X are said to be equivalent if there exists an isomorphism between N and $N'$ that maps each leaf of N to the leaf of $N'$ with the same label.

Given two networks $N,N'$ with $\mathcal {L}(N')\subseteq \mathcal {L}(N)$, we say that N displays $N'$ if $N|\mathcal {L}(N')$ is equivalent to $N'$. Note that this definition in particular applies to the cases that $N'$ is a binet or trinet. In addition, we say that N displays a set $\mathcal {N}$ of networks if N displays each network in $\mathcal {N}$.

Given a network N, we use the notation $\mathbb {T}(N)$ to denote the set of all trinets and binets displayed by N. For a set $\mathcal {N}$ of networks, $\mathbb {T}(\mathcal {N})$ denotes $\bigcup _{N\in \mathcal {N}} \mathbb {T}(N)$. Given a set $\mathbb {T}$ of trinets and/or binets on X and a nonempty subset $X'\subseteq X$, we define the restriction of $\mathbb {T}$ to $X'$ as

$$\begin{aligned} \mathbb {T}|X':= \{T|(\mathcal {L}(T)\cap X') \quad : \quad T\in \mathbb {T} \text{ and } |\mathcal {L}(T)\cap X'| \in \{2,3\} \}. \end{aligned}$$

The following observation will be useful.

Observation 1

Let $\mathbb {T}$ be a set of trinets and binets on X and suppose that there exists a binary level-1 network N on X such that $\mathbb {T}\subseteq \mathbb {T}(N)$. Then, for any nonempty subset $X'$ of X, $N|X'$ is a binary level-1 network displaying $\mathbb {T}|X'$.

Proof

Let $X'$ be a nonempty subset of X and consider a trinet or binet $T'\in \mathbb {T}|X'$. Then there exists a binet or trinet $T\in \mathbb {T}$ such that $T'=T|(\mathcal {L}(T)\cap X')$. Since $T\in \mathbb {T}\subseteq \mathbb {T}(N)$, T is displayed by N. When restricting N to $N|X'$, first the vertices and arcs that are not on a directed path from the lowest stable ancestor of $X'$ to a leaf in $X'$ are deleted. Hence, all vertices and arcs on directed paths from $LSA(X')$ to leaves in $\mathcal {L}(T)\cap X'$ are kept. Thus, $T'=T|(\mathcal {L}(T)\cap X')$ is still displayed. Suppressing indegree-1 outdegree-1 vertices and replacing parallel arcs by single arcs does not change this. Hence, $T'$ is displayed by $N'$. $\square$

We call a network cycle-rooted if its root is contained in a cycle. A cycle-rooted network is called tiny-cycle rooted if its root is in a tiny cycle and large-cycle rooted otherwise. If N is a cycle-rooted binary level-1 network whose root $\rho (N)$ is in cycle C, then there exists a unique reticulation r that is contained in C. We say that a leaf x is high in N if there exists a path from $\rho (N)$ to x that does not pass through r, otherwise we say that x is low in N. If N is not cycle-rooted, then we define all leaves to be high in N. We say that two leaves are at the same elevation in N if they are either both high or both low in N. Two leaves x, y that are both high in N are said to be on the same side in N if x and y are both reachable from the same child of $\rho (N)$ by two directed paths. A bipartition $\{L,R\}$ of the set H of high leaves in N is the bipartition of H induced by N if all leaves in L are on the same side $S_L$ in N and all the leaves in R are on the same side $S_R$ in N, with $S_L\ne S_R$. (Note that one between $S_L$ and $S_R$ could be empty). Finally, if N is cycle-rooted, we say that a subnetwork $N'$ of N is a pendant subnetwork if there exists in N some arc $(u,\rho ')$ that is a cut-arc, i.e., an arc whose removal disconnects the graph, with $\rho '$ the root of $N'$ and u a vertex of the cycle containing the root of N. If, in addition, u is not a reticulation, then $N'$ is said to be a pendant sidenetwork of N. If, in addition, $\mathcal {L}(N')\subseteq S$ with S a part of the bipartition of the high leaves of N induced by N, then we say that $N'$ is a pendant sidenetwork on side S. See Fig. 2 for an illustration of these definitions.

We end this section by giving a short description of the Build algorithm [1, 23], which decides if there exists a rooted tree (i.e. a network without reticulations) displaying a given set of triplets $\mathbb {L}$. The Build algorithm constructs a graph $\mathcal {R}^L(\mathbb {L})$ with a vertex for each taxon and an edge $\{x,y\}$ precisely if there exists a triplet $T_1(x,y;z)\in \mathbb {L}$ for some z. If $\mathcal {R}^L(\mathbb {L})$ is connected, the algorithm halts and reports that there exists no rooted tree displaying $\mathbb {L}$. Otherwise, let $X_1,\ldots ,X_k$ be the vertex sets of the connected components of $\mathcal {R}^L(\mathbb {L})$. The algorithm recursively tries to construct trees displaying $\mathbb {L}|X_1,\ldots \mathbb {L}|X_k$. If such trees exist, Build outputs a rooted tree consisting of a new root with arcs to the roots of the recursively computed trees. Otherwise, the algorithm reports that there exists no solution.

Fig. 2

A binary level-1 network N. Its set of high leaves is $H=\{a, b, c, d, e, f, g, h, i, m\}$. The bipartition of H induced by N is $\{\{a, b\},\{c, d, e, f, g, h, i, m\}\}$. Hence, a and b are on the same side in N and c, d, e, f, g, h, i and m are on the same side in N. The pendant sidenetworks of N are $N(L_1)$, $N(L_2)$, $N(R_1)$ and $N(R_2)$. Leaves j, k and l are low in N

Our algorithm for trinets described in Sect. 4 can be seen as a generalization of the Build algorithm. It uses a graph $\mathcal {R}$ which generalizes the $\mathcal {R}^L$ graph, but also has three additional steps which use different graphs. Our algorithm for binets described in the next section also uses a similar recursive approach. Finally, we note that our algorithms always construct binary networks, but this is just for convenience. These algorithms could be adapted to construct nonbinary networks, just as Build constructs nonbinary trees.

3 Constructing a Network from a Set of Binets

In this section we describe a polynomial-time algorithm for deciding if there exists some binary level-1 network displaying a given set $\mathbb {B}$ of binets, and constructing such a network if it exists. We treat this case separately because it is much simpler than the trinet algorithms and gives an introduction to the techniques we use.

The first step of the algorithm is to construct the graph $\mathcal {R}^b(\mathbb {B})$ ¹, which has a vertex for each taxon and an edge $\{x,y\}$ if (at least) one of N(x; y) and N(y; x) is contained in $\mathbb {B}$.

If the graph $\mathcal {R}^b(\mathbb {B})$ is disconnected and has connected components $X_1,\ldots ,X_p$, then the algorithm constructs a network N by recursively computing networks $N(X_1),\ldots ,N(X_p)$ displaying $\mathbb {B}|X_1,\ldots ,\mathbb {B}|X_p$ respectively, creating a new root node $\rho$ and adding arcs from $\rho$ to the roots of $N(X_1),\ldots ,N(X_p)$, and refining arbitrarily the root $\rho$ in order to make the network binary. See Fig. 3 for an example.

Fig. 3

Example of a step of the algorithm for constructing a network N from the set $\mathbb {B}$ of binets. The graph $\mathcal {R}^b(\mathbb {B})$ has connected components $X_1=\{a, b, c, d, e\}$ and $X_2=\{f, g\}$. Hence, network N is obtained by combining recursively computed networks $N(X_1)$ and $N(X_2)$ by hanging them below a new root. See Fig. 4 for the first recursive step

If the graph $\mathcal {R}^b(\mathbb {B})$ is connected, then the algorithm constructs the graph $\mathcal {K}^b(\mathbb {B})$, which has a vertex for each taxon and an edge $\{x,y\}$ precisely if $T(x,y)\in \mathbb {B}$. In addition, the algorithm constructs the directed graph $\varOmega ^b(\mathbb {B})$, which has a vertex for each connected component of $\mathcal {K}^b(\mathbb {B})$ and an arc $(\pi _1,\pi _2)$ precisely if there exists a binet $N(y;x)\in \mathbb {B}$ with $x\in V(\pi _1)$ and $y\in V(\pi _2)$ (with $V(\pi )$ denoting the vertex set of a given connected component $\pi$).

The algorithm searches for a nonempty strict subset U of the vertices of $\varOmega ^b(\mathbb {B})$ such that there is no arc $(\pi _1,\pi _2)$ with $\pi _1\notin U$ and $\pi _2\in U$. This can be done in polynomial time by collapsing directed cycles until an acyclic digraph is obtained and then searching for an indegree-0 vertex. If there exists no such set U then the algorithm halts and outputs that there exists no solution. Otherwise, let H be the union of the vertex sets of the connected components of $\mathcal {K}^b(\mathbb {B})$ that correspond to elements of U and define $L_{ow}=X{\setminus } H$. The algorithm recursively constructs networks N(H) displaying $\mathbb {B}|H$ and $N(L_{ow})$ displaying $\mathbb {B}|L_{ow}$. Subsequently, the algorithm constructs a network N consisting of vertices $\rho ,v,r$, arcs $(\rho ,v)$, (v, r), $(\rho ,r)$, networks $N(L_{ow}), N(H)$ and an arc from v to the root of N(H) and an arc from r to the root of $N(L_{ow})$. See Fig. 4 for an example of this case.

Fig. 4

Example of the recursive step, which constructs a network $N(X_1)$ from binet set $\mathbb {B}|X_1$, with $\mathbb {B}$ and $X_1$ as in Fig. 3. Network $N(X_1)$ is cycle-rooted because graph $\mathcal {R}^b$ is connected. One possible strict subset of the vertices of $\varOmega ^b(\mathbb {B}|X_1)$ with no incoming arcs is $\{a, b\}$. Hence, $H=\{a, b\}$ can be made the high leaves of the network, and $L_{ow}=\{c, d, e\}$ the low leaves. Combining recursively computed networks N(H) and $N(L_{ow})$ by hanging them below a new cycle as described by the algorithm then gives network $N(X_1)$. Note that other valid subsets of the vertices of $\varOmega ^b(\mathbb {B}|X_1)$ are $\{a, b, d\}$, $\{a, b, c\}$, $\{a, b, c, d\}$ and $\{d\}$, which lead to alternative solutions

Finally, when $|X|\le 2$ (in some recursive step), the problem can be solved trivially. When $|X|=1$, the algorithm outputs a network consisting of a single vertex labelled by the only element of X, which is the root as well as the leaf of the network. When $|X|=2$ and there is a single binet remaining, the algorithm outputs that binet. When $|X|=2$ and there are at least two binets remaining, then the algorithm halts and outputs that there exists no solution.

This completes the description of the algorithm for binets. Clearly, it is a polynomial-time algorithm and its correctness is shown in the following theorem.

Theorem 1

Given a set $\mathbb {B}$ of binets on a set X of taxa, there exists a polynomial-time algorithm that decides if there exists a binary level-1 network on X that displays all binets in $\mathbb {B}$, and that constructs such a network if it exists.

Proof

We prove by induction on |X| that the algorithm described above produces a binary level-1 network on X displaying $\mathbb {B}$ if such a network exists. The induction basis for $|X|\le 2$ is clearly true. Now let $|X|\ge 3$, $\mathbb {B}$ a set of binets on X and assume that there exists some binary level-1 network on X displaying $\mathbb {B}$. There are two cases.

First assume that the graph $\mathcal {R}^b(\mathbb {B})$ is disconnected and has connected components $C_1,\ldots ,C_p$. Then the algorithm recursively computes networks $N|C_1,\ldots ,N|C_p$ displaying the sets $\mathbb {B}|C_1,\ldots$, $\mathbb {B}|C_p$ respectively. Such networks exist by Observation 1 and can be found by the algorithm by induction. It follows that the network N which is constructed by the algorithm displays all binets in $\mathbb {B}$ of which both taxa are in the same connected component of $\mathcal {R}^b(\mathbb {B})$. Each other binet is of the form T(x, y) by the definition of graph $\mathcal {R}^b(\mathbb {B})$. Hence, those binets are also displayed by N, by construction.

Now assume that the graph $\mathcal {R}^b(\mathbb {B})$ is connected. Then we claim that there exists no binary level-1 network displaying $\mathbb {B}$ that is not cycle-rooted. To see this, assume that there exists such a network, let $v_1,v_2$ be the two children of its root and $X_i$ the leaves reachable by a directed path from $v_i$, for $i=1,2$. Then there is no edge $\{a,b\}$ in $\mathcal {R}^b(\mathbb {B})$ for any $a\in X_1$ and $b\in X_2$. Since $X_1\cup X_2=X$, it follows that $\mathcal {R}^b(\mathbb {B})$ is disconnected, which is a contradiction. Hence, any network that is a valid solution is cycle-rooted.

The algorithm then searches for a nonempty strict subset U of the vertices of $\varOmega ^b(\mathbb {B})$ with no incoming arc, i.e., for which there is no arc $(\pi _1,\pi _2)$ with $\pi _1\notin U$ and $\pi _2\in U$. First assume that there exists no such set U. Then the algorithm reports that there exists no solution. To prove that this is correct, assume that $N'$ is some binary level-1 network on X displaying $\mathbb {B}$ and let H be the set of leaves that are high in $N'$. The graph $\mathcal {K}^b(\mathbb {B})$ contains no edges between taxa that are high in $N'$ and taxa that are low in $N'$ (because such taxa x, y cannot be together in a T(x, y) binet). Hence, the set H is a union of vertex sets of connected components of $\mathcal {K}^b(\mathbb {B})$ and their representing vertices of $\varOmega ^b(\mathbb {B})$ form a subset U. If there were an arc $(\pi _1,\pi _2)$ in $\varOmega ^b(\mathbb {B})$ with $\pi _1\notin U$ and $\pi _2\in U$, then there would be a binet $N(y;x)\in \mathbb {B}$ with $x\in V(\pi _1)$ and $y\in V(\pi _2)$. This binet N(y; x) would not be displayed by $N'$ because $y\in H$ and $x\notin H$. Therefore, we conclude that there is no arc $(\pi _1,\pi _2)$ in $\varOmega ^b(\mathbb {B})$ with $\pi _1\notin U$ and $\pi _2\in U$. Hence, we have obtained a contradiction to the assumption that there is no such set U.

Now assume that there exists such a set U. Then the algorithm recursively constructs networks N(H) displaying $\mathbb {B}|H$ and $N(L_{ow})$ displaying $\mathbb {B}|L_{ow}$, with H the union of the vertex sets of the connected components of $\mathcal {K}^b(\mathbb {B})$ corresponding to the elements of U, and with $L_{ow}=X{\setminus } H$. The algorithm then constructs a network N consisting of a cycle with networks N(H) hanging from the side of the cycle and network $N(L_{ow})$ hanging below the cycle, as in Fig. 4. Networks N(H) and $N(L_{ow})$ exist by Observation 1 and can be found by the algorithm by induction. Because these networks display $\mathbb {B}|H$ and $\mathbb {B}|L_{ow}$ respectively, each binet from $\mathbb {B}$ that has both its leaves high or both its leaves low in N is displayed by N. Each other binet is of the form N(x; y) with x low and y high in N, because otherwise there would exist an element in U which would have an incoming arc in $\varOmega ^b(\mathbb {B})$. Hence, such binets are also displayed by N. $\square$

4 Constructing a Network from a Nondense Set of Binets and Trinets

In this section we present an algorithm to construct a binary level-1 network displaying a given nondense set of binets and trinets, if any exists. This algorithm can be regarded as a generalisation of the Build algorithm [1, 23] for checking whether or not there exists a rooted phylogenetic tree displaying a set of triplets.

4.1 Outline

Let $\mathbb {T}$ be a set of binary level-1 trinets and binets on a set X of taxa. In this section we will describe an exponential-time algorithm for deciding whether there exists a binary level-1 network N on X with $\mathbb {T}\subseteq \mathbb {T}(N)$. Note that, if $\mathbb {T}$ contains trinets or binets that are not level-1, we know that such a network cannot exist because all binets and trinets displayed by a binary level-1 network are binary level-1 networks.

Throughout this section, we will assume that there exists some binary level-1 network on X that displays $\mathbb {T}$ and we will show that in this case we can reconstruct such a network N.

Our approach aims at constructing the network N recursively; the recursive steps that are used depend on the structure of N. The main steps of our approach are the following:

• 1. We determine whether the network N is cycle-rooted (see Sect. 4.2);

• 2. If this is the case, we guess the high and low leaves of N (see Sect. 4.3);

• 3. Then, we guess how to partition the high leaves into the “left” and “right” leaves (see Sect. 4.4);

• 4. Finally, we determine how to partition the leaves on each side into the leaves of the different sidenetworks on that side (see Sect. 4.5).

Although we could do Steps 2 and 3 in a purely brute force way, we present several structural lemmas which restrict the search space and will be useful in Sect. 5.

Once we have found a correct partition of the leaves (i.e., after Step 4), we recursively compute networks for each block of the partition and combine them into a single network. In the case that the network is not cycle-rooted, we do this by creating a root and adding arcs from this root to the recursively computed networks. Otherwise, the network is cycle-rooted. In this case, we construct a cycle with outgoing cut-arcs to the roots of the recursively computed networks, as illustrated in Fig. 2.

The fact that we can recursively compute networks for each block of the computed partition follows from Observation 1.

In the next sections we present a detailed description of our algorithm to reconstruct N. We will illustrate the procedure by applying it to the example set of trinets depicted in Fig. 5. The pseudocode is presented in Algorithm 1 and Table 1 gives an overview of the different graphs used by the algorithm.

Fig. 5

The set $\mathbb {T}$ of trinets that we use to illustrate the inner workings of our algorithm

Table 1 Overview of the graphs used by Algorithm 1

4.2 Is the Network Cycle-Rooted?

To determine whether or not N is cycle-rooted, we define a graph $\mathcal {R}(\mathbb {T})$ as follows. The vertex set of $\mathcal {R}(\mathbb {T})$ is the set X of taxa and the edge set has an edge $\{a,b\}$ if there exists a trinet or binet $T\in \mathbb {T}$ with $a,b\in \mathcal {L}(T)$ that is cycle-rooted or contains a common ancestor of a and b different from the root of T (or both). For an example, see Fig. 6.

Fig. 6

The graph $\mathcal {R}(\mathbb {T})$ for the set $\mathbb {T}$ of trinets in Fig. 5. Since $\mathcal {R}(\mathbb {T})$ is connected, any network displaying $\mathbb {T}$ is cycle-rooted

Lemma 1

Let N be a binary level-1 network and $\mathbb {T}\subseteq \mathbb {T}(N)$. If $\mathcal {R}(\mathbb {T})$ is disconnected and has connected components $C_1,\ldots ,C_p$, then $\mathbb {T}$ is displayed by the binary level-1 network $N'$ obtained by creating a new root $\rho$ and adding arcs from $\rho$ to the roots of $N|C_1,\ldots ,N|C_p$, and refining arbitrarily the root $\rho$ in order to make the resulting network binary.

Proof

By Observation 1, $N'$ displays each binet and each trinet of $\mathbb {T}$ whose leaves are all in the same connected component of $\mathcal {R}(\mathbb {T})$. Consider a binet $B\in \mathbb {T}$ on $\{a,b\}$ with a and b in different components. Then there is no edge $\{a,b\}$ in $\mathcal {R}(\mathbb {T})$ and hence B is not cycle-rooted, i.e. $B=T(a,b)$, and B is clearly displayed by $N'$. Now consider a trinet $T\in \mathbb {T}$ on $\{a,b,c\}$ with a, b, c in three different components. Then, none of $\{a,b\},\{b,c\}$ and $\{a,c\}$ is an edge in $\mathcal {R}(\mathbb {T})$. Hence, none of the pairs $\{a,b\},\{b,c\},\{a,c\}$ has a common ancestor other than the root of T. Employing Fig. 1, this is impossible and so T cannot exist. Finally, consider a trinet $T'\in \mathbb {T}$ on $\{a,b,c\}$ with $a,b\in C_i$ and $c\in C_j$ with $i\ne j$. Then there is no edge $\{a,c\}$ and no edge $\{b,c\}$ in $\mathcal {R}(\mathbb {T})$. Consequently, $T'$ is not cycle-rooted and the pairs $\{a,c\}$ and $\{b,c\}$ do not have a common ancestor in $T'$ other than the root of $T'$. Hence, $T'\in \{T_1(a,b;c) , N_3(a;b;c), N_3(b;a;c)\}$. If $T'=T_1(a,b;c)$, then $N|C_i$ displays $T'|C_i=T(a,b)$ and hence $N'$ displays $T'$. If $T'=N_3(a;b;c)$, then $N|C_i$ displays $T'|C_i=N(a;b)$ and, so, $N'$ displays $T'$. Symmetrically, if $T'=N_3(b;a;c)$, then $N|C_i$ displays $T'|C_i=N(b;a)$ and, so, $N'$ displays $T'$. We conclude that $N'$ displays $\mathbb {T}$. $\square$

Hence, if $\mathcal {R}(\mathbb {T})$ is disconnected, we can recursively reconstruct a network for each of its connected components and combine the solutions to the subproblems in the way detailed in Lemma 1. If all input trinets are of the form $T_1(x,y;z)$, then this simulates the Build algorithm [1, 23].

If $\mathcal {R}(\mathbb {T})$ is connected, then we can apply the following lemma:

Lemma 2

Let N be a binary level-1 network on X and $\mathbb {T}\subseteq \mathbb {T}(N)$. If $\mathcal {R}(\mathbb {T})$ is connected and $|X|\ge 2$, then N is cycle-rooted.

Proof

Suppose to the contrary that $\mathcal {R}(\mathbb {T})$ is connected and that N is not cycle-rooted. Let $v_1,v_2$ be the two children of the root of N and $X_i$ the leaves of N reachable by a directed path from $v_i$, for $i=1,2$. Note that $X_1\cap X_2=\emptyset$ and $X_1\cup X_2=X$. Let $a\in X_1$ and $b\in X_2$ and let T be any trinet or binet displayed by N that contains a and b. Then we have that T is not cycle-rooted and that the only common ancestor of a and b in T is the root of T. Hence, there is no edge $\{a,b\}$ in $\mathcal {R}(\mathbb {T})$ for any $a\in X_1$ and $b\in X_2$, which implies that $\mathcal {R}(\mathbb {T})$ is disconnected; a contradiction. $\square$

In the remainder of this section, we assume that $\mathcal {R}(\mathbb {T})$ is connected and thus that N is cycle-rooted.

4.3 Separating the High and the Low Leaves

We define a graph $\mathcal {K}(\mathbb {T})$ whose purpose is to help decide which leaves are at the same elevation in N. The vertex set of $\mathcal {K}(\mathbb {T})$ is the set of taxa X and the edge set contains an edge $\{a,b\}$ if there exists a trinet or binet $T\in \mathbb {T}$ with $a,b\in \mathcal {L}(T)$ and in which a and b are at the same elevation in T.

Lemma 3

Let N be a cycle-rooted binary level-1 network and $\mathbb {T}\subseteq \mathbb {T}(N)$. If C is a connected component of $\mathcal {K}(\mathbb {T})$, then all leaves in C are at the same elevation in N.

Proof

We prove the lemma by showing that there is no edge in $\mathcal {K}(\mathbb {T})$ between any two leaves that are not at the same elevation in N. Let h and $\ell$ be leaves that are, respectively, high and low in N. Then, in any trinet or binet T displayed by N that contains h and $\ell$, we have that T is cycle-rooted and that h is high in T and $\ell$ is low in T. Hence, there is no edge $\{h,\ell \}$ in $\mathcal {K}(\mathbb {T})$. $\square$

We now define a directed graph $\varOmega (\mathbb {T})$ whose purpose is to help decide which leaves are high and which ones are low in N. The vertex set of $\varOmega (\mathbb {T})$ is the set of connected components of $\mathcal {K}(\mathbb {T})$ and the arc set contains an arc $(\pi ,\pi ')$ precisely if there is a cycle-rooted binet or trinet $T\in \mathbb {T}$ with $h,\ell \in \mathcal {L}(T)$ with $h\in V(\pi )$ high in T, $\ell \in V(\pi ')$ low in T. See Fig. 7 for an example for both graphs.

Fig. 7

The graph $\mathcal {K}(\mathbb {T})$ in solid lines and the directed graph $\varOmega (\mathbb {T})$ in dashed lines, for the set $\mathbb {T}$ of trinets in Fig. 5

Lemma 4

Let $\mathbb {T}$ be a set of binets and trinets on a set X of taxa. Let N be a cycle-rooted binary level-1 network displaying $\mathbb {T}$. Then there exists a nonempty strict subset U of the vertices of $\varOmega (\mathbb {T})$ for which there is no arc $(\pi ,\pi ')$ with $\pi '\in U$, $\pi \notin U$ such that the set of leaves that are high in N equals $\cup _{\pi \in U} V(\pi )$.

Proof

Let H be the set of leaves that are high in N. Note that $H\ne \emptyset$. By Lemma 3, H is the union of connected components of $\mathcal {K}(\mathbb {T})$ and hence the union of a set U of vertices of $\varOmega (\mathbb {T})$ that respresent those components. We need to show that there is no arc $(\pi ,\pi ')$ with $\pi '\in U$, $\pi \notin U$ in $\varOmega (\mathbb {T})$. To see this, notice that if there were such an arc, there would be a trinet or binet $T\in \mathbb {T}$ that is cycle-rooted and has leaves $h,\ell \in \mathcal {L}(T)$ with $h\in V(\pi )$ high in T and $\ell \in V(\pi ')$ low in T. However, such a trinet can only be displayed by N if either h is high in N and $\ell$ is low in N or h and $\ell$ are at the same elevation in N. This leads to a contradiction because $h\in V(\pi )$ with $\pi \notin U$ and $\ell \in V(\pi ')$ with $\pi '\in U$ and, hence, h is low in N and $\ell$ is high in N. $\square$

We now distinguish two cases. The first case is that the root of the network is in a cycle with size at least four, i.e., the network is large-cycle rooted. The second case is that the root of the network is in a cycle with size three, i.e., that the network is tiny-cycle rooted. To construct a network from a given set of binets and trinets, the algorithm explores both options.

4.3.1 The Network is Large-Cycle Rooted

In this case, we can simply try all subsets of vertices of $\varOmega (\mathbb {T})$ with no incoming arcs (i.e. arcs that begin outside and end inside the subset). For at least one such set U will hold that $\bigcup _{\pi \in U} V(\pi )$ is the set of leaves that are high in the network by Lemma 4.

A set $\mathbb {T}$ of binets and trinets on a set X of taxa is called semi-dense if for each pair of taxa from X there is at least one binet or trinet that contains both of them. If $\mathbb {T}$ is semi-dense, then we can identify the set of high leaves by the following lemma.

Lemma 5

Let $\mathbb {T}$ be a semi-dense set of binets and trinets on a set X of taxa. Let N be a binary large-cycle rooted level-1 network displaying $\mathbb {T}$. Let H be the set of leaves that are high in N. Then there is a unique indegree-0 vertex $\pi _0$ of $\varOmega (\mathbb {T})$ and $H=V(\pi _0)$.

Proof

Since $\mathbb {T}$ is semi-dense, for any two leaves $h,h'\in H$ that are below different cut-arcs leaving the cycle C containing the root of N, there exists a binet or a trinet T in $\mathbb {T}$ containing both h and $h'$. Then, since T is displayed by N, T has to be a binet or a trinet where h and $h'$ are at the same elevation. This implies that there is an edge $\{h,h'\}$ in $\mathcal {K}(\mathbb {T})$. Then, since there exist at least two different cut-arcs leaving C, the leaves in H are all in the same connected component of $\mathcal {K}(\mathbb {T})$. Then, by Lemma 3, H forms a connected component of $\mathcal {K}(\mathbb {T})$. Hence, H is a vertex of $\varOmega (\mathbb {T})$. This vertex has indegree-0 because no trinet or binet T displayed by N has a leaf $\ell \notin H$ that is high in T and a leaf $h\in H$ that is low in T. Therefore, H is an indegree-0 vertex of $\varOmega (\mathbb {T})$. Moreover, by construction, there is an arc from H to each other vertex of $\varOmega (\mathbb {T})$. Hence, H is the unique indegree-0 vertex of $\varOmega (\mathbb {T})$. $\square$

4.3.2 The Network is Tiny-Cycle Rooted

For this case, we define a modified graph $\mathcal {K}^\dagger (\mathbb {T})$, which is the graph obtained from $\mathcal {K}(\mathbb {T})$ as follows. For each pair of leaves $a,b\in X$, we add an edge $\{a,b\}$ if there is no such edge yet and there exists a large-cycle rooted trinet $T\in \mathbb {T}$ with $a,b\in \mathcal {L}(T)$ (i.e. T is of type $S_1(x,y;z)$ or $S_2(x;y;z)$). The idea behind these extra edges is that if the network is tiny-cycle rooted and it displays a large-cycle rooted trinet, then all leaves of this trinet must be in the same pendant subnetwork and hence at the same elevation.

The directed graph $\varOmega ^\dagger (\mathbb {T})$ is defined in a similar way as $\varOmega (\mathbb {T})$ but its vertex set is the set of connected components of $\mathcal {K}^\dagger (\mathbb {T})$. Its arc set has, as in $\varOmega (\mathbb {T})$, an arc $(\pi ,\pi ')$ if there is a binet or trinet $T\in \mathbb {T}$ that is cycle-rooted and has leaves $h,\ell \in \mathcal {L}(T)$ with $h\in V(\pi )$ high in T, $\ell \in V(\pi ')$ low in T.

Fig. 8

Example for the case that the network is tiny-cycle rooted. From left to right are depicted a set of trinets $\mathbb {T}$, its graphs $\mathcal {K}^\dagger (\mathbb {T})$ (solid) and $\varOmega ^\dagger (\mathbb {T})$ (dashed) and the resulting network N, obtained by combining networks N(H) and $N(L_{ow})$. Note that the two edges labelled $\dagger$ are in $\mathcal {K}^\dagger (\mathbb {T})$ but not in $\mathcal {K}(\mathbb {T})$

Our approach for this case is to take a non-empty strict subset U of the vertices of $\varOmega ^\dagger (\mathbb {T})$ that has no incoming arcs and to take H to be the union of the elements of U. Then, a network displaying $\mathbb {T}$ can be constructed by combining a network N(H) displaying $\mathbb {T}|H$ and a network $N(L_{ow})$ displaying $\mathbb {T}|L_{ow}$, with $L_{ow}=X{\setminus } H$. (An example is depicted in Fig. 8). The next lemma shows the correctness of this step.

Lemma 6

Let $\mathbb {T}$ be a set of binets and trinets on a set X of taxa. Let N be a binary tiny-cycle rooted level-1 network displaying $\mathbb {T}$. Then there is a non-empty strict subset U of the vertices of $\varOmega ^\dagger (\mathbb {T})$ such that there is no arc $(\pi ,\pi ')$ with $\pi '\in U$, $\pi \notin U$. Moreover, if U is any such set of vertices, then there exists a binary tiny-cycle rooted level-1 network $N'$ displaying $\mathbb {T}$ in which $\bigcup _{\pi \in U} V(\pi )$ is the set of leaves that are high in $N'$.

Proof

Let H denote the set of leaves that are high in N. Then, H is the union of the vertex sets of one or more connected components of $\mathcal {K}(\mathbb {T})$ by Lemma 3. Any large-cycle rooted trinet which contains a leaf in H and a leaf not in H cannot be displayed by N because N is tiny-cycle rooted. Hence, H is also the union of one or more connected components of $\mathcal {K}^\dagger (\mathbb {T})$. These components form a subset U of the vertices of $\varOmega ^\dagger (\mathbb {T})$. Furthermore, there is no arc $(\pi ,\pi ')$ with $\pi '\in U$, $\pi \notin U$ since no trinet or binet T displayed by N has a leaf that is in H and high in T and a leaf that is not in H and that is low in T.

Now consider any nonempty strict subset $U'$ of the vertices of $\varOmega ^\dagger (\mathbb {T})$ with no incoming arcs, let $H'$ be the union of the vertex sets of the corresponding connected components of $\mathcal {K}^\dagger (\mathbb {T})$ and let $L_{ow}'=X{\setminus } H'$. Let $N(H')$ be a binary level-1 network displaying $\mathbb {T}|H'$ and let $N(L_{ow}')$ be a binary level-1 network displaying $\mathbb {T}|L_{ow}'$. Such networks exist by Observation 1. Let $N'$ be the network consisting of vertices $\rho ,v,r$, arcs $(\rho ,v)$, (v, r), $(\rho ,r)$, networks $N(L_{ow}'), N(H')$ and an arc from v to the root of $N(H')$ and an arc from r to the root of $N(L_{ow}')$. Clearly, $N'$ is a tiny-cycle rooted level-1 network and $H'$ is the set of leaves that are high in $N'$.

It remains to prove that $N'$ displays $\mathbb {T}$. First observe that for any $h\in H'$ and $\ell \in X{\setminus } H'$, there is no edge $\{h,\ell \}$ in $\mathcal {K}^\dagger (\mathbb {T})$ (because otherwise h and $\ell$ would lie in the same connected component). Hence, by construction of $\mathcal {K}^\dagger (\mathbb {T})$, any binet or trinet containing h and $\ell$ can not be tiny-cycle rooted and cannot have h and $\ell$ at the same elevation. Moreover, in any such binet or trinet, h must be high and $\ell$ must be low, because otherwise there would be an arc entering $U'$ in $\varOmega ^\dagger (\mathbb {T})$.

Consider any trinet or binet $T\in \mathbb {T}$. If the leaves of T are all in $H'$ or all in $L'$ then $T\in \mathbb {T}|H'$ or $T\in \mathbb {T}|L'$ and so T is clearly displayed by $N'$. If T is a binet containing one leaf $h\in H'$ and one leaf $\ell \in X{\setminus } H'$, then T must be $N(\ell ;h)$ (by the previous paragraph) and, again, T is clearly displayed by $N'$. Now suppose that T contains one leaf $h\in H'$ and two leaves $\ell ,\ell '\in X{\setminus } H'$. Since we have argued in the previous paragraph that T is tiny-cycle rooted, T must be of the form $N_2(\ell ,\ell ';h)$, $N_5(\ell ;\ell ';h)$ or $N_5(\ell ';\ell ;h)$. Moreover, since $N(L_{ow}')$ displays the binet on $\ell$ and $\ell '$, and since h is high in T and $\ell ,\ell '$ low, it again follows that T is displayed by $N'$. Finally, assume that T contains two leaves $h,h'\in H'$ and a single leaf $\ell \in X{\setminus } H'$. Then (since T is tiny-cycle rooted) T must be of the form $N_1(h,h';\ell )$ or $N_4(h;h';\ell )$. Since $N(H')$ displays the binet on h and $h'$, it follows that $N'$ again displays T. $\square$

Note that the proof of Lemma 6 describes how to build a tiny-cycle rooted level-1 network displaying $\mathbb {T}$ if such a network exists. Therefore, we assume from now on that the to be constructed network is large-cycle rooted.

4.4 Separating the Left and the Right Leaves

The next step is to divide the set H of leaves that are high in N into the leaves that are “on the left” and the leaves that are “on the right” of the cycle containing the root or, more precisely, to find the bipartition of H induced by some network displaying a given set of binets and trinets. We use the following definition.

Definition 1

A bipartition of some set $H\subseteq X$ is called feasible with respect to a set of binets and trinets $\mathbb {T}$ if the following holds:

• (F1) If there is a binet or trinet $T\in \mathbb {T}$ containing leaves $a,b\in H$ that has a common ancestor in T that is not the root of T, then a and b are in the same part of the bipartition and

• (F2) If there is a trinet $S_1(x,y;z)\in \mathbb {T}$ with $x,y\in H$ and $z\in X{\setminus } H$, then x and y are in different parts of the bipartition.

Note that one part of a feasible bipartition may be empty. The next lemma shows that the bipartition of H induced by N must be feasible. Hence, to find the right bipartion we only need to consider feasible ones.

Lemma 7

Let N be a cycle-rooted binary level-1 network, let $\mathbb {T}\subseteq \mathbb {T}(N)$, let H be the set of leaves that are high in N and let $\{L,R\}$ be the bipartition of H induced by N. Then $\{L,R\}$ is feasible with respect to $\mathbb {T}$.

Proof

First consider a binet or trinet $T\in \mathbb {T}$ containing leaves $a,b\in H$ that have a common ancestor in T that is not the root of T. Since N displays T, it follows that a and b have a common ancestor in N that is not the root of N. Hence, a and b are on the same side in N. Since $\{L,R\}$ is the bipartition of H induced by N, it now follows that a and b are in the same part of the bipartition, as required.

Now consider a trinet $S_1(x,y;z)\in \mathbb {T}$ with $x,y\in H$ and $z\in X{\setminus } H$. Since N displays T, we have that x and y are not on the same side in N. Since $\{L,R\}$ is the bipartition of H induced by N, it follows that x and y are contained in different parts of the bipartition, as required.

We now show how a feasible bipartition of a set $H\subseteq X$ can be found in polynomial time. We define a graph $\mathcal {M}(\mathbb {T},H)=(H,E(\mathcal {M}))$ with an edge $\{a,b\}\in E(\mathcal {M})$ if there is a trinet or binet $T\in \mathbb {T}$ with $a,b\in \mathcal {L}(T)$ distinct and in which there is a common ancestor of a and b that is not the root of T. The idea behind this graph is that leaves that are in the same connected component of this graph have to be in the same part of the bipartition.

Now define a graph $\mathcal {W}(\mathbb {T},H)=(V(\mathcal {W}),E(\mathcal {W}))$ as follows. The vertex set $V(\mathcal {W})$ is the set of connected components of $\mathcal {M}(\mathbb {T},H)$ and there is an edge $\{\pi ,\pi '\}\in E(\mathcal {W})$ precisely if there exists a trinet $S_1(x,y;z)\in \mathbb {T}$ with $x\in V(\pi )$, $y\in V(\pi ')$ and $z\in X{\setminus } H$. The purpose of this graph is to ensure that groups of leaves are in different parts of the bipartition, whenever this is necessary. See Fig. 9 for an example.

Fig. 9

The graph $\mathcal {M}(\mathbb {T},H)$ in solid lines and the graph $\mathcal {W}(\mathbb {T},H)$ in dashed lines, for the set $\mathbb {T}$ of trinets in Fig. 5 and $H=\{a, b, c, d, e, f, g, h, i, m\}$. A proper 2-colouring of $\mathcal {W}(\mathbb {T},H)$ is to color $\{a\}$ and $\{b\}$ in red and $\{c, d, e, f, g, h, i, m\}$ in blue (Color figure online)

Lemma 8

Let $\mathbb {T}$ be a set of binets and trinets on X and $H\subseteq X$. A bipartition $\{L,R\}$ of H is feasible with respect to $\mathbb {T}$ if and only if

• (I) $V(\pi )\subseteq L$ or $V(\pi )\subseteq R$ for all $\pi \in V(\mathcal {W})$ and

• (II) there does not exist $\{\pi ,\pi '\}\in E(\mathcal {W})$ with $(V(\pi )\cup V(\pi '))\subseteq L$ or $(V(\pi )\cup V(\pi '))\subseteq R$.

Proof

The lemma follows directly from observing that (F1) holds if and only if (I) holds and that (F2) holds if and only if (II) holds. $\square$

By Lemma 8, all feasible bipartitions can be found by finding all 2-colourings of the graph $\mathcal {W}(\mathbb {T},H)$. At least one of them is the bipartition induced by a valid solution N (if one exists) by Lemma 7.

For example, consider the input set of trinets $\mathbb {T}$ from Fig. 5. Since $\mathbb {T}$ is not semi-dense, we have to guess which connected components of $\mathcal {K}(\mathbb {T})$ form the set H of leaves that are high in the network (see Sect. 4.3). If we guess $H=\{a,b,c,d,e,f,g,h,i,m\}$, then we obtain the graphs $\mathcal {M}(\mathbb {T},H)$ and $\mathcal {W}(\mathbb {T},H)$ as depicted in Fig. 9. The only possible 2-colouring (up to symmetry) of the graph $\mathcal {W}(\mathbb {T},H)$ is indicated in the figure. From this we can conclude that a and b are on the same side of the network and that all other high leaves (c, d, e, f, g, h, m) are “on the other side” (i.e., none of them is on the same side as a or b).

4.5 Finding the Pendant Sidenetworks

The next step is to divide the leaves of each part of the bipartition of the set of high leaves of the network into the leaves of the pendant sidenetworks. For this, we define the following graph and digraph.

Let $\mathbb {T}$ be a set of binets and trinets on X, let $H\subsetneq X$, let $\{L,R\}$ be some bipartition of H that is feasible with respect to $\mathbb {T}$ and let $S'\subseteq S\in \{L,R\}$. Consider the graph $\mathcal {O}(\mathbb {T},S',H)$ with vertex set $S'$ and an edge $\{a,b\}$ if

• There exists a trinet or binet $T\in \mathbb {T}|S'$ with $a,b\in \mathcal {L}(T)$ that has a cycle that contains the root or a common ancestor of a and b (or both) or;

• There exists a trinet $T\in \mathbb {T}$ with $\mathcal {L}(T)=\{a,b,c\}$ with $c\notin H$ and such that c is low in T and a and b are high in T and both in the same pendant sidenetwork of T or;

• $T_1(a,b;c)\in \mathbb {T}|S'$ for some $c\in S'$.

The directed graph $\mathcal {D}(\mathbb {T},S',H)$ (possibly having loops) has a vertex for each connected component of $\mathcal {O}(\mathbb {T},S',H)$ and it has an arc $(\pi _1,\pi _2)$ (possibly, $\pi _1=\pi _2$) precisely if there is a trinet in $\mathbb {T}$ of the form $S_2(x;y;z)$ with $x\in V(\pi _1)$, $y\in V(\pi _2)$ and $z\notin H$.

For example, Fig. 10 shows the set of trinets from Fig. 5 restricted to the set $S=R=\{c,d,e,f,g,h,i,m\}$. The corresponding graphs $\mathcal {O}(\mathbb {T},R,H)$ and $\mathcal {D}(\mathbb {T},R,H)$, with $H=\{a,b,c,d,e$, $f,g,h,i,m\}$, are depicted in Fig. 11.

Fig. 10

The restricted set of trinets $\mathbb {T}|R$ with $R=\{c, d, e, f, g, h, i, m\}$ and $\mathbb {T}$ the set of trinets in Fig. 5 and $H=\{a, b, c, d, e, f, g, h, i, m\}$

Fig. 11

The graph $\mathcal {O}(\mathbb {T},R,H)$ in solid lines and the digraph $\mathcal {D}(\mathbb {T},R,H)$ in dashed lines, with R and H as in Fig. 10

The following lemma shows that, if the digraph $\mathcal {D}(\mathbb {T},S',H)$ has no indegree-0 vertex, there exists no binary level-1 network displaying $\mathbb {T}$ in which H is the set of high leaves and all leaves in $S'$ are on the same side.

Lemma 9

Let $\mathbb {T}$ be a set of binets and trinets on X, let $H\subsetneq X$, let $\{L,R\}$ be a bipartition of H that is feasible with respect to $\mathbb {T}$ and let $S'\subseteq S\in \{L,R\}$. If the graph $\mathcal {D}(\mathbb {T},S',H)$ has no indegree-0 vertex, then there exists no binary level-1 network N that displays $\mathbb {T}$ in which H is the set of high leaves and all leaves in $S'$ are on the same side.

Proof

Suppose that there exists such a network N. Let $\{L,R\}$ be the bipartition of H induced by N and suppose without loss of generality that $L\cap S' \ne \emptyset$. Let $L_1,\ldots ,L_q$ be the partition of L induced by the pendant sidenetworks of N, ordered from the nearest to the farthest from the root. Let i be the first index for which $L_i\cap S'\ne \emptyset$. Then, by the definition of $\mathcal {O}(\mathbb {T},S',H)$, $L_i\cap S'$ is the union of one or more connected components of $\mathcal {O}(\mathbb {T},S',H)$. Each of these connected components has indegree 0 in $\mathcal {D}(\mathbb {T},S',H)$. $\square$

Let $\mathbb {T},X,H,L$ and R be as above. We present a sidenetwork partitioning algorithm, which proceeds as follows for each $S\in \{L,R\}$. Choose one indegree-0 vertex of $\mathcal {D}(\mathbb {T},S,H)$ and call it $S_1$. This will be the set of leaves of the first pendant sidenetwork on side S. Then, construct the graph $\mathcal {O}(\mathbb {T},S{\setminus } S_1,H)$ and digraph $\mathcal {D}(\mathbb {T},S{\setminus } S_1,H)$, select an indegree-0 vertex and call it $S_2$. Continue like this, i.e. let $S_i$ be an indegree-0 vertex of $\mathcal {D}(\mathbb {T},S{\setminus } (S_1\cup \ldots \cup S_{i-1} ),H)$, until an empty graph or a digraph with no indegree-0 vertex is obtained. In the latter case, there is no valid solution (under the given assumptions) by Lemma 9. Otherwise, we obtain sets $L_1,\ldots ,L_q$ and $R_1,\ldots ,R_{q'}$ containing the leaves of the pendant sidenetworks on both sides.

In the example in Fig. 11, the only indegree-0 vertex of $\mathcal {D}(\mathbb {T},R,H)$ is $\{c,d\}$. Hence, we have $R_1=\{c,d\}$. Since $\mathcal {O}(\mathbb {T},R{\setminus }\{c,d\})$ is connected, $R_2=\{e,f,g,h,i,m\}$ follows.

4.6 Constructing the Network

We build a binary level-1 network $N^*$ based on the sets $H,L_1,\ldots ,L_q, R_1,\ldots ,R_{q'}$ as follows. Let $N(L_i)$ be a binary level-1 network displaying $\mathbb {T}|L_i$ for $i=1,\ldots ,q$ and let $N(R_i)$ be a binary level-1 network displaying $\mathbb {T}|R_i$ for $i=1,\ldots ,q'$ (note that it is possible that one of q and $q'$ is 0.). We can build these networks recursively, and they exist by Observation 1. In addition, we recursively build a network $N(L_{ow})$ displaying $\mathbb {T}|L_{ow}$ with $L_{ow}=X{\setminus } H$. Now we combine these networks into a single network $N^*$ as follows. We create a root $\rho$, a reticulation r, and two directed paths $(\rho ,u_1,\ldots ,u_q,r)$, $(\rho ,v_1,\ldots ,v_{q'},r)$ from $\rho$ to r (if $q=0$ (respectively $q'=0$) then there are no internal vertices on the first (resp. second) path). Then we add an arc from $u_i$ to the root of $N(L_i)$, for $i=1,\ldots ,q$, we add an arc from $v_i$ to the root of $N(R_i)$ for $i=1,\ldots ,q'$ and, finally, we add an arc from r to the root of $N(L_{ow})$. This completes the construction of $N^*$. For an example, see Fig. 2.

We now prove that the network $N^*$ constructed in this way displays the input trinets, assuming that there exists some solution that has H as its set of high leaves and $\{L,R\}$ as the bipartition of H induced by it.

Lemma 10

Let $\mathbb {T}$ be a set of binets and trinets, let N be a cycle-rooted binary level-1 network displaying $\mathbb {T}$, let H be the set of leaves that are high in N and let $\{L,R\}$ be the feasible bipartition of H induced by N. Then the binary level-1 network $N^*$ constructed above displays $\mathbb {T}$.

Proof

The proof is by induction on the number $|\mathcal {L}(\mathbb {T})|$ of leaves in $\mathbb {T}$. The induction basis for $|\mathcal {L}(\mathbb {T})|\le 2$ is trivial. Hence, assume $|\mathcal {L}(\mathbb {T})|\ge 3$.

For each pendant subnetwork $N'$ of $N^*$ with leaf-set $X'$, there exists a binary level-1 network displaying $\mathbb {T}|X'$ by Observation 1. Hence, the network $N'$ that has been computed recursively by the algorithm displays $\mathbb {T}|X'$ by induction. It follows that any trinet or binet whose leaves are all in the same pendant sidenetwork of $N^*$ is displayed by $N^*$. Hence, it remains to consider binets and trinets containing leaves in at least two different pendant subnetworks of $N^*$.

Let $B\in \mathbb {T}$ be a binet on leaves that are in two different pendant subnetworks of $N^*$. If $B=N(y;x)$ then, because B is displayed by N, y is low in N and hence also low in $N^*$. Since x and y are in different pendant subnetworks of $N^*$, it follows that x is high in $N^*$ and hence B is displayed by $N^*$. If $B=T(x,y)$ then there is an edge $\{x,y\}$ in $\mathcal {K}(\mathbb {T})$ and hence x and y are at the same elevation in $N^*$. Since x and y are in different pendant subnetworks, both must be high in $N^*$ and it follows that $N^*$ displays B.

Now consider a trinet $T\in \mathbb {T}$ on leaves x, y, z that are in at least two different pendant subnetworks. At least one of x, y, z is high in $N^*$ because otherwise all three leaves would be in the same pendant subnetwork $N(L_{ow})$, with $L_{ow}=X{\setminus } H$. We now consider the different types of trinet that T can be.

First suppose that $T=T_1(x,y;z)$. Then x, y, z form a clique in $\mathcal {K}(\mathbb {T})$ and hence all of x, y and z are high in $N^*$. Moreover, by feasibility, x and y are in the same part of the bipartition $\{L,R\}$ and hence on the same side in $N^*$. If x and y are in the same pendant subnetwork then the binet $T|\{x,y\}=T(x,y)$ is displayed by this pendant subnetwork. Hence, in that case, T is clearly displayed by $N^*$. Now assume that x and y are in different pendant subnetworks and assume without loss of generality that $x,y\in R$. If $z\in L$ then, again, T is clearly displayed by $N^*$. Hence assume that $x,y,z\in R$. Then, for each set $R'\subseteq R$ containing x, y, z, the graph $\mathcal {O}(\mathbb {T},R',H)$ has an edge between x and y. Hence, either x and y are in the same pedant sidenetwork, or z is in a pendant sidenetwork above the pendant sidenetworks that contain x and y. Hence, T is displayed by $N^*$.

Now suppose that $T\in \{N_1(x,y;z),N_4(x;y;z)\}$. Then there is an edge $\{x,y\}$ in $\mathcal {K}(\mathbb {T})$ and hence x and y are at the same elevation in $N^*$. First note that x, y and z are not all high in $N^*$ because otherwise x, y and z would all be in the same part S of the bipartition $\{L,R\}$ by feasibility and in the same pendant sidenetwork because they form a clique in $\mathcal {O}(\mathbb {T},S,H)$. Hence, z is not at the same elevation as x and y and hence z is not in the same connected component of $\mathcal {K}(\mathbb {T})$ as x and y. Then there is an arc $(\pi ,\pi ')$ in $\varOmega (\mathbb {T})$ with $\pi$ the component containing x and y and $\pi '$ the component containing z. Hence x and y are high in $N^*$ and z is low in $N^*$ (since $\pi '$ has indegree greater than zero). Then, x and y are in the same part S of the bipartition $\{L,R\}$ by feasibility and in the same pendant subnetwork of $N^*$ because there is an edge $\{x,y\}$ in $\mathcal {O}(\mathbb {T},S)$. Hence, since the binet $T|\{x,y\}$ is displayed by the pendant subnetwork containing x and y, we conclude that T is displayed by $N^*$.

Now suppose that $T=S_1(x,y;z)$. We can argue in the same way as in the previous case that x and y are high in $N^*$ and that z is low in $N^*$. By feasibility, x and y are in different parts of the bipartition $\{L,R\}$ and, hence, $N^*$ displays T.

Now suppose that $T\in \{N_2(x,y;z),N_5(x;y;z)\}$. Then we can argue as before that x and y are at the same elevation in $N^*$ and that z is not at the same elevation as x and y and hence that z is not in the same connected component of $\mathcal {K}(\mathbb {T})$ as x and y. Then there is an arc $(\pi ,\pi ')$ in $\varOmega (\mathbb {T})$ with $\pi$ the component containing z and $\pi '$ the component containing x and y. Hence, z is high in $N^*$ and x and y are low in $N^*$. Since the binet $T|\{x,y\}$ is displayed by $N(L_{ow})$, we conclude that T is displayed by $N^*$.

Now suppose that $T=N_3(x;y;z)$. Observe that x, y, z are all high in $N_3(x;y;z)$ because this trinet is not cycle-rooted. Therefore, x, y, z form a clique in $\mathcal {K}(\mathbb {T})$ and hence all of x, y and z are high in $N^*$. Moreover, by feasibility, x and y are in the same part of the bipartition $\{L,R\}$, say in R, and hence on the same side in $N^*$. First suppose that $z\in L$. Then, $\mathbb {T}|R$ contains the binet $T|\{x,y\}$ which is cycle-rooted. Hence, there is an edge $\{x,y\}$ in $\mathcal {O}(\mathbb {T},R,H)$ and x and y are in the same pendant sidenetwork. Since $T|\{x,y\}$ is displayed by this pendant subnetwork, it follows that T is displayed by $N^*$. Now assume that $z\in R$. Then the trinet T is in $\mathbb {T}|R$ and has a common ancestor of x and y contained in a cycle. Hence, as before, x and y are in the same pendant sidenetwork of $N^*$ and, since $T|\{x,y\}$ is displayed by that pendant sidenetwork, it follows that T is displayed by $N^*$.

Finally, suppose that $T=S_2(x;y;z)$. As in the case $T\in \{N_1(x,y;z),N_4(x;y;z)\}$, we can argue that x and y are high in $N^*$ and that z is low in $N^*$. Then, by feasibility, x and y are on the same side S in $N^*$. First suppose that x and y are in the same pendant sidenetwork of $N^*$. Consider an iteration i of the sidenetwork partitioning algorithm with $x,y\in S{\setminus } (S_1\cup \ldots \cup S_{i-1})$. Then there is an arc $(\pi _1,\pi _2)$ in $\mathcal {D}(\mathbb {T},S{\setminus } (S_1\cup \ldots \cup S_{i-1}),H)$ with $x\in V(\pi _1)$ and $y\in V(\pi _2)$ (possibly $\pi _1=\pi _2$). Hence, $S_i$ does not contain y because $\pi _2$ does not have indegree-0. It follows that x and y are in different sidenetworks and that the sidenetwork containing x is above the sidenetwork containing y. Hence, $N^*$ displays T, which concludes the proof of the lemma. $\square$

See Algorithm 1 for the pseudocode of the algorithm and Table 1 for an overview of the definitions of the graphs used in the algorithm. Note that Lemma 5 shows correctness of Lines 14-16, which speed up the algorithm significantly in the case that the input is semi-dense.

Theorem 2

There exists an $O(3^{|X|} poly(|X|))$ time algorithm that constructs a binary level-1 network N displaying a given set $\mathbb {T}$ of binets and trinets on a taxon set X, if such a network exists.

Proof

If the graph $\mathcal {R}(\mathbb {T})$ is disconnected and has connected components $C_1,\ldots ,C_p$, then we recursively compute binary level-1 networks $N_1,\ldots ,N_p$ displaying $\mathbb {T}|C_1,\ldots ,\mathbb {T}|C_p$ respectively. Then, by Lemma 1, $\mathbb {T}$ is displayed by the binary level-1 network $N'$ obtained by creating a root $\rho$ and adding arcs from $\rho$ to the roots of $N|C_1,\ldots ,N|C_p$, and refining the root $\rho$ in order to make the network binary.

If $\mathcal {R}(\mathbb {T})$ is connected, then any binary level-1 network N displaying $\mathbb {T}$ is cycle-rooted by Lemma 2. If there exists such a network that is tiny-cycle rooted, then we can find such a network by Lemma 6.

Otherwise, we can “guess”, using Lemma 4, a set of leaves H such that there exists some binary level-1 network N displaying $\mathbb {T}$ in which H is the set of leaves that are high. Moreover, using Lemma 8, we can “guess” a feasible partition $\{L,R\}$ of H with respect to $\mathbb {T}$ by “guessing” a proper 2-colouring of the graph $\mathcal {W}(\mathbb {T},H)$. The total number of possible guesses for the tripartition $\{L,R,X{\setminus } H\}$ is at most $3^{|X|}$.

If there exists a binary level-1 network $N'$ displaying $\mathbb {T}$ then, by Lemma 10, there exists some tripartition  $(L,R,X{\setminus } H)$ for which network $N^*$ from Lemma 10 displays all binets and trinets in $\mathbb {T}$.

It remains to analyse the running time. Each recursive step takes $O(3^{|X|} poly(|X|))$ time and the number of recursive steps is certainly at most |X|, leading to $O(3^{|X|} poly(|X|))$ in total since, by Observation 1, the various recursive steps are independent of each other. $\square$

Note that the running time analysis in the proof Theorem 2 is pessimistic since, by Lemma 3, the set H of high leaves must be the union of a subset of the vertices of $\varOmega (\mathbb {T})$ with no incoming arcs. Moreover, the number of feasible bipartitions of H is also restricted because each such bipartition must correspond to a 2-colouring of the graph $\mathcal {W}(\mathbb {T},H)$. Hence, the number of possible guesses is restricted (but still exponential).

We conclude this section by extending Theorem 2 to instances containing networks with arbitrarily many leaves.

Corollary 1

There exists an $O(3^{|X|} poly(|X|))$ time algorithm that constructs a binary level-1 network N displaying a given set $\mathcal {N}$ of binary level-1 networks, if such a network exists.

Proof

We apply Theorem 2 to the set $\mathbb {T}(\mathcal {N})$ of binets and trinets displayed by the networks in $\mathcal {N}$. To check that the resulting network N displays $\mathcal {N}$, consider a network $N'\in \mathcal {N}$. Since binary level-1 networks are encoded by their trinets [11], any binary level-1 network displaying $\mathbb {T}(N')$ is equivalent to $N'$. Hence, $N|\mathcal {L}(N')$ is equivalent to $N'$. Therefore, $N'$ is displayed by N. Since $|\mathbb {T}(\mathcal {N})|=O(|X|^3)$, the running time is $O(3^{|X|} poly(|X|))$ as in Theorem 2. $\square$

5 Constructing a Binary Level-1 Network from a Set of Tiny-Cycle Networks in Polynomial Time

Recall that a network is a tiny-cycle network if each cycle consists of exactly three vertices. It is easy to see that each tiny-cycle network is a level-1 network. Note that all binary level-1 binets and trinets except for $S_1(x,y;z)$ and $S_2(x;y;z)$ are tiny-cycle networks. We prove the following.

Fig. 12

Transformation from a binary level-1 network N to a tiny-cycle network $N'$, used in the proof of Theorem 3 (with $n=3$ and $m=2$)

Theorem 3

Given a set $\mathbb {T}$ of tiny-cycle binets and tiny-cycle trinets, we can decide in polynomial time if there exists a binary level-1 network displaying $\mathbb {T}$ and construct such a network if it exists.

Proof

Let N be a binary level-1 network displaying $\mathbb {T}$. If N is not a tiny-cycle network, then we construct a tiny-cycle network $N'$ from N as follows (see Fig. 12 for an illustration). For each cycle of N consisting of internally vertex-disjoint directed paths $(s,v_1,\ldots ,v_n,t)$ and $(s,w_1,\ldots ,w_m,t)$ with $n+m\ge 2$, do the following. Delete arcs $(v_n,t)$ and $(w_m,t)$, suppress $v_n$ and $w_m$, add vertices q and r and arcs (q, r), (r, t), (q, t) and (r, s). Finally, if s is not the root of N, let p be the parent of s in N and replace arc (p, s) by an arc (p, q). Let $N'$ be the obtained network. It is easy to verify that any binary tiny-cycle network that is displayed by N is also displayed by $N'$ and that $N'$ is a tiny-cycle network. Hence, we may restrict our attention to constructing tiny-cycle networks.

The only two cases to consider are that the to be constructed network is not cycle-rooted and that it is tiny-cycle rooted. By Lemmas 1 and 2, we can deal with the first case in the same way as in the polynomial-time algorithm for binets from Sect. 3 with $\mathcal {R}(\mathbb {T})$ instead of $\mathcal {R}^b(\mathbb {B})$. By Lemma 6, we can deal with the second case in the same way as in the polynomial-time algorithm for binets with $\varOmega ^\dagger (\mathbb {T})$ instead of $\varOmega ^b(\mathbb {B})$ (and hence $\mathcal {K}^\dagger (\mathbb {T})$ instead of $\mathcal {K}^b(\mathbb {B})$). $\square$

Note that Theorem 3 applies to sets of binets and trinets that do not contain any trinets of the form $S_1(x,y;z)$ and $S_2(x;y;z)$. The following corollary generalises this theorem to general instances of tiny-cycle networks. It follows from Theorem 3 in the same way as Corollary 1 follows from Theorem 2.

Corollary 2

Given a set $\mathcal {N}$ of tiny-cycle networks, we can decide in polynomial time if there exists a binary level-1 network displaying $\mathcal {N}$ and construct such a network if it exists.

6 Complexity of Constructing a Level-1 Network from a Nondense Set of Trinets

In this section, we show that it is NP-hard to construct a binary level-1 network from a nondense set of trinets. The reduction is a nontrivial adaptation of the reduction given by Jansson, Nguyen and Sung [19] for deciding if there exists a level-1 network that is consistent with a given set of triplets in the following sense. A network N is consistent with a triplet T if N contains a subgraph that is a subdivision of T. The notions of triplet consistency and trinet display are fundamentally different in networks (while they are the same in trees). In particular, a network displays only one trinet on three taxa but may be consistent with two distinct triplets on these three taxa (for example, network N in Fig. 13 is consistent with triplets $T_1(b,x_1;z_1)$ and $T_1(b,z_1;x_1)$ but the only trinet on these taxa that N displays is $S_1(x_1,z_1;b)$). Consequently, Theorem 4 does not follow directly from the result in [19].

Fig. 13

An example of the reduction if the input of the SetSplitting problem is $\mathcal {C}=\{\{x, y, z\},\{q, x, z\}\}$ (with $q<x<y<z$). A valid set splitting is $\{\{q, z\}, \{x, y\}\}$ and the network N indicated in the figure displays all trinets produced by the reduction

Because trinets provide more information than triplets, one might hope that constructing a network from trinets is computationally easier than from triplets. However, Theorem 4 shows that this is (in the considered setting) not the case. The proof uses a reduction from SetSplitting, which is similar to the reduction in [19]. However, with trinets it is much more difficult to enforce a simple structure (a cycle with one leaf below it and all other leaves on its left and right sides) without enforcing on which side each leaf is. To achieve this, the reduction uses three different types of trinets, and it is not clear if the problem remains NP-hard if only trinets of type $S_1(x,y;z)$ or only trinets of type $S_2(x;y;z)$ are present.

Theorem 4

Given a set of trinets $\mathbb {T}$, it is NP-hard to decide if there exists a binary level-1 network N displaying $\mathbb {T}$. In addition, it is NP-hard to decide if there exists such a network with a single reticulation.

Proof

We reduce from the NP-hard problem SetSplitting [6].

The SetSplitting problem is defined as follows. Given a set U and a collection $\mathcal {C}$ of size-3 subsets of U, decide if there exists a bipartition of U into sets A and B such that for each $C\in \mathcal {C}$ holds that $C\cap A\ne \emptyset$ and $C\cap B\ne \emptyset$? If such a bipartition exists, then we call it a set splitting for $\mathcal {C}$.

The reduction is as follows. For an example see Fig. 13. Assume that $\mathcal {C}=\{C_1,\ldots ,C_k\}$, with $k\ge 1$, and furthermore that the elements of U are totally ordered (by an operation $<$). We create a taxon set X and a trinet set $\mathbb {T}$ on X as follows. For each $u\in U$, put a taxon $u_0$ in X. In addition, add a special taxon b to X. Then, for each $C_i=\{u,v,w\}$ with $u<v<w$, add taxa $u_i,u_i',v_i,v_i',w_i,w_i'$ to X and add the following trinets to $\mathbb {T}$: $T_1(v_i,v_i';u_i)$, $T_1(w_i,w_i';v_i)$, $T_1(u_i,u_i';w_i)$, $S_2(v_i;v_i';b)$, $S_2(w_i;w_i';b)$, $S_2(u_i;u_i';b)$, $S_1(u_i,u_0;b)$, $S_1(v_i,v_0;b)$, $S_1(w_i,w_0;b)$, resulting in $\mathbb {T}$ comprising of three different types of trinets. This completes the reduction.

First we show that, if there exists a set splitting for $\mathcal {C}$, then there exists a network N on X that displays $\mathbb {T}$ and has exactly one reticulation. Let $\{A,B\}$ be a set splitting for $\mathcal {C}$. We construct a network N whose root is in a cycle and each arc leaving this cycle ends in a leaf. Hence, N has precisely one reticulation, whose child is leaf. Label this leaf by taxon b. Let $\{L,R\}$ be the bipartition of $X{\setminus }\{b\}$ induced by N. Then, for each $u\in A$ we put $u_0$ in L and $u_i$ and $u_i'$ for $i\ge 1$ in R. Symmetrically, for each $u\in B$ we put $u_0$ in R and $u_i$ and $u_i'$ for $i\ge 1$ in L. It remains to describe the order of the leaves on each side of the network. For each $i\in \{1,\ldots ,k\}$ and for any two leaves $x_i,y_i$ that are on the same side in N, put $x_i$ above $y_i$ and $y_i'$ if $x<y$ (and put $y_i$ above $x_i$ and $x_i'$ if $y>x$). In addition, put each $x_i$ above $x_i'$. The ordering can be completed arbitrarily. For an example, see the network in Fig. 13. To see that N displays $\mathbb {T}$, first observe that all trinets of the form $S_2(x_i;x_i';b)$ are displayed by N because we put $x_i$ above $x_i'$ and on the same side. In addition, all trinets of the form $S_1(x_i,x_0;b)$ are also displayed by N because $x_i$ and $x_0$ are on opposite sides of N. Now consider a constraint $C_i=\{u,v,w\}\in \mathcal {C}$ with $u<v<w$. Since $\{A,B\}$ is a set splitting, $|C_i\cap A|=2$ or $|C_i\cap B|=2$. Suppose that u and v are in the same set, say $u,v\in A$. The other two cases can be dealt with in a similar manner. It then follows that $w\in B$ and hence that $u_i,v_i,u_i',v_i'\in R$ and $w_i,w_i'\in L$. It then follows that trinets $T_1(w_i,w_i';v_i)$ and $T_1(u_i,u_i';w_i)$ are displayed by N. Moreover, since $u<v$, we have that $u_i$ is above $v_i$ and $v_i'$. Hence, also trinet $T_1(v_i,v_i';u_i)$ is displayed by N. We conclude that $\mathbb {T}$ is displayed by N.

It remains to show that if there exists a network on X that displays $\mathbb {T}$, then there exists a set splitting A, B for $\mathcal {C}$. So assume that there exists a network N on X that displays $\mathbb {T}$. From Lemma 2 it follows that N is cycle-rooted. By Lemma 3, all leaves in $X{\setminus }\{b\}$ are at the same elevation in N. Consequently, by Lemma 4, the leaves in $X{\setminus }\{b\}$ are all high in N and b is low in N. Let $\{L,R\}$ be the bipartition of $X{\setminus }\{b\}$ induced by N. Define $A=\{u\in U \mid u_0 \in L\}$ and $B = \{u\in U \mid u_0\in R\}$. We claim that A and B form a set splitting for $\mathcal {C}$. To show this, assume the contrary, i.e., that there exists some constraint $C_i=\{u,v,w\}\in \mathcal {C}$, with $u<v<w$, such that either $u,v,w\in A$ or $u,v,w\in B$. Assume without loss of generality that $u,v,w\in A$. Then $u_0,v_0,w_0\in L$. Hence, $u_i,v_i,w_i\in R$ since the trinets $S_1(u_i,u_0;b)$, $S_1(v_i,v_0;b)$ and $S_1(w_i,w_0;b)$ are contained in $\mathbb {T}$. Then, since $S_2(u_i;u_i';b)\in \mathbb {T}$, we obtain that $u_i'\in R$. Moreover, $u_i$ and $u_i'$ are in different sidenetworks of N. Then, since $T_1(u_i,u_i';w_i)\in \mathbb {T}$, the sidenetwork containing $w_i$ is strictly above the sidenetwork containing $u_i$. However, it follows in the same way from trinets $S_2(v_i;v_i';b)$ and $T_1(v_i,v_i';u_i)$ that the sidenetwork of N containing $u_i$ is strictly above the sidenetwork containing $v_i$. Furthermore, it follows from the trinets $S_2(w_i;w_i';b)$ and $T_1(w_i,w_i';v_i)$ that the sidenetwork containing $v_i$ is strictly above the sidenetwork containing $w_i$. Hence, we have obtained a contradiction. It follows that A and B form a set splitting of $\mathcal {C}$, completing the proof. $\square$

7 Concluding Remarks

We have presented an exponential time algorithm for determining whether or not an arbitrary set of binets and trinets is displayed by a level-1 network, shown that this problem is NP-hard, and given some polynomial time algorithms for solving it in certain special instances. It would be interesting to know whether other special instances are also solvable in polynomial time (for example, when either $S_1(x,y;z)$-type or $S_2(x;y;z)$-type trinets are excluded).

We note that the problem of deciding if a set of binets and trinets is displayed by a level-1 network remains NP-hard when the input set is semi-dense, i.e. for each combination of two taxa it contains at least one binet or trinet containing those two taxa. Although the trinet set produced in the proof of Theorem 4 is not semi-dense, it is not difficult to make it semi-dense without affecting the reduction, by adding a binet T(x, y) for all $x,y\in X{\setminus }\{b\}$.

As mentioned in the introduction, our algorithms can be regarded as a supernetwork approach for constructing phylogenetic networks. It is therefore worth noting that our main algorithms extend to the case where the input consists of a collection of binary level-1 networks, where each input network is allowed to have any number of leaves.

Furthermore, we have shown that constructing a binary level-1 network from a set of trinets is NP-hard in general. One could instead consider the problem of constructing such networks from networks on (at least) m leaves, $3 \le m \le |X|$ (or m-nets for short). However, it can be shown that it is also NP-hard to decide if a set of level-1 m-nets is displayed by a level-1 network or not. This can be shown by a simple reduction from the problem for trinets.

It would also be of interest to develop algorithms to reconstruct level-k networks for $k\ge 2$ from m-nets (a binary network is said to be level-k if every biconnected component contains at most k reticulations [4]). Note that the trinets displayed by a level-2 network always encode the network [16], but that in general trinets do not encode level-k networks [9]. Therefore, in light also of the results in this paper, we anticipate that these problems might be quite challenging in general. Even so, it could still be very useful to develop heuristics for tackling such problems as this has proven very useful in both supertree and phylogenetic network construction.